Drought Assessment Based on Fused Satellite and Station Precipitation Data: An Example from the Chengbi River Basin, China
Abstract
:1. Introduction
2. Study Area and Data Sets
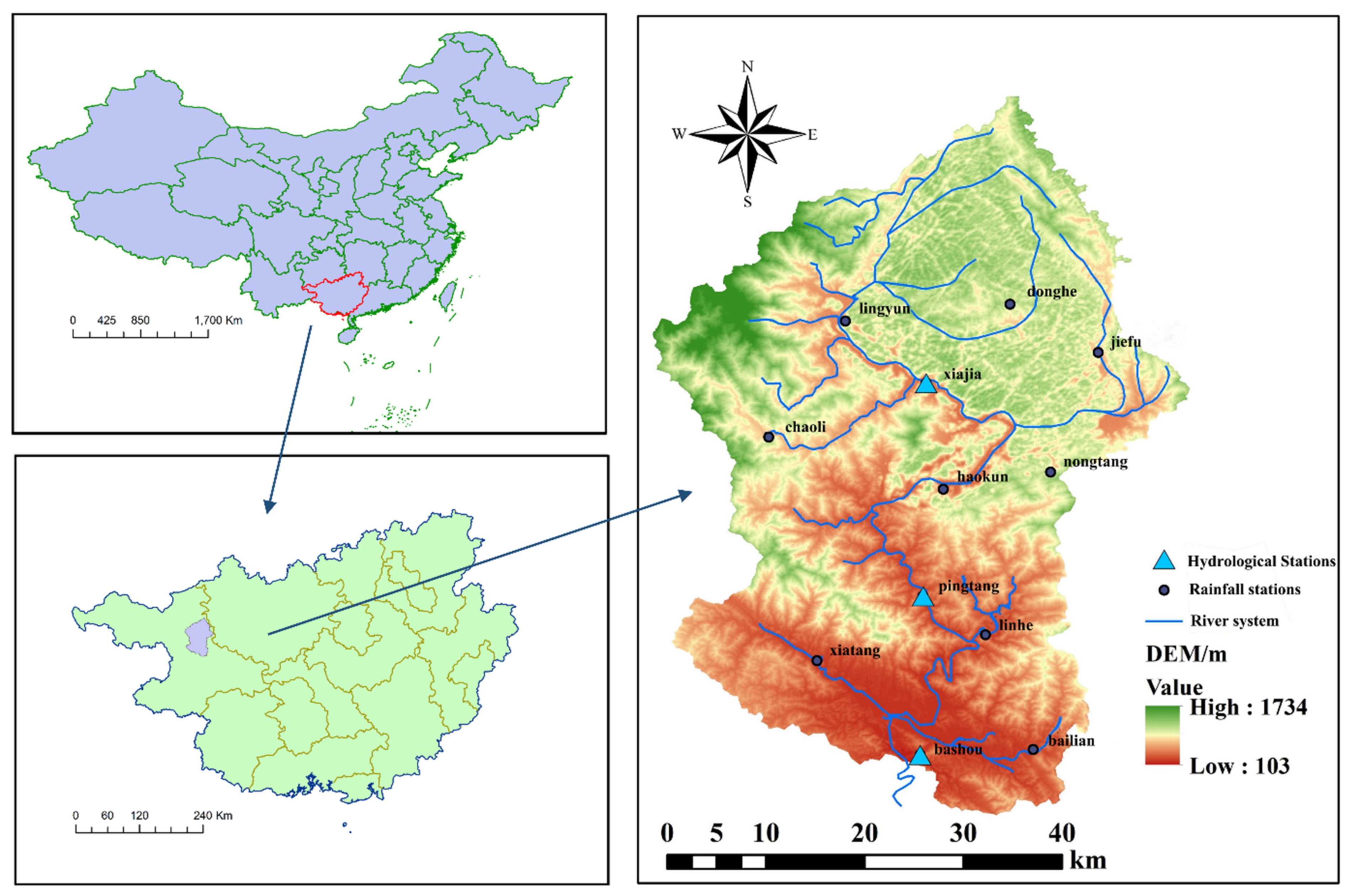
2.1. Study Area
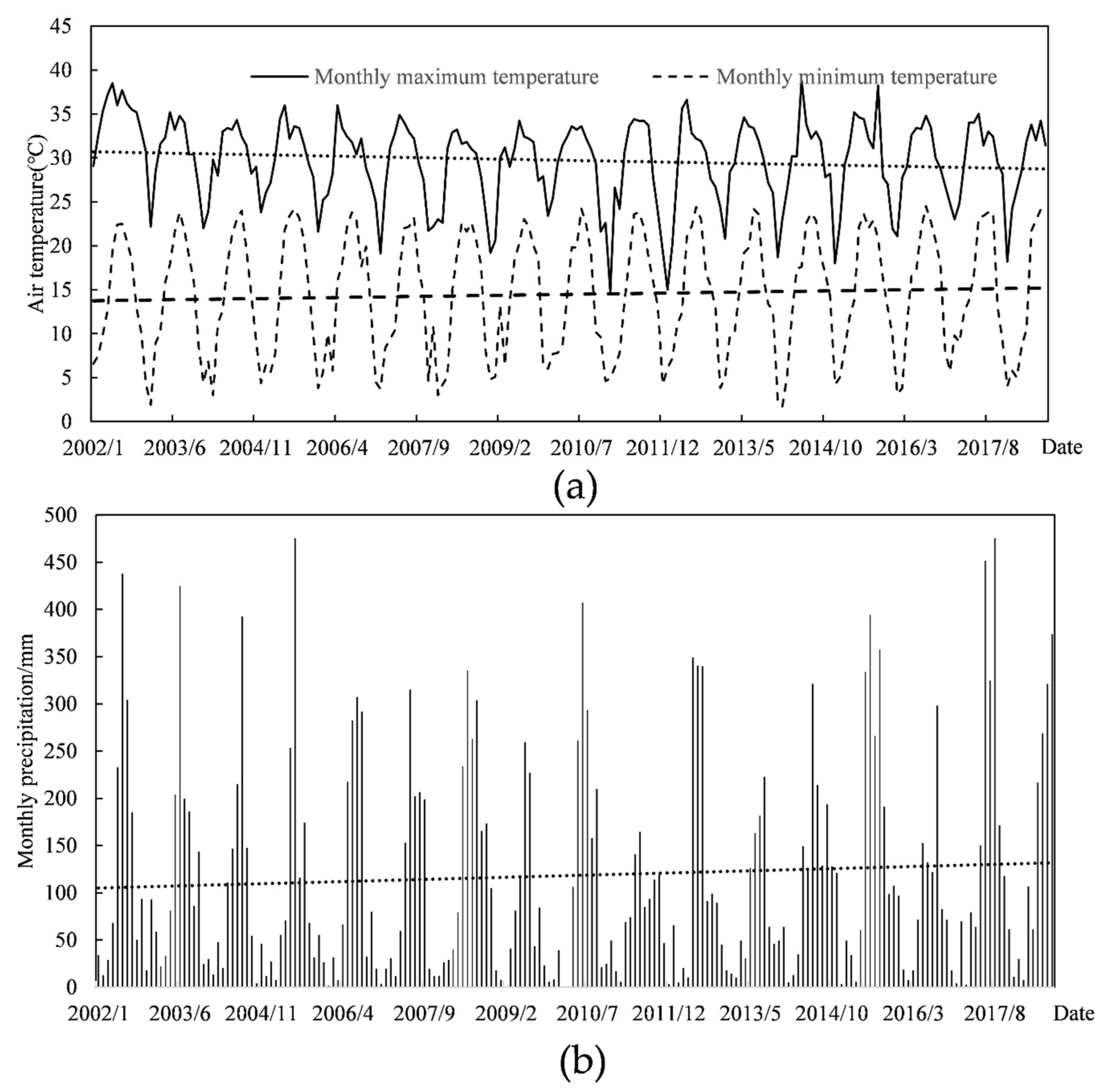
2.2. Data Sets
2.2.1. Satellite Data
2.2.2. DEM Data
2.2.3. Measured Data
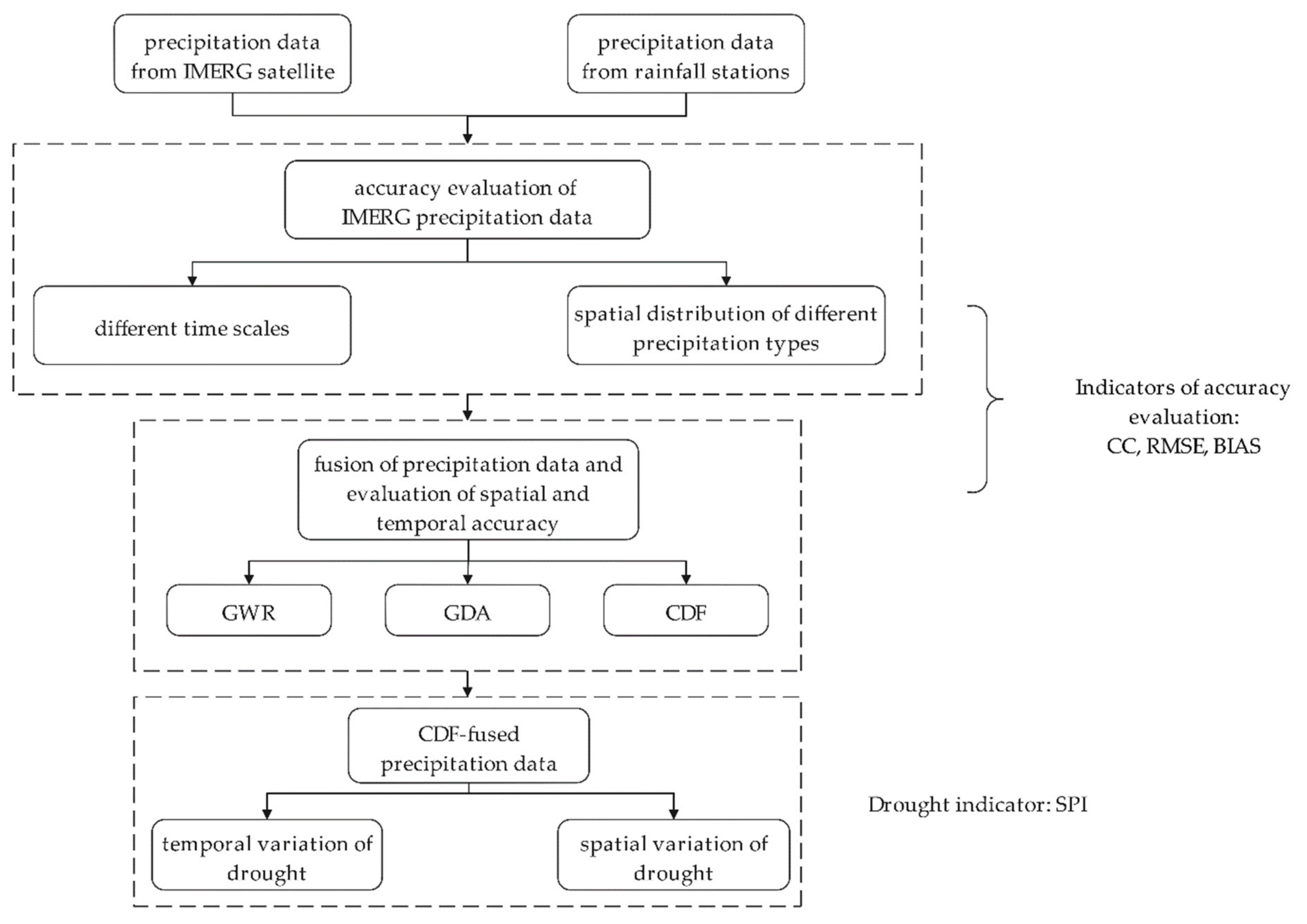
3. Methodology
3.1. Evaluation Indicators
3.2. Methodology of Precipitation Data Fusion
3.2.1. Geographically Weighted Regression (GWR)
3.2.2. Geographical Difference Analysis (GDA)
3.2.3. Cumulative Distribution Function (CDF)
3.3. Standardized Precipitation Index (SPI)
4. Results
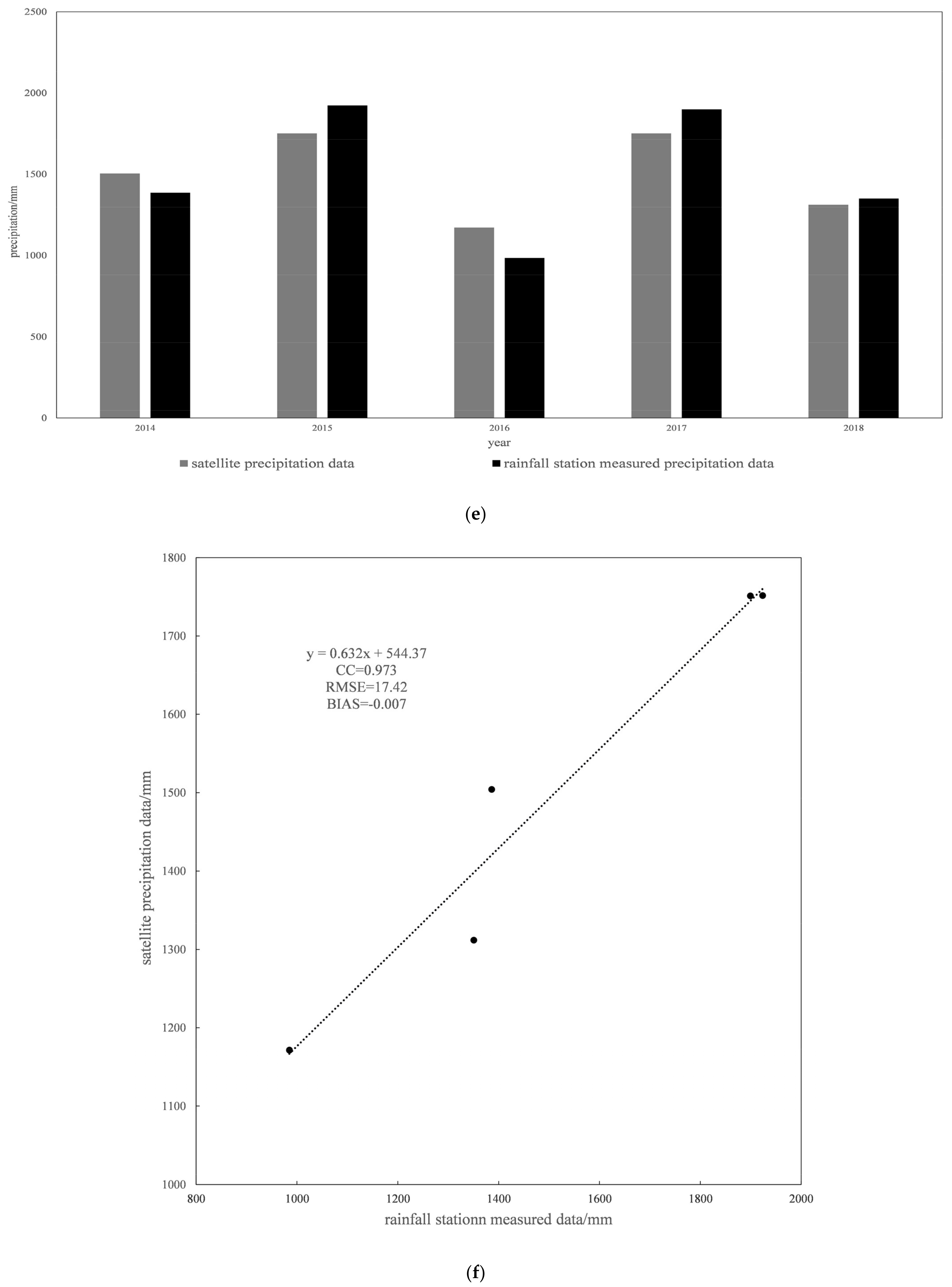
4.1. Data Accuracy of IMERG Precipitation Products
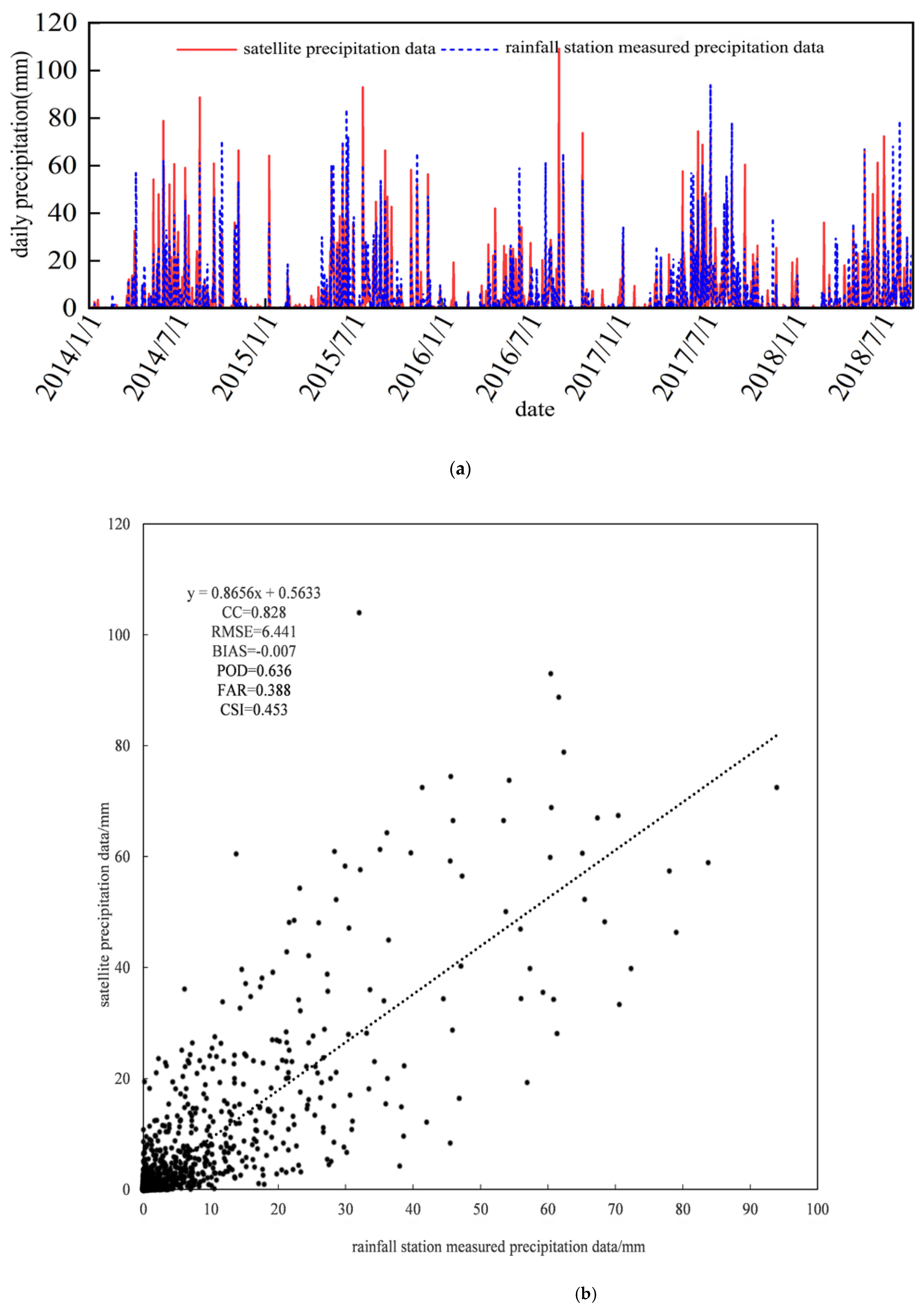
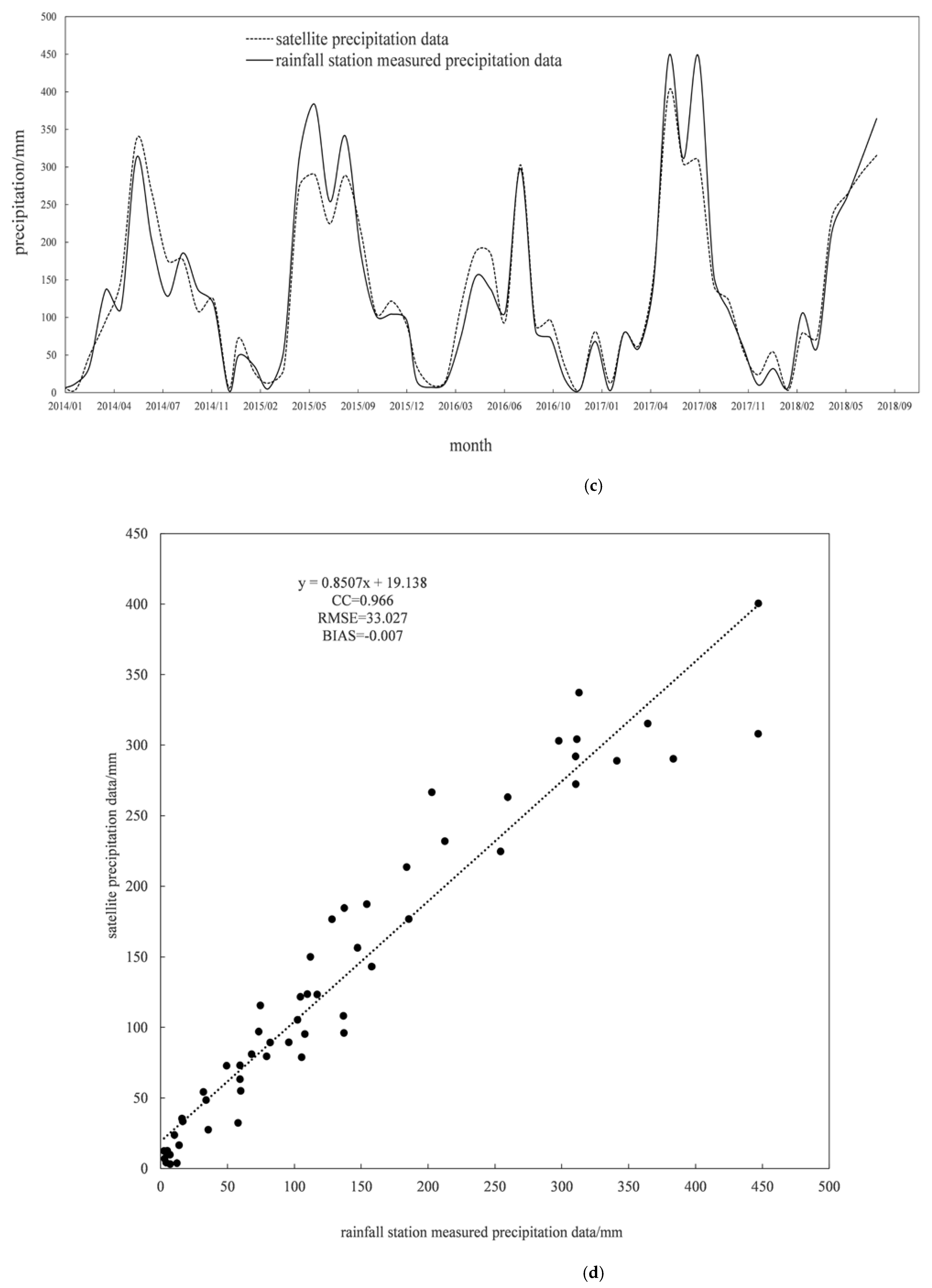
4.1.1. Data Accuracy in the Time Dimension
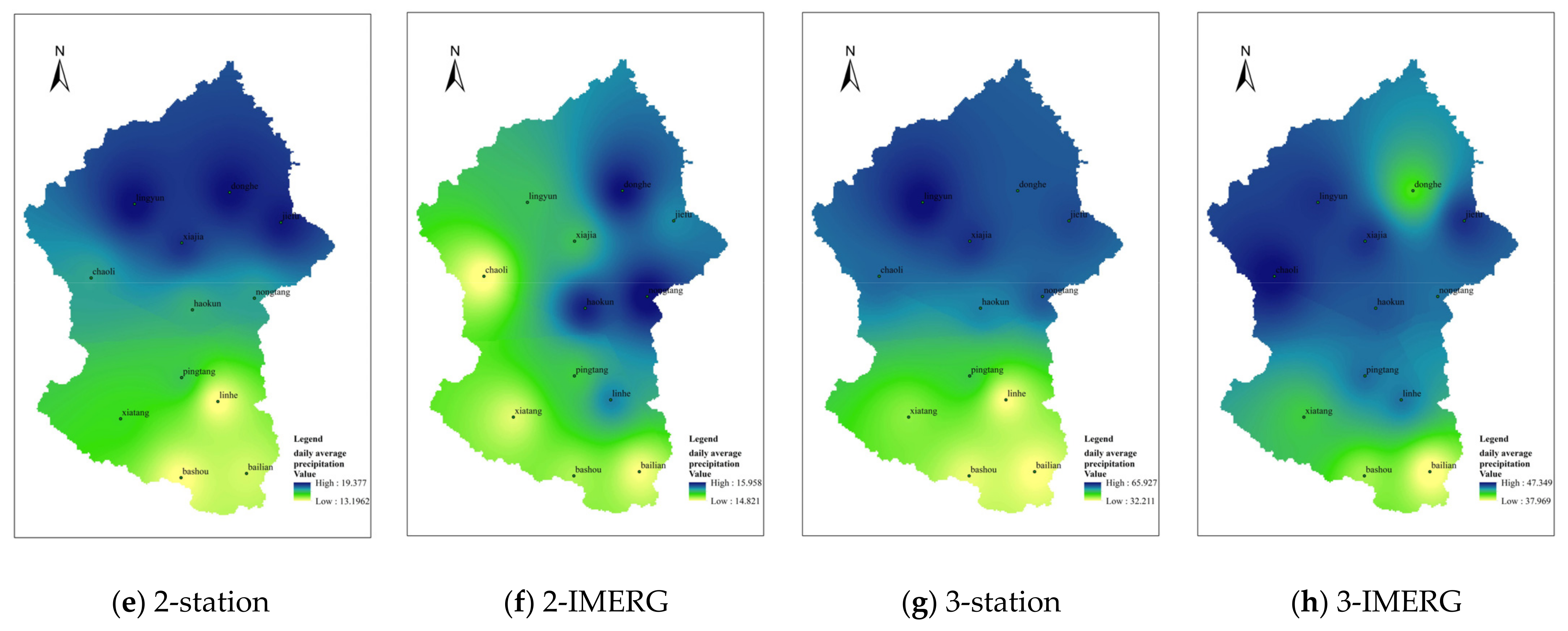
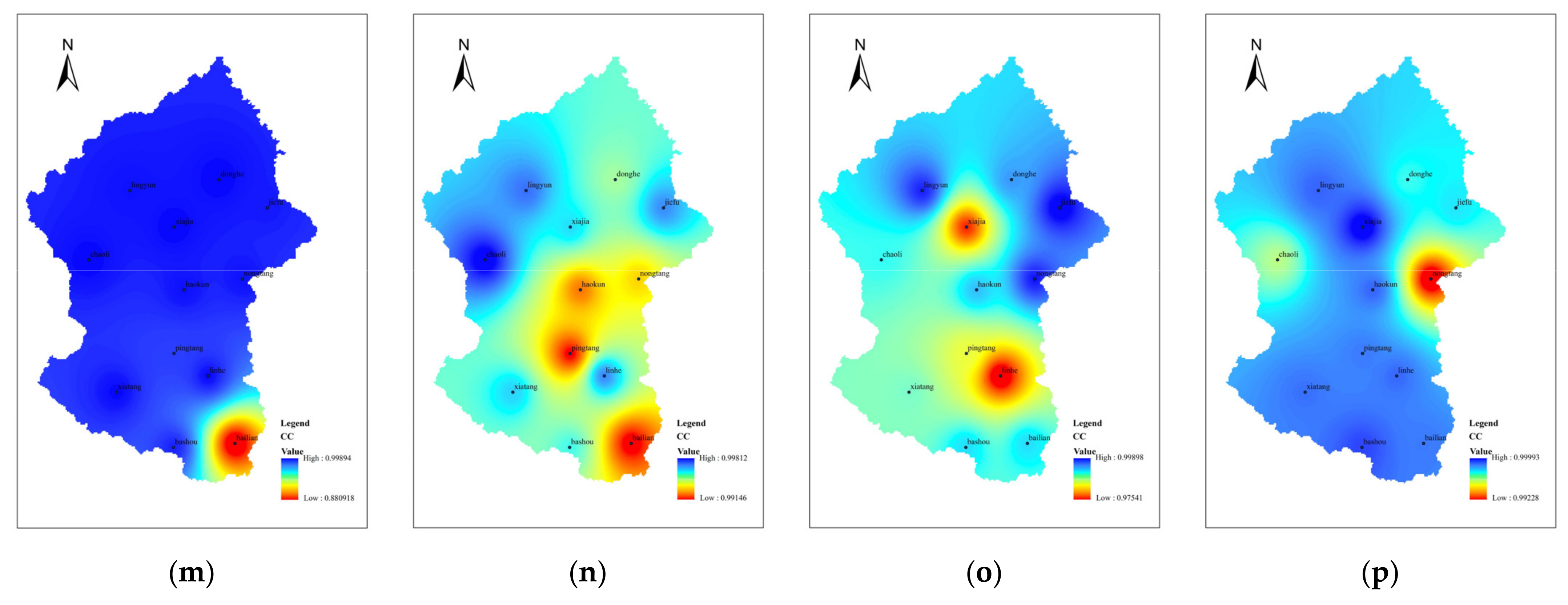
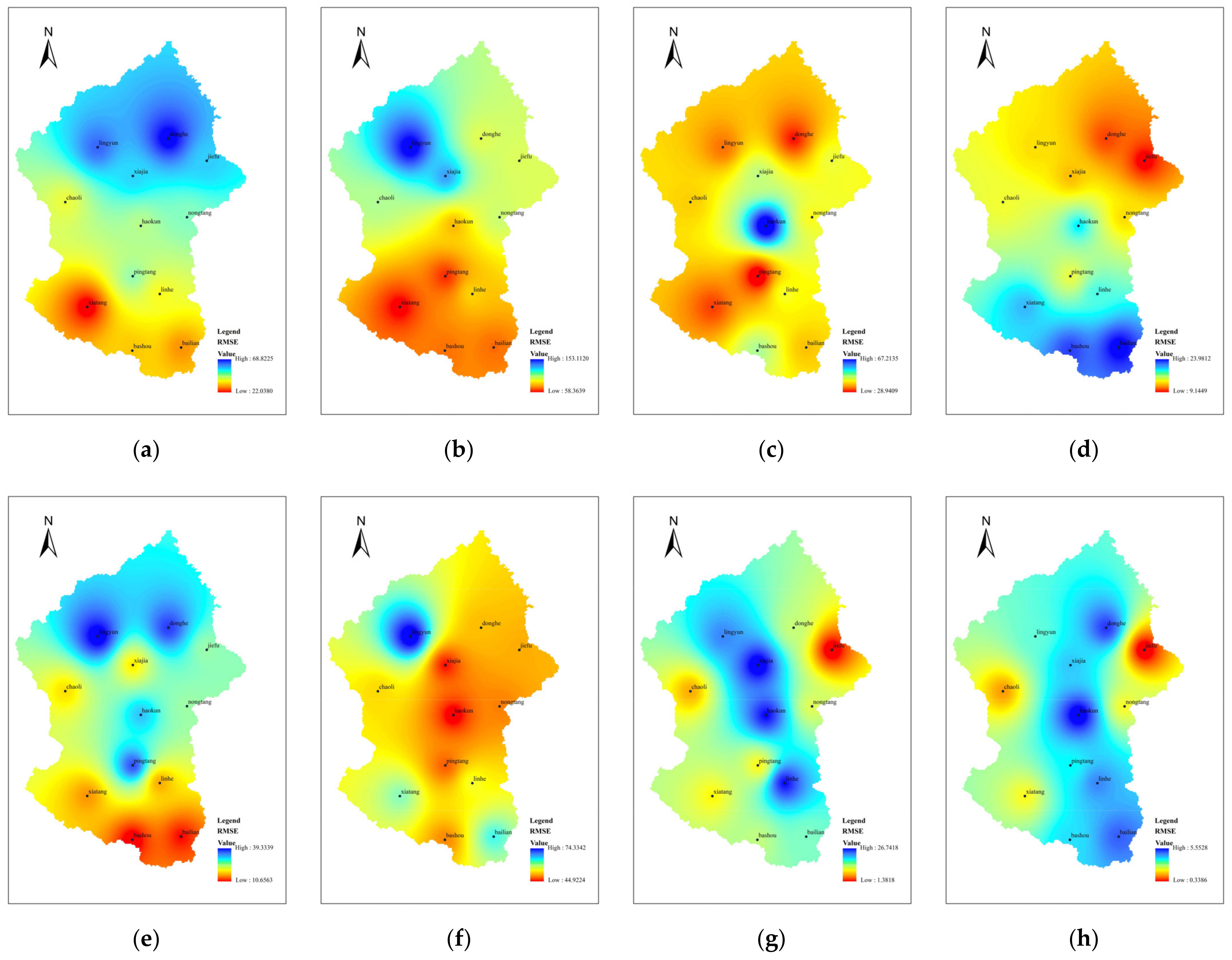
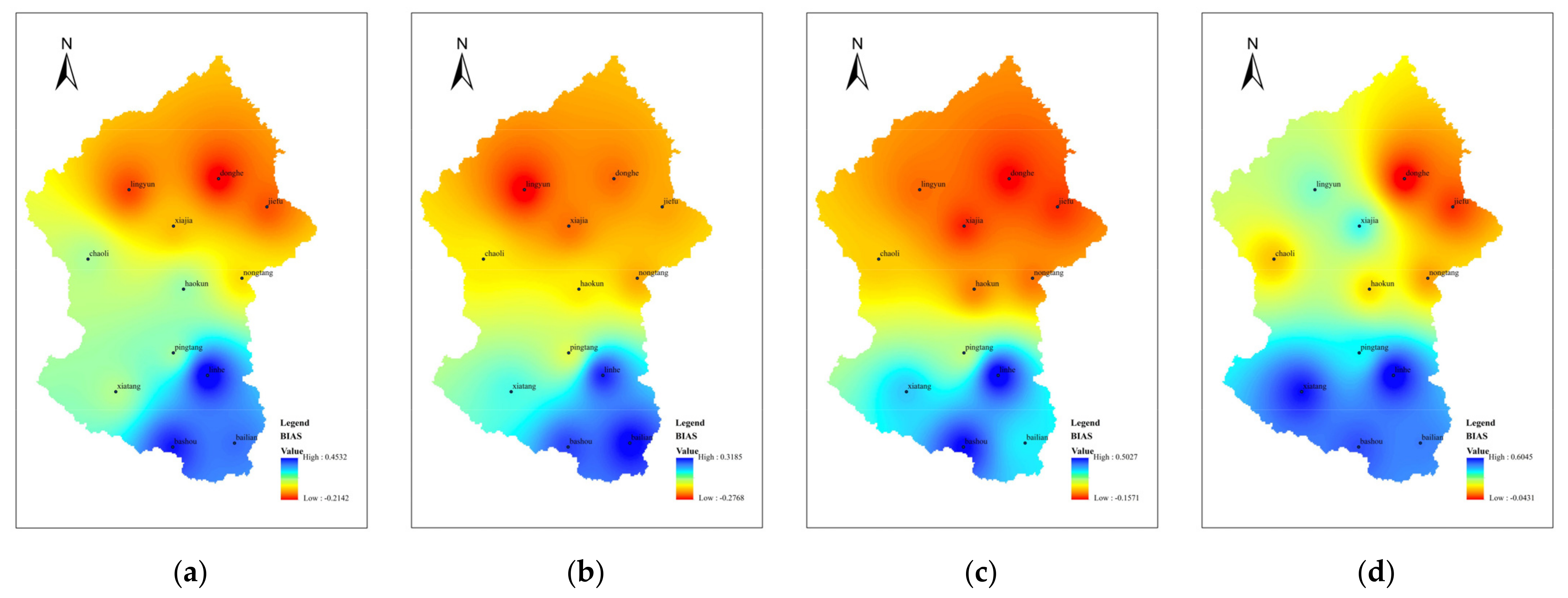
4.1.2. Data Accuracy in Spatial Dimension
4.2. Accuracy of Fused Precipitation Data
4.2.1. Data Accuracy in the Time Dimension
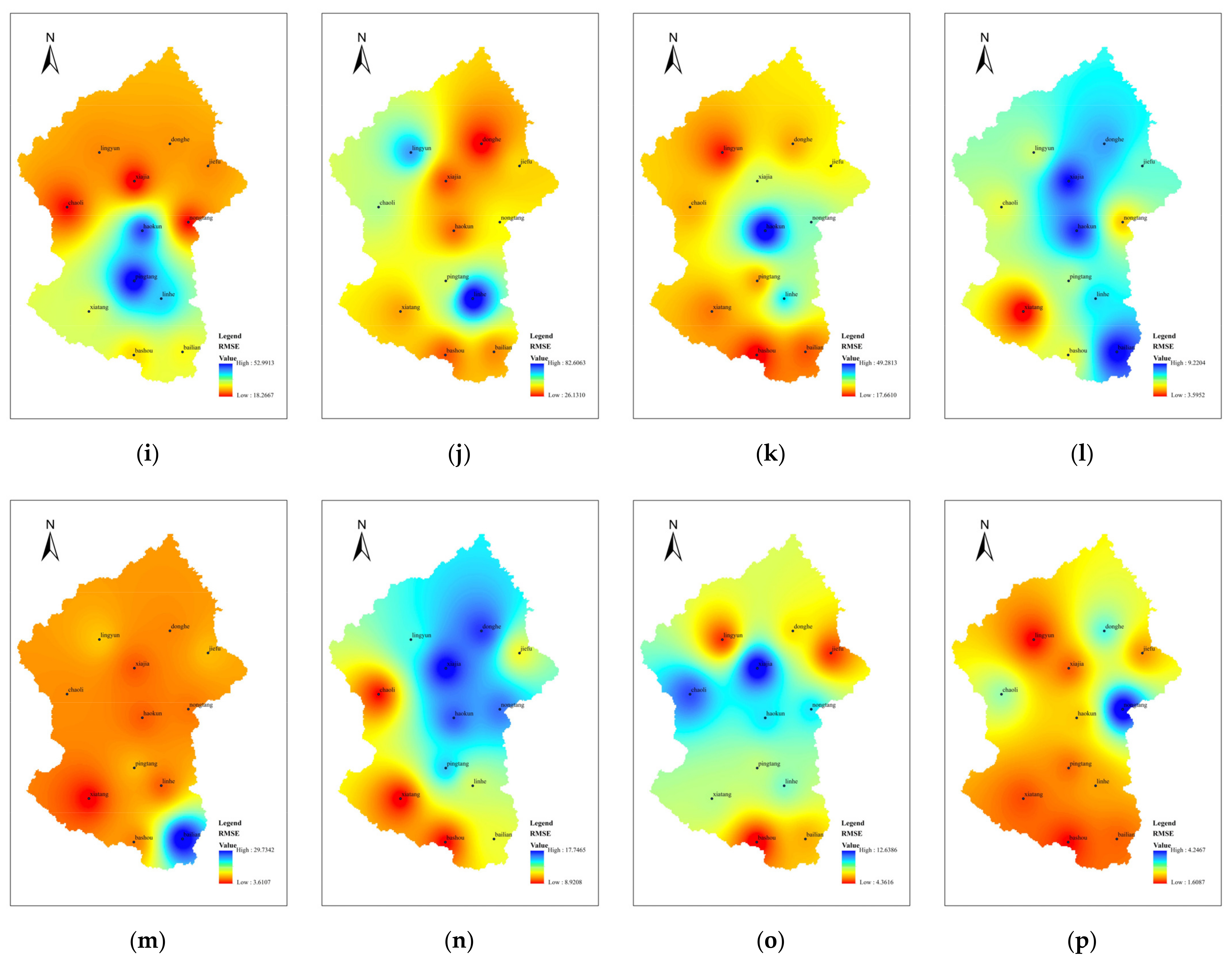
4.2.2. Data Accuracy in the Spatial Dimension
4.3. Drought Analysis
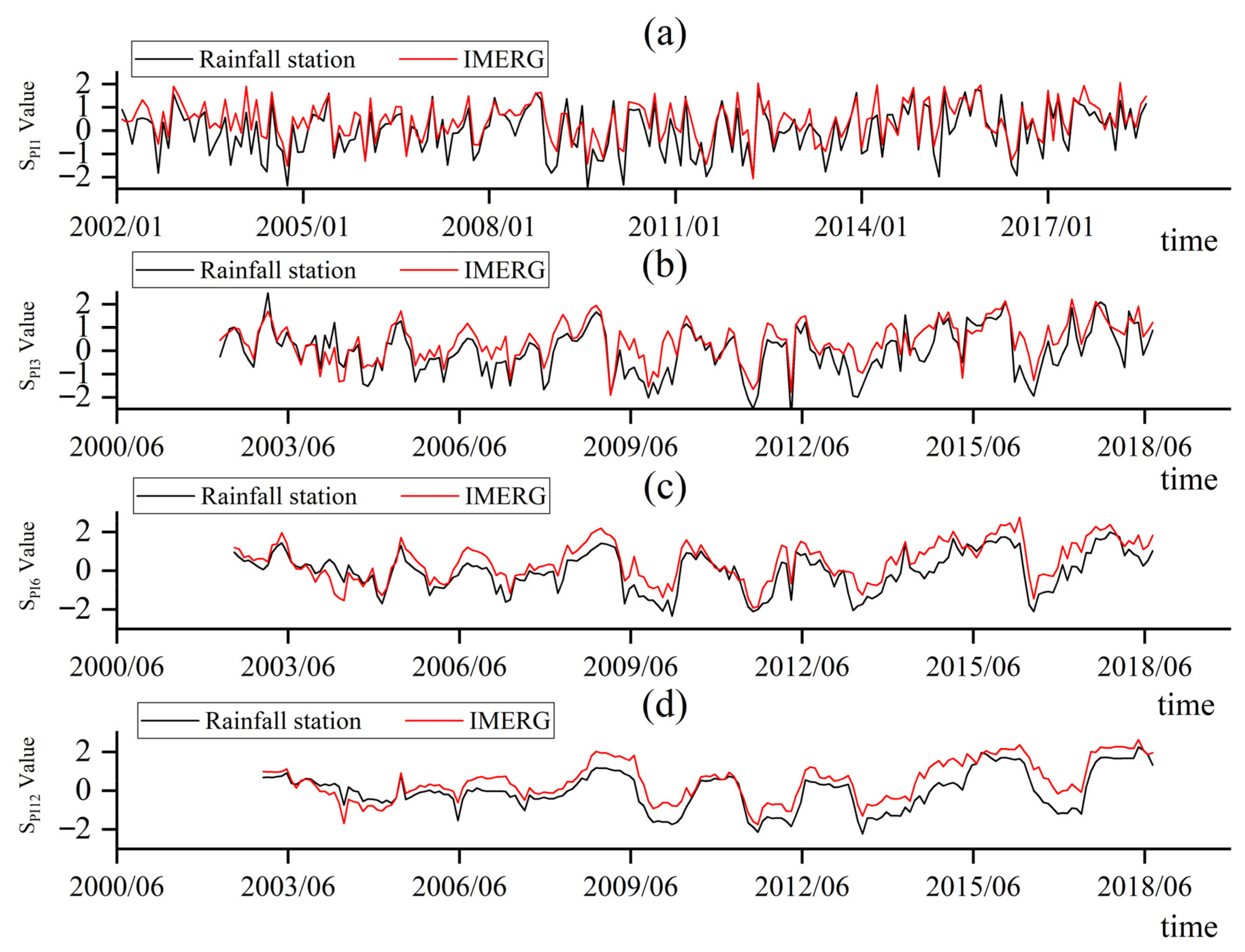
4.3.1. Temporal Evolutionary Characteristics of Droughts
4.3.2. Spatial Distribution of Droughts
5. Discussion
5.1. Explanation of Some Phenomena
5.2. Comparison with Previous Results
5.3. Advantages and Disadvantages
5.4. Suggestions
6. Summary and Conclusions
- (1)
- Temporally, the CC values of satellite precipitation and station precipitation increase with increasing time scale, the overall BIAS values remain basically the same, and the RMSE values are the smallest at the daily scale. Spatially, IMERG precipitation data overestimate actual precipitation in the southern part of the basin and underestimate actual precipitation in the northern part of the basin.
- (2)
- The quality of the CDF-fused precipitation data is better than the other two fusion methods, and the best values of CC, RMSE, and BIAS are 0.997, 4.222, and 0 in each season, respectively.
- (3)
- The drought analysis shows that the Chengbi River Basin is in a cycle of drought and flooding, with flooding occurring more often during the rainy season, while other periods show a dry state. In October–December 2014, the standardized precipitation index was mostly between +1 and −1, with spatial expressions of slight drought, normal conditions, and slight flooding.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, S.; Wang, Y.; Chang, J.; Guo, A.; Li, Z. Research on spatio-temporal evolution of drought patterns in the Yellow River Basin. J. Hydraul. Eng. 2019, 50, 1231–1241. [Google Scholar]
- Liu, T.; Krop, R.; Haigh, T.; Smith, K.H.; Svoboda, M. Valuation of Drought Information: Understanding the Value of the US Drought Monitor in Land Management. Water 2021, 13, 112. [Google Scholar] [CrossRef]
- Fowler, H.; Kilsby, C. A weather-type approach to analysing water resource drought in the Yorkshire region from 1881 to 1998. J. Hydrol. 2002, 262, 177–192. [Google Scholar] [CrossRef]
- Svoboda, M.D.; Fuchs, B.A.; Poulsen, C.C.; Nothwehr, J.R. The drought risk atlas: Enhancing decision support for drought risk management in the United States. J. Hydrol. 2015, 526, 274–286. [Google Scholar] [CrossRef] [Green Version]
- Rippey, B.R. The U.S. drought of 2012. Weather Clim. Extrem. 2015, 10, 57–64. [Google Scholar] [CrossRef] [Green Version]
- Mitra, S.; Srivastava, P. Comprehensive Drought Assessment Tool for Coastal Areas, Bays, and Estuaries: Development of a Coastal Drought Index. J. Hydrol. Eng. 2021, 26, 04020055. [Google Scholar] [CrossRef]
- Oh, K.; Yu, I.; Kim, H.; Kim, S.; Kim, L.-H.; Jeong, S. Drought assessment based on real-time drought index. Desalination Water Treat. 2014, 53, 3111–3117. [Google Scholar] [CrossRef]
- Shah, D.; Mishra, V. Integrated Drought Index (IDI) for Drought Monitoring and Assessment in India. Water Resour. Res. 2020, 56, e2019WR026284. [Google Scholar] [CrossRef]
- Sojka, M.; Jaskula, J.; Wielgosz, I. Drought Risk Assessment in the Kopel River Basin. J. Ecol. Eng. 2017, 18, 134–141. [Google Scholar] [CrossRef]
- Thomas, T.; Jaiswal, R.K.; Galkate, R.; Nayak, P.C.; Ghosh, N.C. Drought indicators-based integrated assessment of drought vulnerability: A case study of Bundelkhand droughts in central India. Nat. Hazards 2016, 81, 1627–1652. [Google Scholar] [CrossRef]
- Wickham, E.D.; Bathke, D.; Abdel-Monem, T.; Bernadt, T.; Bulling, D.; Pytlik-Zillig, L.; Stiles, C.; Wall, N. Conducting a drought-specific THIRA (Threat and Hazard Identification and Risk Assessment): A powerful tool for integrating all-hazard mitigation and drought planning efforts to increase drought mitigation quality. Int. J. Disaster Risk Reduct. 2019, 39, 101227. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wang, Y.M.; Chang, J.X.; Yao, J.; Huang, Q. Integrated assessment for hydrometeorological drought based on Markov chain model. Nat. Hazards 2016, 84, 1137–1160. [Google Scholar] [CrossRef]
- Perez, F.; De Stefano, M.; Disabato, F.; Vigna, R. The ITHACA Early Warning System for drought monitoring: First prototype test for the 2010 Sahel crisis. Ital. J. Remote Sens. 2012, 44, 181–195. [Google Scholar] [CrossRef]
- Saghafian, B.; Hamzekhani, F.G. Hydrological drought early warning based on rainfall threshold. Nat. Hazards 2015, 79, 815–832. [Google Scholar] [CrossRef]
- Wang, Y.T.; Jiang, M.X.; Zhang, H.X.; Huang, W.; Destech Publicat, I. Development of Guizhou Drought Monitoring and Early Warning and Disaster Evaluation System. In Proceedings of the 3rd International Conference on Green Materials and Environmental Engineering (GMEE), Beijing, China, 22–22 October 2017; pp. 61–66. [Google Scholar]
- McEvoy, D.J.; Hobbins, M.; Brown, T.J.; VanderMolen, K.; Wall, T.; Huntington, J.L.; Svoboda, M. Establishing Relationships between Drought Indices and Wildfire Danger Outputs: A Test Case for the California-Nevada Drought Early Warning System. Climate 2019, 7, 52. [Google Scholar] [CrossRef] [Green Version]
- Barrett, A.B.; Duivenvoorden, S.; Salakpi, E.E.; Muthoka, J.M.; Mwangi, J.; Oliver, S.; Rowhani, P. Forecasting vegetation condition for drought early warning systems in pastoral communities in Kenya. Remote Sens. Environ. 2020, 248, 111886. [Google Scholar] [CrossRef]
- Sharafi, L.; Zarafshani, K.; Keshavarz, M.; Azadi, H.; Van Passel, S. Drought risk assessment: Towards drought early warning system and sustainable environment in western Iran. Ecol. Indic. 2020, 114, 106276. [Google Scholar] [CrossRef]
- Van Ginkel, M.; Biradar, C. Drought Early Warning in Agri-Food Systems. Climate 2021, 9, 134. [Google Scholar] [CrossRef]
- Botterill, L.C.; Hayes, M.J. Drought triggers and declarations: Science and policy considerations for drought risk management. Nat. Hazards 2012, 64, 139–151. [Google Scholar] [CrossRef] [Green Version]
- Kulirova, P.; Vopravil, J.; Batysta, M.; Mendel Univ, B. Integrated Drought Management System in Central and Eastern Europe. In Proceedings of the International Conference on Soil—The Non-Renewable Environmental Resource, Brno, Czech Republic, 7–9 September 2015; pp. 159–168. [Google Scholar]
- Al-Faraj, F.A.M.; Scholz, M.; Tigkas, D.; Boni, M. Drought indices supporting drought management in transboundary watersheds subject to climate alterations. Water Policy 2015, 17, 865–886. [Google Scholar] [CrossRef]
- Hong, I.; Lee, J.H.; Cho, H.S. National drought management framework for drought preparedness in Korea (lessons from the 2014-2015 drought). Water Policy 2016, 18, 89–106. [Google Scholar] [CrossRef]
- Jéssica, G.N.; Daniel, A.; Helizani, C.B.; Christopher, M.U.N.; Sergio, N.D.; Anderson, L.R.; Ivo, Z.G. Evaluating the Latest IMERG Products in a Subtropical Climate: The Case of Paraná State, Brazil. Remote Sens. 2021, 13, 906. [Google Scholar]
- Chengcheng, M.; Xingguo, M.; Suxia, L.; Shi, H. Extensive evaluation of IMERG precipitation for both liquid and solid in Yellow River source region. Atmos. Res. 2021, 256, 105570. [Google Scholar]
- Zhu, S.; Shen, Y.; Ma, Z. A New Perspective for Charactering the Spatio-temporal Patterns of the Error in GPM IMERG over Mainland China. Earth Space Sci. 2021, 8, 1–16. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Mohammed, S.A.; Hamouda, M.A.; Mohamed, M.M. Impact of Topography and Rainfall Intensity on the Accuracy of IMERG Precipitation Estimates in an Arid Region. Remote Sens. 2020, 13, 13. [Google Scholar] [CrossRef]
- Tan, M.L.; Duan, Z. Assessment of GPM and TRMM Precipitation Products over Singapore. Remote Sens. 2017, 9, 720. [Google Scholar] [CrossRef] [Green Version]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef] [Green Version]
- Moazami, S.; Najafi, M. A comprehensive evaluation of GPM-IMERG V06 and MRMS with hourly ground-based precipitation observations across Canada. J. Hydrol. 2020, 594, 125929. [Google Scholar] [CrossRef]
- Ayat, H.; Evans, J.P.; Behrangi, A. How do different sensors impact IMERG precipitation estimates during hurricane days? Remote Sens. Environ. 2021, 259, 112417. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Nakhjiri, N. A near real-time satellite-based global drought climate data record. Environ. Res. Lett. 2012, 7, 044037. [Google Scholar] [CrossRef] [Green Version]
- Hnilica, J.; Hanel, M.; Pus, V. Multisite bias correction of precipitation data from regional climate models. Int. J. Climatol. 2017, 37, 2934–2946. [Google Scholar] [CrossRef]
- Yilmaz, M. Drought analysis of Konya Closed Basin with the use of TMPA satellite-based precipitation data. J. Fac. Eng. Archit. Gazi Univ. 2017, 32, 541–549. [Google Scholar] [CrossRef] [Green Version]
- Katiraie-Boroujerdy, P.-S.; Naeini, M.R.; Asanjan, A.A.; Chavoshian, A.; Hsu, K.-L.; Sorooshian, S. Bias Correction of Satellite-Based Precipitation Estimations Using Quantile Mapping Approach in Different Climate Regions of Iran. Remote Sens. 2020, 12, 2102. [Google Scholar] [CrossRef]
- Le, X.-H.; Lee, G.; Jung, K.; An, H.-U.; Lee, S.; Jung, Y. Application of Convolutional Neural Network for Spatiotemporal Bias Correction of Daily Satellite-Based Precipitation. Remote Sens. 2020, 12, 2731. [Google Scholar] [CrossRef]
- Wei, L.; Jiang, S.; Ren, L.; Zhang, L.; Wang, M.; Duan, Z. Preliminary Utility of the Retrospective IMERG Precipitation Product for Large-Scale Drought Monitoring over Mainland China. Remote Sens. 2020, 12, 2993. [Google Scholar] [CrossRef]
- Montaseri, M.; Amirataee, B. Comprehensive stochastic assessment of meteorological drought indices. Int. J. Clim. 2016, 37, 998–1013. [Google Scholar] [CrossRef]
- Nasrollahi, M.; Khosravi, H.; Moghaddamnia, A.; Malekian, A.; Shahid, S. Assessment of drought risk index using drought hazard and vulnerability indices. Arab. J. Geosci. 2018, 11, 606. [Google Scholar] [CrossRef]
- Samantaray, A.K.; Singh, G.; Ramadas, M.; Panda, R.K. Drought hotspot analysis and risk assessment using probabilistic drought monitoring and severity-duration-frequency analysis. Hydrol. Processes 2019, 33, 432–449. [Google Scholar] [CrossRef]
- Shengle, C.A.O.; Yanling, W.; Ru’an, Y.U.N. Study on drought assessment and forecast method of Shandong Province. J. Shandong Univ. (Eng. Sci.) 2006, 36, 58–61. [Google Scholar]
- Guoqing, S. Drought Risk Assessment in the South-to-North Water Transferred Areas. South—North Water Transf. Water Sci. Technol. 2008, 6, 14–17. [Google Scholar]
- Xu, J.; Pan, D. Comprehensive Assessment of Drought Severity Based onIts Evolution Course Simulation. J. Yangtze River Sci. Res. Inst. 2014, 31, 16–22. [Google Scholar]
- Fernandez, C.; Vega, J.A.; Fonturbel, T.; Jimenez, E. Streamflow drought time series forecasting: A case study in a small watershed in North West Spain. Stoch. Environ. Res. Risk Assess. 2009, 23, 1063–1070. [Google Scholar] [CrossRef]
- Liu, Y.W.; Wang, W.; Hu, Y.M.; Liang, Z.M. Drought assessment and uncertainty analysis for Dapoling basin. Nat. Hazards 2014, 74, 1613–1627. [Google Scholar] [CrossRef]
- Mo, C.; Ruan, Y.; Xiao, X.; Lan, H.; Jin, J. Impact of climate change and human activities on the baseflow in a typical karst basin, Southwest China. Ecol. Indic. 2021, 126, 107628. [Google Scholar] [CrossRef]
- Mo, C.X.; Ruan, Y.L.; He, J.Q.; Jin, J.L.; Liu, P.; Sun, G.K. Frequency analysis of precipitation extremes under climate change. Int. J. Climatol. 2019, 39, 1373–1387. [Google Scholar] [CrossRef]
- Linfei, Y.; Guoyong, L.; Andre, P.; Jian, P. A Comprehensive Evaluation of Latest GPM IMERG V06 Early, Late and Final Precipitation Products across China. Remote Sens. 2021, 13, 1208. [Google Scholar]
- Yang, X.; Lu, Y.; Tan, M.L.; Li, X.; Wang, G.; He, R. Nine-Year Systematic Evaluation of the GPM and TRMM Precipitation Products in the Shuaishui River Basin in East-Central China. Remote Sens. 2020, 12, 1042. [Google Scholar] [CrossRef] [Green Version]
- Ren, M.; Xu, Z.; Pang, B.; Liu, W.; Liu, J.; Du, L.; Wang, R. Assessment of Satellite-Derived Precipitation Products for the Beijing Region. Remote Sens. 2018, 10, 1914. [Google Scholar] [CrossRef] [Green Version]
- Dezfooli, D.; Abdollahi, B.; Hosseini-Moghari, S.-M.; Ebrahimi, K. A comparison between high-resolution satellite precipitation estimates and gauge measured data: Case study of Gorganrood basin, Iran. J. Water Supply Res. Technol. -Aqua 2018, 67, 236–251. [Google Scholar] [CrossRef]
- Vasvari, V. Calibration of tipping bucket rain gauges in the Graz urban research area. Atmos. Res. 2005, 77, 18–28. [Google Scholar] [CrossRef]
- Bruster-Flores, J.L.; Ortiz-Gómez, R.; Ferriño-Fierro, A.L.; Guerra-Cobián, V.H.; Burgos-Flores, D.; Lizárraga-Mendiola, L.G. Evaluation of Precipitation Estimates CMORPH-CRT on Regions of Mexico with Different Climates. Water 2019, 11, 1722. [Google Scholar] [CrossRef] [Green Version]
- Foody, G.M. Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI-rainfall relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Bastiaanssen, W.G.M. Local calibration of remotely sensed rainfall from the TRMM satellite for different periods and spatial scales in the Indus Basin. Int. J. Remote Sens. 2012, 33, 2603–2627. [Google Scholar] [CrossRef]
- Calheiros, R.V.; Zawadzki, I.I. Reflectivity-Rain Rate Relationships for Radar Hydrology in Brazil. J. Appl. Meteorol. 1987, 26, 118–132. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Dabanli, I.; Mishra, A.K.; Sen, Z. Long-term spatio-temporal drought variability in Turkey. J. Hydrol. 2017, 552, 779–792. [Google Scholar] [CrossRef]
- Wang, L.; Yu, H.; Yang, M.; Yang, R.; Gao, R.; Wang, Y. A drought index: The standardized precipitation evapotranspiration runoff index. J. Hydrol. 2019, 571, 651–668. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, Y.; Wu, Y.; Wang, G.; Wu, W.; Jin, J.; He, R.; Liu, C. Research on the Quality Evaluation of GPM Satellite Precipitation Data Products -Taking the Yarlung Zangbo River as an Example. China Rural. Water Hydropower 2021, 6, 91–97. [Google Scholar]
- Sheau Tieh, N.; Tangang, F.; Juneng, L. Bias correction of global and regional simulated daily precipitation and surface mean temperature over Southeast Asia using quantile mapping method. Glob. Planet. Chang. 2017, 149, 79–90. [Google Scholar] [CrossRef] [Green Version]
- Lei, H.; Ma, J.; Li, H.; Wang, J.; Shao, D.; Zhao, H. Bias Correction of Climate Model Precipitation in the Upper Heihe River Basin based on Quantile Mapping Method. Plateau Meteorol. 2020, 39, 266–279. [Google Scholar]
- Gao, Y.; Liu, X.; Leng, X.; Zhang, Y.; Dong, J.; Fan, C. Spatio-temporal drought patterns in Guangxi Province based on principal component analysis. Acta Ecol. Sin. 2020, 40, 5591–5601. [Google Scholar]



| Station | Latitude (°) | Longitude (°) | Altitude (m) | Average Annual Precipitation (mm) | Maximum Annual Precipitation (mm) | Minimum Annual Precipitation (mm) |
|---|---|---|---|---|---|---|
| Bashou | 23.95 | 106.642 | 263 | 1074 | 1422 | 803 |
| Pingtang | 24.094 | 106.645 | 314 | 1250 | 1792 | 805 |
| Haokun | 24.192 | 106.663 | 408 | 1424 | 2009 | 816 |
| Lingyun | 24.345 | 106.574 | 689 | 1660 | 2381 | 995 |
| Xiatang | 24.036 | 106.548 | 206 | 1093 | 1682 | 743 |
| Bailian | 23.955 | 106.745 | 277 | 1098 | 1536 | 671 |
| Linhe | 24.059 | 106.701 | 245 | 975 | 1476 | 554 |
| Chaoli | 24.239 | 106.504 | 801 | 1446 | 2087 | 876 |
| Xiajia | 24.289 | 106.648 | 592 | 1500 | 2303 | 905 |
| Nongtang | 24.207 | 106.761 | 883 | 1497 | 2123 | 929 |
| Jiefu | 24.316 | 106.804 | 689 | 1659 | 2305 | 1068 |
| Donghe | 24.36 | 106.724 | 1004 | 1573 | 2409 | 956 |
| Station | CC | RMSE (mm) | BIAS | POD | FAR | CSI |
|---|---|---|---|---|---|---|
| Bashou | 0.756 | 7.966 | 0.334 | 0.463 | 0.665 | 0.241 |
| Pingtang | 0.724 | 8.971 | 0.06 | 0.526 | 0.661 | 0.260 |
| Haokun | 0.676 | 10.379 | −0.051 | 0.531 | 0.637 | 0.275 |
| Lingyun | 0.707 | 10.841 | −0.206 | 0.546 | 0.610 | 0.295 |
| Xiatang | 0.733 | 8.320 | 0.201 | 0.409 | 0.607 | 0.251 |
| Bailian | 0.732 | 8.248 | 0.314 | 0.420 | 0.634 | 0.243 |
| Linhe | 0.716 | 8.903 | 0.391 | 0.436 | 0.669 | 0.232 |
| Chaoli | 0.636 | 11.123 | −0.072 | 0.530 | 0.610 | 0.290 |
| Xiajia | 0.706 | 10.411 | −0.15 | 0.545 | 0.623 | 0.286 |
| Nongtang | 0.659 | 11.304 | −0.094 | 0.546 | 0.610 | 0.295 |
| Jiefu | 0.714 | 10.293 | −0.184 | 0.545 | 0.588 | 0.307 |
| Donghe | 0.674 | 10.638 | −0.170 | 0.552 | 0.551 | 0.329 |
| Station | CC | RMSE (mm) | BIAS |
|---|---|---|---|
| Bashou | 0.954 | 47.384 | 0.334 |
| Pingtang | 0.941 | 40.941 | 0.060 |
| Haokun | 0.900 | 57.837 | −0.051 |
| Lingyun | 0.924 | 82.958 | −0.206 |
| Xiatang | 0.947 | 41.312 | 0.201 |
| Bailian | 0.963 | 45.187 | 0.314 |
| Linhe | 0.938 | 53.995 | 0.391 |
| Chaoli | 0.902 | 64.846 | −0.072 |
| Xiajia | 0.920 | 72.980 | −0.150 |
| Nngtang | 0.920 | 58.574 | −0.094 |
| Jiefu | 0.941 | 68.744 | −0.184 |
| Donghe | 0.945 | 60.421 | −0.170 |
| Station | CC | RMSE (mm) | BIAS |
|---|---|---|---|
| Bashou | 0.904 | 391.603 | 0.334 |
| Pingtang | 0.984 | 136.061 | 0.060 |
| Haokun | 0.964 | 173.531 | −0.051 |
| Lingyun | 0.975 | 460.281 | −0.206 |
| Xiatang | 0.982 | 268.582 | 0.201 |
| Bailian | 0.921 | 374.023 | 0.314 |
| Linhe | 0.923 | 434.951 | 0.391 |
| Chaoli | 0.834 | 311.194 | −0.072 |
| Xiajia | 0.959 | 393.479 | −0.150 |
| Nongtang | 0.933 | 234.845 | −0.094 |
| Jiefu | 0.947 | 399.423 | −0.184 |
| Donghe | 0.979 | 396.214 | −0.170 |
| Type | Time | Frequency | Station | |
|---|---|---|---|---|
| Minimum Value (mm) | Maximum Value (mm) | |||
| 0 | 746 | 0.437793 | 0 | 0 |
| 1 | 697 | 0.409038 | 0.047738 | 8.069297 |
| 2 | 204 | 0.119718 | 8.085273 | 31.69781 |
| 3 | 57 | 0.033451 | 32.36669 | 94.86293 |
| Data Types | Indicators | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|---|
| Satellite | CC | 0.519 | 0.735 | 0.695 | 0.669 |
| RMSE (mm) | 91.977 | 239.693 | 94.388 | 31.439 | |
| BIAS | 0.039 | −0.057 | 0.046 | 0.271 | |
| GDA | CC | 0.857 | 0.957 | 0.971 | 0.971 |
| RMSE (mm) | 56.893 | 102.983 | 31.812 | 7.231 | |
| BIAS | −0.071 | −0.035 | 0.011 | 0.012 | |
| GWR | CC | 0.813 | 0.951 | 0.913 | 0.884 |
| RMSE (mm) | 60.462 | 101.253 | 53.534 | 13.781 | |
| BIAS | 0.049 | 0.007 | 0.007 | 0.021 | |
| CDF | CC | 0.992 | 0.997 | 0.993 | 0.990 |
| RMSE (mm) | 13.607 | 25.355 | 15.663 | 4.222 | |
| BIAS | 0.011 | 0.001 | 0.000 | 0.001 |
| SPI Value | Drought and Flood Scale | SPI Value | Drought and Flood Scale |
|---|---|---|---|
| 2.0 ≤ SPI | extreme flood | −1.0 < SPI ≤ −0.5 | slight drought |
| 1.5 < SPI ≤ 2.0 | severe flood | −1.5 < SPI ≤ −1.0 | moderate drought |
| 1.0 < SPI ≤ 1.5 | moderate flood | −2.0 < SPI ≤ −1.5 | severe drought |
| 0.5 < SPI ≤ 1.0 | slight flood | SPI ≤ −2.0 | extreme drought |
| −0.5 < SPI ≤ 0.5 | no drought or flood |
| Data Types | Date | Xiajia | Lingyun | Donghe | Jiefu | Nongtang | Haokun |
|---|---|---|---|---|---|---|---|
| October 2014 | −0.99 | −0.3 | −0.36 | −0.83 | −0.7 | −0.78 | |
| Station Data | November 2014 | −0.13 | 0.44 | 0.27 | −0.23 | 0.36 | 0.08 |
| December 2014 | −0.07 | 0.51 | 0.25 | −0.01 | 0.65 | 0.15 | |
| October 2014 | −0.57 | −0.51 | −0.54 | −0.67 | −0.66 | −0.75 | |
| Fused data | November 2014 | −0.23 | −0.17 | −0.24 | −0.3 | −0.31 | −0.27 |
| December 2014 | −0.06 | −0.03 | −0.1 | −0.11 | −0.15 | −0.14 | |
| Data Types | Date | Pingtang | Xiatang | Chaoli | Linhe | Bailian | Bashou |
| October 2014 | −1.14 | −0.94 | −0.69 | −1.12 | −1.18 | −0.9 | |
| Station Data | November 2014 | −0.21 | 0.03 | −0.07 | −0.26 | −0.65 | 0.1 |
| December 2014 | 0.06 | −0.03 | 0.23 | −0.23 | −0.21 | −0.12 | |
| October 2014 | −1.04 | −1 | −0.65 | −1.19 | −1.12 | −1.11 | |
| Fused data | November 2014 | −0.22 | −0.19 | −0.15 | −0.32 | −0.27 | −0.27 |
| December 2014 | −0.12 | −0.09 | −0.05 | −0.26 | −0.16 | −0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, C.; Meng, X.; Ruan, Y.; Wang, Y.; Lei, X.; Xing, Z.; Lai, S. Drought Assessment Based on Fused Satellite and Station Precipitation Data: An Example from the Chengbi River Basin, China. ISPRS Int. J. Geo-Inf. 2022, 11, 48. https://doi.org/10.3390/ijgi11010048
Mo C, Meng X, Ruan Y, Wang Y, Lei X, Xing Z, Lai S. Drought Assessment Based on Fused Satellite and Station Precipitation Data: An Example from the Chengbi River Basin, China. ISPRS International Journal of Geo-Information. 2022; 11(1):48. https://doi.org/10.3390/ijgi11010048
Chicago/Turabian StyleMo, Chongxun, Xuechen Meng, Yuli Ruan, Yafang Wang, Xingbi Lei, Zhenxiang Xing, and Shufeng Lai. 2022. "Drought Assessment Based on Fused Satellite and Station Precipitation Data: An Example from the Chengbi River Basin, China" ISPRS International Journal of Geo-Information 11, no. 1: 48. https://doi.org/10.3390/ijgi11010048
APA StyleMo, C., Meng, X., Ruan, Y., Wang, Y., Lei, X., Xing, Z., & Lai, S. (2022). Drought Assessment Based on Fused Satellite and Station Precipitation Data: An Example from the Chengbi River Basin, China. ISPRS International Journal of Geo-Information, 11(1), 48. https://doi.org/10.3390/ijgi11010048







