Positioning Localities for Vague Spatial Location Description: A Supervaluation Semantics Approach
Abstract
:1. Introduction
- (1)
- Construction of vague location description representation model considering multi-factors. Based on the cognitive mechanism of spatial location, a unified framework of spatial location description is proposed, which defines the following three cognitive factors: reference frame, spatial object and spatial relationship. The framework is used to illustrate the vagueness of different cognitive and abstract levels in the location description. Different from the traditional spatial information modeling, which focuses on spatial relationship, this paper establishes the vagueness relation and influence among different information factors by the strategy of multi-factors representation. It not only combs the source of vagueness in location description more comprehensively, but also enhances the interpretability of semantics of vague location description.
- (2)
- A supervaluationist theory-based positioning method for vague spatial location description is proposed. Based on the basic principles of supervaluation semantics, precisification models of vague predicates are constructed for spatial object and spatial relationship. From the three aspects of extension, anti-extension and penumbra, the threshold range of the cut-off point in the precisification model is set according to the location description context, so as to obtain precisification results in different situations. Location description as the expression of the result of personal spatial cognition is strongly subjective. In this method, different contexts are supervalued separately, making the inferred spatial location in real world more suitable for personalized subjective cognition.
2. Related Work
2.1. Vague Location Description and Positioning Method
2.2. Supervaluation Theory and Its Application in Geography
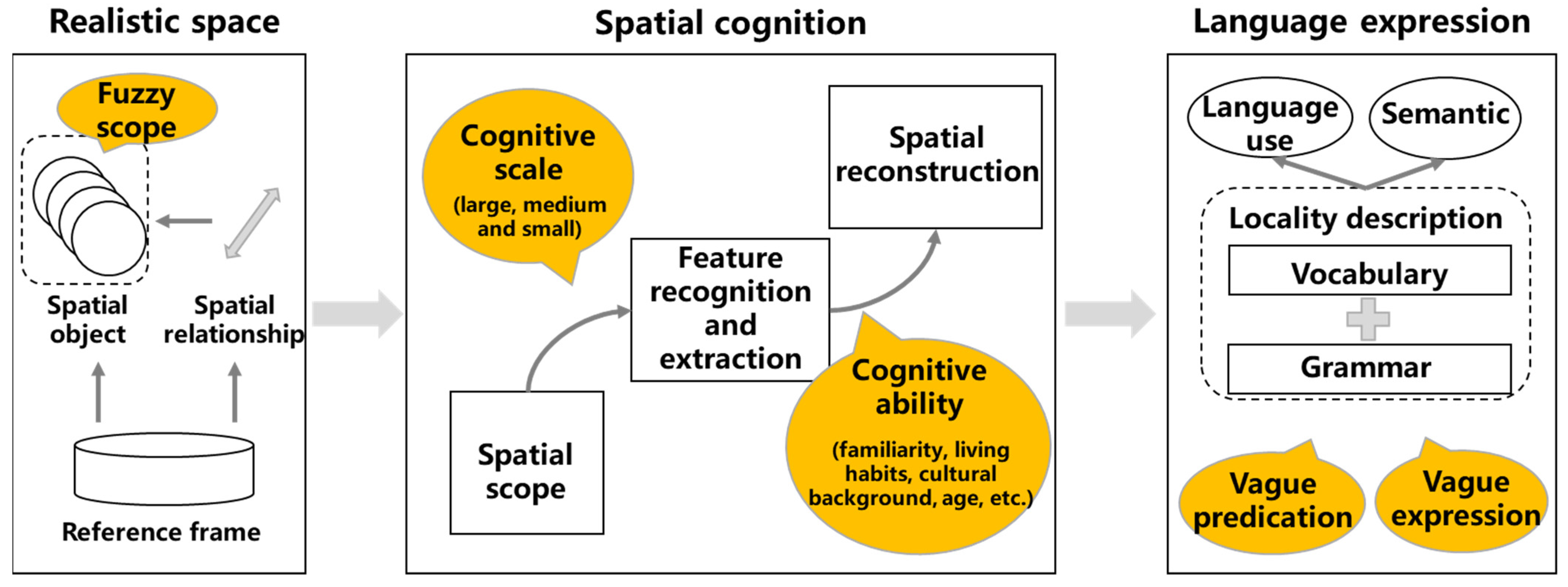
3. Spatial Location Description and Its Vagueness
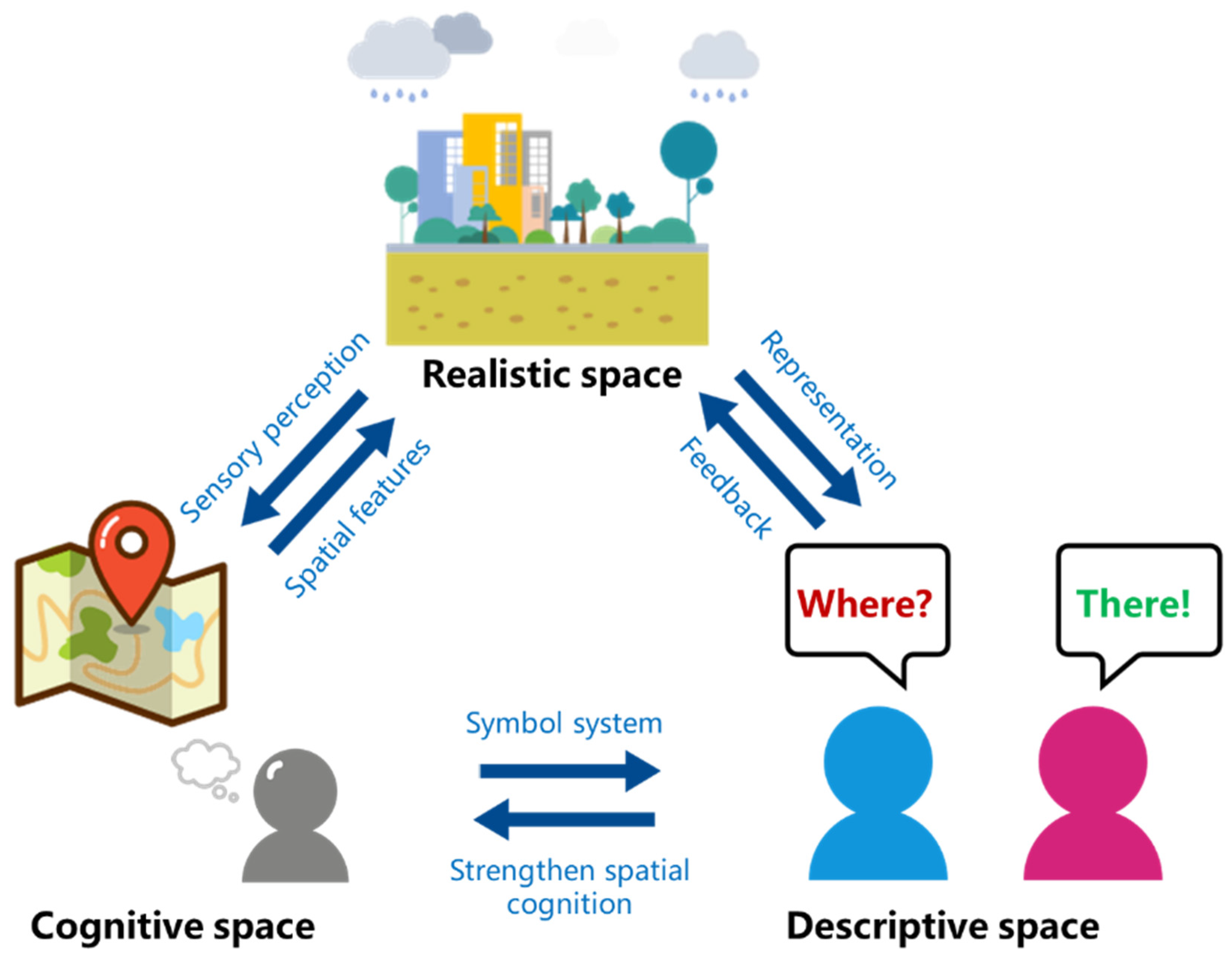
3.1. From Spatial Cognition to Location Description
3.2. Expression of Location Description
3.2.1. Reference Frame
3.2.2. Spatial Object
3.2.3. Spatial Relationship
3.3. Multi-Level Vagueness of Location Description
3.3.1. Vagueness of the Concept of Spatial Object
3.3.2. Vagueness in the Process of Spatial Cognition
3.3.3. Vagueness Enhanced by Natural Language
4. Positioning Model Based on Supervaluation Semantics
4.1. Basic Ideas of Supervaluationist Theory
- (1)
- Extension and anti-extension. Some lexical items, such as “forest”, “far”, “near” and so on, belong to the predicates, which are used in natural language to show the nature, characteristics or relationship between objects. Within a certain domain, the set of objects that can definitely be applied to a predicate is an extension of the predicate. On the contrary, the set of objects that cannot definitely be applied to this predicate is anti-extension. For instance, in the domain of “restaurants near the supermarket”, the restaurant 500 m away is in the extension of the predicate “near”, whereas the restaurant 2000 m away is in the anti-extension of the predicate “near”.
- (2)
- Penumbra. Beyond the extension and anti-extension is the boundary case of the predicate, which is the penumbra, also known as truth-value gaps. The existence of penumbra results in vague predicates that are neither true nor false. Because the supervaluation contains the truth-value gap, the classical two-valued principle is invalid for the supervaluationist theory. Following the previous instance, the restaurant 1000 m is the boundary case, thus the distance of 1000 m is in the penumbra of the predicate “near”.
- (3)
- Precisification. According to the supervaluationist theory, vagueness results from semantic incompleteness or indeterminacy of vague predicates, which makes the sentences containing vague predicates can be interpreted in different ways [62]. The use of more precise statements to explain each way is precisification. The aim of precisification is to minimize and eliminate the penumbra of vague predicates, and gradually enlarge the range of extension and anti-extension of predicates to make them admissible precisifications, which is a reasonable and cognitive way of precisification. Under each admissible precisification, vague predicates are actually refined into precise predicates, and the sentences containing vague predicates can be assigned values in the way of classical logic. The purpose of supervaluation is to transcend the classical assignment that corresponds to each precisification.
- (4)
- Cut-off point. The cut-off point is a concept based on precisification, which is used to explain precisification in different contexts [63]. Following the previous instance, the 800m can be used as a cut-off point, with restaurants below 800m being included in the extension of “near”, and all other restaurants in the anti-extension of “near”. This is a kind of precisification of “near”, and the result is a predicate without vagueness. By choosing different cut-off points, different precisification of the vague predicate can be obtained. It is important to note that the boundary case of the vague predicate is already determined. Therefore, any cut-off point of precisification should be appropriate and admissible, and not be inconsistent with non-boundary cases. Continuing the previous instance, it is not appropriate to use 400 m as a cut-off point for the precisification of the “near”. Because this cut-off is within the known extension of the “near”. Consequently, the cut-off point should be derived from the boundary case.
4.2. Positioning Model of Single Spatial Assertion
4.2.1. Basic Framework of the Positioning Model
- Vague spatial object model
- 2.
- Vague distance relation model
- 3.
- Vague direction relation model
4.2.2. Calculating Thresholds from Context-Dependent Observations
- Threshold of vague spatial object
- 2.
- Threshold of vague distance relation
- 3.
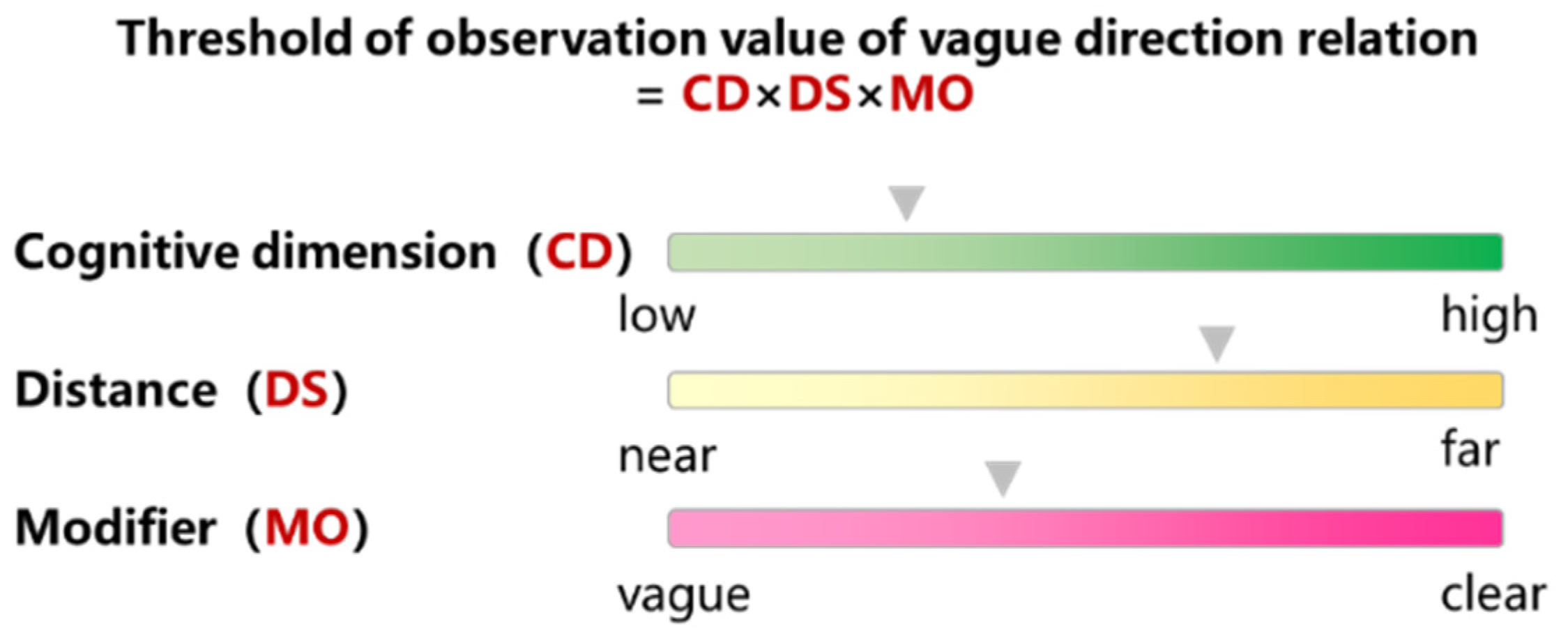
- Threshold of vague direction relation
4.2.3. Threshold Comparison between Different Contexts
- (1)
- Equality (ci ≈ cj). If the two contexts ci and cj are the same in terms of the observations, then they are likely to be equal and are recorded as ci ≈ cj. In the instance above, c2! ≈ c3.
- (2)
- General (ci⊐cj). After ignoring observations, if there are:The formula indicates that the contexts ci is at least as generic as the contexts cj (recorded as ci⊒cj). If ci⊒cj but does not have cj⊒ci, then ci is more general than cj (recorded as ci⊐cj). In the instance above, c2⊐c3.
- (3)
- Identifiability (ci≺cj). Taking the predicate “near” as an example, if all is “near” in ci and is also “near” in cj, then ci has at least the same identifiability as cj (recorded as ci≼cj). If ci≼cj but does not have cj≼ci, then cj has a stronger identifiability (recorded as ci≺cj). In the instance above, c2≺c3.
4.3. Positioning Model of Compound Spatial Assertion
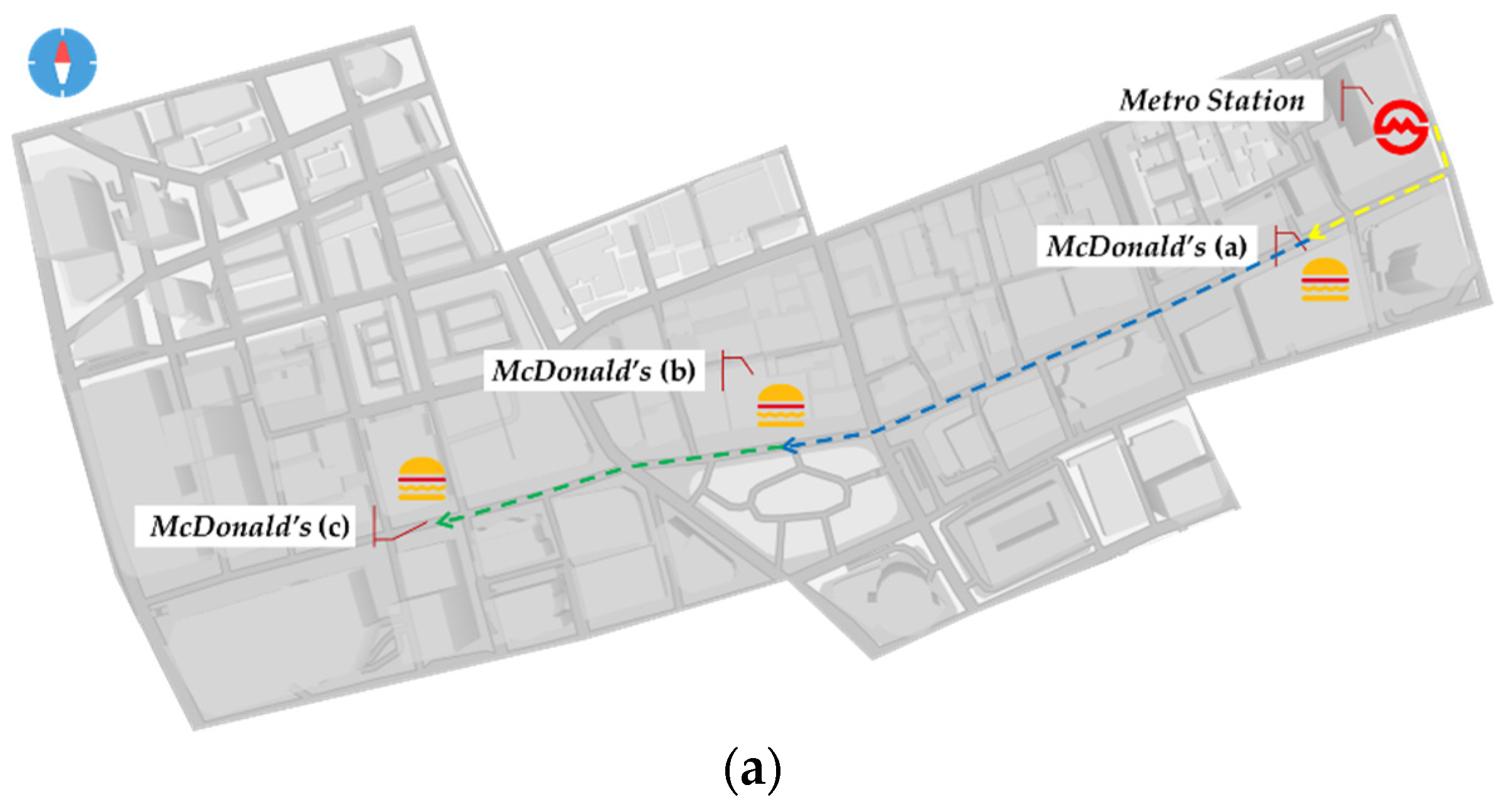
5. Case Study
5.1. Positioning Localities Based on Single Spatial Assertion
5.2. Positioning Localities Based on Compound Spatial Assertion
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Núñez, R.; Allen, M.; Gao, R.; Rigoli, C.; Relaford-Doyle, J.; Semenuks, A. What happened to cognitive science? Nat. Hum. Behav. 2019, 3, 782–791. [Google Scholar] [CrossRef] [PubMed]
- Cohn, A.G.; Hazarika, S.M. Qualitative spatial representation and reasoning: An overview. Fund. Inform. 2001, 46, 1–29. [Google Scholar]
- Renz, J. Qualitative spatial reasoning with topological information. J. Mol. Struct. Theochem. 2002, 579, 191–203. [Google Scholar]
- Wang, Y.; Fan, H.; Chen, R. Indoors Locality Positioning Using Cognitive Distances and Directions. Sensors 2017, 17, 2828. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vasardani, M.; Winter, S.; Richter, K.F. Locating place names from place descriptions. Int. J. Geogr. Inf. Sci. 2013, 27, 2509–2532. [Google Scholar] [CrossRef]
- Richter, D.; Winter, S.; Richter, K.F.; Stirling, L. Granularity of locations referred to by place descriptions. Comput. Environ. Urban 2013, 41, 88–99. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, Q.; Wieczorek, J.; Goodchild, M.F. Positioning localities based on spatial assertions. Int. J. Geogr. Inf. Sci. 2009, 23, 1471–1501. [Google Scholar] [CrossRef]
- Krishnapuram, R.; Keller, J.M.; Ma, Y. Quantitative analysis of properties and spatial relations of fuzzy image regions. IEEE Trans. Fuzzy Syst. 1993, 1, 222–233. [Google Scholar] [CrossRef] [Green Version]
- Ittelson, W.H. Environment Perception and Contemporary Perceptual Theory; Seminar: New York, NY, USA, 1976; pp. 141–154. [Google Scholar]
- Bloch, I.; Colliot, O.; Cesar, R.M. On the ternary spatial relation “Between”. IEEE Trans. Syst. Man Cybern. Part B 2006, 36, 312–327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takemura, C.M.; Cesar, R.M.; Bloch, I. Modeling and measuring the spatial relation “along”: Regions, contours and fuzzy sets. Pattern Recogn. 2012, 45, 757–766. [Google Scholar] [CrossRef]
- Chen, J.; Jia, H.; Liu, D.; Zhang, C. Composing Cardinal Direction Relations Basing on Interval Algebra. In Proceedings of the International Conference on Knowledge Science, Engineering and Management, Belfast, UK, 1–3 September 2010; Bi, Y., Williams, M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Du, S.; Guo, L.; Wang, Q. A model for describing and composing direction relations between overlapping and contained regions. Inform. Sci. 2008, 178, 2928–2949. [Google Scholar] [CrossRef]
- Deng, M.; Li, Z. A Statistical Model for Directional Relations between Spatial Objects. Geoinformatica 2008, 12, 193–217. [Google Scholar] [CrossRef]
- Claramunt, C.; Thériault, M. Fuzzy semantics for direction relations between composite regions. Inform. Sci. 2004, 160, 73–90. [Google Scholar] [CrossRef]
- Karbou, F.; Karbou, F. An interval approach to fuzzy surroundedness and fuzzy spatial relations. In Proceedings of the International Conference of the North American Fuzzy Information Processing Society—NAFIPS, Atlanta, GA, USA, 13–15 July 2000. [Google Scholar]
- Pizzi, N.J.; Pedrycz, W. Fuzzy Set Theoretic Adjustment to Training Set Class Labels Using Robust Location Measures. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks, Como, Italy, 27 July 2000. [Google Scholar]
- Rao, J.R.; Saraswati, K. Facility location problem on a network under multiple criteria—Fuzzy set theoretic approach. Int. J. Geogr. Inf. Sci. 2008, 19, 2555–2559. [Google Scholar] [CrossRef]
- Fatmi, M.R.; Habib, M.A.; Chowdhury, S. A Longitudinal Investigation of Residential Location: Fuzzy Logic-Based Choice Set Generation and Panel Location Choice Models. In Proceedings of the International Choice Modelling Conference, Austin, TX, USA, 10–13 May 2015. [Google Scholar]
- Montello, D.R.; Goodchild, M.F.; Gottsegen, J.; Fohl, P. Where’s Downtown? Behavioral Methods for Determining Referents of Vague Spatial Queries. Spat. Cogn. Comput. 2003, 3, 185–204. [Google Scholar]
- Jones, C.B.; Purves, R.S.; Clough, P.D.; Joho, H. Modelling vague places with knowledge from the Web. Int. J. Geogr. Inf. Sci. 2008, 22, 1045–1065. [Google Scholar] [CrossRef] [Green Version]
- Cheng, T.; Molenaar, M.; Lin, H. Formalizing fuzzy objects from uncertain classification results. Int. J. Geogr. Inf. Sci. 2001, 15, 27–42. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy sets and probability: Misunderstandings, bridges and gaps. In Proceedings of the Second IEEE International Conference on Fuzzy Systems, San Francisco, CA, USA, 28 March–1 April 1993. [Google Scholar]
- Porter, B. Supervaluations and the Strict-Tolerant Hierarchy. J. Philos. Logic 2021, 50, 1–20. [Google Scholar] [CrossRef]
- Keefe, R. Vagueness: Supervaluationism. Philos. Compass 2008, 3, 315–324. [Google Scholar] [CrossRef]
- Fine, K. Vagueness, truth and logic. Synthese 1975, 30, 265–300. [Google Scholar] [CrossRef]
- Dietz, R.; Moruzzi, S. Supernumeration: Vagueness and Numbers. In Cuts and Clouds: Vagueness, Its Nature and Its Logic; Simons, P., Ed.; Oxford University Press: Oxford, UK, 2010; pp. 482–490. [Google Scholar]
- Varzi, A.C. Supervaluationism and Its Logics. Mind 2007, 116, 633–676. [Google Scholar] [CrossRef]
- Montello, D.R. Scale and multiple psychologies of space. In Proceedings of the Spatial Information Theory, Marciana Marina, Italy, 19–22 September 1993; Frank, A.U., Campari, I., Eds.; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Du, S.; Wang, Q.; Qing, Q. Fuzzy Description and Composition Reasoning of Spatial Relation; Science Press: Beijing, China, 2007; pp. 154–196. [Google Scholar]
- Iii, A. Natural language processing for a location-based services system. J. Acoust. Soc. Am. 2008, 125, 1845. [Google Scholar]
- Ma, C.J.; Fang, J.Y. Interactive Location-Based Services Combined with Natural Language. In Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, Shanghai, China, 21–25 September 2007. [Google Scholar]
- Qiao, Z. Fuzziness-vagueness-generality-ambiguity. J. Pragmat. 1998, 29, 13–31. [Google Scholar]
- Goyal, R.K.; Egenhofer, M.J. Consistent queries over cardinal directions across different levels of detail. In Proceedings of the 11th International Workshop on Database and Expert Systems Applications, London, UK, 4–8 September 2000. [Google Scholar]
- Du, S.; Guo, L.; Wang, Q. A scale-explicit model for checking directional consistency in multi-resolution spatial data. Int. J. Geogr. Inf. Sci. 2010, 24, 465–485. [Google Scholar] [CrossRef]
- Tang, X.; Qin, K. Direction-relation similarity model based on fuzzy close-degree. In Proceedings of the 2010 IEEE International Conference on Progress in Informatics and Computing, Shanghai, China, 10–12 December 2010. [Google Scholar]
- Gong, Y.; Wu, L.; Lin, Y.; Liu, Y. Probability issues in locality descriptions based on Voronoi neighbor relationship. J. Vis. Lang. Comput. 2012, 23, 213–222. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Mark, D.M.; Egenhofer, M.J. Modeling Spatial Relations between Lines and Regions: Combining Formal Mathematical Models and Human Subjects Testing. Am. Cartogr. 1994, 21, 195–212. [Google Scholar]
- Xu, J. Formalizing natural-language spatial relations descriptions with fuzzy decision tree algorithm. Int. J. Geogr. Inf. Sci. 2007, 4, 377–395. [Google Scholar] [CrossRef]
- Xu, J. Formalizing the Natural-language Descriptions about the Spatial Relations between Linear Geographic Objects. J. Remote Sens. 2007, 2, 152–158. [Google Scholar]
- Xu, J.; Pan, X.; Zhao, J.; Fu, H. Virtual Reality-Based Fuzzy Spatial Relation Knowledge Extraction Method for Observer-Centered Vague Location Descriptions. ISPRS Int. J. Geo-Inf. 2021, 10, 833. [Google Scholar] [CrossRef]
- Blaschke, T.; Merschdorf, H.; Cabrera-Barona, P.; Gao, S.; Papadakis, E.; Kovacs-Györi, A. Place versus Space: From Points, Lines and Polygons in GIS to Place-Based Representations Reflecting Language and Culture. ISPRS Int. J. Geo-Inf. 2018, 7, 452. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Zhang, H.; Yang, H. Urban Functional Zone Recognition Integrating Multisource Geographic Data. Remote Sens. 2021, 13, 4732. [Google Scholar] [CrossRef]
- Wieczorek, J.; Guo, Q.; Hijmans, R.J. The point-radius method for georeferencing locality descriptions and calculating associated uncertainty. Int. J. Geogr. Inf. Sci. 2004, 18, 745–767. [Google Scholar] [CrossRef]
- Cohn, A.G.; Gotts, N.M. The ‘egg-yolk’ representation of regions with indeterminate boundaries. In Geographic Objects with Indeterminate Boundaries; Burrough, P.A., Frank, A., Eds.; Taylor & Francis: London, UK, 1996; Volume 2, pp. 171–187. [Google Scholar]
- Chen, J.; Shaw, S.L. Representing the Spatial Extent of Places Based on Flickr Photos with a Representativeness-Weighted Kernel Density Estimation; Geographic Information Science. GIScience 2016. Lecture Notes in Computer Science; Miller, J., O’Sullivan, D., Wiegand, N., Eds.; Springer: Cham, Switzerland, 2016; Volume 9927. [Google Scholar]
- Bäcklund, H.; Hedblom, A.; Neijman, N. A Density-Based Spatial Clustering of Application with Noise. Available online: https://weber.itn.liu.se/~aidvi/courses/06/dm/Seminars2011/DBSCAN(4).pdf (accessed on 11 November 2021).
- Cunha, E.; Martins, B. Using one-class classifiers and multiple kernel learning for defining imprecise geographic regions. Int. J. Geogr. Inf. Sci. 2014, 28, 2220–2241. [Google Scholar] [CrossRef]
- Liu, K.; Yin, L.; Lu, F.; Mou, N. Visualizing and exploring POI configurations of urban regions on POI-type semantic space. Cities 2020, 99, 102610. [Google Scholar] [CrossRef]
- Mehlberg, H. Book Reviews: The Reach of Science. Science 1958, 128, 1078–1079. [Google Scholar]
- Van Fraassen, B. Singular Terms, Truth-Value Gaps, and Free Logic. J. Philos. 1966, 63, 481–495. [Google Scholar] [CrossRef]
- Morreau, M. What vague objects are like. J. Philos. 2002, 99, 333–361. [Google Scholar] [CrossRef]
- Kulik, L. Vague spatial reasoning based on supervaluation. Geogr. Domain Geo-Graph. Inf. Syst. 2000, 19, 73–80. [Google Scholar]
- Minock, M.; Mollevik, J. Context-dependent ‘near’ and ‘far’ in spatial databases via supervaluation. Data Knowl. Eng. 2013, 86, 295–305. [Google Scholar] [CrossRef]
- Kulik, L. A Geometric Theory of Vague Boundaries Based on Supervaluation. In Proceedings of the International Conference on Spatial Information Theory, Morro Bay, CA, USA, 19–23 September 2001; Montello, D.R., Ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Bennett, B. Application of Supervaluation Semantics to Vaguely Defined Spatial Concepts. In Proceedings of the International Conference on Spatial Information Theory, Morro Bay, CA, USA, 19–23 September 2001; Montello, D.R., Ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Rodrigues, E.J.; Santos, P.E.; Lopes, M.; Bennett, B.; Oppenheimer, P.E. Standpoint semantics for polysemy in spatial prepositions. J. Log. Comput. 2020, 30, 635–661. [Google Scholar] [CrossRef]
- Santos, P.; Bennett, B.; Sakellariou, G. Supervaluation semantics for an inland water feature ontology. In Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence, Edinburgh, UK, 30 July–5 August 2005. [Google Scholar]
- Bolotin, A. Quantum Supervaluationism. J. Math. Phys. 2017, 58, 122106. [Google Scholar] [CrossRef]
- Bell, S. Spatial cognition and scale: A child’s perspective. J. Environ. Psychol. 2002, 22, 9–27. [Google Scholar] [CrossRef]
- Lei, L.; Lin, C. A Modal Supervaluation Description Logic for Characterization of Vague Concepts: Its semantics and a tableau algorithm for it. Log. J. IGPL 2006, 14, 873–888. [Google Scholar]
- Rohrs, B. Supervaluational propositional content. Synthese 2016, 194, 2185–2201. [Google Scholar] [CrossRef]
- Bencivenga, E. Supervaluations and theories. Grazer Philos. Stud. 1984, 21, 89–98. [Google Scholar]
- Minock, M.J. Vague Relations in Spatial Databases. In Proceedings of the International Conference on Application of Natural Language to Information Systems, Cardiff, UK, 23–25 June 2010. [Google Scholar]
- Straccia, U. Towards spatial reasoning in fuzzy description logics. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju, Korea, 20–24 August 2009; pp. 512–517. [Google Scholar] [CrossRef] [Green Version]
- Edoh-Alove, E.; Bimonte, S.; Pinet, F.; Bédard, Y. Exploiting Spatial Vagueness in Spatial OLAP: Towards a New Hybrid Risk-Aware Design Approach. In Proceedings of the 16th AGILE International Conference on Geographic Information Science, Leuven, Belgium, 14–17 May 2013. [Google Scholar]
- Dilo, A.; de By, R.A.; Stein, A. Metrics for vague spatial objects based on the concept of mass. In Proceedings of the 2007 IEEE International Fuzzy Systems Conference, London, UK, 23–26 July 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Cheng, T.; Fisher, P.; Li, Z. Double Vagueness: Effect of Scale on the Modelling of Fuzzy Spatial Objects. In Developments in Spatial Data Handling; Fisher, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 1, pp. 299–313. [Google Scholar]
- Xu, J.; Pan, X. A Fuzzy Spatial Region Extraction Model for Object’s Vague Location Description from Observer Perspective. ISPRS Int. J. Geo-Inf. 2020, 9, 703. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, H.; Wang, C.; Hou, Z.; Zheng, Z.; Shen, S.; Cheng, Q.; Feng, Z.; Wang, X.; Lv, H.; et al. Geoscience knowledge graph in the big data era. Sci. China Earth Sci. 2021, 64, 1105–1114. [Google Scholar] [CrossRef]






| Type | Description | Advantage | Disadvantage | |
|---|---|---|---|---|
| Two-valued logic method | Cone-shaped model | The reference object is replaced by the reference object’s center of mass, and the plane space is divided into four directions of east, south, west, and north around the center of mass of the reference object. | The model is simple, and the regions are clearly divided. | Inability to handle entanglement, intersection, horseshoe shape, etc., sometimes leads to misjudgment. |
| Triangular model | The expansion of the four-direction cone-shaped model and the eight-direction cone-shaped model. | The triangular model takes into account the influence of the shape and size of the space target on the spatial relationship to a certain extent. | When the distance of the space target is far, the ability to distinguish the directional relationship is weak. | |
| Minimum bounding rectangle model | The projections of the two targets on the X and Y axes are used to establish the smallest rectangle to approximate the direction relation of the original target. It is an extended model of the triangular model. | Taking into account the shape and size of spatial entities, with the help of the reflexivity of the semantics of orientation relations. | The use of semantic reflexivity to accurately describe the positional relationship has limitations, and it cannot be described formally and judged effectively. | |
| 4-intersection model (4IM) | Based on the point set topology, it is defined by the intersection of the boundary and the inner point set, and divided according to its content. | Because it only uses the “empty” and “non-empty” of point set intersection to distinguish the relation, the method is simple. | There are many cases that are clearly distinguishable by people, but the model is powerless. | |
| 9-intersection model (9IM) | Introduce the “complement” of the point set and construct a 9-intersection spatial relationship model consisting of the boundary, the interior, and the complementary point set. | The 9-intersection model improves the 4-intersection model and enhances the uniqueness of the plane-line and line-line spatial relationships. | There is not much improvement in the representation of the spatial relationship of plane-plane, point-point, point-line, and point-plane. | |
| 9-intersection model based on dimension extension | Use dimension expansion method to expand 9IM. The dimensionality of the intersection between the boundary, interior and complement of the point, line, and plane is used as the framework for the description of the spatial relationship. | It is helpful to classify various spatial topological relations more accurately. | The operation complexity of the model is high. | |
| 9-intersection model based on Voronoi graph | The Voronoi region is used to replace the “complement” of the spatial target in the 9IM, and a nine tuples model of spatial relationships based on Voronoi is developed. | It can distinguish the neighboring and separated relationships of spatial objects, avoiding the difficulty of calculating the external relationships of spatial objects. | The operation complexity of the model is high. | |
| Fuzzy logic method | Cognitive experiment | A group of people were selected to judge the vagueness of the objects studied in the form of questionnaires. | The combination of geography and psychology embodies the subjectivity of vagueness factor. | The cost of collecting experimental data is high, and the reliability of sample group affects the accuracy of results. |
| Knowledge base | The spatial relationship between the observer and the object is represented by spatial knowledge, and the mapping relationship between “phrases” and “regions” is established. | Summarize and analyze the experience of experts in the field and existing research results to form a spatial knowledge base. | The type and breadth of spatial knowledge involved in the knowledge base are limited. | |
| Geographic information retrieval | Through the analysis of the geographic content contained in the web page, the scope of a vague entity can be determined. | There is no need to conduct a large-scale questionnaire survey, and it is more convenient for the membership function of multiple geographic elements. | The selected search concept is prone to have the characteristics of population density or other tendencies, and the experimental results are prone to bias. | |
| Remote sensing image classification | Ground feature classification method based on remote sensing image. | The modeling process is clear. | It is only applicable to geographical elements that can be distinguished by remote sensing, and the accuracy of the vague range is directly restricted by the classification accuracy. | |
| Other method | Point-radius method | A point and a circle with a certain radius around the point to describe the location. | The model is simple and convenient for data storage. | the coordinates of all objects are represented by points, the actual shape and size of the objects are not considered. |
| Egg-folk model | Based on the minimum and maximum range to describe the uncertain region of the geographic entity. | Supports some explanations of important inferences involving the relationship between vague spatial scopes. | It is unable to deal with the complex constraints that a region may expand between its maximum and minimum values, and it is difficult to reflect the actual spatial distribution of objects. | |
| Spatial clustering method | Clustering fuzzy place-name data, and the range of convex hull of the cluster with the most points is the approximate space range of the fuzzy place names. | No assumptions are attached to the data distribution, and the characteristics of the distribution range of spatial data are studied from the data sample itself. | The choice of spatial clustering algorithm is critical to the vague range result. | |
| Factor | Asserted? | Context Semantics | Observations | Threshold Range |
|---|---|---|---|---|
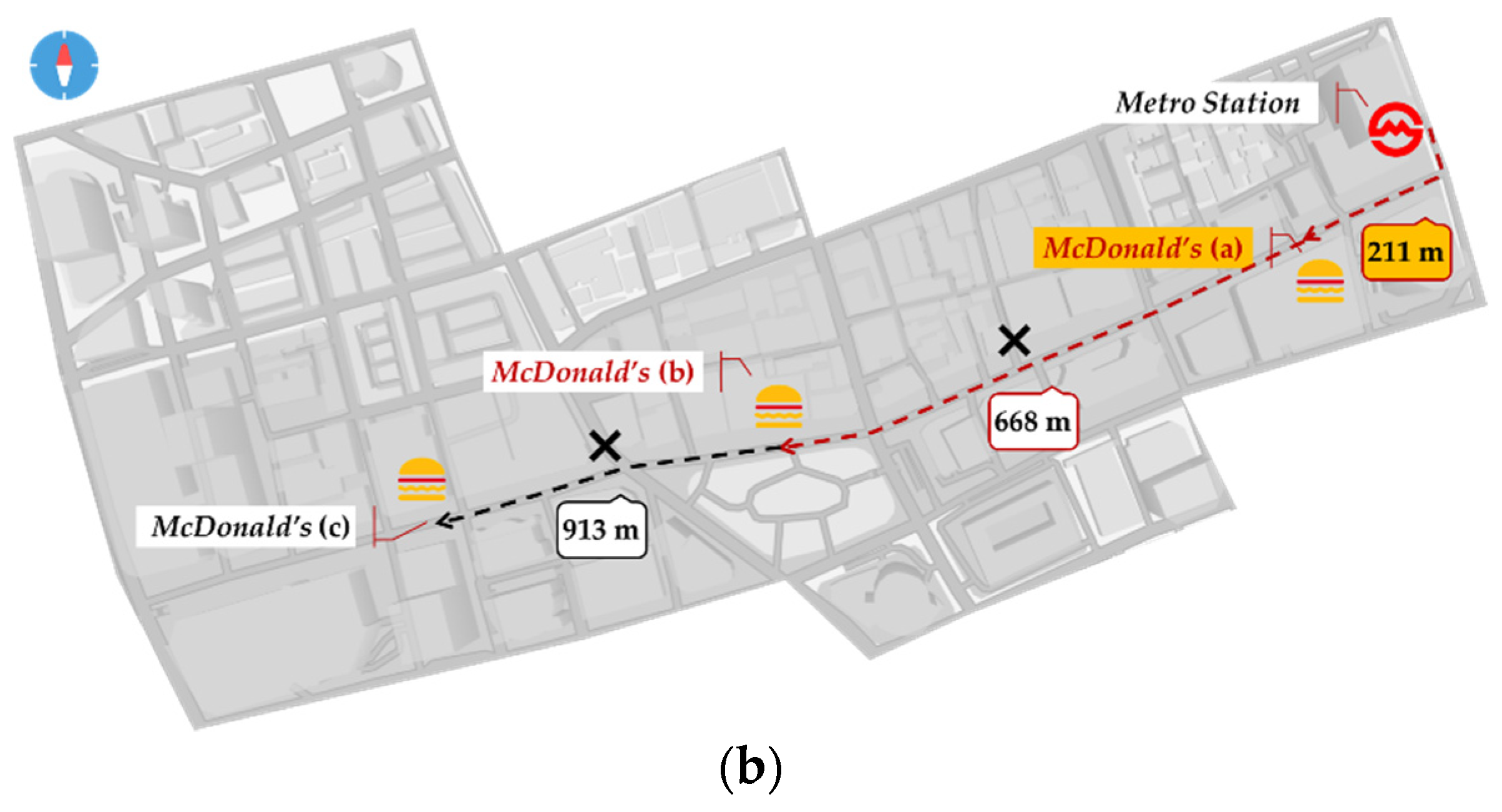
| Movement mode | Yes | Walk, ≤10min | 300 m | ①300 × 1.0 × 1.0 = 300, the range is [0, 300 m] ②300 × 0.8 × 1.0 = 240, the range is [0, 240 m] ③780 × 1.0 × 1.0 = 780, the range is [0, 780 m] ④780 × 0.8 × 1.0 = 624, the range is [0, 624 m] |
| Bike, ≤5min | 780 m | |||
| Terrain environment | No | - | - | |
| Accessibility | Yes | High road | ×1.0 | |
| Auxiliary road | ×0.8 | |||
| Weather condition | Yes | Sunny | ×1.0 | |
| Modifiers | No | - | - |
| Type | Factor | Asserted? | Context Semantics | Observations | Threshold Range |
|---|---|---|---|---|---|
| Distance relation | Movement mode | Yes | Walk, ≤10min | 300 m | [0, 300 m] |
| Terrain environment | No | - | - | ||
| Accessibility | Yes | Road | ×1.0 | ||
| Weather condition | No | Sunny | ×1.0 | ||
| Modifiers | No | - | - | ||
| Direction relation | Cognitive dimensions | Yes | East, 4 dimensions | [−45°, 45°) | [−45°, 45°) |
| Distance | Yes | Near | ×1.0 | ||
| Modifiers | No | - | - |
| Type | Factor | Asserted? | Context Semantics | Observations | Threshold Range |
|---|---|---|---|---|---|
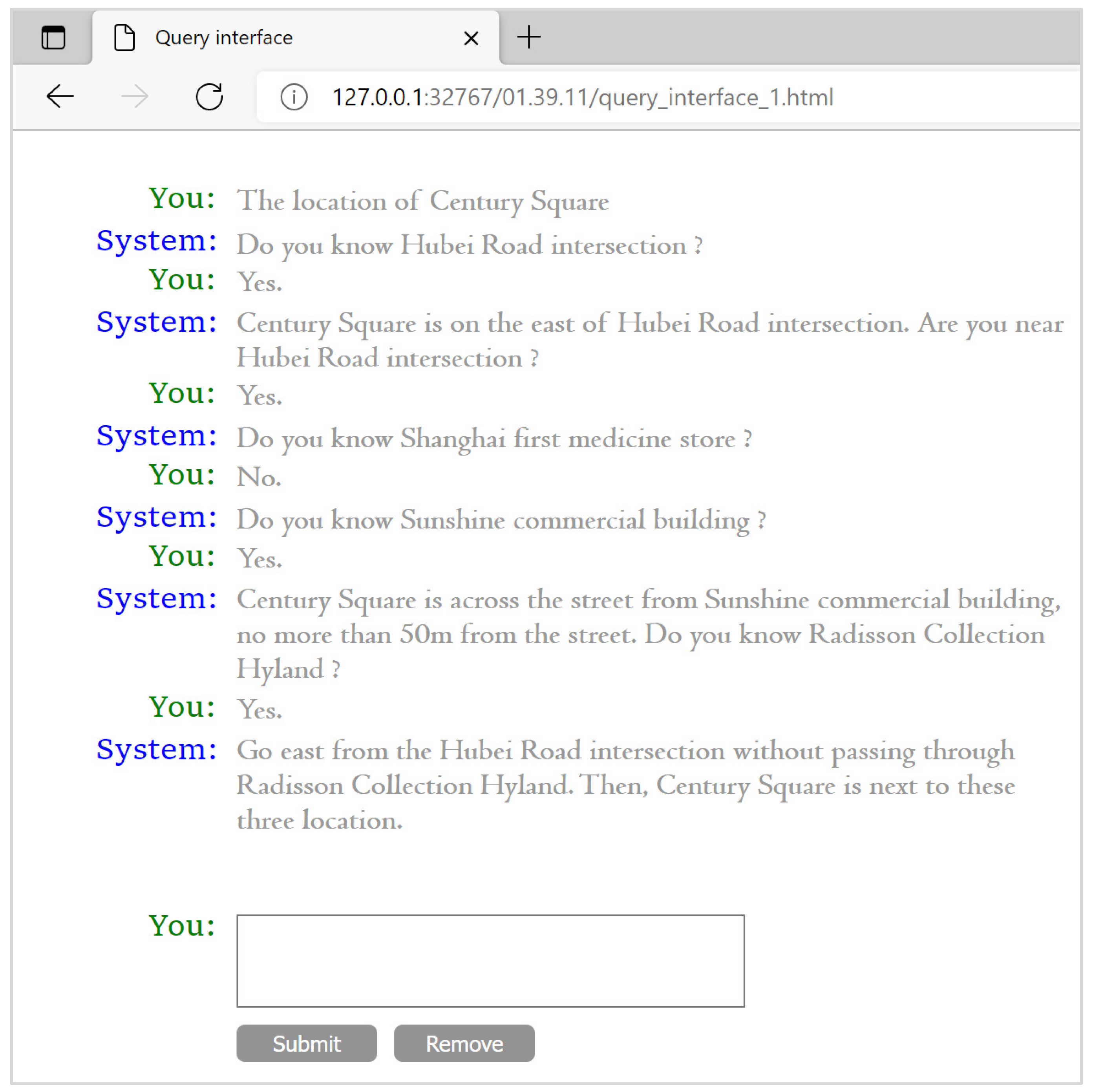
| Distance relation | Movement mode | Yes | Stand | [0, 50 m] | [0, 50 m] |
| Terrain environment | No | - | - | ||
| Accessibility | Yes | Road | ×1.0 | ||
| Weather condition | No | - | - | ||
| Modifiers | No | - | - | ||
| Direction relation | Cognitive dimensions | Yes | One side, 2 dimensions | 1 1 | 1 1 |
| Distance | Yes | Near | ×1.0 | ||
| Modifiers | Yes | Opposite | - |
| Type | Factor | Asserted? | Context semantics | Observations | Threshold Range |
|---|---|---|---|---|---|
| Direction relation | Cognitive dimensions | Yes | West, 4 dimensions | [135°, 225°) | [135°, 225°) |
| Distance | No | - | - | ||
| Modifiers | No | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, P.; Zhang, X.; Zhang, C.; Dang, Y. Positioning Localities for Vague Spatial Location Description: A Supervaluation Semantics Approach. ISPRS Int. J. Geo-Inf. 2022, 11, 68. https://doi.org/10.3390/ijgi11010068
Ye P, Zhang X, Zhang C, Dang Y. Positioning Localities for Vague Spatial Location Description: A Supervaluation Semantics Approach. ISPRS International Journal of Geo-Information. 2022; 11(1):68. https://doi.org/10.3390/ijgi11010068
Chicago/Turabian StyleYe, Peng, Xueying Zhang, Chunju Zhang, and Yulong Dang. 2022. "Positioning Localities for Vague Spatial Location Description: A Supervaluation Semantics Approach" ISPRS International Journal of Geo-Information 11, no. 1: 68. https://doi.org/10.3390/ijgi11010068
APA StyleYe, P., Zhang, X., Zhang, C., & Dang, Y. (2022). Positioning Localities for Vague Spatial Location Description: A Supervaluation Semantics Approach. ISPRS International Journal of Geo-Information, 11(1), 68. https://doi.org/10.3390/ijgi11010068







