Multifractal Correlation between Terrain and River Network Structure in the Yellow River Basin, China
Abstract
:1. Introduction
2. Materials and Methods
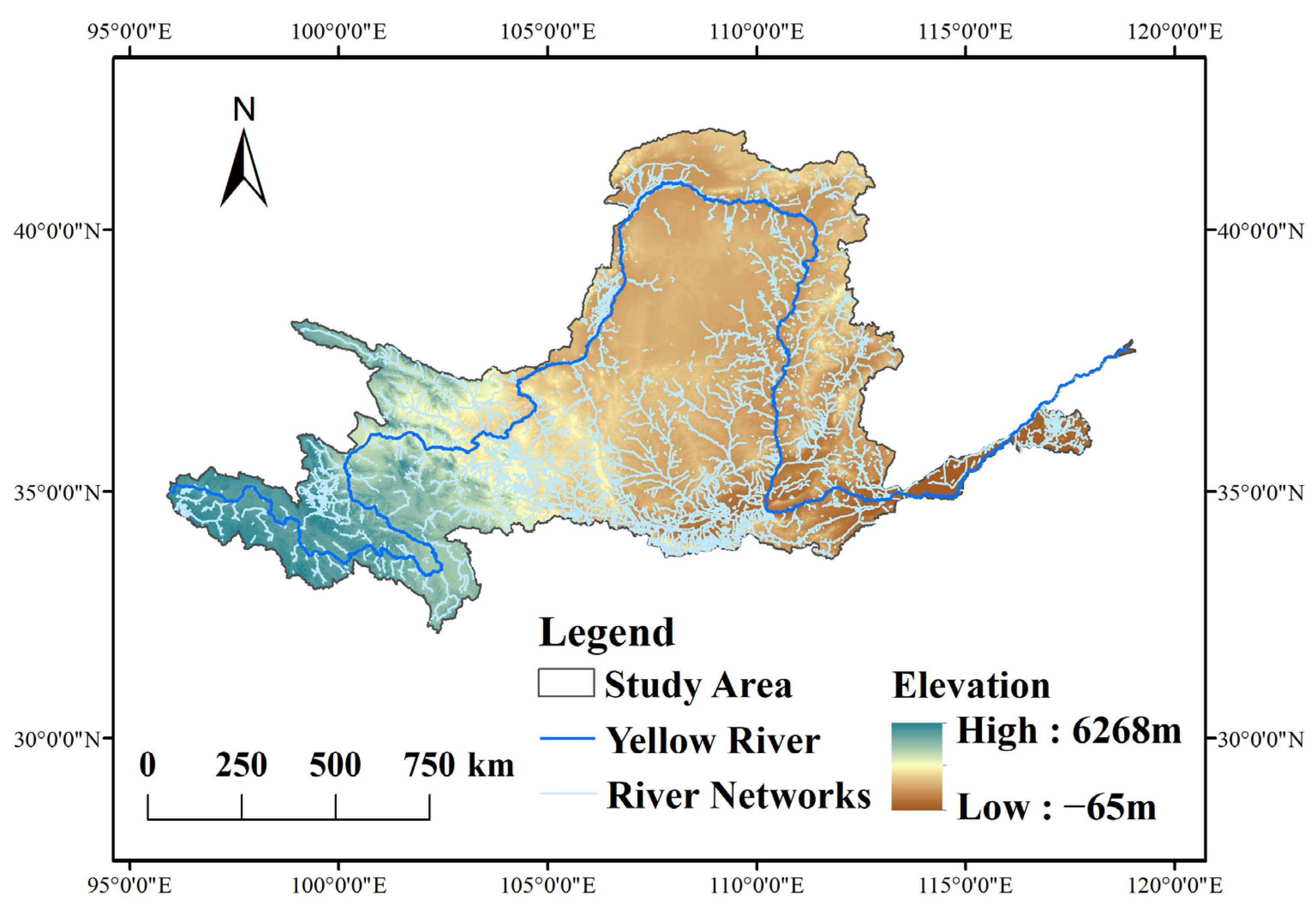
2.1. Study Area
2.2. Data Description
2.3. Method
2.3.1. Multifractal Analysis
2.3.2. The Geographical Detectors
2.3.3. Geographically Weighted Regression
3. Results
3.1. Multifractal Analysis
3.2. Geographical Detection Analysis and Influence of Topography on the River Network
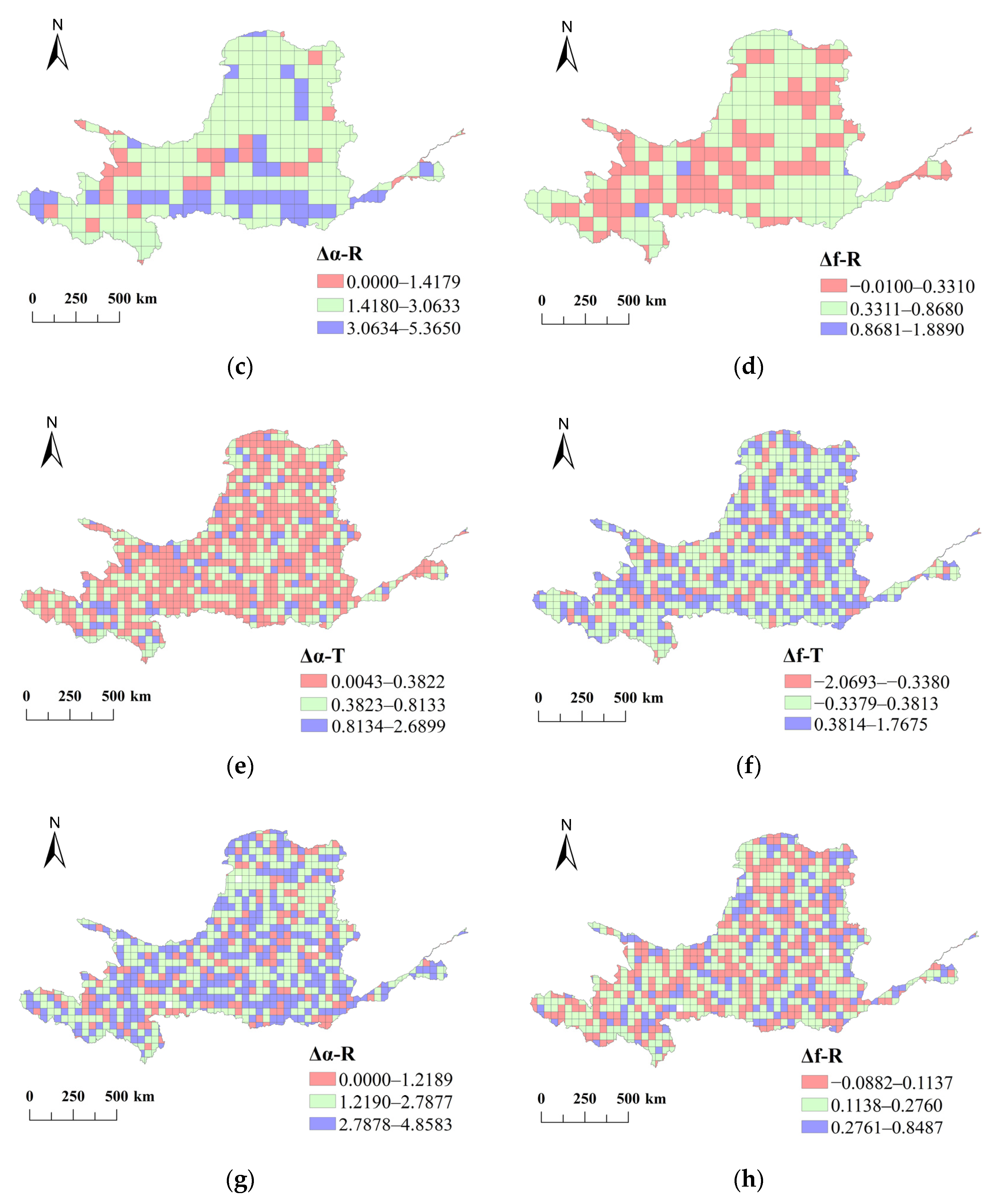
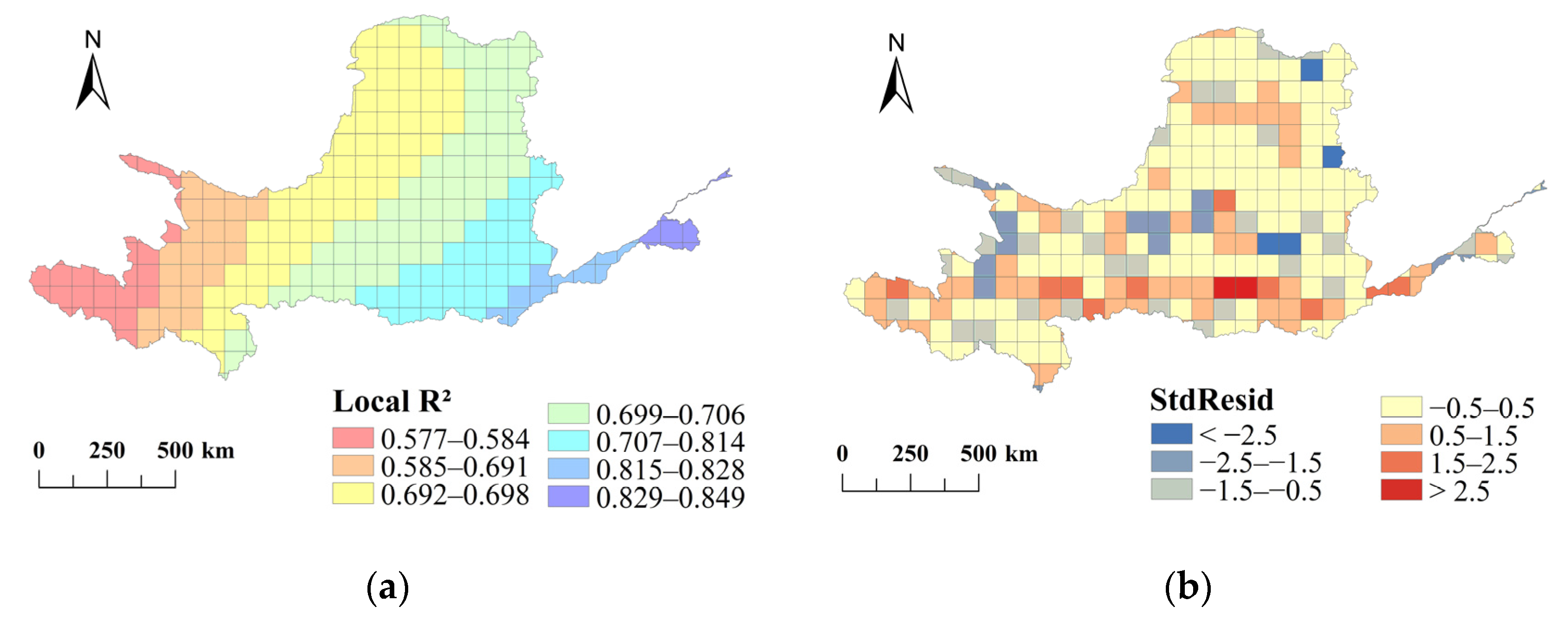
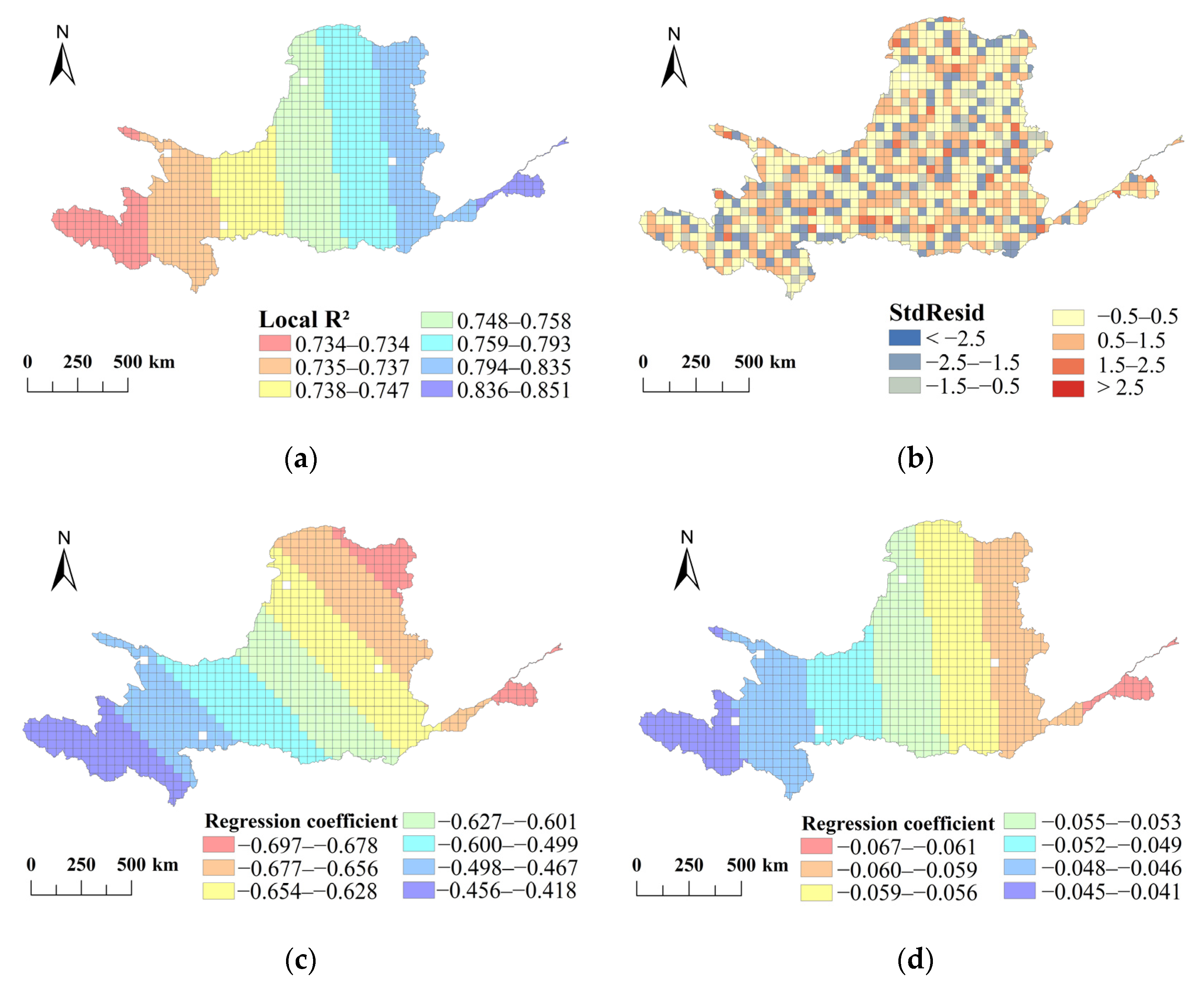
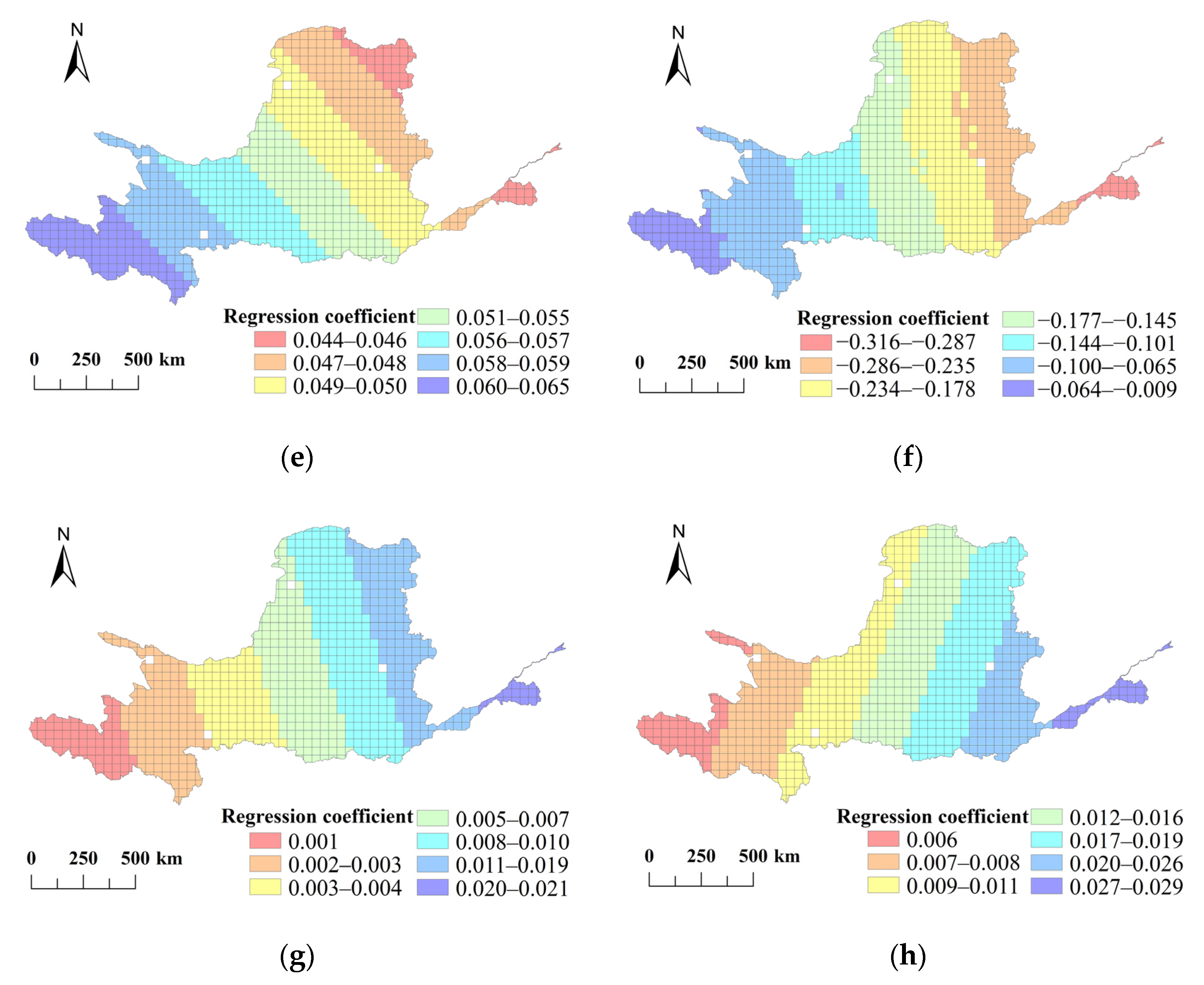
3.3. Correlation between Topography and River Network Structure
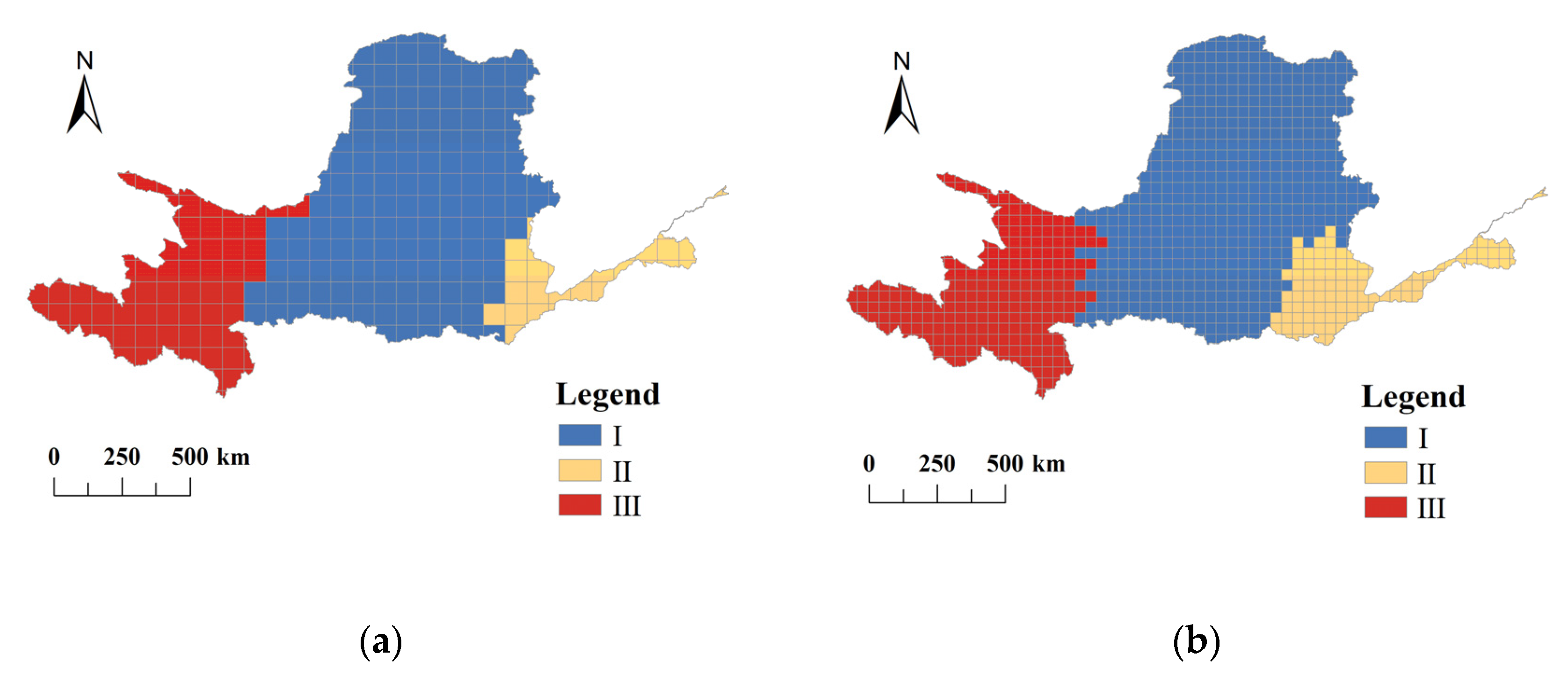
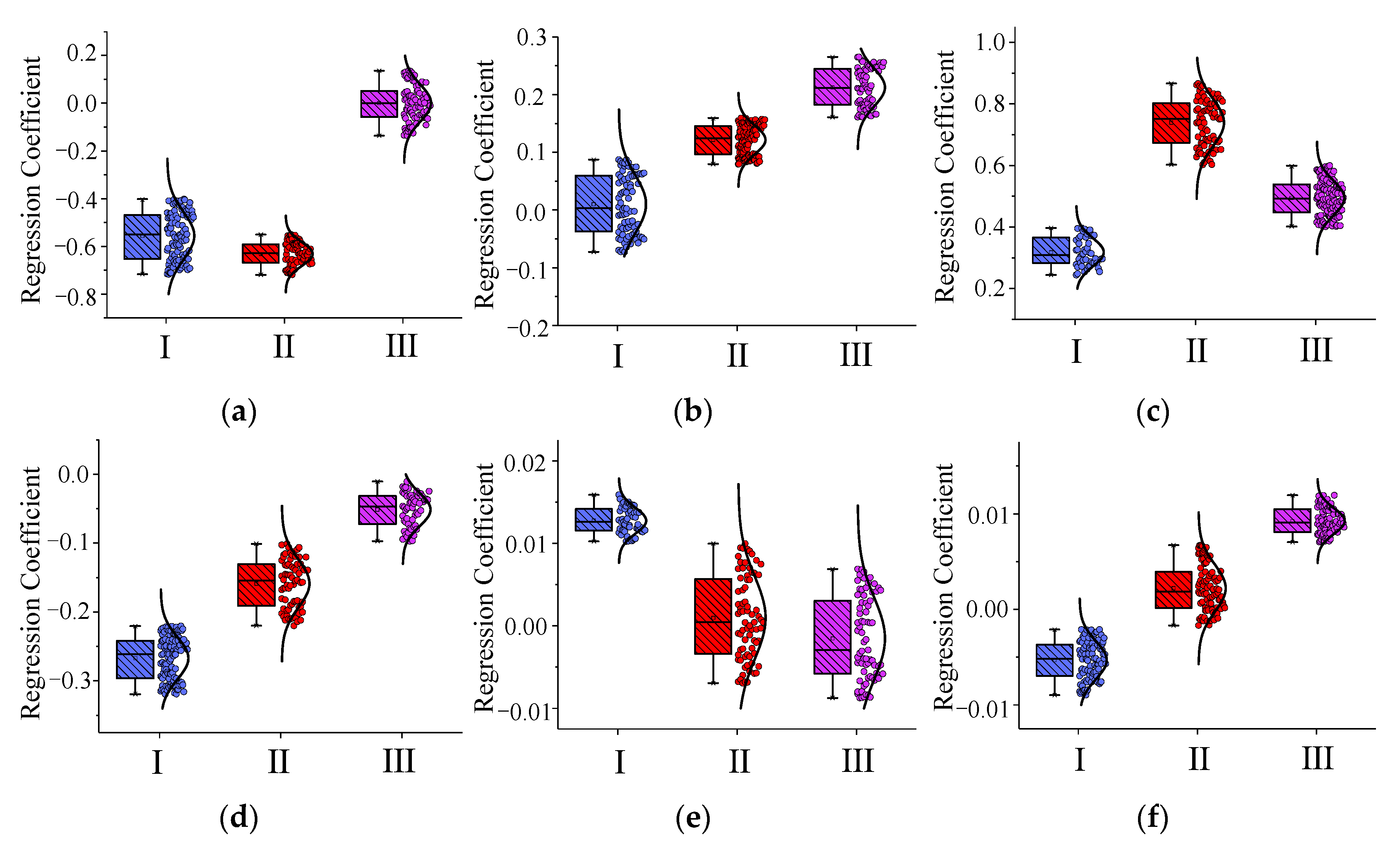
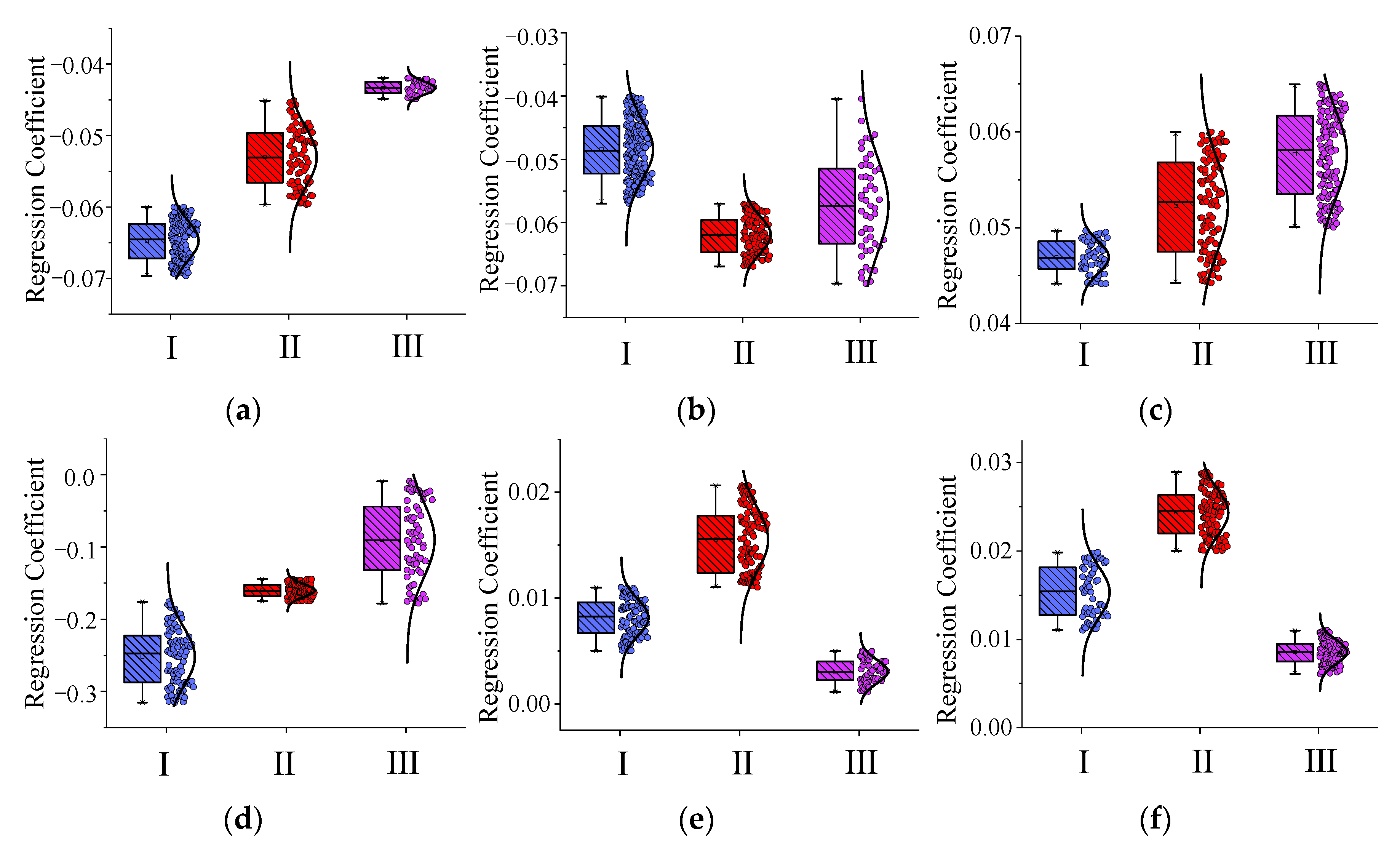
3.4. Cluster Analysis of Geographically Weighted Regression Coefficients
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi-Bin, M.A.; Yu-Lun, A.N. Auto-classification of Landform in Karst Region Based on ASTER GDEM. Sci. Geogr. Sin. 2012, 32, 368–373. [Google Scholar]
- Tang, G. Progress of DEM and digital terrain analysis in china. Acta Geogr. Sin. 2014, 69, 1305–1325. [Google Scholar]
- Meng, X.; Zhang, P.; Li, J.; Ma, C.; Liu, D. The linkage between box-counting and geomorphic fractal dimensions in the fractal structure of river networks: The junction angle. Hydrol. Res. 2020, 51, 1397–1408. [Google Scholar] [CrossRef]
- Czuba, J.A.; Foufoula-Georgiou, E.; Gran, K.B.; Belmont, P.; Wilcock, P.R. Interplay between spatially explicit sediment sourcing, hierarchical river-network structure, and in-channel bed material sediment transport and storage dynamics. J. Geophys. Res. Earth Surf. 2017, 122, 1090–1120. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Zabalza-Martínez, J.; Borràs, G.; López-Moreno, J.; Pla, E.; Pascual, D.; Savé, R.; Biel, C.; Funes, I.; Azorin-Molina, C. Extreme hydrological events and the influence of reservoirs in a highly regulated river basin of northeastern Spain. J. Hydrol. Reg. Stud. 2017, 12, 13–32. [Google Scholar] [CrossRef]
- Fox, C.A. River Basin Development. Int. Encycl. Hum. Geogr. (2nd Ed.) 2020, 90, 1–8. [Google Scholar] [CrossRef]
- Fotherby, L.M. Valley confinement as a factor of braided river pattern for the Platte River. Geomorphology 2009, 103, 562–576. [Google Scholar] [CrossRef]
- Wu, S.; Li, J.; Huang, G.H. A study on DEM-derived primary topographic attributes for hydrologic applications: Sensitivity to elevation data resolution. Appl. Geogr. 2008, 28, 210–223. [Google Scholar] [CrossRef]
- Shi, W.Z.; Wang, B.; Yan, T. Accuracy Analysis of Digital Elevation Model Relating to Spatial Resolution and Terrain Slope by Bilinear Interpolation. Math. Geosci. 2014, 46, 445–481. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Analysis of errors of derived slope and aspect related to DEM data properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Liu, B.Y.; Nearing, M.A.; Risse, L.M. Slope Length Effects on Soil Loss for Steep Slopes. Soil Sci. Soc. Am. J. 2000, 64, 1759–1763. [Google Scholar] [CrossRef] [Green Version]
- Liu, P. Influence of Relief Degree of Land Surface on Street Network Complexity in China. ISPRS Int. J. Geo-Inf. 2021, 10, 705. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mukherjee, S.; Garg, R.D.; Bhardwaj, A.; Raju, P.L.N. Evaluation of topographic index in relation to terrain roughness and DEM grid spacing. J. Earth Syst. Sci. 2013, 122, 869–886. [Google Scholar] [CrossRef] [Green Version]
- Luo, M.; Xu, Y.; Mu, K.; Wang, R.; Yang, P. Spatial variation of the hypsometric integral and the implications for local base levels in the Yanhe River, China. Arab. J. Geosci. 2018, 11, 366. [Google Scholar] [CrossRef]
- Horton, R.E. Drainage-basin characteristics. Eos Trans. Am. Geophys. Union 1932, 13, 350–361. [Google Scholar] [CrossRef]
- Schneider, A.; Jost, A.; Coulon, C.; Silvestre, M.; Théry, S.; Ducharne, A. Global-scale river network extraction based on high-resolution topography and constrained by lithology, climate, slope, and observed drainage density. Geophys. Res. Lett. 2017, 44, 2773–2781. [Google Scholar] [CrossRef] [Green Version]
- Tucker, G.E.; Catani, F.; Rinaldo, A.; Bras, R.L. Statistical analysis of drainage density from digital terrain data. Geomorphology 2001, 36, 187–202. [Google Scholar] [CrossRef]
- Perron, J.T.; Richardson, P.W.; Ferrier, K.L.; Laptre, M. The root of branching river networks. Nature 2012, 492, 100–103. [Google Scholar] [CrossRef]
- Chen, X.B.; Wang, Y.C.; Jinren, N.I. Structural characteristics of river networks and their relations to basin factors in the Yangtze and Yellow River basins. Sci. China Tech. Sci. 2019, 62, 11. [Google Scholar] [CrossRef]
- Zhou, F.; Huihua, L.; Liu, C. Change of river system in the Lixiahe region during urbanization. South-North Water Transf. Water Sci. Technol. 2018, 16, 118–126. [Google Scholar]
- Liu, Z.; Han, L.; Du, C.; Cao, H.; Wang, H. Fractal and Multifractal Characteristics of Lineaments in the Qianhe Graben and Its Tectonic Significance Using Remote Sensing Images. Remote Sens. 2021, 13, 587. [Google Scholar] [CrossRef]
- Krupiński, M.; Wawrzaszek, A.; Drzewiecki, W.; Jenerowicz, M.; Aleksandrowicz, S. What Can Multifractal Analysis Tell Us about Hyperspectral Imagery? Remote Sens. 2020, 12, 4077. [Google Scholar] [CrossRef]
- Qin, Z.L.; Wang, J.X.; Lu, Y. Multifractal Characteristics Analysis Based on Slope Distribution Probability in the Yellow River Basin, China. ISPRS Int. J. Geo-Inf. 2021, 10, 337. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bartolo, S.; Veltri, M.; Primavera, L. Estimated generalized dimensions of river networks. J. Hydrol. 2006, 322, 181–191. [Google Scholar] [CrossRef]
- Bartolo, S.D.; Gabriele, S.; Gaudio, R. Multifractal behaviour of river networks. Hydrol. Earth Syst. Sci. 2000, 4, 105–112. [Google Scholar] [CrossRef] [Green Version]
- Parisi, G.; Frisch, U. On the singularity structure of fully developed turbulence in Turbulence and predictability in geophysical fluid dynamics and climate dynamics. Am. J. Theol. Philos. 1985, 88, 71–88. [Google Scholar]
- Benzi, R.; Paladin, G.; Parisi, G.; Vulpiani, A. On the multifractal nature of fully developed turbulence and chaotic systems. J. Phys. A Gen. Phys. 1999, 17, 3521–3531. [Google Scholar] [CrossRef]
- Xu, S.; Yu, Z.; Yang, C.; Ji, X.; Ke, Z. Trends in evapotranspiration and their responses to climate change and vegetation greening over the upper reaches of the Yellow River Basin. Agric. For. Meteorol. 2018, 263, 118–129. [Google Scholar] [CrossRef]
- Ge, Q.; Xu, W.; Fu, M.; Han, Y.; An, G.; Xu, Y. Ecosystem service values of gardens in the Yellow River Basin, China. J. Arid. Land 2022, 14, 284–296. [Google Scholar] [CrossRef]
- Seo, Y.; Schmidt, A.R.; Kang, B. Multifractal properties of the peak flow distribution on stochastic drainage networks. Stoch. Environ. Res. Risk Assess. 2014, 28, 1157–1165. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Zhan-Bin, L.I.; Peng, L.I.; Ke-Xin, L.U. Multifractal arithmethic for watershed topographic feature. Adv. Water Sci. 2009, 20, 385–391. [Google Scholar] [CrossRef]
- Aharony, A. Measuring multifractals. Phys. D Nonlinear Phenom. 1989, 38, 1–4. [Google Scholar] [CrossRef]
- Rolph, S. Fractal Geometry: Mathematical Foundations and Applications. Math. Gaz. 1990, 74, 288–317. [Google Scholar]
- Halsey, T.; Jensen, M.; Kadanoff, L.; Procaccia, I.; Shraiman, B. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A Third 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Gaudio, R.; Bartolo, S.; Primavera, L.; Veltri, M.; Gabriele, S. Procedures in multifractal analysis of river networks: A state of the art review. Water Energy Abstr. 2005, 15, 5. [Google Scholar]
- Wawrzaszek, A.; Echim, M.; Bruno, R. Multifractal Analysis of Heliospheric Magnetic Field Fluctuations observed by Ulysses. Astrophys. J. 2019, 876, 153. [Google Scholar] [CrossRef] [Green Version]
- Wawrzaszek, A.; Echim, M.; Macek, W.M.; Bruno, R. Evolution of Intermittency in the Slow and Fast Solar Wind Beyond the Ecliptic Plane. Astrophys. J. 2016, 814, L19. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Qin, Z.; Shi, Y.; Yao, J. Multifractal Analysis of River Networks under the Background of Urbanization in the Yellow River Basin, China. Water 2021, 13, 2347. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Christakos, G.; Liao, Y.; Zhang, T.; Gu, X.; Zheng, X. Geographical Detectors-Based Health Risk Assessment and its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Wang, J.F.; Zhang, T.L.; Fu, B.J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically Weighted Regression. J. R. Stat. Soc. Ser. D 2017, 47, 431–443. [Google Scholar] [CrossRef]
- Xiong, Y.; Li, Y.; Xiong, S.; Wu, G.; Deng, O. Multi-scale spatial correlation between vegetation index and terrain attributes in a small watershed of the upper Minjiang River. Ecol. Indic. 2021, 126, 107610. [Google Scholar] [CrossRef]
- Akaike, H.T. A new look at the statistical model identification. Autom. Control IEEE Trans. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Tu, J. Spatially varying relationships between land use and water quality across an urbanization gradient explored by geographically weighted regression. Appl. Geogr. 2011, 31, 376–392. [Google Scholar] [CrossRef]
- Pike, R.J.; Evans, I.S.; Hengl, T. Geomorphometry: A Brief Guide. Dev. Soil Sci. 2009, 33, 3–30. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale Analysis of Topographic Surface Roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1200–1213. [Google Scholar] [CrossRef]


| Range | Total Number | Category | The Range of q Value | The Range of Boxes Size e |
|---|---|---|---|---|
| Yellow River Basin | 1 | Topography | [−30, 30], | [30 m, 40,000 m], |
| River Network | [−21, 21], | [30 m, 40,000 m], | ||
| 80 km × 80 km grids | 262 | Topography | [−30, 30], | [30 m, 20,000 m], |
| River Network | [−15, 15], | [30 m, 20,000 m], | ||
| 40 km × 40 km grids | 893 | Topography | [−45, 45], | [30 m, 20,000 m], |
| River Network | [−25, 25], | [30 m, 20,000 m], |
| Dimension | Name | Symbol | Unit | Description |
|---|---|---|---|---|
| Multifractal characteristics | The width of the multifractal spectrum | — | It is used to represent the degree of inhomogeneity, irregularity, and complexity of the terrain in the study area. | |
| The difference of the multifractal spectrum | — | It is used to reflect the difference of quantity distribution of the maximum- and minimum-probability subsets of the watershed characteristic information. | ||
| Capacity dimension | — | It is equivalent to the box fractal dimension, reflecting the complexity of the research object. | ||
| Information dimension | — | It adds coverage probability on the basis of the capacity dimension. | ||
| Correlation dimension | — | It is used to reflect the degree of connection between subjects. | ||
| Topographic relief factors | Average elevation | H | Meter (m) | It represents the average elevation of the region and reflects the overall elevation of the region. It is calculated using a DEM with a resolution of 30 m. |
| Maximum elevation | Meter (m) | It represents the maximum elevation of the region and reflects the overall elevation of the region. It is calculated using a DEM with a resolution of 30 m. | ||
| Minimum elevation | Meter (m) | It represents the minimum elevation of the region and reflects the overall elevation of the region. It is calculated using a DEM with a resolution of 30 m. | ||
| Topographic relief | Meter (m) | It represents the difference between the maximum and minimum values of regional elevation and reflects the relief of regional terrain. It is calculated using a DEM with resolution of 30 m. | ||
| Topographic roughness | R | — | It represents the roughness of the terrain [47]. It is calculated using a DEM with resolution of 30 m. | |
| Slope factors | slope | S | Degree (°) | It represents the average slope of the region. It is calculated using a DEM with a resolution of 30 m. |
| Slope aspect | SA | Degree (°) | It represents the average slope aspect of the region. It is calculated using a DEM with a resolution of 30 m. | |
| Slope length | SL | Meter (m) | It represents the average slope length of the region. It is calculated using a DEM with a resolution of 30 m. |
| Dimension | Explanatory Variable Name | 40 km × 40 km Grids | 80 km × 80 km Grids | ||||
|---|---|---|---|---|---|---|---|
| Significance Level | q Value | Rank | Significance Level | q Value | Rank | ||
| Multifractal characteristics | The width of the multifractal spectrum | 0.01 | 0.501 | 1 | 0.01 | 0.407 | 1 |
| The difference of the multifractal spectrum | 0.01 | 0.265 | 2 | 0.01 | 0.217 | 2 | |
| Capacity dimension | ― | 0.263 | ― | ― | 0.205 | ― | |
| Information dimension | ― | 0.125 | ― | ― | 0.135 | ― | |
| Correlation dimension | ― | 0.002 | ― | ― | 0.039 | ― | |
| Topographic relief factors | Average elevation | 0.01 | 0.133 | 4 | 0.01 | 0.108 | 4 |
| Maximum elevation | 0.01 | 0.124 | 5 | 0.01 | 0.101 | 5 | |
| Minimum elevation | 0.05 | 0.113 | 6 | 0.1 | 0.098 | 6 | |
| Topographic relief | ― | 0.050 | ― | ― | 0.037 | ― | |
| Topographic roughness | ― | 0.024 | ― | ― | 0.057 | ― | |
| Slope factors | slope | 0.01 | 0.245 | 3 | 0.01 | 0.199 | 3 |
| Slope aspect | ― | 0.087 | ― | ― | 0.018 | ― | |
| Slope length | ― | 0.046 | ― | ― | 0.079 | ― | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Z.; Wang, J. Multifractal Correlation between Terrain and River Network Structure in the Yellow River Basin, China. ISPRS Int. J. Geo-Inf. 2022, 11, 519. https://doi.org/10.3390/ijgi11100519
Qin Z, Wang J. Multifractal Correlation between Terrain and River Network Structure in the Yellow River Basin, China. ISPRS International Journal of Geo-Information. 2022; 11(10):519. https://doi.org/10.3390/ijgi11100519
Chicago/Turabian StyleQin, Zilong, and Jinxin Wang. 2022. "Multifractal Correlation between Terrain and River Network Structure in the Yellow River Basin, China" ISPRS International Journal of Geo-Information 11, no. 10: 519. https://doi.org/10.3390/ijgi11100519
APA StyleQin, Z., & Wang, J. (2022). Multifractal Correlation between Terrain and River Network Structure in the Yellow River Basin, China. ISPRS International Journal of Geo-Information, 11(10), 519. https://doi.org/10.3390/ijgi11100519





