Figure 1.
The first level hexagonal and pentagonal cells on the icosahedron.
Figure 1.
The first level hexagonal and pentagonal cells on the icosahedron.
Figure 2.
Different grid division rules. (a) Diamond hierarchical subdivision; (b) Triangular hierarchical subdivision; (c) Hexagonal hierarchical subdivision.
Figure 2.
Different grid division rules. (a) Diamond hierarchical subdivision; (b) Triangular hierarchical subdivision; (c) Hexagonal hierarchical subdivision.
Figure 3.
Different spherical grids. (a) diamond grid; (b) triangular grid; and (c) hexagonal grid.
Figure 3.
Different spherical grids. (a) diamond grid; (b) triangular grid; and (c) hexagonal grid.
Figure 4.
Basic diamond code on icosahedron.
Figure 4.
Basic diamond code on icosahedron.
Figure 5.
Second level Z-curve of different grids in a basic diamond plane. (a) Hexagon Z-curve; (b) diamond Z-curve; (c) triangle Z-curve.
Figure 5.
Second level Z-curve of different grids in a basic diamond plane. (a) Hexagon Z-curve; (b) diamond Z-curve; (c) triangle Z-curve.
Figure 6.
The process of converting DHC code to DZC code of the second level. (a) Second level DHC code; (b) Second level Hilbert curve; (c) 1-order Hilbert recursive curve; (d) Second level Z-curve; (e) Second level DZC code.
Figure 6.
The process of converting DHC code to DZC code of the second level. (a) Second level DHC code; (b) Second level Hilbert curve; (c) 1-order Hilbert recursive curve; (d) Second level Z-curve; (e) Second level DZC code.
Figure 7.
Corresponding relationship between hexagon grid and triangle grid.
Figure 7.
Corresponding relationship between hexagon grid and triangle grid.
Figure 8.
Icosahedral hexagonal cell type.
Figure 8.
Icosahedral hexagonal cell type.
Figure 9.
Triangle selection rules of HtoTcode for spatial discrete line and surface data. (a) Edge adjacency; (b) Corner adjacency and the (n − 1)th triangle is a lower triangle; and (c) Corner adjacency and the (n − 1)th triangle is an upper triangle.
Figure 9.
Triangle selection rules of HtoTcode for spatial discrete line and surface data. (a) Edge adjacency; (b) Corner adjacency and the (n − 1)th triangle is a lower triangle; and (c) Corner adjacency and the (n − 1)th triangle is an upper triangle.
Figure 10.
Corresponding relationship of different cells. (a) Corresponding relationship between hexagon grid and diamond grid; (b) Corresponding relationship between triangle grid and diamond grid.
Figure 10.
Corresponding relationship of different cells. (a) Corresponding relationship between hexagon grid and diamond grid; (b) Corresponding relationship between triangle grid and diamond grid.
Figure 11.
Efficiency comparison diagram between GtoG and longitude–latitude method expressing discrete lines. (a) Efficiency comparison curve between HtoTcode and longitude–latitude method, and (b) Efficiency comparison curve between TtoDcode and longitude–latitude method.
Figure 11.
Efficiency comparison diagram between GtoG and longitude–latitude method expressing discrete lines. (a) Efficiency comparison curve between HtoTcode and longitude–latitude method, and (b) Efficiency comparison curve between TtoDcode and longitude–latitude method.
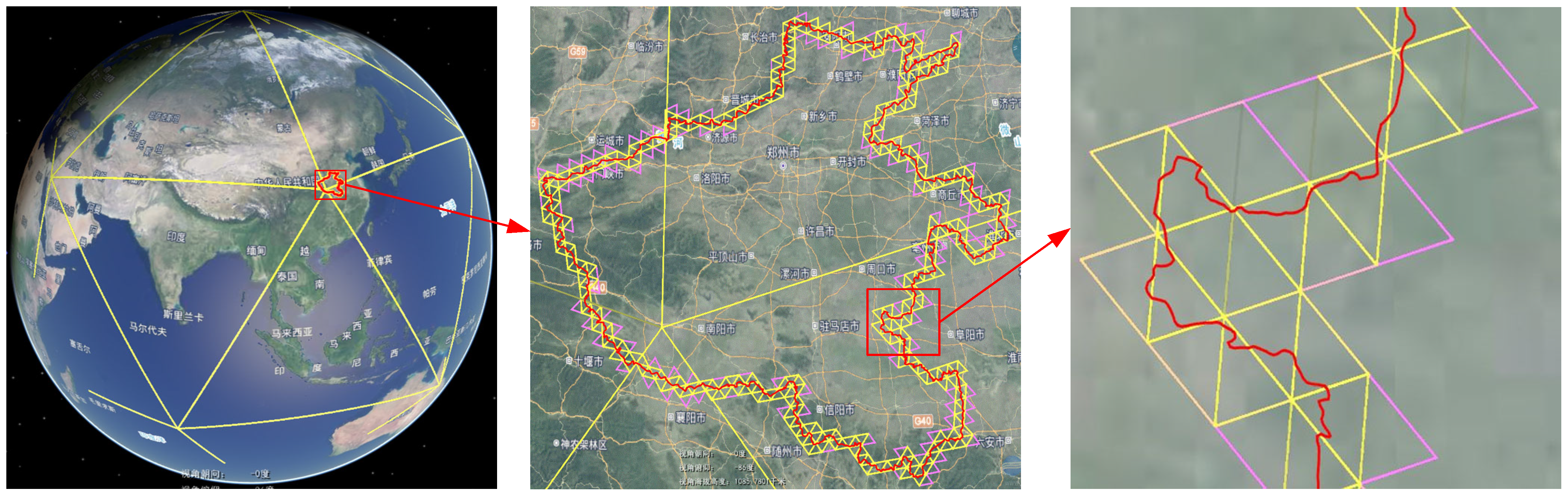
Figure 12.
The ninth level HtoTcode discrete line.
Figure 12.
The ninth level HtoTcode discrete line.
Figure 13.
The ninth level TtoDcode discrete line.
Figure 13.
The ninth level TtoDcode discrete line.
Figure 14.
The different grid codes of the sixth, seventh and eighth levels of Globeland30 land coverage data in Henan Province before and after HtoTcode conversion. (a) The sixth level hexagonal grid code of land coverage data in Henan Province, (b) The sixth level HtoTcode triangle grid code of land coverage data in Henan Province, (c) The seventh level hexagonal grid code of land coverage data in Henan Province, (d) The seventh level Htotcode triangle grid code of land coverage data in Henan Province, (e) The eighth level hexagonal grid code of land coverage data in Henan Province, (f) The eighth level Htotcode triangle grid code of land coverage data in Henan Province.
Figure 14.
The different grid codes of the sixth, seventh and eighth levels of Globeland30 land coverage data in Henan Province before and after HtoTcode conversion. (a) The sixth level hexagonal grid code of land coverage data in Henan Province, (b) The sixth level HtoTcode triangle grid code of land coverage data in Henan Province, (c) The seventh level hexagonal grid code of land coverage data in Henan Province, (d) The seventh level Htotcode triangle grid code of land coverage data in Henan Province, (e) The eighth level hexagonal grid code of land coverage data in Henan Province, (f) The eighth level Htotcode triangle grid code of land coverage data in Henan Province.
Figure 15.
The different grid codes of the sixth, seventh and eighth levels of Globeland30 land coverage data in Henan Province before and after TtoDcode conversion. (a) The sixth level triangle grid code of land coverage data in Henan Province, (b) The sixth level TtoDcode diamond grid code of land coverage data in Henan Province, (c)The seventh level triangle grid code of land coverage data in Henan Province, (d) The seventh level TtoDcode diamond grid code of land coverage data in Henan Province, (e) The eighth level triangle grid code of land coverage data in Henan Province, (f) The eighth level TtoDcode diamond grid code of land coverage data in Henan Province.
Figure 15.
The different grid codes of the sixth, seventh and eighth levels of Globeland30 land coverage data in Henan Province before and after TtoDcode conversion. (a) The sixth level triangle grid code of land coverage data in Henan Province, (b) The sixth level TtoDcode diamond grid code of land coverage data in Henan Province, (c)The seventh level triangle grid code of land coverage data in Henan Province, (d) The seventh level TtoDcode diamond grid code of land coverage data in Henan Province, (e) The eighth level triangle grid code of land coverage data in Henan Province, (f) The eighth level TtoDcode diamond grid code of land coverage data in Henan Province.
Figure 16.
Comparison diagram of the ninth level triangle discrete lines of HtoTcode and longitude–latitude. (a) The ninth level triangle discrete lines of longitude–latitude; (b) the ninth level triangle discrete lines of longitude–latitude; (c) the ninth level discrete lines superposition of longitude–latitude and HtoTcode.
Figure 16.
Comparison diagram of the ninth level triangle discrete lines of HtoTcode and longitude–latitude. (a) The ninth level triangle discrete lines of longitude–latitude; (b) the ninth level triangle discrete lines of longitude–latitude; (c) the ninth level discrete lines superposition of longitude–latitude and HtoTcode.
Figure 17.
Comparison diagram of the ninth level diamond discrete lines of TtoDcode and longitude–latitude. (a) The ninth level diamond discrete lines of longitude–latitude; (b) the ninth level diamond discrete lines of TtoDcode; (c) the ninth level discrete lines superposition of longitude–latitude and TtoDcode.
Figure 17.
Comparison diagram of the ninth level diamond discrete lines of TtoDcode and longitude–latitude. (a) The ninth level diamond discrete lines of longitude–latitude; (b) the ninth level diamond discrete lines of TtoDcode; (c) the ninth level discrete lines superposition of longitude–latitude and TtoDcode.
Figure 18.
Hexagonal grid to triangular grid. (a) Hexagonal grid cells; (b) Triangles obtained by decomposing hexagons; (c) Coordinate systems for triangular and hexagonal grids, xt and yt are triangular grid coordinate systems, xh and yh are hexagonal coordinate systems.
Figure 18.
Hexagonal grid to triangular grid. (a) Hexagonal grid cells; (b) Triangles obtained by decomposing hexagons; (c) Coordinate systems for triangular and hexagonal grids, xt and yt are triangular grid coordinate systems, xh and yh are hexagonal coordinate systems.
Figure 19.
Triangular grid to hexagonal grid. (a) Triangular grid, its origin and coordinate system; (b) Vectors chosen to aggregate a hexagonal cell in triangular grid; (c) There are three possibilities to choose the origin of the aggregation conversion illustrated by salmon, green and blue points.
Figure 19.
Triangular grid to hexagonal grid. (a) Triangular grid, its origin and coordinate system; (b) Vectors chosen to aggregate a hexagonal cell in triangular grid; (c) There are three possibilities to choose the origin of the aggregation conversion illustrated by salmon, green and blue points.
Figure 20.
Hexagonal grids with different subdivision structures. (a) Aperture 4 hexagonal grid; (b) Aperture 7 hexagonal grid; (c) Aperture 3 hexagonal grid.
Figure 20.
Hexagonal grids with different subdivision structures. (a) Aperture 4 hexagonal grid; (b) Aperture 7 hexagonal grid; (c) Aperture 3 hexagonal grid.
Figure 21.
Correspondence between hexagonal grids and triangular grids.
Figure 21.
Correspondence between hexagonal grids and triangular grids.
Figure 22.
Octahedral planar expansion and hexagonal cell classification. (a) Basic diamond code of octahedron; (b) Octahedral hexagonal cell type.
Figure 22.
Octahedral planar expansion and hexagonal cell classification. (a) Basic diamond code of octahedron; (b) Octahedral hexagonal cell type.
Table 1.
Discrete global grid subdivision and index structure.
Table 1.
Discrete global grid subdivision and index structure.
| Author | Subdivision Method | Index Structure |
|---|
| Dutton, G.H. [19] | Triangular grid of regular octahedral | Hierarchy code |
| White, D. [20] | Diamond grids of regular icosahedral and octahedral | Morton code |
| Bartholdi, J.J. [21] | Triangular grid of polyhedron | Space filling curve |
| Górski, K.M., et al. [22] | 1:4 subdivided HEALPix grid of diamond dodecahedron | Hierarchy code |
| Sahr, K. [23] | Aperture 3 hexagonal grid of regular icosahedral | MGBT hierarchy code |
| Xuesheng Zhao et al. [24] | Variable longitude–latitude DQG grid | Degenerate quadtree code |
| Vince, A. et al. [25] | Aperture 3 hexagonal grid of regular icosahedral | PYXIS hierarchy code |
| Ali Mahdavi Amiri [26] | 1-to-2 refinement squares grid of cube | Hierarchy code and coordinate code |
| Gibb, R.G. [27] | 1:9 subdivided rHEALPix grid of cube | Z-curve |
| Veach, E. et al. [28] | Aperture 4 square grid of cube | Hilbert curve |
| Uber Technologies [29] | Aperture 7 hexagonal tessellation of
the icosahedron | Hierarchy code |
| Bingxian Lin et al. [30] | Regular icosahedral triangular grid | Z-curve |
| Jin Ben et al. [31] | Regular icosahedral aperture 3 hexagonal grid | Hierarchy code |
| Sahr, K. [32] | Regular icosahedral mixed aperture hexagonal grid | Hierarchical linear index code |
| Hall, J. et al. [33] | Aperture 4 triangular grid of triacontahedron | Z-curve |
| Rui Wang et al. [34] | Regular icosahedral mixed aperture 3 and 4 hexagonal grid | Hierarchy code |
Table 2.
GtoG mapping rule index table corresponding to hexagonal cell type.
Table 2.
GtoG mapping rule index table corresponding to hexagonal cell type.
Table 3.
Htotcode rule of the (n − 1)th hexagon cell A.
Table 3.
Htotcode rule of the (n − 1)th hexagon cell A.
| Hn−1 and Hn Coordinate Relationship | Tdn−1 | Triangle Cells Selected |
|---|
| and | – | and |
| and | – | and |
| and | – | and |
| and | – | and |
| and | 0 | and |
| and | 1 | and |
| and | 0 | and |
| and | 1 | and |
Table 4.
Htotcode rule of the (n − 1)th hexagon cell B1.
Table 4.
Htotcode rule of the (n − 1)th hexagon cell B1.
| HDn−1 | HDn | Hn−1 and Hn Coordinate Relationship | Tdn−1 | Triangle Cells Selected |
|---|
| | | – | and |
| 0 | and |
| 1 | and |
| | | – | and |
| 0 | and |
| 1 | and |
| | | – | , and |
| – | and |
| | | – | , and |
| – | and |
Table 5.
Htotcode rule of the (n − 1)th hexagon cell B2.
Table 5.
Htotcode rule of the (n − 1)th hexagon cell B2.
| HDn−1 | HDn | Hn−1 and Hn Coordinate Relationship | Tdn−1 | Triangle Cells Selected |
|---|
| | | – | and |
| 1 | and |
| 0 | and |
| | | – | and |
| – | , and |
| | | – | and |
| – | , and |
Table 6.
Htotcode rule of the (n − 1)th hexagon cell B3.
Table 6.
Htotcode rule of the (n − 1)th hexagon cell B3.
| HDn−1 | HDn | Hn−1 and Hn Coordinate Relationship | Tdn−1 | Triangle Cells Selected |
|---|
| | | – | , and |
| – | and |
| | | – | , and |
| – | and |
| | | – | and |
| 1 | and |
| 0 | and |
| | | – | and |
| 1 | and |
| 0 | and |
Table 7.
Htotcode rule of the (n − 1)th hexagon cell B4.
Table 7.
Htotcode rule of the (n − 1)th hexagon cell B4.
| HDn−1 | HDn | Hn−1 and Hn Coordinate Relationship | Tdn−1 | Triangle Cells Selected |
|---|
| | | – | , and |
| – | and |
| | | – | , and |
| – | and |
| | | – | and |
| 1 | and |
| 0 | and |
Table 8.
Htotcode rule of the (n − 1)th hexagon cell C1.
Table 8.
Htotcode rule of the (n − 1)th hexagon cell C1.
| HDn−1 | HDn | Hn−1 and Hn Coordinate Relationship | Tdn−1 | Triangle Cells Selected |
|---|
| | | – | and |
| 0 | and |
| 1 | and |
| | – | and |
| 0 | and |
| 1 | and |
| | | – | and |
| 0 | and |
| 1 | and |
| | – | and |
| 0 | and |
| 1 | and |
| | – | – | and |
| | – | , and |
| – | and |
| | – | – | and |
| | – | , and |
| – | and |
| | – | – | and |
| | – | , and |
| – | and |
Table 9.
Htotcode rule of the (n − 1)th hexagon cell C1 and the nth hexagon cell E2.
Table 9.
Htotcode rule of the (n − 1)th hexagon cell C1 and the nth hexagon cell E2.
| HDn−1 | HDn | HDn+1 | Triangle Cells Selected |
|---|
| | | and |
| , and |
| , and |
| and |
| | | , and |
| , and |
| and |
| and |
| | | , and |
| and |
| and |
| , and |
| | | and |
| and |
| , and |
| , and |
| | | and |
| , and |
| , and |
| and |
Table 10.
Htotcode rule of the (n − 1)th hexagon cell C2.
Table 10.
Htotcode rule of the (n − 1)th hexagon cell C2.
| HDn−1 | HDn | Hn−1 and Hn Coordinate Relationship | Triangle cells selected |
|---|
| | – | and |
| | , and |
| and |
| | | , and |
| and |
| – | and |
| | | , and |
| and |
| – | and |
| | | , and |
| and |
| – | and |
Table 11.
Htotcode rule of the (n − 1)th hexagon cell C3.
Table 11.
Htotcode rule of the (n − 1)th hexagon cell C3.
| HDn−1 | HDn | Hn−1 and Hn Coordinate Relationship | Tdn−1 | Triangle Cells Selected |
|---|
| | | – | , and |
| – | and |
| – | – | and |
| | – | – | and |
| | – | , and |
| – | and |
| | – | – | and |
| | – | , and |
| – | and |
| | | – | and |
| 0 | and |
| 1 | and |
| | – | and |
| 1 | and |
| 0 | and |
| | | – | and |
| 0 | and |
| 1 | and |
| | – | and |
| 1 | and |
| 0 | and |
Table 12.
Htotcode rule of the (n − 1)th hexagon cell C3 and the nth hexagon cell E1.
Table 12.
Htotcode rule of the (n − 1)th hexagon cell C3 and the nth hexagon cell E1.
| HDn−1 | HDn | HDn+1 | Triangle Cells Selected |
|---|
| | | and |
| , and |
| , and |
| and |
| | | and |
| and |
| , and |
| , and |
| | | , and |
| and |
| and |
| , and |
| | | , and |
| , and |
| and |
| and |
| | | and |
| , and |
| , and |
| and |
Table 13.
Htotcode rule of the (n − 1)th hexagon cell E1.
Table 13.
Htotcode rule of the (n − 1)th hexagon cell E1.
| HDn−1 | HDn | HDn−2 | Triangle Cells Selected |
|---|
| | | and |
| , and |
| , and |
| and |
| | and |
| and |
| , and |
| , and |
| | , and |
| and |
| and |
| , and |
| | , and |
| , and |
| and |
| and |
| | and |
| , and |
| , and |
| and |
Table 14.
Htotcode rule of the (n − 1)th hexagon cell E2.
Table 14.
Htotcode rule of the (n − 1)th hexagon cell E2.
| HDn−1 | HDn | HDn−2 | Triangle Cells Selected |
|---|
| | | and |
| , and |
| , and |
| and |
| | and |
| and |
| , and |
| , and |
| | , and |
| and |
| and |
| , and |
| | , and |
| , and |
| and |
| and |
| | and |
| , and |
| , and |
| and |
Table 15.
Htotcode rule of the (n − 1)th hexagon cell E3.
Table 15.
Htotcode rule of the (n − 1)th hexagon cell E3.
| HDn−1 | HDn | Triangle Cells Selected |
|---|
| | and |
| and |
| | and |
| and |
| | and |
| and |
| | and |
| and |
Table 16.
Comparison of efficiency and accuracy of HtoTcode and longitude–latitude expressing discrete points.
Table 16.
Comparison of efficiency and accuracy of HtoTcode and longitude–latitude expressing discrete points.
| Points | HtoTcode Efficiency (ms) | Longitude-Latitude Efficiency (ms) | Efficiency Ratio | Maximum Distance Difference Between Center Points (m) | Average Diameter of 20 Level Hexagonal Cells (m) | Length Ratio |
|---|
| 104 | 0.041 | 153 | 3731 | 4.90734 | 7.68543 | 0.639 |
| 105 | 0.408 | 1561 | 3825 | 4.90734 | 7.68543 | 0.639 |
| 106 | 4 | 17,518 | 4379 | 4.90734 | 7.68543 | 0.639 |
| 107 | 41 | 497,062 | 12,123 | 4.90734 | 7.68543 | 0.639 |
Table 17.
Comparison of efficiency and accuracy of TtoDcode and longitude–latitude expressing discrete points.
Table 17.
Comparison of efficiency and accuracy of TtoDcode and longitude–latitude expressing discrete points.
| Points | TtoDcode Efficiency (ms) | Longitude–latitude Efficiency (ms) | Efficiency Ratio | Maximum Distance difference Between Center Points (m) | Average Diameter of 20 Level Hexagonal Cells (m) | Length Ratio |
|---|
| 104 | 0.04 | 153 | 3825 | 2.45551 | 5.43442 | 0.452 |
| 105 | 0.4 | 1544 | 3860 | 2.45551 | 5.43442 | 0.452 |
| 106 | 4 | 17,197 | 4299 | 2.45551 | 5.43442 | 0.452 |
| 107 | 43 | 492,169 | 11,445 | 2.45551 | 5.43442 | 0.452 |
Table 18.
Comparison of efficiency and accuracy of HtoTcode and longitude–latitude expressing discrete lines.
Table 18.
Comparison of efficiency and accuracy of HtoTcode and longitude–latitude expressing discrete lines.
| Level | HtoTcode
Efficiency (ms) | Longitude–Latitude (ms) | Efficiency Ratio | Maximum Distance Difference between Center Points (m) | Average Diameter of Hexagonal Cells (m) | Length Ratio |
|---|
| 17 | 69 | 10,769 | 156 | 38.9844 | 61.48344 | 0.634 |
| 18 | 121 | 14,544 | 120 | 19.4925 | 30.74172 | 0.634 |
| 19 | 241 | 23,058 | 95 | 9.7465 | 15.37086 | 0.634 |
| 20 | 476 | 43,368 | 91 | 4.87417 | 7.68543 | 0.634 |
| 21 | 900 | 105,699 | 117 | 2.43893 | 3.842715 | 0.635 |
| 22 | 2312 | 306,969 | 132 | 1.22316 | 1.921358 | 0.637 |
Table 19.
Comparison of efficiency and accuracy of TtoDcode and longitude–latitude expressing discrete lines.
Table 19.
Comparison of efficiency and accuracy of TtoDcode and longitude–latitude expressing discrete lines.
| Level | TtoDcode Efficiency (ms) | Longitude–Latitude (ms) | Efficiency Ratio | Maximum Distance Difference between Center Points (m) | Average Diameter of Triangular Cells (m) | Length Ratio |
|---|
| 17 | 6 | 11,202 | 1867 | 31.9519 | 43.4754 | 0.735 |
| 18 | 12 | 15,065 | 1255 | 15.9762 | 21.7377 | 0.735 |
| 19 | 22 | 24,251 | 1102 | 7.98812 | 10.8688 | 0.735 |
| 20 | 43 | 46,911 | 1090 | 3.99632 | 5.43442 | 0.735 |
| 21 | 80 | 114,516 | 1431 | 2.00041 | 2.71721 | 0.736 |
| 22 | 168 | 339,406 | 2020 | 1.0047 | 1.3586 | 0.740 |
Table 20.
Comparison of efficiency and accuracy of HtoTcode and longitude–latitude expressing discrete area.
Table 20.
Comparison of efficiency and accuracy of HtoTcode and longitude–latitude expressing discrete area.
| Level | HtoTcode
Efficiency (ms) | Longitude–Latitude
Efficiency (ms) | Efficiency Ratio | Number of Hexagonal Cells | Number of Triangle Cells | Relative Area
Deviation |
|---|
| 11 | 3 | 108,748 | 36,249 | 14,124 | 27,910 | 0.012305 |
| 12 | 17 | 418,611 | 24,624 | 55,507 | 110,340 | 0.006138 |
| 13 | 63 | 1,652,347 | 26,227 | 219,917 | 438,486 | 0.003066 |
| 14 | 297 | 6,632,788 | 22,332 | 875,486 | 1,748,282 | 0.001533 |
Table 21.
Comparison of efficiency and accuracy of TtoDcode and longitude–latitude expressing discrete area.
Table 21.
Comparison of efficiency and accuracy of TtoDcode and longitude–latitude expressing discrete area.
| Level | TtoDcode Efficiency (ms) | Longitude–Latitude
Efficiency (ms) | Efficiency Ratio | Number of Triangle Cells | Number of Diamond Cells | Relative Area
Deviation |
|---|
| 10 | 0.09 | 27,313 | 303,478 | 7225 | 3677 | 0.017854 |
| 11 | 0.32 | 106,014 | 331,294 | 28,072 | 14,165 | 0.009191 |
| 12 | 1 | 419,343 | 419,343 | 110,719 | 55,632 | 0.004922 |
| 13 | 5 | 1,719,359 | 343,871 | 439,279 | 220,202 | 0.002561 |
Table 22.
HtoTcode rule of the (n − 1)th hexagon cell C1 and the nth hexagon cell E2.
Table 22.
HtoTcode rule of the (n − 1)th hexagon cell C1 and the nth hexagon cell E2.
| HDn−1 | HDn | Triangle Cells Selected |
|---|
| | and |