Optimizing the Spatial Location of Street Lights in Belle Isle, Michigan

Abstract

Improved street lighting can provide better use of public space and helps to promote safety while driving or walking. In terms of balancing benefits and impacts, on the basis of cost saving, this research adopts two prominent mathematical models, the maximal coverage location problem and the location set covering problem, to optimize street light locations. By comparing with the currently installed lights following the rule of thumb, the mathematical models in this research achieve the effect of saving electric energy while meeting residents’ traffic safety needs and living conditions. Furthermore, the models can provide greater coverage of illumination using the same amount of energy.

1. Introduction

Street lighting, being one of the important uses of artificial lighting, dramatically influences our living environment in many facets. There are profound perceived benefits for human well-being that are provided by street lighting, such as increasing opportunities for economically productive activity, energy-saving activity, and social interaction activity [1,2,3,4]. For instance, street lighting reduces time consumption for work and social activities, facilitates leisure and recreational activities, reduces crime and vehicle accident rates, etc. [5,6,7]. Of course, some negative impacts are also associated with street lighting, such as altering and reshaping the ecosystem, energy consumption, emission and pollution generation, and physiological disruptions. Therefore, the design process of street lighting is a crucial precondition in evaluating the above-mentioned impacts. The variables of the street lighting design process consist of lamp output in lumens, luminaire optics, height and spacing of the lamp post, risk of gare, type of road surface, spatial requirements of locating street lights, etc. Accordingly, the use of scientific methods (i.e., maximal coverage location and location set covering) to optimize street light location by considering a mixed combination of parameters is extremely valuable to electric energy saving, residents’ traffic safety, living conditions, etc. In this paper, we mainly focus on the investigation of spatial constraints for lamp post position, together with crash risk, pedestrian hindrance, and maintenance access, as our key factors to balance the benefits and costs of street lighting as a public service [8,9,10,11,12].

Street lighting plays an indispensable role in supporting economic, social, and environmental activities. Incorporating geographical information systems (GIS) with street lighting coverage applied in community safety planning activities has effectively eliminated the probability for criminal behavior and reduced the fear of crime [13,14,15,16]. In addition, lamp spot coverage and design material of lighting are also undeniable factors that impact pedestrians’ and drivers’ visual ability to prevent road accidents [17].

Bullough et al. (2013) combined visual coverage area analysis with a statistical association between lighting and nighttime crashes and demonstrated an improvement in traffic safety where changes in the night to day crash ratio did not exceed 13% [18]. Moreover, street lighting enhances neighborhood cohesiveness, community activity, and sociocultural lives [19].

The costs of street lighting are also more severe through inefficient planning and monitoring. The International Dark-Sky Association (IDSA) claims that 15 million tons of CO₂ are emitted each year to power residential outdoor lighting in the U.S., and 30% of outdoor lighting in the U.S. alone is wasted, costing USD 3.3 billion [20]. Climate Week NYC, an annual event that has taken place every year since 2009 to bring international leaders from business, government, and civil society to showcase global climate action, has called on every single city and utility around the world to switch their street lighting to LED to reduce energy consumption and emission pollution. For animals and other natural creatures, the impact of artificial lighting has been potentially linked to adverse changes in migration patterns, reproduction, and communication [21]. In this sense, the spatial efficiency of street light location planning is both an effective means and a compelling need for scholars to investigate the balance between the benefits and potential costs of the street lighting problem.

Little research has been conducted on the street lighting location problem. Up to now, only a few research papers have focused on the street lighting location problem [22,23,24]. In general, location analysis has been widely studied in the fields of geography and operations research/management science (OR/MS). Location analysis has evolved over time with the power of mathematical models since the classic seminal work of Weber (1990). Interested readers may refer to several detailed reviews of facility location models over the decades [25,26,27,28].

Based on the space of location decisions, location models can often be classified into two categories: continuous-space models in the plane and discrete-space models on a network. In a continuous space, a location is presented by two coordinates, which can be defined as decision variables for a mathematical model. However, due to the form of calculating travel distance between two locations, a continuous-space model is often nonlinear, which makes the problem very hard to solve. Therefore, most location models in OR/MS for real-world applications are formulated based on a network, which consists of nodes and arcs. Normally, a node represents a demand area and/or a candidate site for locating a facility, while an arc represents the route between two nodes. Travel distance, time, or cost may be associated with each arc. Mathematically, the location decision at each candidate node can be defined as a binary decision variable for a mathematical model. Note that one necessary task before building such a model is to find a finite set of candidate locations.

The first location problem on a network using a mathematical programming model was known as the p-median problem [29], which was to find the optimal locations of p facilities on a network to minimize the demand weighted average distance between demand nodes and the nearest of the selected facilities. Since then, numerous mathematical programming models for a variety of location problems have been proposed. One of the most popular location models on a network is the covering problem, which has a large number of applications in the real world, such as locating schools, police stations, fire stations, ambulance stations, hospitals, post offices, bank branches, etc. [30]. One fundamental requirement for covering problems is that a demand node must be served by at least one facility within a given distance threshold.

Among covering problems, two particular types have received massive attention due to their wide applicability: the maximal coverage location problem (MCLP) [25,31,32,33,34] and the location set covering problem (LSCP) [29,35,36]. The MCLP aims to locate a fixed number of facilities to maximize the total covered demand, while the objective of the LSCP is to locate a minimum number of servers so that each demand node must be covered. We note that both the MCLP and LSCP can be applied to the street lighting location problem that we investigate in this paper.

More recently, increasing attention has been drawn to analyzing location problems using GIS in both geography and OR/MS. The maturity of GIS and mathematical models together can advance spatial analysis capabilities and offer substantial potential for continued and sustained theoretical and empirical evolution. Murray [10] provided an overview of linkages between location analysis and GIS to highlight how GIS has contributed to location science in terms of data input, visualization, problem solution, and theoretical advances. Alexandris and Giannikos [37] proposed a model of MCLP with the notion of complementary partial coverage and used a GIS to better represent demand. Rajagopalan et al. [35] studied a multi-period LSCP for the dynamic redeployment of emergency medical services, to determine the minimum number of ambulances and locations to meet the coverage requirements and visualized by a geographic tool. To maximize coverage of continuous demand in multiple siting facilities, Murray et al. [8] investigated a case study using a geocomputational heuristic, in which detailed geometric techniques could be utilized for solving a complex MCLP model. Calderin et al. [38] discussed the development of GIS software to model and solve MCLP, as well as data management and visualization of solutions by meta-heuristic algorithms. GIS could display solutions for the MCLP and LSCP in maps, and based on visualization, different analyses could be performed.

This paper aims to study the street lighting location problem by applying the two covering models: the MCLP and LSCP. Although those models are widely used in different situations of site selection of emergency services, and as far as we know, there is very limited literature that has developed mathematical programming models for the street lighting location problem. Murray and Feng (2016) investigated a small-sized problem with no more than 30 street lights to be located. In contrast, we consider a general methodology for large-sized applications and apply our methodology in a real case study with approximately 200 street lights to be located.

The main contributions of this paper lie in three aspects. First, this paper formally proposes the street lighting maximal coverage location problem (SLMCLP) and street lighting location set covering problem (SLLSCP) and further develops the mathematical formulations of the problems, which could then be solved by professional software packages (solvers). Second, we describe the application of our methodology through a large-sized real case study, which integrates mathematical models with GIS. Third, we conduct sensitivity analysis and provide managerial insights for policymakers and urban designers.

The rest of the paper is organized as follows: Section 2 presents the two models of SLMCLP and SLLSCP and the solution methods. Section 3 discusses the background of this research and data processing. Results and sensitivity analysis are also presented in this section. The last section concludes the paper with a discussion and concluding remarks.

2. Models and Solution Methods

The Federal Highway Administration (FHWA), an agency within the U.S. Department of Transportation, prepared the FHWA Lighting Handbook to provide guidance and support to state/local government and lighting designers [39]. From this handbook, the federal guidance and recommendations regarding roadway lighting, as well as general considerations of lighting imparts, are introduced in detail [39]. The standards and guidelines of street lighting are stipulated by local agencies and are similar among different cities. For example, the City of San José designed a public streetlight replacement and installation design guide in 2016 [40]; the City of Nashville separates street light poles into residential and urban streetscape categories [41]. Other cities, e.g., Los Angeles [42], Santa Barbara [43], Denver [44], and Washington D.C. [45] also have their own standards.

In our case study, the Public Lighting Authority (PLA), an independent agency, managed the restoration of the street light system in Detroit. PLA transferred the system operation and maintenance to the serving utility, DTE Energy [46]. One of the co-authors is from a local engineering agency that contracted with DTE Energy for the design and installation of the street lights in Belle Isle. The following standards/guidelines are operationalized during the construction:

• Road centerlines are covered by street lights (distance between a point on a road centerline and its nearest street light not to exceed 150 ft);
• Road intersections should be covered by at least two street lights.

Next, we present two covering models that are applicable to the street lighting location problem in detail.

2.1. Street Lighting Maximal Coverage Location Problem (SLMCLP)

The MCLP was first introduced by Church and ReVelle (1974). The aim of the model is to maximize the coverage of a population with limited resources. The MCLP considers a discrete set of demand nodes and a discrete set of nodes where facilities can be located. Each demand node has an associated demand, representing its level of importance, and some nodes can remain uncovered. The objective of the MCLP is to find the optimal locations of $p$ facilities to maximize coverage of the demand.

Applying the MCLP for street lighting, we must modify the original model by taking the road infrastructure and street lighting standards/guidelines into account. Specifically, we consider a discrete set of potential street light locations, which are usually along the road and can be generated automatically in GIS. Further, we consider a discrete set of points on road centerlines as demand notes, which can again be generated automatically in GIS. Details on how we selected the potential street light locations and the points on road centerlines for the case study are described in Section 3.3. The distance between any two nodes is calculated as the shortest separation in GIS, more narrowly, the Euclidean metric, which is the straight-line distance used to measure the distances between nodes. Given the distance and a coverage distance threshold, we can then determine whether each point on road centerlines can be covered by each potential street light location. The objective of the SLMCLP is to find the optimal locations of $p$ street lights to maximize the coverage, which is defined as the number of covered points on road centerlines.

In summary, the parameters and decision variables for the SLMCLP are defined as follows:

• $i$ ($k)$, $I$: the index and set of potential street light locations;
• $j$, $J$: the index and set of points on road centerlines;
• $D$: coverage distance (distance between a point on a road centerline and its nearest street light) threshold;
• $d_{ij}$: $\left\{0;1\right\}$ a binary parameter that equals 1 if the distance from potential street light $i$ to point $j$ is smaller than or equal to $D$, 0 otherwise;
• $b_j$: the number of street lights required to cover point $j$;
• $p$: number of street lights to be located;
• $x_i$: $\left\{0;1\right\}$ a binary decision variable that equals 1 if potential street light $i$ is located, 0 otherwise;
• $y_j$: $\left\{0;1\right\}$ a binary decision variable that equals 1 if point $j$ is covered by one or more street lights located within a distance of $D$, 0 otherwise.

The SLMCLP can then be formulated as an integer programming model as follows:

$$Max:{\displaystyle \sum }_{j\in J}{y}_j$$

(1)

Subject to:

$${\displaystyle \sum }_{i\in I}{d}_{ij}{x}_i\ge b_j{y}_j\hspace{1em}\forall j\in J$$

(2)

$${\displaystyle \sum }_{i\in I}{x}_i=p$$

(3)

$$x_i=\left\{0,1\right\},\forall i\in I$$

(4)

$$y_j=\left\{0,1\right\},\forall j\in J$$

(5)

The objective function (1) is to maximize the number of covered points on road center lines. Constraint (2) states that a point on road centerlines is covered only when one or more street lights are located within a distance $D$ from this point. Note that for a regular point j that is not at a road intersection, $b_j$ = 1; otherwise, $b_j$ = 2. Constraint (3) ensures that the number of street lights to be located is $p$. Constraints (4) and (5) require that the decision variables must take on integer values.

We note that integer programming belongs to mathematical programming, and also this type of model involves combinatorial optimization. Further, the MCLP is an NP-hard (nondeterministic polynomial-time) problem (Church and ReVelle 1976), and so is the SLMCLP. This implies that the computation time to find the optimal solution grows exponentially with problem size. Therefore, it is computationally very difficult to find the optimal solution for extremely large-sized problems.

2.2. Street Lighting Location Set Covering Problem (SLLSCP)

Following the LSCP, the SLLSCP is to locate a minimum number of street lights so that each node on road centerlines must be covered. Given the same parameters and decision variables defined in Section 2.1, the SLLSCP can be formulated as an integer programming model as follows:

$$Min:{\displaystyle \sum }_{i\in I}{x}_i$$

(6)

Subject to: (4), (5), and

$${\displaystyle \sum }_{i\in I}{d}_{ij}{x}_i\ge b_j\hspace{1em}j\in J$$

(7)

The objective function (6) is to minimize the number of street lights to be located. Constraint (7) states that every point on road centerlines must be covered. Similarly, the SLLSCP is also an NP-hard problem.

2.3. Solution Methods

There are a number of ways to solve a mathematical programming problem [47]. Professional software packages, known as solvers, exist for solving a generic mathematical programming problem. Solvers based on exact or heuristic algorithms can find the optimal or a near-optimal solution directly. Alternatively, researchers develop their own heuristic algorithms dedicated to a particular type of problem, such as greedy heuristic, tabu search, genetic algorithm, etc. [48].

For the case study investigated in Section 3, we used GAMS/CPLEX 12.0 (GAMS Development Corp., Fairfax, VA), which is one of the most powerful professional solvers for integer programming (https://www.gams.com/, accessed on 29 January 2022). GAMS provides a modeling environment, i.e., generating integer programs, and CPLEX is the optimizer used to find optimal solutions. This software was used for two main reasons. First, it is commercial software and one of the most widely used optimization software in both academia and industry in operations research. Second, one of the authors has intense experience using this software. All runs were performed in a PC with Intel Core i5-3470 3.2 GHz Quad-Core and 8GB RAM. We note that the case study is actually a medium-sized problem, and therefore, GAMS/CPLEX can solve the problem optimally within an hour. However, for extremely large-sized problems, there may be a need to develop efficient heuristic algorithms.

3. Case Study

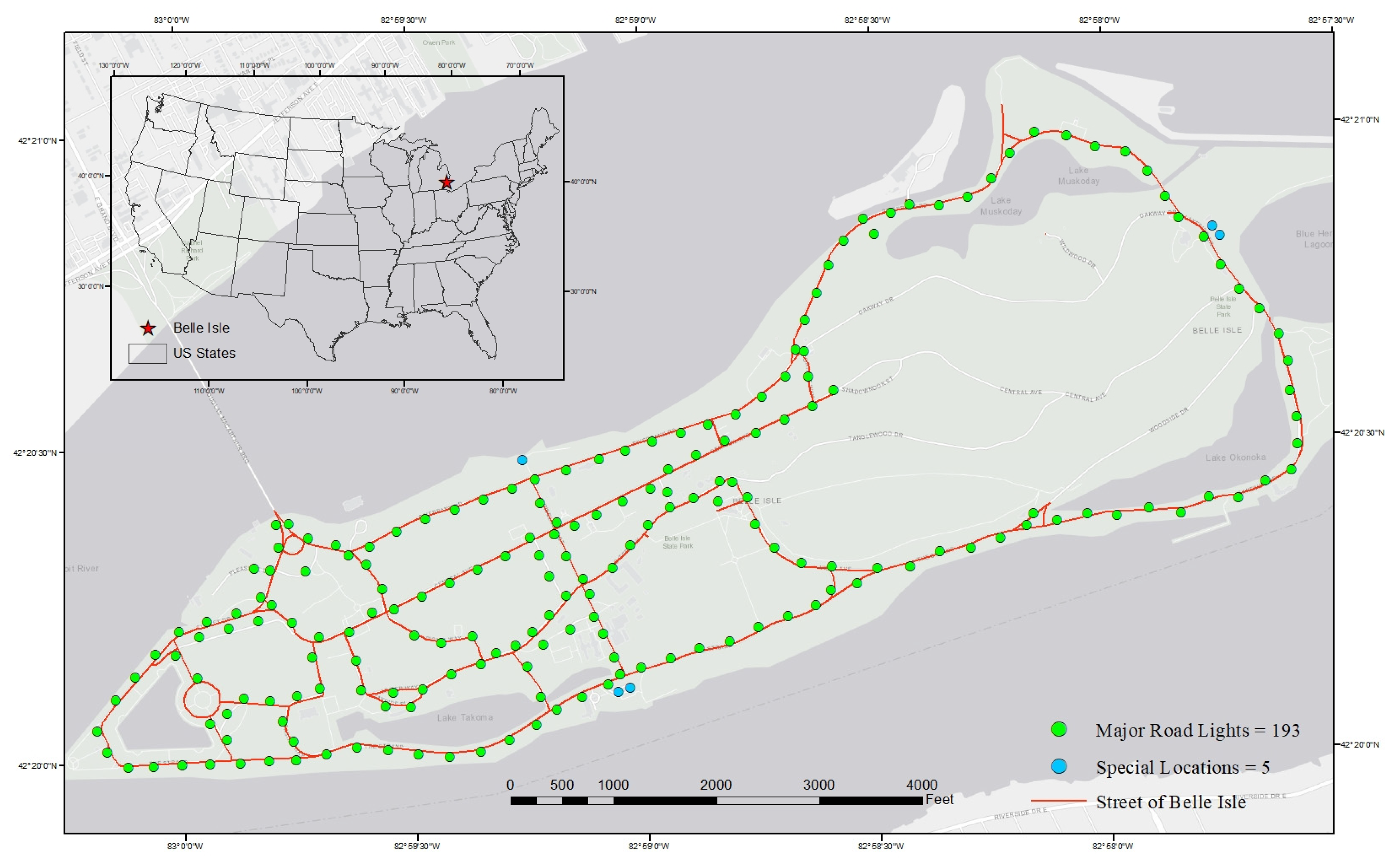
3.1. Background

It is well known that the city of Detroit, Michigan, declared bankruptcy in 2013, and it has struggled with a bad economic situation for a long period of time. As a result, the city of Detroit has suffered from old and poor infrastructure for long durations. In 2014, the Public Lighting Authority (PLA) inspected all of the street lights within the 139 square miles of the city boundary and found that roughly 40 percent of the city’s street lights did not work [46]. From 2014, the PLA started a project called “Relighting Detroit” with USD 185 million in bond funding, which was a collaboration between the city and the state to relight the city’s streets with LED lights. By replacing the old high-pressure sodium lights, planting new foundations and poles, and building new lights in less than 3 years, the PLA claims that 99 percent of street lights are on at any given time [49,50].

As a Detroit gem, Belle Isle Park received its relighting plan in 2016. Within the limitation of the budget, the PLA tried to cover more area on the island with the least cost. Before the relighting plan, there were 506 street lights with high-pressure sodium luminaires covering the major roads and streets on the island. Considering energy usage, power cable system planning and construction cost, fancy viewing, and environmental protection reasons, the PLA decided to build new solar street lights on the island.

3.2. Data Source

According to the PLA data, there were 661 high-pressure sodium lights on the other side of the Douglas MacArthur Bridge on Belle Isle. Among them, 506 lights were placed on the major road that the PLA plans to light in the relighting project. The road data come from the US Census Bureaus, and the total length of the major road is 10.65 miles. According to the solar luminaire’s parameter and the PLA’s requirement, we agree that each solar street light pole has a maximum effective range of 150 feet. Designed by experienced electrical engineers, 193 new solar street lights were planted by the major road. Five new lights were placed to cover special locations, two of them for a parking lot and one for a walking trail. Figure 1 shows the current configuration of all solar street lights in Belle Isle designed on the basis of experience.

3.3. Data Preprocessing

All of the street lights have to be placed on the Right of Way (ROW) that is owned by the State of Michigan. Right of Way is a type of easement granted or reserved over the land for transportation or electrical purposes. In Michigan, it can be used to build street lights and electrical lines. Based on the Right of Way information and map from the State of Michigan and Wayne County, we took the Trimble Geo7X handheld data collector to collect the Right of Way data in the field. The average error for the Right of Way data were less than 8 inches. Within the 20.93 miles of Right of Way, we created 37,125 street light locations as candidates by selecting one every 5 feet along the road. Thus, they are uniformly distributed along the road. These points were created by using the Create Random Points tool, which is one set of Sampling tools in the ArcGIS software. ArcGIS Collector was used to collect the field data with the help of the Trimble Geo7X device. It could provide accuracy as good as 1.5 inches.

To present the coverage of the road by street light locations, we also created 15,280 points on the major road centerline, again by selecting one every 5 feet along the road. In order to be as accurate as possible, while keeping in mind the computational power, the range of 5 feet was chosen as a test value in this research. We calculated a distance matrix between every candidate street light location and every point of the road centerline (37,125 × 15,280), using the Euclidean distance, which is how light travels. Based on this distance matrix, we calculated $d_{ij}$ for the SLMCLP and SLLSCP.

In order to obtain the intersections of the major road, we used the Intersect tool from ArcMap 10.6.1 to find 18 major road intersection points that must be covered by at least two lights. Right of Way data and intersections are shown in Figure 2.

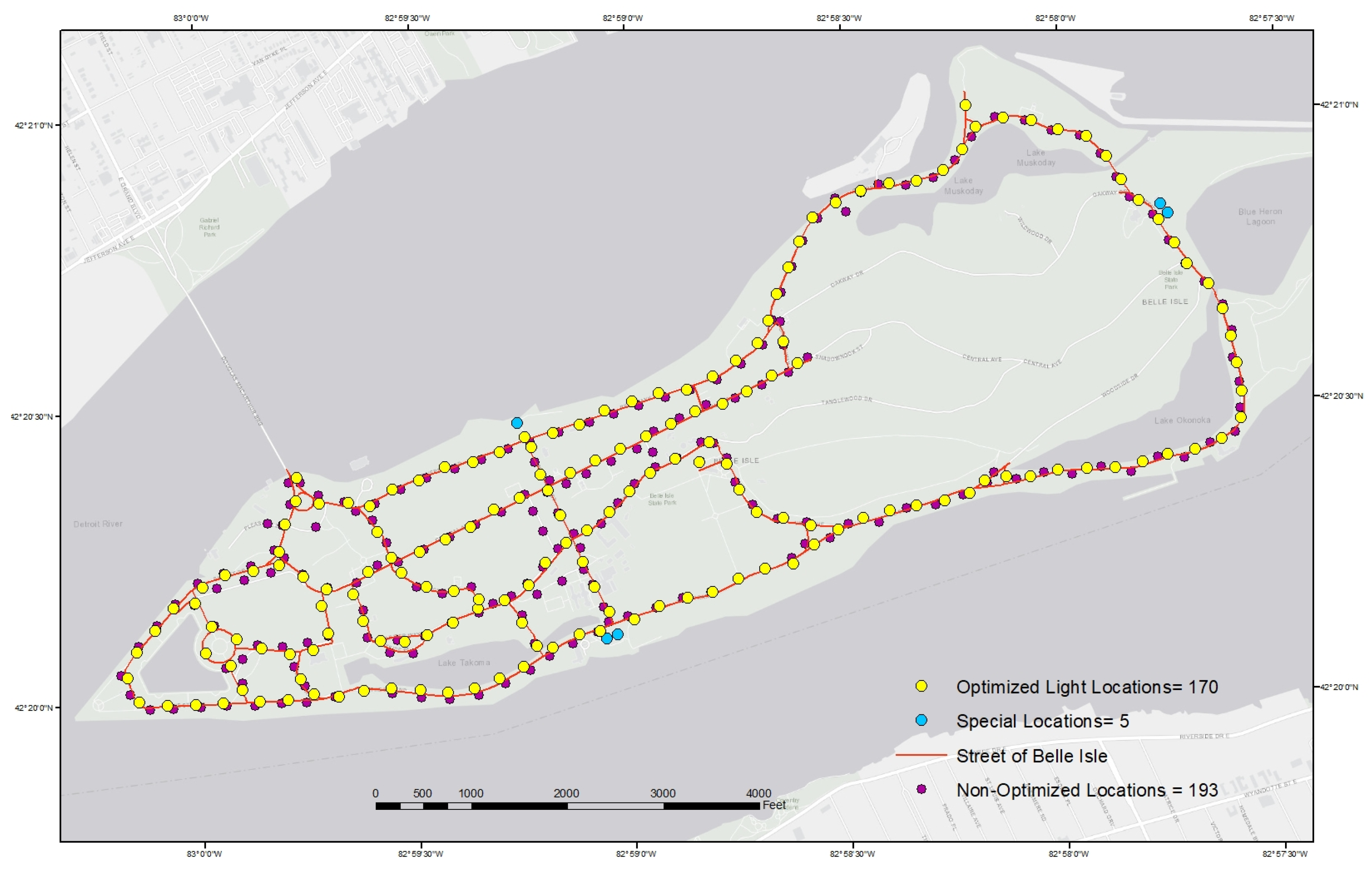
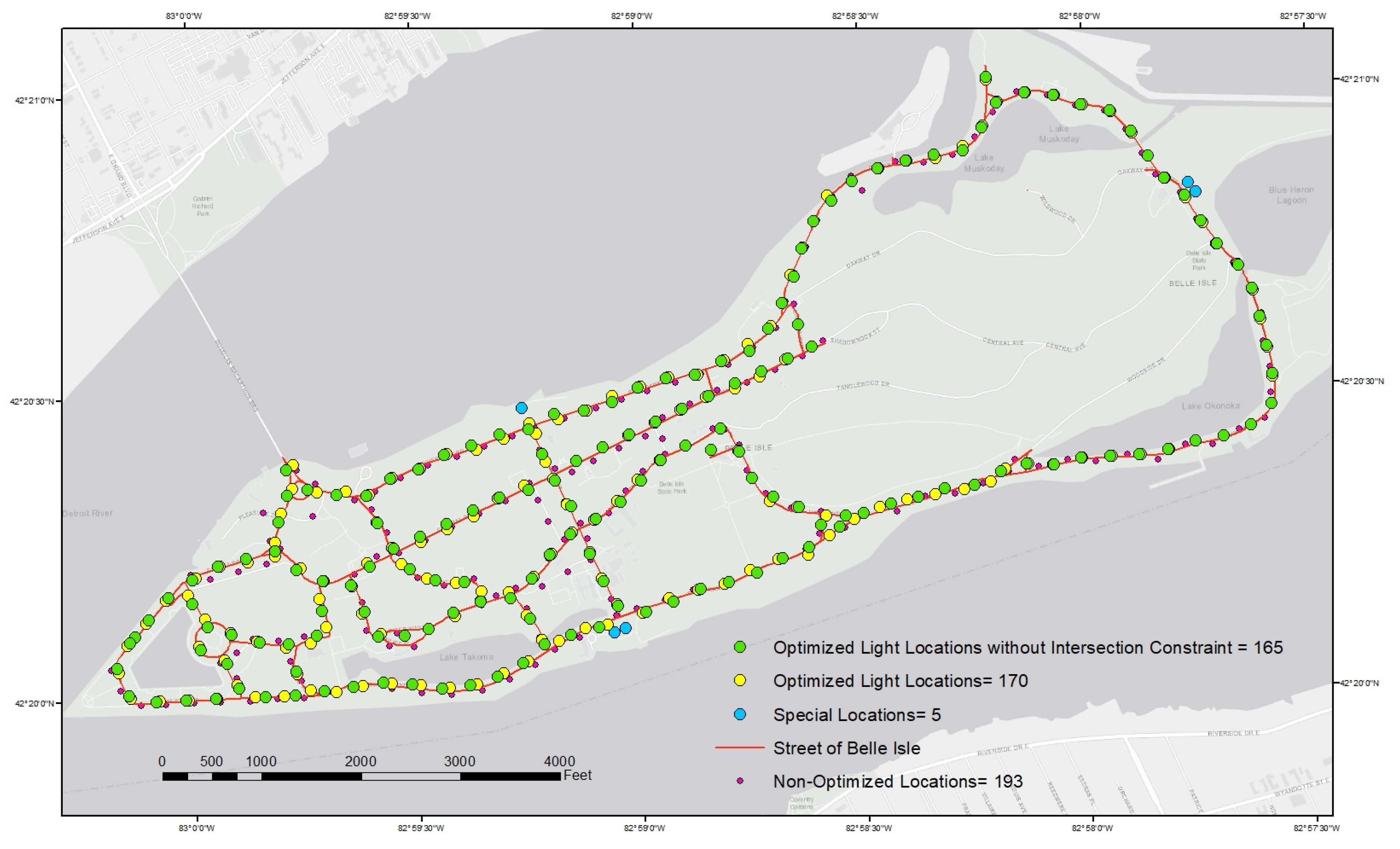
3.4. Results

3.4.1. Scenario 1: Cover All Road Centerline Points with a Minimum Number of Lights

The SLLSCP applies to this scenario. The following standards and guidelines need to be satisfied: (1) all the points from the road centerline should be efficiently covered by at least one street light within 150 ft; (2) the intersections should be covered by at least two street lights.

GAMS/CPLEX solves this problem to optimality within an hour. From Figure 3, the optimal solution shows that 170 street light locations can cover the entire road centerline in Belle Isle. Therefore, the number of street lights could be reduced by over 10%, from 193 to 170, by using our method. Given each street light pole costs about USD 2000 to USD 3000 for installation (https://www.ledsmaster.com/channel/How-Much-Do-Street-Lights-Cost-Replacing-and-Running-the-Street-Lamp--77.html) (accessed on 25 July 2021), this result indicates a cost saving of about USD 46,000 to USD 69,000. This cost saving is only on street lights themselves, not including the designs of the lights, management fees, and the fees on supporting facilities and maintenance. According to the information from one of the co-authors who participated in the real projects, the estimated cost saving can be up to USD 80,000 to USD 103,500.

By comparing our optimal solution and the current solution closely, we can find that although the patterns of the distribution of street lights are similar, most of the current street light locations are not in our optimal solution. Many of the optimal locations often shift from the current locations by 10–50 feet. We also find that the current solution does not actually satisfy both two parts of the above requirements. For example, compared with the 100% coverage of the optimized solutions, the current planning only covers 96.3% of the road centerline. Recall that the current solution was designed by experienced lighting engineers; this comparison clearly shows the power of a sophistical mathematical model over the experience of humans for this type of problem. Note that the reduction may be even greater for a large-sized problem.

To verify our model, the Trimble GPS device was used to collect the existing light locations and ROW path in Belle Isle Island. We calculated the light coverage for the road of the current street light locations and optimized locations with the same parameters. We found that the optimal solution could provide better light coverage with fewer street lights. We did not mean 100% using the optimized solutions to build the street lights since any building plan has to be confirmed and verified by experienced engineers and other specialists. Nevertheless, it will be a very good supporting tool or idea for experienced engineers, or a starting reference during the planning process.

3.4.2. Scenario 2: Cover All Road Centerline Points with a Minimum Number of Lights without the Intersection Constraint

To examine the impact of the intersection constraint, we resolve the SLLSCP without the constraint. The solution indicates 165 street lights to be located, i.e., reducing 5 locations. This is the minimum number of street lights to cover the entire road centerline in Belle Isle. If there is a budget problem for the policymakers, this scenario can be an alternative solution for them. Lower costs satisfy the basic guidelines and requirements of the street lights coverage in the study area. Figure 4 presents the distributions of the optimized street light locations without the constraint that the intersections should be covered by at least two street lights.

3.5. Sensitivity Analysis

In this sensitivity analysis, we apply the SLMCLP to study how much the entire road centerline can at most be covered by locating a certain number of street lights. Figure 5 below shows the percentage of coverage of the road centerline with respect to the number of street lights. The percentage of coverage tends to be linearly related to the number of street lights when it is less than 160, which already gives almost 99% of coverage. This may be helpful for city planners to estimate the outcome given a limited budget.

4. Discussion

The street lighting maximal coverage location problem (SLMCLP) and street lighting location set covering problem (SLLSCP) are discussed and developed in this paper. Through the results of the mathematical models, it has been proved that this solution is possible. The optimized solutions cover a larger lighting area or more roads with more efficiency and less expenditure by comparison with manual manipulation. First of all, the optimized street lights increased lighting coverage. There are many inevitable mistakes and errors during manual planning, while the mathematical optimization models can reach 100% coverage of all the roads according to our demands without any omission. Secondly, mathematically optimized street lighting locations can save a lot of costs and avoid unnecessary waste while providing greater coverage. We have to point out that manual planning will inevitably result in many unwarranted duplications of coverage due to inaccuracies by following the same rules and limitations; that is to say, many places and roads without any special significance will be covered by different street lights. Thirdly, the time cost on the street light optimization algorithm is much less than that of manual planning. Even if we admit that manual planning can be more nuanced, we can also verify the locations of the street light manually after using the mathematical optimization models, which can still save a large amount of time by comparing it with manual planning from scratch.

In a practical sense, this research demonstrates a real street lighting planning situation. PLA planted 193 solar street lamps in Belle Isle, Michigan, in 2016, which covers around 96% of the main roads. If the optimization method in this paper is adopted for street lighting planning, by satisfying the same conditions, only 170 street lights are needed to cover 100% of all the intersections and roads. The optimization solutions can save 12 percent of the number of street lights and about USD 100,000 in cost. The purpose of this paper was to provide an idea by using mathematical models with real-life data. The reality may be much more complicated than our mathematical models; therefore, all the construction process should be verified by human experts, engineers, and spatial planners.

The intensity of the saving is quite significant. If the study area extends to the whole Detroit area, in which the PLA rebuilt 65,000 street lights in 2016 (http://www.publiclightingauthority.org/construction-schedule/) (accessed on 25 November 2019), the saving of street lights number can be 7800. Even if 5 percent of the special locations are not accounted for and 5 percent of the fault tolerance is allowed, Detroit could actually save around 7000 street lights, which is at least USD 28 million in taxpayer savings. Those saved costs and resources could be spent on other infrastructure projects. Even if we fully invest in the street light projects, we can use the saved resources to improve the street lamp density or light intensity in specific areas or places with a high crime rate, where the incidence of traffic accidents is high, or where there are many pedestrians at night.

What is more important is that this paper aims to find and solve the crucial social needs that affect people’s daily lives by using advanced location models and methods with GIS and the optimization method. The idea can also be extended to other public sector services, such as site selection for fire stations and ambulances. As already observed in many industries, analytics and artificial intelligence, based on mathematical models and algorithms, have made a significant impact on decision making. We believe that this is the trend for urban planning too. Although this is a finished project, site visits and validation were conducted in order to verify the mathematical model. Regardless of the actual situation, this model can be used as an important reference before the actual construction in the future.

5. Conclusions

Several limitations in this research need to be acknowledged. First of all, this study focused on discrete-space models. Although these models, including the SLMCLP and SLLSCP, can be efficiently used to solve the location problem, street light placement is a continuous-space facility sitting problem since street lighting as an entity can be located anywhere along the road. In future research, continuous-space models should be considered to solve the street lighting location problem. Furthermore, the objective of this research was only targeted at reducing costs, which may not be comprehensive in real life. More objectives, for example, reducing the crime rate or creating pleasant environments could be considered to maintain the sustainable development and ecological balance of the city.

While considering the applications related to street lighting, there are large quantities of resources to use, from local agencies or state/federal standards and guidelines. Given the specificity of nighttime lighting of streets in the field of outdoor, these resources are constantly updating and changing. There’s plenty of room to learn about optimizing visibility for motorists and pedestrians while coordinating or balancing the relationship between side environmental impacts and optimal cost effectiveness of safety improvements. Facts show that the rule of thumb is not always accurate or efficient; our findings and results show better improvement of electric energy in the study area of Belle Isle, Michigan. Although the lights have already been installed, this research will benefit the decision-making process in future urban design projects. Undoubtedly, researchers will continue to improve the models and provide better approaches to optimize where street lighting is beneficial most.