Modeling and Querying Fuzzy SOLAP-Based Framework

Abstract

Nowadays, with the rise of sensor technology, the amount of spatial and temporal data is increasing day by day. Modeling data in a structured way and performing effective and efficient complex queries has become more essential than ever. Online analytical processing (OLAP), developed for this purpose, provides appropriate data structures and supports querying multidimensional numeric and alphanumeric data. However, uncertainty and fuzziness are inherent in the data in many complex database applications, especially in spatiotemporal database applications. Therefore, there is always a need to support flexible queries and analyses on uncertain and fuzzy data, due to the nature of the data in these complex spatiotemporal applications. FSOLAP is a new framework based on fuzzy logic technologies and spatial online analytical processing (SOLAP). In this study, we use crisp measures as input for this framework, apply fuzzy operations to obtain the membership functions and fuzzy classes, and then generate fuzzy association rules. Therefore, FSOLAP does not need to use predefined sets of fuzzy inputs. This paper presents the method used to model the FSOLAP and manage various types of complex and fuzzy spatiotemporal queries using the FSOLAP framework. In this context, we describe how to handle non-spatial and fuzzy spatial queries, as well as spatiotemporal fuzzy query types. Additionally, while FSOLAP primarily includes historical data and associated queries and analyses, we also describe how to handle predictive fuzzy spatiotemporal queries, which typically require an inference mechanism.

1. Introduction

Recently, the amount and variety of data used for analytical purposes have greatly increased. In order to improve the data to be analyzed, it is necessary to use expertise and a suitable application for the processing and interpretation of these data. For this purpose, various methods and applications have been developed to analyze large amounts of data. One of the most common developed applications is online analytical processing (OLAP) [1]. OLAP enables data analysis and query processes to help in decision-making about the data source. It is a computational method that allows users to quickly and selectively extract and query data for analysis from different perspectives. OLAP has emerged because classic databases cannot be used in decision-making and require expertise in data access. While traditional databases are concerned with the retention of data and the efficient management of online transactions, OLAP is concerned with the efficient analytics of online data.

In addition, conventional data mining techniques are insufficient in the area of spatiotemporal database applications because they often require intensive computations and involve complex differential equations and computational algorithms [2]. However, we need to perform effective and efficient querying with a colossal amount of spatiotemporal data. One of the widely used geospatial data mining tools is spatial online analytical processing (SOLAP), which enables the exploration of data cubes to extract new information effectively and efficiently [3]. SOLAP can also be defined as a platform supporting fast and easy spatiotemporal querying. It allows data mining following a multidimensional approach comprised of levels of aggregation.

Researchers working with OLAP mainly use numerical and statistical models [4,5,6], which generally use precise values as input and output. Furthermore, SOLAP provides querying and analysis of numeric and alphanumeric multidimensional data. However, there is a need to support flexible queries on uncertain and fuzzy data, due to the nature of complex applications such as meteorological and spatiotemporal applications. Uncertainty and fuzziness are inherent features of most meteorological applications [7]. That is, spatial and temporal information and various relationships in these applications frequently involve uncertainty and fuzziness. For example, in describing a rainy region, the region’s boundary is a fuzzy concept. Likewise, in estimating a weather event, the need to determine its position at a particular time, or its time of occurrence at a specific location, gives rise to fuzzy estimations.

The most common reasons for various types of uncertainties in spatiotemporal applications are:

• Some spatial information is inherently imprecise or fuzzy. The locations of events, spatial relationships, and various geometric and topological properties usually involve multiple forms of uncertainty [7].
• Most natural phenomena have fuzzy boundaries due to the transitional nature of variation in their aspects (e.g., high humidity and low temperature cause precipitation at a certain altitude) [8,9,10].
• Obtaining precise data is tedious and unnecessary most of the time, and we may only be able to give a range of values within which the exact numbers would fall. For instance, we may need the number of “cloudy” or “partly cloudy” days for some areas within a certain period. In this request, the user specifies the cloudiness criteria in linguistic terms instead of giving numeric degrees of cloudiness (e.g., 2/8 or 7/8) [11].

The use of OLAP is mainly related to querying and analyzing historical data, but we also need to make predictions based on spatiotemporal data. In this study, we describe how to handle predictive fuzzy spatiotemporal queries that require an inference mechanism. We also show that various complex queries, including predictive fuzzy spatiotemporal queries, are effectively and efficiently handled using our fuzzy spatial OLAP framework. We do this with the support of the association rules and fuzzy inference system (FIS) components of the FSOLAP framework. In other words, the FIS component included in the FSOLAP framework supports fuzzy predictive query types.

Spatial–temporal database applications naturally contain hierarchical data structures. Spatial data include hierarchical breakdowns such as country–region–city, while temporal data have hierarchical relationships at levels such as year–month–day. SOLAP was developed to provide effective and efficient analysis and querying of hierarchical data. Spatial and temporal information and various associations in spatial–temporal applications frequently involve uncertainty and fuzziness, which are inherent features of most of these applications [7] (e.g., in describing a rainy region). In addition, since spatial–temporal applications are complex, they are challenging to analyze with conventional logic approaches. Fuzzy logic can be used for situations in which conventional logic technologies are ineffective, such as applications [2,12,13,14,15,16,17,18,19,20,21] and systems [22,23] that mathematical models cannot precisely describe, those with significant uncertainties or contradictory conditions, and linguistically controlled applications or systems. The concepts of SOLAP and fuzzy logic can be combined to benefit from both to provide an effective and efficient platform for spatiotemporal applications. The aim of this study is to propose a new framework, FSOLAP, to take advantage of both SOLAP and fuzzy logic to provide analytics and querying of imprecise spatiotemporal data and to extend the framework with inference ability.

Our study aims to find spatiotemporal patterns in data which have spatiotemporal characteristics, in order to perform data analytics and querying. Researchers [24,25] typically use synthetic or semi-synthetic data to demonstrate the performance of their compound models in data science applications. The use of synthetic data makes it impossible to represent the true efficiency and accuracy of the model. Validation of the FSOLAP framework on a big database under the fuzzy spatial–temporal data model is vital. However, it is not easy to find real data to study. In our study, thanks to the Turkish State Meteorological Service, we were able to use a real meteorological dataset containing spatiotemporal features and measurement attributes as a case study to test our framework and models. It was shown that a fuzzy approach is suitable for handling spatiotemporal data. Therefore, we present our approach for dealing with different types of fuzzy spatiotemporal queries using FSOLAP. In this context, the FSOLAP framework is modeled, and the methods for supporting fuzzy non-spatial, fuzzy spatial, and fuzzy spatiotemporal query types using FSOLAP are explained. In general, the FSOLAP framework includes SOLAP, a fuzzy module, a fuzzy knowledge base (FKB), and a fuzzy inference system (FIS), as explained in Section 2.2. This framework allows us to make efficient and flexible fuzzy queries and analyses on spatiotemporal data.

The main contribution of this study is the development of FSOLAP as a new fuzzy SOLAP-based framework, allowing effective and efficient analysis and querying of spatiotemporal data. FSOLAP supports the fuzzy spatiotemporal predictive query, which is a new query type that has not been proposed before, as well as the complex type of fuzzy spatial queries present in the literature.

More specifically, the contributions of this study are as follows. We propose a fuzzy SOLAP-based complex system (FSOLAP) for analytics on fuzzy spatiotemporal data and for predictive analysis of various spatiotemporal events, including support for various querying capabilities, visualization of data, and analysis. The SOLAP server and its multidimensional expression (MDX) query processor is modified to support various flexible and complex queries. An optimal number of fuzzification clusters is calculated and integrated into the FSOLAP framework as an automated process. Moreover, fuzzy sets are generated automatically and used to create fuzzy association rules. The appropriate minsup and minconf values related to fuzzy association rule generation are also determined. In addition, an analysis of the performance of the framework is undertaken using a real meteorological dataset. Average CPU usage, memory usage, and query execution time for running each query type included in the FSOLAP framework are measured. A pruning method based on confidence measures that removes complex rules in the generated fuzzy association rule set to speed up the inference performance is also applied. Additionally, fuzzy association rule weighting for rule-based pruning is performed on the generated rules. Thus, we derive accurate inferences from the fuzzy association rules.

The organization of this paper is as follows. Background information, related works, proposed architecture, and supported query types are given in Section 2. The execution of queries and experimental results are explained in Section 3. In Section 4, the results of the study are discussed and compared with those of previous studies. Finally, in Section 5, the conclusions and future work are presented.

2. Materials and Methods

Here, we first introduce the related work in Section 2.1 and then explain the FSOLAP framework and its components in Section 2.2. FSOLAP query management is presented and the structure of the modules explained in Section 2.3. Brief information about the dataset used to confirm the performance of the framework is given in Section 2.4. Finally, we present the supported complex and fuzzy queries in Section 2.5.

2.1. Background and Related Works

The increase in spatial data and human limitations in analyzing spatial data in detail make querying spatial databases crucial for spatiotemporal applications. In recent years, many studies [2,5,26] have addressed the issue of performing data mining tasks on data warehouses. Some of them [26,27] are explicitly interested in mining patterns and association rules in data cubes. For instance, Imieli’nski et al. [27] state that OLAP is closely intertwined with association rules and shares with association rules the goal of finding patterns in the data. Data mining techniques such as association rule mining can be used together with OLAP to extract knowledge from data cubes. Spatial data mining can be performed in a spatial data cube as well as in a spatial database. For this purpose, J. Han constructed GeoMiner [4], a spatial OLAP and data mining system prototype. Another proposed study [26] considers a framework for mining association rules from data cubes according to a sum-based aggregate measure, which is more general than frequencies provided by the count measure. The mining process is guided by a meta-rule, is context-driven by analysis objectives, and exploits aggregate measures to revisit the definitions of support and confidence. These studies profit from the hierarchical aspect of cube dimensions to mine association rules at different levels of granularity, such as spatial and temporal hierarchies.

Supporting spatial queries is one of the key features in spatial database management systems, due to the broad range of applications. Providing these types of queries involves introducing spatial components such as fuzzy topological relations into relational and object-relational databases. Fuzzy topological relations between fuzzy regions are explained in [28] and shown in Figure 1b. The formal definitions of the fuzzy topological relations can be explained as follows.

Let A be a set of attributes under consideration and let a region be a fuzzy subset defined in two-dimensional space $R^2$ over A. We can define the membership function of the region as $\mu :X\times Y\times A\to [0,1]$, where X and Y are the sets of coordinates defining the region. Each point $(x,y)$ within the region is assigned a membership value for an attribute $a\in A$. We show a fuzzy region in Figure 1a, which has a core, an indeterminate boundary, an exterior, and $\alpha -cut$ levels.

The concept of the $\alpha -cut$ level region is used to approximate the indeterminate boundaries of a fuzzy region and is defined as follows:

$$R_{\alpha }=\left\{(x,y,a)\right|{\mu }_R(x,y,a)\ge \alpha \}(0<\alpha <1)$$

(1)

The degree of the fuzzy relation is measured by aggregating the $\alpha -cut$ levels of fuzzy regions. The basic probability assignment $m\left(R_{\alpha i}\right)$, which can be interpreted as the probability that $R_{\alpha i}$ is the true representative of R, is defined as in [29,30]:

$$m\left(R_{\alpha i}\right)={\alpha }_i-{\alpha }_{i+1},1\le i\le n,n\in N,1={\alpha }_1>{\alpha }_2>\dots >{\alpha }_n>{\alpha }_{n+1}=0$$

(2)

Assuming that $\tau (R,S)$ is the value representing the topological relation between two fuzzy regions R and S, and $\tau (R_{\alpha i},R_{\alpha j})$ is the value representing the topological relation between two $\alpha -cut$ level regions $R_{\alpha i}$ and $S_{\alpha j}$, the general relation between two fuzzy regions can be determined by

$$\tau (R,S)=\sum _{i=1}^n\sum _{j=1}^{m}m\left(R_{\alpha i}\right)m\left(S_{\alpha j}\right)\tau (R_{\alpha i},S_{\alpha j})$$

(3)

For example, the overlap relation between two fuzzy regions can be approximated by using the formula above as follows:

$$\tau (R,S)=\sum _{i=1}^n\sum _{j=1}^{m}m\left(R_{\alpha i}\right)m\left(S_{\alpha j}\right){\tau }_{overlap}(R_{\alpha i},S_{\alpha j})$$

(4)

Since spatial OLAP querying deals with some concepts expressed in verbal language, fuzziness is frequently involved in spatial OLAP. Hence, the ability to query spatial data under fuzziness is an essential characteristic of any spatial database. The studies in [25,31] discuss the directional and topological relationships in fuzzy concepts. Some earlier works [24,32] provide a basis for fuzzy querying capabilities based on a binary model to support queries of this nature. Another study [33] considers unary operators for querying fuzzy multidimensional databases. The study discusses the properties of unary operators on fuzzy cubes and investigates the combination of several queries to explore the possibility of the definition of an algebra to manipulate fuzzy cubes. All these studies mainly focus on modeling basic fuzzy object types and operations, leaving aside the processing of more advanced queries.

In existing fuzzy OLAP studies [12,13,14,15], OLAP mining and fuzzy data mining are combined to take advantage of the fact that fuzzy set theory treats numeric values more naturally, increases understanding, and extracts more generalizable rules. Fuzzy OLAP is performed on fuzzy multidimensional databases. The multidimensional data model of data warehouses is extended to manage the imperfect and imprecise data (e.g., cold days) of the real world. These studies typically focus on finding knowledge about fuzzy spatial data, but more complex queries (e.g., select cold regions) are not considered.

In studies [16,17] on fuzzy spatial querying, neither SOLAP nor MDX query supports are used, but an extension to the standard Structured Query Language (SQL) is used to support spatial and temporal data. The authors combine and extend techniques developed in spatial and fuzzy data mining to deal with the uncertainty of typical spatial data, though they were not concerned about the performance side of the queries. In another study [18], fuzzy logic is integrated into spatial databases to help with decision support and OLAP query processes. In this study, the design of the fuzzy spatial data warehouse methodology is presented, but the effectiveness and efficiency are not discussed.

In addition, there are studies [19,20] on the nearest-neighbor and range types of queries in the field of fuzzy spatial queries. These studies consider range and nearest-neighbor queries in the context of fuzzy objects with indeterminate boundaries. They show that processing these types of queries in spatial OLAP is essential, but the query types are too limited. Support for complex spatial query types is still required.

Special structures have been developed for efficient and effective queries on fuzzy spatiotemporal data [21,34]. In these studies, novel indexes such as R*-tree [35] and X-tree [36] were used for efficient and effective queries, but there were no queries showing the benefits of spatial OLAP.

2.2. FSOLAP Framework

The FSOLAP framework provides for fuzzy spatial–temporal data analytics and flexible and complex querying. The framework includes a multilayered system architecture that consists of four layers. The layers are data sources, structured data, logic, and presentation layers (from the bottom to the top). The system architecture of FSOLAP is represented in Figure 2.

At the bottom of the system, there are text files, database tables, and shape files. These structures contain the pure data which may be gathered from a web service or collected from a website. Data are migrated to the structured data layer via extract, transform, and load (ETL) operations from this layer. ETL operations are mainly related to reading files, preprocessing data, cleaning data, and validating data operations.

The data layer includes semi-structured or structured data such as a relational database, fuzzified data, and a fuzzy rule set. ETL output data, the fuzzification phase, and fuzzy association rule generation are handled in this layer. The upper layer is called the logic layer, and it requests data from the data layer using SQL or JavaScript Object Notation (JSON) requests. The data layer returns the requested data via SQL tuples, Java Database Connectivity (JDBC) result sets, or JSON responses. The data layer also provides fuzzy querying on PostGIS database data supported by the fuzzy logic module.

The logic layer contains systems that provide spatial, non-spatial, temporal, and fuzzy data mining tools, and a set of fuzzy functions used for fuzzification/defuzzification. It also includes data analytics and visualization platforms that help in visual pattern detection. The reporting tools that provide standard reports on the data are integrated into this layer. The SOLAP server is another central part of this layer that supports SOLAP data cube operations and multidimensional expression (MDX) querying. We integrated a fuzzy inference system and a fuzzy logic module for spatial data mining tasks. The fuzzy logic module was assembled to support fuzzy operations such as membership calculation, fuzzy clustering, and fuzzy class identification.

The presentation layer is shown at the top of our proposed architecture in Figure 2. This layer provides a categorized and simplified system structure. We can demonstrate the data on a map with a cartography viewer. We can also design a new SOLAP cube with hierarchies and measurements using the SOLAP data cube designer. In addition, the SOLAP cube data viewer allows querying of the data using user-friendly query interfaces for data selection. The data selection corresponds to the process of obtaining a subcube from the SOLAP cube via an MDX query. The definition of a subcube is as follows.

Let $D_s\subseteq D$ be a non-empty set of p dimensions $\{D_1,D_2,\dots ,D_p\}$ from data cube $C(p\le d)$. The p-tuple $\{{\Theta }_1,{\Theta }_2,\dots ,{\Theta }_p\}$ defines a subcube on C according to $D_s$ $iff{\forall }_i\in \{1,\dots ,p\},{\Theta }_i\ne \varnothing$, and there exists a unique j such that ${\Theta }_i\subseteq A_{ij}$, which can be visualized as shown in Figure 3.

Data selection does not always involve running a simple MDX query; it includes complex fuzzy queries based on the requirements of the data analytics. In data analytics, a hierarchical query is also necessary for certain situations. In this case, it is essential to use structures that support hierarchical querying. SOLAP enables querying and analysis of multidimensional numeric and alphanumeric data. However, there is still a need to support flexible queries on uncertain and fuzzy data due to the nature of complex applications such as meteorological and other spatiotemporal applications. The framework supports data analytics with the management of fuzzy spatiotemporal queries. FSOLAP can handle a variety of complex queries, including fuzzy spatiotemporal queries, which are dealt with effectively and efficiently using our FSOLAP framework.

2.3. FSOLAP Query Management

This section describes the architecture and query types that support fuzzy spatiotemporal queries on spatial OLAP-based structures. In the FSOLAP framework, we typically achieve query management through two main structures, as shown in Figure 4. One of these is the data layer, where we prepare, format, and query data. The other is the query module, which contains the frontend presented to the user for querying and query management components.

2.3.1. Data Layer

The raw data are structured after ETL operations and inserted into the PostgreSQL database at the data layer. SOLAP cube metadata are constructed by using the data in the database via the SOLAP cube designer. Then, for each attribute in SOLAP, the appropriate number of clusters is specified using X-means clustering [37].

X-means clustering is a variation of K-means clustering that refines cluster assignments by repeatedly attempting subdivision and keeping the best resulting splits, until some criterion is reached [37]. Algorithm 1, for X-means clustering, consists mainly of two operations repeated until completion.

Algorithm 1 Algorithm of X-means Clustering

Input: given sets of data to be clustered: $d_1$, …, $d_n$ Output: $K\leftarrow$ number of clusters 1: Improve-Params ← run conventional K-means to convergence 2: Improve-Structure ← find out if and where new centroids should appear 3: if $K>K_{max}$ then 4:  stop and report best scoring model found during the search 5: else if $K<=K_{max}$then 6:  Go to 1 7: end if 8: returnK

The objective function of K-means is as follows:

$$J=\sum _{j=1}^k\sum _{i=1}^n\mid \mid x_i^j-c_j\mid {\mid }^2$$

(5)

where $\mid \mid x_i^j-c_j\mid {\mid }^2$ is a chosen distance measure between a data point $x_i^j$ and the cluster centre $c_j$, which is an indicator of the distance of the n data points from their respective cluster centres.

The determined number of clusters is used as input when fuzzifying each attribute with the fuzzy c-means (FCM) clustering algorithm [38,39].

FCM is based on minimization of the following objective function:

$$J_m=\sum _{i=1}^N\sum _{j=1}^C{u}_{ij}\mid \mid x_i-c_j\mid {\mid }^2,1\le m<\infty$$

(6)

where m is any real number greater than 1, $u_{ij}$ is the degree of membership of $x_i$ in the cluster j, $x_i$ is the ith value of d-dimensional measured data, $c_j$ is the d-dimension center of the cluster, and $\mid \mid \ast \mid \mid$ is any norm expressing the similarity between any measured data point and the center [39]. Fuzzy partitioning is carried out through an iterative optimization of the objective function shown above, updating the membership $u_{ij}$ and the cluster centers $u_j$ by:

$$u_{ij}=\left(\frac{1}{{\sum }_{k=1}^C{u}_{ij}{(\frac{\mid \mid x_i-c_j\mid \mid }{\mid \mid x_i-c_k\mid \mid })}^{\frac{2}{m-1}})}\right)$$

(7)

$$c_j=\frac{{\sum }_{i=1}^N{u}_{ij}^m·x_i}{{\sum }_{i=1}^N{u}_{ij}^m}$$

(8)

This iteration will stop when $ma{x}_{ij}=|u_{ij}^{(k+1)}-u_{ij}^{\left(k\right)}|<\delta$, where $\delta$ is a termination criterion between 0 and 1, whereas k represents the iteration steps. This procedure converges to a local minimum or a saddle point of $J_m$ [39]. The algorithm is composed of the following steps:

• Initialize $U=\left[u_{ij}\right]$ matrix, $U^{\left(0\right)}$
• At k-step: calculate the center vectors $C^{\left(k\right)}=\left[c_j\right]$ with $U^{\left(k\right)}$

  $$c_j=\frac{{\sum }_{i=1}^N{u}_{ij}^m·x_i}{{\sum }_{i=1}^N{u}_{ij}^m}$$

  (9)
• Update $U^{\left(k\right)}$, $U^{(k+1)}$

  $$u_{ij}=\left(\frac{1}{{\sum }_{k=1}^C{u}_{ij}{(\frac{\mid \mid x_i-c_j\mid \mid }{\mid \mid x_i-c_k\mid \mid })}^{\frac{2}{m-1}})}\right)$$

  (10)
• If $\mid \mid U^{(k+1)}-U^{\left(k\right)}\mid \mid <\delta$ then STOP, otherwise return to step 2.

After determining the fuzzy clusters and membership functions, fuzzy association rules are generated on the fuzzified attributes with the FP-growth algorithm [40]. Association finds rules about items that appear together in an event such as a purchase transaction.

The problem of association rule mining is defined as follows. Let $I=\{i_1,i_2,···,i_n\}$ be a set of n binary attributes called items. Let $D=\{t_1,t_2,···,t_m\}$ be a set of transactions called the database. Each transaction in D has a unique transaction ID and contains a subset of the items in I. A rule is defined as an implication of the form $X\Rightarrow Y$, where X, $Y\subseteq I$. A rule is defined only between a set and a single item, $X\Rightarrow i_j$ for $i_j\in I$. Every rule is composed of two different sets of items, also known as itemsets, X and Y, where:

• X is called the antecedent or left-hand side (LHS);
• Y is called the consequent or right-hand side (RHS).

A heuristic approach is applied to generate a proper number of association rules. First, a different number of rules is generated by parametrically changing the minsup and minconf values for the FP-growth algorithm. After running FP-growth, the generated ruleset is tested with test data for making inferences. Then, the accuracy values of the inferences produced with the test data are calculated. Finally, the proper number of fuzzy association rules is obtained when no change in the accuracy is calculated according to the number of rules. However, this ruleset may contain duplicative rules. We need to reduce the number of rules with confidence-based rule pruning to prevent duplication. We used a rule-based pruning algorithm [41] that removes the unnecessarily complex rules, as shown in Algorithm 2.

Algorithm 2 Algorithm of Fuzzy Association Rule Pruning Based on Confidence

Input: given the sets of several length rules: $S_1$, …, $S_L$  $L\leftarrow$ max length($R_L$), l = 1, …, M  J is an empty set Output: $RB$: pruned fuzzy association rule base with reduced number of rules 1: fori = L, …, 2 do 2:  for all $RϵS_i$ do 3:   for all $R^{\prime }ϵS_{i-1}$ do 4:    if size($R^{\prime }\cap R$) = i then 5:     $J\leftarrow J$ ∪ index of $R^{\prime }$ 6:    end if 7:   end for 8:   if max($FC\left(R_J\right))>FC\left(R\right)$) − $\epsilon$ then 9:    delete R from the rule base $RB$ 10:   end if 11:  end for 12: end for 13: return $RB$

The pruning method compares the most comprehensive rules with shorter ones. A general rule which contains more minor rules is removed from the rule base when the maximal confidence of a fuzzy association rule ($FC$) value of the more minor rules is higher than the $FC$ value of the broad rule minus $\epsilon$, the correction factor (initially set to 2 percent). This rule pruning method offers shorter rules in the rule base. Although the pruned rule base contains fewer rules, the new classifier has the same classification accuracy as the unpruned rule base.

The fact that pruned rules have different weights during inference is a factor that affects accuracy. Results produced by association rules that make inferences for the same attribute in proportion to their weights should be considered. For this reason, a weighting process for the rules in the association rule set was performed. This study uses an interest measure called Rule Power Factor (RPF) [42] to give weight to each fuzzy association rule and to mine the fuzzy association rule between them. The equation of the RPF is as follows:

$$RFP(X\to Y)=support(X\cup Y)\ast confidence(X\cup Y)$$

(11)

where support and confidence are defined as follows:

$$support(X\to Y)=\frac{\mathit{number} \mathit{of} \mathit{tuples} \mathit{containing} \mathit{both} X \mathit{and} Y}{\mathit{total} \mathit{number} \mathit{of} \mathit{tuples}}$$

(12)

$$confidence(X\to Y)=\frac{\mathit{number} \mathit{of} \mathit{tuples} \mathit{containing} \mathit{both} X \mathit{and} Y}{\mathit{number} \mathit{of} \mathit{tuples} \mathit{containing} X}$$

(13)

2.3.2. Query Module

The query module (QM) is the component which handles query operations. Basically, it includes a fuzzy module (FM), a fuzzy knowledge base (FKB), a fuzzy inference system (FIS), a query parser (QPr), a query processor (QPc), and a query interface (QIn), as shown in Figure 4. User queries are entered into the system via the query interface. The QIn component receives user queries and sends these queries to the QPr. After the query is evaluated, the query results are displayed to the user.

There are two user interfaces for querying meteorological phenomena and meteorological data. Before querying meteorological phenomena, it is necessary to determine the association rules of related phenomena. For this purpose, the rules regarding the meteorological phenomenon can be defined with the expert rule definition interface shown in Figure 5.

In this interface, after the type and fuzzy class of a phenomenon are determined, the fuzzy association rule is produced by selecting the meteorological attribute and fuzzy class that are the antecedents of the relevant event. These fuzzy association rules are stored in the FKB and then used in the meteorological phenomenon inquiry interface, as shown in Figure 6.

In addition, meteorological data can be queried by selecting the attribute and the spatial and temporal criteria using the interface, as shown in Figure 7. The query results are represented in a list, and the spatial information is shown on a map.

In the meteorological phenomenon inquiry process, the association rules of the relevant event are selected from the FKB. In the antecedent part of these rules, fuzzy attributes and classes are determined and used as query criteria. The user can insert the spatial and temporal conditions into the requirements of the MDX query. Query results are fetched after executing the built MDX query on the SOLAP server. Again, query results are displayed in a list, and spatial information is shown on a map. Figure 8 shows how the selected criteria are used in the interface when building the MDX query.

The QPr component parses and interprets the user query and determines which elements will process the query. The QPc module works as a subcomponent responsible for running the query on the related systems and collecting and displaying the results. In other words, the QPc component plays a coordinating role in query processing. QPc performs the communication and interactions between the SOLAP, the FIS, and the fuzzy module. It receives user queries, analyzes them, sends requests to the SOLAP and/or to the FKB/FM, retrieves the results, and sends them to the query interface.

The fuzzy module is the component that provides crisp-to-fuzzy or fuzzy-to-crisp transformations using fuzzification and defuzzification operations. In this module, using the FCM algorithm, fuzzy clustering is performed to generate membership classes and determine membership values. FCM needs the number of clusters as a parameter. Therefore, we used X-means clustering to determine the appropriate number of clusters and to cross-check the cluster with elbow [43] and silhouette [44] methods. In addition, the definitions of uncertain types, similarity relations, and membership functions are stored in the fuzzy data map.

The fuzzy knowledge base (FKB) produces and stores fuzzy association rules. After fuzzifying the meteorological data on SOLAP, the fuzzy association rules are generated with the FP-growth algorithm and stored in the FKB. The resulting extensive list of rules is pruned using a confidence-measure-based pruning method [41] for performance improvement. The rules in the FKB are used in the case of inference as input for the FIS.

The FIS is utilized to support prediction-type queries. While querying, the fuzzy association rule required for each criterion is requested from the FKB and sent to the FIS. In addition, the FM provides the fuzzy membership classes and membership values required for the values in the query as input to the FIS. This interface works as follows. $A^{\prime }=F\left(x_0\right)$, where $x_0$ is a crisp value defined in the input universe ∪, $A_0$ is a fuzzy set defined in the same universe, and F is a fuzzifier operator. The FIS is based on the application of the generalized modus ponens, an extension of the classical modus ponens proposed by Zadeh, where:

$$\frac{\left(\mathrm{If}X\mathrm{is}A\mathrm{then}Y\mathrm{is}B\right)\cap \left(X\mathrm{is}{A}^{\prime }\right)}{\left(Y\mathrm{is}{B}^{\prime }\right)}$$

(14)

where X and Y are linguistic variables, A and B are fuzzy sets, and $B^{\prime }$ is the output fuzzy set inferred. To achieve this, the system firstly obtains the degree of matching of each rule by applying a conjunctive operator, and then infers the output fuzzy sets by means of a fuzzy implication operator. The FIS produces the same number of output fuzzy sets as the number of rules collected in the FKB.

The SOLAP server acts as a database server for objects and provides an application that stores measurement results, including spatiotemporal hierarchies, and supports MDX query types. We used the GeoMondrian SOLAP server [45] in our system. After the ETL process, the meteorological data are inserted onto the spatial OLAP server. These data are stored on the spatial OLAP server as spatial, temporal, and measurement-value hierarchies. The spatial hierarchy has region, city, and station breakdowns. Spatial hierarchy can be achieved with a foreign key, as in classical relational databases, or with a minimum bounded rectangle (MBR) structure supporting the spatial structure. The temporal hierarchy is organized according to year, month, and day divisions. Furthermore, each measurement result is available in a hierarchical structure in SOLAP.

We extended the MDX query and modified the GeoMondrian SOLAP server to support fuzzy queries. In general, the user asks for the fuzzy spatial or non-spatial objects that meet the conditions of the predefined rules within a specified time interval, when querying. The rules can be evaluated by examining the topological relations between fuzzy regions and fuzzy objects. To support this, the fuzzify_measure and fuzzify_geo methods are implemented in the MDX query processor of the SOLAP server. The fuzzify_measure method uses the hierarchy for the non-spatial attributes, while the fuzzify_geo method uses the hierarchy for the spatial attributes. The spatial hierarchy is used while detecting the fuzzy relationships such as around, inside, covers, etc., of two different spatial data items that are related to each other, using the fuzzify_geo method. To develop these methods, the geomondrian.jar Java library [45], which is used by the GeoMondrian SOLAP server for querying, was edited. We modified the MondrianServerImpl.java, Query.java, and Parser.java classes in this Java library by adding fuzzify_measure and fuzzify_geo methods. The MondrianServerImpl.java class contains keywords such as Filter, Member, Where, etc., which are used in the query. The fuzzify_measure and fuzzify_geo methods are inserted as keywords to this class. The Query.java class parses the MDX query with the help of the Parser.java class, then determines the query parts and parameters. While parsing the MDX query in the Parser.java class, fuzzy methods are identified using the keywords defined in the MondrianServerImpl.java class. The fuzzy module is integrated with its API while implementing these methods. The parameters of the methods are fuzzified in the fuzzy module via the API. The query results are fetched by processing the fuzzified parameter, and the fuzzy criterion is entered into the query with the relevant operator. While the query processor creates an MDX query, it fuzzifies the parameters that are associated with fuzzy methods and transforms them into a standard MDX query. In the query process, attributes are fuzzified via the fuzzy module and made suitable for the MDX query structure. Similarly, geometric features are fuzzified during queries and handled using the spatial functions provided with PostGIS.

The algorithm for implementing queries is given in Algorithm 3, and some sample queries are defined in Section 2.5.

Algorithm 3 The generic query evaluation algorithm

Input: The user $query$ with set of column members $CLN$ and predicates $PR$ Output: Set of retrieved/predicted objects $RSL$  Initialization:  $F{T}_p\leftarrow \left\{\right\}$  //fuzzy membership terms  $FAR\leftarrow \left\{\right\}$  //fuzzy association rules  $S{P}_t\leftarrow \left\{\right\}$  //spatial terms  $NS{P}_t\leftarrow \left\{\right\}$  //non-spatial terms, measurement  $D_s\leftarrow \left\{\right\}$  //SOLAP data cube query result holder  $S_O\leftarrow \left\{\right\}$  //satisfying-objects 1: Retrieve and Parse ($query$) 2: if query includes prediction predicate($PR$) then 3:  Send query to FKB with ($CLN$, $PR$) 4:  Transfer to FIS with ($CLN$, $PR$) 5:  $FAR\leftarrow$ Retrieve fuzzy association rules from FKB with ($CLN$, $PR$) 6:  $F{T}_p\leftarrow$ Retrieve fuzzy memberships from FM with ($CLN$, $PR$) 7:  $S{P}_t\leftarrow$ Defuzzify spatial predicates with ($CLN$) 8:  $NS{P}_t\leftarrow$ Defuzzify non-spatial predicates with ($PR$) 9:  $D_s\leftarrow$ Query spatial temporal data from SOLAP with ($S{P}_t$, $NS{P}_t$) 10:  $S_O\leftarrow$ Make prediction with ($FAR$, $F{T}_p$, $D_s$) 11:  return $S_O$ 12: else 13:  if query is spatial then 14:   $S{P}_t\leftarrow$ Defuzzify spatial predicates with ($CLN$) 15:   $NS{P}_t\leftarrow$ Defuzzify non-spatial predicates with ($PR$) 16:   $D_s\leftarrow$ Query spatial temporal data from SOLAP with ($S{P}_t$, $NS{P}_t$) 17:   $S_O\leftarrow$ Fuzzify satisfying objects with ($D_s$) 18:   return $S_O$ 19:  else 20:   $NS{P}_t\leftarrow$ Defuzzify non-spatial predicates with ($PR$) 21:   $D_s\leftarrow$ Query spatial temporal data from SOLAP with ($NS{P}_t$) 22:   $S_O\leftarrow$ Fuzzify satisfying objects with ($D_s$) 23:   return $S_O$ 24:  end if 25: end if

2.4. Data Sets

In this study, we utilized a spatiotemporal database including real meteorological measurements that have been observed and collected in Turkey over many years. The spatial extent of Turkey is 36${}^{\circ }$ N to 42${}^{\circ }$ N in latitude and from 26${}^{\circ }$ E to 45${}^{\circ }$ E in longitude. The meteorological data measurement interval of the study was 1970 to 2017. There are seven geographical regions in Turkey. These geographical regions are separated according to their climate, location, flora and fauna, human habitat, agricultural diversities, transportation, topography, etc. The names of the regions are: Mediterranean, Black Sea, Marmara, Aegean, Central Anatolia, Eastern Anatolian, and Southeastern Anatolia. There are meteorological measurement data in our meteorological database from 1161 meteorological observation stations. These stations were selected from different geographical regions. Sample data from different meteorological stations are given in

Table 1. Meteorological station samples from station database table.

Station No	Station Name	City	Town	Latitude (${}^{\circ }$)	Longitude (${}^{\circ }$)	Altitude (m)
17038	Trabzon	Trabzon	Ortahisar	40.99	39.78	39
17040	Rize	Rize	Merkez	41.04	40.50	3
17050	Edirne	Edirne	Merkez	41.67	26.55	51
17064	İstanbul	İstanbul	Kartal	40.91	29.15	18

.

Tables in the Meteorological Database

In this study, we used database tables containing ten types of meteorological measurements for our various queries. The types of meteorological measurements were: daily vapor pressure, daily hours of sunshine, daily maximum speed and direction of the wind, daily average actual pressure, daily average cloudiness, daily average relative humidity, daily average speed of the wind, daily average temperature, daily total rainfall—manual and daily total rainfall—omgi. The database table names of the measurement types and the details of each measurement are described in

Table 2. Database tables and descriptions.

Table Name	Description	Units
station	Station code, names, city, and coordinates	latitude, longitude, and altitude
vapor-pressure	Daily vapor pressure	hectopascal (1 hPa = 100 Pa)
sunshine-hour	Daily hours of sunshine	hours
speed-direction-wind	Daily max speed and direction of the wind	meter/second and direction
average-pressure	Daily average actual pressure	hectopascal (1 hPa = 100 Pa)
cloudiness	Daily average cloudiness	8 octa
average-humidity	Daily average relative humidity	percentage
average-speed-wind	Daily average speed of the wind	meter per second
average-temperature	Daily average temperature	celsius
total-rainfall-manual	Daily total rainfall—manual	kg per meter square
total-rainfall-omgi	Daily total rainfall—omgi	kg per meter square

.

These tables contain daily measurements from 1 January 1970 to 1 January 2017. Each table record consists of a station number, measurement type, measurement date, and measurement value. Sample data for the daily average speed of the wind are given in

Table 3. Sample data for daily average wind speed table.

Station No	Station Name	Year	Month	Day	The Daily Average Speed of Wind (m/s)
8541	HASSA	1977	1	1	1.3
8541	HASSA	1977	1	2	1.1
8541	HASSA	1977	1	3	3.1
8541	HASSA	1977	1	4	3.4

.

2.5. Supported Query Types

After illustrating the architecture of the proposed environment for fuzzy spatiotemporal querying, we apply the following procedures to handle the various query types employing the given components.

2.5.1. Fuzzy Non-Spatial Query

This query type asks for fuzzy data not dealing with spatial attributes. The QM, the FM, and the SOLAP server components are working in the execution step and the query flow is given in Figure 9:

• The QM retrieves the user query, parses it, and sends it to the FM.
• The QM asks the SOLAP server for data using the query. The objects retrieved by the QM are sent to the FM component to fuzzify the result.
• Fuzzified query results are displayed in the QM component.

Query1:Find all the cities at risk of flooding.

The query is expressed in MDX, which is an OLAP query language which provides a specialized syntax for querying and manipulating the multidimensional data stored in OLAP cubes [46]. While it is possible to translate some of these queries into traditional SQL, this would frequently require the synthesis of clumsy SQL expressions, even for elementary MDX expressions. Furthermore, many OLAP vendors have used MDX, and it has become the standard for OLAP systems. While it is not an open standard, it is embraced by a wide range of OLAP vendors. Therefore, we extended MDX with fuzzy operators and wrote the query specified above in MDX form, using the query parameters shown in Figure 10.

To query the database, we first need to defuzzfy the fuzzy expression part of the query. The query processor requests the FM to defuzzify the fuzzy expression in the query. The fuzzy term is defuzzified according to the fuzzy membership function, as shown in Figure 11. The heavy class in the query has a triangular-shaped membership function defined by the triple (7.5, 8.5, 9.5) that overlaps the membership function of the overmuch class in the range [7.5, 8.5]. In this case, the heavy class includes measurements between 8.0 and 9.5. The query processor of the GeoMondrian rearranges the MDX query with the crisp values after defuzzification and executes it in the SOLAP server. As a result of the query on the SOLAP server, the results matching the searched criteria contain crisp data. We again fuzzify the crisp values in the resulting data with the help of the FM. Here, the fuzzification subcomponent in the FM includes a triangular or trapezoidal membership function for each measurement result. It generates fuzzy class and membership values as output, using the crisp value of input from the relevant membership function. Finally, the results are displayed to the user, including fuzzy terms. For our example, we show the R1 and R4 records in

Table 4. Sample data for rainfall in database.

ID	Date	City	Crisp Val.	Fuzzy Val.
R1	19 August 2016	Ankara	8.6	heavy (0.7)
R2	19 August 2016	Konya	4.9	low (0.7)
R3	19 August 2016	Adana	4.1	very-low (0.6)
R4	19 August 2016	Rize	8.8	heavy (0.8)

as the query result that meets the criteria.

Suppose we execute this query in a relational database. In that case, we need to thoroughly scan all records, because it is necessary to calculate the rainfall value and find the queried value by grouping based on the city within the station measurement records. The cost of scanning all the data and grouping them is critical; the query execution time is related to the number of records in the database. In the FSOLAP environment, it is not necessary to access all records for the objects that satisfy the query criteria, due to the help of the hierarchical structure. The calculation of the measurements of the cities with which the stations are connected does not imply such a cost. Therefore, the cost of searching rainy stations is limited to the number of stations registered in the database, and the query execution time is less than the relational database query execution time.

2.5.2. Fuzzy Spatial Query

Fuzzy spatial queries allow the user to interrogate fuzzy spatial objects and their relationships. The QM, the FM, and the SOLAP server components are employed to fetch query results, as shown in Figure 12. The user asks for the objects that have topological relations with the entities under inquiry.

Query2:Retrieve the appropriate cities for the installation of a solar power plant

A fuzzy rule definition uses linguistic values, as shown below in the FKB regarding suitable places for solar power plants.

Figure 13 shows how we implemented the MDX query with the parameters entered from the query interface.

In this query, regions in the south of Turkey with a very high sunshine duration are considered. The intersection of areas with positionally high sunshine hour and south fields are taken into account. We explained the operational structure of the fuzzify_measure method in the previous query. Here, the fuzzify_geo method is also used. This method is run on the FM and determines the overlap relation between two geometric objects given as parameters. There are as many accesses in the query process as the number of stations in the database. On the other hand, the execution time for the relational database query, given in the following, can be longer due to the averaging of sunshine hour measurements and joining these with the stations.

In this query, cities with an average daily sunshine duration of more than seven hours are regarded as having a high sunshine duration. These cities are in the Mediterranean and Southeastern Anatolia regions in the south of the country.

2.5.3. Fuzzy Spatiotemporal Query

In this type of query, the user asks for the fuzzy spatial objects that meet the conditions of the predefined rules within a specified time interval. The rules can be evaluated by an examination of the topological relations between fuzzy regions and fuzzy objects. The query flow is shown in Figure 14.

Query3:Retrieve locations around Ankara that were at high risk of freezing between 7 January 2012 and 14 January 2012.

The FKB contains the following fuzzy rule definition that uses linguistic values regarding freezing events.

The query syntax’s implementation in MDX is represented in Figure 15.

In addition to the previous query, we can make more specific queries using date attribute conditions. The handling of the fuzzy predicates in the query operation is the same as for the fuzzy spatial query. For the distance attribute, the membership classes in the fuzzy data map are NEAR, CLOSE, and AROUND. We create these fuzzy classes by calculating the paired distances for the geometric data of the stations and applying fuzzy clustering of these values. However, the date predicate greatly reduces the amount of data to be retrieved from the database. As we mentioned earlier, this situation, which requires a full scan of an index-less relational database, is easily handled using the temporal hierarchy in the SOLAP environment. The execution time of the query depends on the number of stations in the database. Relational database systems must be fully searched for temperature and cloudiness between the given dates. In this case, the query execution time is proportional to the number of records and the number of stations in the database.

2.5.4. Fuzzy Spatiotemporal Predictive Query

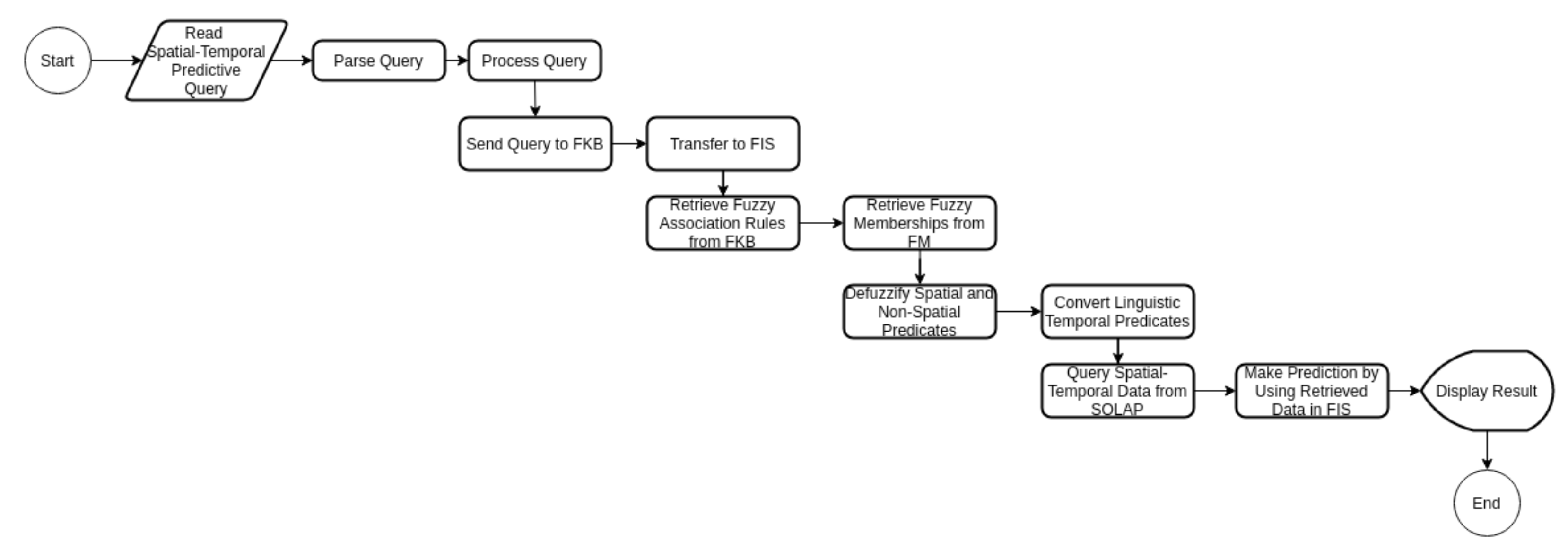
This type of query asks for fuzzy spatial relations and a specified time with inference. The QM, the FM, the FIS, the FKB, and the SOLAP server components are employed to fetch query results, and the query flow is shown in Figure 16. The QM retrieves the user query, parses it, and sends it to the FM for defuzzification. If the QM detects the inference operand in the query, it sends the conditions to the FKB for inference. When the FKB receives the request from the QM, it determines the fuzzy association rules and sends them to the FIS, and the FIS obtains membership classes/functions from the fuzzy data map subcomponent. The FIS makes predictions with the given parameters and the collected knowledge, and then it sends the inference back to the QM.

Query4:Is there a possibility of a windstorm around Izmir during the last week of December?

The FKB contains the following rules for meteorological events that occur depending on wind speed.

Unlike other query types, the antecedent part of the association rules is not used in the FKB as a criterion when considering predictive queries. Since the purpose here is to predict the conditions that are the antecedents of the meteorological phenomenon in question, we do not include these fields in the query. Other fuzzy attributes are used as criteria in the MDX query. In addition, the spatial and temporal criteria entered into the interface are used for querying. When the QM detects the PREDICT expression in the query, it recognizes that the query requires an inference mechanism. The MDX query constructed with the criteria entered into the meteorological phenomenon query UI is illustrated in Figure 17.

We previously mentioned that the fuzzy association rules which are expert-defined are stored in the FKB. The fuzzy association rules defined for the relevant phenomenon are chosen in the meteorological phenomenon inquiry. The antecedent of each rule is used to look for the fuzzy attribute and membership class found in the consequent part of the fuzzy association rules. In other words, the rules which include these antecedents in the FKB are selected as a consequence of the rules in the fuzzy association rules, and this process is demonstrated in Figure 18.

We create inferences for each row fetched from the MDX query by running the rules selected from the fuzzy association rule set in the FIS, as shown in Figure 19. The minimum value is calculated by multiplying the results by the weight value of each association rule. The same fuzzy class result is determined by taking the maximum value among the minimum values. If the result value meets the expected criteria, the relevant MDX query result row is marked as satisfied. The results marked as satisfied are shown on the results list and the map.

A sample inference is given in Figure 20. In this example, consider a current situation where the relative humidity is 48%, the temperature is +25${}^{\circ }$, and the cloudiness is 3/8. We want to predict the sunshine hours using this information. The relative humidity of 48% is translated into the linguistic variable value of $\{0.3,0.7,0,0,0\}$ which can be interpreted as “less, normal”. Similarly, linguistic translation can be given as “hot, boiling” for temperature and “partly sunny, partly cloudy” for cloudiness. After all the input variables have been converted to linguistic variable values, the fuzzy inference step can identify the rules that apply to the current situation and can compute the values of the output linguistic variable. As seen in the figure, the five rules of thumb can be translated into a fuzzy rule base using these linguistic terms to describe the meteorological prediction. The rules are selected according to the consequent part. There are three proper rules which have a sunshine hours consequent and can be used for inference. After the rules are executed, the center of gravity method is used to calculate the final predicted value.

3. Experimental Results

3.1. Platform

We achieved reasonable performance of the prototype application in the environment and with the specifications, technology, and tools specified below.

• Application development environment: Eclipse IDE 2021-03;
• System: Windows 10 x64, Intel i5-7200U CPU, 16 GB RAM;
• Java: 1.8.0-281, Java HotSpot Client 64-bit Server VM 25.281-b09;
• SOLAP: GeoMondrian 1.0 Server;
• DBMS: PostgreSQL 13.3 64-bit;
• FIS: jFuzzyLogic.jar;
• Data Size: approximately 10 GB data consisting of 1161 stations and 15 M records for each measurements (15 M × 10 measurement types).

3.2. Performance Results

We measured the average CPU usage, memory usage, and execution time by running each query type in the fuzzy SOLAP-based framework and the PostgreSQL database. Here, average CPU usage is the average CPU usage rate measured during querying. Similarly, average memory usage is the average memory usage measured in megabytes (MB) during querying. The execution time is the average of the measurements obtained over several query runs.

First, we addressed some of the high-level factors that affect the query performance with regard to CPU usage, memory usage, and execution time. Data size directly affects the performance of the query because the query uses one or more tables with millions of rows or more. Joins are another factor affecting performance; if the query joins two tables, increasing the row count of the result set substantially, the query is likely to be slow. Aggregations also affect performance, as combining multiple rows to produce a result requires more computation than simply retrieving those rows.

In addition to obtaining this information, we also performed the roll-up function provided by SOLAP for aggregating with the UNION operator in relational database queries. In this case, aggregating N dimensions requires N such unions in an SQL query. Another essential issue to consider in terms of query performance is that of cross-tabulations. While SOLAP supports such operations naturally, SQL requires an even more complicated combination of unions and GROUP BY clauses for cross-tabulations. An N-dimensional cross-tabulation requires a $2^N$-way union of $2^N$ different GROUP BY operators to build the underlying representation. In most relational databases, this results in $2^N$ scans of the data and $2^N$ sorts or hashes.

The CPU usage for the queries was measured over several query runs, and the average CPU usage for all query types was calculated. The results are given in

Table 5. Comparision of average CPU usages between FSOLAP and relational database SQL queries.

	FSOLAP Query Ave. CPU Usage (%)	Relational Database SQL Query Ave. CPU Usage (%)
Query1	29.2	33.7
Query2	30.3	36.6
Query3	30.1	31.3
Query4	30.9	Not Supported

.

The average CPU usages of the FSOLAP-based query and the relational database query are compared in the column chart shown in Figure 21.

Similar to the computational power requirement, the measurement results for the average memory usage are given in

Table 6. Comparision of average memory usages between FSOLAP and relational database SQL queries.

	FSOLAP Query Ave. Memory Usage (MB)	Relational Database SQL Query Ave. Memory Usage (MB)
Query1	150	278
Query2	228	330
Query3	115	229
Query4	217	Not Supported

.

The average memory usages of the queries are represented graphically in Figure 22. According to this chart, relational database queries consume more memory than FSOLAP-based queries.

A comparison of the execution times of the queries was used as part of the performance testing, and the results are shown in

Table 7. Comparison of average execution times between FSOLAP and relational database SQL queries.

	FSOLAP Query Ave. Execution Time (ms)	Relational Database SQL Query Ave. Execution Time (ms)
Query1	596,480	1,630,362
Query2	257,054	643,642
Query3	18,314	172,303
Query4	183,717	Not Supported

.

We have shown the time spent between starting the query and finishing the query graphically for each query in Figure 23. The graph shows that relational database queries have a longer execution time.

The implementation of Query 1 in the relational database requires the $havingavg$ operation as an aggregation for all cities. This requires a great deal of CPU and memory resource usage. Along with these, it also causes a long query time. Query 2 requires $havingavg$ as an aggregation along with a spatial search. A spatial data search uses index matches with the join operand in the query. This query requires more CPU and memory than other queries, but the query time is comparatively less than Query 1 since the query has a spatial restriction. Query 3, on the other hand, is better in terms of resource usage as it possesses additional time restrictions compared to Query 2, but it also takes less query time. The aggregation process in the queries involves the CPU usage, the union, and the join operands, affecting the memory usage. According to the query criteria, the amount of data in the query process determines the query time. When we evaluate the performance tests in general, we observe that FSOLAP-based query operations require fewer resources and less time than relational database queries. While we obtain adequate CPU and memory usage results, especially in queries containing spatial and temporal criteria, we obtain better results in terms of execution time. In addition, FSOLAP performs well in prediction-type queries, which are not supported for relational database queries.

Based on our experimental analysis and considering all the parameters mentioned, FSOLAP-based querying is preferred over relational database querying, as FSOLAP offers scalability with low resource usage.

4. Discussion

In this paper, we introduced FSOLAP as a new fuzzy SOLAP-based framework to compound the advantages of fuzzy and SOLAP concepts and explained how it supports complex fuzzy spatial queries. We tested the efficiency and effectiveness of FSOLAP in a meteorological application with spatial and temporal hierarchical data, using fuzzy spatial and fuzzy spatiotemporal query types. Moreover, we showed that the fuzzy logic approach is an effective approach for complex applications such as spatiotemporal data with fuzzy spatial queries containing fuzzy terms. In addition, we explained how we handled fuzzy spatiotemporal predictive queries using the inference capability, which has not been previously discussed in the literature. We integrated these queries into FSOLAP with the use of an FIS. It was shown that FSOLAP handles queries effectively and efficiently using fewer resources compared to a relational database system, based on average CPU usage, average memory usage, and average execution time for each type of query. While SOLAP handles hierarchical data naturally, SQL does so with the union operator, which requires high CPU and memory usage as the test results showed. Similarly, SOLAP handles the operation performed by SQL using the group by statement with its core functionality. In extensive performance tests, complex queries structurally containing a group by statement have been shown to require less CPU and memory usage in FSOLAP compared to SQL queries. The average CPU and memory usage of queries during execution is proportionally similar, but the query execution time does not have the same trend. This is because the criteria for query types are determined by the amount of data the query retrieves and processes. As the number of restrictions in query types increased, query execution time decreased inversely.

Related studies on fuzzy SOLAP-based data mining and querying were investigated with regard to whether they have the following concepts or features: fuzziness, OLAP, SOLAP, data mining, inference, temporal querying, fuzzy querying, fuzzy spatial querying, fuzzy predictive querying, high visualization, easy use and performance evaluation. A system known as a fuzzy storage assignment system (FSAS) that provides fuzziness, OLAP, data mining, inference, and fuzzy querying based on fuzzy OLAP was proposed in the study by Lam et al. [15]. Their study was aimed at increasing the availability of decision support data and converting human knowledge into a system for tackling the storage location assignment problem. In another study, David et al. [18] researched fuzzy spatial data warehouses. They proposed a model that supports fuzziness, OLAP, SOLAP, data mining, inference, fuzzy querying, and fuzzy spatial querying. Their work represented a part of the Intelligent Geographical Project (IGP), which integrated fuzzy logic with spatial databases to help in the decision support and OLAP querying processes. Boutkhoum and Hanine [13] also developed software for complex decision-making problems. The software implementation was an integrated decision-making prototype based on an OLAP system and multicriteria analysis (MCA) to generate a hybrid analysis process dealing with complex multicriteria decision-making situations. Their proposal included fuzziness, OLAP, data mining, inference, temporal querying, and fuzzy querying. Ladner et al. [17] studied the use of fuzzy set approaches in spatial data mining to integrate their GIDB geospatial system. They presented an approach to discovering association rules for fuzzy spatial data where they were interested in correlations of spatially related data such as directional or geometric relationships of soil types. They combined and extended techniques developed in spatial and fuzzy data mining to deal with the uncertainty found in typical spatial data, supporting fuzziness, data mining, inference, fuzzy querying, and fuzzy spatial querying. FSOLAP and some related approaches in the literature are compared according to their concepts and characteristics in

Table 8. Comparision of FSOLAP and existing approaches.

	FSAS [15]	IGP [18]	OLAP MCA [13]	GIDB [17]	FSOLAP
Fuzziness	✓	✓	✓	✓	✓
OLAP	✓	✓	✓		✓
SOLAP		✓		✓	✓
Data Mining	✓	✓	✓	✓	✓
Inference	✓	✓	✓	✓	✓
Temporal Querying			✓		✓
Fuzzy Querying	✓	✓	✓	✓	✓
Fuzzy Spatial Querying		✓		✓	✓
Fuzzy Predictive Querying					✓
High Visualization	✓		✓
Performance Evaluation					✓
Easy to Use	✓		✓

.

Although the FSOLAP framework brings together the strengths of fuzzy and SOLAP concepts for spatiotemporal applications and offers effective and efficient querying, it has difficulty in defining the expert rules in the representative application domain. As shown in the example queries, the expert-defined rules that the queries refer to must be defined in the system by domain experts. This situation makes it difficult for naïve users to use the framework without the help of a domain expert. Moreover, although FSOLAP provides some visualization, this functionality needs improvement as it is a spatiotemporal application. Future studies aimed at making the framework easy to use can be applied in this context. The realization of these studies would also make it possible to use this framework of analysis and inference in different fields such as agriculture, maritime transport, and others. For example, in the field of agriculture, a future study may develop an early warning system that can alert farmers by mapping the risk of frost.

5. Conclusions

This study proposed a framework based on fuzzy SOLAP (FSOLAP) to analyze fuzzy spatiotemporal data and make predictive analyses of various spatiotemporal events. To achieve this, fuzzy and SOLAP were harmonized to take advantage of the strengths of these two concepts. Moreover, an inference capability was added to the framework to support the predictive type of queries. In summary, some modifications of the SOLAP server and MDX queries were implemented, fuzzification operations were performed, association rules were generated, and pruning and weighting rules were applied to assemble the framework. Then, the performance of the framework was represented by non-spatial, spatial, spatiotemporal, and predictive fuzzy complex queries. We used a case study of a real database involving meteorological objects with specific spatial and temporal attributes. This study showed that the use of fuzzy concepts and SOLAP for spatiotemporal applications was effective and efficient, which was confirmed by both the implementation of query types and performance tests. Features provided by FSOLAP were compared with features in related works, and FSOLAP was shown to have a much broader functionality than the approaches used in similar studies in the literature. Making the framework easy to use for naïve users and enabling it to be utilized in other fields are suggested as avenues for future studies.

The main objective of this paper was to describe a generic fuzzy querying approach to process complex and flexible queries using the FSOLAP framework. We also aimed to manage uncertainty in spatiotemporal database applications when querying the database. A real-life database that involves meteorological objects with certain spatial and temporal attributes was used as a case study. The proposed mechanism was implemented and several implementation issues that arose when querying the database were discussed.

This study used meteorological aspects and geographic data as spatiotemporal objects. Furthermore, the inference system in the fuzzy SOLAP environment integrated the model with a fuzzy inference system for allowing prediction over spatiotemporal data. As a result, a fuzzy spatiotemporal predictive query could be executed by using the framework.

Modeling and querying spatiotemporal data requires further research in future studies. The model and method presented in this study could be adjusted and/or extended to other fields of application such as agriculture, environment, etc. We implemented some of the fuzzy methods needed in this study, but the set of fuzzy methods should be further extended to different areas. This study implemented a generic fuzzy querying approach to process complex and fuzzy queries using our FSOLAP framework. In this context, the framework supports non-spatial and fuzzy spatial queries as well as fuzzy spatiotemporal query types. The processing of fuzzy aggregation queries and the corresponding algorithms may be studied in future work to explain the involvement of fuzzy spatial hierarchical relationships among members in the computation of the aggregation of numerical measures.