A New Graph-Based Fractality Index to Characterize Complexity of Urban Form
Abstract
:1. Introduction
- 1.
- Introducing a new graph convolution neural network framework on irregular building distributions to describe their local spatial and attribute features for each building, as well as their global statistical features;
- 2.
- Devising a method under the second fractal definition to synthesize fractal patterns by an established square-based fractal regime, the Sierpinski carpet, that can be used as training and validation datasets;
- 3.
- Showing how the proposed GFI can compensate for the inability of either the fractal dimension or ht-index (or its derivative: cumulative rate of growth index, CRG) to integrate the fractal-related computations with both spatial and aspatial aspects.
2. Related Work
2.1. Complexity of Urban Morphology
2.2. Graph Convolutional Networks
3. Methods
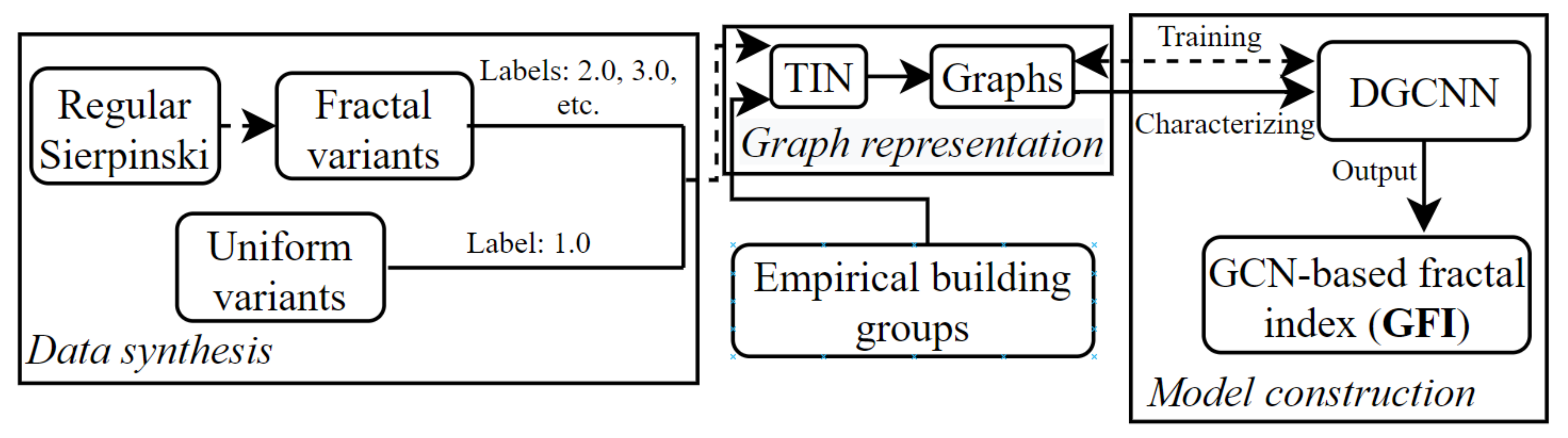
3.1. Framework for Characterizing Complexity of Building Distributions
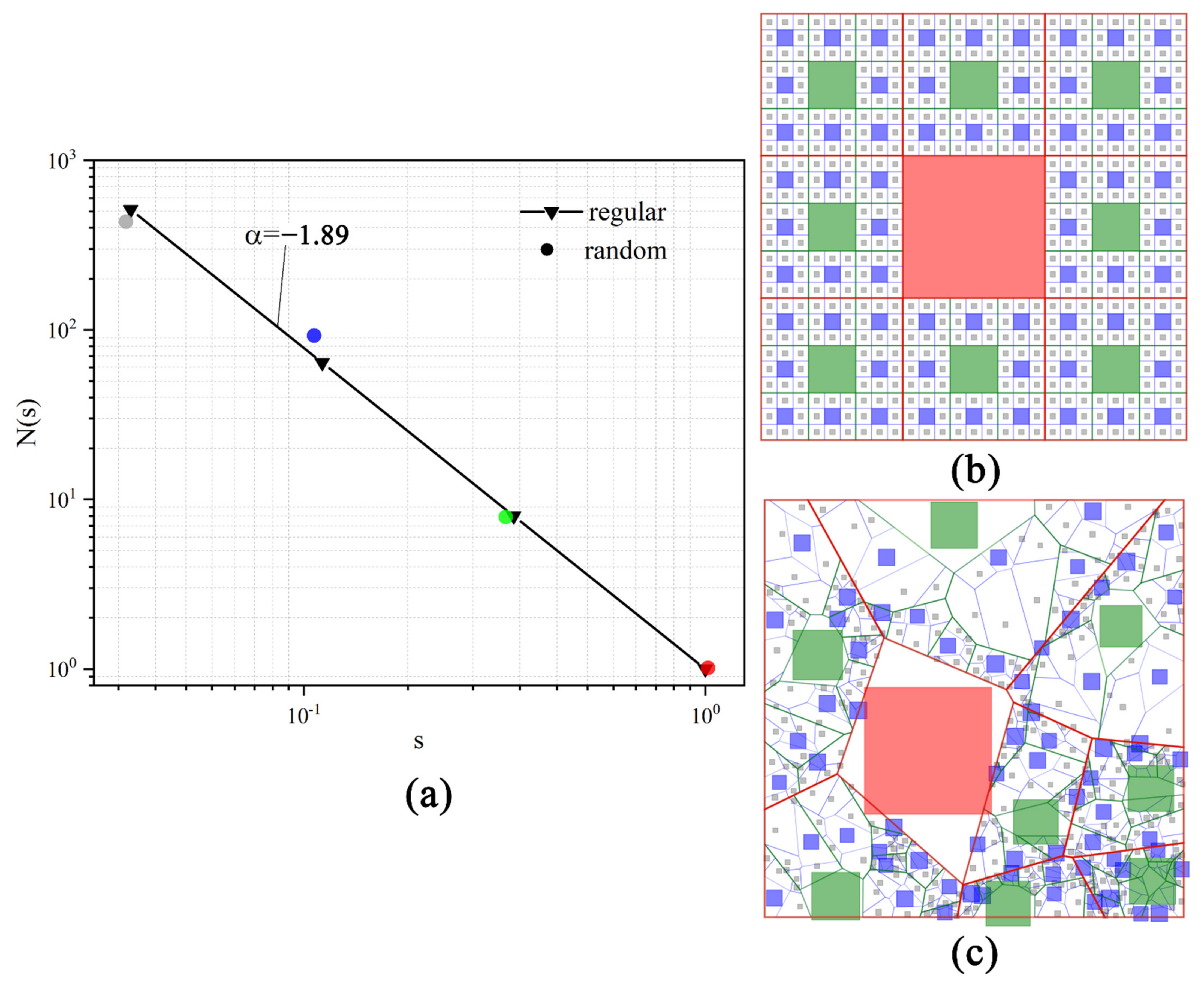
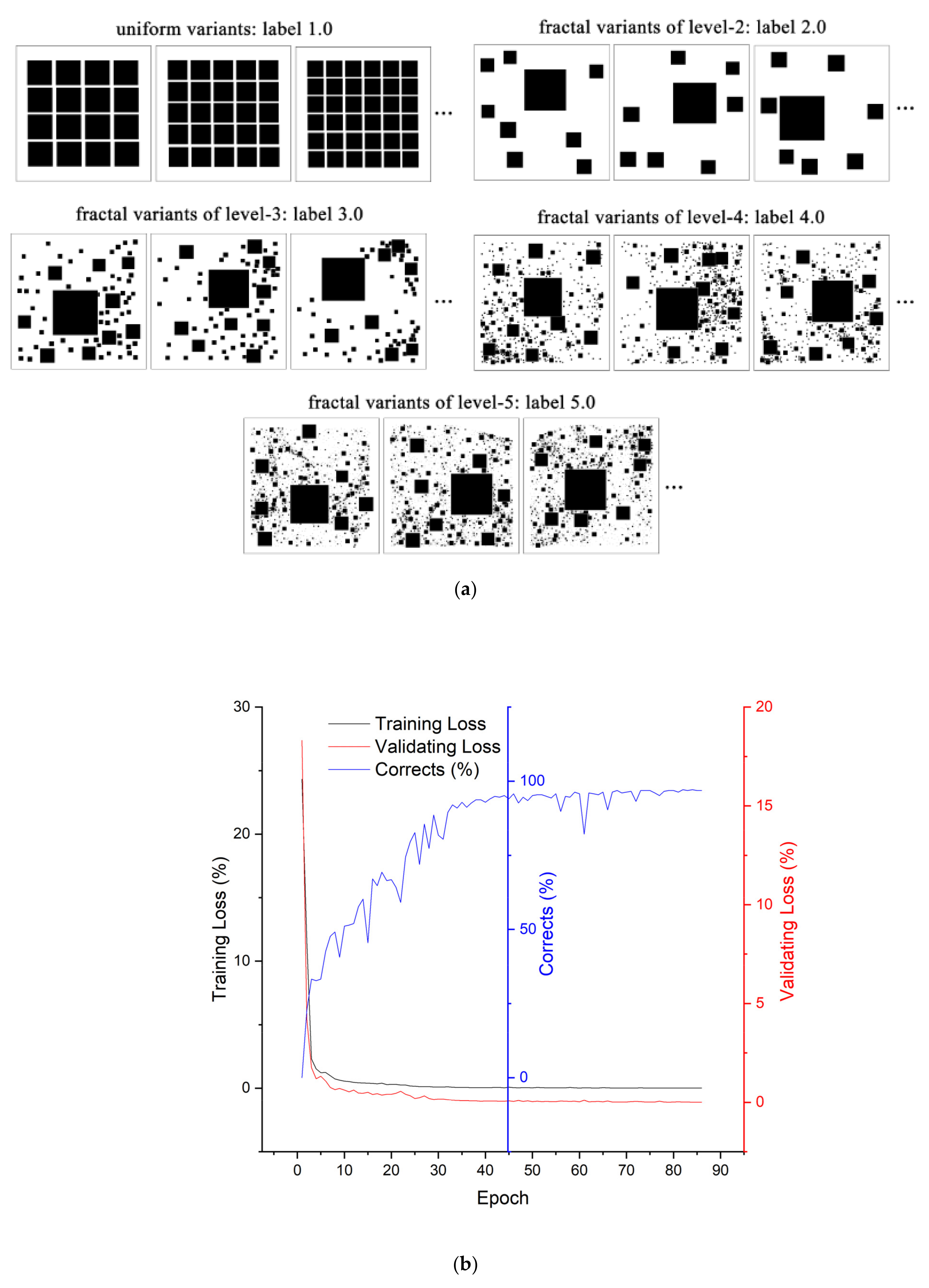
3.2. Synthetic Fractals and Uniform Variants
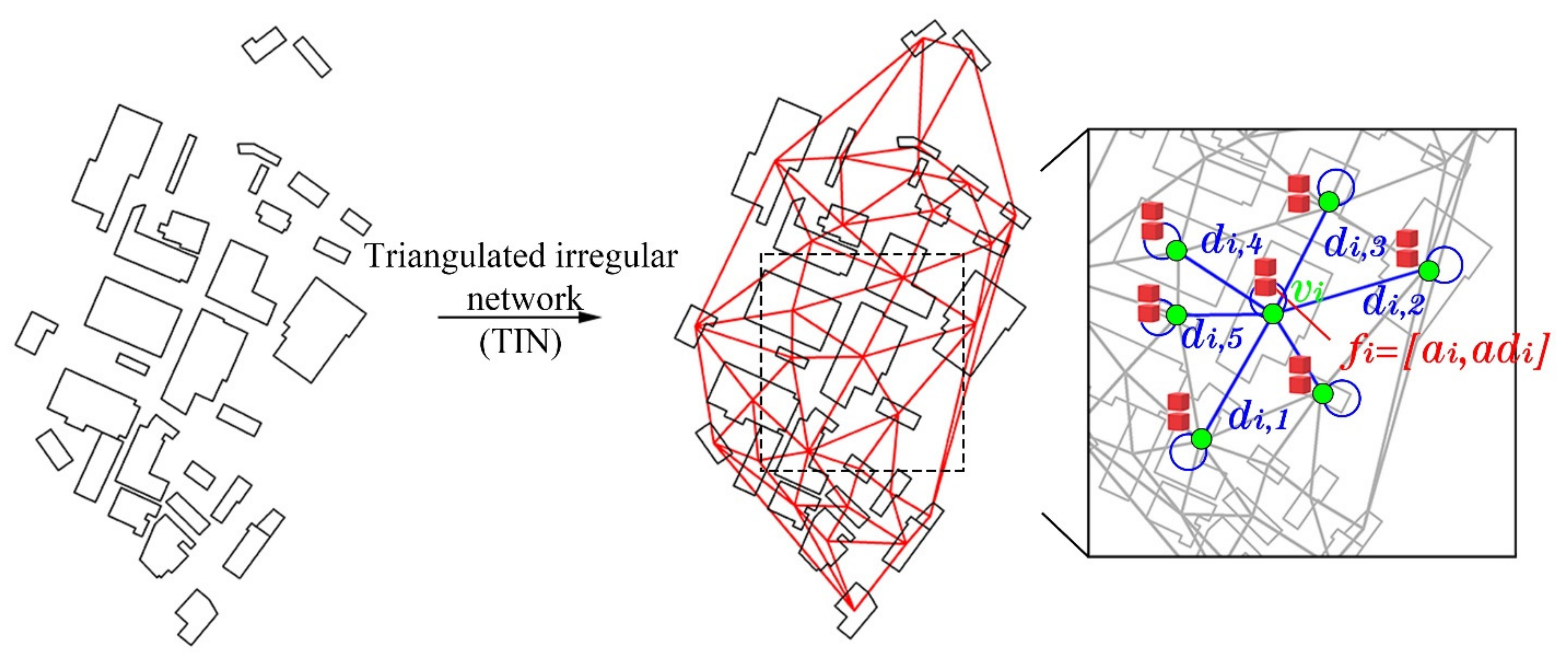
3.3. Graph Representations for Building Groups
3.4. DGCNN Model
3.4.1. GCN Layers
3.4.2. The SortPooling Layer
4. Synthetic Variants and Model Training
5. Case Studies
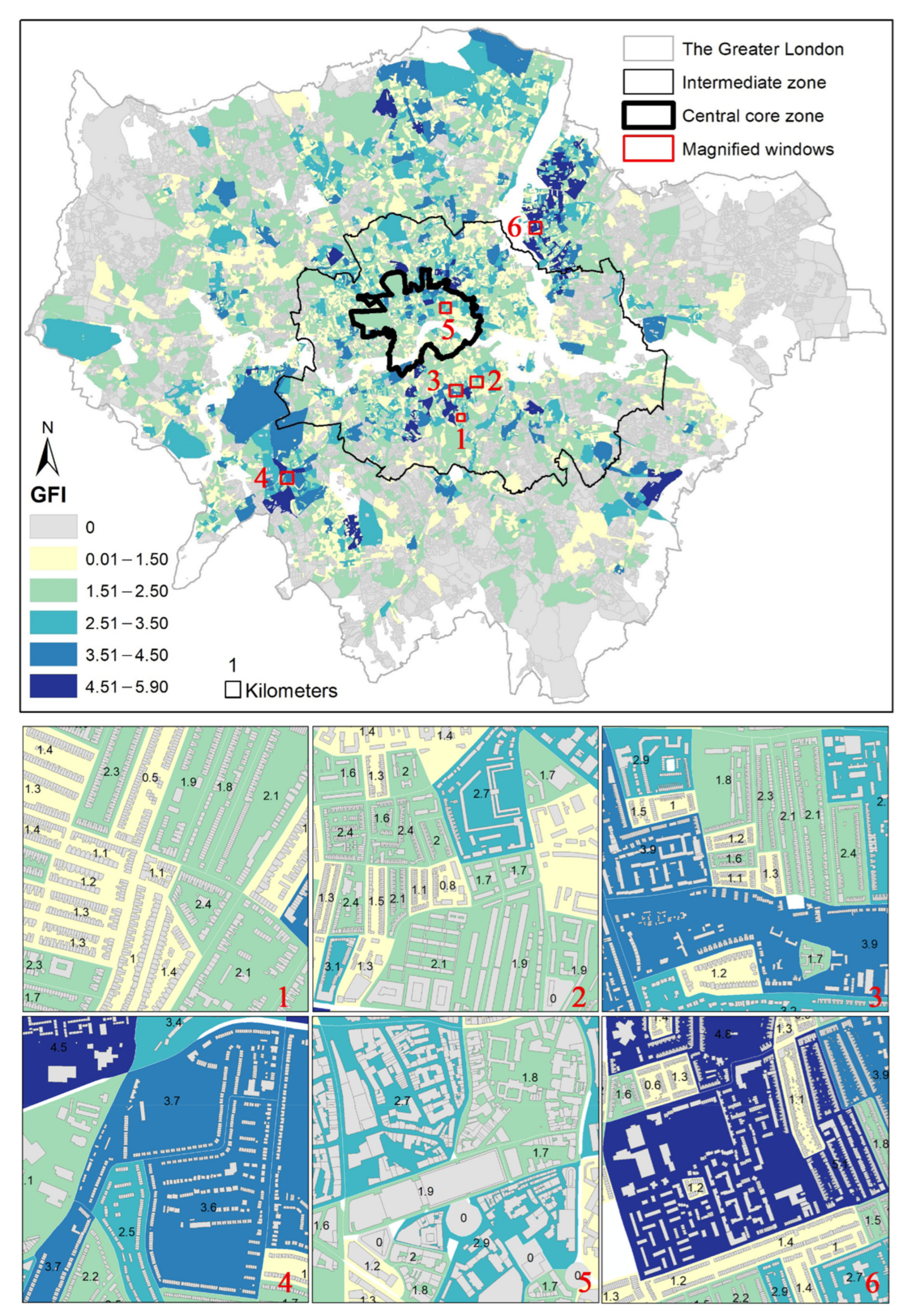
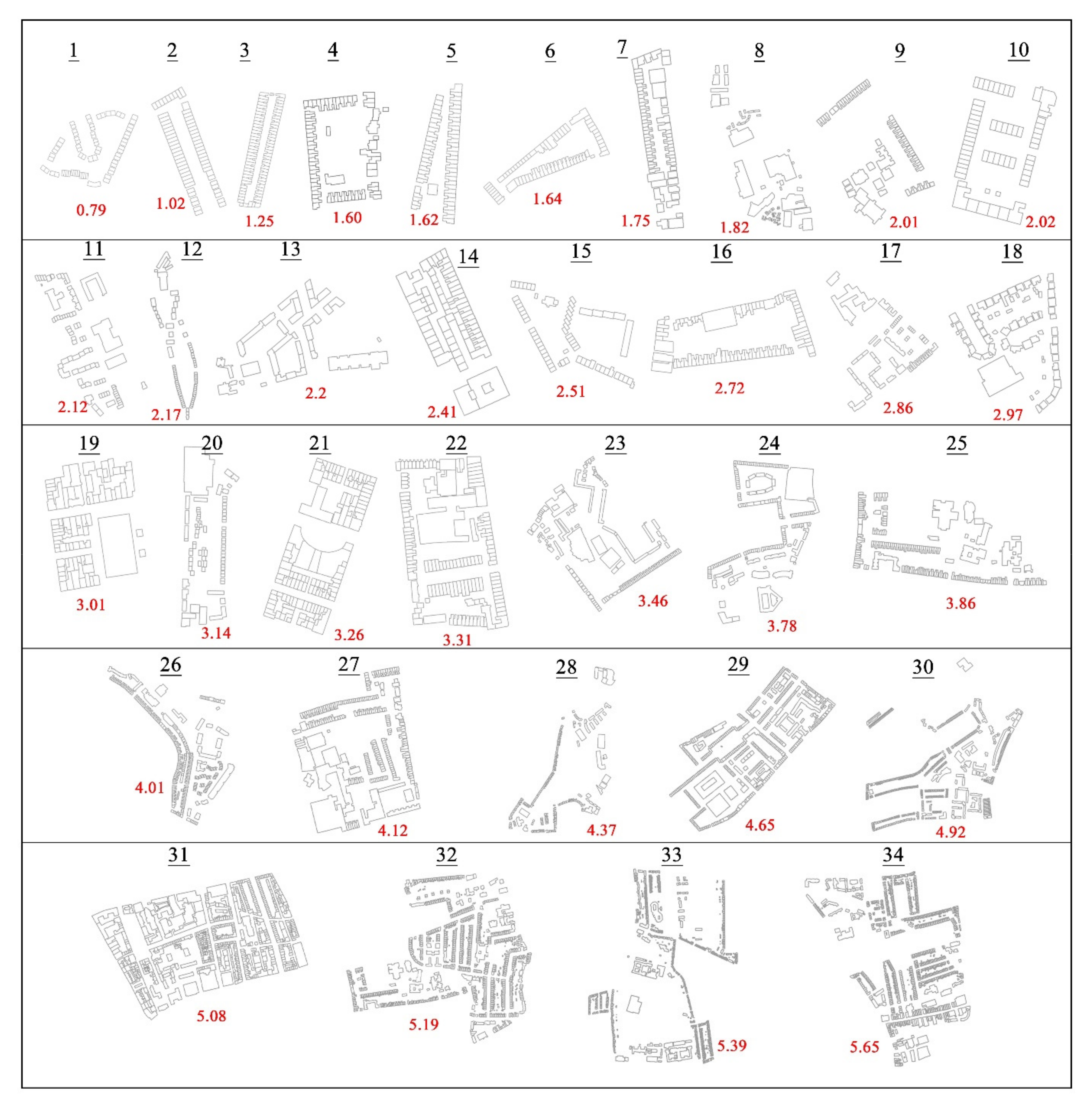
5.1. Building Footprints in Blocks
5.2. Building Footprints in Neighborhood
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Mandelbrot, B.B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lauwerier, H. Fractals: Endlessly Repeated Geometrical Figures; Gill-Hoffstädt, S., Translator; Princeton University Press: Princeton, NJ, USA, 1991. [Google Scholar]
- Jiang, B.; Yin, J. Ht-Index for Quantifying the Fractal or Scaling Structure of Geographic Features. Ann. Assoc. Am. Geogr. 2013, 104, 530–540. [Google Scholar] [CrossRef]
- Jiang, B.; Brandt, S.A. A Fractal Perspective on Scale in Geography. ISPRS Int. J. Geo. Inf. 2016, 5, 95. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Ma, D. How Complex Is a Fractal? Head/tail Breaks and Fractional Hierarchy. J. Geovisualization Spat. Anal. 2018, 2, 6. [Google Scholar] [CrossRef] [Green Version]
- Batty, M.; Longley, P.A. Fractal Cities: A Geometry of Form and Function; Academic Press Inc.: San Diego, CA, USA, 1994. [Google Scholar]
- Tannier, C.; Thomas, I.; Vuidel, G.; Frankhauser, P. A Fractal Approach to Identifying Urban Boundaries. Geogr. Anal. 2011, 43, 211–227. [Google Scholar] [CrossRef]
- Tannier, C.; Thomas, I. Defining and characterizing urban boundaries: A fractal analysis of theoretical cities and Belgian cities. Comput. Environ. Urban Syst. 2013, 41, 234–248. [Google Scholar] [CrossRef]
- Thomas, I.; Frankhauser, P. Fractal Dimensions of the Built-up Footprint: Buildings versus Roads. Fractal Evidence from Antwerp (Belgium). Environ. Plan. B Plan. Des. 2013, 40, 310–329. [Google Scholar] [CrossRef]
- Rootzén, H.; Segers, J.; Wadsworth, J.L. Multivariate generalized Pareto distributions: Parametrizations, representations, and properties. J. Multivar. Anal. 2018, 165, 117–131. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhou, J. Introduction to Graph Neural Networks. Synth. Lect. Artif. Intell. Mach. Learn. 2020, 14, 1–127. [Google Scholar] [CrossRef]
- Batty, M. Inventing Future Cities; Batty, M., Ed.; The MIT Press: Cambridge, MA, USA, 2019. [Google Scholar] [CrossRef]
- Ma, D.; Osaragi, T.; Oki, T.; Jiang, B. Exploring the heterogeneity of human urban movements using geo-tagged tweets. Int. J. Geogr. Inf. Sci. 2020, 34, 2475–2496. [Google Scholar] [CrossRef]
- D’Acci, L. Mathematics of Urban Morphology; Luca, D., Ed.; Birkhäuser: Basel, Switzerland, 2019. [Google Scholar]
- Hillier, B.; Hanson, J. The Social Logic of Space; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1984. [Google Scholar] [CrossRef]
- Zhang, X.; Stoter, J.; Ai, T.; Kraak, M.J.; Molenaar, M. Automated evaluation of building alignments in generalized maps. Int. J. Geogr. Inf. Sci. 2013, 27, 1550–1571. [Google Scholar] [CrossRef]
- Zhang, X.; Ai, T.; Stoter, J. Characterization and detection of building patterns in cartographic data: Two algorithms. In Advances in Spatial Data Handling and GIS; Springer: Berlin/Heidelberg, Germany, 2012; pp. 93–107. [Google Scholar]
- Zhao, R.; Ai, T.; Yu, W.; He, Y.; Shen, Y. Recognition of building group patterns using graph convolutional network. Cartogr. Geogr. Inf. Sci. 2020, 47, 400–417. [Google Scholar] [CrossRef]
- He, X.; Zhang, X.; Xin, Q. Recognition of building group patterns in topographic maps based on graph partitioning and random forest. ISPRS J. Photogramm. Remote Sens. 2018, 136, 26–40. [Google Scholar] [CrossRef]
- Du, S.; Zhang, F.; Zhang, X. Semantic classification of urban buildings combining VHR image and GIS data: An improved random forest approach. ISPRS J. Photogramm. Remote Sens. 2015, 105, 107–119. [Google Scholar] [CrossRef]
- Niu, N.; Liu, X.; Jin, H.; Ye, X.; Liu, Y.; Li, X.; Chen, Y.; Li, S. Integrating multi-source big data to infer building functions. Int. J. Geogr. Inf. Sci. 2017, 31, 1871–1890. [Google Scholar] [CrossRef]
- Lüscher, P.; Weibel, R.; Burghardt, D. Integrating ontological modelling and Bayesian inference for pattern classification in topographic vector data. Comput. Environ. Urban Syst. 2009, 33, 363–374. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Yan, H.; Ai, T.; Chen, J. Automated building generalization based on urban morphology and Gestalt theory. Int. J. Geogr. Inf. Sci. 2004, 18, 513–534. [Google Scholar] [CrossRef]
- Batty, M.; Kim, K.S. Form Follows Function: Reformulating Urban Population Density Functions. Urban Stud. 1992, 29, 1043–1069. [Google Scholar] [CrossRef]
- Thomas, I.; Frankhauser, P.; De Keersmaecker, M.-L. Fractal dimension versus density of built-up surfaces in the periphery of Brussels. Pap. Reg. Sci. 2007, 86, 287–308. [Google Scholar] [CrossRef]
- Sémécurbe, F.; Tannier, C.; Roux, S.G. Applying two fractal methods to characterise the local and global deviations from scale-invariance of built patterns throughout mainland France. J. Geogr. Syst. 2019, 21, 271–293. [Google Scholar] [CrossRef] [Green Version]
- Lagarias, A.; Prastacos, P. Comparing the urban form of South European cities using fractal dimensions. Environ. Plan. B Urban Anal. City Sci. 2018, 47, 1149–1166. [Google Scholar] [CrossRef]
- Thomas, I.; Frankhauser, P.; Badariotti, D. Comparing the fractality of European urban neighbourhoods: Do national contexts matter? J. Geogr. Syst. 2010, 14, 189–208. [Google Scholar] [CrossRef]
- Gao, P.; Liu, Z.; Xie, M.; Tian, K.; Liu, G. CRG Index: A More Sensitive Ht-Index for Enabling Dynamic Views of Geographic. Features Prof. Geogr. 2015, 68, 533–545. [Google Scholar] [CrossRef]
- Gao, P.; Zhao, L.; Kun, T.; Gang, L. Characterizing traffific conditions from the perspective of spatial-temporal heterogeneity. ISPRS Int. J. Geo. Inf. 2016, 5, 34. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.; Liu, Z.; Liu, G.; Zhao, H.; Xie, X. Unified metrics for characterizing the fractal nature of geographic features. Ann. Am. Assoc. Geogr. 2017, 107, 1315–1331. [Google Scholar] [CrossRef]
- Jiang, B. Head/Tail Breaks: A New Classification Scheme for Data with a Heavy-Tailed Distribution. Prof. Geogr. 2013, 65, 482–494. [Google Scholar] [CrossRef]
- Ren, Z.; Jiang, B.; Seipel, S. Capturing and Characterizing Human Activities Using Building Locations in America. ISPRS Int. J. Geo. Inf. 2019, 8, 200. [Google Scholar] [CrossRef] [Green Version]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019; pp. 1–17. [Google Scholar]
- Hu, W.; Yan, L.; Liu, K.; Wang, H. A Short-term Traffic Flow Forecasting Method Based on the Hybrid PSO-SVR. Neural Process. Lett. 2015, 43, 155–172. [Google Scholar] [CrossRef]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion Convolutional Recurrent Neural Network. In International Conference on Learning Representations; University of California: Oakland, CA, USA, 2018; Volume 1090, pp. 1–15. [Google Scholar]
- Jin, G.; Cui, Y.; Zeng, L.; Tang, H.; Feng, Y.; Huang, J. Urban ride-hailing demand prediction with multiple spatio-temporal information fusion network. Transp. Res. Part C Emerg. Technol. 2020, 117, 102665. [Google Scholar] [CrossRef]
- Yi, X.; Zhang, J.; Wang, Z.; Li, T.; Zheng, Y. Deep Distributed Fusion Network for Air Quality Prediction. In Proceedings of the KDD ’18: 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 19–23 August 2018. [Google Scholar] [CrossRef]
- Yu, L.; Jiao, C.; Xin, H.; Wang, Y.; Wang, K. Prediction on Housing Price Based on Deep Learning. Int. J. Comput. Inf. Eng. 2018, 12, 90–99. [Google Scholar] [CrossRef]
- Yildirimoglu, M.; Kim, J. Identification of communities in urban mobility networks using multi-layer graphs of network traffic. Transp. Res. Part C Emerg. Technol. 2018, 89, 254–267. [Google Scholar] [CrossRef]
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning convolutional neural networks for graphs. In International Conference on Machine Learning; ICML 2016 4; PMLR: New York, NY, USA, 2016; pp. 2958–2967. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar] [CrossRef]
- Zheng, C.; Fan, X.; Wang, C.; Qi, J. GMAN: A Graph Multi-Attention Network for Traffic Prediction. Proc. Conf. AAAI Artif. Intell. 2020, 34, 1234–1241. [Google Scholar] [CrossRef]
- Wu, Y.; Lian, D.; Xu, Y.; Wu, L.; Chen, E. Graph Convolutional Networks with Markov Random Field Reasoning for Social Spammer Detection. Proc. Conf. AAAI Artif. Intell. 2020, 34, 1054–1061. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Yin, H. A graph convolutional neural network for classification of building patterns using spatial vector data. ISPRS J. Photogramm. Remote Sens. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Yan, X.; Ai, T.; Yang, M.; Tong, X. Graph convolutional autoencoder model for the shape coding and cognition of buildings in maps. Int. J. Geogr. Inf. Sci. 2020, 35, 490–512. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, Z.; Neumann, M.; Chen, Y. An end-to-end deep learning architecture for graph classification. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 4438–4445. [Google Scholar]
- Sankaranarayanan, S.; Balaji, Y.; Jain, A.; Lim, S.N.; Chellappa, R. Learning from Synthetic Data: Addressing Domain Shift for Semantic Segmentation. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 3752–3761. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; W.H. Freeman and Company: New York, NY, USA, 1977. [Google Scholar]
- Van Pabst, L.v.L.; Jense, H. Dynamic Terrain Generation Based on Multifractal Techniques. In High Performance Computing for Computer Graphics and Visualisation; Springer: New York, NY, USA, 1996; pp. 186–203. [Google Scholar] [CrossRef]
- Re, A.D.L.; Abad, F.; Camahort, E.; Juan, M.C. Tools for Procedural Generation of Plants in Virtual Scenes. In Lecture Notes in Computer Science; Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics 5545 LNCS (PART 2); Springer: Berlin/Heidelberg, Germany, 2009; pp. 801–810. [Google Scholar]
- Vicsek, T.; Gould, H. Fractal Growth Phenomena. Comput. Phys. 1989, 3, 108. [Google Scholar] [CrossRef]
- Thomas, I.; Frankhauser, P.; Biernacki, C. The morphology of built-up landscapes in Wallonia (Belgium): A classification using fractal indices. Landsc. Urban Plan. 2008, 84, 99–115. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. Adv. Neural Inf. Process. Syst. 2016, 59, 3844–3852. [Google Scholar]
- Micheli, A. Neural Network for Graphs: A Contextual Constructive Approach. IEEE Trans. Neural Netw. 2009, 20, 498–511. [Google Scholar] [CrossRef]
- Atwood, J.; Towsley, D. Diffusion-convolutional neural networks. Adv. Neural Inf. Process. Syst. 2016, 29. Available online: https://cpb-us-w2.wpmucdn.com/sites.coecis.cornell.edu/dist/9/287/files/2019/08/Towsley-6-6212-diffusion-convolutional-neural-networks.pdf (accessed on 10 February 2022).
- Heaven, D. Why deep-learning AIs are so easy to fool. Nature 2019, 574, 163–166. [Google Scholar] [CrossRef] [PubMed]
- Gahegan, M. Fourth paradigm GIScience? Prospects for automated discovery and explanation from data. Int. J. Geogr. Inf. Sci. 2019, 34, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Hajrasoulih, A.; del Rio, V.; Francis, J.; Edmondson, J. Urban form and mental wellbeing: Scoping a theoretical framework for action. J. Urban Des. Ment. Health 2018, 5. Available online: https://www.urbandesignmentalhealth.com/journal-5---urban-form-and-mental-wellbeing.html (accessed on 10 February 2022).
- McCormack, G.R.; Cabaj, J.; Orpana, H.; Lukic, R.; Blackstaffe, A.; Goopy, S.; Hagel, B.; Keough, N.; Martinson, R.; Chapman, J.; et al. Evidence synthesis A scoping review on the relations between urban form and health: A focus on Canadian quantitative evidence. Health Promot. Chronic Dis. Prev. Can. 2019, 39, 187–200. [Google Scholar] [CrossRef] [PubMed]
- Trowbridge, M.J.; Gurka, M.J.; O’Connor, R.E. Urban Sprawl and Delayed Ambulance Arrival in the U.S. Am. J. Prev. Med. 2009, 37, 428–432. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Bandyopadhyay, S.; Ramamritham, K.; Jana, A. Pinch analysis to reduce fire susceptibility by redeveloping urban built forms. Clean Technol. Environ. Policy 2020, 22, 1531–1546. [Google Scholar] [CrossRef]
- Haifler, T.Y.; Fisher-Gewirtzman, D. Urban Wellbeing, As Influenced by Densification Rates and Building Typologies—A Virtual Reality Experiment. In Anthropocene, Design in the Age of Humans, Proceedings of the 25th CAADRIA Conference, Bangkok, Thailand, 5–6 August 2020; Chulalongkorn University: Bangkok, Thailand, 2020; pp. 661–670. [Google Scholar]
- Amcoff, J. Ny studie om segregation: Urban form kan vara viktigare än bostadsblandning. Plan Tidskr. För Samhällsplanering 2022, 1–2, 64–69. (In Swedish) [Google Scholar]
- Amcoff, J. Searching for new ways to achieve mixed neighbourhoods. Cities 2022, 121, 103496. [Google Scholar] [CrossRef]

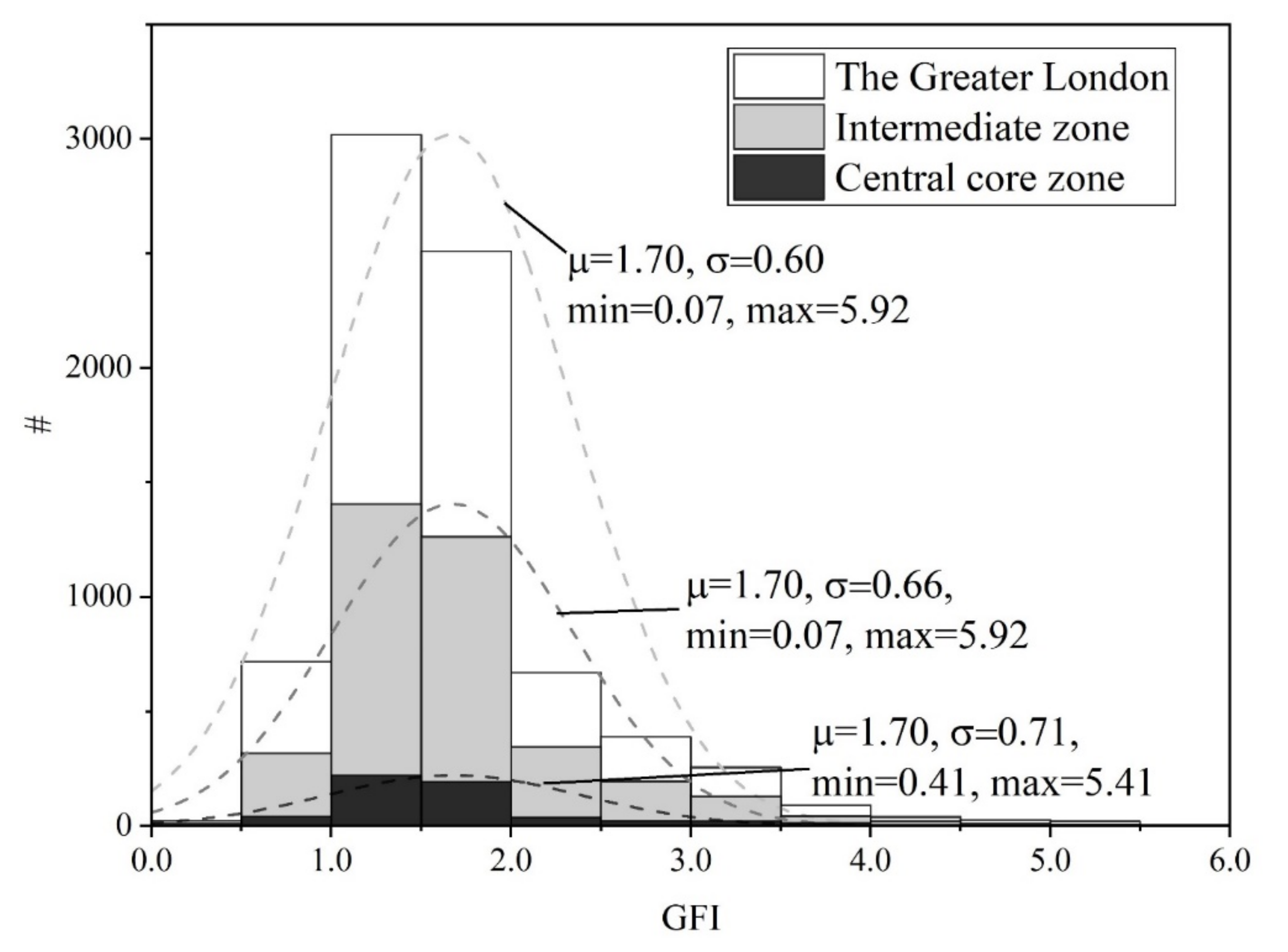

| Area km2 (%) | # of Buildings (%) | # of Street Blocks (%) | |
|---|---|---|---|
| The Greater London | 1594.31(100) | 472,295(100) | 24,009(100) |
| Intermediate zone | 348.63(21.87) | 204,449(43.29) | 8960(37.32) |
| Central core zone | 33.52(2.10) | 26,305(5.57) | 967(4.03) |
| ID | # | Density | GFI | Area | Distance | FD | ||
|---|---|---|---|---|---|---|---|---|
| ht-A | CRG-A | ht-D | CRG-D | |||||
| 1 | 69 | 0.14 | 0.79 | 1 | 0 | 1 | 0 | 1.71 |
| 2 | 63 | 0.19 | 1.02 | 3 | 1.18 | 1 | 0 | 1.77 |
| 3 | 78 | 0.27 | 1.25 | 1 | 0 | 1 | 0 | 1.78 |
| 4 | 66 | 0.19 | 1.60 | 4 | 3.23 | 4 | 3.38 | 1.67 |
| 5 | 68 | 0.22 | 1.62 | 3 | 1.21 | 1 | 0 | 1.78 |
| 6 | 64 | 0.14 | 1.64 | 4 | 3.43 | 4 | 3.69 | 1.76 |
| 7 | 64 | 0.24 | 1.75 | 4 | 3.51 | 3 | 2.00 | 1.72 |
| 8 | 66 | 0.13 | 1.82 | 2 | 1383.86 | 5 | 5.15 | 1.68 |
| 9 | 65 | 0.10 | 2.01 | 3 | 3.11 | 1 | 0 | 1.64 |
| 10 | 61 | 0.22 | 2.02 | 3 | 2.60 | 1 | 0 | 1.77 |
| 11 | 76 | 0.14 | 2.12 | 4 | 6.20 | 5 | 4.75 | 1.63 |
| 12 | 75 | 0.12 | 2.17 | 4 | 4.60 | 3 | 2.03 | 1.47 |
| 13 | 36 | 0.15 | 2.20 | 3 | 2.43 | 4 | 3.26 | 1.64 |
| 14 | 61 | 0.50 | 2.41 | 4 | 5.01 | 4 | 3.46 | 1.84 |
| 15 | 63 | 0.12 | 2.51 | 3 | 2.63 | 2 | 28.68 | 1.70 |
| 16 | 72 | 0.23 | 2.72 | 4 | 4.83 | 5 | 4.92 | 1.76 |
| 17 | 62 | 0.08 | 2.86 | 3 | 4.80 | 5 | 5.37 | 1.59 |
| 18 | 67 | 0.19 | 2.97 | 3 | 2.07 | 3 | 1.56 | 1.66 |
| 19 | 73 | 0.37 | 3.01 | 3 | 2.75 | 3 | 1.71 | 1.85 |
| 20 | 73 | 0.13 | 3.14 | 3 | 3.60 | 3 | 2.04 | 1.69 |
| 21 | 113 | 0.41 | 3.26 | 4 | 7.19 | 3 | 1.85 | 1.83 |
| 22 | 131 | 0.38 | 3.31 | 3 | 4.45 | 1 | 0 | 1.81 |
| 23 | 138 | 0.11 | 3.46 | 3 | 4.84 | 3 | 2.09 | 1.59 |
| 24 | 172 | 0.15 | 3.78 | 4 | 7.33 | 6 | 6.66 | 1.63 |
| 25 | 166 | 0.15 | 3.86 | 3 | 5.60 | 1 | 0 | 1.63 |
| 26 | 289 | 0.10 | 4.01 | 5 | 9.09 | 3 | 2.91 | 1.58 |
| 27 | 231 | 0.22 | 4.12 | 4 | 10.22 | 5 | 5.12 | 1.66 |
| 28 | 239 | 0.07 | 4.37 | 4 | 6.69 | 4 | 4.36 | 1.47 |
| 29 | 502 | 0.19 | 4.65 | 4 | 6.50 | 4 | 4.37 | 1.61 |
| 30 | 712 | 0.07 | 4.92 | 4 | 6.28 | 2 | 51.18 | 1.48 |
| 31 | 665 | 0.25 | 5.08 | 3 | 3.73 | 4 | 3.66 | 1.73 |
| 32 | 752 | 0.12 | 5.19 | 5 | 6.95 | 1 | 0 | 1.56 |
| 33 | 803 | 0.07 | 5.39 | 4 | 9.90 | 4 | 5.06 | 1.44 |
| 34 | 988 | 0.10 | 5.65 | 5 | 7.82 | 7 | 8.90 | 1.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Seipel, S.; Brandt, S.A.; Ma, D. A New Graph-Based Fractality Index to Characterize Complexity of Urban Form. ISPRS Int. J. Geo-Inf. 2022, 11, 287. https://doi.org/10.3390/ijgi11050287
Ma L, Seipel S, Brandt SA, Ma D. A New Graph-Based Fractality Index to Characterize Complexity of Urban Form. ISPRS International Journal of Geo-Information. 2022; 11(5):287. https://doi.org/10.3390/ijgi11050287
Chicago/Turabian StyleMa, Lei, Stefan Seipel, Sven Anders Brandt, and Ding Ma. 2022. "A New Graph-Based Fractality Index to Characterize Complexity of Urban Form" ISPRS International Journal of Geo-Information 11, no. 5: 287. https://doi.org/10.3390/ijgi11050287
APA StyleMa, L., Seipel, S., Brandt, S. A., & Ma, D. (2022). A New Graph-Based Fractality Index to Characterize Complexity of Urban Form. ISPRS International Journal of Geo-Information, 11(5), 287. https://doi.org/10.3390/ijgi11050287






