Harmonizing Full and Partial Matching in Geospatial Conflation: A Unified Optimization Model
Abstract
:1. Introduction
2. Background
2.1. Similarity Measures
2.2. Extracting Match Relations
2.3. Optimized Conflation Models
2.4. Related Works
3. Methods
3.1. Unifying Bidirectional Matching Model (U-bimatching)
3.2. Reducing Spurious Assignments Using Auxiliary Measures (Name Similarity)
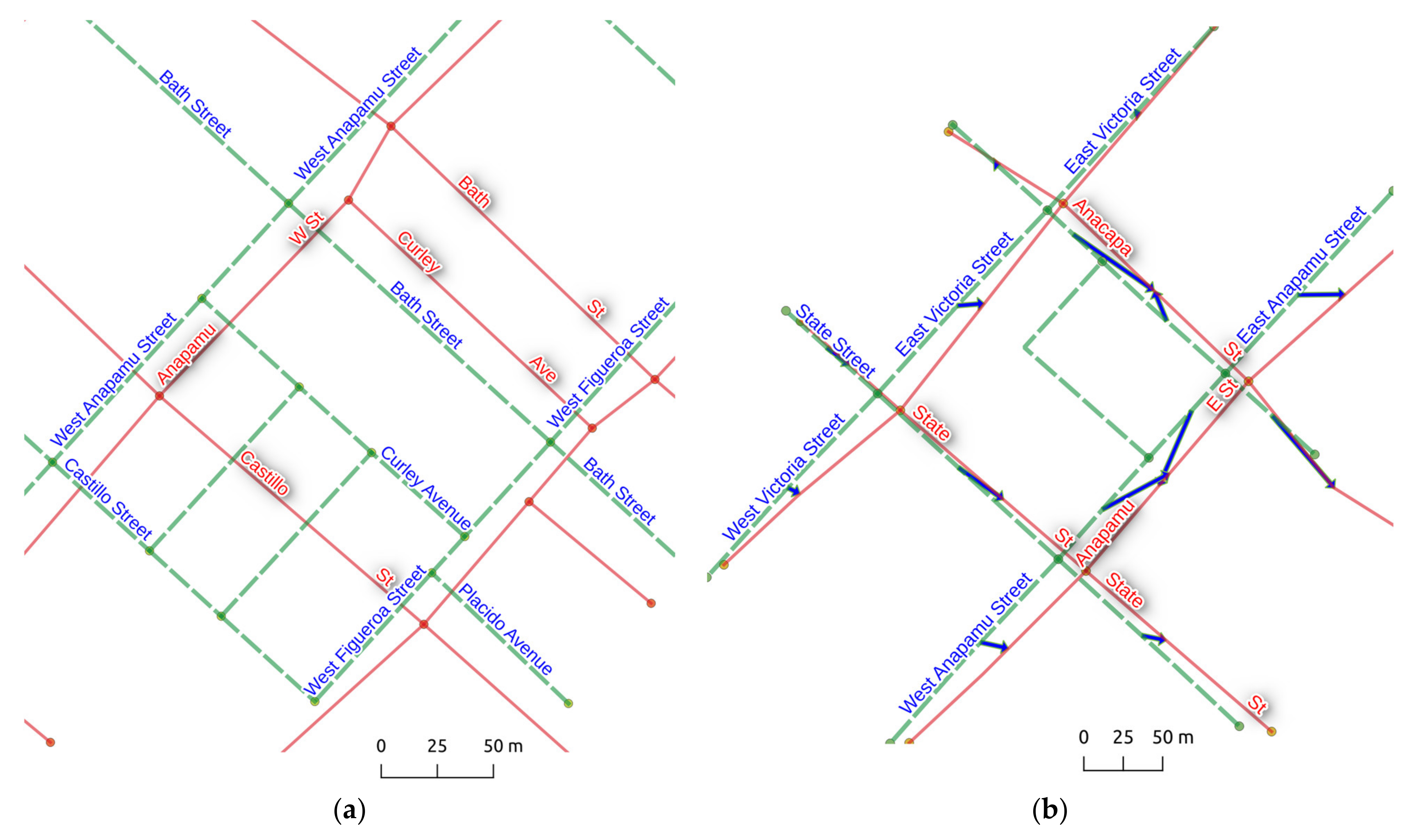
4. Results
4.1. Experiment Settings
4.2. Evaluation Criteria
4.3. Performance Results
4.3.1. Precision
4.3.2. Recall
4.3.3. F-Score
4.3.4. Percentage of Full Matches
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Frank, A.U. Why is scale an effective descriptor for data quality? The physical and ontological rationale for imprecision and level of detail. In Research Trends in Geographic Information Science; Springer: Berlin/Heidelberg, Germany, 2009; pp. 39–61. [Google Scholar]
- Saalfeld, A. A fast rubber-sheeting transformation using simplicial coordinates. Am. Cartogr. 1985, 12, 169–173. [Google Scholar] [CrossRef]
- Saalfeld, A. Conflation automated map compilation. Int. J. Geogr. Inf. Syst. 1988, 2, 217–228. [Google Scholar] [CrossRef]
- Walter, V.; Fritsch, D. Matching spatial data sets: A statistical approach. Int. J. Geogr. Inf. Sci. 1999, 13, 445–473. [Google Scholar] [CrossRef]
- McKenzie, G.; Janowicz, K.; Adams, B. A weighted multi-attribute method for matching user-generated points of interest. Cartogr. Geogr. Inf. Sci. 2014, 41, 125–137. [Google Scholar] [CrossRef]
- Pendyala, R.M. Development of GIS-Based Conflation Tools for Data Integration and Matching; Florida Dept. of Transportation: Lake City, FL, USA, 2002. [Google Scholar]
- Masuyama, A. Methods for detecting apparent differences between spatial tessellations at different time points. Int. J. Geogr. Inf. Sci. 2006, 20, 633–648. [Google Scholar] [CrossRef]
- Xavier, E.M.A.; Ariza-López, F.J.; Ureña-Cámara, M.A. A survey of measures and methods for matching geospatial vector datasets. ACM Comput. Surv. 2016, 49, 1–34. [Google Scholar] [CrossRef]
- Li, L.; Goodchild, M.F. An optimisation model for linear feature matching in geographical data conflation. Int. J. Image Data Fusion 2011, 2, 309–328. [Google Scholar] [CrossRef]
- Beeri, C.; Kanza, Y.; Safra, E.; Sagiv, Y. Object fusion in geographic information systems. In Proceedings of the Thirtieth International Conference on Very Large Data Bases, Toronto, ON, Canada, 31 August–3 September 2004; Volume 30, pp. 816–827. [Google Scholar]
- Corral, A.; Manolopoulos, Y.; Theodoridis, Y.; Vassilakopoulos, M. Algorithms for processing k-closest-pair queries in spatial databases. Data Knowl. Eng. 2004, 49, 67–104. [Google Scholar] [CrossRef] [Green Version]
- Goodchild, M.F.; Hunter, G.J. A simple positional accuracy measure for linear features. Int. J. Geogr. Inf. Sci. 1997, 11, 299–306. [Google Scholar] [CrossRef]
- Tong, X.; Liang, D.; Jin, Y. A linear road object matching method for conflation based on optimization and logistic regression. Int. J. Geogr. Inf. Sci. 2014, 28, 824–846. [Google Scholar] [CrossRef]
- Rosen, B.; Saalfeld, A. Match criteria for automatic alignment. In Proceedings of the 7th International Symposium on Computer-Assisted Cartography (Auto-Carto 7), Washington, DC, USA, 11–14 March 1985; pp. 1–20. [Google Scholar]
- Cobb, M.A.; Chung, M.J.; Iii, H.F.; Petry, F.E.; Shaw, K.B.; Miller, H.V. A rule-based approach for the conflation of attributed vector data. GeoInformatica 1998, 2, 7–35. [Google Scholar] [CrossRef]
- Filin, S.; Doytsher, Y. Detection of corresponding objects in linear-based map conflation. Surv. Land Inf. Syst. 2000, 60, 117–128. [Google Scholar]
- Li, L.; Goodchild, M.F. Optimized feature matching in conflation. In Proceedings of the Geographic Information Science: 6th International Conference, GIScience, Zurich, Switzerland, 14–17 September 2010; pp. 14–17. [Google Scholar]
- Lei, T.; Lei, Z. Optimal spatial data matching for conflation: A network flow-based approach. Trans. GIS 2019, 23, 1152–1176. [Google Scholar] [CrossRef]
- Lei, T.L. Geospatial data conflation: A formal approach based on optimization and relational databases. Int. J. Geogr. Inf. Sci. 2020, 34, 2296–2334. [Google Scholar] [CrossRef]
- Lei, T.L. Large scale geospatial data conflation: A feature matching framework based on optimization and divide-and-conquer. Comput. Environ. Urban Syst. 2021, 87, 101618. [Google Scholar] [CrossRef]
- Zhang, M. Methods and Implementations of Road-Network Matching. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2009. [Google Scholar]
- Vilches-Blázquez, L.M.; Ramos, J.Á. Semantic conflation in GIScience: A systematic review. Cartogr. Geogr. Inf. Sci. 2021, 48, 512–529. [Google Scholar] [CrossRef]
- Hackeloeer, A.; Klasing, K.; Krisp, J.M.; Meng, L. Road network conflation: An iterative hierarchical approach. In Progress in Location-Based Services 2014; Springer: Berlin/Heidelberg, Germany, 2015; pp. 137–151. [Google Scholar]
- Guo, Q.; Xu, X.; Wang, Y.; Liu, J. Combined matching approach of road networks under different scales considering constraints of cartographic generalization. IEEE Access 2019, 8, 944–956. [Google Scholar] [CrossRef]
- Liu, L.; Ding, X.; Zhu, X.; Fan, L.; Gong, J. An iterative approach based on contextual information for matching multi-scale polygonal object datasets. Trans. GIS 2020, 24, 1047–1072. [Google Scholar] [CrossRef]
- Memduhoglu, A.; Basaraner, M. An approach for multi-scale urban building data integration and enrichment through geometric matching and semantic web. Cartogr. Geogr. Inf. Sci. 2022, 49, 1–17. [Google Scholar] [CrossRef]
- Hillier, F.S.; Lieberman, G.J. Introduction to Operations Research, 8th ed.; McGraw-Hill: New York, NY, USA, 2005; p. 1088. [Google Scholar]
- Xavier, E.M.; Ariza-López, F.J.; Ureña-Cámara, M.A. MatchingLand, geospatial data testbed for the assessment of matching methods. Sci. Data 2017, 4, 170180. [Google Scholar] [CrossRef] [PubMed] [Green Version]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, T.L.; Lei, Z. Harmonizing Full and Partial Matching in Geospatial Conflation: A Unified Optimization Model. ISPRS Int. J. Geo-Inf. 2022, 11, 375. https://doi.org/10.3390/ijgi11070375
Lei TL, Lei Z. Harmonizing Full and Partial Matching in Geospatial Conflation: A Unified Optimization Model. ISPRS International Journal of Geo-Information. 2022; 11(7):375. https://doi.org/10.3390/ijgi11070375
Chicago/Turabian StyleLei, Ting L., and Zhen Lei. 2022. "Harmonizing Full and Partial Matching in Geospatial Conflation: A Unified Optimization Model" ISPRS International Journal of Geo-Information 11, no. 7: 375. https://doi.org/10.3390/ijgi11070375
APA StyleLei, T. L., & Lei, Z. (2022). Harmonizing Full and Partial Matching in Geospatial Conflation: A Unified Optimization Model. ISPRS International Journal of Geo-Information, 11(7), 375. https://doi.org/10.3390/ijgi11070375





