A Lightweight Long-Term Vehicular Motion Prediction Method Leveraging Spatial Database and Kinematic Trajectory Data
Abstract
:1. Introduction
- A novel personalized LVMP method based on spatial database and kinematic trajectory data is proposed. Different from existing historical data-based methods that learn knowledge from huge volumes of data, our method retrieves relevant information based on spatial relations through a well-organized spatial database. In addition, the neglected personal factors in the present methods, such as driver and vehicle information, are taken into account in this paper.
- A spatial database system is initially embedded in a classical KF framework. This combination makes our system lightweight and the utilization of a spatial search makes our algorithm able to find the most spatially related data quickly.
- Both accuracy and efficiency of algorithms are discussed in this paper.
2. Related Work
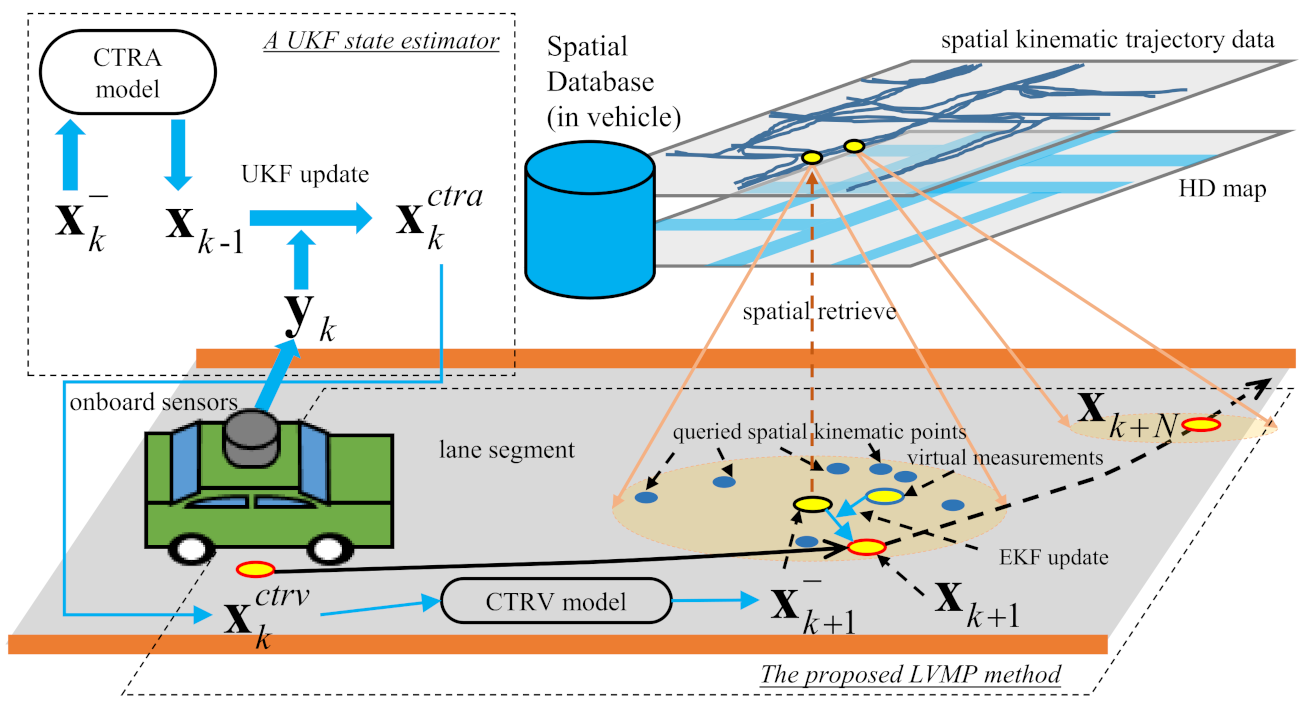
3. System Overview
- A UKF state estimator. In real-world studies, prior to motion prediction, a real-time vehicle state estimator is necessary to reduce sensor noises; in our system, an unscented Kalman filter (UKF) that cooperates with a CTRA model is adopted. The UKF fuses information from the CTRA model and onboard sensors to make a reliable real-time vehicle state estimate at 10 Hz.
- A spatial database for kinematic trajectory data management. The spatial database that maintains kinematic trajectory data and HD maps is a crucial component. The kinematic trajectory data, which contain spatial information, are stored in the spatial database to leverage a quick spatial query to realize real-time LVMP. The kinematic data are linked to the HD maps to facilitate the spatial query.
- The lightweight LVMP algorithm. The utilization of the spatial database and EKF makes our method lightweight. The quick spatial search functions of the database provide the most spatially related information to our algorithm and thus we do not need to learn knowledge from huge amounts of data. The efficient EKF ensures real-time data processing.
4. Methodology
4.1. Vehicle State Estimation
4.2. Vehicle Motion Prediction
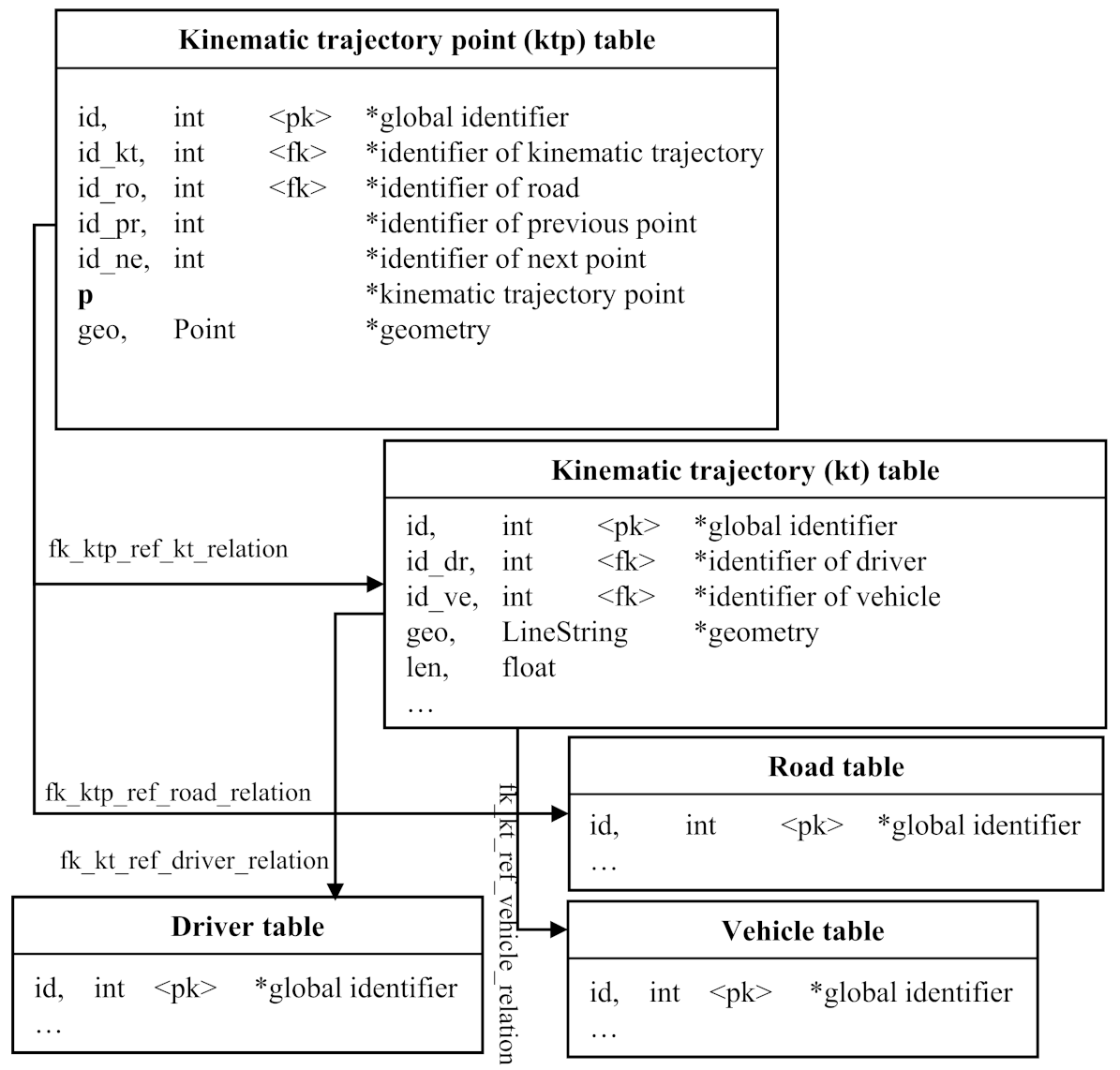
4.2.1. Spatial Kinematic Trajectory Database
- semantic attributes: such as corresponding driver and vehicle information.
- topological attributes: such as the road a point located in; previous/next point.
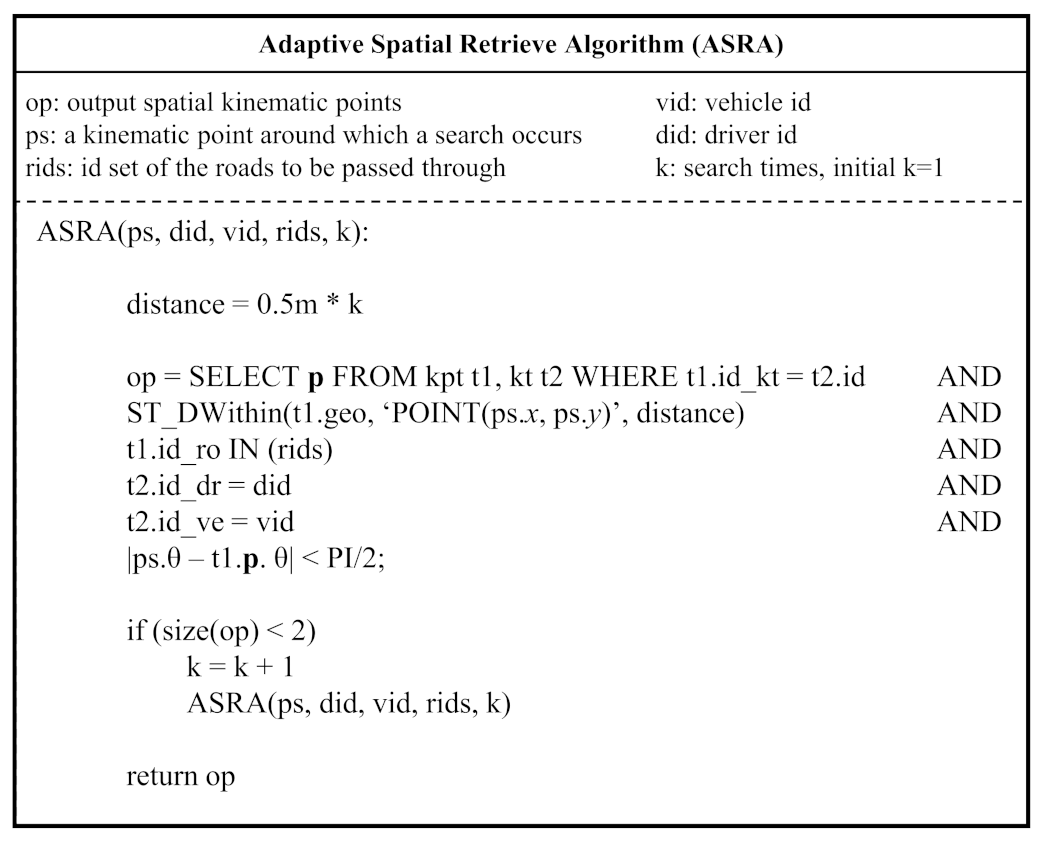
4.2.2. Adaptive Spatial Retrieve Algorithm (ASRA)
- Spatial rules: the points must be within a certain distance 0.5 m * k, where k < 5, and the heading difference must be less than ; otherwise, the points are kicked out; if k ≥ 5 and the point number is less than 2, the search fails.
- Topological rules: the points must be located on the road that the vehicle is driving on; otherwise, the points are kicked out.
- Semantic rules: the points must be produced by the same vehicle that is driven by the same person; otherwise, the points are kicked out.
4.2.3. EKF Framework for Kinematic Trajectory Data Integration
(Process 1) Predicting
(Process 2) Spatial Search and Virtual Measurement Calculation
(Process 3) Updating
5. Experiments
5.1. Experimental Configurations
5.2. Accuracy Performance Evaluations
5.2.1. Used Metrics
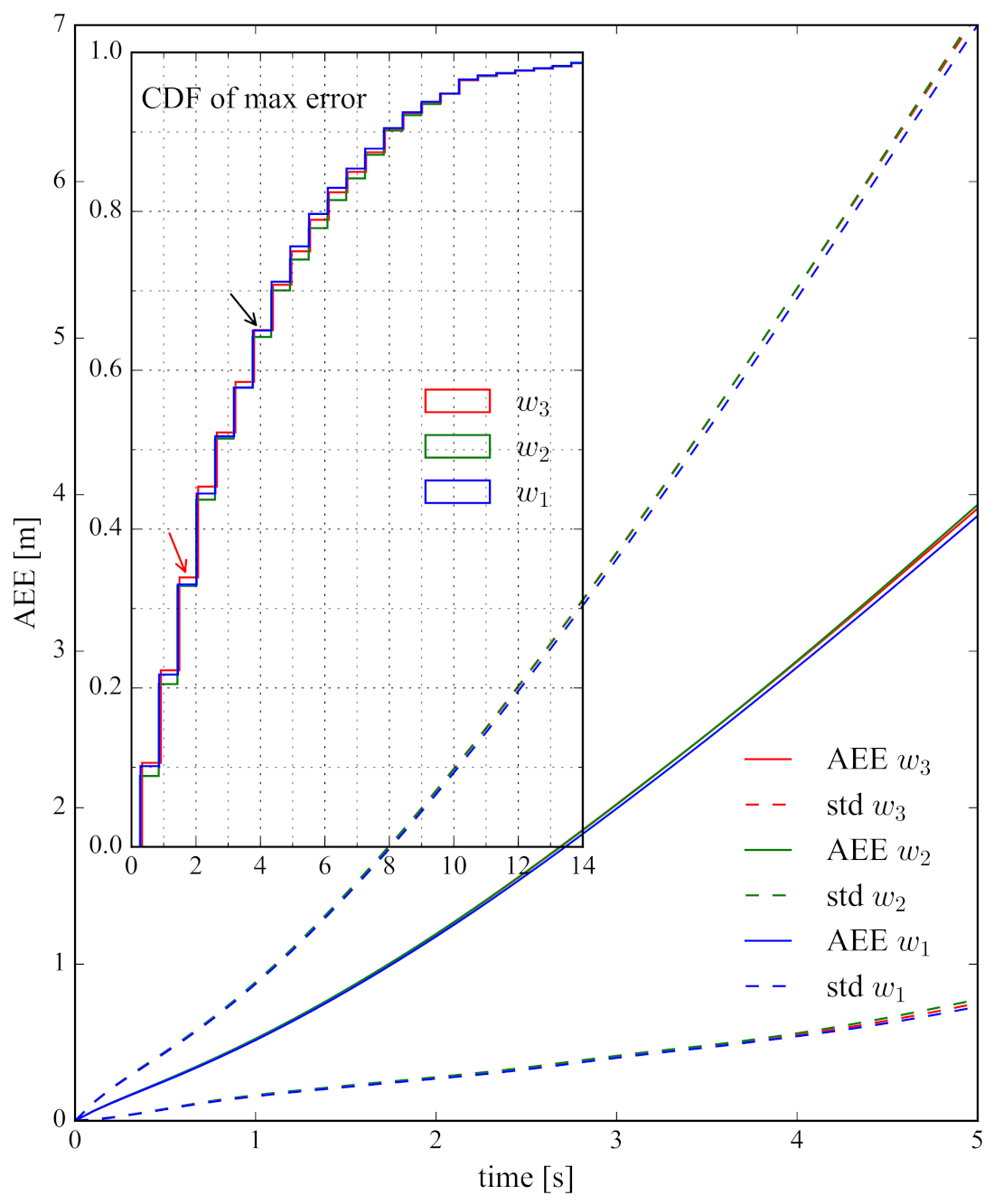
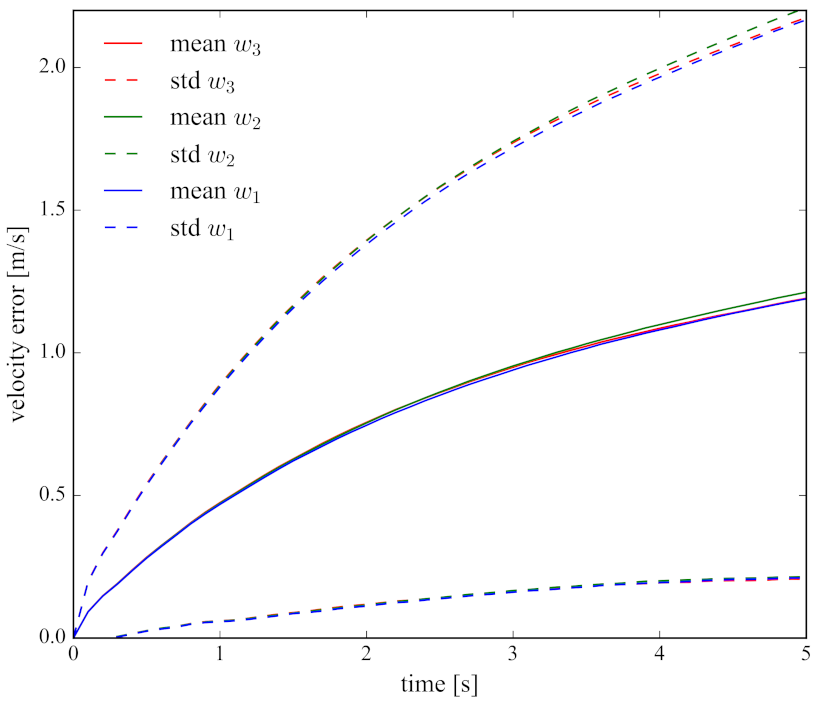
5.2.2. Using Different Weighting Functions
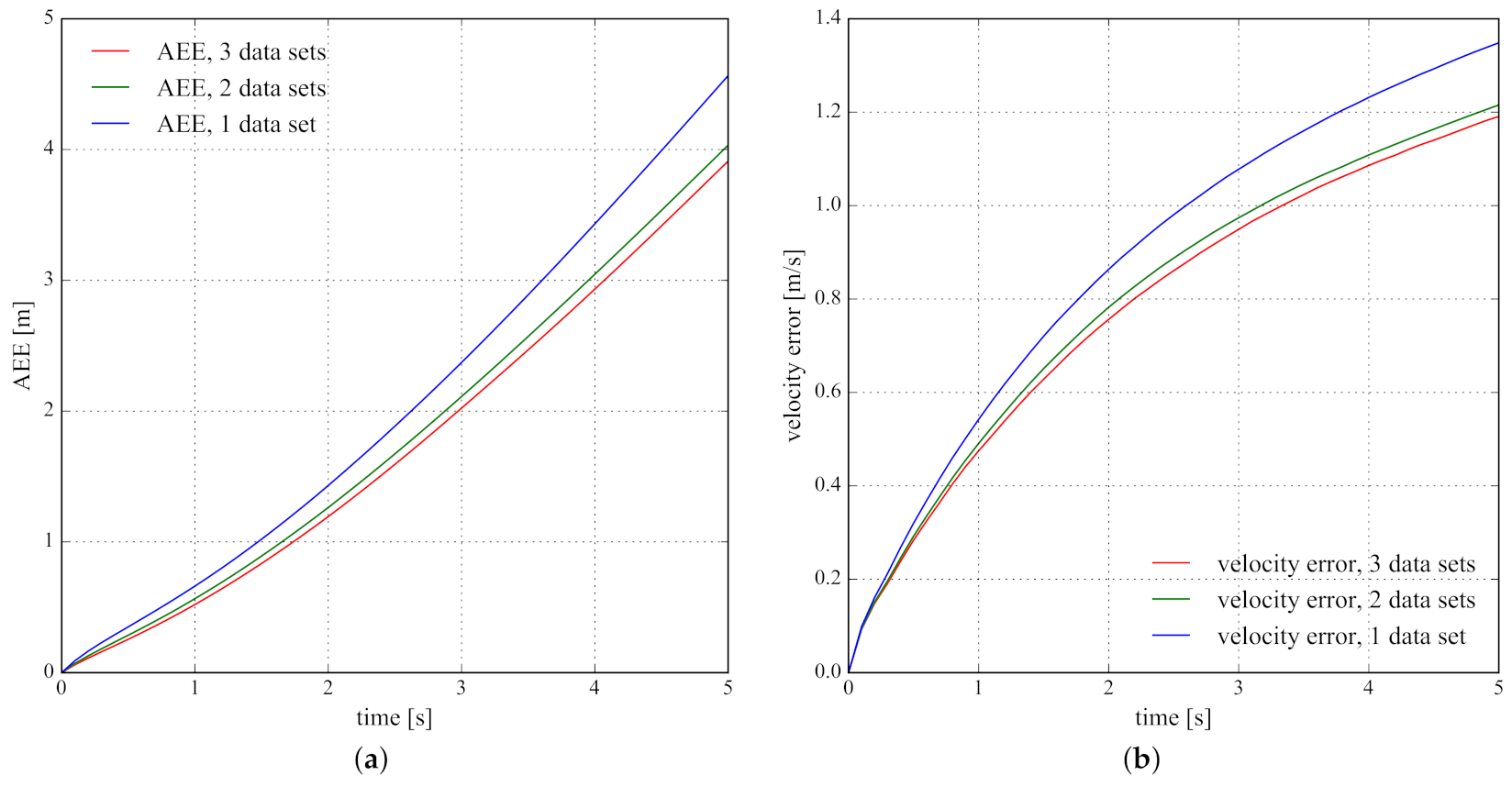
5.2.3. Using Different Data Sets
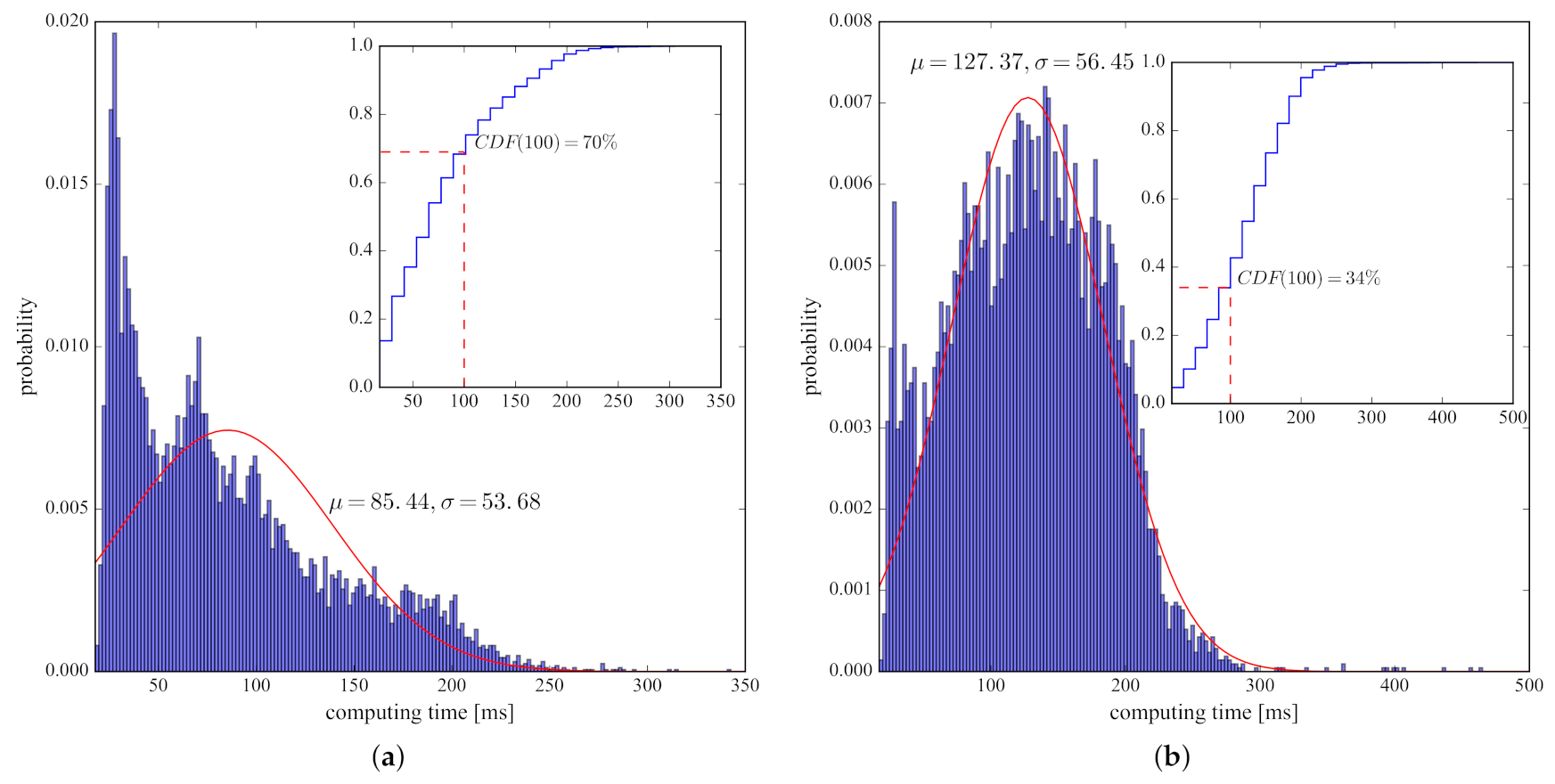
5.3. Efficiency Performance Evaluations
6. Future Work
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pihrt, J.; Šimánek, P. Spatiotemporal Prediction of Vehicle Movement Using Artificial Neural Networks. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 4–9 June 2022; pp. 734–739. [Google Scholar] [CrossRef]
- Lefèvre, S.; Vasquez, D.; Laugier, C. A survey on motion prediction and risk assessment for intelligent vehicles. Robomech J. 2014, 1, 1. [Google Scholar]
- Tan, H.S.; Huang, J. DGPS-Based Vehicle-to-Vehicle Cooperative Collision Warning: Engineering Feasibility Viewpoints. IEEE Trans. Intell. Transp. Syst. 2006, 7, 415–428. [Google Scholar]
- Lytrivis, P.; Thomaidis, G.; Tsogas, M.; Amditis, A. An Advanced Cooperative Path Prediction Algorithm for Safety Applications in Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2011, 12, 669–679. [Google Scholar]
- Hermes, C.; Wohler, C.; Schenk, K.; Kummert, F. Long-term Vehicle Motion Prediction. In Proceedings of the Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009. [Google Scholar]
- Jeong, D.; Baek, M.; Lee, S.S. Long-term prediction of vehicle trajectory based on a deep neural network. In Proceedings of the International Conference on Information & Communication Technology Convergence, Jeju, Korea, 18–20 October 2017. [Google Scholar]
- Altché, F.; de La Fortelle, A. An LSTM network for highway trajectory prediction. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 353–359. [Google Scholar] [CrossRef]
- Jiang, R.; Xu, H.; Gong, G.; Kuang, Y.; Liu, Z. Spatial-Temporal Attentive LSTM for Vehicle-Trajectory Prediction. ISPRS Int. J. Geo-Inf. 2022, 11, 354. [Google Scholar] [CrossRef]
- Lin, L.; Li, W.; Bi, H.; Qin, L. Vehicle Trajectory Prediction Using LSTMs with Spatial-Temporal Attention Mechanisms. IEEE Intell. Transp. Syst. Mag. 2022, 14, 197–208. [Google Scholar] [CrossRef]
- Petrich, D.; Dang, T.; Kasper, D.; Breuel, G.; Stiller, C. Map-based long term motion prediction for vehicles in traffic environments. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), The Hague, The Netherlands, 6–9 October 2013. [Google Scholar]
- Yalamanchi, S.; Huang, T.K.; Haynes, G.C.; Djuric, N. Long-term prediction of vehicle behavior using short-term uncertainty-aware trajectories and high-definition maps. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar]
- Lu, T.; Watanabe, Y.; Yamada, S.; Takada, H. Comparative evaluation of Kalman filters and motion models in vehicular state estimation and path prediction. J. Navig. 2021, 74, 1142–1160. [Google Scholar]
- Kawasaki, A.; Tasaki, T. Trajectory Prediction of Turning Vehicles based on Intersection Geometry and Observed Velocities. In Proceedings of the IEEE Intelligent Vehicles Symposium, Changshu, China, 26–30 June 2018; pp. 511–516. [Google Scholar]
- Tao, L.; Watanabe, Y.; Li, Y.; Yamada, S.; Takada, H. Collision Risk Assessment Service for Connected Vehicles: Leveraging Vehicular State and Motion Uncertainties. IEEE Internet Things J. 2021, 8, 11548–11560. [Google Scholar] [CrossRef]
- Hafner, M.R.; Cunningham, D.; Caminiti, L.; Vecchio, D.D. Cooperative Collision Avoidance at Intersections: Algorithms and Experiments. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1162–1175. [Google Scholar] [CrossRef]
- Joerer, S.; Segata, M.; Bloessl, B.; Cigno, R.L.; Sommer, C.; Dressler, F. A Vehicular Networking Perspective on Estimating Vehicle Collision Probability at Intersections. IEEE Trans. Veh. Technol. 2014, 63, 1802–1812. [Google Scholar] [CrossRef]
- Shan, M.; Worrall, S.; Nebot, E. Long Term Vehicle Motion Prediction and Tracking in Large Environments. In Proceedings of the IEEE International Conference on Intelligent Transportation Systems (ITSC’11), Washington, DC, USA, 5–7 October 2011. [Google Scholar]
- Xu, Y.; Liu, X.; Cao, X.; Huang, C.; Liu, E.; Qian, S.; Liu, X.; Wu, Y.; Dong, F.; Qiu, C.W.; et al. Artificial intelligence: A powerful paradigm for scientific research. Innovation 2021, 2, 100179. [Google Scholar] [CrossRef]
- Quan, T.; Firl, J. Modelling of traffic situations at urban intersections with probabilistic non-parametric regression. In Proceedings of the Intelligent Vehicles Symposium, Gold Coast, QLD, Australia, 23–26 June 2013. [Google Scholar]
- Gindele, T.; Brechtel, S.; Dillmann, R. Learning Driver Behavior Models from Traffic Observations for Decision Making and Planning. Intell. Transp. Syst. Mag. IEEE 2015, 7, 69–79. [Google Scholar] [CrossRef]
- Zhang, K.; Feng, X.; Wu, L.; He, Z. Trajectory Prediction for Autonomous Driving Using Spatial-Temporal Graph Attention Transformer. IEEE Trans. Intell. Transp. Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, W.; Hu, X.; Xu, P.; Zhou, S.; Cai, M. Vehicle Trajectory Prediction in Connected Environments via Heterogeneous Context-Aware Graph Convolutional Networks. IEEE Trans. Intell. Transp. Syst. 2022, 1–13. [Google Scholar] [CrossRef]
- Schmidt, J.; Jordan, J.; Gritschneder, F.; Dietmayer, K. CRAT-Pred: Vehicle Trajectory Prediction with Crystal Graph Convolutional Neural Networks and Multi-Head Self-Attention. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 7799–7805. [Google Scholar] [CrossRef]
- Baumann, U.; Guiser, C.; Herman, M.; Zollner, J.M. Predicting Ego-Vehicle Paths from Environmental Observations with a Deep Neural Network. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018. [Google Scholar]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Wan, E.A.; Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, 4 October 2000. [Google Scholar]
- PostGIS. Available online: http://www.postgis.org (accessed on 23 June 2022).
- Kato, S.; Takeuchi, E.; Ishiguro, Y.; Ninomiya, Y.; Takeda, K.; Hamada, T. An Open Approach to Autonomous Vehicles. IEEE Micro 2015, 48, 60–68. [Google Scholar] [CrossRef]
- Kato, S.; Tokunaga, S.; Maruyama, Y.; Maeda, S.; Hirabayashi, M.; Kitsukawa, Y.; Monrroy, A.; Ando, T.; Fujii, Y.; Azumi, T. Autoware on Board: Enabling Autonomous Vehicles with Embedded Systems. In Proceedings of the 2018 ACM/IEEE 9th International Conference on Cyber-Physical Systems (ICCPS), Porto, Portugal, 11–13 April 2018. [Google Scholar]
- Autoware. Available online: https://github.com/autowarefoundation/autoware (accessed on 7 August 2022).
- Robot Operating System. Available online: http://www.ros.org (accessed on 23 June 2022).



| Study | Genre | Input | Output | Methodology | Scenario | DCC | Personalized |
|---|---|---|---|---|---|---|---|
| [4] | physical model based | vehicle state | position | kinematic models, Dempster–Shafer reasoning system | campus | No | No |
| [5] | trajectory matching based | odometry data, HDT 1 | position, velocity, yaw and yaw angle | particle filter, trained trajectory classifier | intersection | Yes | No |
| [8] | machine learning based | the first 3 s historical trajectories, HDT | position | LSTM | highway | Yes | No |
| [13] | map-aided | HD maps, vehicle state | position, velocity | EKF, cubic polynomial fitting | intersection | No | No |
| [11] | hybrid | HDT, HD maps | position | Uncertainty-aware Stitching | intersection | Yes | No |
| ours | spatial historical data based | vehicle state, spatial kinematic data | position, velocity | EKF, spatial search | campus | No | Yes |
| Trajectory | Mean v () | Std v () | Mean a () | Std a () | Driver | Vehicle | Point Number |
|---|---|---|---|---|---|---|---|
| 5.82139 | 2.65461 | 0.04619 | 0.62621 | Yamata | PHV001 | 3895 | |
| 5.25437 | 2.23874 | 0.04669 | 0.51137 | Yamata | PHV001 | 4142 | |
| 5.49708 | 2.01545 | 0.05826 | 0.47457 | Yamata | PHV001 | 4075 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, L.; Watanabe, Y.; Takada, H. A Lightweight Long-Term Vehicular Motion Prediction Method Leveraging Spatial Database and Kinematic Trajectory Data. ISPRS Int. J. Geo-Inf. 2022, 11, 463. https://doi.org/10.3390/ijgi11090463
Tao L, Watanabe Y, Takada H. A Lightweight Long-Term Vehicular Motion Prediction Method Leveraging Spatial Database and Kinematic Trajectory Data. ISPRS International Journal of Geo-Information. 2022; 11(9):463. https://doi.org/10.3390/ijgi11090463
Chicago/Turabian StyleTao, Lu, Yousuke Watanabe, and Hiroaki Takada. 2022. "A Lightweight Long-Term Vehicular Motion Prediction Method Leveraging Spatial Database and Kinematic Trajectory Data" ISPRS International Journal of Geo-Information 11, no. 9: 463. https://doi.org/10.3390/ijgi11090463
APA StyleTao, L., Watanabe, Y., & Takada, H. (2022). A Lightweight Long-Term Vehicular Motion Prediction Method Leveraging Spatial Database and Kinematic Trajectory Data. ISPRS International Journal of Geo-Information, 11(9), 463. https://doi.org/10.3390/ijgi11090463






