Assessing Regional Development Balance Based on Zipf’s Law: The Case of Chinese Urban Agglomerations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Source
2.2. Research Methods
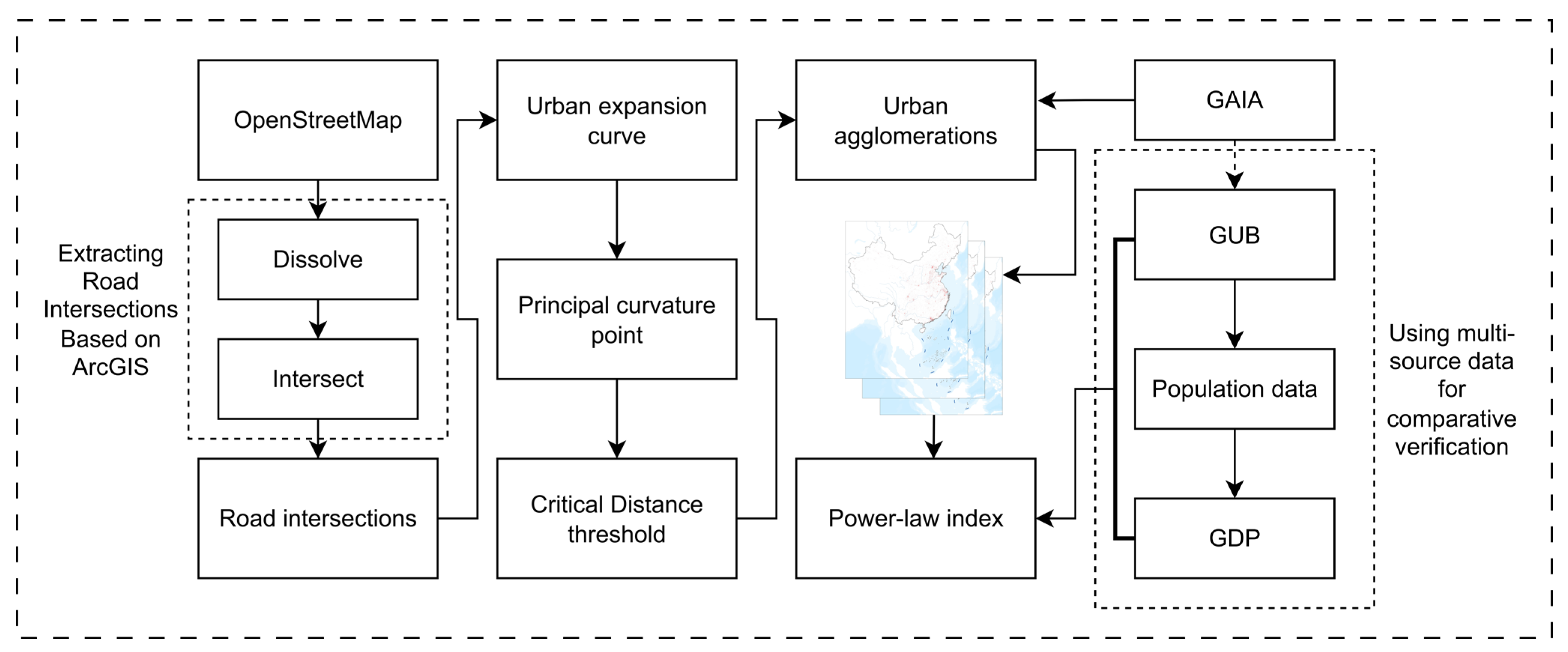
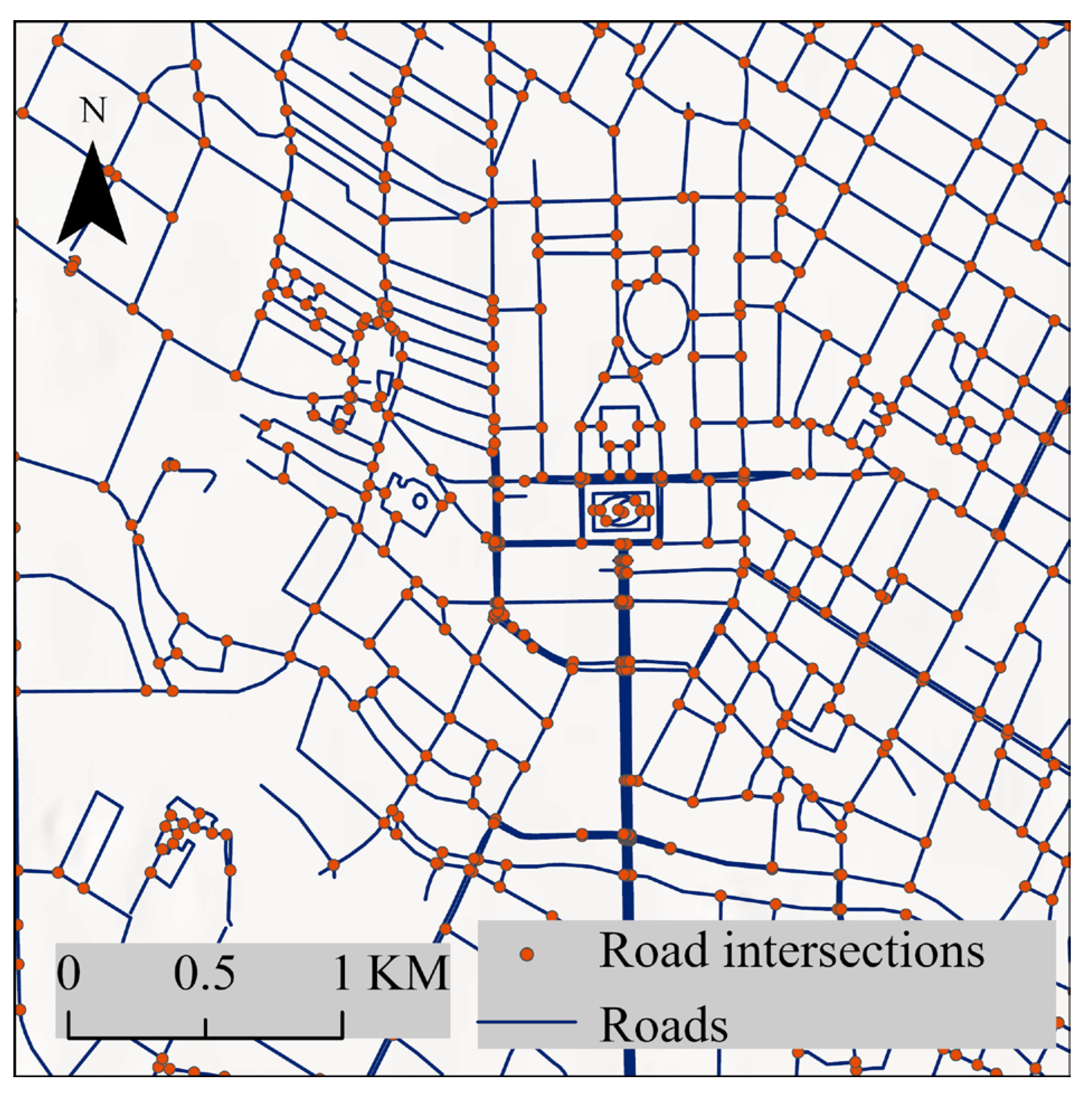
2.2.1. Experimental Procedure
2.2.2. Urban Expansion Curve
2.2.3. Zipf’s Law
3. Results
3.1. Urban Agglomerations
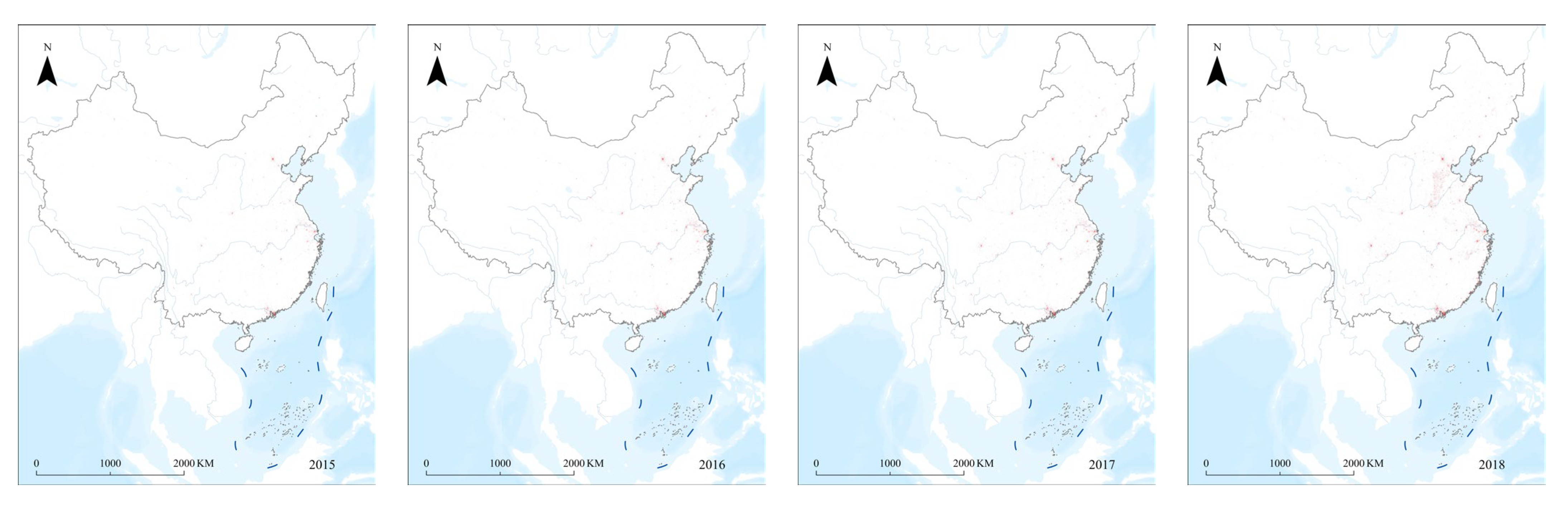
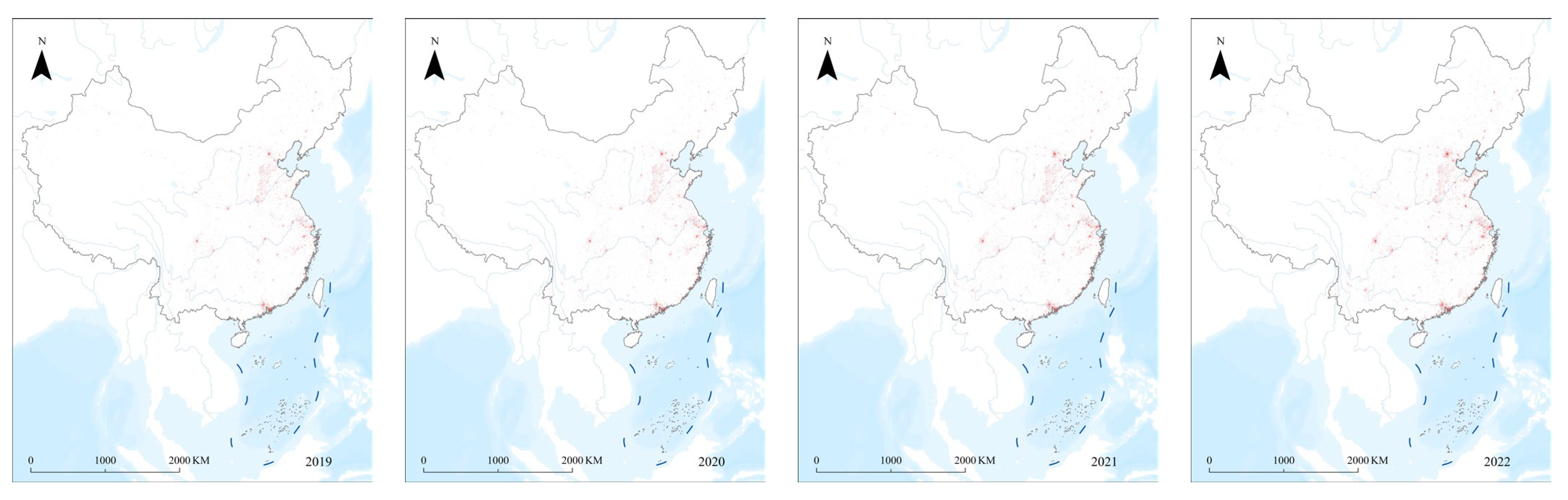
3.1.1. National-Scale Agglomeration Characteristics
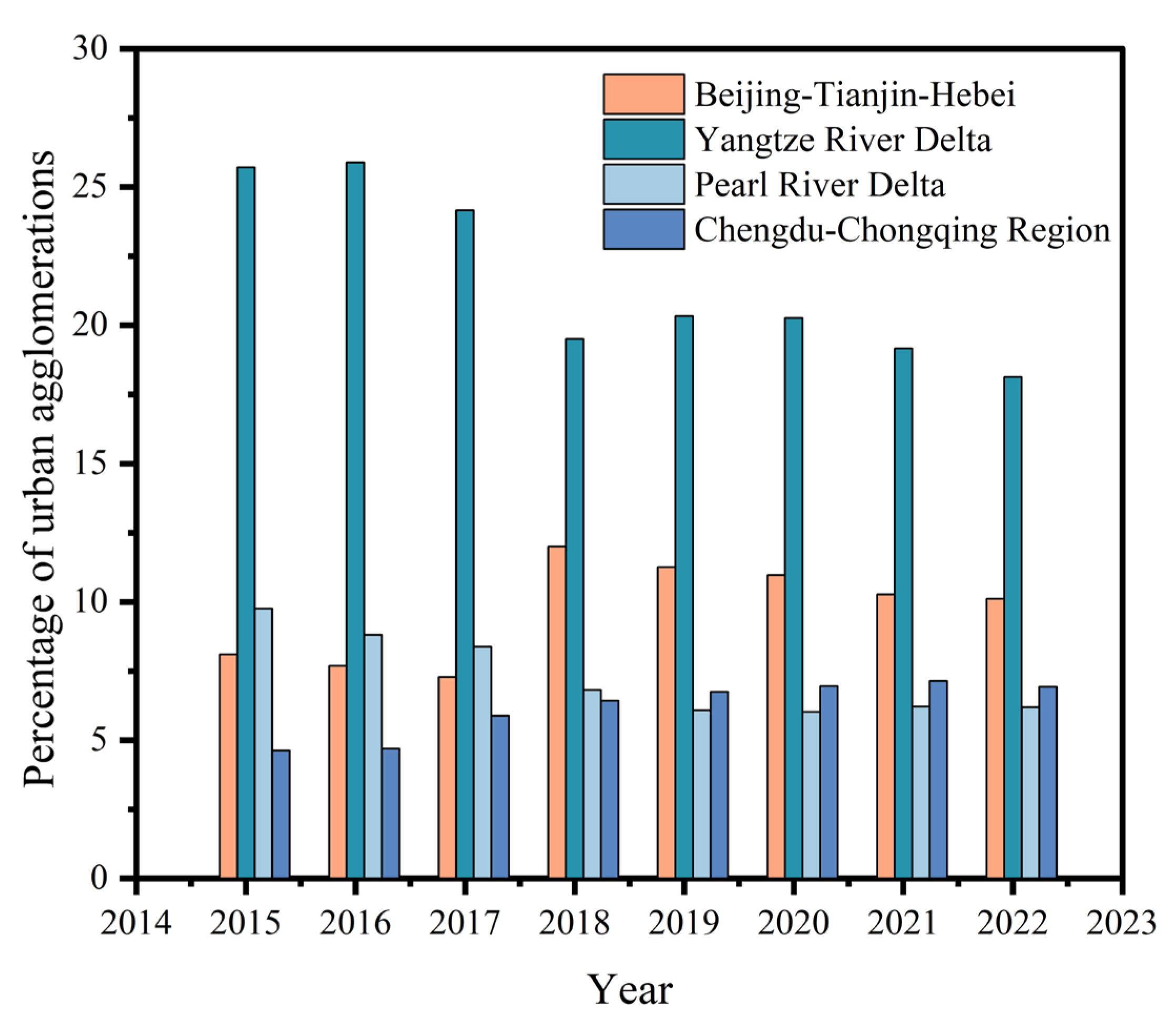
3.1.2. Regional-Scale Aggregation Characteristics
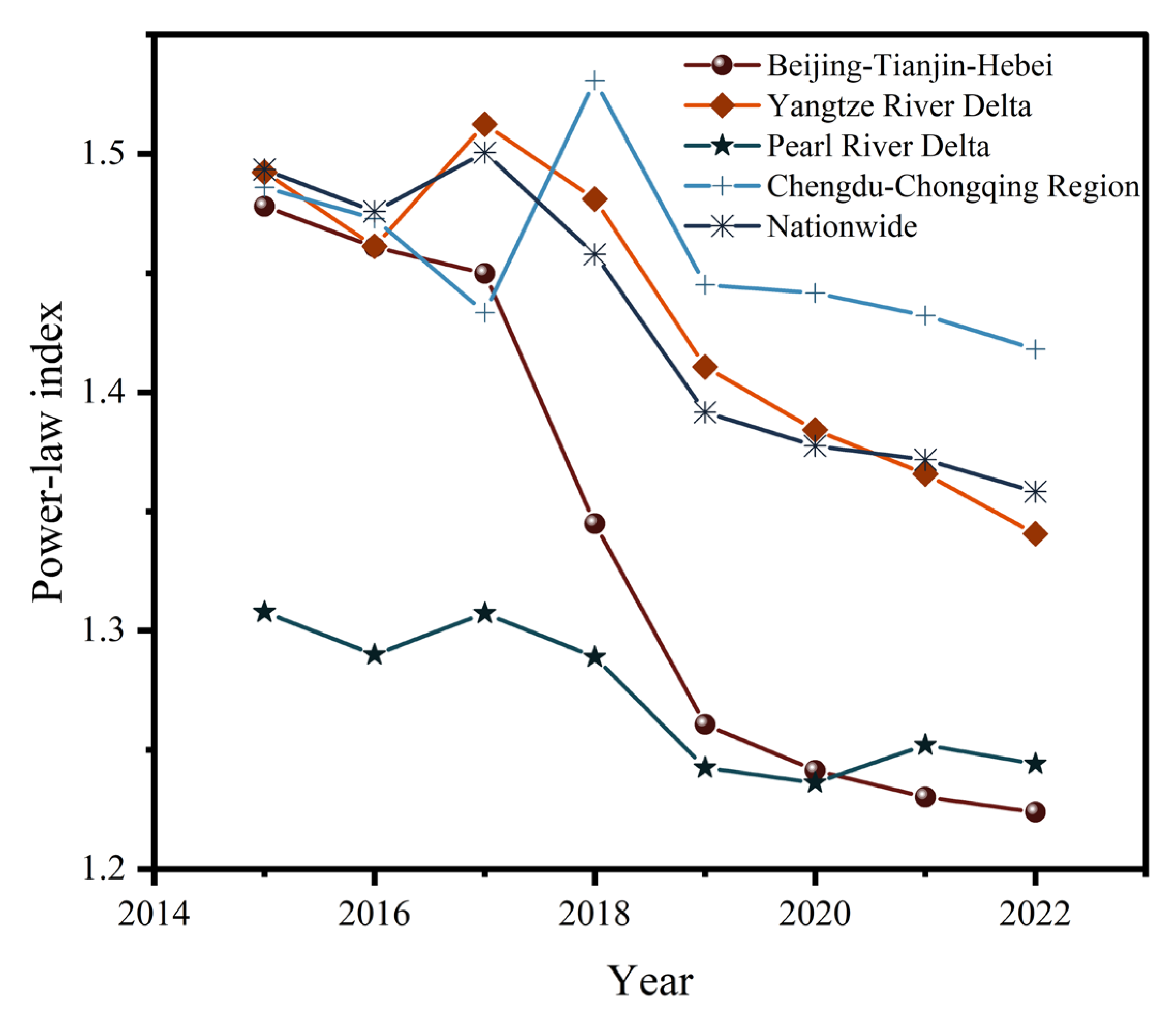
3.2. Power-Law Index
4. Discussion
5. Conclusions
- (1)
- From 2015 to 2022, the growth rate of the number of urban agglomerations and the growth rate of the area in China show a simultaneous growth or decrease. The regions with the most significant growth of urban agglomerations in China are the Beijing–Tianjin–Hebei region, Yangtze River Delta region, Pearl River Delta region, and Chengdu–Chongqing region. The number of agglomerations in the Yangtze River Delta and Pearl River Delta regions decreases year by year, while the number of urban agglomerations in the Beijing–Tianjin–Hebei and Chengdu–Chongqing regions increases year by year. The regions with earlier urban development have a high proportion of urban agglomerations in the early stage and a low proportion in the later stage.
- (2)
- China’s urban agglomerations conform to the power-law distribution law and do not conform to Zipf’s law. From 2015 to 2022, the power-law index of national urban agglomerations decreases year by year, the agglomerations between cities increase, and the unevenness of regional development increases.
- (3)
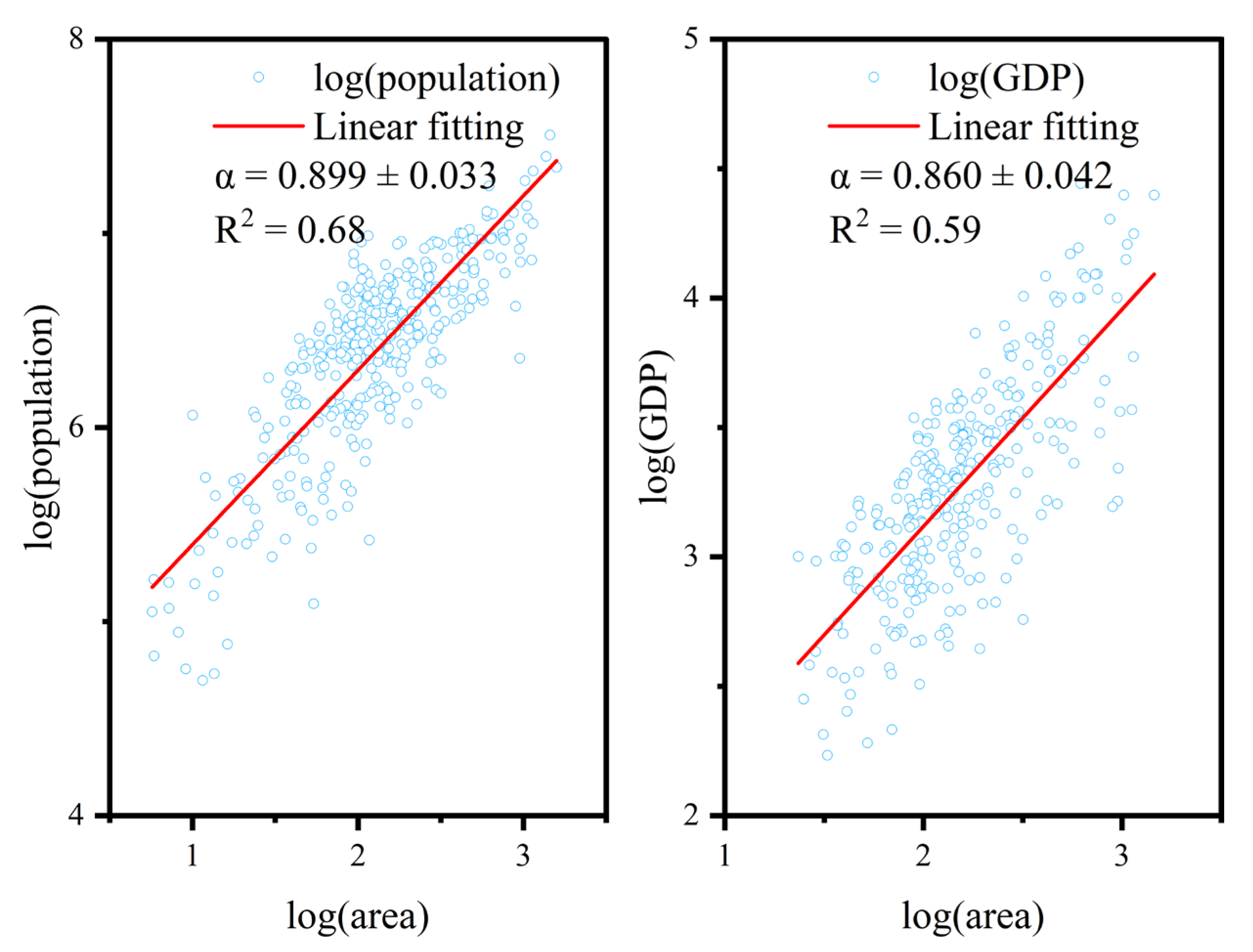
- There is a significant correlation between the road network and population data. Chinese urban agglomerations extracted based on road intersections exhibit a linear relationship with officially published population and economic data, indicating that urban agglomerations are expanding faster than the population and economic growth rates.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Li, Y. Revitalize the world’s countryside. Nature 2017, 548, 275–277. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, M.; Zhu, Y.; Chen, Z.; Huang, X. Urban expansion and the urban–rural income gap: Empirical evidence from China. Cities 2022, 129, 103831. [Google Scholar] [CrossRef]
- Zhang, X.; Pan, M. Emerging rural spatial restructuring regimes in China: A tale of three transitional villages in the urban fringe. J. Rural Stud. 2022, 93, 287–300. [Google Scholar] [CrossRef]
- Qu, L.; Li, Y.; Feng, W. Spatial-temporal differentiation of ecologically-sustainable land across selected settlements in China: An urban-rural perspective. Ecol. Indic. 2020, 112, 105783. [Google Scholar] [CrossRef]
- Li, L.; Ma, S.; Zheng, Y.; Xiao, X. Integrated regional development: Comparison of urban agglomeration policies in China. Land Use Policy 2022, 114, 105939. [Google Scholar] [CrossRef]
- The Central People’s Government of the People’s Republic of China. Outline of the 13th Five Year Plan for National Economic and Social Development of the People’s Republic of China. Available online: http://www.gov.cn/xinwen/2016-03/17/content_5054992.htm (accessed on 8 April 2023).
- Batty, M. The Size, Scale, and Shape of Cities. Science 2008, 319, 769–771. [Google Scholar] [CrossRef]
- Jiang, B.; Jia, T. Zipf’s Law for All the Natural Cities in the United States: A Geospatial Perspective. Int. J. Geogr. Inf. Sci. 2010, 25, 1269–1281. [Google Scholar] [CrossRef]
- Mori, T.; Smith, T.E.; Hsu, W.-T. Common power laws for cities and spatial fractal structures. Proc. Natl. Acad. Sci. USA 2020, 117, 6469–6475. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, Y.; Zhu, D.; Dong, L.; Liu, Y. Metrogan: Simulating urban morphology with generative adversarial network. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 2482–2492. [Google Scholar]
- Overman, H.G.; Ioannides, Y.M. Cross-sectional evolution of the US city size distribution. J. Urban Econ. 2001, 49, 543–566. [Google Scholar] [CrossRef]
- González-Val, R. The evolution of US city size distribution from a long-term perspective (1900–2000). J. Reg. Sci. 2010, 50, 952–972. [Google Scholar] [CrossRef]
- Sun, X.; Yuan, O.; Xu, Z.; Yan, h.; Liu, Q.; Wu, L. Did Zipf’s Law hold for Chinese cities and why? Evidence from multisource data. Land Use Policy 2021, 106, 105460. [Google Scholar] [CrossRef]
- Wang, H.; Ning, X.; Zhang, H.; Liu, Y. Urban Expansion Analysis of China’s Prefecture Level City from 2000 to 2016 using High-Precision Urban Boundary. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 7514–7517. [Google Scholar]
- Kong, L.; He, Z.; Chen, Z.; Luo, M.; Du, Z.; Zhu, F.; He, L. Spatial Distribution and Morphological Identification of Regional Urban Settlements Based on Road Intersections. ISPRS Int. J. Geo-Inf. 2021, 10, 4. [Google Scholar] [CrossRef]
- Zhou, Y.; Shi, Y. Toward establishing the concept of physical urban area in China. Acta Geogr. Sin. 1995, 50, 289–301. [Google Scholar]
- Ma, S.; Long, Y. Identifying Spatial Cities in China at the Community Scale. J. Urban Reg. Plan. 2019, 11, 37–50. [Google Scholar]
- Gong, P.; Li, X.; Wang, J.; Bai, Y.; Zhou, Y. Annual maps of global artificial impervious area (GAIA) between 1985 and 2018. Remote Sens. Environ. 2019, 236, 11510. [Google Scholar] [CrossRef]
- Qin, Y.; Xiao, X.; Dong, J.; Chen, B.; Liu, F.; Zhang, G.; Zhang, Y.; Wang, J.; Wu, X.J.I.J.o.P.; Sensing, R. Quantifying annual changes in built-up area in complex urban-rural landscapes from analyses of PALSAR and Landsat images. ISPRS J. Photogramm. Remote Sens. 2017, 124, 89–105. [Google Scholar] [CrossRef]
- Li, X.; Gong, P.; Zhou, Y.; Wang, J.; Bai, Y.; Chen, B.; Hu, T.; Xiao, Y.; Xu, B.; Yang, J. Mapping global urban boundaries from the global artificial impervious area (GAIA) data. Environ. Res. Lett. 2020, 15, 094044. [Google Scholar] [CrossRef]
- Tan, X.; Chen, Y. Urban boundary identification based on neighborhood dilation. Prog. Geogr. 2015, 34, 1259–1265. [Google Scholar]
- Long, Y. Redefining Chinese city system with emerging new data. Appl. Geogr. 2016, 75, 36–48. [Google Scholar] [CrossRef]
- Rozenfeld, H.D.; Rybski, D.; Gabaix, X.; Makse, H.A. The Area and Population of Cities: New Insights from a Different Perspective on Cities. Am. Econ. Rev. 2011, 101, 2205–2225. [Google Scholar] [CrossRef]
- Tannier, C.; Thomas, I.; Vuidel, G.; Frankhauser, P. A fractal approach to identifying urban boundaries. Geogr. Anal. 2011, 43, 211–227. [Google Scholar] [CrossRef]
- Zhang, H.; Lan, T.; Li, Z. Fractal evolution of urban street networks in form and structure: A case study of Hong Kong. Int. J. Geogr. Inf. Sci. 2022, 36, 1100–1118. [Google Scholar] [CrossRef]
- Agostinho, F.; Costa, M.; Coscieme, L.; Almeida, C.M.; Giannetti, B.F. Assessing cities growth-degrowth pulsing by emergy and fractals: A methodological proposal. Cities 2021, 113, 103162. [Google Scholar] [CrossRef]
- Li, D.; Li, X. An Overview on Data Mining of Nighttime Light Remote Sensing. Acta Geod. Cartogr. Sin. 2015, 44, 591–601. [Google Scholar]
- Chen, S.; Zhang, H.; Ou, X. Study on the spatial-temporal differentiation of road network density and its relationship with urban form in Greater Bay Area of Guangdong, Hong Kong and Macao. In Proceedings of the 3rd International Conference on Internet of Things and Smart City (IoTSC 2023), Chongqing, China, 24–26 March 2023; pp. 310–319. [Google Scholar]
- He, B.; Guo, R.; Li, M.; Jing, Y.; Zhao, Z.; Zhu, W.; Zhang, C.; Zhang, C.; Ma, D. The fractal or scaling perspective on progressively generated intra-urban clusters from street junctions. Int. J. Digit. Earth 2023, 16, 1944–1961. [Google Scholar] [CrossRef]
- Miao, H. Analysis of the evolutionary characteristics of city size distribution of prefecture-level cities in China. Inq. Econ. Issues 2014, 113–121. [Google Scholar] [CrossRef]
- Chen, Z.; Wei, Y.; Shi, K.; Zhao, Z.; Wang, C.; Wu, B.; Qiu, B.; Yu, B. The potential of nighttime light remote sensing data to evaluate the development of digital economy: A case study of China at the city level. Comput. Environ. Urban Syst. 2022, 92, 101749. [Google Scholar] [CrossRef]
- Chen, Y. Exploring the level of urbanization based on Zipf’s scaling exponent. Phys. A Stat. Mech. Appl. 2020, 566, 125620. [Google Scholar] [CrossRef]
- Wan, G.; Zhu, D.; Wang, C.; Zhang, X. The size distribution of cities in China: Evolution of urban system and deviations from Zipf’s law. Ecol. Indic. 2020, 111, 106003. [Google Scholar] [CrossRef]
- Holmes, T.J.; Lee, S. Cities as Six-by-Six-Mile Squares: Zipf’s Law? In Agglomeration Economics; Glaeser, E.L., Ed.; The University of Chicago Press: Chicago, IL, USA, 2010; Volume 3, pp. 105–131. [Google Scholar]
- Arshad, S.; Hu, S.; Ashraf, B.N. Zipf’s Law, the Coherence of the Urban System and City Size Distribution: Evidence from Pakistan. Phys. A Stat. Mech. Appl. 2019, 513, 87–103. [Google Scholar] [CrossRef]
- Cao, W.; Dong, L.; Wu, L.; Liu, Y. Quantifying urban areas with multi-source data based on percolation theory. Remote Sens. Environ. 2020, 241, 111730. [Google Scholar] [CrossRef]
- Holz, C.A.J.S.E.J. Chinese Statistics: Classification Systems and Data Sources. SSRN Electron. J. 2013, 54, 532–571. [Google Scholar]
- Gibson, J.; Li, C. The erroneous use of china’s population and per capita data: A structured review and critical test. J. Econ. Surv. 2017, 31, 905–922. [Google Scholar] [CrossRef]
- Nitsch, V. Zipf zipped. J. Urban Econ. 2005, 57, 86–100. [Google Scholar] [CrossRef]
- Kosmopoulou, G.; Buttry, N.; Johnson, J.; Kallsnick, A. Suburbanization and the rank-size rule. Appl. Econ. Lett. 2007, 14, 1–4. [Google Scholar] [CrossRef]
- Wang, D.; Kong, L.; Chen, Z.; Yang, X.; Luo, M. Physical Urban Area Identification Based on Geographical Data and Quantitative Attribution of Identification Threshold: A Case Study in Chongqing Municipality, Southwestern China. Land 2023, 12, 30. [Google Scholar] [CrossRef]
- Hu, T.; Huang, X.; Li, X.; Liang, L.; Xue, F. Toward a better understanding of urban sprawl: Linking spatial metrics and landscape networks dynamics. In Computational Urban Planning and Management for Smart Cities; Springer: Cham, Switzerland, 2019; pp. 163–178. [Google Scholar]
- National Bureau of Statistics. China Statistical Yearbook. Available online: http://www.stats.gov.cn/sj/ndsj/ (accessed on 8 April 2023).
- Bettencourt, L.; Zünd, D. Demography and the Emergence of Universal Patterns in Urban Systems. Nat. Commun. 2020, 11, 4584. [Google Scholar] [CrossRef]
- Eeckhout, J. Gibrat’s Law for (All) Cities. Am. Econ. Rev. 2004, 94, 1429–1451. [Google Scholar] [CrossRef]
- Dietzel, C.; Herold, M.; Hemphill, J.J.; Clarke, K.C. Spatio-temporal dynamics in California’s Central Valley: Empirical links to urban theory. Int. J. Geogr. Inf. Sci. 2005, 19, 175–195. [Google Scholar] [CrossRef]
- Bosch, M.; Jaligot, R.; Chenal, J. Spatiotemporal patterns of urbanization in three Swiss urban agglomerations: Insights from landscape metrics, growth modes and fractal analysis. Landsc. Ecol. 2020, 35, 879–891. [Google Scholar] [CrossRef]
- Yin, C.; Meng, F.; Yang, X.; Yang, F.; Fu, P.; Yao, G.; Chen, R. Spatio-temporal evolution of urban built-up areas and analysis of driving factors—A comparison of typical cities in north and south China. Land Use Policy 2022, 117, 106114. [Google Scholar] [CrossRef]
- Wei, W.; Shi, P.J.; Zhou, J.J.; Xie, B.B. The Road Network Density and Spatial Dependence Analysis Based on Basin Scale—A Case Study on Shiyang River Basin. Appl. Mech. Mater. 2014, 505–506, 750–754. [Google Scholar] [CrossRef]
- Benguigui, L.; Czamanski, D.; Marinov, M.; Portugali, Y.J.E. When and where is a city fractal? Environ. Plan. B:Plan. Des. 2000, 27, 507–519. [Google Scholar] [CrossRef]
- Chen, Y. Approaches to estimating fractal dimension and identifying fractals of urban form. Prog. Geogr. 2017, 36, 529–539. [Google Scholar]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. Mapping Urban Areas with Integration of DMSP/OLS Nighttime Light and MODIS Data Using Machine Learning Techniques. Remote Sens. 2015, 7, 12419–12439. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Lawrence, W.T.; Elvidge, C.D.; Paul, T.; Levine, E.; Privalsky, M.V.; Brown, V. Using nighttime DMSP/OLS images of city lights to estimate the impact of urban land use on soil resources in the United States. Remote Sens. Environ. 1997, 59, 105–117. [Google Scholar] [CrossRef]
- Gabaix, X. Zipf’s law for cities: An explanation. Q. J. Econ. 1999, 114, 739–767. [Google Scholar] [CrossRef]
- Feng, W.; Li, B.; Chen, Z.; Liu, P. City size based scaling of the urban internal nodes layout. PLoS ONE 2021, 16, e0250348. [Google Scholar] [CrossRef]
- Arcaute, E.; Hatna, E.; Ferguson, P.; Youn, H.; Johansson, A.; Batty, M. Constructing cities, deconstructing scaling laws. J. R. Soc. Interface 2015, 12, 20140745. [Google Scholar] [CrossRef]
- Sahitya, K.S.; Prasad, C. Urban road network structural analysis and its relation with human settelements using geographical information systems. Suranaree J. Sci. Technol. 2021, 28, 010084. [Google Scholar]
- Ji, W.; Wang, Y.; Zhuang, D.; Song, D.; Shen, X.; Wang, W.; Li, G. Spatial and temporal distribution of expressway and its relationships to land cover and population: A case study of Beijing, China. Transp. Res. Part D Transp. Environ. 2014, 32, 86–96. [Google Scholar] [CrossRef]
- National Bureau of Statistics. Major Figures on 2020 Population Census of China. Available online: http://www.stats.gov.cn/sj/pcsj/rkpc/d7c/ (accessed on 9 August 2023).
- National Bureau of Statistics. China Statistical Yearbook 2020. Available online: http://www.stats.gov.cn/sj/ndsj/2020/indexch.htm (accessed on 9 August 2023).
- Tannier, C.; Thomas, I. Defining and characterizing urban boundaries: A fractal analysis of theoretical cities and Belgian cities. Comput. Environ. Urban Syst. 2013, 41, 234–248. [Google Scholar] [CrossRef]
- Wang, J.; Lu, F.; Liu, S. A classification-based multifractal analysis method for identifying urban multifractal structures considering geographic mapping. Comput. Environ. Urban Syst. 2023, 101, 101952. [Google Scholar] [CrossRef]
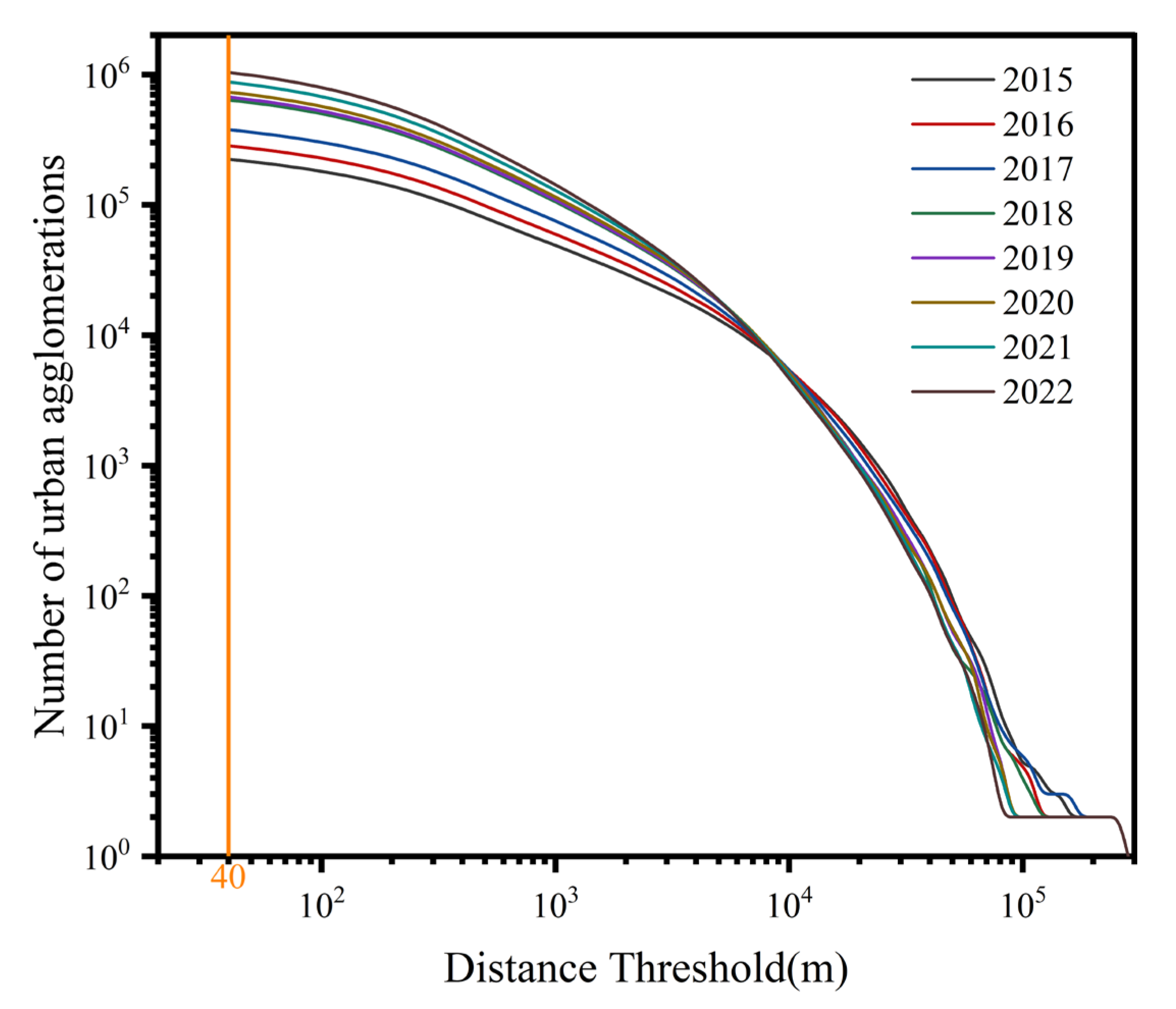

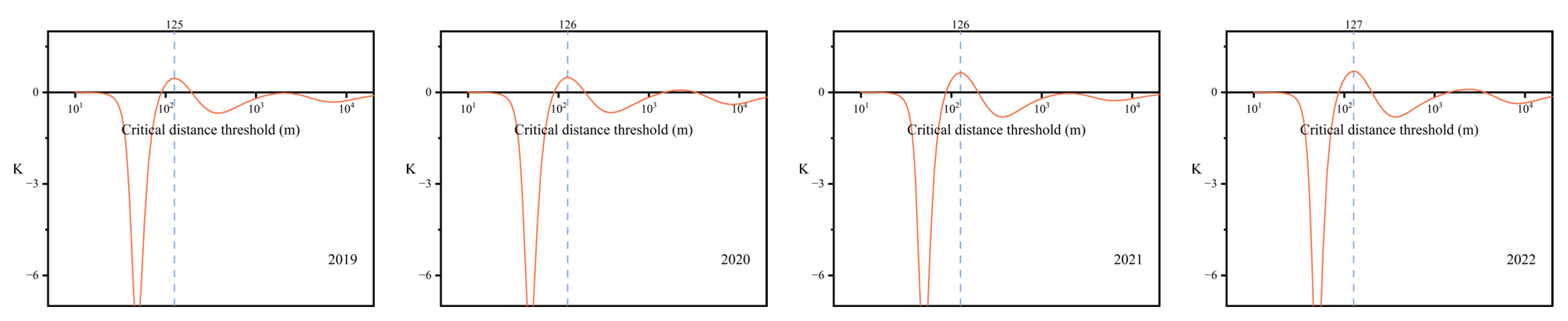




| Year | Main Curvature Point (K) | Critical Distance Threshold (m) | R2 |
|---|---|---|---|
| 2015 | 0.176 | 121 | 0.99479 |
| 2016 | 0.333 | 123 | 0.99524 |
| 2017 | 0.118 | 119 | 0.99598 |
| 2018 | 0.103 | 117 | 0.996 |
| 2019 | 0.460 | 125 | 0.99441 |
| 2020 | 0.487 | 126 | 0.99418 |
| 2021 | 0.645 | 126 | 0.99393 |
| 2022 | 0.696 | 127 | 0.99376 |
| Year | Area (km2) | Cities | Year | Area (km2) | Cities |
|---|---|---|---|---|---|
| 2015 | 211.23 | Beijing | 2019 | 399.02 | Hong Kong, Shenzhen |
| 75.32 | Shenzhen | 305.08 | Beijing | ||
| 70.00 | Shanghai | 216.90 | Chengdu | ||
| 68.43 | Shenzhen | 167.78 | Guangzhou | ||
| 64.49 | Hong Kong | 137.92 | Shanghai | ||
| 2016 | 226.64 | Beijing | 2020 | 409.44 | Hong Kong, Shenzhen |
| 97.92 | Guangzhou | 344.07 | Beijing | ||
| 92.68 | Shenzhen | 241.59 | Chengdu | ||
| 80.73 | Shenzhen | 174.48 | Guangzhou | ||
| 77.64 | Shanghai | 144.13 | Shanghai | ||
| 2017 | 223.18 | Beijing | 2021 | 450.41 | Hong Kong, Shenzhen |
| 198.6 | Shenzhen | 411.53 | Beijing | ||
| 106.96 | Guangzhou | 253.02 | Chengdu | ||
| 80.01 | Shanghai | 190.58 | Guangzhou | ||
| 72.49 | Hong Kong | 153.13 | Shanghai | ||
| 2018 | 348.27 | Hong Kong, Shenzhen | 2022 | 639.32 | Beijing |
| 267.66 | Beijing | 602.97 | Hong Kong, Shenzhen | ||
| 168.13 | Chengdu | 272.78 | Chengdu | ||
| 136.35 | Guangzhou | 248.95 | Suqian | ||
| 115.77 | Shanghai | 206.07 | Guangzhou |
| Year | Beijing–Tianjin–Hebei | Yangtze River Delta | Pearl River Delta | Chengdu–Chongqing Region | Nationwide |
|---|---|---|---|---|---|
| 2015 | 1.4780 | 1.4923 | 1.3078 | 1.4859 | 1.4934 |
| [1.4753,1.4807] | [1.4912,1.4933] | [1.3065,1.3092] | [1.4833,1.4886] | [1.4929,1.4940] | |
| 2016 | 1.4609 | 1.4612 | 1.2899 | 1.4728 | 1.4759 |
| [1.4586,1.4632] | [1.4604,1.4620] | [1.2888,1.2911] | [1.4699,1.4757] | [1.4754,1.4763] | |
| 2017 | 1.4499 | 1.5124 | 1.3073 | 1.4334 | 1.5005 |
| [1.4478,1.4520] | [1.5115,1.5133] | [1.3063,1.3083] | [1.4316,1.4351] | [1.5001,1.5009] | |
| 2018 | 1.3449 | 1.4810 | 1.2889 | 1.5308 | 1.4579 |
| [1.3433,1.3465] | [1.4801,1.4817] | [1.2882,1.2897] | [1.5295,1.5322] | [1.4576,1.4582] | |
| 2019 | 1.2606 | 1.4107 | 1.2425 | 1.4451 | 1.3917 |
| [1.2590,1.2622] | [1.4101,1.4113] | [1.2417,1.2433] | [1.4438,1.4465] | [1.3914,1.3920] | |
| 2020 | 1.2413 | 1.3842 | 1.2362 | 1.4416 | 1.3775 |
| [1.2398,1.2428] | [1.3836,1.3848] | [1.2354,1.2369] | [1.4404,1.4428] | [1.3772,1.3778] | |
| 2021 | 1.2302 | 1.3658 | 1.2520 | 1.4322 | 1.3718 |
| [1.2289,1.2316] | [1.3653,1.3664] | [1.2512,1.2528] | [1.4311,1.4333] | [1.3715,1.3721] | |
| 2022 | 1.2239 | 1.3407 | 1.2441 | 1.4181 | 1.3583 |
| [1.2223,1.2251] | [1.3402,1.3412] | [1.2433,1.2449] | [1.4171,1.4191] | [1.3580,1.3586] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Wu, Q.; Deng, J.; Bai, L.; Chen, Z.; Du, Z.; Luo, M. Assessing Regional Development Balance Based on Zipf’s Law: The Case of Chinese Urban Agglomerations. ISPRS Int. J. Geo-Inf. 2023, 12, 472. https://doi.org/10.3390/ijgi12120472
Kong L, Wu Q, Deng J, Bai L, Chen Z, Du Z, Luo M. Assessing Regional Development Balance Based on Zipf’s Law: The Case of Chinese Urban Agglomerations. ISPRS International Journal of Geo-Information. 2023; 12(12):472. https://doi.org/10.3390/ijgi12120472
Chicago/Turabian StyleKong, Liang, Qinglin Wu, Jie Deng, Leichao Bai, Zhongsheng Chen, Zhong Du, and Mingliang Luo. 2023. "Assessing Regional Development Balance Based on Zipf’s Law: The Case of Chinese Urban Agglomerations" ISPRS International Journal of Geo-Information 12, no. 12: 472. https://doi.org/10.3390/ijgi12120472
APA StyleKong, L., Wu, Q., Deng, J., Bai, L., Chen, Z., Du, Z., & Luo, M. (2023). Assessing Regional Development Balance Based on Zipf’s Law: The Case of Chinese Urban Agglomerations. ISPRS International Journal of Geo-Information, 12(12), 472. https://doi.org/10.3390/ijgi12120472








