Geological Hazard Assessment of Secondary Collapses Due to Volcanic Earthquakes on Changbai Mountain in China
Abstract
1. Introduction
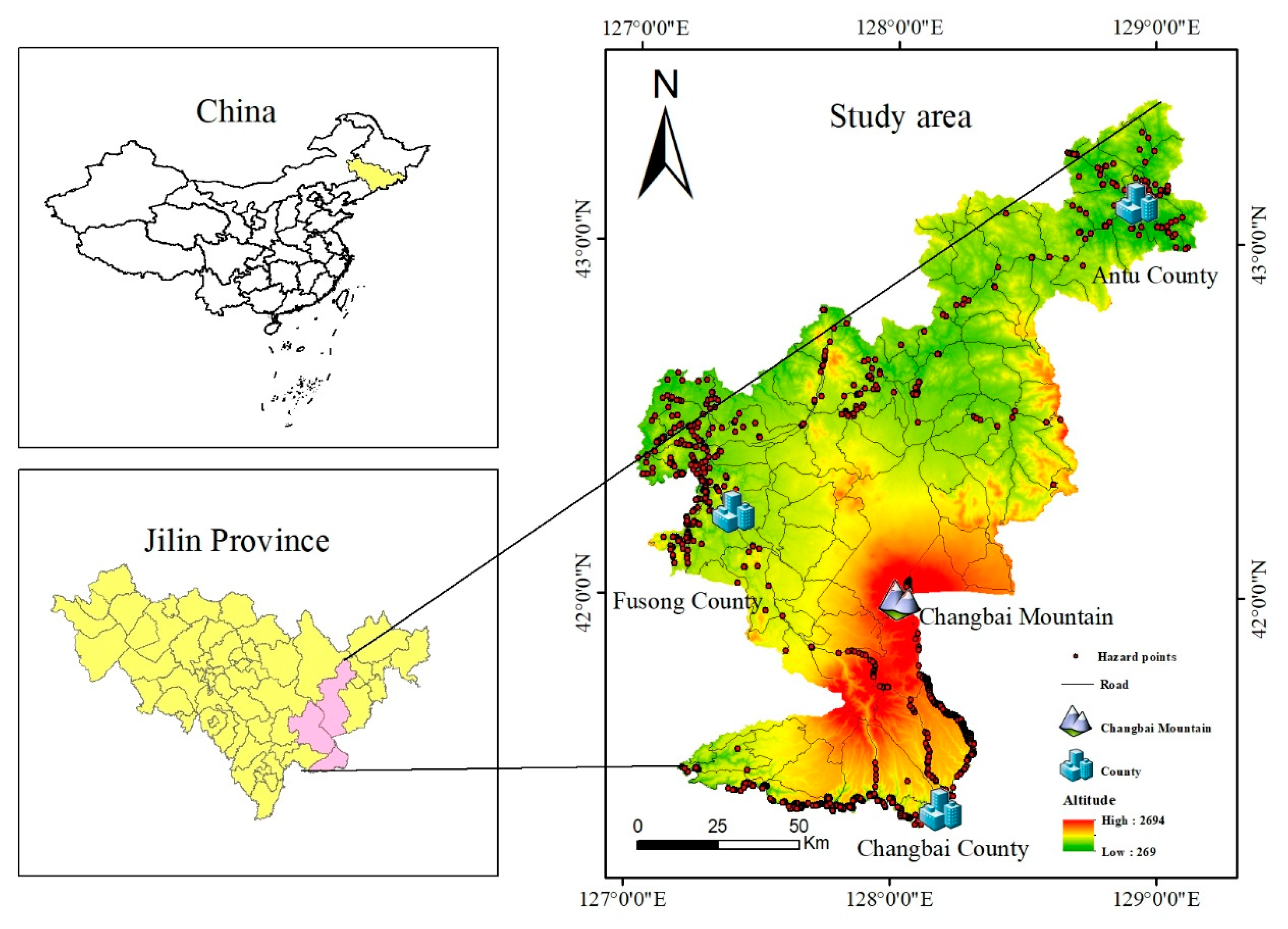
2. Study Area
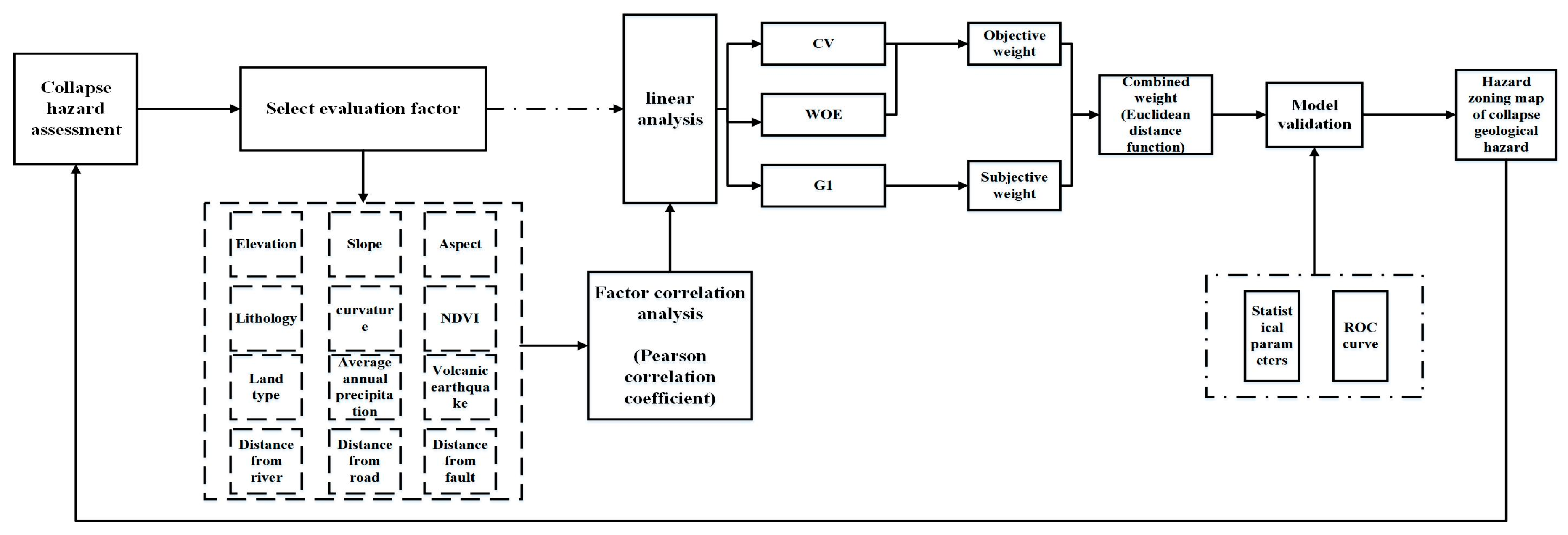
3. Methods and Data
3.1. Index Selection
3.2. Building an Evaluation Model
3.2.1. Order Relation Analysis Method (G1 Method)
- (1)
- Deterministic order relation
- (2)
- Judge the importance ratio
- (3)
- Calculation of weight coefficient
3.2.2. Weight of Evidence (WOE)
- (1)
- Calculate a prior probability
- (2)
- Weight calculation
- (3)
- Calculate a posteriori probability
3.2.3. Coefficient of Variance (CV)
- (1)
- Standardized treatment.
- (2)
- Calculate the coefficient of variation and weight value.
3.2.4. Combination Weight
- (1)
- Build a combination weight model.
- (2)
- Based on the Euclidean distance function, establish the equations.
- (3)
- Calculate the combined weight value.
4. Result and Discussion
4.1. Evaluation Index Correlation Analysis
4.2. Comparative Analysis of Evaluation Models
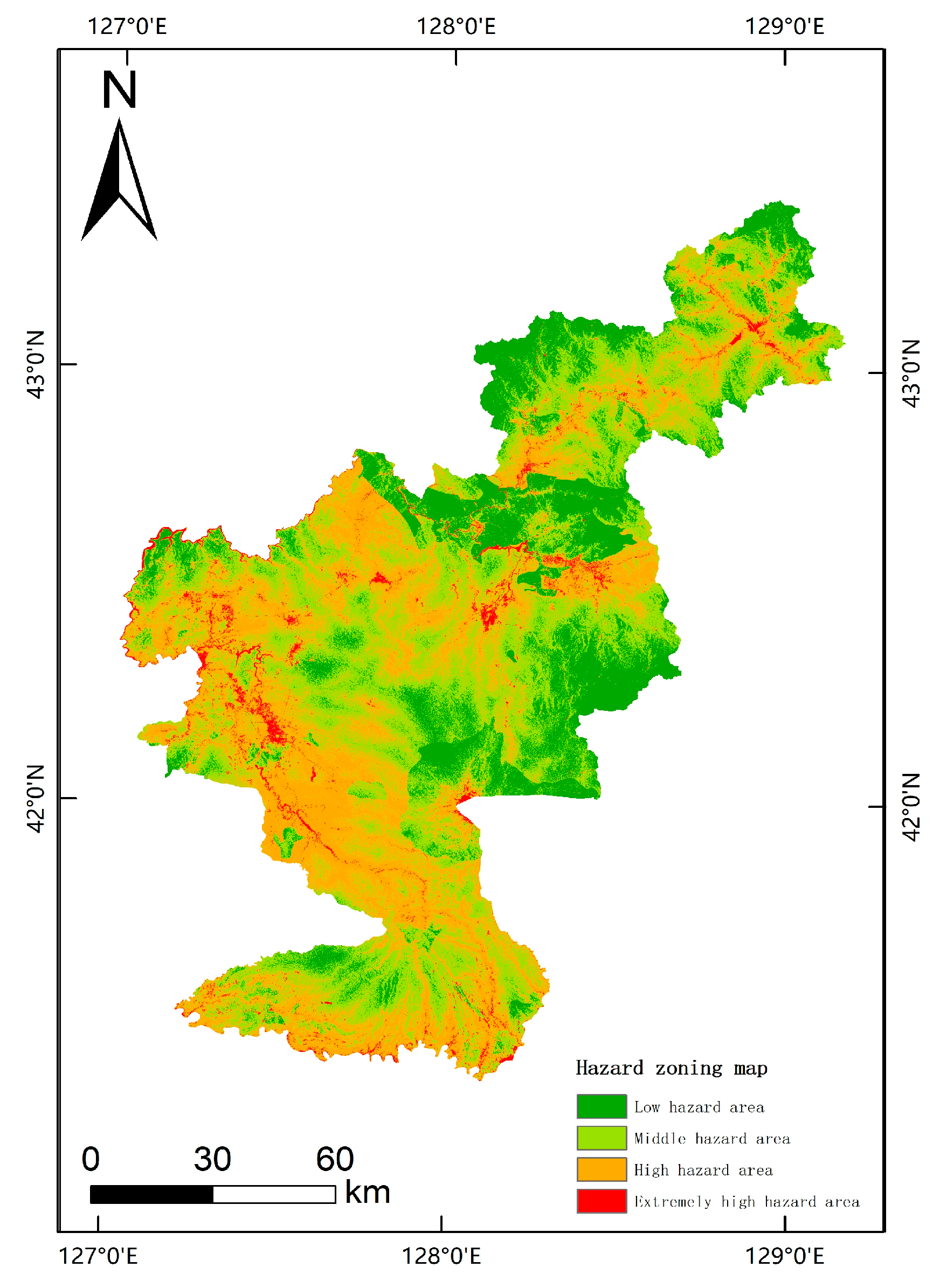
4.3. Hazard Map Analysis of Collapse Geological Hazard
4.4. Model Accuracy Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mulero, D.L.; Njå, O.; Fernández, C.L. Landslide risk management in the urban development of sandnes (norway). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-3/W4, 327–334. [Google Scholar] [CrossRef]
- Cui, P.; Peng, J.; Shi, P.; Tang, H.; Ouyang, C.; Zou, Q.; Liu, L.; Li, C.; Lei, Y. Scientific challenges of research on natural hazards and disaster risk. Geogr. Sustain. 2021, 2, 216–223. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Z.; Gao, G.; Guo, J.; Xue, P. Disaster probability, optimal government expenditure for disaster prevention and mitigation, and expected economic growth. Sci. Total Environ. 2019, 709, 135888. [Google Scholar] [CrossRef]
- Chen, Q.-F.; Ai, Y.; Chen, Y. Overview of deep structures under the Changbaishan volcanic area in Northeast China. Sci. China Earth Sci. 2019, 62, 935–952. [Google Scholar] [CrossRef]
- Liu, G.M.; Sun, Y.T.; Li, T.; Zhong, G.P.; Gong, Z.; Su, X.T. The geochemical monitoring of volcanic gases in the Tianchi Area of the Changbaishan mountains and discussion of their data processing methods. Bull. Mineral. Petrol. Geochem. 2018, 37, 621–628+795. [Google Scholar] [CrossRef]
- Pederson, C.A.; Santi, P.M.; Pyles, D.R. Relating the compensational stacking of debris-flow fans to characteristics of their underlying stratigraphy: Implications for geologic hazard assessment and mitigation. Geomorphology 2015, 248, 47–56. [Google Scholar] [CrossRef]
- Yanar, T.; Kocaman, S.; Gokceoglu, C. Use of Mamdani Fuzzy Algorithm for Multi-Hazard Susceptibility Assessment in a Developing Urban Settlement (Mamak, Ankara, Turkey). ISPRS Int. J. Geo-Inf. 2020, 9, 114. [Google Scholar] [CrossRef]
- Gill, J.C.; Malamud, B.D. Anthropogenic processes, natural hazards, and interactions in a multi-hazard framework. Earth-Sci. Rev. 2017, 166, 246–269. [Google Scholar] [CrossRef]
- de Vita, S.; Sansivero, F.; Orsi, G.; Marotta, E. Cyclical slope instability and volcanism related to volcano-tectonism in resurgent calderas: The Ischia island (Italy) case study. Eng. Geol. 2006, 86, 148–165. [Google Scholar] [CrossRef]
- Miles, S.B.; Keefer, D.K. Evaluation of CAMEL—Comprehensive areal model of earthquake-induced landslides. Eng. Geol. 2008, 104, 1–15. [Google Scholar] [CrossRef]
- Keefer, D.K.; Wasowski, J.; Del Gaudio, V. Special issue from the European Geosciences Union Symposium on landslides induced by earthquake and volcanic activity. Eng. Geol. 2006, 86, 85–86. [Google Scholar] [CrossRef]
- ElGharbawi, T.; Tamura, M. Coseismic and postseismic deformation estimation of the 2011 Tohoku earthquake in Kanto Region, Japan, using InSAR time series analysis and GPS. Remote Sens. Environ. 2015, 168, 374–387. [Google Scholar] [CrossRef]
- Tamura, J.; Okada, T. Ambient noise tomography in the Naruko/Onikobe volcanic area, NE Japan: Implications for geofluids and seismic activity. Earth Planets Space 2016, 68, 5. [Google Scholar] [CrossRef]
- Huang, Y.-D.; Yao, L.K.; Guo, C.W.; Guo, H.Q. Distribution law of earthquake-induced collapse and landslide in intensity regions VII to IX. J. Basic Sci. Eng. Ing. 2015, 23, 92–102. [Google Scholar]
- Zhang, J.Q.; Fan, J.R.; Yan, D.; Guo, F.F.; Su, F.H. Sensitivity evaluation to the earthquake-induced landslide and collapse: A case study of Beichuan county, Sichuan province. J. Sichuan Univ. (Eng. Sci. Ed.) 2009, 41, 140–145. [Google Scholar] [CrossRef]
- Lin, J.; Chen, W.; Qi, X.; Hou, H. Risk assessment and its influencing factors analysis of geological hazards in typical mountain environment. J. Clean. Prod. 2021, 309, 127077. [Google Scholar] [CrossRef]
- Koradecka, D.; Pośniak, M.; Widerszal-Bazyl, M.; Augusty Nska, D.; Radkiewicz, P. A comparative study of objective and subjective assessment of occupational risk. Int. J. Occup. Saf. Ergon. 2010, 16, 3–22. [Google Scholar] [CrossRef]
- Tan, Q.; Bai, M.; Zhou, P.; Hu, J.; Qin, X. Geological hazard risk assessment of line landslide based on remotely sensed data and GIS. Measurement 2021, 169, 108370. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Gessler, P.E.; Foltz, R.B.; Elliot, W.J. Spatial prediction of landslide hazard using logistic regression and ROC analysis. Trans. GIS 2006, 10, 395–415. [Google Scholar] [CrossRef]
- Zheng, Q.; Lyu, H.M.; Zhou, A.; Shen, S.L. Risk assessment of geohazards along Cheng-Kun railway using fuzzy AHP incorporated into GIS. Geomat. Nat. Hazards Risk 2021, 12, 1508–1531. [Google Scholar] [CrossRef]
- Chen, L.; Wang, W.; Zhang, W. Risk Evaluation of Regional Collapses Geological Hazard Based on D-S Evidence Theory-A case study of Haiyuan active fault belt in Ningxia Province. Energy Procedia 2012, 16, 371–376. [Google Scholar] [CrossRef]
- Sun, X.; Yu, C.; Li, Y.; Rene, N.N. Susceptibility Mapping of Typical Geological Hazards in Helong City Affected by Volcanic Activity of Changbai Mountain, Northeastern China. ISPRS Int. J. Geo-Inf. 2022, 11, 344. [Google Scholar] [CrossRef]
- Liu, X. Hazard Assessment of Landslide and Collapse Induced by Volcanic Eruption in Changbai Mountains. Master’s Thesis, Jilin University, Changchun, China, 2016. [Google Scholar]
- Ding, Y.-H. The Relationship between Earthquake Collapse and Seismic Parameters and Its Application in Slope Earthquake Damage Prediction. Chin. J. Geophys. 1999, S1, 101–107. [Google Scholar]
- Grant, A.; Wartman, J.; Abou-Jaoude, G. Multimodal method for coseismic landslide hazard assessment. Eng. Geol. 2016, 212, 146–160. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, M.-S.; Xue, Q.; Wu, S.-D. Risk-based evaluation on geological environment carrying capacity of mountain city—A case study in Suide County, Shaanxi Province, China. J. Mt. Sci. 2018, 15, 2730–2740. [Google Scholar] [CrossRef]
- Sun, D.; Chen, Y.; Li, X.; Huang, C.; Su, H.; Chen, R. Control and Application of Terrain Curvature on Dynamic Disasters: A Case Study of Coal and Gas Outbursts in the Pingdingshan Mining Area, China. Adv. Civ. Eng. 2021, 2021, 1–6. [Google Scholar] [CrossRef]
- Ye, Q.; Yu, S.; Liu, J.; Zhao, Q.; Zhao, Z. Aboveground biomass estimation of black locust planted forests with aspect variable using machine learning regression algorithms. Ecol. Indic. 2021, 129, 107948. [Google Scholar] [CrossRef]
- Batar, A.; Watanabe, T. Landslide Susceptibility Mapping and Assessment Using Geospatial Platforms and Weights of Evidence (WoE) Method in the Indian Himalayan Region: Recent Developments, Gaps, and Future Directions. ISPRS Int. J. Geo-Inf. 2021, 10, 114. [Google Scholar] [CrossRef]
- Dai, K.; Chen, C.; Shi, X.; Wu, M.; Feng, W.; Xu, Q.; Liang, R.; Zhuo, G.; Li, Z. Dynamic landslides susceptibility evaluation in Baihetan Dam area during extensive impoundment by integrating geological model and InSAR observations. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103157. [Google Scholar] [CrossRef]
- Meinhardt, M.; Fink, M.; Tünschel, H. Landslide susceptibility analysis in central Vietnam based on an incomplete landslide inventory: Comparison of a new method to calculate weighting factors by means of bivariate statistics. Geomorphology 2015, 234, 80–97. [Google Scholar] [CrossRef]
- Manzo, G.; Tofani, V.; Segoni, S.; Battistini, A.; Catani, F. GIS techniques for regional-scale landslide susceptibility assessment: The Sicily (Italy) case study. Int. J. Geogr. Inf. Sci. 2013, 27, 1433–1452. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Sharma, L.P.; Patel, N.; Debnath, P.; Ghose, M.K. Assessing landslide vulnerability from soil characteristics—A GIS-based analysis. Arab. J. Geosci. 2011, 5, 789–796. [Google Scholar] [CrossRef]
- Zope, P.E.; Eldho, T.I.; Jothiprakash, V. Impacts of land use–land cover change and urbanization on flooding: A case study of Oshiwara River Basin in Mumbai, India. Catena 2016, 145, 142–154. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Y.; Zhai, E.; Ye, P. Coupling analysis of the heat-water dynamics and frozen depth in a seasonally frozen zone. J. Hydrol. 2020, 593, 125603. [Google Scholar] [CrossRef]
- Ye, F.; Sun, J.; Wang, Y.; Nedjah, N.; Bu, W. A novel method for the performance evaluation of institutionalized collaborative innovation using an improved G1-CRITIC comprehensive evaluation model. J. Innov. Knowl. 2023, 8, 100289. [Google Scholar] [CrossRef]
- Behera, S.; Panigrahi, M.K. Gold prospectivity mapping and exploration targeting in Hutti-Maski schist belt, India: Synergistic application of Weights-of-Evidence (WOE), Fuzzy Logic (FL) and hybrid (WOE-FL) models. J. Geochem. Explor. 2022, 235, 106963. [Google Scholar] [CrossRef]
- Wu, Z.; Lv, H.; Meng, Y.; Guan, X.; Zang, Y. The determination of flood damage curve in areas lacking disaster data based on the optimization principle of variation coefficient and beta distribution. Sci. Total Environ. 2021, 750, 142277. [Google Scholar] [CrossRef] [PubMed]
- Puth, M.-T.; Neuhäuser, M.; Ruxton, G.D. Effective use of Spearman’s and Kendall’s correlation coefficients for association between two measured traits. Anim. Behav. 2015, 102, 77–84. [Google Scholar] [CrossRef]
- Martens, F.K.; Tonk, E.C.; Kers, J.G.; Janssens, A.C.J. Small improvement in the area under the receiver operating characteristic curve indicated small changes in predicted risks. J. Clin. Epidemiol. 2016, 79, 159–164. [Google Scholar] [CrossRef]

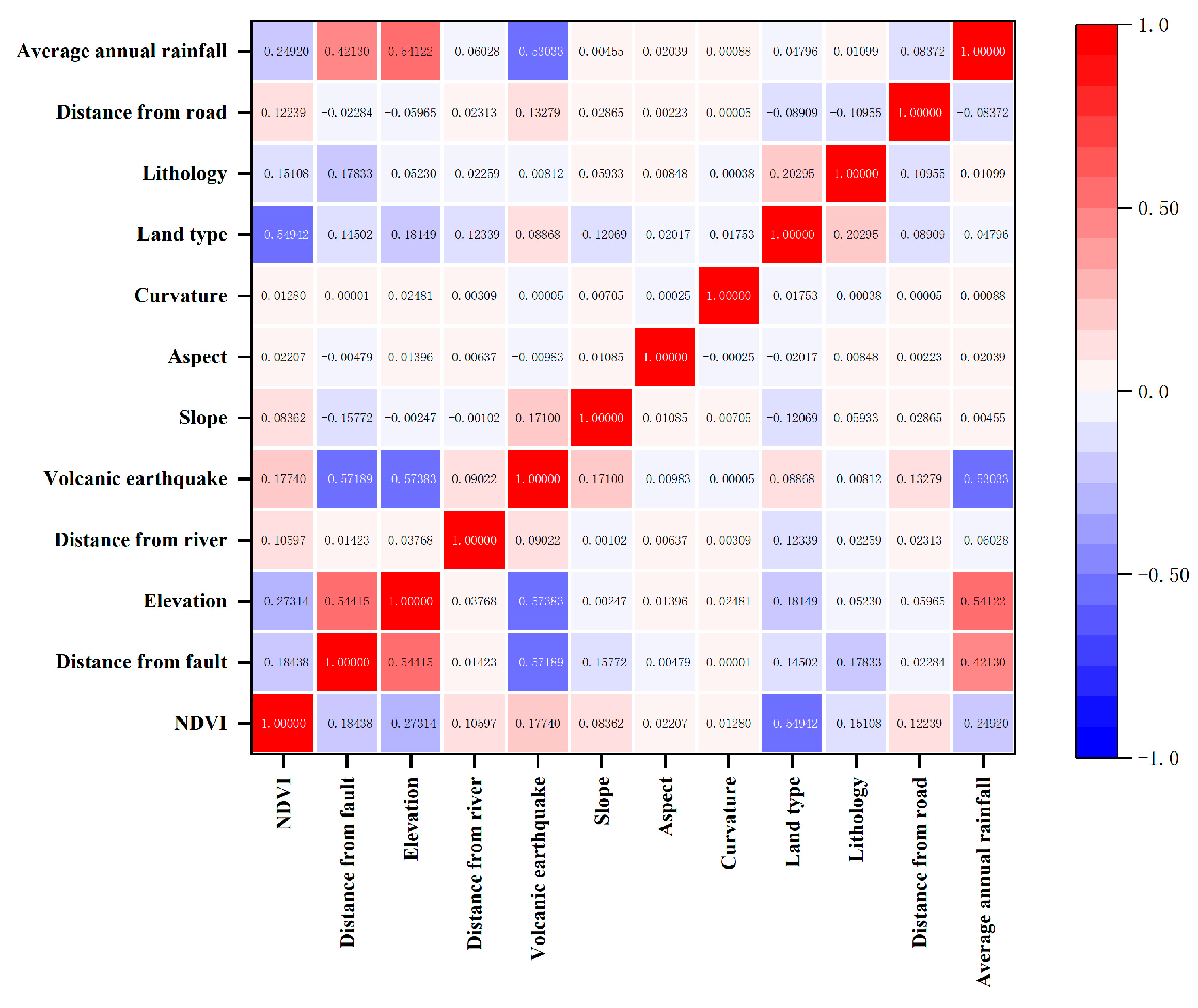

| Criteria | Evaluation Indicators | Principle of Selection |
|---|---|---|
| Topographic features | Elevation | The vegetation coverage, sunlight exposure area and water catchment of slopes at different elevations, with varying impacts on the rock and soil mass of slopes [25]. |
| Slope | When the slope exceeds a certain value, it will intensify the gravity effect, easily causing the sliding and collapse of rock layers and soil, especially under the influence of natural disasters such as rainy seasons or earthquakes. Therefore, slope is one of the important factors in the occurrence of collapse geological hazard [26]. | |
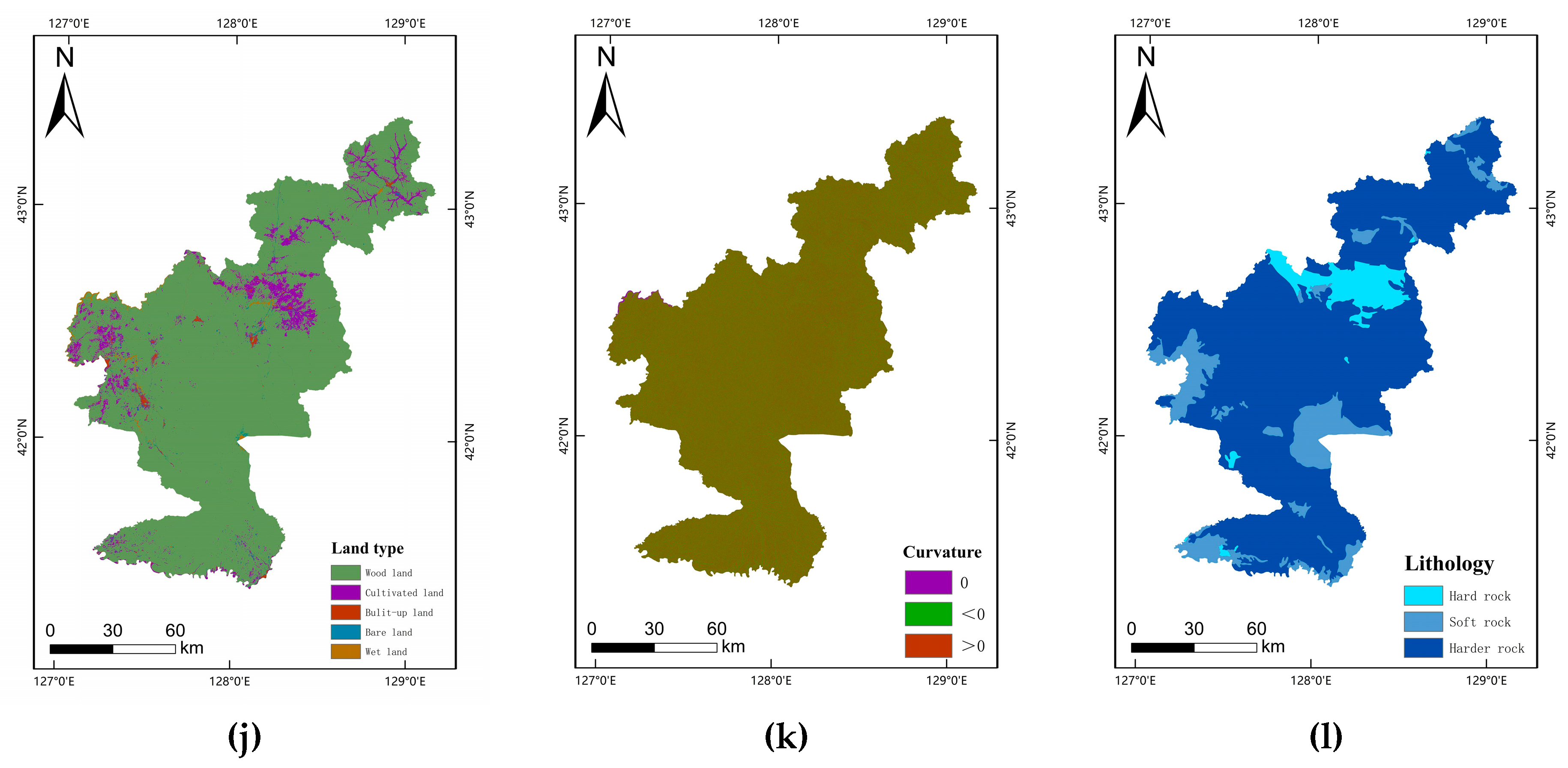
| Curvature | The value of the curvature reflects the shape of the slope, including concave slopes, convex slopes, straight slopes, etc. Convex slopes will form a phenomenon of stress concentration at the slope corner, resulting in a decrease in the stability of the slope. The middle part of the concave slope is prone to strong erosion, which is also not conducive to the stability of the slope [27]. | |
| Aspect | Different slope directions are exposed to sunlight and precipitations for different time ranges, which further affects the distribution of vegetation on the slope, the weathering degree of rock and soil, and then the occurrence of geological hazard [28]. | |
| Rock and soil mass | Lithology | Formation lithology is the material condition for forming geological hazards. Different formation lithologies have different shear and weathering resistance of rock mass. According to the analysis and statistics of the formation lithology in the study area, geological hazards of collapse mainly occur in hard rock layers [29]. |
| Geological structure | Distance from fault | The strength of the rock and soil around the fault zone is low, and the weathering resistance is weak, which can lead to unstable joint surfaces, and then induce the occurrence of collapse geological hazards [30]. |
| Meteorology and hydrology | Distance from river | Drainage affects the stability of the slope, mainly manifested in scouring and eroding the slope toe, changing the original slope gradient and reducing the strength of the slope [31]. |
| Human engineering activities | Distance from road | Through statistical analysis, it is found that more than 80% of the collapse geological hazard in the study area is affected by human engineering activities. Among them, the construction of roads is the primary factor affecting the stability of slopes, with the excavation, backfilling and stacking of materials during the construction process [32]. |
| Vegetation cover | NDVI | The vegetation normalization index can significantly reflect the spatial distribution of vegetation in the study area. The smaller the NDVI value is, the sparser the vegetation is. The higher the NDVI value is, the higher the vegetation coverage is. Areas with high vegetation cover are less susceptible to erosion than bare areas [33]. |
| Land use type | The type of land use can objectively reflect the natural environment and human engineering activities in the study area, both of which will affect the occurrence of geological hazards to a certain extent [34,35]. | |
| Inducing factor | Volcanic earthquake | The study area is close to the crater of Changbai Mountain, and volcanic activity has occurred frequently in recent years, so volcanic earthquake is selected as the inducing factor for consideration. |
| Average annual precipitation | Rainfall may induce slope instability and deformation. Part of the rainfall will form surface runoff and scour the slope surface. At the same time, part of the rain will penetrate into the slope, changing the stress balance inside the slope, and further inducing the occurrence of collapse geological hazards [36]. |
| Indicator | Data Source |
|---|---|
| DEM | Geospatial Date Cloud (http://www.gscloud.cn, accessed on 2 June 2022) |
| Lithology | National Geological Archives Date Center (http://dc.ngac.org.cn/Home, accessed on 1 January 2021) |
| Distance from fault | |
| Distance from river | National Catalogue Service For Geographic Information (https://www.webmap.cn, accessed on 29 April 2022) |
| Distance from road | |
| NDVI | Google Earth Engine (https://code.earthengine.google.com, accessed on 1 July 2022) |
| Land type | National Tibetan Plateau Date Center (http://data.tpdc.ac.cn, accessed on 20 July 2021) |
| Average annual precipitation | China Meteorological Date Service Center (http://data.cma.cn, accessed on 1 January 2022) |
| Volcanic earthquake | Seismic ground motion parameters zonation map of China GB18306-2015 (https://www.gb18306.net, accessed on 1 June 2022) |
| rk | Explain |
|---|---|
| 1.0 | Xk−1 and Xk are equally important |
| 1.1 | Xk−1 and Xk are between equally important and slightly important |
| 1.2 | Xk−1 is slightly more important than Xk |
| 1.3 | Xk−1 and Xk are between slightly important and obviously important |
| 1.4 | Xk−1 is obviously more important than Xk |
| 1.5 | Xk−1 and Xk are between obviously important and strongly important |
| 1.6 | Xk−1 is strongly more important than Xk |
| 1.7 | Xk−1 and Xk are between strongly important and extremely important |
| 1.8 | Xk−1 is extremely more important than Xk |
| Evidence Factors | Classification | Number of Cells | Number of Hazards | ||||
|---|---|---|---|---|---|---|---|
| NDVI | 0–0.58 | 313,974 | 63 | 1.47667 | −0.05182 | 1.52849 | 0.00020065 |
| 0.58–0.72 | 668,216 | 144 | 1.54806 | −0.12761 | 1.67567 | 0.00021550 | |
| 0.72–0.82 | 1,425,234 | 204 | 1.13882 | −0.16501 | 1.30383 | 0.00014313 | |
| 0.82–0.89 | 3,273,150 | 278 | 0.61684 | −0.16813 | 0.78497 | 0.00008493 | |
| 0.89–1 | 15,634,670 | 288 | −0.91162 | 0.97320 | −1.88482 | 0.00001842 | |
| Distance from fault (m) | 0–1000 | 1,180,622 | 109 | 0.70029 | −0.06132 | 0.76160 | 0.00009232 |
| 1000–2000 | 1,151,732 | 77 | 0.37750 | −0.02655 | 0.40404 | 0.00006686 | |
| 2000–3000 | 1,082,263 | 67 | 0.30059 | −0.01893 | 0.31952 | 0.00006191 | |
| 3000–4000 | 1,021,729 | 54 | 0.14243 | −0.00774 | 0.15017 | 0.00005285 | |
| >4000 | 16,878,898 | 670 | −0.14386 | 0.41198 | −0.55583 | 0.00003969 | |
| Elevation (m) | 269–600 | 3,311,114 | 455 | 1.09804 | −0.45801 | 1.55605 | 0.00013742 |
| 600–800 | 7,462,661 | 235 | −0.37541 | 0.15582 | −0.53123 | 0.00003149 | |
| 800–1000 | 4,965,081 | 73 | −1.13707 | 0.18754 | −1.32460 | 0.00001470 | |
| 1000–1300 | 3,650,234 | 91 | −0.60902 | 0.09007 | −0.69909 | 0.00002493 | |
| 1300–1600 | 1,322,724 | 74 | 0.19932 | −0.01470 | 0.21402 | 0.00005595 | |
| 1600–2700 | 603,430 | 49 | 0.57192 | −0.02274 | 0.59465 | 0.00008120 | |
| Distance from river (m) | 0–1000 | 8,966,141 | 734 | 0.58003 | −0.84561 | 1.42564 | 0.00008186 |
| 1000–2000 | 6,678,777 | 134 | −0.82619 | 0.22840 | −1.05458 | 0.00002006 | |
| 2000–3000 | 3,607,311 | 75 | −0.79056 | 0.10554 | −0.89611 | 0.00002079 | |
| 3000–4000 | 1,476,359 | 26 | −0.95657 | 0.04481 | −1.00138 | 0.00001761 | |
| >4000 | 586,656 | 8 | −1.21234 | 0.01969 | −1.23203 | 0.00001364 | |
| Volcanic earthquake | 0.088–0.034 | 4,741,785 | 200 | −0.08316 | 0.02257 | −0.10574 | 0.00004218 |
| 0.034–0.025 | 6,448,480 | 173 | −0.53564 | 0.16542 | −0.70105 | 0.00002683 | |
| 0.025–0.019 | 5,894,248 | 456 | 0.52348 | −0.30506 | 0.82854 | 0.00007736 | |
| 0.019–0.014 | 2,504,709 | 27 | −1.44743 | 0.09699 | −1.54442 | 0.00001078 | |
| 0.014–0.011 | 1,726,022 | 121 | 0.42493 | −0.04778 | 0.47271 | 0.00007010 | |
| Slope (°) | 0–7 | 7,842,641 | 89 | −1.39604 | 0.36327 | −1.75931 | 0.00001135 |
| 7–13 | 6,599,765 | 156 | −0.66226 | 0.19657 | −0.85883 | 0.00002364 | |
| 13–20 | 3,953,879 | 175 | −0.03498 | 0.00780 | −0.04277 | 0.00004426 | |
| 20–40 | 2,739,782 | 382 | 1.11257 | −0.35836 | 1.47093 | 0.00013943 | |
| >40 | 179,177 | 175 | 3.06003 | −0.18894 | 3.24898 | 0.00097669 | |
| Aspect | North | 2,877,596 | 72 | −0.60537 | 0.06848 | −0.67385 | 0.00002502 |
| Northeast | 2,689,788 | 109 | −0.12318 | 0.01660 | −0.13978 | 0.00004052 | |
| East | 2,621,511 | 153 | 0.24164 | −0.03908 | 0.28072 | 0.00005836 | |
| Southeast | 2,277,835 | 210 | 0.69886 | −0.12899 | 0.82785 | 0.00009219 | |
| South | 2,580,040 | 163 | 0.32090 | −0.05351 | 0.37441 | 0.00006318 | |
| Southwest | 2,652,967 | 142 | 0.15509 | −0.02414 | 0.17923 | 0.00005352 | |
| West | 2,901,265 | 78 | −0.53352 | 0.06311 | −0.59663 | 0.00002688 | |
| Northwest | 2,714,242 | 50 | −0.91158 | 0.08368 | −0.99526 | 0.00001842 | |
| Curvature | <0 | 10,199,533 | 534 | 0.13300 | −0.13986 | 0.27286 | 0.00005236 |
| 0 | 1,168,179 | 36 | −0.39701 | 0.01882 | −0.41583 | 0.00003082 | |
| >0 | 9,947,532 | 407 | −0.11358 | 0.08980 | −0.20338 | 0.00004091 | |
| Land type | Wood land | 19,448,699 | 662 | −0.29759 | 1.30354 | −1.60113 | 0.00003404 |
| Cultivated land | 1,383,114 | 107 | 0.52346 | −0.04891 | 0.57236 | 0.00007736 | |
| Bulit-up land | 159,839 | 79 | 2.37842 | −0.07679 | 2.45521 | 0.00049425 | |
| Bare land | 192,787 | 117 | 2.58384 | −0.11847 | 2.70231 | 0.00060689 | |
| Wet land | 130,805 | 12 | 0.69394 | −0.00620 | 0.70014 | 0.00009174 | |
| Lithology | Harder rock | 17,130,568 | 638 | −0.20760 | 0.56954 | −0.77714 | 0.00003724 |
| Soft rock | 2,874,907 | 308 | 0.84908 | −0.23383 | 1.08291 | 0.00010713 | |
| Hard rock | 1,309,769 | 31 | −0.66095 | 0.03117 | −0.69212 | 0.00002367 | |
| Distance from road (m) | 0–1000 | 2,615,504 | 669 | 1.71947 | −1.02350 | 2.74298 | 0.00025578 |
| 1000–2000 | 2,195,692 | 66 | −0.42192 | 0.03877 | −0.46069 | 0.00003006 | |
| 2000–3000 | 1,988,314 | 38 | −0.87479 | 0.05825 | −0.93305 | 0.00001911 | |
| 3000–4000 | 1,734,351 | 23 | −1.24024 | 0.06105 | −1.30128 | 0.00001326 | |
| >4000 | 12,781,383 | 181 | −1.17459 | 0.71054 | −1.88513 | 0.00001416 | |
| Average annual precipitation (mm) | 570–650 | 2,987,969 | 137 | 0.00032 | −0.00005 | 0.00038 | 0.00004585 |
| 650–750 | 10,682,978 | 411 | −0.17513 | 0.14964 | −0.32477 | 0.00003847 | |
| 750–850 | 7,096,453 | 379 | 0.15288 | −0.08604 | 0.23893 | 0.00005341 | |
| 850–950 | 483,402 | 31 | 0.33585 | −0.00930 | 0.34515 | 0.00006413 | |
| 950–1100 | 64,442 | 19 | 1.86161 | −0.01661 | 1.87823 | 0.00029484 |
| Evaluation Factor | Average | Standard Deviation | Coefficient of Variation | Weight Value |
|---|---|---|---|---|
| Land type | 5,421,204.4 | 7,116,344.351 | 1.312686965 | 0.142485503 |
| NDVI | 8,158,410.4 | 4,468,700.668 | 0.547741588 | 0.059454568 |
| Aspect | 14,315,560.75 | 5,201,882.555 | 0.363372602 | 0.039442251 |
| Elevation | 14,400,680.5 | 11,112,883.19 | 0.771691532 | 0.083763197 |
| Slope | 13,640,479.6 | 7,542,532.487 | 0.552952147 | 0.060020147 |
| Distance from fault | 8,808,624.4 | 4,764,803.379 | 0.540924799 | 0.05871464 |
| Volcanic earthquake | 22,137,892 | 17,042,856.53 | 0.769850017 | 0.08356331 |
| Lithology | 44,195,626 | 42,385,456.04 | 0.959041875 | 0.104099125 |
| Distance from river | 30,206,968.2 | 29,026,962.87 | 0.960935989 | 0.104304721 |
| Curvature | 51,661,842 | 36,488,511.95 | 0.706295218 | 0.076664759 |
| Distance from road | 17,785,890 | 12,496,151.36 | 0.702587914 | 0.07626235 |
| Average annual precipitation | 11,986,172.4 | 12,282,169.97 | 1.02469492 | 0.11122543 |
| Evaluation Factor | Subjective Weight | Objective Weight | Combined Weight |
|---|---|---|---|
| Land type | 0.178790582 | 0.142485503 | 0.159863837 |
| NDVI | 0.112872842 | 0.059454568 | 0.08502456 |
| Aspect | 0.054433277 | 0.039442251 | 0.04661808 |
| Elevation | 0.045361064 | 0.083763197 | 0.065381056 |
| Slope | 0.148992152 | 0.060020147 | 0.102608822 |
| Distance from fault | 0.094060702 | 0.05871464 | 0.075633916 |
| Volcanic earthquake | 0.022367388 | 0.08356331 | 0.054270352 |
| Lithology | 0.065319932 | 0.104099125 | 0.085536495 |
| Distance from river | 0.078383918 | 0.104304721 | 0.091897081 |
| Curvature | 0.034893126 | 0.076664759 | 0.056669723 |
| Distance from road | 0.135447411 | 0.07626235 | 0.104592759 |
| Average annual precipitation | 0.029077605 | 0.11122543 | 0.07190332 |
| Classification | Area (km2) | Number of Hazard Points | Density of Hazard Points (km−2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| G1 | WOE-CV | Combined Weight | G1 | WOE-CV | Combined Weight | G1 | WOE-CV | Combined Weight | |
| Low | 2947 | 2346 | 3098 | 26 | 38 | 23 | 0.009 | 0.016 | 0.007 |
| Middle | 5934 | 6797 | 7080 | 145 | 130 | 97 | 0.024 | 0.019 | 0.014 |
| High | 4931 | 6436 | 5424 | 235 | 432 | 465 | 0.048 | 0.067 | 0.086 |
| very high | 2211 | 444 | 421 | 571 | 377 | 392 | 0.258 | 0.850 | 0.932 |
| Classification | Area (km2) | Proportion (%) | Number of Hazard Points | Proportion of Hazard Points (%) |
|---|---|---|---|---|
| Low-hazard area | 3097.64 | 19.33 | 23 | 2.35 |
| Middle-hazard area | 7080.22 | 44.19 | 97 | 9.93 |
| High-hazard area | 5423.77 | 33.85 | 465 | 47.59 |
| Very-high hazard area | 420.72 | 2.63 | 392 | 40.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Z.; Lang, Q.; Zhang, Y.; Zhang, J.; Yu, C.; Wu, C. Geological Hazard Assessment of Secondary Collapses Due to Volcanic Earthquakes on Changbai Mountain in China. ISPRS Int. J. Geo-Inf. 2023, 12, 307. https://doi.org/10.3390/ijgi12080307
Pan Z, Lang Q, Zhang Y, Zhang J, Yu C, Wu C. Geological Hazard Assessment of Secondary Collapses Due to Volcanic Earthquakes on Changbai Mountain in China. ISPRS International Journal of Geo-Information. 2023; 12(8):307. https://doi.org/10.3390/ijgi12080307
Chicago/Turabian StylePan, Zengkai, Qiuling Lang, Yichen Zhang, Jiquan Zhang, Chenglong Yu, and Chenyang Wu. 2023. "Geological Hazard Assessment of Secondary Collapses Due to Volcanic Earthquakes on Changbai Mountain in China" ISPRS International Journal of Geo-Information 12, no. 8: 307. https://doi.org/10.3390/ijgi12080307
APA StylePan, Z., Lang, Q., Zhang, Y., Zhang, J., Yu, C., & Wu, C. (2023). Geological Hazard Assessment of Secondary Collapses Due to Volcanic Earthquakes on Changbai Mountain in China. ISPRS International Journal of Geo-Information, 12(8), 307. https://doi.org/10.3390/ijgi12080307






