Towards Topological Geospatial Conflation: An Optimized Node-Arc Conflation Model for Road Networks
Abstract
:1. Introduction
2. Background
2.1. Similarity Measures
2.2. Match Selection Methods
2.3. Optimized Conflation Modeling
3. Method
3.1. Topological Relations in Matching
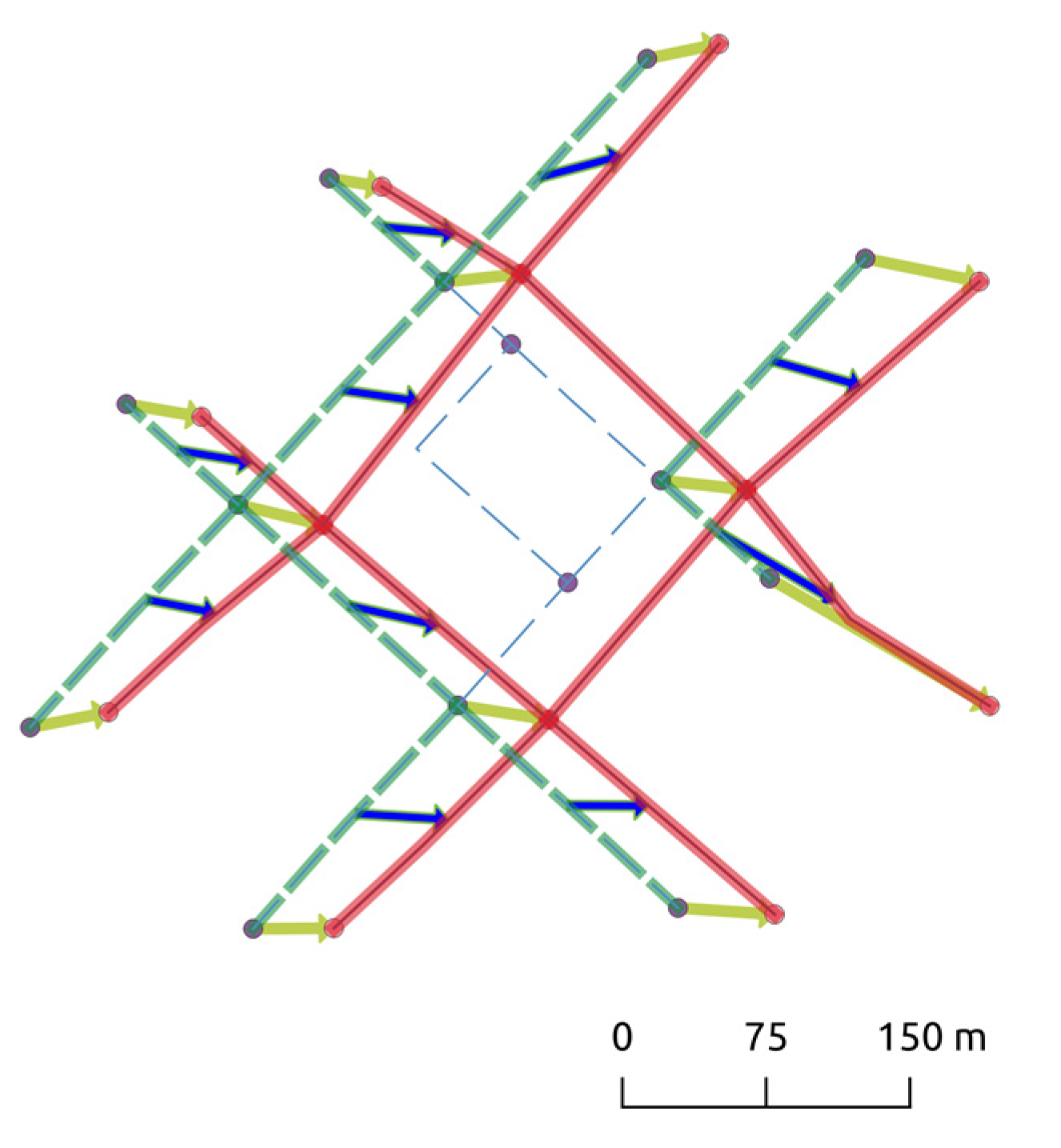
3.2. A Node-Arc Topological Matching Model
- The right-hand side is the sum of the degrees of all nodes in that are matched. By construction, the matched nodes and edges in form a subnetwork of for which because compatibility constraints (6) through (9) require all nodes associated with the matched edges to also be matched, and the objective function (1) ensures that no other nodes are matched. Because each edge is connected to two nodes, and according to a well-known fact in graph theory, the sum of the degrees of the said subnetwork of is equal to twice the number of edges, the latter of which is exactly the left-hand side. Therefore, .
- Because the en-matching model is a one-to-one matching model, the number of matched edges (and nodes) in network is the same as that in network . Therefore, we also have .
- Therefore, we have . □
4. Experiments
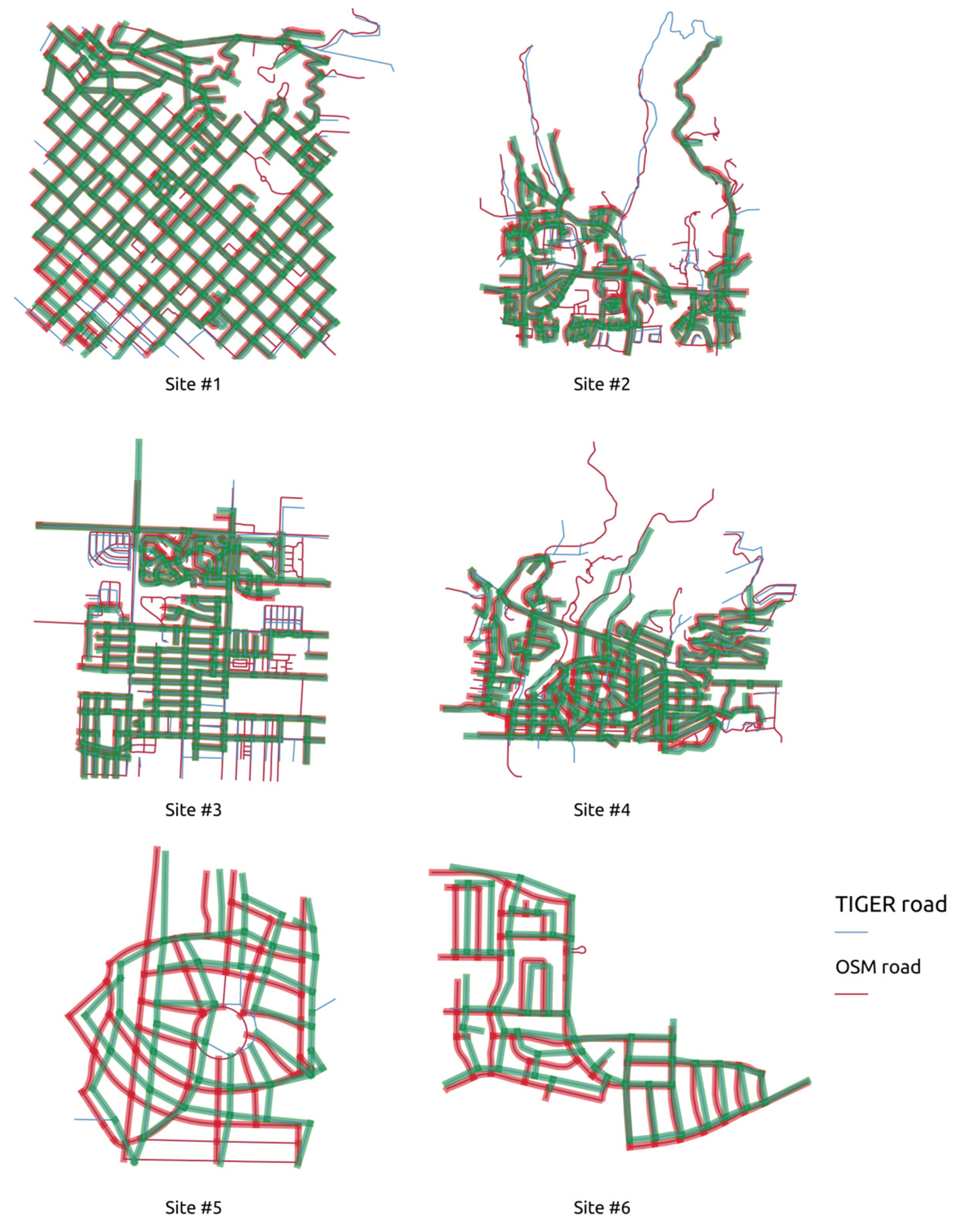
4.1. Experimental Settings
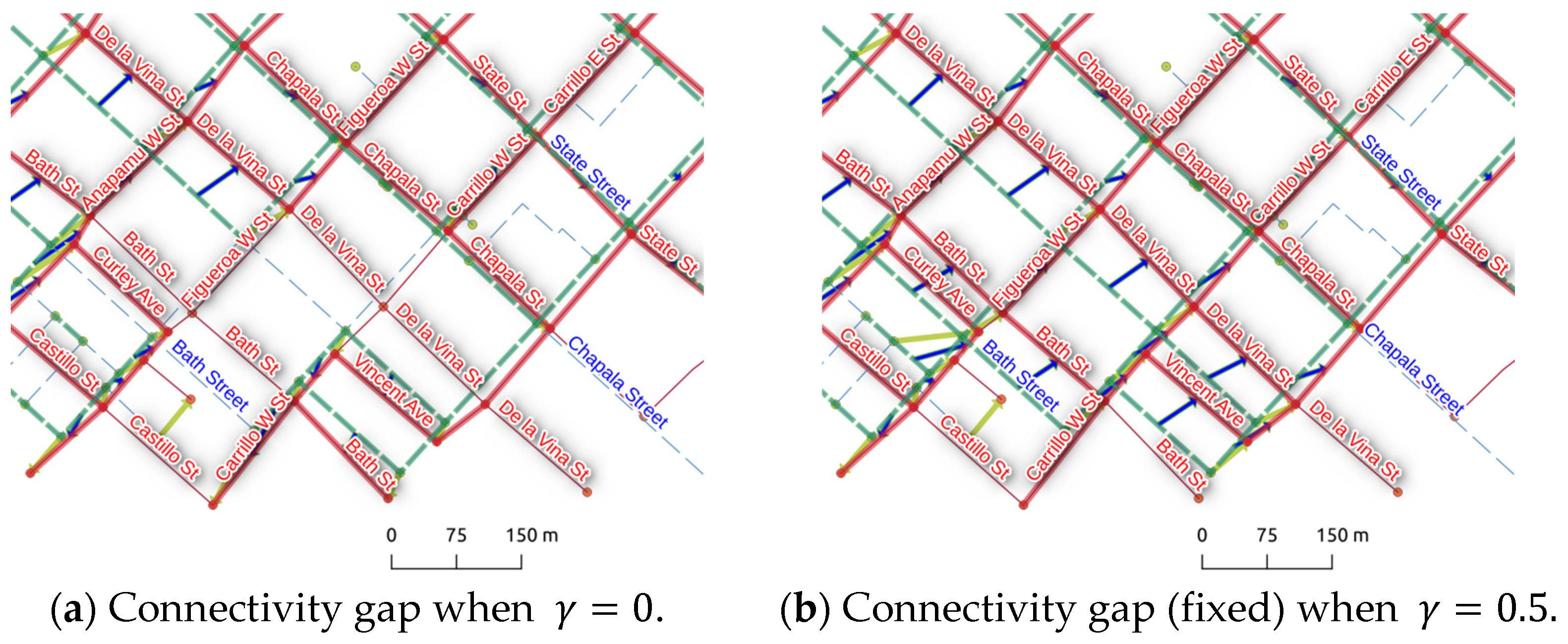
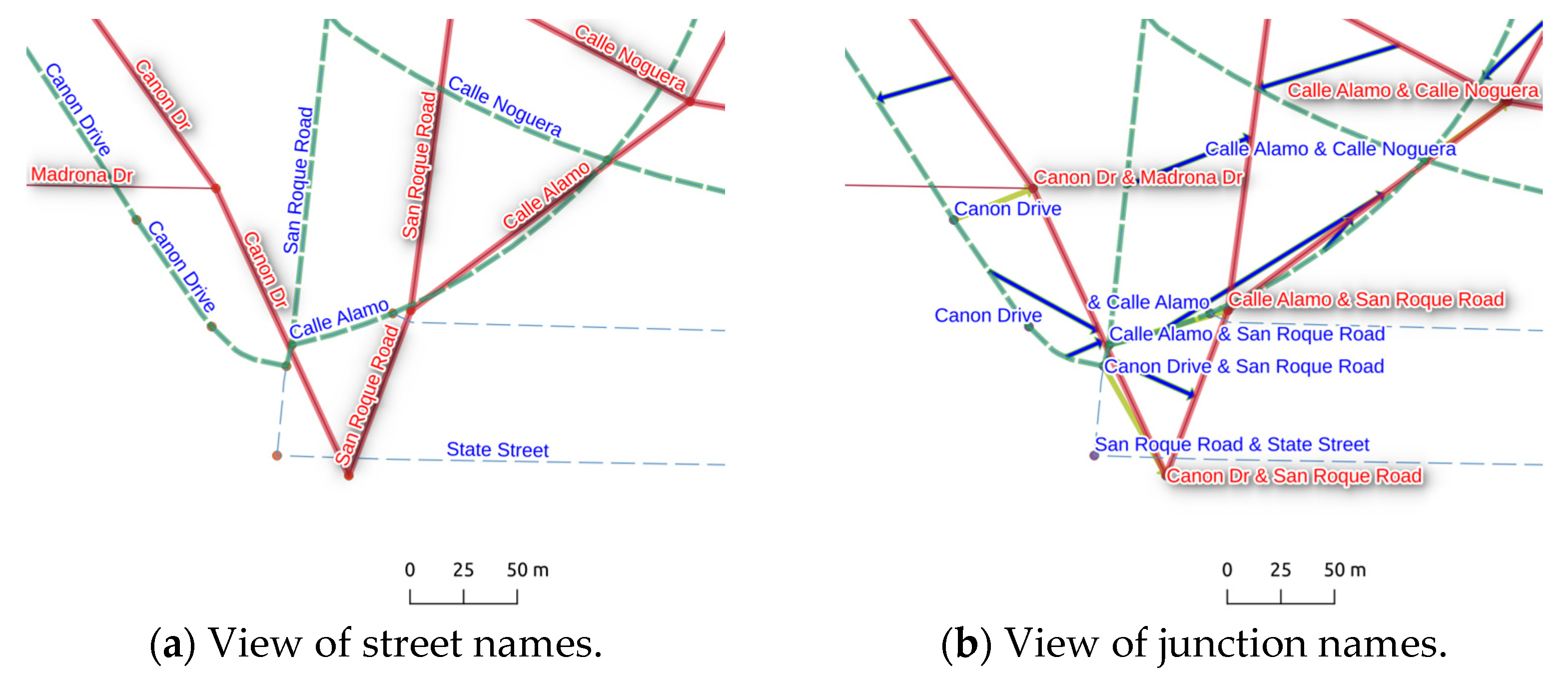
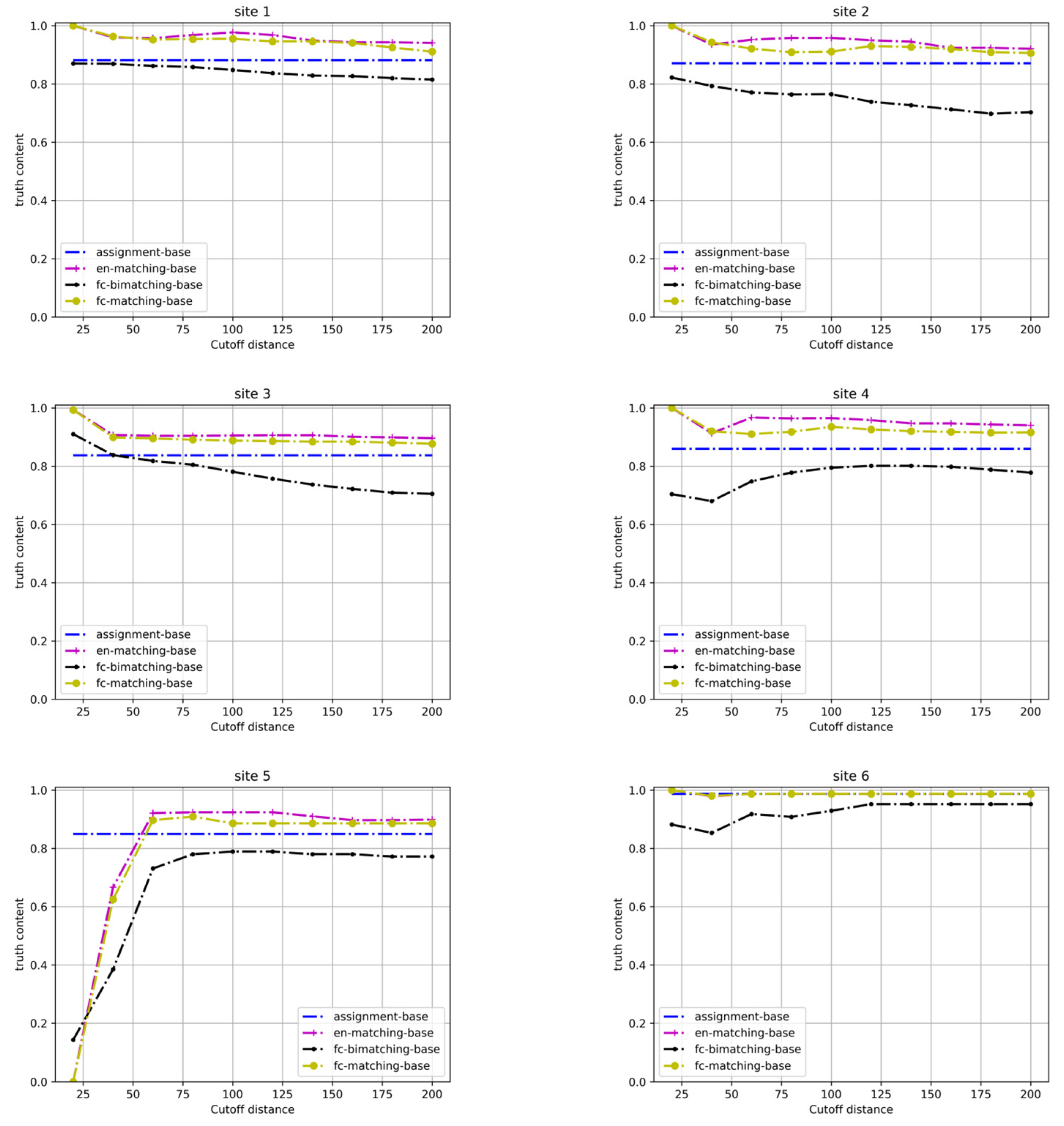
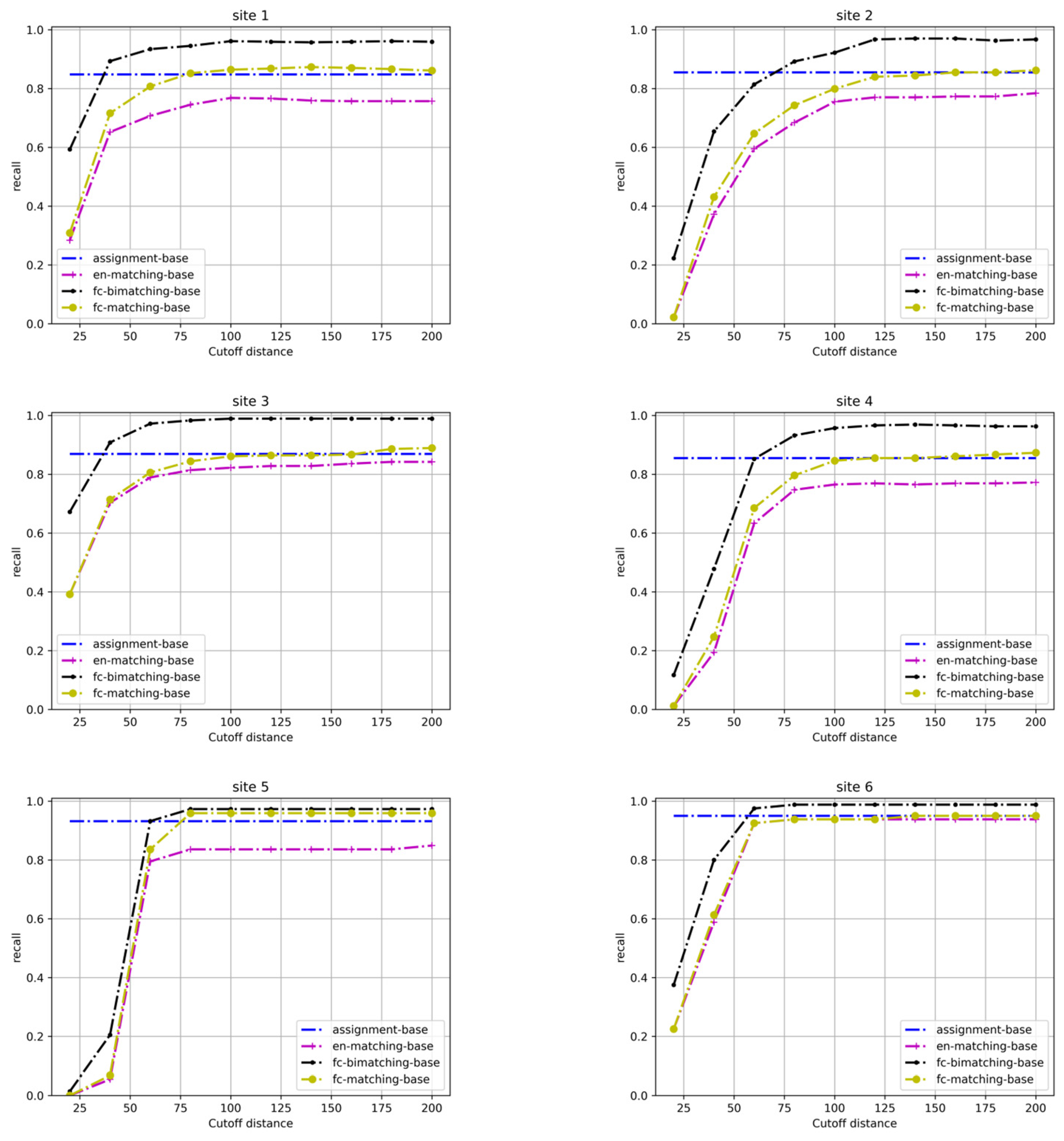
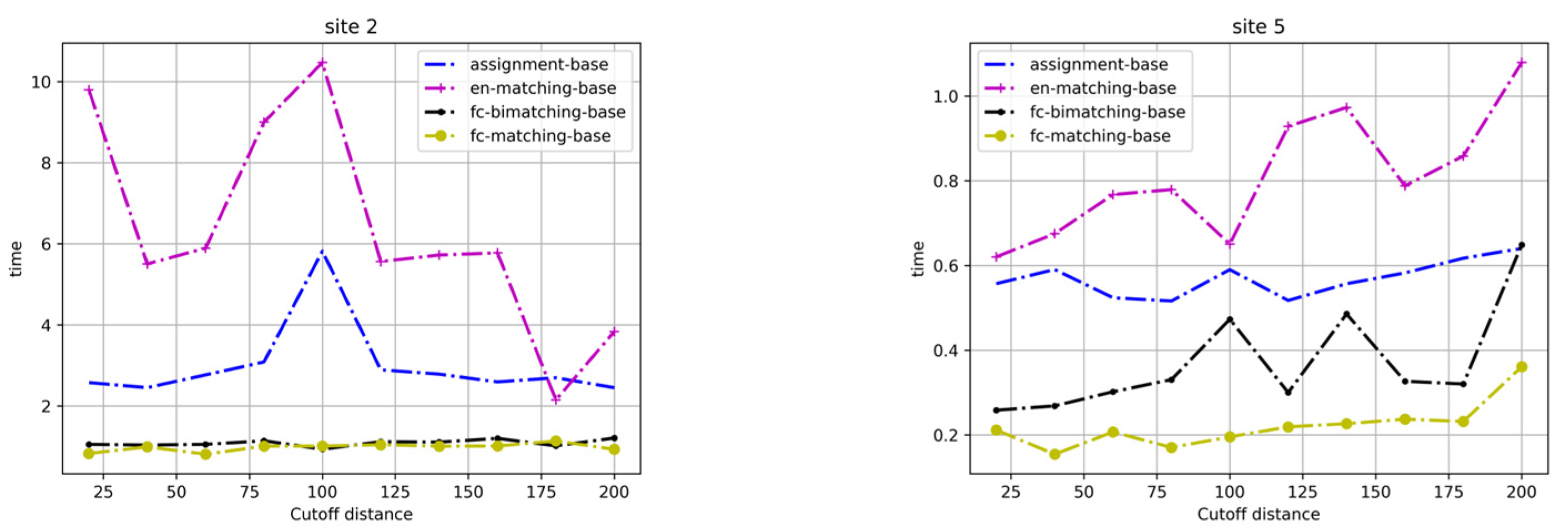
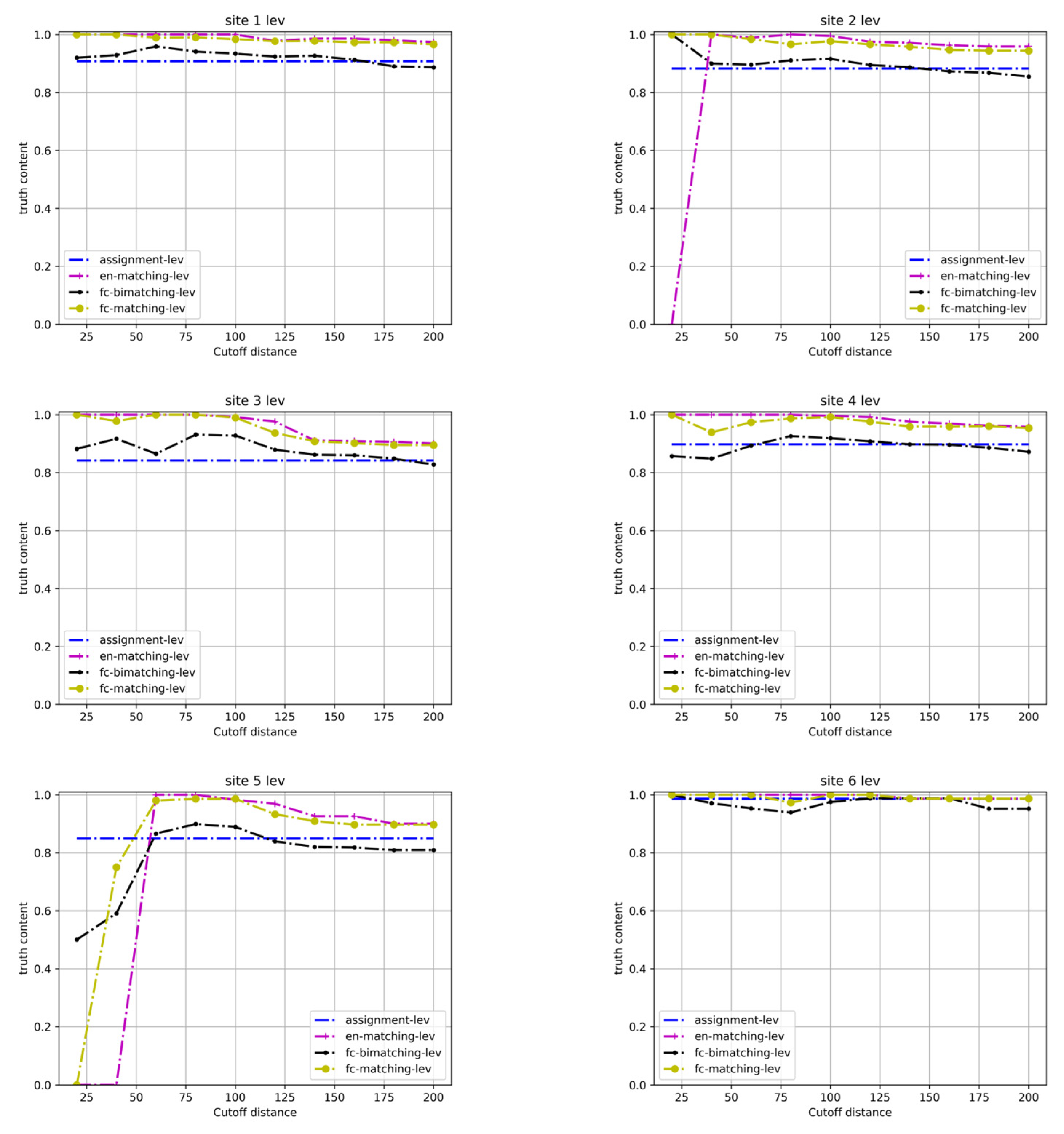
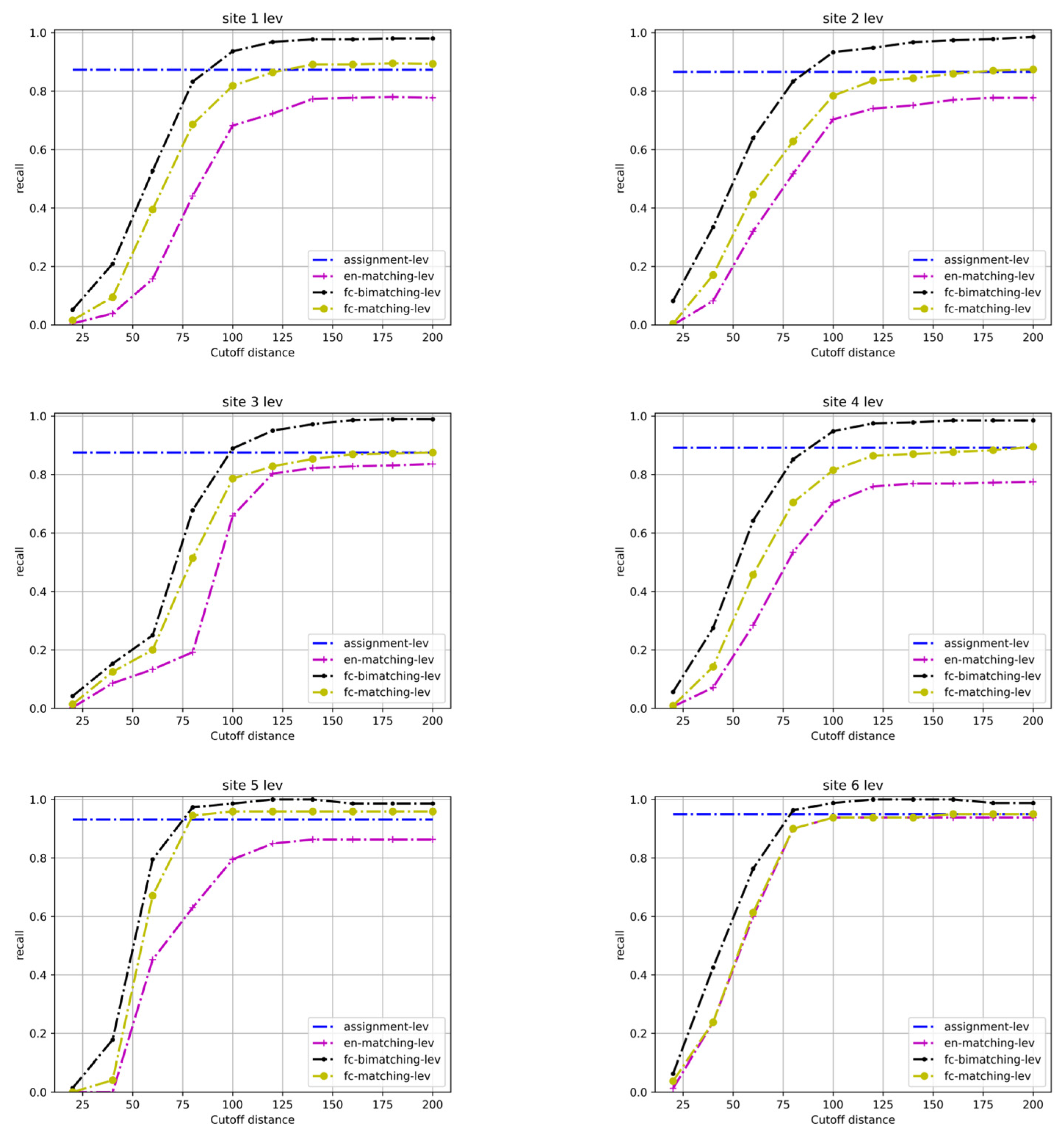
4.2. Experimental Results
5. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosen, B.; Saalfeld, A. Match Criteria for Automatic Alignment. In Proceedings of the 7th International Symposium on Computer-Assisted Cartography (Auto-Carto 7), Washington, DC, USA, 11–14 March 1985; pp. 1–20. [Google Scholar]
- Saalfeld, A. Conflation automated map compilation. Int. J. Geogr. Inf. Syst. 1988, 2, 217–228. [Google Scholar] [CrossRef]
- Cobb, M.A.; Chung, M.J.; Iii, H.F.; Petry, F.E.; Shaw, K.B.; Miller, H.V. A rule-based approach for the conflation of attributed vector data. GeoInformatica 1998, 2, 7–35. [Google Scholar] [CrossRef]
- Filin, S.; Doytsher, Y. Detection of corresponding objects in linear-based map conflation. Surv. Land Inf. Syst. 2000, 60, 117–128. [Google Scholar]
- Masuyama, A. Methods for detecting apparent differences between spatial tessellations at different time points. Int. J. Geogr. Inf. Sci. 2006, 20, 633–648. [Google Scholar] [CrossRef]
- Pendyala, R.M. Development of GIS-Based Conflation Tools for Data Integration and Matching; Florida Department of Transportation: Lake City, FL, USA, 2002.
- Ruiz, J.J.; Ariza, F.J.; Ureña, M.A.; Blázquez, E.B. Digital map conflation: A review of the process and a proposal for classification. Int. J. Geogr. Inf. Sci. 2011, 25, 1439–1466. [Google Scholar] [CrossRef]
- Xavier, E.M.A.; Ariza-López, F.J.; Ureña-Cámara, M.A. A survey of measures and methods for matching geospatial vector datasets. ACM Comput. Surv. 2016, 49, 1–34. [Google Scholar] [CrossRef]
- MacEachren, A.M. Compactness of geographic shape: Comparison and evaluation of measures. Geogr. Ann. Ser. B Hum. Geogr. 1985, 67, 53–67. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, X.; Molenaar, M.; Stoter, J.; Kraak, M.-J.; Ai, T. Pattern classification approaches to matching building polygons at multiple scales. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 19–24. [Google Scholar] [CrossRef]
- Tang, W.; Hao, Y.; Zhao, Y.; Li, N. Research on areal feature matching algorithm based on spatial similarity. In Proceedings of the 2008 Chinese Control and Decision Conference, Yantai, China, 2–4 July 2008; pp. 3326–3330. [Google Scholar]
- Tong, X.; Shi, W.; Deng, S. A probability-based multi-measure feature matching method in map conflation. Int. J. Remote Sens. 2009, 30, 5453–5472. [Google Scholar] [CrossRef]
- Wentz, E.A. Shape Analysis in GIS. In Proceedings of the Auto-Carto, Seattle, WA, USA, 7–10 April 1997; Volume 13, pp. 7–10. [Google Scholar]
- Eiter, T.; Mannila, H. Computing discrete fréchet distance. Citeseer 1994. [Google Scholar]
- Chambers, E.W.; De Verdiere, E.C.; Erickson, J.; Lazard, S.; Lazarus, F.; Thite, S. Homotopic fréchet distance between curves or, walking your dog in the woods in polynomial time. Comput. Geom. 2010, 43, 295–311. [Google Scholar] [CrossRef]
- Arkin, E.M.; Chew, L.P.; Huttenlocher, D.P.; Kedem, K.; Mitchell, J.S. An Efficiently Computable Metric for Comparing Polygonal Shapes; Cornell University: Ithaca, NY, USA, 1991. [Google Scholar]
- Lei, T.L.; Wang, R. Conflating linear features using turning function distance: A new orientation-sensitive similarity measure. Trans. GIS 2021, 25, 1249–1276. [Google Scholar] [CrossRef]
- Harvey, F.; Vauglin, F.; Ali, A.B.H. Geometric matching of areas, comparison measures and association links. In Proceedings of the 8th International Symposium on Spatial Data Handling, Vancouver, BC, Canada, 11–15 July 1998; pp. 557–568. [Google Scholar]
- Huh, Y.; Yu, K.; Heo, J. Detecting conjugate-point pairs for map alignment between two polygon datasets. Comput. Environ. Urban Syst. 2011, 35, 250–262. [Google Scholar] [CrossRef]
- Fan, H.; Zipf, A.; Fu, Q.; Neis, P. Quality assessment for building footprints data on OpenStreetMap. Int. J. Geogr. Inf. Sci. 2014, 28, 700–719. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Hunter, G.J. A simple positional accuracy measure for linear features. Int. J. Geogr. Inf. Sci. 1997, 11, 299–306. [Google Scholar] [CrossRef]
- Li, L.; Goodchild, M.F. Optimized feature matching in conflation. In Proceedings of the Geographic Information Science: 6th International Conference, GIScience, Zurich, Switzerland, 14–17 September 2010; pp. 14–17. [Google Scholar]
- McKenzie, G.; Janowicz, K.; Adams, B. A weighted multi-attribute method for matching user-generated points of interest. Cartogr. Geogr. Inf. Sci. 2014, 41, 125–137. [Google Scholar] [CrossRef]
- Liadis, J.S. GPS TIGER accuracy analysis tools (GTAAT) evaluation and test results. US Bur. Census Div. Geogr. TIGER Oper. Branch 2000. [Google Scholar]
- Zandbergen, P.A.; Ignizio, D.A.; Lenzer, K.E. Positional Accuracy of TIGER 2000 and 2009 Road Networks. Trans. GIS 2011, 15, 495–519. [Google Scholar] [CrossRef]
- Church, R.; Curtin, K.; Fohl, P.; Funk, C.; Goodchild, M.F.; Kyriakidis, P.; Noronha, V. Positional distortion in geographic data sets as a barrier to interoperation. In Proceedings of the ACSM Annual Convention, Baltimore, MD, USA, 27 February–5 March 1998. [Google Scholar]
- Lei, T.L. Geospatial data conflation: A formal approach based on optimization and relational databases. Int. J. Geogr. Inf. Sci. 2020, 34, 2296–2334. [Google Scholar] [CrossRef]
- Beeri, C.; Kanza, Y.; Safra, E.; Sagiv, Y. Object fusion in geographic information systems. In Proceedings of the Thirtieth International Conference on Very Large Data Bases, Toronto, ON, Canada, 31 August–3 September 2004; Volume 30, pp. 816–827. [Google Scholar]
- Hillier, F.S.; Lieberman, G.J. Introduction to Operations Research, 8th ed.; McGraw-Hill: New York, NY, USA, 2005; p. 1088. [Google Scholar]
- Li, L.; Goodchild, M.F. An optimisation model for linear feature matching in geographical data conflation. Int. J. Image Data Fusion 2011, 2, 309–328. [Google Scholar] [CrossRef]
- Tong, X.; Liang, D.; Jin, Y. A linear road object matching method for conflation based on optimization and logistic regression. Int. J. Geogr. Inf. Sci. 2013, 28, 824–846. [Google Scholar] [CrossRef]
- Lei, T.; Lei, Z. Optimal spatial data matching for conflation: A network flow-based approach. Trans. GIS 2019, 23, 1152–1176. [Google Scholar] [CrossRef]
- Revelle, C.; Marks, D.; Liebman, J.C. An Analysis of Private and Public Sector Location Models. Manag. Sci. 1970, 16, 692–707. [Google Scholar] [CrossRef]
- ReVelle, C. Facility siting and integer-friendly programming. Eur. J. Oper. Res. 1993, 65, 147–158. [Google Scholar] [CrossRef]
- Lei, T.L. Large scale geospatial data conflation: A feature matching framework based on optimization and divide-and-conquer. Comput. Environ. Urban Syst. 2021, 87, 101618. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Z.; Lei, T.L. Towards Topological Geospatial Conflation: An Optimized Node-Arc Conflation Model for Road Networks. ISPRS Int. J. Geo-Inf. 2024, 13, 15. https://doi.org/10.3390/ijgi13010015
Lei Z, Lei TL. Towards Topological Geospatial Conflation: An Optimized Node-Arc Conflation Model for Road Networks. ISPRS International Journal of Geo-Information. 2024; 13(1):15. https://doi.org/10.3390/ijgi13010015
Chicago/Turabian StyleLei, Zhen, and Ting L. Lei. 2024. "Towards Topological Geospatial Conflation: An Optimized Node-Arc Conflation Model for Road Networks" ISPRS International Journal of Geo-Information 13, no. 1: 15. https://doi.org/10.3390/ijgi13010015
APA StyleLei, Z., & Lei, T. L. (2024). Towards Topological Geospatial Conflation: An Optimized Node-Arc Conflation Model for Road Networks. ISPRS International Journal of Geo-Information, 13(1), 15. https://doi.org/10.3390/ijgi13010015





