Beyond the Road: A Regional Perspective on Traffic Congestion in Metro Atlanta
Abstract
:1. Introduction
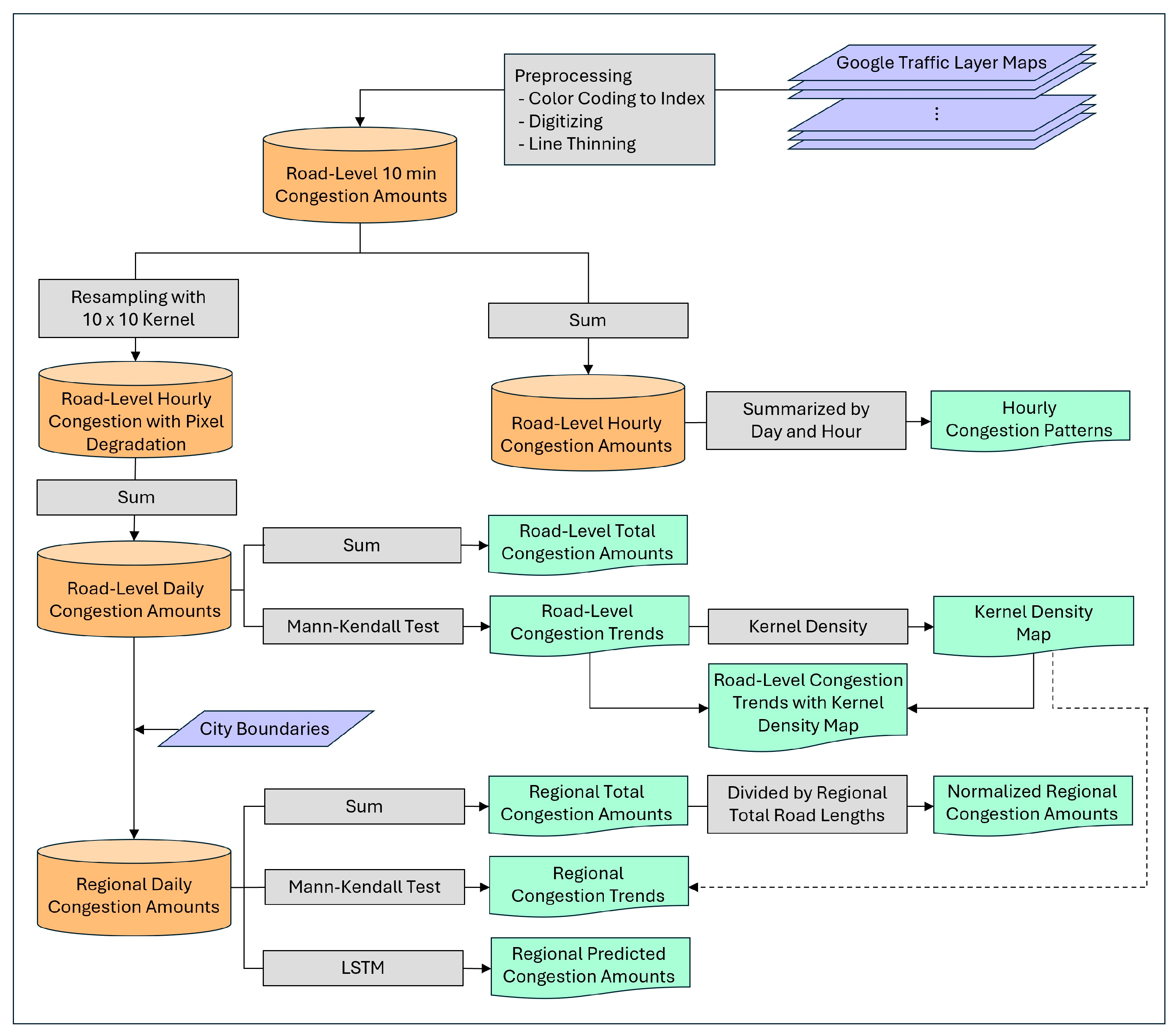
2. Materials and Methods
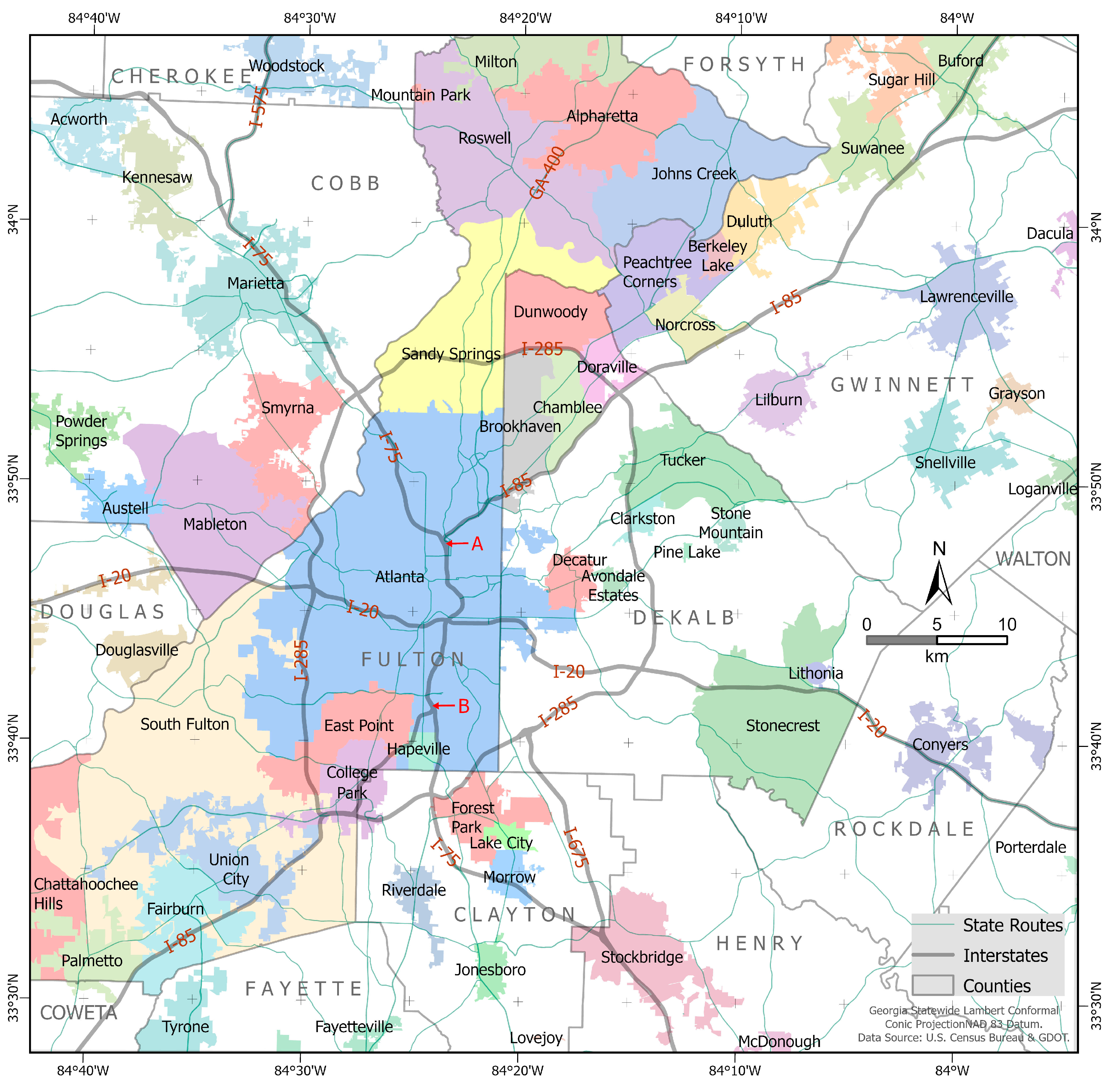
2.1. Study Area and Data
2.2. Spatial and Temporal Patterns
2.3. Trend Analysis
2.4. Regional Analysis
3. Results
3.1. Temporal and Spatial Patterns
3.2. Temporal Trends
3.3. Regional Variations
3.4. Predicted Trends
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Federal Highway Administration. Traffic Congestion and Reliability: Linking Solutions to Problems. 2004. Available online: https://ops.fhwa.dot.gov/congestion_report_04/index.htm (accessed on 27 November 2024).
- Hennessy, D.A. Social, Personality, and Affective Constructs in Driving. In Handbook of Traffic Psychology; Porter, B., Ed.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 149–164. [Google Scholar] [CrossRef]
- Noratikah, W.; Ghazali, B.W.; Nurhamizah, C.; Zulkifli, A.B.; Ponrahomo, Z. The Effect of Traffic Congestion on Quality of Community Life. In Proceedings of the ICRP 2019—4th International Conference on Rebuilding Place, George Town, Malaysia, 6–7 November 2019. [Google Scholar] [CrossRef]
- Beckmann, M.J. Traffic Congestion and What to Do About It. Transp. B Transp. Dyn. 2013, 1, 103–109. [Google Scholar] [CrossRef]
- Khalid, A.; Vaughn, C. Application of System Selection Tool to Traffic Congestion in Metro Atlanta: A Case Study. In Proceedings of the 2011 ASEE Annual Conference & Exposition, Vancouver, BC, Canada, 26–29 June 2011. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, K.; Das, P. Study on Road Traffic Congestion: A Review. In Recent Trends in Communication and Electronics; CRC Press: Boca Raton, FL, USA, 2021; pp. 230–240. [Google Scholar] [CrossRef]
- Duranton, G.; Turner, M.A. The Fundamental Law of Road Congestion: Evidence from US Cities. Am. Econ. Rev. 2011, 101, 2616–2652. [Google Scholar] [CrossRef]
- Mann, A. What’s Up with That: Building Bigger Roads Actually Makes Traffic Worse. WIRED, 17 June 2014. Available online: https://www.wired.com/2014/06/wuwt-traffic-induced-demand/ (accessed on 27 November 2024).
- Djahel, S.; Doolan, R.; Muntean, G.-M.; Murphy, J. A Communications-Oriented Perspective on Traffic Management Systems for Smart Cities: Challenges and Innovative Approaches. IEEE Commun. Surv. Tutor. 2015, 17, 125–151. [Google Scholar] [CrossRef]
- Afrin, T.; Yodo, N. A Survey of Road Traffic Congestion Measures Towards a Sustainable and Resilient Transportation System. Sustainability 2020, 12, 4660. [Google Scholar] [CrossRef]
- Atlanta Regional Commission. 2050 Metropolitan Transportation Plan. 2024. Available online: https://atlantaregional.org/what-we-do/transportation-planning/metropolitan-transportation-plan/ (accessed on 27 November 2024).
- Delaware Valley Regional Planning Commission. Congestion Management Process. 2023. Available online: https://www.dvrpc.org/reports/24135.pdf (accessed on 27 November 2024).
- Code of Federal Regulations. Title 23—Highways. Available online: https://www.ecfr.gov/current/title-23/chapter-I/subchapter-E/ (accessed on 27 November 2024).
- Zhang, K.; Sun, D.; Shen, S.; Zhu, Y. Analyzing Spatiotemporal Congestion Patterns on Urban Roads Based on Taxi GPS Data. J. Transp. Land Use 2017, 10, 675–694. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Prioritization of Public Transportation Investments: A Guide for Decision-Makers; TCRP Research Report 227 for TCRP Project H-58; The National Academies Press: Washington, DC, USA, 2021. [Google Scholar] [CrossRef]
- Rahman, M.M.; Najaf, P.; Fields, M.G.; Thill, J.C. Traffic Congestion and Its Urban Scale Factors: Empirical Evidence from American Urban Areas. Int. J. Sustain. Transp. 2021, 16, 406–421. [Google Scholar] [CrossRef]
- Lomax, T.; Turner, S.; Shunk, G. NCHRP Report 398: Quantifying Congestion: Volume 1—Final Report; Transportation Research Board, National Research Council: Washington, DC, USA, 1997. Available online: http://onlinepubs.trb.org/onlinepubs/nchrp/nchrp_rpt_398.pdf (accessed on 21 January 2025).
- INRIX. 2023 INRIX Global Traffic Scorecard. 2024. Available online: https://inrix.com/scorecard/ (accessed on 27 November 2024).
- Google. Google Maps Platform. Available online: https://developers.google.com/maps/documentation/routes/compute_route_directions (accessed on 27 November 2024).
- Wang, F.; Xu, Y. Estimating O–D Travel Time Matrix by Google Maps API: Implementation, Advantages, and Implications. Ann. GIS 2011, 17, 199–209. [Google Scholar] [CrossRef]
- Marasco, D.; Murray-Tuite, P.; Guikema, S.; Logan, T. Time to Leave: An Analysis of Travel Times During the Approach and Landfall of Hurricane Irma. Nat. Hazards 2020, 103, 2459–2487. [Google Scholar] [CrossRef]
- Zafar, N.; Ul Haq, I. Traffic Congestion Prediction Based on Estimated Time of Arrival. PLoS ONE 2020, 15, e0238200. [Google Scholar] [CrossRef]
- Gong, F.-Y. Modeling Walking Accessibility to Urban Parks Using Google Maps Crowdsourcing Database in the High-Density Urban Environments of Hong Kong. Sci. Rep. 2023, 13, 20798. [Google Scholar] [CrossRef]
- Seong, J.; Kim, Y.; Goh, H.; Kim, H.; Stanescu, A. Measuring Traffic Congestion with Novel Metrics: A Case Study of Six U.S. Metropolitan Areas. ISPRS Int. J. Geo-Inf. 2023, 12, 130. [Google Scholar] [CrossRef]
- Kim, Y. Prediction of Traffic Congestion Using a Time-Series Model and Spatiotemporal Data: A Case Study of the Atlanta Downtown Connector. Geogr. Bull. 2023, 64, 93–102. Available online: https://digitalcommons.kennesaw.edu/thegeographicalbulletin/vol64/iss2/7 (accessed on 27 November 2024).
- Ji, S.; Seong, J.; Stanescu, A.; Hwang, C.S.; Lee, Y. Spatiotemporal Traffic Database Construction with Google Real-Time Traffic Information and Spatiotemporal Congestion Pattern Analysis: A Case Study of Montgomery County, Maryland, U.S.A. J. Korean Geogr. Soc. 2021, 56, 265–276. [Google Scholar] [CrossRef]
- ESRI. How Kernel Density Works. ArcGIS Pro 3.4 Reference Manual. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-analyst/how-kernel-density-works.htm (accessed on 27 November 2024).
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall: London, UK, 1986; 175p. [Google Scholar] [CrossRef]
- Hirsh, R.M.; Slack, J.R.; Smith, R.A. Techniques of Trend Analysis for Monthly Water-Quality Data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Helsel, D.R.; Mueller, D.K.; Slack, J.R. Computer Program for the Kendall Family of Trend Tests; U.S. Geological Survey: Reston, VA, USA, 2006. Available online: https://pubs.usgs.gov/sir/2005/5275/pdf/sir2005-5275.pdf (accessed on 27 November 2024).
- U.S. Bureau of the Census. Geographic Areas Reference Manual. 1994. Available online: https://purl.fdlp.gov/GPO/LPS53335 (accessed on 27 November 2024).
- U.S. Bureau of the Census. TIGER Geodatabases. 2023. Available online: https://www.census.gov/geographies/mapping-files/time-series/geo/tiger-geodatabase-file.html (accessed on 27 November 2024).
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Akhtar, M.; Moridpour, S. A Review of Traffic Congestion Prediction Using Artificial Intelligence. J. Adv. Transp. 2021, 2021, 8878011. [Google Scholar] [CrossRef]
- Giles, C.L.; Lawrence, S.; Tsoi, A.C. Noisy Time Series Prediction Using Recurrent Neural Networks and Grammatical Inference. Mach. Learn. 2001, 44, 161–183. [Google Scholar] [CrossRef]
- Xu, F. Research on Traffic Flow Prediction Method Based on LSTM Model and PSO-LSTM Model. Appl. Comput. Eng. 2024, 101, 154–163. [Google Scholar] [CrossRef]
- Mojtaba, M.; Abdoul-Ahad, C.; Farshid, A. The Short-Term Prediction of Daily Traffic Volume for Rural Roads Using Shallow and Deep Learning Networks: ANN and LSTM. J. Supercomput. 2023, 79, 17475–17494. [Google Scholar] [CrossRef]
- Scikit-Learn. StandardScaler. Available online: https://scikit-learn.org/1.5/modules/generated/sklearn.preprocessing.StandardScaler.html (accessed on 27 November 2024).
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar] [CrossRef]
- American Transportation Research Institute. Top 100 Truck Bottlenecks—2023. Available online: https://truckingresearch.org/2023/02/top-100-truck-bottlenecks-2023/ (accessed on 27 November 2024).
- Almatar, K.M. Traffic Congestion Patterns in the Urban Road Network: (Dammam Metropolitan Area). Ain Shams Eng. J. 2023, 14, 101886. [Google Scholar] [CrossRef]
- Wei, X.; Ren, Y.; Shen, L.; Shu, T. Exploring the Spatiotemporal Pattern of Traffic Congestion Performance of Large Cities in China: A Real-Time Data-Based Investigation. Environ. Impact Assess. Rev. 2022, 95, 106808. [Google Scholar] [CrossRef]
- Agarwal, A. A Comparison of Weekend and Weekday Travel Behavior Characteristics in Urban Areas. USF Tampa Graduate Theses and Dissertations, University of South Florida, Tampa, FL, USA, 2004. Available online: https://digitalcommons.usf.edu/etd/936 (accessed on 12 November 2024).
- Perimeter Community Improvement Districts. Consolidated Plan: Perimeter in Progress, 2021 Update. 2021. Available online: https://perimeteratl.com/wp-content/uploads/2023/11/PCID-2021-Consolidated-Plan-Final-compressed.pdf (accessed on 27 November 2024).
- City of Cumming, Georgia. Comprehensive Plan 2022–2042. 2022. Available online: https://www.cityofcumming.net/wp-content/uploads/2022/10/Cumming-Comp-Plan-Adopted-10-4-2022.pdf (accessed on 27 November 2024).
- Byahut, S.; Ghosh, S.; Masilela, C. Urban Transformation for Sustainable Growth and Smart Living: The Case of the Atlanta Beltline. In Smart Living for Smart Cities; Springer Nature: Singapore, 2020; Chapter 13. [Google Scholar] [CrossRef]



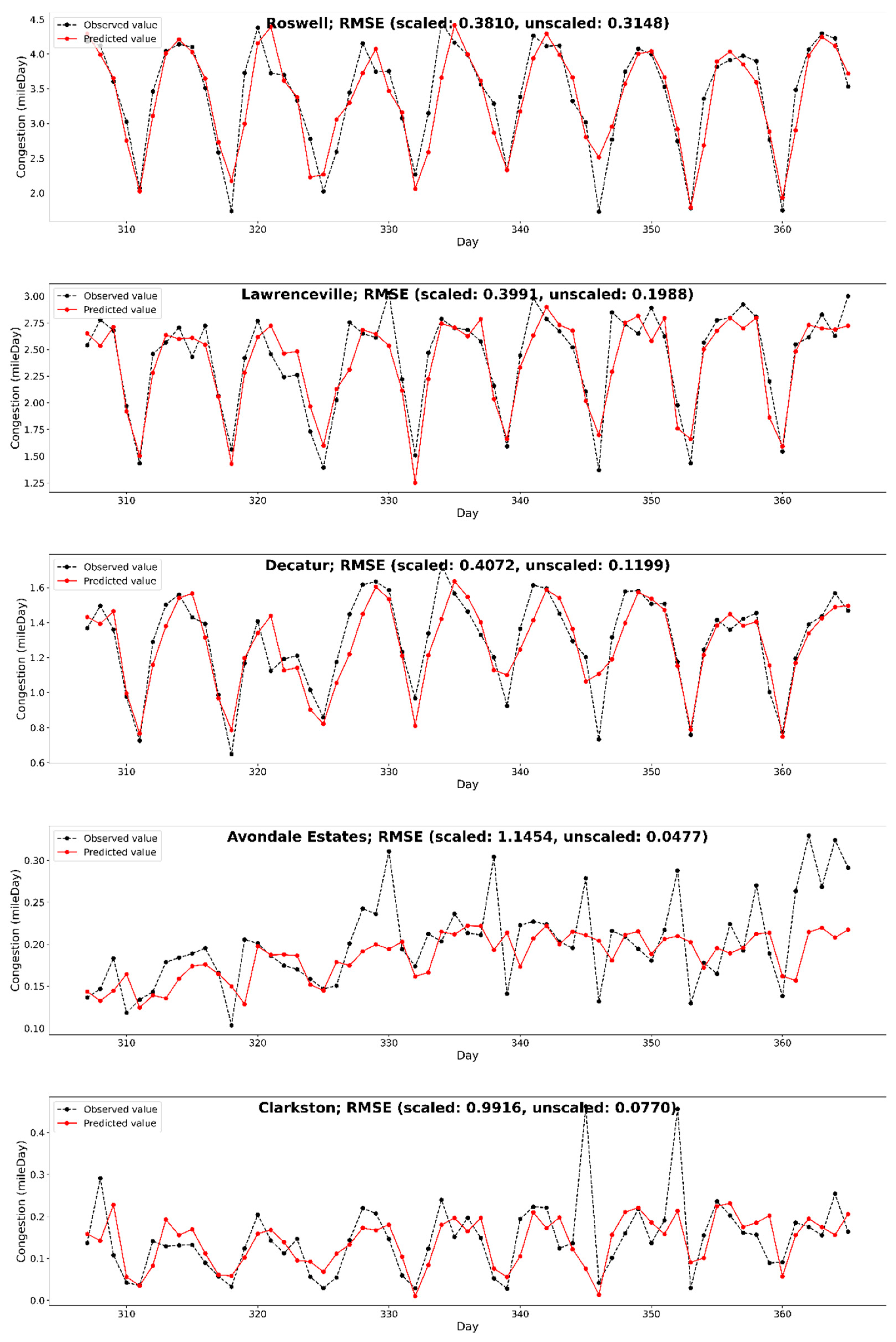
| City | Hidden Nodes | Hidden Layers | Learning Rate | Epochs | Validation Loss (MSE) | Test Loss (RMSE) |
|---|---|---|---|---|---|---|
| =Alpharetta | 32 | 3 | 0.001 | 10 | 0.5166 | 0.7514 |
| Atlanta | 32 | 3 | 0.001 | 50 | 0.4699 | 0.5882 |
| Austell | 64 | 3 | 0.001 | 50 | 0.1744 | 0.6153 |
| Avondale Estates | 32 | 3 | 0.001 | 30 | 0.5011 | 1.1454 |
| Berkeley Lake | 32 | 2 | 0.001 | 50 | 0.3281 | 0.4386 |
| Brookhaven | 64 | 3 | 0.001 | 10 | 0.2856 | 0.6604 |
| Chamblee | 32 | 3 | 0.001 | 10 | 0.3629 | 0.7643 |
| Clarkston | 64 | 3 | 0.001 | 50 | 0.4368 | 0.9916 |
| College Park | 32 | 3 | 0.001 | 10 | 0.3440 | 0.8407 |
| Conyers | 64 | 1 | 0.001 | 50 | 0.2763 | 0.4838 |
| Decatur | 64 | 3 | 0.001 | 50 | 0.4953 | 0.4072 |
| Doraville | 64 | 2 | 0.001 | 50 | 0.3425 | 0.5002 |
| Duluth | 64 | 3 | 0.001 | 30 | 0.3166 | 0.4143 |
| Dunwoody | 64 | 2 | 0.001 | 30 | 0.2611 | 0.6023 |
| East Point | 32 | 3 | 0.001 | 10 | 0.0834 | 0.7783 |
| Fairburn | 64 | 1 | 0.001 | 50 | 0.3219 | 0.9189 |
| Forest Park | 64 | 3 | 0.001 | 50 | 0.2174 | 0.4509 |
| Grayson | 32 | 1 | 0.001 | 50 | 0.9174 | 0.5089 |
| Hapeville | 32 | 1 | 0.001 | 30 | 3.5845 | 0.5690 |
| Johns Creek | 64 | 2 | 0.001 | 30 | 0.2328 | 0.4692 |
| Jonesboro | 32 | 2 | 0.001 | 10 | 0.4641 | 0.5824 |
| Kennesaw | 64 | 2 | 0.001 | 10 | 0.4040 | 0.4689 |
| Lake City | 64 | 1 | 0.001 | 10 | 0.4584 | 0.7992 |
| Lawrenceville | 64 | 2 | 0.001 | 50 | 0.1322 | 0.3991 |
| Lilburn | 64 | 3 | 0.001 | 30 | 0.1656 | 0.5162 |
| Lithonia | 64 | 3 | 0.001 | 50 | 0.2241 | 0.6889 |
| Mableton | 64 | 2 | 0.001 | 30 | 0.3516 | 0.5291 |
| Marietta | 32 | 2 | 0.001 | 50 | 0.3235 | 0.7732 |
| Morrow | 32 | 1 | 0.001 | 10 | 0.6072 | 0.8320 |
| Norcross | 32 | 3 | 0.001 | 30 | 0.4845 | 0.4294 |
| Peachtree Corners | 32 | 1 | 0.001 | 50 | 0.3721 | 0.4398 |
| Riverdale | 64 | 3 | 0.001 | 50 | 0.4331 | 0.6334 |
| Roswell | 32 | 3 | 0.001 | 50 | 0.1941 | 0.3810 |
| Sandy Springs | 64 | 1 | 0.001 | 50 | 0.2399 | 0.4413 |
| Smyrna | 64 | 1 | 0.001 | 50 | 0.4179 | 0.5925 |
| Snellville | 64 | 3 | 0.001 | 30 | 0.2003 | 0.5568 |
| South Fulton | 64 | 2 | 0.001 | 50 | 0.0873 | 0.5208 |
| Stockbridge | 32 | 3 | 0.001 | 50 | 0.3996 | 0.7355 |
| Stone Mountain | 32 | 1 | 0.001 | 50 | 0.2845 | 0.5909 |
| Stonecrest | 32 | 2 | 0.001 | 50 | 0.2060 | 0.9212 |
| Suwanee | 64 | 3 | 0.001 | 10 | 0.6972 | 0.7017 |
| Tucker | 64 | 3 | 0.001 | 10 | 0.4993 | 0.4598 |
| Union City | 32 | 1 | 0.001 | 10 | 0.2348 | 0.7230 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seong, J.C.; Lee, S.; Cho, Y.; Hwang, C. Beyond the Road: A Regional Perspective on Traffic Congestion in Metro Atlanta. ISPRS Int. J. Geo-Inf. 2025, 14, 61. https://doi.org/10.3390/ijgi14020061
Seong JC, Lee S, Cho Y, Hwang C. Beyond the Road: A Regional Perspective on Traffic Congestion in Metro Atlanta. ISPRS International Journal of Geo-Information. 2025; 14(2):61. https://doi.org/10.3390/ijgi14020061
Chicago/Turabian StyleSeong, Jeong Chang, Seungyeon Lee, Yoonjae Cho, and Chulsue Hwang. 2025. "Beyond the Road: A Regional Perspective on Traffic Congestion in Metro Atlanta" ISPRS International Journal of Geo-Information 14, no. 2: 61. https://doi.org/10.3390/ijgi14020061
APA StyleSeong, J. C., Lee, S., Cho, Y., & Hwang, C. (2025). Beyond the Road: A Regional Perspective on Traffic Congestion in Metro Atlanta. ISPRS International Journal of Geo-Information, 14(2), 61. https://doi.org/10.3390/ijgi14020061






