Estimating the Potential for Rooftop Generation of Solar Energy in an Urban Context Using High-Resolution Open Access Geospatial Data: A Case Study of the City of Tromsø, Norway
Abstract
1. Introduction
2. Materials and Methods
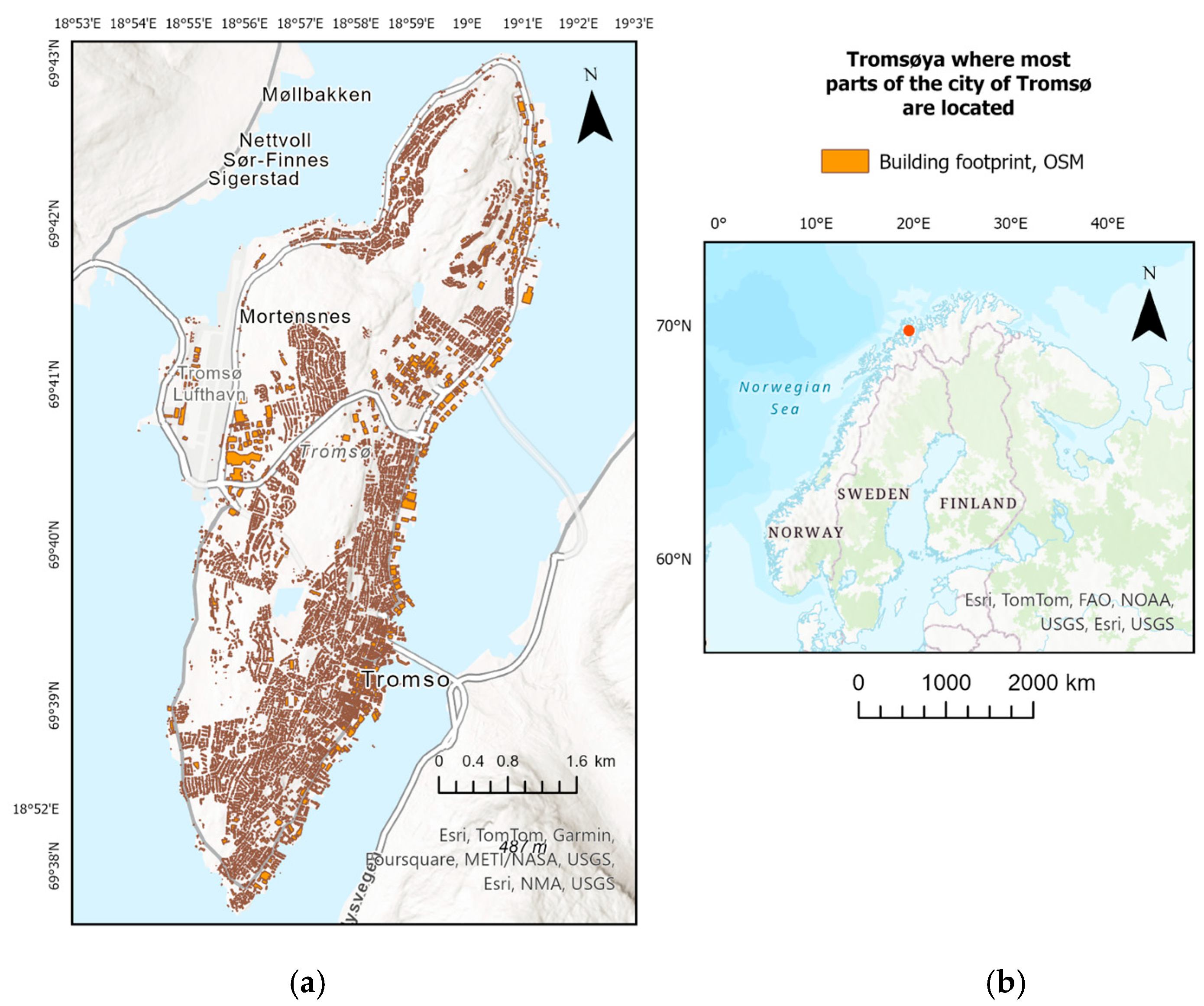
2.1. Study Area
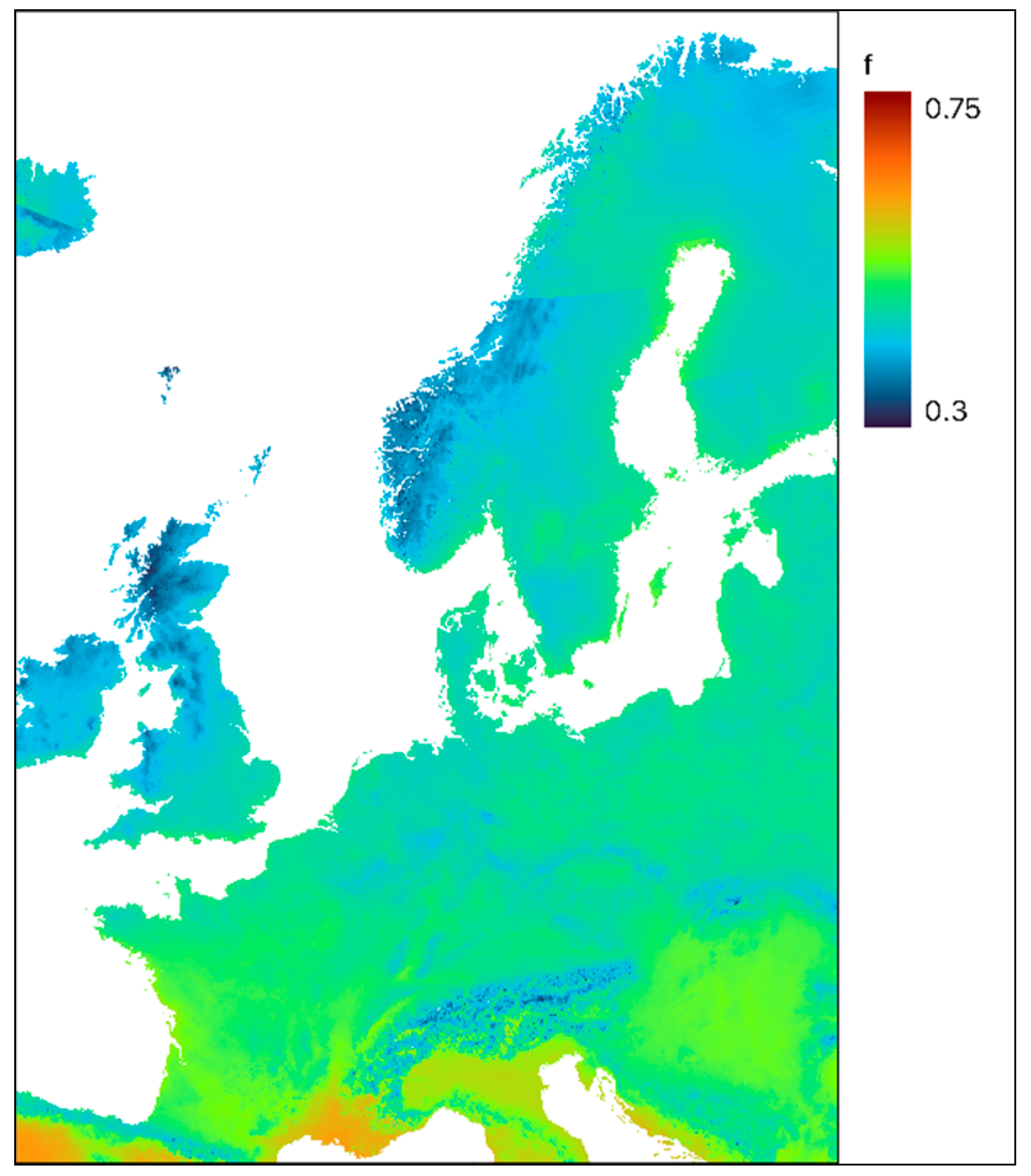
2.2. PV Generation Model
2.3. Selecting Usable Areas of Roofs
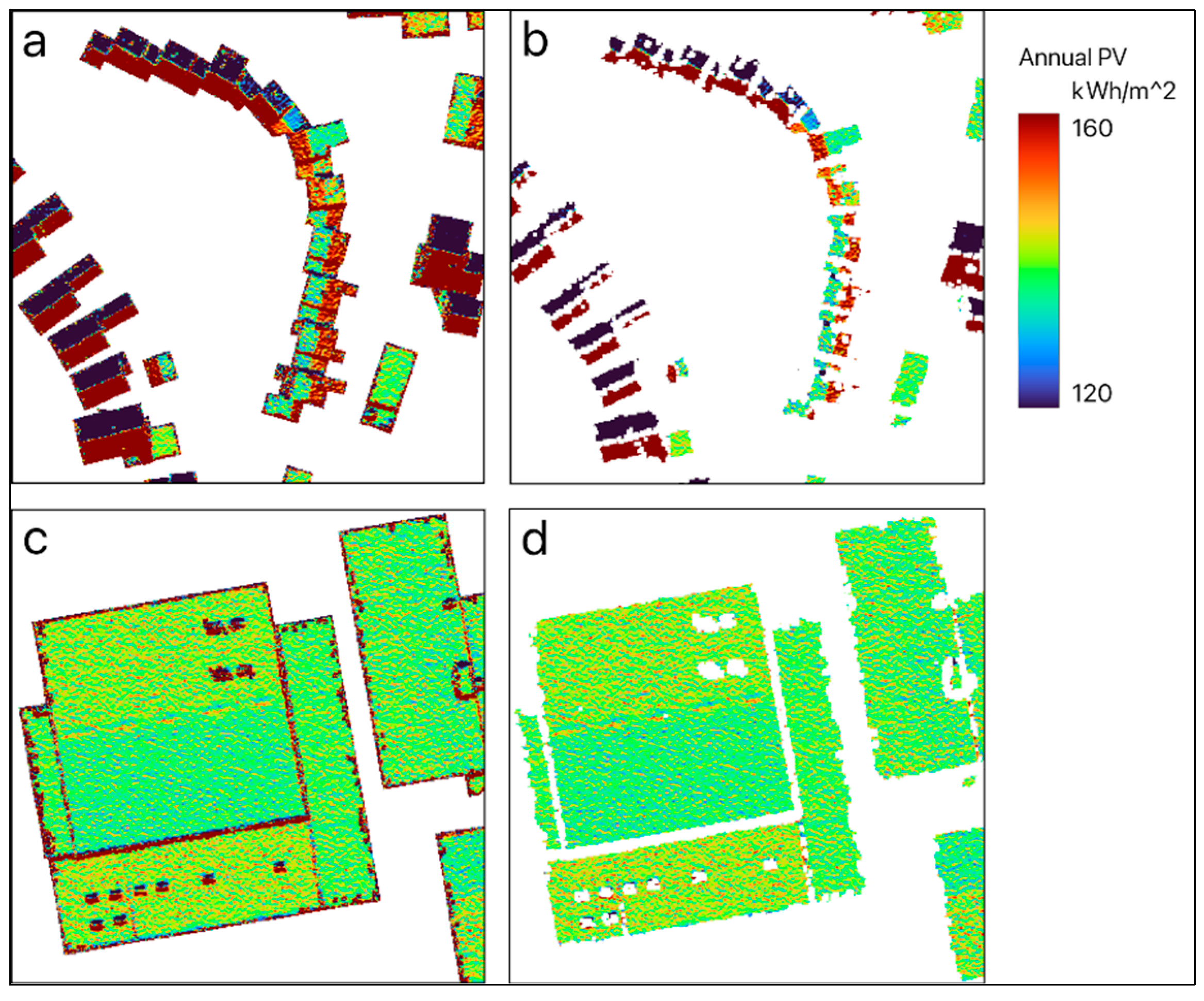
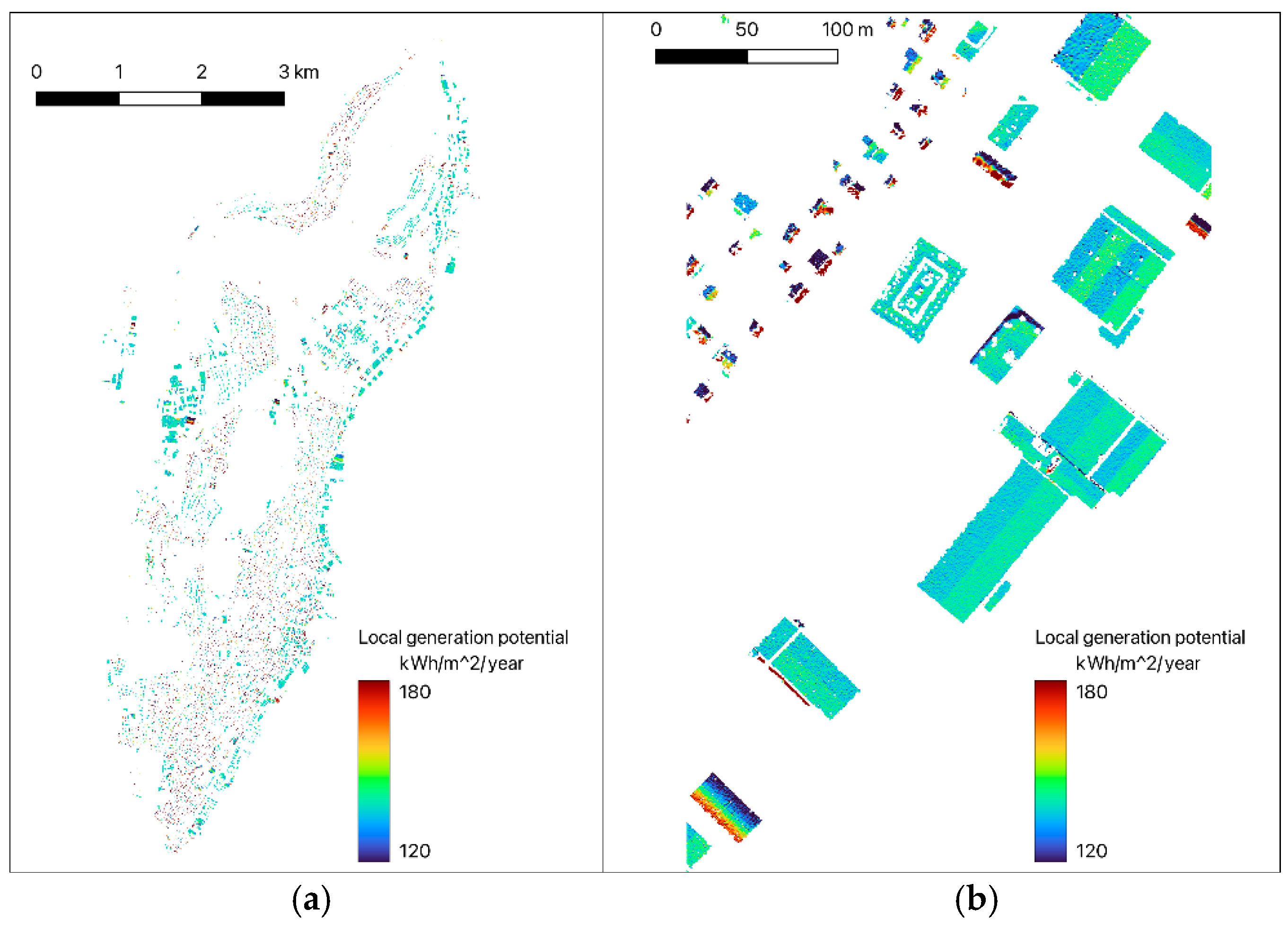
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Global Market Outlook for Solar Power 2024–2028. Intersolar Europe, Global Solar Council (GSC). 2024. Available online: https://www.solarpowereurope.org/insights/outlooks/global-market-outlook-for-solar-power-2024-2028/detail (accessed on 12 September 2024).
- Norway 2022 Energy Policy Review. IEA Publications. 2022. Available online: https://iea.blob.core.windows.net/assets/de28c6a6-8240-41d9-9082-a5dd65d9f3eb/NORWAY2022.pdf (accessed on 27 September 2024).
- Lee, H.; Calvin, K.; Dasgupta, D.; Krinner, G.; Mukherji, A.; Thorne, P.; Trisos, C.; Romero, J.; Aldunce, P.; Barrett, K.; et al. IPCC, 2023: Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Muellejans, H.; Pavanello, D.; Sample, T.; Kenny, R.; Shaw, D.; Field, M.; Dunlop, E.; Stoyanova Lyubenova, T.; Mihaylov, B.; Antonelli, A.; et al. State-of-the-Art Assessment of Solar Energy Technologies; EUR 31189 EN, JRC130086; Publications Office of the European Union: Luxembourg, 2022; ISBN 978-92-76-55849-1. [Google Scholar] [CrossRef]
- Molnár, G.; Ürge-Vorsatz, D.; Chatterjee, S. Estimating the global technical potential of building-integrated solar energy production using a high-resolution geospatial model. J. Clean. Prod. 2022, 375, 134133. [Google Scholar] [CrossRef]
- Bódis, K.; Kougias, I.; Jäger-Waldau, A.; Taylor, N.; Szabó, S. A high-resolution geospatial assessment of the rooftop solar photovoltaic potential in the European Union. Renew. Sustain. Energy Rev. 2019, 114, 109309. [Google Scholar] [CrossRef]
- Kapsalis, V.; Maduta, C.; Skandalos, N.; Bhuvad, S.S.; D’Agostino, D.; Yang, R.J.; Udayraj Parker, D.; Karamanis, D. Bottom-up energy transition through rooftop PV upscaling: Remaining issues and emerging upgrades towards NZEBs at different climatic conditions. Renew. Sustain. Energy Transit. 2024, 5, 100083. [Google Scholar] [CrossRef]
- Chen, L.; Hu, Y.; Wang, R.; Li, X.; Chen, Z.; Hua, J.; Osman, A.I.; Farghali, M.; Huang, L.; Li, J.; et al. Green building practices to integrate renewable energy in the construction sector: A review. Environ. Chem. Lett. 2023, 22, 751–784. [Google Scholar] [CrossRef]
- Maka, A.O.M.; Ghalut, T.; Elsaye, E. The pathway towards decarbonisation and net-zero emissions by 2050: The role of solar energy technology. Green Technol. Sustain. 2024, 2, 100107. [Google Scholar] [CrossRef]
- Joshi, S.; Zakeri, B.; Mittal, S.; Mastrucci, A.; Holloway, P.; Krey, V.; Shukla, P.R.; O’Gallachoir, B.; Glynn, J. Global high-resolution growth projections dataset for rooftop area consistent with the shared socioeconomic pathways, 2020–2050. Sci. Data 2024, 11, 563. [Google Scholar] [CrossRef]
- EU/2024/1275. Directive (EU) 2024/1275 of the European Parliament and of the Council of 24 April 2024 on the Energy Performance of Buildings (Recast) (Text with EEA Relevance). Available online: https://eur-lex.europa.eu/eli/dir/2024/1275/oj (accessed on 9 February 2025).
- EU. Energy Performance of Buildings Directive. Available online: https://energy.ec.europa.eu/topics/energy-efficiency/energy-efficient-buildings/energy-performance-buildings-directive_en (accessed on 11 February 2025).
- Kakoulaki, G.; Taylor, N.; Szabo, S.; Kenny, R.; Chatzipanagi, A.; Jäger-Waldau, A. Communication on the potential of applied PV in the European Union: Rooftops, reservoirs, roads (R3). EPJ Photovolt. 2024, 15, 2. [Google Scholar] [CrossRef]
- Mathew, T.C.; Nagaraja Pandian, S. Unveiling the shadows: A qualitative exploration of barriers to rooftop solar photovoltaic adoption in residential sectors. Clean Energy 2024, 8, 218–228. [Google Scholar] [CrossRef]
- Bernardi, M.; Ferralis, N.; Wan, J.H.; Villalon, R.; Grossman, J.C. Solar energy generation in three dimensions. Energy Environ. Sci. 2012, 5, 6880. [Google Scholar] [CrossRef]
- Khan, M.I.; Al Huneidi, D.I.; Asfand, F.; Al-Ghamdi, S.G. Climate Change Implications for Optimal Sizing of Residential Rooftop Solar Photovoltaic Systems in Qatar. Sustainability 2023, 15, 16815. [Google Scholar] [CrossRef]
- Jouttijärvi, S.; Lobaccaro, G.; Kamppinen, A.; Miettunen, K. Benefits of bifacial solar cells combined with low voltage power grids at high latitudes. Renew. Sustain. Energy Rev. 2022, 161, 112354. [Google Scholar] [CrossRef]
- Akbarinejad, T.; Machlein, E.; Bertolin, C.; Lobaccaro, G.; Salaj, A.T. Enhancing the deployment of solar energy in Norwegian high-sensitive built environments: Challenges and barriers—A scoping review. Front. Built Environ. 2023, 9, 1285127. [Google Scholar] [CrossRef]
- Sicard, M.; Kageyama, M.; Charbit, S.; Braconnot, P.; Madeleine, J.-B. An energy budget approach to understand the Arctic warming during the Last Interglacial. Clim. Past 2022, 18, 607–629. [Google Scholar] [CrossRef]
- Formolli, M.; Kleiven, T.; Lobaccaro, G. Assessing solar energy accessibility at high latitudes: A systematic review of urban spatial domains, metrics, and parameters. Renew. Sustain. Energy Rev. 2023, 177, 113231. [Google Scholar] [CrossRef]
- Formolli, M.; Lobaccaro, G.; Kanters, J. Solar Energy in the Nordic Built Environment: Challenges, Opportunities and Barriers. Energies 2021, 14, 8410. [Google Scholar] [CrossRef]
- Formolli, M.; Schön, P.; Kleiven, T.; Lobaccaro, G. Solar accessibility in high latitudes urban environments: A methodological approach for street prioritization. Sustain. Cities Soc. 2024, 103, 105263. [Google Scholar] [CrossRef]
- Gholami, H. Technical potential of solar energy in buildings across Norway: Capacity and demand. Sol. Energy 2024, 278, 112758. [Google Scholar] [CrossRef]
- The Energy Commission. 2023. Available online: https://www.regjeringen.no/no/dokumenter/nou-2023-3/id2961311/ (accessed on 10 October 2024).
- Bjørndalen, J.; Fiskvik, I.H.; Hadizadeh, M.; Horschig, T.; Ingeberg, K. Energy Transition Norway 2050. DNV AS. Available online: https://www.dnv.com/publications/energy-transition-norway-2024/ (accessed on 10 October 2024).
- Solar Power Potential on Built-Up Areas in Norway. 2024. Available online: https://solenergiklyngen.no/wp-content/uploads/2024/10/Solkraftpotensial-pa-nedbygde-arealer-i-Norge_final.pdf (accessed on 10 October 2024).
- Socioeconomic Analysis of 8 TWh Solar Power. 2024. Available online: https://solenergiklyngen.no/wp-content/uploads/2024/03/240321-DNV-Menon-Solrapport-6.pdf (accessed on 10 October 2024).
- Eikeland, O.F.; Apostoleris, H.; Santos, S.; Ingebrigtsen, K.; Boström, T.; Chiesa, M. Rethinking the role of solar energy under location specific constraints. Energy 2022, 211, 118838. [Google Scholar] [CrossRef]
- Lingfors, D. Solar Variability Assessment in the Built Environment: Model Development and Application to Grid Integration. Ph.D. Thesis, Acta Universitatis Upsaliensis, Uppsala, Sweden, 2017. [Google Scholar]
- Lingfors, D.; Bright, J.M.; Engerer, N.A.; Ahlberg, J.; Killinger, S.; Widén, J. Comparing the capability of low- and high-resolution LiDAR data with application to solar resource assessment, roof type classification and shading analysis. Appl. Energy 2017, 205, 1216–1230. [Google Scholar] [CrossRef]
- Kakoulaki, G.; Martinez, A.; Florio, P. Non-Commercial Light Detection and Ranging (LiDAR) Data in Europe; Publications Office of the European Union: Luxemburg, 2021; Available online: https://op.europa.eu/en/publication-detail/-/publication/0a79fa74-2c29-11ec-bd8e-01aa75ed71a1/language-en (accessed on 3 September 2024).
- Huang, Y.; Chen, Z.; Wu, B.; Chen, L.; Mao, W.; Zhao, F.; Wu, J.; Wu, J.; Yu, B. Estimating Roof Solar Energy Potential in the Downtown Area Using a GPU-Accelerated Solar Radiation Model and Airborne LiDAR Data. Remote Sens. 2015, 7, 17212–17233. [Google Scholar] [CrossRef]
- Kodysh, J.B.; Omitaomu, O.A.; Bhaduri, B.L.; Neish, B.S. Methodology for estimating solar potential on multiple building rooftops for photovoltaic systems. Sustain. Cities Soc. 2013, 8, 31–41. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Pearce, J.M.; Harrap, R.; Barber, G. The Application of LiDAR to Assessment of Rooftop Solar Photovoltaic Deployment Potential in a Municipal District Unit. Sensors 2012, 12, 4534–4558. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Liu, Z.; Huang, Y.; Wei, M.; Yuan, B. Estimation of Rooftop Solar Photovoltaic Potential Based on High-Resolution Images and Digital Surface Models. Buildings 2023, 13, 2686. [Google Scholar] [CrossRef]
- Nelson, J.R.; Grubesic, T.H. The use of LiDAR versus unmanned aerial systems (UAS) to assess rooftop solar energy potential. Sustain. Cities Soc. 2020, 61, 102353. [Google Scholar] [CrossRef]
- Nys, G.-A.; Poux, F.; Billen, R. CityJSON Building Generation from Airborne LiDAR 3D Point Clouds. ISPRS Int. J. Geo-Inf. 2020, 9, 521. [Google Scholar] [CrossRef]
- Lingfors, D.; Killinger, S.; Engerer, N.A.; Widén, J.; Bright, J.M. Identification of PV system shading using a LiDAR-based solar resource assessment model: An evaluation and cross-validation. Sol. Energy 2018, 159, 157–172. [Google Scholar] [CrossRef]
- Lingfors, D.; Shepero, M.; Good, C. Modelling City Scale Spatio-temporal Solar Energy Generation and Electric Vehicle Charging Load. In Proceedings of the 8th International Workshop on the Integration of Solar Power into Power Systems, Stockholm, Sweden, 16–17 October 2018. [Google Scholar]
- Gooding, J.; Crook, R.; Tomlin, A.S. Modelling of roof geometries from low-resolution LiDAR data for city-scale solar energy applications using a neighbouring buildings method. Appl. Energy 2015, 148, 93–104. [Google Scholar] [CrossRef]
- Manni, M.; Nocente, A.; Kong, G.; Skeie, K.; Fan, H.; Lobaccaro, G. Solar energy digitalization at high latitudes: A model chain combining solar irradiation models, a LiDAR scanner, and high-detail 3D building model. Front. Energy Res. 2022, 10, 1082092. [Google Scholar] [CrossRef]
- Kozlovas, P.; Gudzius, S.; Ciurlionis, J.; Jonaitis, A.; Konstantinaviciute, I.; Bobinaite, V. Assessment of Technical and Economic Potential of Urban Rooftop Solar Photovoltaic Systems in Lithuania. Energies 2023, 16, 5410. [Google Scholar] [CrossRef]
- Larsen, A. Solar Photovoltaic Potential on Commercial Buildings in Arctic Latitudes. Master’s Thesis, UiT The Arctic University of Norway UiT Norges Arktiske Universitet, Tromsø, Norway, 2022. Available online: https://hdl.handle.net/10037/26152 (accessed on 15 October 2024).
- Liang, J.; Gong, J.; Xie, X.; Sun, J. Solar3D: An Open-Source Tool for Estimating Solar Radiation in Urban Environments. ISPRS Int. J. Geo-Inf. 2020, 9, 524. [Google Scholar] [CrossRef]
- Melius, J.; Margolis, R.; Ong, S. Estimating Rooftop Suitability for PV: A Review of Methods, Patents, and Validation Techniques. National Renewable Energy Laboratory. 2013. Available online: https://www.nrel.gov/docs/fy14osti/60593.pdf (accessed on 12 September 2024).
- ArcGIS Pro. Version Spatial Analyst Toolbox. [Computer Software]. Esri. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-analyst/area-solar-radiation.htm (accessed on 25 October 2024).
- Neteler, M.; Mitasova, H. Open Source GIS; Springer US: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Hofierka, J.; Suri, M. The solar radiation model for Open source GIS: Implementation and applications. In Proceedings of the International GRASS Users Conference, Trento, Italy, 11–13 September 2002. [Google Scholar]
- Conrad, O. Potential Incoming Solar Radiation, [Computer Software]. 2010. Available online: https://saga-gis.sourceforge.io/saga_tool_doc/6.1.0/ta_lighting_2.html (accessed on 25 October 2024).
- Kaňuk, J.; Zubal, S.; Šupinský, J.; Šašak, J.; Bombara, M.; Sedlák, V.; Gallay, M.; Hofierka, J.; Onačillová, K. Testing of V3.Sun Module Prototype for Solar Radiation Modelling on 3d Objects with Complex Geometric Structure. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-4/W15, 35–40. [Google Scholar] [CrossRef]
- Amillo, G.; Huld, T. Performance Comparison of Different Models for the Estimation of Global Irradiance on Inclined Surfaces: Validation of the Model Implemented in PVGIS; Publications Office: Luxembourg, 2013; Available online: https://op.europa.eu/en/publication-detail/-/publication/4ef8c4e1-4397-4e27-8487-448786327f27/language-en (accessed on 15 October 2024).
- Amillo, G.; Taylor, N.; Martinez, A.M. Adapting PVGIS to Trends in Climate, Technology and User Needs. In Proceedings of the 38th European Photovoltaic Solar Energy Conference and Exhibition (PVSEC), Online, 6–10 September 2021; pp. 907–911. [Google Scholar] [CrossRef]
- Mueller, R.; Behrendt, T.; Hammer, A.; Kemper, A. A New Algorithm for the Satellite-Based Retrieval of Solar Surface Irradiance in Spectral Bands. Remote Sens. 2012, 4, 622–647. [Google Scholar] [CrossRef]
- Margolis, R.; Gagnon, P.; Melius, J.; Phillips, C.; Elmore, R. Using GIS-based methods and lidar data to estimate rooftop solar technical potential in US cities. Environ. Res. Lett. 2017, 12, 074013. [Google Scholar] [CrossRef]
- Martínez-Rubio, A.; Sanz-Adan, F.; Santamaría-Peña, J.; Martínez, A. Evaluating solar irradiance over facades in high building cities, based on LiDAR technology. Appl. Energy 2016, 183, 133–147. [Google Scholar] [CrossRef]
- Ni, H.; Wang, D.; Zhao, W.; Jiang, W.; Mingze, E.; Huang, C.; Yao, J. Enhancing rooftop solar energy potential evaluation in high-density cities: A Deep Learning and GIS based approach. Energy Build. 2024, 309, 113743. [Google Scholar] [CrossRef]
- Schuffert, S.; Voegtle, T.; Tate, N.; Ramirez, A. Quality Assessment of Roof Planes Extracted from Height Data for Solar Energy Systems by the EAGLE Platform. Remote Sens. 2015, 7, 17016–17034. [Google Scholar] [CrossRef]
- Prieto, I.; Izkara, J.L.; Usobiaga, E. The Application of LiDAR Data for the Solar Potential Analysis Based on Urban 3D Model. Remote Sens. 2019, 11, 2348. [Google Scholar] [CrossRef]
- Yan, L.; Zhu, R.; Kwan, M.-P.; Luo, W.; Wang, D.; Zhang, S.; Wong, M.S.; You, L.; Yang, B.; Chen, B.; et al. Estimation of urban-scale photovoltaic potential: A deep learning-based approach for constructing three-dimensional building models from optical remote sensing imagery. Sustain. Cities Soc. 2023, 93, 104515. [Google Scholar] [CrossRef]
- Falklev, E.H. Mapping of Solar Energy Potential on Tromsøya Using Solar Analyst in ArcGIS. Master’s Thesis, UiT The Arctic University of Norway UiT Norges Arktiske Universitet, Tromsø, Norway, 2017. [Google Scholar]
- Statistics Norway. Annual Report 2020. Available online: https://www.ssb.no/en (accessed on 5 June 2024).
- Boström, T.; Good, C. Long-Term PV Performance at High Latitudes. Department of Technology and Safety UiT the Arctic University of Norway, Tromso, Norway. 2024; manuscript in preparation. [Google Scholar]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Pfeifroth, U.; Kothe, S.; Müller, R.; Trentmann, J.; Hollmann, R.; Fuchs, P.; Werscheck, M. Surface Radiation Data Set—Heliosat (SARAH)—Edition 2 (Version 2.0, p. 7.1 TiB) [NetCDF-4]. 2017. Satellite Application Facility on Climate Monitoring (CM SAF). Available online: https://doi.org/10.5676/EUM_SAF_CM/SARAH/V002 (accessed on 4 September 2024).
- Adjiski, V.; Kaplan, G.; Mijalkovski, S. Assessment of the solar energy potential of rooftops using LiDAR datasets and GIS based approach. Int. J. Eng. Geosci. 2023, 8, 188–199. [Google Scholar] [CrossRef]
- Alhamwi, A.; Medjroubi, W.; Vogt, T.; Agert, C. GIS-based urban energy systems models and tools: Introducing a model for the optimisation of flexibilisation technologies in urban areas. Appl. Energy 2017, 191, 1–9. [Google Scholar] [CrossRef]
- Biljecki, F.; Chow, Y.S.; Lee, K. Quality of crowdsourced geospatial building information: A global assessment of OpenStreetMap attributes. Build. Environ. 2023, 237, 110295. [Google Scholar] [CrossRef]
- PVsyst SA. PVsyst Photovoltaic Software v7. PVsyst SA. Satigny, Switzerland. Available online: https://www.pvsyst.com/ (accessed on 15 October 2024).
- Eikeland, O.F. Investigation of Photovoltaic Energy Yield on Tromsøya by Mapping Solar Potential in ArcGIS. Master’s Thesis, Faculty of Science and Technology, UiT The Arctic University of Norway, Tromsø, Norway, 2019. Available online: https://hdl.handle.net/10037/16580 (accessed on 15 October 2024).
- Yang, Y.; Campana, P.E.; Stridh, B.; Yan, J. Potential analysis of roof-mounted solar photovoltaics in Sweden. Appl. Energy 2020, 279, 115786. [Google Scholar] [CrossRef]
- Romero Rodríguez, L.; Duminil, E.; Sánchez Ramos, J.; Eicker, U. Assessment of the photovoltaic potential at urban level based on 3D city models: A case study and new methodological approach. Sol. Energy 2017, 146, 264–275. [Google Scholar] [CrossRef]
- Vargas-Munoz, J.E.; Srivastava, S.; Tuia, D.; Falcão, A.X. OpenStreetMap: Challenges and Opportunities in Machine Learning and Remote Sensing. IEEE Geosci. Remote Sens. Mag. 2021, 9, 184–199. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, F.; Li, S.; Mao, J.; Xu, H.; Ju, W.; Liu, X.; Wu, J.; Min, K.; Zhang, X.; et al. Solar energy potential of urban buildings in 10 cities of China. Energy 2020, 196, 117038. [Google Scholar] [CrossRef]
- Gagnon, P.; Margolis, R.; Melius, J.; Phillips, C.; Elmore, R. Estimating rooftop solar technical potential across the US using a combination of GIS-based methods, lidar data, and statistical modeling. Environ. Res. Lett. 2018, 13, 024027. [Google Scholar] [CrossRef]

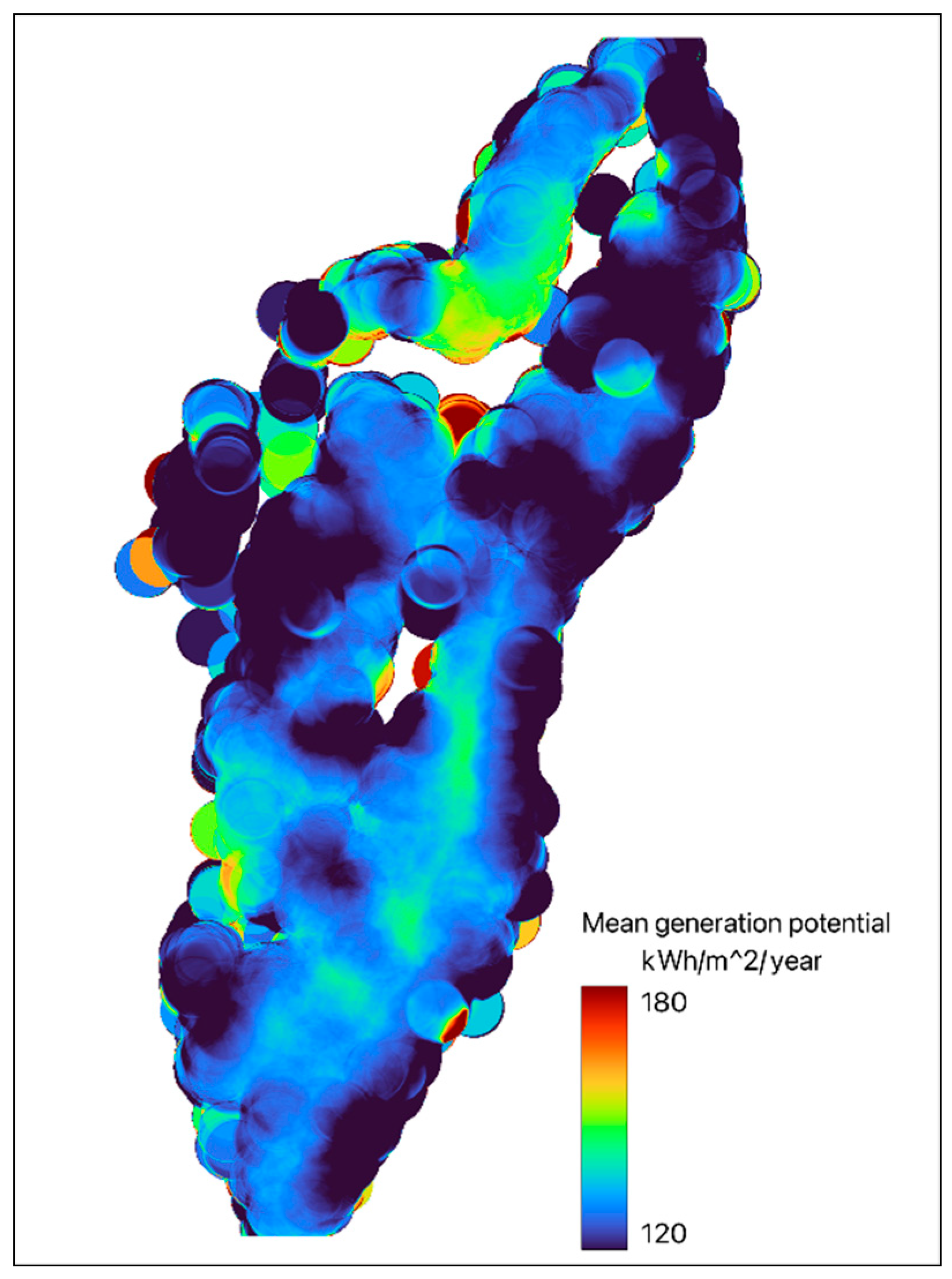
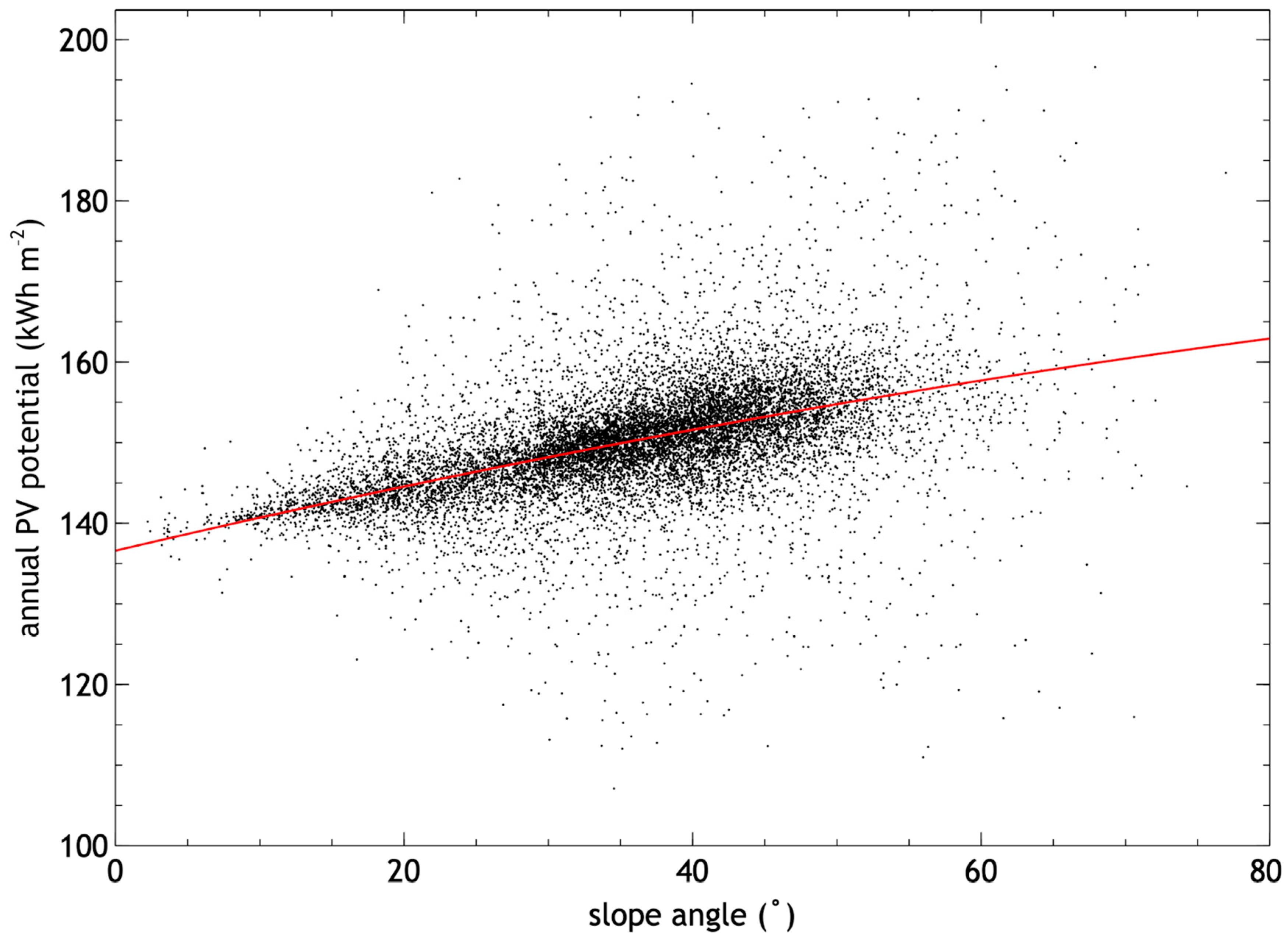
| Total (GWh) | Annual Energy Generation (kWh/m2/year) | Average Slope (°) | Average Usable Area (m2) | Average Area (m2) | Number | Class |
|---|---|---|---|---|---|---|
| 86 | 149.0 | 37.1 | 59 | 168 | 10,211 | residential |
| 31 | 143.8 | 27.9 | 395 | 793 | 555 | commercial |
| 19 | 144.3 | 28.3 | 691 | 1274 | 199 | civic |
| 16 | 145.0 | 27.5 | 530 | 968 | 211 | education |
| 8 | 150.1 | 35.0 | 13 | 45 | 4342 | outbuildings |
| 17 | 142.3 | 23.6 | 543 | 748 | 227 | warehouses |
| 11 | 142.4 | 31.9 | 356 | 483 | 238 | industrial |
| 15 | 142.8 | 37.3 | 272 | 378 | 394 | unknown |
| 203 | 16,377 | TOTAL |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rees, G.; Hebryn-Baidy, L.; Good, C. Estimating the Potential for Rooftop Generation of Solar Energy in an Urban Context Using High-Resolution Open Access Geospatial Data: A Case Study of the City of Tromsø, Norway. ISPRS Int. J. Geo-Inf. 2025, 14, 123. https://doi.org/10.3390/ijgi14030123
Rees G, Hebryn-Baidy L, Good C. Estimating the Potential for Rooftop Generation of Solar Energy in an Urban Context Using High-Resolution Open Access Geospatial Data: A Case Study of the City of Tromsø, Norway. ISPRS International Journal of Geo-Information. 2025; 14(3):123. https://doi.org/10.3390/ijgi14030123
Chicago/Turabian StyleRees, Gareth, Liliia Hebryn-Baidy, and Clara Good. 2025. "Estimating the Potential for Rooftop Generation of Solar Energy in an Urban Context Using High-Resolution Open Access Geospatial Data: A Case Study of the City of Tromsø, Norway" ISPRS International Journal of Geo-Information 14, no. 3: 123. https://doi.org/10.3390/ijgi14030123
APA StyleRees, G., Hebryn-Baidy, L., & Good, C. (2025). Estimating the Potential for Rooftop Generation of Solar Energy in an Urban Context Using High-Resolution Open Access Geospatial Data: A Case Study of the City of Tromsø, Norway. ISPRS International Journal of Geo-Information, 14(3), 123. https://doi.org/10.3390/ijgi14030123









