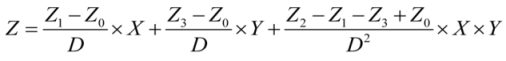Multi-Temporal Time-Dependent Terrain Visualization through Localized Spatial Correspondence Parameterization
Abstract
:1. Introduction

- Modelling complexity—the topographic reality that is based on 3D physical objects is normally very complex: geometric and semantic information—to name a few;
- Multi-resolution and multi-representation—when dealing with multi-epoch and multi-source terrain representation the physical objects representing terrain are rarely of the same nature;
- Presentation and appearance—usually when representing 3D terrain data the viewer will demand the representation to be as true-to-nature as possible and not derived by data symbols and annotation;
- Animation—terrain animation has to preserve the quality and accuracy of given data, as well as be realistic and continuous throughout the simulation;
- Simulations and multi-temporal representations—chosen algorithm needs to handle the general problem of physical objects (or skeletons) derived deformation instead of treating each area of anatomy as a special case;
- Topologies and morphologies—are to be preserved or otherwise created if derived by the deformation process, while maintaining the realistic nature of representation.
2. Related Work

- Vertex Correspondence, i.e., figuring out which vertex in one object should blend with another vertex in the other object; this can be defined in the problem at hand as spatial correspondence, i.e., which entity (and parts of entity) in one topographic dataset corresponds to another entity in the other topographic dataset, while the correspondence is modelled and quantified by transformation parameters. A trivial solution to this is to leave it to the animator himself to decide, i.e., manual sampling of selection of points, which will define the connectivity between both physical objects, thus finding their mutual coordinates connectivity.
- Vertex Path (trajectory problem), i.e., figuring out what path the vertices should take to get from one object space to the other. This problem can be resolved only after the vertex correspondence problem is solved. This problem stems from the question of how to transform the source object points to the destination object points. The trivial solution for this is the substitution of linear transformation between the points. As stated earlier, this is not usually the preferred natural and realistic solution, so more complex solutions are required to solve this, such as, including distortions and squinting in the intermediate objects to maintain natural visualization (e.g., [8,9]).
3. Proposed Approach


- Global rough registration, whereas choosing a common framework for both DTMs (and, thus, solving the datum and coordinate system ambiguities existing between DTMs before performing transformation, as outlined in Figure 1). This is achieved while implementing the Hausdorff distance algorithm that registers sets of selective unique homologous entities (objects) existing in both topographies’ skeleton structure. The skeleton structure of each DTM is identified via a novel topographical maxima interest point identification algorithm;
- Matching—since global registration is achieved and datum ambiguities are resolved, local matching is carried out while implementing the Iterative Closest Point (ICP) algorithm for rigid surfaces matching. This stage is essential for achieving precise reciprocal modelling framework between the two datasets, thus establishing localized transformation quantification;
- Integration schema, which consists of the modelling inter-relations quantification evaluated in the local matching. Since transformation is extracted via ICP on a local level, this quantification is needed to be densified for all points existing in that level, i.e., extracting transformation values for each DTM point independently to be transformed from one topographic dataset to the other. This densification is carried out via designated interpolation mechanisms, which are further developed to suit the task at hand (discussed in Section 4.2).
3.1. Correspondences Extraction

3.2. Path Evaluation
- Among the DTPM matrix’s grid-nodes (space-domain) to maintain continuity, while moving among cells. This computation is designated for the calculation of position-derived six parameter transformation values. These values are required to transform a grid-point that exists in the source dataset to its corresponding position in the target dataset;
- In-between the topographic datasets/DTMs (time-domain). Spatially, it can be depicted as if the intermediate topography is situated in the space between the source and target topographies. The position of the intermediate topographic dataset is defined by the time-proportion and the magnitude of the transformations involved in the process.
4. Algorithm Outline
4.1. Local Matching (Vertex Correspondence)
4.1.1. General


4.1.2. Non-Rigid Bodies Constraints
- Wide-coverage DTMs represent different data-characteristics—namely, level-of-detail and resolution—implying that existing ICP homologous points is not at all explicit;
- DTMs acquired on different times (epochs) will surely represent different terrain topography and morphology (either natural or artificial activities);
- Data and measurement errors can reflect on the points’ positional certainty on a relatively large scale.
- The corresponding coordinates of the paired-up nearest neighbor i {f(x,y,z)i} fit geometrically to a local cell-plane in frame f. Cell-plane geometry is defined here by a localized bi-linear interpolation: z(x,y) = a0+ a × x + a2 × y + a3 × x × y, which is probably the most common way to calculate heights within a bounded rectangular grid-cell. The four coefficients {a0,a1,a2,a3} are calculated based on the cell’s corner heights, depicted in Equation (3) and Figure 6 (In cases where the triangulated irregular network (TIN) structure of topographic datasets is used, slight modifications of these equations are required to fit TIN’s triangular-plane characteristics. Still, though this data-structure is becoming, nowadays, more commonly used, mainly for data acquired by airborne laser scanning (ALS) technology, most of existing wide coverage DTMs are still stored and analyzed as a raster structure; thus, this will not be addressed here);
- The line-equation, derived from the coordinates of point i transformed from frame g (denoted by gt(x,y,z)i, where t stands for transformed) to frame f with the best known transformation parameters and the paired-up nearest neighbor, i, in frame, f {f(x,y,z)i}, is perpendicular to the local cell-plane in frame, f, in the X direction (achieved by the first order derivative). This constraint validates that counterpart points, gt(x,y,z)i and f(x,y,z)i, are the closest ones existing based on the shortest Euclidian distance;
- The same constraint outlined in 2 is applied, only here, the line-equation is perpendicular to the local cell-plane in frame f in the Y direction:






4.2. Spatial Correspondence Parameterization (Vertex Path)
4.2.1. Translation Values

4.2.2. Rotation Values



5. Statistical Analysis
5.1. Translation Parameters

5.2. Rotation Parameters




| Parameter | Difference values | |
|---|---|---|
| Mean | SD | |
| dφ (deg) | −0.0033 | 0.0041 |
| dκ (deg) | 0.00005 | 0.0003 |
| dω (deg) | −0.0042 | 0.0048 |
6. Results


7. Conclusions and Discussion
Conflict of Interest
References
- Mach, R.; Petschek, P. Visualization of Digital Terrain and Landscape Data: A Manual, 1st ed.; Springer: Heidelberg, Germany, 2007. [Google Scholar]
- Nebiker, S. Support for Visualisation and Animation in a Scalable 3D GIS Environment: Motivation, Concepts and Implementation. In Proceedings of ISPRS Workshop on Visualization and Animation of Reality-Based 3D Models, Vulpera, Switzerland, 24–28 February 2003.
- Stasko, J.T. The path-transition paradigm: A practical methodology for adding animation to program interfaces. J. Visual. Lang. Computing 1990, 1, 213–236. [Google Scholar] [CrossRef]
- Turk, G.; O’Brien, J.F. Shape Transformation Using Variational Implicit Functions. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 8–13 August 1999; pp. 335–342.
- Thomas, F.; Johnston, O. Disney Animation: The Illusion of Life; Disney Editions: New York, NY, USA, 1981. [Google Scholar]
- Mohr, A.; Gleicher, M. Building efficient, accurate character skins from examples. ACM Trans. Graph. 2003, 22, 562–568. [Google Scholar]
- Watt, A.; Watt, M. Advanced Animation and Rendering Techniques; ACM: New York, NY, USA, 1992. [Google Scholar]
- Wang, R.; Pulli, K.; Popovi, J. Real-time enveloping with rotational regression. ACM Trans. Graph. 2007, 26, 73/1–73/9. [Google Scholar]
- Yu, Y.; Zhou, K.; Xu, D.; Shi, X.; Bao, H.; Guo, B.; Shum, H.Y. Mesh editing with poisson-based gradient field manipulation. ACM Trans. Graph. 2004, 23, 644–651. [Google Scholar] [CrossRef]
- Gomes, J.; Darsa, L.; Costa, B.; Velho, L. Warping & Morphing of Graphical Objects (The Morgan Kaufmann Series in Computer Graphics and Geometric Modeling); Morgan Kaufman: San-Francisco, CA, USA, 1998. [Google Scholar]
- Lazarus, F.; Verroust, A. Three-dimensional metamorphosis: a survey. Visual Comput. 1998, 14, 373–389. [Google Scholar] [CrossRef]
- Wolberg, G. Image morphing: A survey. Visual Comput. 1998, 14, 360–372. [Google Scholar] [CrossRef]
- Alexa, M.; Cohen-Or, D.; Levin, D. As-Rigid-As-Possible Shape Interpolation. In Proceedings of the 27th Annual International Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 25–27 July 2000; pp. 157–164.
- Zhang, H.; Sheffer, A.; Cohen-Or, D.; Zhou, Q.; van Kaick, O.; Tagliasacchi, A. Deformation-Driven Shape Correspondence. In Proceedings of Symposium on Geometry Processing 2008, Copenhagen, Denmark, 2–4 July 2008; pp. 1431–1439.
- Zöckler, M.; Stalling, D.; Hege, H.C. Fast and intuitive generation of geometric shape transitions. Visual Comput. 2000, 16, 241–253. [Google Scholar]
- Dalyot, S.; Doytsher, Y. A Hierarchical Approach toward 3-D Geospatial Data Set Merging. In Representing, Modelling and Visualizing the Natural Environment: Innovations in GIS 13; Mount, N., Harvey, G., Aplin, P., Priestnall, G., Eds.; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2008; pp. 195–220. [Google Scholar]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Doytsher, Y.; Hall, J.K. Interpolation of DTM using bi-directional third-degree parabolic equations, with FORTRAN subroutines. Comput. Geosci. 1997, 23, 1013–1020. [Google Scholar] [CrossRef]
- Foley, J.D.; van Dam, A.; Feiner, S.K.; Hughes, J.F. Computer Graphics Principles and Practice, 2nd ed.; Addison-Wesley: Reading, MA, USA, 1990. [Google Scholar]
- Cayley, A. An Elementary Treatise on Elliptic Functions; Dover Publications: New York, NY, USA, 1961. [Google Scholar]
- Shoemake, K. Animating Rotation with Quaternion Curves. In Proceedings of Proceedings of the 12th Annual Conference on Computer Graphics and Interactive Techniques, San Francisco, CA, USA, 22–26 July 1985; Volume 19, pp. 245–254.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dalyot, S.; Doytsher, Y. Multi-Temporal Time-Dependent Terrain Visualization through Localized Spatial Correspondence Parameterization. ISPRS Int. J. Geo-Inf. 2013, 2, 456-479. https://doi.org/10.3390/ijgi2020456
Dalyot S, Doytsher Y. Multi-Temporal Time-Dependent Terrain Visualization through Localized Spatial Correspondence Parameterization. ISPRS International Journal of Geo-Information. 2013; 2(2):456-479. https://doi.org/10.3390/ijgi2020456
Chicago/Turabian StyleDalyot, Sagi, and Yerach Doytsher. 2013. "Multi-Temporal Time-Dependent Terrain Visualization through Localized Spatial Correspondence Parameterization" ISPRS International Journal of Geo-Information 2, no. 2: 456-479. https://doi.org/10.3390/ijgi2020456
APA StyleDalyot, S., & Doytsher, Y. (2013). Multi-Temporal Time-Dependent Terrain Visualization through Localized Spatial Correspondence Parameterization. ISPRS International Journal of Geo-Information, 2(2), 456-479. https://doi.org/10.3390/ijgi2020456