Improved Jitter Elimination and Topology Correction Method for the Split Line of Narrow and Long Patches
Abstract
:1. Introduction
2. Related Works
- Rounded skeleton lines. Lee [6] and Montanari [7] proposed rounded skeleton line methods, i.e., medial axis splitting methods. These rounded skeleton lines are calculated using a Voronoi diagram of the polygon boundary and its vertices. Rounded skeleton lines consist of two parts, namely parabolas and straight lines. The parabolas make the lines smoother at polygon bends. However, this algorithm is considerably complex in design. Consequently, it is difficult to optimize the structural characteristics of the geographic features further.
- Triangulation-based skeleton lines. Owing to the excellent properties of Delaunay triangulation, such as proximity, optimality, regionality, and convexity polygons [8,9], scholars have performed considerable research [10,11,12] on the extraction of polygon skeleton lines based on Delaunay triangulation as well as the practical applications. DeLucia and Black [13] first proposed the extraction of polygon skeleton lines based on a CDT and classified the triangles in the triangular mesh into three categories based on the number of polygonal edges present at the three sides of a triangle. Skeleton line extraction for each type of triangle was described, and this formed the foundation for subsequent research.
- Straight skeleton lines. Aichholzer et al. [21] proposed a straight skeleton line construction method; the skeleton lines extracted using this method are structurally simple, containing only line segments. The initial algorithm is only applicable to simple polygons. Das et al. [22] extended the scope of the algorithm to the monotone polygon. A simple polygon P is said to be monotone with respect to a line L if its intersection (if any) with any line perpendicular to L is connected. Eppstein and Erickson [23] improved the efficiency of the algorithm by using a technique developed by Eppstein for maintaining the extreme of binary functions.
3. Advantages and Disadvantages of Straight Skeletons
3.1. Original Method for Straight Skeletons
3.1.1. Advantages
3.1.2. Disadvantages
3.2. Optimization Method for Straight Skeletons
3.2.1. Topologically Constrained Correcting Algorithm
3.2.2. Skeleton Elimination Algorithm
3.2.3. Connection Point Reconstruction Algorithm
3.2.4. Existing Problems in the Optimization Method
4. Improved Jitter Elimination and Topology Correction Method for the Split Line
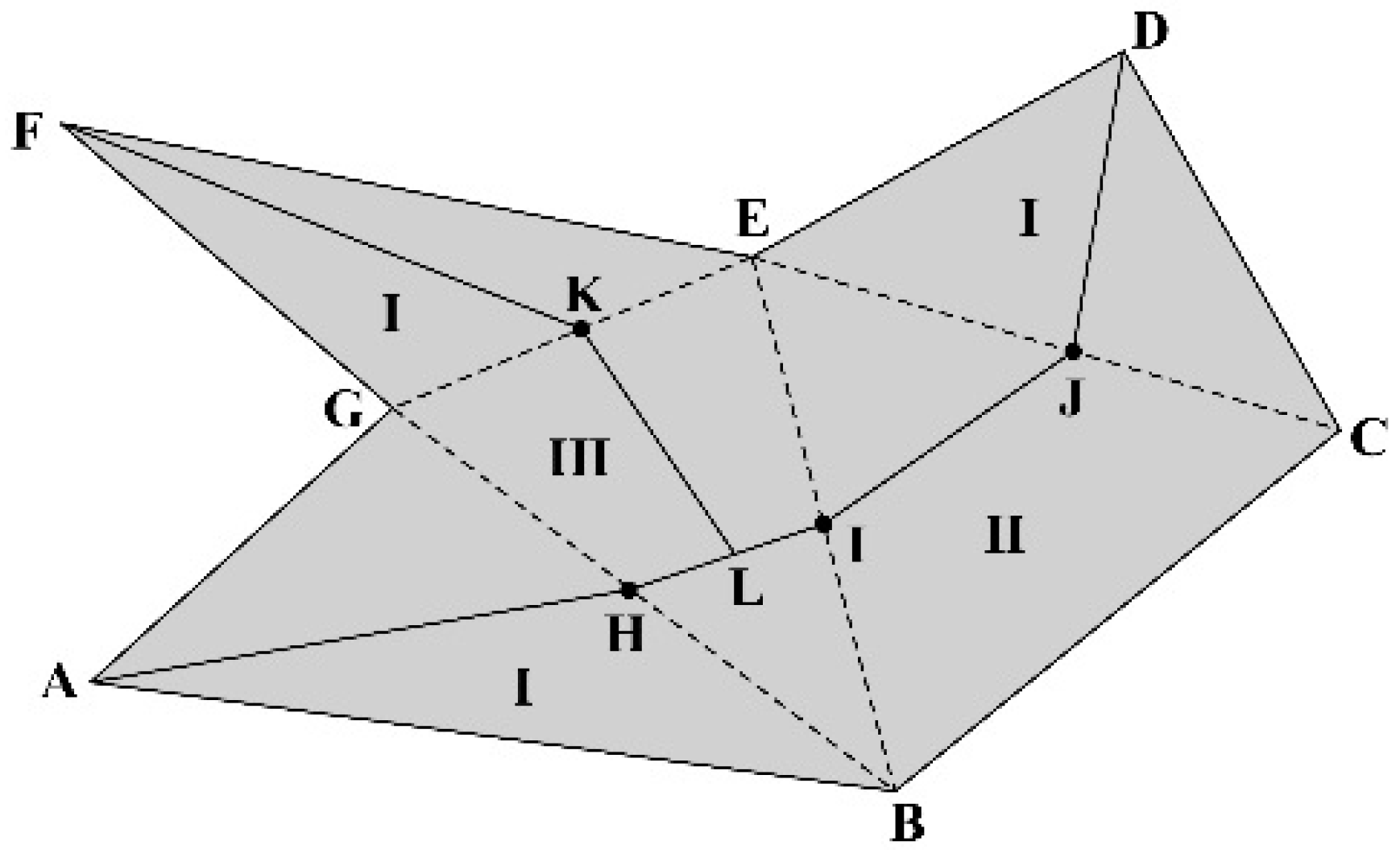
4.1. Delaunay Triangulation
4.2. Split Line Jitter Removal Based on Geometric Features
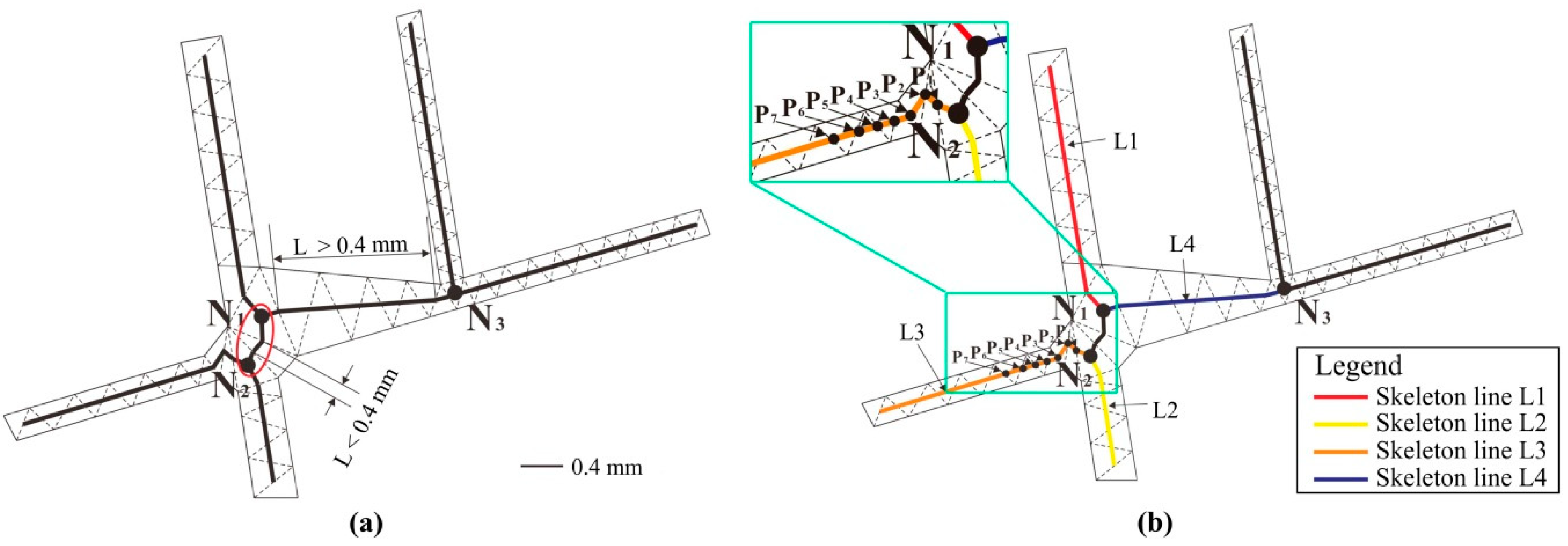
4.2.1. Spike Jitter Adjustment Algorithm
4.2.2. Jitter Adjustment Algorithm for the Branch Junctions
- (1)
- Branch skeleton lines with the same direction are connected preferentially to a straight line. The other branch skeleton lines are extended to this straight line along their respective directions.
- (2)
- If two skeleton lines which are in the same direction did not exist, the Euclidean distance between the nodes is taken as a similarity measurement. The fitting node is aggregated to the geometric center of the aggregation zone. The branch skeleton lines then are connected to the fitting nodes along their respective directions.
4.3. Split Line Topology Correction
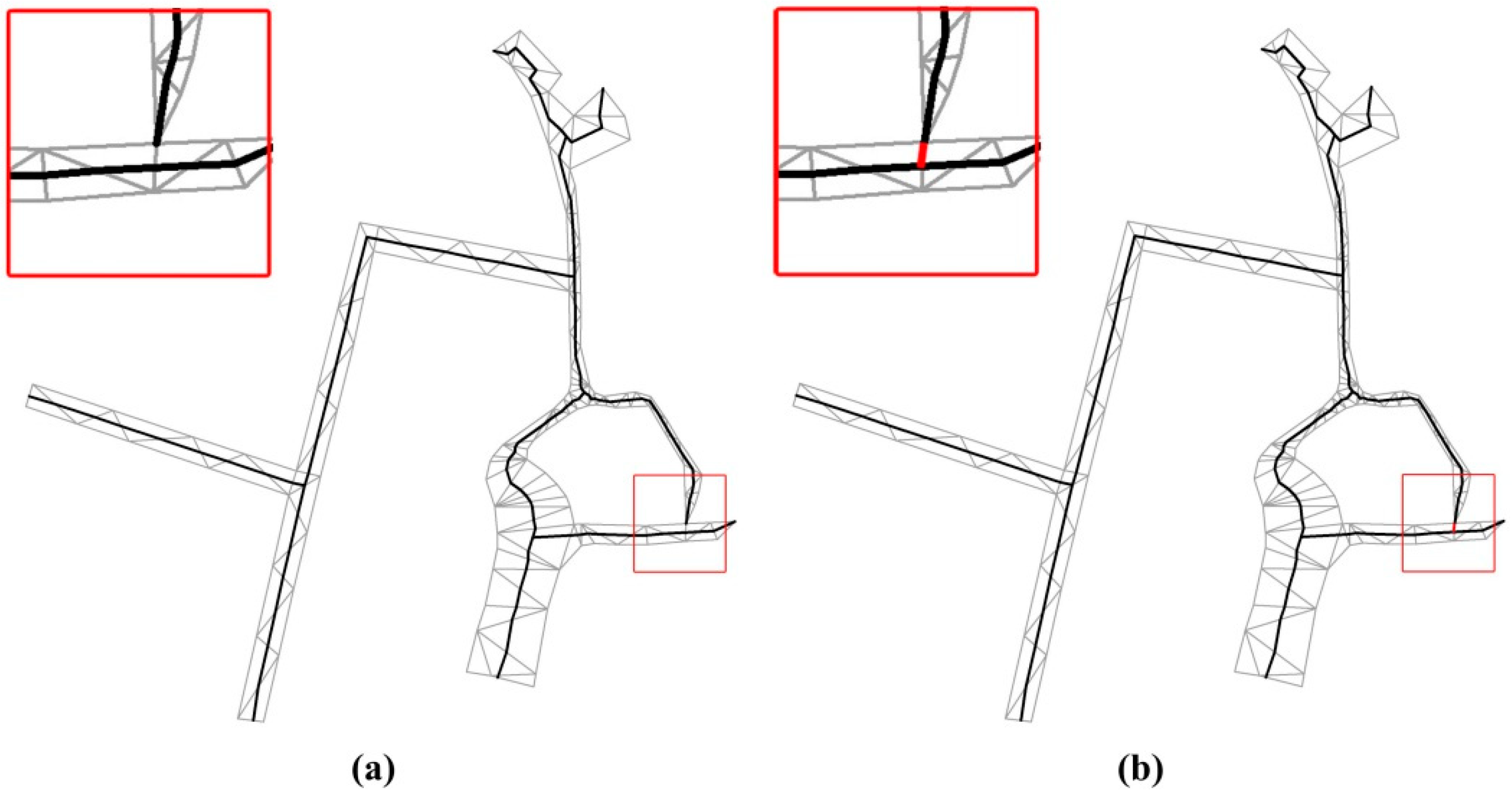
4.3.1. Topology Correction for Nodes with Degree 1
4.3.2. Topology Correction for Nodes with Degree 2
- (1)
- If the area is inside the polygon and has a split line associated with point O, no action is taken.
- (2)
- If the area is inside the polygon and does not have a split line associated with point O, the closest point method is applied to correct it with the split line.
- (3)
- If the area is outside the polygon, no action is taken.
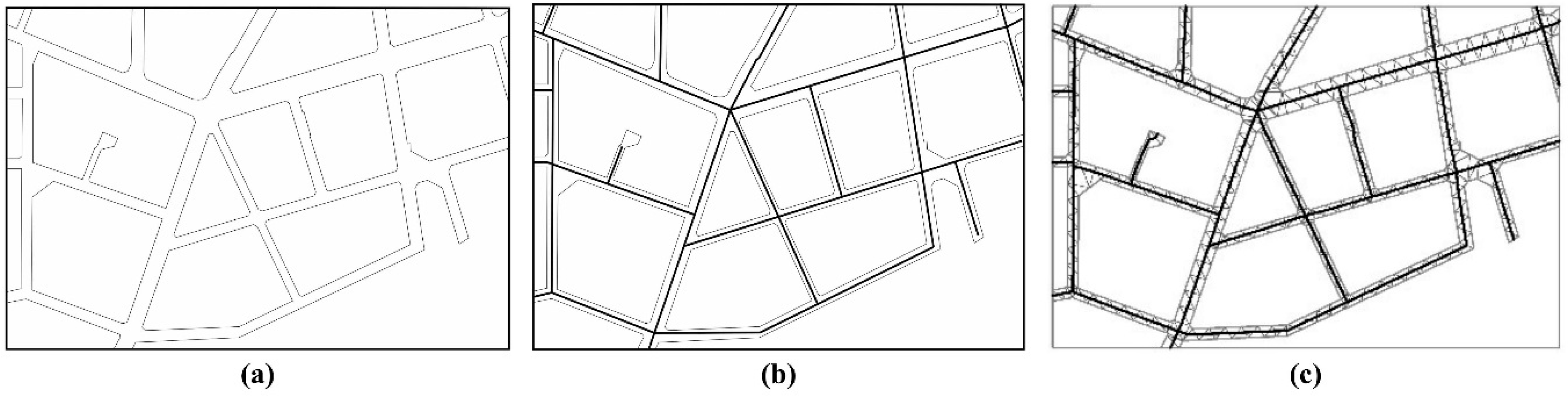
5. Experiments and Results
5.1. Reliability Test and Analysis
5.2. Superiority Test and Analysis
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van Oosterom, P. The GAP-tree, an approach to ‘on-the-fly’ map generalization of an area partitioning. In GIS and Generalization, Methodology and Practice; CRC Press: Boca Raton, FL, USA, 1995; pp. 120–132. [Google Scholar]
- Beard, K.; Mackaness, W. Generalization operations and supporting structures. In Auto-Carto 10: Technical Papers of the 1991 ACSM-ASPRS Annual Convention; ACSM-ASPRS: Baltimore, ML, USA, 1991; Volume 6, pp. 29–45. [Google Scholar]
- McMaster, R.B.; Shea, K.S. Generalization in Digital Cartography; Association of American Geographers: Washington, DC, USA, 1992. [Google Scholar]
- Mitropoulos, V.; Xydia, A.; Nakos, B.; Vescoukis, V. The use of epsilon convex area for attributing bends along a cartographic line. In Proceedings of the 22nd International Cartographic Conference, La Corona, Spain, 9–16 July 2005. [Google Scholar]
- Muller, J.C. Fractal and Automated Line Generalization. Cartogr. J. 1987, 24, 27–34. [Google Scholar] [CrossRef]
- Lee, D.T. Medial axis transformation of a planar shape. IEEE Trans. Pattern Anal. Mach. Intell. 1982, 4, 363–369. [Google Scholar] [CrossRef] [PubMed]
- Montanari, U. A method for obtaining skeletons using a quasi-Euclidean distance. J. ACM 1968, 15, 600–624. [Google Scholar] [CrossRef]
- Ruas, A. Multiple paradigms for automating map generalization: Geometry, topology, hierarchical partitioning and local triangulation. ACSM/ASPRS Annu. Conv. Expos. 1995, 4, 68–69. [Google Scholar]
- Ware, J.M.; Jones, C.B.; Bundy, G.L. A Triangulated Spatial Model for Cartographic Generalization of Areal Objects. In Advance in GIS Research II, Proceedings of the 7th International Symposium on Spatial Data Handling, Delft, The Netherlands, 12–16 August 1996; Kraak, M.J., Molenaar, M., Eds.; Taylor & Francis: London, UK, 1997; pp. 173–192. [Google Scholar]
- Cao, T.; Edelsbrunner, H.; Tan, T. Proof of correctness of the digital Delaunay triangulation algorithm. Comput. Geom. Theory Appl. 2015, 48, 507–519. [Google Scholar] [CrossRef]
- Sintunata, V.; Aoki, T. Skeleton extraction in cluttered image based on delaunay triangulation. In Proceedings of the 2016 IEEE International Symposium on Multimedia (ISM), San Jose, CA, USA, 11–13 December 2016; pp. 365–366. [Google Scholar]
- Yu, W. Assessing the implications of the recent community opening policy on the street centrality in China: A GIS-based method and case study. Appl. Geogr. 2017, 89, 61–76. [Google Scholar] [CrossRef]
- DeLucia, A.A.; Black, R.T. A Comprehensive Approach to Automatic Feature Generalization. In Proceedings of the 13th Conference of the International Cartographic Association, Morelia, Mexico, 12–21 October 1987; pp. 173–191. [Google Scholar]
- Li, Z. Algorithmic Foundation of Multi-Scale Spatial Representation; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Zou, J.J.; Yan, H. Skeletonization of ribbon-like shapes based on regularity and singularity analyses. IEEE Trans. Syst. Man Cybern. Part B 2001, 31, 401–407. [Google Scholar]
- Morrison, P.; Zou, J.J. Triangle refinement in a constrained Delaunay triangulation skeleton. Pattern Recognit. 2007, 40, 2754–2765. [Google Scholar] [CrossRef]
- Penninga, F.; Verbree, E.; Quak, W.; van Oosterom, P. Construction of the Planar Partition Postal Code Map Based on Cadastral Registration. GeoInformatica 2005, 9, 181–204. [Google Scholar] [CrossRef] [Green Version]
- Uitermark, H.; Vogels, A.; Van Oosterom, P. Semantic and Geometric Aspects of Integrating Road Networks. In Proceedings of the Second International Conference on Interoperating Geographic Information Systems (INTEROP’99), Zürich, Switzerland, 10–12 March 1999; Vþkovski, A., Brassel, K.E., Schek, H.-J., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 177–188. [Google Scholar]
- Jones, C.B.; Bundy, G.L.; Ware, M.J. Map Generalization with a Triangulated Data Structure. Cartogr. Geogr. Inf. Syst. 1995, 22, 317–331. [Google Scholar]
- Gao, P.; Minami, M.M. Raster-to-vector Conversion: A Trend Line Intersection Approach to Junction Enhancement. In Proceedings of the 11th International Symposium on Computer-Assisted Cartography, Minneapolis, MN, USA, 30 October–1 November 1993; pp. 297–304. [Google Scholar]
- Aichholzer, O.; Aurenhammer, F.; Alberts, D.; Gärtner, B. A Novel Type of Skeleton for Polygons. J. Univers. Comput. Sci. 1996, 1, 752–761. [Google Scholar]
- Das, G.K.; Mukhopadhyay, A.; Nandy, S.C.; Patil, S.; Rao, S.V. Computing the straight skeleton of a monotone polygon in O(nlogn) time. In Proceedings of the 22nd Annual Canadian Conference on Computational Geometry, Winnipeg, MB, Canada, 9–11 August 2010; pp. 207–210. [Google Scholar]
- Eppstein, D.; Erickson, J. Raising roofs, crashing cycles, and playing pool: Applications of a data structure for finding pairwise interactions. Discret. Comput. Geom. 1999, 22, 569–592. [Google Scholar] [CrossRef]
- Haunert, J.H.; Sester, M. Using the straight skeleton for generalization in a multiple representation environment. In Proceedings of the 8th ICA Workshop on Generalization and Multiple Representation, Leicester, UK, 20–21 August 2004. [Google Scholar]
- Haunert, J.H.; Sester, M. Area collapse and road centerlines based on straight skeletons. GeoInformatica 2008, 12, 169–191. [Google Scholar] [CrossRef]
- Ai, T.; Yang, F.; Li, J. Land-use Data Generalization for the Database Construction of the Second Land Resource Survey. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 887–891. (In Chinese) [Google Scholar]
- Meijers, M.; Savino, S.; Van Oosterom, P. SPLITAREA: An algorithm for weighted splitting of faces in the context of a planar partition. Int. J. Geogr. Inf. Sci. 2016, 30, 1522–1551. [Google Scholar] [CrossRef]














| Jitter Elimination | Topology Correction | Total | |||
|---|---|---|---|---|---|
| Spike Jitters | Jitters in Branch Junctions | Nodes with Degree 1 | Nodes with Degree 2 | ||
| Number | 621 | 456 | 1513 | 3 | 2593 |
| Proportion (%) | 23.95 | 17.59 | 58.35 | 0.11 | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Yin, Y.; Wu, P.; Liu, X.; Guo, P. Improved Jitter Elimination and Topology Correction Method for the Split Line of Narrow and Long Patches. ISPRS Int. J. Geo-Inf. 2018, 7, 402. https://doi.org/10.3390/ijgi7100402
Li C, Yin Y, Wu P, Liu X, Guo P. Improved Jitter Elimination and Topology Correction Method for the Split Line of Narrow and Long Patches. ISPRS International Journal of Geo-Information. 2018; 7(10):402. https://doi.org/10.3390/ijgi7100402
Chicago/Turabian StyleLi, Chengming, Yong Yin, Pengda Wu, Xiaoli Liu, and Peipei Guo. 2018. "Improved Jitter Elimination and Topology Correction Method for the Split Line of Narrow and Long Patches" ISPRS International Journal of Geo-Information 7, no. 10: 402. https://doi.org/10.3390/ijgi7100402
APA StyleLi, C., Yin, Y., Wu, P., Liu, X., & Guo, P. (2018). Improved Jitter Elimination and Topology Correction Method for the Split Line of Narrow and Long Patches. ISPRS International Journal of Geo-Information, 7(10), 402. https://doi.org/10.3390/ijgi7100402




