Identification of Experimental and Control Areas for CCTV Effectiveness Assessment—The Issue of Spatially Aggregated Data
Abstract
:1. Introduction
2. Methodological Challenges in Evaluating Effectiveness of CCTV Using the Quasi-Experimental Method
3. Description of the Method Developed
- The experimental area must have at least two cameras per 1 km of street length. This criterion is intended to exclude streets barely affected by the intervention.
- The number of crime incidents preceding the intervention (installation of a camera) should be no less than 20.
- The total number of crime incidents should not be less than 100 in the ten-year period included in the analysis.
- Crime incidents data were acquired for the period ranging from 2005 to 2014; we needed at least one year before and two years after the intervention in order to assess its impact. A two-year period was needed because the exact date of the CCTV camera installation was not known. If a camera is installed in December, the impact of this action will appear in the second year. In our study, only streets on which the first camera was installed no earlier than 2006 and no later than 2013 were taken into account.
- First, the aggregation to quarterly crime data has been chosen due to rare occurring crimes. We aggregated quarterly crime incident data for each street and subsequently standardized them by dividing them by the length of the street. Aggregating crime incidents to shorter time frames would have resulted in many streets with few crime incidents or without any, while aggregating to larger time frames would have reduced time series to such short ones that comparing experimental and control areas would have been impossible.
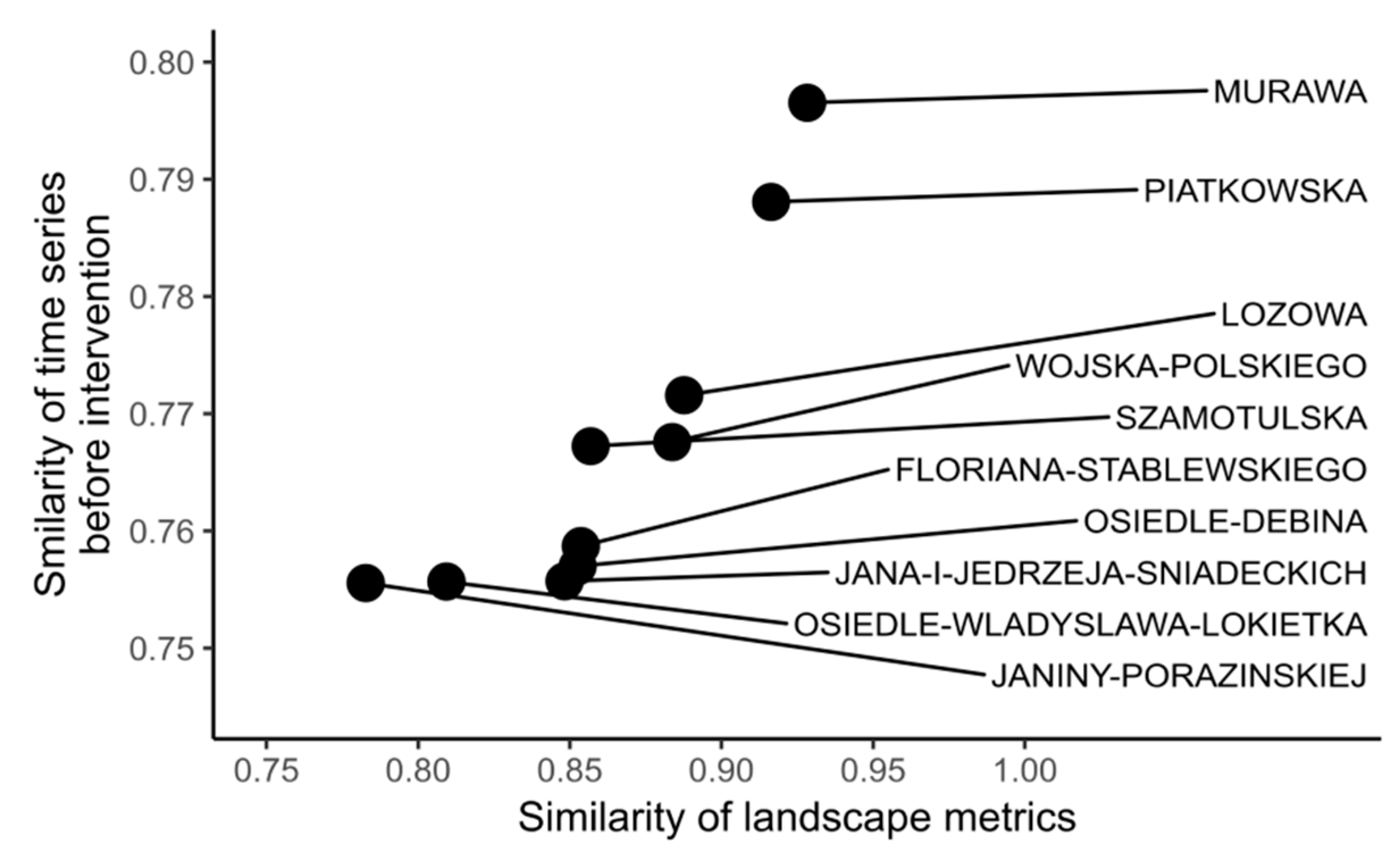
- Second, to find control areas with a similar crime density, i.e., similar number of crimes per 1 km of street length, we calculated the Euclidean distance for each experimental area. The Euclidean distance is a good measure for changes of proportions of land-cover types between two time series. It is calculated as:where , . Values of vectors and represent the number of crime incidents per kilometer in each consecutive quarter (i) prior to the intervention. For each pair of values , small differences are suppressed towards zero and large ones are penalized. The formula is calculated for the experimental area and every street that could become its control area. For example, having a street Q (an experimental area on which a camera has been installed in 2014) and a street P (a possible control area), we have a time series consisting of four quarters before intervention. Supposing the crime density in the experimental area (Q) equals to 10, 9, 8, 7, and the corresponding values for control areas (P) are 8, 5, 3, and 11, the Euclidean distance between the two areas equals to 7.8. The higher the Euclidean distance, the more dissimilar the crime densities are between experimental and control areas, and vice versa.Since the distribution of Euclidean distances was strongly right-skewed, we decided to declare a mean distance of seven crimes per 1 km of street length per a quarter of a year as the maximum distance of similarity. In other words, any control area that exceeds this distance is treated as completely dissimilar to its compared experimental area. The remaining distances with values ≤7 were subsequently standardized and inversed. This resulted in a similarity measure where 0 meant that two areas were fully dissimilar (the Euclidean distance was equal to 7 or more), and 1 that their time series were identical (the Euclidean distance was equal to 0). Using this procedure, the distance of 3.5 had a similarity measure of 0.5 and the distance of 6 resulted in a similarity measure of 0.14. This allowed us to select the 10 most similar control areas in terms of crime densities prior to the intervention. The streets, however, could have had similar time series due to sheer coincidence, which could have happened especially for short time series, such as one year. Therefore, experimental and control areas had to be evaluated in terms of their similarity of landscape as well.
- We evaluated the similarity of the landscape between the experimental area and its pre-selected control areas. We calculated the Euclidean distance regarding the landscape metrics, i.e.,where , . Values of vectors and represent percentages of each landscape type (i) in the experimental (r) and the corresponding control area (s). As in the case of , for each pair of values , small differences are suppressed towards zero and large ones are penalized.
4. Testing the Method in a Case Study
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lim, H.; Kim, C.; Eck, J.E.; Kim, J. The crime-reduction effects of open-street CCTV in South Korea. Secur. J. 2016, 29, 241–255. [Google Scholar] [CrossRef]
- Gill, M.; Spriggs, A. Assessing the Impact of CCTV; Home Office Research: London, UK, 2005. [Google Scholar]
- La Vigne, N.G.; Lowry, S.S.; Markman, J.A.; Dwyer, A.M. Evaluating the Use of Public Surveillance Cameras for Crime Control and Prevention; Urban Institute: Washington, DC, USA, 2011. [Google Scholar]
- Farrington, D.P.; Gill, M.; Waples, S.J.; Argomaniz, J. The effects of closed-circuit television on crime: Meta-analysis of an English national quasi-experimental multi-site evaluation. J. Exp. Criminol. 2007, 3, 21–38. [Google Scholar] [CrossRef]
- Farrington, D.P.; Painter, K.A. How to evaluate the impact of CCTV on crime. Crime Prev. Community Saf. 2003, 5, 7–16. [Google Scholar] [CrossRef]
- Caplan, J.M.; Kennedy, L.W.; Petrossian, G. Police-monitored CCTV cameras in Newark, NJ: A quasi-experimental test of crime deterrence. J. Exp. Criminol. 2011, 7, 255–274. [Google Scholar] [CrossRef]
- Weisburd, D.; Petrosino, A.; Fronius, T. Randomized Experiments in Criminology and Criminal Justice. In Encyclopedia of Criminology and Criminal Justice; Springer: New York, NY, USA, 2014; pp. 4283–4291. [Google Scholar]
- Brown, B. CCTV in Town Centres: Three Case Studies; Police Research Group: London, UK, 1995; ISBN 1858934737. [Google Scholar]
- Bowers, K.J.; Johnson, S.D. Measuring the geographical displacement and diffusion of benefit effects of crime prevention activity. J. Quant. Criminol. 2003, 19, 275–301. [Google Scholar] [CrossRef]
- Welsh, B.C.; Farrington, D.P. Crime Prevention Effects of Closed Circuit Television: A Systematic Review; Home Office Research: London, UK, 2002; Volume 252. [Google Scholar]
- Cerezo, A. CCTV and crime displacement: A quasi-experimental evaluation. Eur. J. Criminol. 2013, 10, 222–236. [Google Scholar] [CrossRef]
- Phomikong, P.; Fukushima, M.; Jutagate, T. Investigation of impact of river damming to the migrations of mekong fishes by” before-after control-impact” quasi-experimental sampling in the tributaries. In Proceedings of the 51st Kasetsart University Annual Conference, Bangkok, Thailand, 5–7 February 2013. [Google Scholar]
- Abbema, E.A.; Van Assema, P.; Kok, G.J.; De Leeuw, E.; De Vries, N.K. Effect evaluation of a comprehensive community intervention aimed at reducing socioeconomic health inequalities in the Netherlands. Health Promot. Int. 2004, 19, 141–156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salkind, N. Encyclopedia of Measurement and Statistics; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 2007; ISBN 9781412916110. [Google Scholar]
- Cook, T.D.; Campbell, D.T.; Shadish, W. Experimental and Quasi-Experimental Designs for Generalized Causal Inference; Houghton Mifflin: Boston, MA, USA, 2002. [Google Scholar]
- Welsh, B.C.; Farrington, D.P. Effects of closed-circuit television on crime. Ann. Am. Acad. Polit. Soc. Sci. 2003, 587, 110–135. [Google Scholar] [CrossRef]
- Piza, E.L.; Caplan, J.M.; Kennedy, L.W. Analyzing the Influence of Micro-Level Factors on CCTV Camera Effect. J. Quant. Criminol. 2014, 30, 237–264. [Google Scholar] [CrossRef]
- Park, H.H.; Oh, G.S.; Paek, S.Y. Measuring the crime displacement and diffusion of benefit effects of open-street CCTV in South Korea. Int. J. Law Crime Justice 2012, 40, 179–191. [Google Scholar] [CrossRef]
- Ratcliffe, J.H.; Taniguchi, T.; Taylor, R.B. The crime reduction effects of public CCTV cameras: A multi-method spatial approach. Justice Q. 2009, 26, 746–770. [Google Scholar] [CrossRef]
- Planells, S. Essays on the Economics of Crime: Determinants of Crime in an Urban Context; Universitat de Barcelona: Barcelona, Spain, 2015. [Google Scholar]
- Aebi, M.F.; Linde, A. Is there a crime drop in Western Europe? Eur. J. Crim. Policy Res. 2010, 16, 251–277. [Google Scholar] [CrossRef]
- Heidensohn, F.; Farrell, M. Crime in Europe; Routledge: London, UK, 1993; ISBN 0203423151. [Google Scholar]
- Tonry, M. Why crime rates are falling throughout the Western world. Crime Justice 2014, 43, 1–63. [Google Scholar] [CrossRef]
- Farrall, S. Outlining the Crime Drop. In Re-Examining the Crime Drop; Springer: Berlin, Germany, 2017; pp. 1–8. [Google Scholar]
- Farrell, G.; Tilley, N.; Tseloni, A. Why the crime drop? Crime Justice 2014, 43, 421–490. [Google Scholar] [CrossRef]
- Siemaszko, A. Are criminologists at risk of unemployment? [Czy kryminologom grozi bezrobocie?]. In Crime Atlas in Poland. [Atlas przestępczości w Polsce]; Oficyna Naukowa: Warsaw, Poland, 2015; Volume 5, p. 227. [Google Scholar]
- Boessen, A.; Hipp, J.R. Close-Ups and the Scale of Ecology: Land Uses and the Geography of Social Context and Crime. Criminology 2015, 53, 399–426. [Google Scholar] [CrossRef]
- Ceccato, V.; Oberwittler, D. Comparing spatial patterns of robbery: Evidence from a Western and an Eastern European city. Cities 2008, 25, 185–196. [Google Scholar] [CrossRef]
- Kennedy, E.; Kennedy, L.W. Using dasymetric mapping for spatially aggregated crime data. J. Quant. Criminol. 2004, 20, 243–262. [Google Scholar] [CrossRef]
- Raphael, S.; Winter-Ebmer, R. Identifying the Effect of Unemployment on Crime. J. Law Econ. 2001, 44, 259–283. [Google Scholar] [CrossRef] [Green Version]
- Stucky, T.D.; Ottensmann, J.R. Land use and violent crime. Criminology 2009, 47, 1223–1264. [Google Scholar] [CrossRef] [Green Version]
- Sypion-Dutkowska, N.; Leitner, M. Land use influencing the spatial distribution of urban crime: A case study of Szczecin, Poland. ISPRS Int. J. Geo-Inf. 2017, 6, 74. [Google Scholar] [CrossRef]
- Farrington, D.P. Evaluating a community crime prevention program. Evaluation 1997, 3, 157–173. [Google Scholar] [CrossRef]
- Braga, A.A.; Weisburd, D.L.; Waring, E.J.; Mazerolle, L.G.; Spelman, W.; Gajewski, F. Problem-oriented policing in violent crime places: A randomized controlled experiment. Criminology 1999, 37, 541–580. [Google Scholar] [CrossRef]
- Farrington, D.P.; Welsh, B.C. Randomized experiments in criminology: What have we learned in the last two decades? J. Exp. Criminol. 2005, 1, 9–38. [Google Scholar] [CrossRef]
- Ariel, B.; Farrar, W.A.; Sutherland, A. The Effect of Police Body-Worn Cameras on Use of Force and Citizens’ Complaints Against the Police: A Randomized Controlled Trial. J. Quant. Criminol. 2015, 31, 509–535. [Google Scholar] [CrossRef]
- Louvet, R.; Aryal, J.; Josselin, D.; Genre-Grandpierre, C. R as a GIS: Illustrating scale and aggregation problems with forest fire data. Procedia Environ. Sci. 2015, 27, 66–69. [Google Scholar] [CrossRef]
- Lisiecka, K. GIS in Analyses of Spatiotemporal Crime Diversity by the Example of Poznań [GIS w analizach zróżnicowania czasoprzestrzennego przestępczości na przykładzie Poznania]. Available online: https://www.arcanagis.pl/gis-w-analizach-zroznicowania-czasoprzestrzennego-przestepczosci-na-przykladzie-poznania/ (accessed on 1 March 2018).
- Cattell, V. Poor people, poor places, and poor health: The mediating role of social networks and social capital. Soc. Sci. Med. 2001, 52, 1501–1516. [Google Scholar] [CrossRef]
- Wolfe, M.K.; Mennis, J. Does vegetation encourage or suppress urban crime? Evidence from Philadelphia, PA. Landsc. Urban Plan. 2012, 108, 112–122. [Google Scholar] [CrossRef]
- Alberti, M.; Marzluff, J.M. Ecological resilience in urban ecosystems: Linking urban patterns to human and ecological functions. Urban Ecosyst. 2004, 7, 241–265. [Google Scholar] [CrossRef]
- Stewart, B.; Neily, P. A Procedural Guide for Ecological Landscape Analysis; Nova Scotia: Truro, NS, Canada, 2008. [Google Scholar]
- Alberti, M.; Marzluff, J.M.; Shulenberger, E.; Bradley, G.; Ryan, C.; Zumbrunnen, C. Integrating humans into ecology: Opportunities and challenges for studying urban ecosystems. Urban Ecol. 2008, 53, 143–158. [Google Scholar] [CrossRef]
- Kuo, F.E.; Sullivan, W.C. Environment and crime in the inner city does vegetation reduce crime? Environ. Behav. 2001, 33, 343–367. [Google Scholar] [CrossRef]
- Gau, J.M.; Corsaro, N.; Brunson, R.K. Revisiting broken windows theory: A test of the mediation impact of social mechanisms on the disorder-fear relationship. J. Crim. Justice 2014, 42, 579–588. [Google Scholar] [CrossRef]
- Poister, T.H. Transit-Related Crime in Suburban Areas. J. Urban Aff. 1996, 18, 63–75. [Google Scholar] [CrossRef]
- Loukaitou-Sideris, A.; Liggett, R.; Iseki, H. The Geography of Transit Crime: Documentation and evaluation of crime incidence on and around the Green Line stations in Los Angeles. J. Plan. Educ. Res. 2002, 22, 135–151. [Google Scholar] [CrossRef]
- McCord, E.S.; Ratcliffe, J.H. Intensity value analysis and the criminogenic effects of land use features on local crime patterns. Crime Patterns Anal. 2009, 2, 17–30. [Google Scholar]
- Crewe, K. Linear Parks and Urban Neighbourhoods: A Study of the Crime Impact of the Boston South-west Corridor. J. Urban Des. 2001, 6, 245–264. [Google Scholar] [CrossRef]
- Anliu, J. Crime Analysis in the City of Baton Rouge and BREC Park Based on Crime Location Quotient and Hotspot Method. Master’s Thesis, Louisiana State University, Baton Rouge, LA, USA, 2017. [Google Scholar]
- Dąbrowski, A. The methodology for creating high-resolution land cover data from the existing spatial data [Metodyka opracowywania szczegółowych map pokrycia terenu na podstawie istniejących źródeł danych przestrzennych]. Probl. Ekol. Kraj. 2016, 43, 105–121. [Google Scholar]
- McGarigal, K.; Cushman, S.A.; Neel, M.C.; Ene, E. FRAGSTATS v4: Spatial Pattern Analysis Program. for Categorical and Continuous Maps; University of Massachusetts: Amherst, MA, USA, 2012; Available online: http://www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 19 October 2018).
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Aggarwal, C.C.; Reddy, C.K. Data Clustering: Algorithms and Applications; CRC press: Boca Raton, FL, USA, 2013. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dąbrowski, A.; Matczak, P.; Wójtowicz, A.; Leitner, M. Identification of Experimental and Control Areas for CCTV Effectiveness Assessment—The Issue of Spatially Aggregated Data. ISPRS Int. J. Geo-Inf. 2018, 7, 471. https://doi.org/10.3390/ijgi7120471
Dąbrowski A, Matczak P, Wójtowicz A, Leitner M. Identification of Experimental and Control Areas for CCTV Effectiveness Assessment—The Issue of Spatially Aggregated Data. ISPRS International Journal of Geo-Information. 2018; 7(12):471. https://doi.org/10.3390/ijgi7120471
Chicago/Turabian StyleDąbrowski, Adam, Piotr Matczak, Andrzej Wójtowicz, and Michael Leitner. 2018. "Identification of Experimental and Control Areas for CCTV Effectiveness Assessment—The Issue of Spatially Aggregated Data" ISPRS International Journal of Geo-Information 7, no. 12: 471. https://doi.org/10.3390/ijgi7120471
APA StyleDąbrowski, A., Matczak, P., Wójtowicz, A., & Leitner, M. (2018). Identification of Experimental and Control Areas for CCTV Effectiveness Assessment—The Issue of Spatially Aggregated Data. ISPRS International Journal of Geo-Information, 7(12), 471. https://doi.org/10.3390/ijgi7120471





