Advanced Sidereal Filtering for Mitigating Multipath Effects in GNSS Short Baseline Positioning

Abstract

Advanced sidereal filtering (ASF) is an observation-domain sidereal filtering that adopts the repeat time of each individual satellite separately rather than the mean repeat time, adopted by the modified sidereal filtering (MSF). To evaluate the performance of ASF, we apply the method to filter the multipath for a short baseline based on a dual-antenna Global Navigation Satellite System (GNSS) receiver. The errors from satellite and receiver clocks, satellite orbit, troposphere, ionosphere, and antenna phase center variations are greatly eliminated by single difference between the two antennas because they are connected to the same receiver clock. The performances of ASF are compared with MSF to evaluate the gain for multipath mitigation. Comparisons indicate that ASF slightly outperforms MSF when the repeat time values of all satellites incorporated in data processing are within the normal range (86,145–86,165 s), but the difference of variance reduction rate between ASF and MSF is statistically significant. When the data of a satellite with repeat time outside the normal range are included, the performances of MSF become much worse, but ASF is almost not affected. This advantage of ASF over MSF is important because the proportion of the days on which at least one satellite’s repeat time exceeds the normal range reaches 71.19% based on the statistics on the data of 2014 and 2015. After applying ASF multipath corrections on the test days, the averages of standard deviations of north, east, and up component are reduced from 3.8 to 2.1 mm, 3.2 to 1.7 mm, and 7.6 to 4.3 mm, respectively. Comparison between applying ASF with the single-day model and with the seven-day model indicates that the former is generally more effective in multipath reduction.

1. Introduction

The Global Navigation Satellite System (GNSS) technique serves a wide range of applications in geoscience fields, e.g., GNSS geodesy [1,2], GNSS seismology [3,4,5], and GNSS meteorology [6,7,8]. Great application potential of this technique stimulates scientists to persistently pursue higher accuracy and precision of GNSS positioning. Among the remaining errors in the positioning, multipath effect, highly depending on the site-specific local environment [9], is an important error source existing in both absolute and relative positioning. For Global Positioning System (GPS), the satellites revisit a static ground station with the period near a sidereal day (23 h 56 min 04 s). Accordingly, the multipath effects, depending on the geometric relationships between the station and GPS satellites, repeat with the same period. On the basis of this time domain repeatability, Bock [10] and Genrich and Bock [11] proposed a method named sidereal filtering to mitigate GPS multipath effects. Due to its easy operation and high efficiency in multipath reduction, sidereal filtering is widely used, e.g., in improving detection of fault slips and seismic displacements [3,12,13,14] and in ameliorating calibration of absolute GPS antenna phase center variations [15,16].

Sidereal filtering mitigates multipath errors for a specific day with a correction model constructed from the observable residuals (or coordinate residuals) of the previous day or the previous several days. Different studies may use the data of different number of days to form the correction model, for example, Genrich and Bock [11] used the coordinate residual time series of the previous day as the multipath correction values (single-day model); Nikolaidis et al. [3] and Langbein and Bock [17] used that of the previous three and five days to form the correction model (multiple-day model), respectively. Ragheb et al. [18] compared multipath correction models constructed from observable residuals (or coordinate residuals) of different number of days, and their result showed that using those of seven days to construct the model resulted in best multipath mitigation. Dong et al. [19] conducted a similar experiment for finding the optimal number of days for model construction, and their result is consistent with that of Ragheb et al. [18].

The real repeat time of a GPS satellite is not exactly equal to a sidereal day [15]. Using a nominal sidereal day as the multipath repeat time to implement sidereal filtering will not achieve its full potential of multipath mitigation. Hence, for improving sidereal filtering, methods of acquiring accurate multipath repeat time have been extensively researched (e.g., [16,18,20,21,22,23,24]). With those methods, the repeat time of each satellite can be estimated. Most previous studies adopted mean repeat time of all satellites to implement sidereal filtering, which is referred to as modified sidereal filtering (MSF). However, the repeat time values of GPS satellites are satellite-dependent, and using the mean repeat time to represent those of all satellites will inevitably cause accuracy loss. The optimal way to implement sidereal filtering is to mitigate the multipath effects with the repeat time of each satellite separately, which is referred to as advanced sidereal filtering (ASF) [19]. ASF is an observation-domain sidereal filtering, which adopts the multipath correction model that is constructed from observable residuals relating to individual satellites.

Zhong et al. [25] and Ye et al. [26] constructed ‘single-differenced’ (between antennas) observable residuals (each relates to a single satellite) from double-differenced observable residuals by introducing an extra constraint, and then constructed multipath models for implementing ASF. Nevertheless, the ‘single-differenced’ observable residuals they derived were based on the assumption of ‘zero mean’ (weighted mean of all single-differenced observable residuals at each epoch equals zero) [27] and hence were heavily assumption-dependent [28]. Atkins et al. [29] and Geng et al. [30] implemented ASF in un-differenced GNSS precise point positioning (PPP); nevertheless, the PPP based un-differenced observable residuals possibly includes other errors, such as un-modeled receiver clock error and troposphere delay. As a result, using multipath correction model constructed from those ‘impure’ residuals deteriorates the performance of ASF.

An emerging dual-antenna clock synchronized GNSS receiver [28] provides a unique opportunity to implement the ASF approach. The single difference between the two antennas of this receiver is able to cancel out both receiver and satellite clock errors. For a short baseline, the other error sources except multipath, such as troposphere and ionosphere delays, are also greatly eliminated. Hence, this type of receiver has wide applications, including attitude determination, ground-based carrier phase wind-up calibration, and phase center variation correction [28,31]. Using such single-differenced observable residuals, we are able to isolate the multipath errors much thoroughly, and to avoid ad-hoc ‘zero-mean’ assumption [25,26] and un-modeled errors from un-differenced observable residuals [29,30]. Thus the assessment of ASF is more accurate and objective. On the other hand, by applying ASF to improve the baseline solutions, we are able to acquire the knowledge of how high a precision the new receiver can achieve, and of the capability of the new receiver for further applications, such as structure dynamic displacement detection [32,33]. This study focuses on GPS multipath mitigation for a short baseline based on a dual-antenna clock synchronized GNSS receiver. Section 2 presents data collection and methods. Section 3 shows the analysis of GPS orbit repeat time, assessment of ASF in multipath mitigation, and comparison of ASF with single-day model and with seven-day day model. Section 4 discusses some results obtained from real collected data, including optimal cutoff frequency and ASF correction model. The last section summarizes the entire study.

2. Data and Methods

2.1. Data Collection

We deployed the two antennas of a clock synchronized GNSS receiver on the roof of a building located in the campus of East China Normal University (Figure 1). One antenna was mounted on a concrete pillar about one meter high. The other antenna was set on the top of an air-conditioner compressor about 1.8 m high. The length of the baseline between the two antennas is about 12.5 m. Data were collected continuously at the sample rate of 1 s from day of year (DOY) 335 to 354, 2014 (1 to 20 December 2014).

2.2. Methods

The basic carrier phase observation equation is

$$\lambda {\phi }_i^s(t)={\rho }_i^s(t)+c(d{t}_r-d{t}^s)+\lambda (N_i^s+U_r+U^s)-I+T+P_i^s+M_i^s+{\epsilon }_i$$

(1)

where $s$, $r$, and $i$ are the satellite index, receiver index, and antenna index, respectively. $c$ is the speed of light. $\lambda$ is the wavelength of carrier phase. ${\phi }_i^s(t)$ is the carrier phase observable. ${\rho }_i^s(t)$ is the geometric distance between satellite and receiving antenna. $N_i^s$ is the integer ambiguity. $d{t}_r$ and $d{t}^s$ are the receiver and satellite clock offsets. $I$ and $T$ are the ionosphere and troposphere delay. $P_i^s$ is the antenna phase center variation. $M_i^s$ is the multipath error. $U_r$ and $U^s$ are the un-calibrated phase delays (UPD) in receiver and satellite, respectively [34]. ${\epsilon }_i$ is the observation noise.

Single difference between the two antennas cancels out $d{t}^s$ and $U^s$, and it greatly eliminates $I$ and $T$ because the baseline is extremely short and the height difference between the two antennas is small (about 0.8 m). $d{t}_r$ and $U_r$ are also eliminated since the two antennas are connected to the same receiver (also the same clock). The types of the two antennas are the same, hence the effect of $P_i^s$ can be mitigated by the single difference with setting the two antennas to the same orientation. The single difference equation then can be written as

$$\begin{array}{ll}\Delta {\phi }_{}^s(t)& ={\phi }_1^s(t)-{\phi }_2^s(t)\\ & =\frac{1}{\lambda }({\rho }_1^s(t)-{\rho }_2^s(t))+(N_1^s-N_2^s)+\frac{1}{\lambda }(M_1^s-M_2^s)+\frac{1}{\lambda }({\epsilon }_1-{\epsilon }_2)\\ & =\frac{1}{\lambda }\Delta {\rho }_{}^s(t)+\Delta N_{}^s+\frac{1}{\lambda }\Delta M_{}^s+\epsilon \end{array}$$

(2)

In practice, we notice that the UPD in receiver ($U_r$) cannot be completely eliminated by the single difference; a satellite-independent bias exists in single-differenced observables, which may be caused by hardware bias or cable length [19]. This bias or un-eliminated part of $U_r$ is nearly constant every epoch. We name the bias as constant bias (CB) and use $\Delta b$ to denote it. Equation (2) is rewritten as

$$\Delta {\phi }_{}^s(t)=\frac{1}{\lambda }\Delta {\rho }_{}^s(t)+\Delta N_{}^s+\Delta b+\frac{1}{\lambda }\Delta M_{}^s+\epsilon$$

(3)

In our experiment, we adopted L1 carrier phase observables to form single-differenced observation equations and estimated the baseline components by two steps. In the first step, the a priori values of the baseline components with centimeter-level accuracy were substituted into Equation (3) to solve the sum (float) of ambiguity ($\Delta N_{}^s$) and CB ($\Delta b$) for each satellite at an epoch. Because the integer part of CB is not separable from the integer ambiguity, we solved the sum of integer ambiguity and integer part of CB. For an epoch, we choose the satellite with smallest post-fit residual to round the sum of ambiguity and CB to its nearest integer. Then, with substituting this solved ‘ambiguity’ and the a priori baseline components into Equation (3), we were able to estimate the fractional part of CB and the sum of integer ambiguity and integer part of CB for other satellites. The estimated sum of integer ambiguity and integer part of CB was rounded to its nearest integer for each satellite. In the second step, with the estimated integer ‘ambiguity’, the baseline components, along with the fractional part of CB ($\Delta b$), were re-estimated with least square algorithm for the epoch. In the following sections, CB ($\Delta b$) refers to its fractional part. To avoid the multipath level being affected by common parameters, the data were processed epoch by epoch separately.

After baseline estimation, the post-fit single-differenced observable residuals (e.g., Figure 2, blue line) mainly contain multipath errors and observation noise. The denoised residuals can be used to construct a multipath model to correct the data of the other day. Nonetheless, because multipath errors (original in GPS observables) are distributed into both the estimated parameters (baseline components and CB) and residuals after least squares adjustment, the post-fit residuals only include part of the multipath errors. Hence, the multipath correction model generated from these residuals has limited efficiency in multipath mitigation. To construct a more complete multipath correction model, we recalculated the single-differenced residuals by fixing the four estimated parameters (CB and three baseline components) to their daily average values. The recalculated residuals contain almost all multipath errors, so that they are generally larger than the original post-fit residuals (Figure 2). The differences between the two kind of observable residuals are especially distinct at both ends of the time series, when the satellite runs in low elevation angles (Figure 2).

For eliminating the multipath of the applied day, we implemented ASF in five steps:

• Calculating the repeat time of each satellite;
• Estimating the parameters (CB and three baseline components) with ambiguity resolution for the previous day;
• Recalculating the residuals with the parameters being fixed to their daily average values and low-pass filtering the recalculated residual time series;
• Shifting the recalculated residual time series for each satellite with its own repeat time to construct the multipath correction model;
• Correcting the multipath errors in single-differenced observables with the model and estimating the baseline components and CB for the applied day.

For comparison, we also implemented MSF in our experiment. The only difference between implementing MSF and ASF is step 4. For MSF, the recalculated residual time series for all satellites are shifted with the same repeat time (mean repeat time) to construct the multipath correction model. To evaluate the effectiveness of ASF and MSF in multipath mitigation, we utilized the variance reduction rate as an index. We calculated the variance reduction rate for each coordinate component (north, east, and up) and also 3D variance reduction rate [18], which integrate the variance reduction rates of the three components into one index. The 3D variance is given as

$${\delta }_{3D}^2=({\delta }_N^2+{\delta }_E^2+{\delta }_U^2)$$

(4)

where ${\delta }_N^2$, ${\delta }_E^2$, and ${\delta }_U^2$ are the variances of the time series of north, east, and up baseline component. The 3D variance reduction rate is given as

$$R=\left(1-\frac{{\delta }_{3D\_corre}^2}{{\delta }_{3D\_uncorre}^2}\right)\times 100\%$$

(5)

where ${\delta }_{3D\_corre}^2$ and ${\delta }_{3D\_uncorre}^2$ are the 3D variances of baseline solutions estimated from multipath corrected and uncorrected observables, respectively.

3. Results

The structure of this ‘Results’ section is shown in Figure 3. Firstly, two years’ repeat time values for each GPS satellite were calculated, and different types of time series of orbit repeat time were presented. The repeat time values of some satellites may distinctly deviate from the values of other satellites (referred to as ‘abnormal’ repeat time in Figure 3). The proportion of the days when these ‘abnormal’ repeat times existed were calculated. Secondly, for achieving better multipath mitigation, the optimal cutoff frequency of the low-pass filter was determined in terms of maximal variance reduction rate. The impacts of including a satellite with ‘abnormal’ repeat time in data processing on ASF and MSF were analyzed. To illustrate the effectiveness of ASF, maximal correlation coefficients between the residual time series generated from ASF-corrected observables and the residual time series of its former day (multipath correction values) were calculated, and were compared with those between the without-ASF-corrected counterparts and the residual time series of the former day. The improvements in standard deviation (STD) and variance after implementing ASF and MSF were displayed. For comparing the variance reduction rates of ASF and MSF, t-test hypothesis testing was used to determine the significance of the statistical difference between them. Lastly, the results of ASF with the single-day model and seven-day model were compared and analyzed.

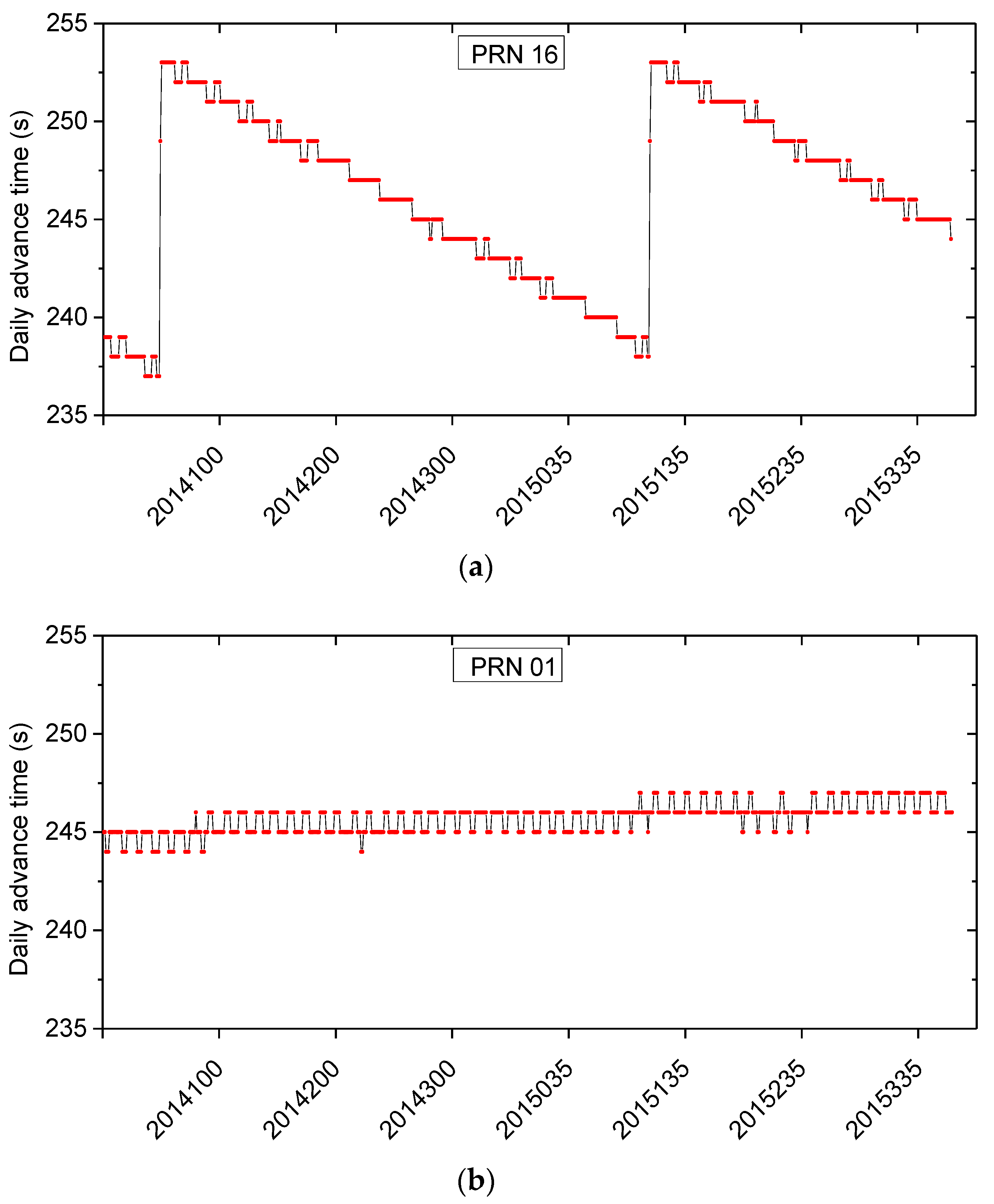
3.1. Orbit Repeat Time

The first step to implement ASF is to obtain the repeat time of each satellite. To understand the characteristic of its variation, we calculated the repeat time of each satellite from 2014 to 2015. The ‘aspect repeat time’ method (ARTM) [21,22,23], which calculates the repetition of satellite ground tracking, was adopted to estimate the repeat time. The repeat time estimates of all satellites are mainly distributed in the range of 86,145 s to 86,165 s (Figure 4), which we refer to as the normal range. In terms of daily advance time (86,400 s minus the repeat time), the normal range is [235, 255] s.

Time series of the satellites’ repeat times from 2014 to 2015 mainly present three types (Figure 5). Time series of the first type have secular drifts and small amplitude oscillations (e.g., Figure 5a), which are caused by resonance effects with the tesseral harmonics in the Earth’s gravity field and by lunar perturbations, respectively [20]. Abrupt steps exist in the time series of this type caused by orbit maintenance maneuvering [21]. The first type is the most common one, to which the time series of 23 satellites belonged. The time series of the second type (e.g., Figure 5b), to which the time series of the repeat time of satellite PRN 01, 27, and 28 belonged, have slower long-term drifts than those of the first type. The time series of the third type show obvious jumps (e.g., Figure 5c), which are caused by significant satellite orbit maneuvers [21]. During 2014 and 2015, six satellites (PRN 04, 08, 13, 19, 20, and 22) encountered such maneuvers (Figure 4).

The repeat time of GPS satellites affected by significant orbit maneuvers may deviate from the normal range by more than 100 s (Figure 4 and Figure 5c). During 2014 and 2015, there were 210 days when the repeat time values of all available satellites were within the normal range ([235, 255] s), which only accounted for 28.81% of the total 730 days (Figure 6). The proportions of the days with one, two, and three satellites whose repeat time were out of the normal range were 44.17%, 14.95%, and 12.07%, respectively (Figure 6). In other words, the proportion was as high as 71.19% for the days with at least one satellite’s repeat time outside the normal range, indicating that it is very common to encounter such a satellite in daily GPS data processing. For traditional sidereal filtering (using nominal sidereal day), the satellites with repeat time outside the normal range have to be excluded from data processing. In ASF, however, the multipath errors for each satellite are corrected separately, which provides the possibility to include satellites with ‘abnormal’ repeat time in data processing. We will investigate the use of such a satellite in ASF in section “Impact of the satellite with ‘abnormal’ repeat time”.

3.2. ASF Multipath Mitigation

3.2.1. Cutoff Frequency

Recalculated single-differenced observable residuals contain multipath errors and observation noise. To construct a ‘clear’ multipath correction model, residual time series should be low-pass filtered to remove the noise. We adopted Chebyshev type II filter to reduce the high-frequency observation noise. The cutoff frequency for implementing Chebyshev type II filter is a key factor to remove the observation noise, which determines what frequency band of components will be filtered from the residual time series. We tested a few representative cutoff frequencies (0.2, 0.08, 0.04, 0.03, 0.02, and 0.01 Hz) to find out the optimal one. From DOY 335 to 353, 2014, the residual time series of each day were low-pass filtered with the representative cutoff frequencies separately, and then were adopted to construct ASF and MSF correction models for each subsequent day. The GPS observables corrected by multipath models (both ASF and MSF models), constructed from the residual time series filtered by different cutoff frequencies, were used to estimate the baseline components, respectively, for each day of DOY 336 to 354, 2014. Meanwhile, the original (uncorrected) observables were used to estimate the baseline solutions for comparison. For each cutoff frequency, the averages of daily 3D variance reduction rates (relative to variance of solutions estimated from uncorrected observables) for ASF and MSF correction (from DOY 336 to 354) are shown in Figure 7. When the cutoff frequency is 0.02 Hz, the 3D variance reduction rates for both ASF and MSF correction are maximal.

In our data, the observation noise mainly covers the frequency range of 0.02 to 0.5 Hz (e.g., Figure 8). For brevity, Figure 8 only shows the power spectral density (PSD) of the up (height) baseline component solutions of DOY 342, 2014. The solutions of north and east component, and the solutions of other days yield similar results and lead to the same conclusions. The ASF or MSF multipath correction models constructed from the unfiltered (without low-pass filtering) residuals incorporate all the observation noise. Using these models to correct the GPS observables increases their noise level, as Figure 8a shows that the noise level of baseline solutions estimated from the ASF or MSF corrected observables is higher than that of solutions estimated from the uncorrected observables. Adopting 0.02 Hz as the cutoff frequency, the low-pass filter removes almost all observation noise from the residuals. The multipath correction models constructed from these residuals are nearly free of the contamination of observation noise, thus, after ASF or MSF correction, the noise level of the solutions does not increase (Figure 8b). In the range of 0.02 to 0.5 Hz, with a lower cutoff frequency, the low-pass filter removes more observation noise and also more multipath errors from the residual time series. The removal of more observation noise from the residuals improves the residual-constructed multipath correction models, whereas the removal of more multipath components from the residuals lowers the completeness of the residual-constructed multipath models. As the cutoff frequency decreases from 0.5 to 0.02 Hz, the gain in variance reduction from the removal of more observation noise surpasses the loss from the removal of more multipath, as a result, the performances of ASF and MSF in variance reduction are getting better (Figure 7). However, the gain is exceeded by the loss as cutoff frequency decreases from 0.02 to 0.01 Hz, thus, the 3D variance reduction rate for the cutoff frequency of 0.01 Hz is smaller than that for the cutoff frequency of 0.02 Hz (Figure 7).

In general, ASF outperforms MSF in both the low-frequency band ([0.001, 0.02] Hz) and high-frequency band ([0.02, 0.5] Hz) (Figure 8a). As the cutoff frequency reduces from 0.5 to 0.02 Hz, the correction values in the models for mitigating the high-frequency multipath become less, and thus the advantages of ASF over MSF, in high-frequency multipath mitigation, become less as well. Consequently, the differences in 3D variance reduction rate between ASF and MSF correction become smaller as the cutoff frequency decreases (Figure 7). Our data show that the frequency bands of multipath and observation noise overlap, and the optimal cutoff frequency is 0.02 Hz in terms of maximal 3D variance reduction rate. We use this cutoff frequency for the following sections.

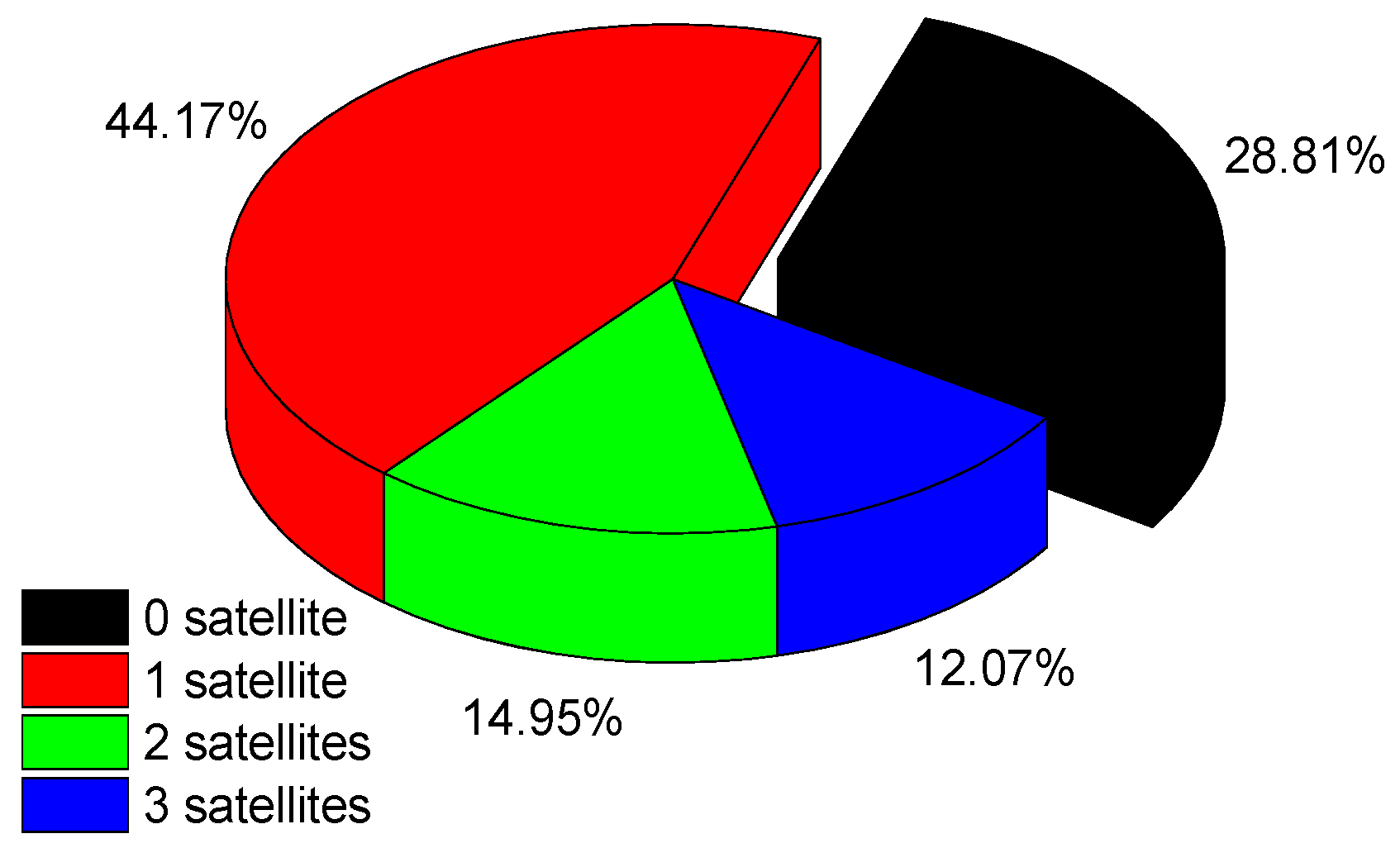
3.2.2. Impact of the Satellite with ‘Abnormal’ Repeat Time

In the section ‘cutoff frequency’, Figure 7 shows that the difference in 3D variance reduction rate between ASF and MSF correction is notable for the cutoff frequency of 0.02 Hz. We adopted all the satellites in data processing in that section. During DOY 335 to 354, 2014, the repeat time values of GPS satellite PRN 13 were about 100 to 110 s (Figure 4 and Figure 5c), which deviated from the normal range ([235, 255] s). Because the MSF approach adopts the mean repeat time of all satellites, including a satellite with repeat time outside the normal range in data processing reduces its effectiveness of multipath mitigation. Previous studies removed these satellites from MSF implementation to avoid their adverse impacts (e.g., [20,23]). Likewise, we excluded the satellite PRN 13 and reprocessed the data. The results show that after PRN 13 is excluded, the 3D variance reduction rate of MSF correction for each day increases evidently (Figure 9a black and blue marks), whereas that of ASF correction for each day does not change significantly (Figure 9b). When the PRN 13 is excluded, though the 3D variance reduction rates of MSF correction are very close to those of ASF correction, the latter ones are slight larger than the former ones for each day (Figure 9a red and blue marks). Notice that, since DOY 352, 2014, though the PRN 13 has been removed from data processing, the differences in 3D variance reduction rate between ASF and MSF correction are evidently larger than before (Figure 9a red and blue marks). The repeat time values of PRN 20 were about 120 to 130 s from DOY 352, 2014 to DOY 175, 2015. Including PRN 20 in data processing degrades the effectiveness of MSF correction, while it has no significant impacts on ASF correction. Consequently, the differences of 3D variance reduction rate between ASF and MSF correction after DOY 352 are larger than those before DOY 352.

3.2.3. Multipath Reduction

We compared the baseline components and the CB estimated from original (uncorrected) GPS observables with those estimated from ASF corrected observables for each day from DOY 336 to 354, 2014. The results of all the 19 days are similar. For brevity, we only show the solutions of DOY 342, 2014 in Figure 10. Due to the presence of multipath effects, the time series of solutions estimated from the original (uncorrected) observables fluctuate (Figure 10a). After ASF correction, the multipath error in GPS observables are effectively mitigated, thus, the time series of solutions estimated from these corrected observables are much more stable (Figure 10b).

ASF uses recalculated observable residuals (low-pass filtered) of a satellite to correct the observables of the same satellite for the subsequent day. The basis for this application is high correlation between residual time series (for the same satellites) of two consecutive days. We fixed one time series and shifted the other one epoch by epoch, and then calculated each correlation coefficient and searched the maximal value, named maximal correlation coefficient.

Table 1. The maximal correlation coefficients between residual time series from each two consecutive days from DOY 335 to 354 for each satellite. The residuals from the former day of each two consecutive days were derived from uncorrected observables, and the residuals from the latter day were derived from observables without ASF corrections (WSF) and with ASF corrections, respectively. Values in ‘WSF’ (‘ASF’) columns are the maximal correlation coefficients between latter day time series of residuals from uncorrected (ASF-corrected) observables and former day residual time series. Due to space limitation, data of part of satellites and on part of days are shown in the table. The full table is provided in Appendix A Table A1.

PRN	DOY 341		DOY 342		DOY 343
	WSF	ASF	WSF	ASF	WSF	ASF
1	0.945	0.069	0.960	0.008	0.980	0.022
7	0.961	0.058	0.962	0.008	0.968	0.024
10	0.940	0.056	0.952	0.012	0.941	0.022
11	0.970	0.040	0.981	0.007	0.984	0.018
12	0.979	0.009	0.979	0.018	0.979	0.032
20	0.956	0.008	0.966	0.035	0.985	0.048
21	0.982	0.015	0.982	0.008	0.967	0.011
30	0.959	0.037	0.971	0.015	0.955	0.036
31	0.985	0.020	0.987	0.021	0.982	0.013
32	0.941	0.030	0.976	0.014	0.971	0.009

shows high correlation between residual time series of two consecutive days (‘WSF’ columns). Without ASF correction, the maximal correlation coefficients are in the range of 0.623 to 0.989 (refer to

Table A1. The maximal correlation coefficients between residual time series from each two consecutive days from DOY 335 to 354 for each satellite. The residuals from the former day of each two consecutive days were derived from uncorrected observables, and the residuals from the latter day were derived from observables without ASF corrections (WSF) and with ASF corrections respectively. Values in ‘WSF’ (‘ASF’) columns are the maximal correlation coefficients between latter day time series of residuals from uncorrected (ASF-corrected) observables and former day residual time series. Symbol ‘/’ represents that the data was not available for the corresponding satellite on that day, except for PRN 13, which we excluded from the data processing. Value ‘0.000’ in the table means that the maximal correlation coefficient is very small (smaller than 5 × 10⁻⁴).

PRN	DOY 336		DOY 337		DOY 338		DOY 339		DOY 340
	WSF	ASF	WSF	ASF	WSF	ASF	WSF	ASF	WSF	ASF
1	0.9	0.014	0.925	0.065	0.943	0.04	0.962	0.063	0.961	0
2	0.947	0.012	0.969	0.016	0.971	0.064	0.862	0.012	0.877	0.059
3	/	/	/	/	/	/	/	/	/	/
4	0.984	0	0.953	0.055	0.96	0.135	0.985	0.059	0.979	0.034
5	0.909	0.002	0.914	0.009	0.965	0.178	0.923	0.039	0.937	0
6	0.941	0.042	0.948	0	0.964	0.051	0.957	0.069	0.963	0.043
7	0.976	0.023	0.944	0	0.933	0.113	0.964	0.049	0.958	0.007
8	/	/	/	/	/	/	/	/	/	/
9	0.969	0.01	0.962	0.038	0.956	0.029	0.975	0.071	0.984	0.043
10	0.912	0.011	0.914	0	0.935	0.033	0.949	0.046	0.962	0.024
11	0.968	0	0.947	0	0.957	0.12	0.984	0.017	0.96	0
12	0.973	0	0.962	0	0.966	0.09	0.971	0.039	0.98	0
13	/	/	/	/	/	/	/	/	/	/
14	0.98	0	0.948	0	0.95	0.058	0.981	0	0.983	0
15	0.912	0	0.921	0.033	0.976	0	0.876	0.005	0.889	0
16	0.973	0.029	0.908	0.004	0.916	0.086	0.982	0.041	0.979	0.01
17	0.959	0	0.939	0.041	0.957	0	0.979	0	0.978	0.019
18	0.927	0.02	0.905	0	0.934	0.09	0.975	0	0.98	0.019
19	0.964	0.041	0.92	0.071	0.927	0.05	0.974	0	0.955	0.019
20	0.954	0.045	0.93	0.131	0.931	0	0.977	0.028	0.966	0.038
21	0.848	0.056	0.84	0.001	0.951	0.036	0.953	0.04	0.952	0.022
22	0.968	0	0.774	0	0.754	0.1	0.983	0.011	0.985	0.027
23	0.949	0.027	0.933	0.059	0.915	0	0.962	0.032	0.977	0.047
24	0.937	0.001	0.94	0.042	0.968	0.018	0.657	0.003	0.623	0.055
25	0.975	0.06	0.932	0.137	0.939	0	0.972	0.007	0.975	0.042
26	/	/	/	/	/	/	0.907	0.003	/	/
27	0.976	0.009	0.915	0	0.913	0.133	0.984	0.043	0.978	0.037
28	0.925	0.008	0.889	0.009	0.922	0.003	0.97	0.065	0.955	0.061
29	0.934	0	0.83	0.073	0.866	0	0.909	0.039	0.905	0.005
30	0.975	0.002	0.959	0	0.96	0.032	0.89	0.031	0.89	0.04
31	0.984	0.019	0.939	0.083	0.949	0	0.982	0.009	0.986	0.032
PRN	DOY 341		DOY 342		DOY 343		DOY 344		DOY 345
	WSF	ASF	WSF	ASF	WSF	ASF	WSF	ASF	WSF	ASF
1	0.945	0.069	0.96	0.008	0.98	0.022	0.918	0.065	0.914	0.088
2	0.976	0	0.977	0.032	0.961	0.009	0.983	0.008	0.937	0.059
3	/	/	/	/	/	/	/	/	/	/
4	0.981	0	0.986	0.01	0.984	0.031	0.914	0	0.925	0.18
5	0.965	0.111	0.972	0.013	0.958	0.009	0.975	0.018	0.943	0.008
6	0.944	0.027	0.954	0.022	0.958	0.005	0.959	0.063	0.942	0.052
7	0.961	0.058	0.962	0.008	0.968	0.024	0.854	0	0.863	0.066
8	/	/	/	/	/	/	/	/	/	/
9	0.982	0.094	0.978	0.013	0.974	0.032	0.919	0	0.891	0.021
10	0.94	0.056	0.952	0.012	0.941	0.022	0.942	0.016	0.924	0.034
11	0.97	0.04	0.981	0.007	0.984	0.018	0.85	0	0.849	0.118
12	0.979	0.009	0.979	0.018	0.979	0.032	0.976	0	0.956	0.099
13	/	/	/	/	/	/	/	/	/	/
14	0.984	0.02	0.982	0.013	0.983	0.016	0.923	0.013	0.925	0.071
15	0.981	0	0.975	0.019	0.97	0.041	0.98	0.003	/	/
16	0.974	0.016	0.983	0.007	0.977	0.051	0.868	0	0.889	0.094
17	0.959	0	0.959	0.031	0.978	0.013	0.957	0.046	0.97	0
18	0.984	0.015	0.978	0.017	0.979	0.021	0.968	0	0.936	0.057
19	0.954	0.02	0.975	0	0.977	0.029	0.871	0.086	0.882	0.018
20	0.956	0.008	0.966	0.035	0.985	0.048	0.911	0.076	0.913	0
21	0.982	0.015	0.982	0.008	0.967	0.011	0.867	0.088	0.883	0
22	0.986	0.014	0.985	0.012	0.982	0.011	0.792	0	0.781	0.088
23	0.97	0.03	0.963	0.018	0.98	0.054	0.87	0.014	0.849	0
24	0.987	0.02	0.983	0.02	0.978	0.02	0.975	0.007	0.967	0
25	0.973	0.005	0.97	0.009	0.974	0.032	0.95	0.145	0.949	0
26	/	/	0.964	0.004	0.963	0.031	0.979	0.034	0.941	0.064
27	0.981	0.01	0.985	0.007	0.985	0.027	0.812	0	0.821	0.153
28	0.915	0.013	0.923	0.013	0.976	0.039	0.906	0.021	0.921	0.092
29	0.979	0.026	0.973	0.024	0.962	0.002	0.875	0.149	0.854	0
30	0.959	0.037	0.971	0.015	0.955	0.036	0.937	0	0.93	0.099
31	0.985	0.02	0.987	0.021	0.982	0.013	0.868	0.137	0.884	0
32	0.941	0.03	0.976	0.014	0.971	0.009	0.729	0	0.775	0
PRN	DOY 346		DOY 347		DOY 348		DOY 349		DOY 350
	WSF	ASF	WSF	ASF	WSF	ASF	WSF	ASF	WSF	ASF
1	0.964	0.032	0.981	0.06	0.974	0.023	0.974	0.032	0.976	0.062
2	0.953	0.053	0.973	0.055	0.969	0	0.896	0.046	0.912	0.013
3	/	/	0.79	0.175	0.962	0.008	0.953	0.015	0.885	0.024
4	0.982	0.034	0.985	0.038	0.982	0	0.976	0.034	0.972	0.044
5	0.951	0.044	0.972	0	0.964	0.092	0.895	0.032	0.895	0.024
6	0.935	0.022	0.973	0.049	0.961	0.036	0.893	0.018	0.808	0.075
7	0.958	0.068	0.951	0.088	0.971	0.047	0.899	0.042	0.907	0.06
8	/	/	/	/	/	/	/	/	/	/
9	0.96	0.017	0.974	0.035	0.978	0.07	0.947	0.035	0.872	0.002
10	0.934	0.036	0.95	0.024	0.95	0.063	0.824	0.002	0.827	0.024
11	0.978	0.059	0.983	0	0.976	0	0.97	0.033	0.971	0.054
12	0.963	0.061	0.978	0.012	0.972	0.056	0.946	0.004	0.87	0.023
13	/	/	/	/	/	/	/	/	/	/
14	0.97	0.027	0.976	0.022	0.982	0.03	0.967	0.005	0.98	0
15	/	/	0.971	0.016	0.976	0	0.948	0.049	0.88	0.04
16	0.978	0.016	0.981	0.043	0.98	0	0.979	0.033	0.975	0.029
17	0.977	0.058	0.98	0.076	0.961	0	0.938	0	0.761	0.026
18	0.97	0	0.967	0.02	0.974	0	0.926	0.004	0.951	0.029
19	0.965	0.006	0.972	0	0.963	0.04	0.955	0.007	0.962	0.007
20	0.974	0	0.981	0	0.967	0.028	0.965	0.006	/	/
21	0.962	0.045	0.978	0.004	0.983	0.015	0.93	0.009	0.953	0.006
22	0.971	0.031	0.977	0.016	0.981	0	0.967	0.011	0.97	0.071
23	0.945	0.023	0.966	0.031	0.96	0.022	0.944	0	0.839	0.032
24	0.974	0.077	0.976	0.019	0.977	0.049	0.936	0.005	0.936	0.026
25	0.973	0.007	0.974	0.006	0.959	0.034	0.936	0	0.919	0.014
26	/	/	/	/	/	/	0.955	0.032	0.931	0.005
27	0.981	0.061	0.979	0.01	0.983	0.041	0.983	0.002	0.98	0.036
28	0.955	0	0.979	0.045	0.926	0.047	0.916	0.024	0.729	0.03
29	0.962	0.006	0.957	0	0.979	0.043	0.874	0	0.926	0.029
30	0.957	0.051	0.949	0.014	0.978	0.03	0.892	0.006	0.923	0.047
31	0.976	0.051	0.983	0.051	0.983	0.035	0.973	0	0.982	0.083
32	0.968	0.053	0.973	0.001	0.957	0.027	0.964	0.003	0.962	0.064
PRN	DOY 351		DOY 352		DOY 353		DOY 354
	WSF	ASF	WSF	ASF	WSF	ASF	WSF	ASF
1	0.984	0	0.978	0	0.984	0.02	0.986	0
2	0.938	0.051	0.952	0	0.95	0.019	0.961	0.011
3	0.923	0	0.96	0.108	0.947	0.098	0.976	0.108
4	0.987	0	0.982	0	0.987	0.03	0.989	0.019
5	0.941	0.003	0.961	0.014	0.949	0.026	0.956	0.019
6	0.842	0.044	0.943	0	0.928	0	0.96	0.07
7	0.904	0.095	0.974	0.028	/	/	/	/
8	/	/	/	/	/	/	/	/
9	0.894	0.013	0.967	0.029	0.95	0.014	0.976	0.032
10	0.881	0.005	0.935	0.032	0.919	0	0.94	0.021
11	0.985	0.021	0.977	0	0.986	0.027	0.986	0.012
12	0.907	0	0.976	0.035	0.972	0.008	0.979	0.027
13	/	/	/	/	/	/	/	/
14	0.977	0.011	0.981	0.081	0.977	0.039	0.981	0.028
15	0.917	0.003	0.98	0	0.982	0.021	0.98	0.024
16	0.984	0.003	0.978	0.003	0.964	0.015	0.983	0.081
17	0.821	0.015	0.949	0	0.923	0.046	0.968	0
18	0.932	0.008	0.979	0.027	0.98	0	0.979	0.013
19	0.978	0.036	0.972	0.01	0.971	0.024	0.979	0.017
20	/	/	0.727	0	0.832	0.013	0.897	0.015
21	0.949	0.03	0.982	0.018	0.979	0	0.98	0.023
22	0.977	0.056	0.985	0.01	0.983	0	0.981	0.033
23	0.865	0.075	0.953	0.07	0.923	0.018	0.967	0.052
24	0.943	0.01	0.974	0.034	0.981	0	0.978	0.02
25	0.934	0.044	0.98	0.019	0.976	0.005	0.974	0.004
26	0.949	0.021	0.977	0.014	0.969	0.01	0.975	0.043
27	0.985	0.006	0.983	0.02	0.98	0.024	0.988	0.07
28	0.795	0.085	0.926	0.032	0.906	0	0.965	0.024
29	0.901	0.02	0.978	0.025	0.978	0.015	0.975	0.024
30	0.91	0.018	0.982	0.005	0.975	0.004	0.985	0.012
31	0.987	0.035	0.985	0.018	0.983	0	0.988	0.003
32	0.977	0.038	0.968	0.032	0.953	0	0.977	0.039

); most values (87.5%) are larger than 0.9. After ASF correction, the maximal correlation coefficients decrease prominently (Table 1 ‘ASF’ columns); the range is reduced to (0, 0.18) (refer to Table A1). Significant reductions of maximal correlation coefficients verify the effectiveness of ASF in multipath mitigation.

For the all 19 days, ASF corrections improve the average STD of the north component from 3.8 to 2.1 mm, the east component from 3.2 to 1.7 mm, and the up component from 7.6 to 4.3 mm (

Table 2. The variances of baseline components estimated from the original observables (without any sidereal filtering), MSF-corrected observables, and ASF-corrected observables, respectively, for each day from DOY 336 to 354. Numbers in parentheses are variance reduction rates (relative to variances from ‘Without SF’); the unit ‘%’ is omitted for saving table space. Due to space limitation, data of part days are shown in the table. The full table is provided in Appendix A Table A2. The values in the last row (row ‘Ave.’) in this table are the same as those in Table A2, which are the averages of corresponding columns (averages of the values of all 19 days).

DOY	Variances of Time Series of Baseline Components (mm2)
	Without SF			MSF			ASF
	N	E	U	N	E	U	N	E	U
336	14.81	10.50	60.37	4.52 (69.48)	3.00 (71.43)	19.73 (67.32)	4.51 (69.55)	2.99 (71.52)	19.57 (67.58)
341	13.58	10.00	56.40	4.78 (64.80)	2.84 (71.60)	18.16 (67.80)	4.77 (64.87)	2.82 (71.80)	18.06 (67.98)
342	13.52	10.18	56.66	3.80 (71.89)	2.67 (73.77)	16.23 (71.36)	3.78 (72.04)	2.66 (73.87)	16.11 (71.57)
353	14.79	10.05	53.52	4.08 (72.41)	2.77 (72.44)	18.35 (65.71)	3.88 (73.77)	2.66 (73.53)	16.91 (68.40)
354	13.61	9.72	52.16	3.98 (70.76)	2.73 (71.91)	17.94 (65.61)	3.84 (71.79)	2.62 (73.05)	16.72 (67.94)
Ave.	14.08	10.35	57.09	4.55 (67.68)	3.02 (70.82)	18.99 (66.74)	4.51 (67.97)	2.99 (71.11)	18.65 (77.12)

row ‘Ave.’ shows the corresponding variances). With PRN 13 excluded, MSF corrections achieve the similar improvement of STD or variance; the variances of baseline components estimated from the MSF-corrected observables are generally several hundredth of millimeter lager than those estimated from ASF-corrected observables (Table 2, also refer to

Table A2. The variances of baseline components estimated from the original observables (without any sidereal filtering), MSF-corrected observables, and ASF-corrected observables, respectively, for each day from DOY 336 to 354. Numbers in parentheses are variance reduction rates (relative to variances from ‘Without SF’); the unit ‘%’ is omitted for saving table space. The values in the last row (row ‘Ave.’) are the averages of corresponding columns.

DOY	Variances of Time Series of Baseline Components (mm2)
	Without SF			MSF			ASF
	N	E	U	N	E	U	N	E	U
336	14.81	10.50	60.37	4.52 (69.48)	3.00 (71.43)	19.73 (67.32)	4.51 (69.55)	2.99 (71.52)	19.57 (67.58)
337	13.96	10.50	60.08	5.28 (62.18)	3.46 (67.05)	21.03 (65.00)	5.20 (62.75)	3.40 (67.62)	20.53 (65.83)
338	14.65	10.14	56.09	5.56 (62.05)	3.45 (65.98)	20.12 (64.13)	5.53 (62.25)	3.44 (66.07)	20.03 (64.29)
339	14.36	10.48	57.79	5.36 (62.67)	3.10 (70.42)	19.88 (65.60)	5.35 (62.74)	3.08 (70.61)	19.79 (65.76)
340	14.59	10.23	60.26	4.41 (69.77)	2.84 (72.24)	18.50 (69.30)	4.35 (70.19)	2.79 (72.73)	18.10 (69.96)
341	13.58	10.00	56.40	4.78 (64.80)	2.84 (71.60)	18.16 (67.80)	4.77 (64.87)	2.82 (71.80)	18.06 (67.98)
342	13.52	10.18	56.66	3.80 (71.89)	2.67 (73.77)	16.23 (71.36)	3.78 (72.04)	2.66 (73.87)	16.11 (71.57)
343	13.73	10.40	57.06	3.87 (71.81)	2.69 (74.13)	16.18 (71.64)	3.85 (71.96)	2.68 (74.23)	16.11 (71.77)
344	13.05	10.27	53.92	5.32 (59.23)	3.69 (64.07)	21.48 (60.16)	5.30 (59.39)	3.67 (64.26)	21.33 (60.44)
345	16.10	12.51	66.65	6.23 (61.30)	4.20 (66.43)	26.08 (60.87)	6.21 (61.43)	4.19 (66.51)	25.94 (61.08)
346	14.68	10.61	60.06	4.77 (67.51)	3.30 (68.90)	20.93 (65.15)	4.76 (67.57)	3.30 (68.90)	20.86 (65.27)
347	14.36	10.25	58.68	4.36 (69.64)	2.89 (71.80)	18.09 (69.17)	4.35 (69.71)	2.88 (71.90)	17.94 (69.43)
348	13.55	10.12	56.54	4.81 (64.50)	2.89 (71.44)	18.80 (66.75)	4.80 (64.58)	2.88 (71.54)	18.72 (66.89)
349	13.48	10.50	56.10	3.64 (73.00)	2.66 (74.67)	16.29 (70.96)	3.63 (73.07)	2.64 (74.86)	16.18 (71.16)
350	13.61	10.11	55.86	3.93 (71.12)	2.77 (72.60)	16.70 (70.10)	3.92 (71.20)	2.76 (72.70)	16.59 (70.30)
351	13.54	10.06	53.73	3.88 (71.34)	2.68 (73.36)	17.46 (67.50)	3.87 (71.42)	2.67 (73.46)	17.36 (67.69)
352	13.48	9.97	52.79	3.90 (71.07)	2.71 (72.82)	18.94 (64.12)	3.81 (71.74)	2.60 (73.92)	17.58 (66.70)
353	14.79	10.05	53.52	4.08 (72.41)	2.77 (72.44)	18.35 (65.71)	3.88 (73.77)	2.66 (73.53)	16.91 (68.40)
354	13.61	9.72	52.16	3.98 (70.76)	2.73 (71.91)	17.94 (65.61)	3.84 (71.79)	2.62 (73.05)	16.72 (67.94)
Ave.	14.08	10.35	57.09	4.55 (67.68)	3.02 (70.82)	18.99 (66.74)	4.51 (67.97)	2.99 (71.11)	18.65 (77.12)

). Table 2 also shows the variance reduction rates; the values for ASF and MSF are very close, which are in the range of 60% to 80% for all the three baseline components (refer to Table A2).

We adopted the t-test to investigate whether the difference between ASF and MSF in variance reduction is statistically significant. The null hypothesis ($H_0$) and alternative hypothesis ($H_1$) are as follows,

$$\{\begin{array}{c}{H}_0:Diff\le 0\\ H_1:Diff>0\end{array}$$

(6)

$Diff$ denotes the variance reduction rate of ASF minus that of MSF. The p-value for the north, east, and up components are 0.002, 0.001, and 0.003, which are all less than 0.01, indicating strong evidence in favor of the alternative hypothesis. In other words, it is statistically significant that applying ASF results in lager variance reduction rate than MSF for each baseline component.

3.3. Single-Day Model Versus Seven-Day Model

In previous sections, the ASF or MSF model for correcting the data of a day was constructed from the residuals of the previous day (Single-day model). However, many studies adopted the multiple-day model to implement sidereal filtering (e.g., [3,18,19,30]). To investigate which type of model is better for ASF, we applied ASF correction on DOY 347 to 354 with the single-day and seven-day models (constructed from residuals of the previous seven days), respectively. Each correction value in a seven-day model is the average of the corresponding residuals from the previous seven days. Our results show that, in general, ASF with the single-day model performs better than ASF with the seven-day model in variance reduction (Figure 11).

From different days, the residual time series relating to the same satellite are correlated. For each satellite, we searched the maximal correlation coefficients between the residual time series from DOY 347 and that from DOY 341, 342, 343, 344, 345, and 346, respectively. The results show that, for a satellite, the maximal correlation coefficient between the residual time series from two different days generally reduces as the interval of the two days increases (Figure 12). A seven-day model is constructed by averaging the corresponding residuals from the previous seven days, whereas a single-day model is constructed from the residuals of the previous day only. Comparing with the residuals from two or more days before, those from the previous day have higher correlation with the residuals from the applied day (Figure 12). Thus, correction values from the single-day model are better correlated with the residuals (or multipath errors) of the applied day than those from seven-day model, which accounts for the higher variance reduction rate when applying ASF correction with the single-day model rather than the seven-day model.

In Figure 11, an exception occurs on DOY 348, where the 3D variance reduction rate of ASF correction with the single-day model is less than that with the seven-day model. Closer inspection indicates that the data of PRN 26 were not observed on DOY 346 and 347, but they were observed on DOY 348 and on DOY 341 to 345. The single-day model for DOY 348 was constructed from the residuals of DOY 347, and the seven-day model was constructed from the residuals of DOY 341 to 347. Thus, the multipath correction values for PRN 26 were absent in the single-day model, but were present in the seven-day model, and that caused the exception on DOY 348.

4. Discussions

With a certain cutoff frequency, the low-pass filter denoises the residual time series for constructing the multipath correction models. For different purposes or different applied data, the selected cutoff frequencies can be different. For example, Genrich and Bock [11] chose 0.02 Hz as the cutoff frequency for filtering the most observation noise from their data, while Atkins et al. [29] selected 0.2 Hz as the cutoff frequency to preserve any short-period (5 to 20 s) multipath component in the corrections. In this study, we choose 0.02 Hz as the cutoff frequency to achieve the maximal variance reduction. Our data show that there is no clear boundary between the frequency band of multipath errors and observation noise. Thus, choosing a cutoff frequency is a tradeoff between removing more noise from the residual time series and keeping more multipath components in these time series that are used to construct the models.

Our experiment demonstrates that ASF with the single-day model is generally better than that with the seven-day model in multipath mitigation. However, Ragheb et al. [18] and Dong et al. [19] concluded that stacking the residuals of seven days generated the best correction model for sidereal filtering. The reason for the different results is that we used the low-pass filtered residual time series to construct the multipath correction models, whereas they used the unfiltered ones. A single-day multipath correction model constructed from the unfiltered residuals is significantly affected by the observation noise. For a seven-day model, each correction value is the average of the residuals of the selected days. The averaging, in essence, is a low-pass filter, which reduces the noise level of the multipath correction model. In their studies, the seven-day model or other multiple-day models had lower noise levels than the single-day model, and hence the former outperformed the latter in variance reduction. Geng et al. [30] also reported that the multiple-day model was better than the single-day model. It is because their PPP derived residuals possibly included orbit error and troposphere delay, which contaminated the multipath correction models. Averaging of the multiple-day’s residuals alleviates the contaminations of these errors. In this study, however, the residuals for multipath model construction are free of these errors and are low-pass filtered, thus, averaging of multiple-day’s residuals will not improve the correction model.

5. Conclusions

Advanced sidereal filtering (ASF) effectively mitigates multipath errors. After ASF correction, the average 3D variance of the baseline solutions was reduced by 67.96% for the 19 experimental days. In general, ASF is more effective in multipath reduction than modified sidereal filtering (MSF), which is statistically significant. Including a satellite with repeat time deviating from the normal range ([235, 255] s) in data processing deteriorates the performances of MSF, but almost does not affect the performances of ASF. The single-day multipath correction model has higher correlation with the multipath of the applied day than the seven-day model, and hence ASF adopting the single-day model is more efficient in multipath mitigation than that adopting the seven-day model. After ASF correction, the average standard deviations of the horizontal components are less than 2.5 mm, and the vertical component is less than 5 mm, indicating that the applications of dual-antenna clock synchronized GNSS receivers could be extended to high precision deformation monitoring.

This study focused on applying ASF to mitigate the multipath of GPS carrier phase observables for a short baseline based on a dual-antenna clock synchronized GNSS receiver. The ASF method can also be applied to other GNSS systems, such as GLONASS, GALILEO, and BDS (BeiDou navigation satellite system), as long as it adopts the repeat time of each satellite of the corresponding system. Future work will incorporate multi-GNSS observables for baseline estimation and investigate whether the precision of the solutions could be further improved.