Analysis of Thematic Similarity Using Confusion Matrices

Abstract

The confusion matrix is the standard way to report on the thematic accuracy of geographic data (spatial databases, topographic maps, thematic maps, classified images, remote sensing products, etc.). Two widely adopted indices for the assessment of thematic quality are derived from the confusion matrix. They are overall accuracy (OA) and the Kappa coefficient (ĸ), which have received some criticism from some authors. Both can be used to test the similarity of two independent classifications by means of a simple statistical hypothesis test, which is the usual practice. Nevertheless, this is not recommended, because different combinations of cell values in the matrix can obtain the same value of OA or ĸ, due to the aggregation of data needed to compute these indices. Thus, not rejecting a test for equality between two index values does not necessarily mean that the two matrices are similar. Therefore, we present a new statistical tool to evaluate the similarity between two confusion matrices. It takes into account that the number of sample units correctly and incorrectly classified can be modeled by means of a multinomial distribution. Thus, it uses the individual cell values in the matrices and not aggregated information, such as the OA or ĸ values. For this purpose, it is considered a test function based on the discrete squared Hellinger distance, which is a measure of similarity between probability distributions. Given that the asymptotic approximation of the null distribution of the test statistic is rather poor for small and moderate sample sizes, we used a bootstrap estimator. To explore how the p-value evolves, we applied the proposed method over several predefined matrices which are perturbed in a specified range. Finally, a complete numerical example of the comparison of two matrices is presented.

1. Introduction

Geographic data (spatial databases, topographic maps, thematic maps, classified images, remote sensing products, etc.) supports decision-making in several fields, such as climate change, crop forecasting, forest fires, national defense, civil protection and spatial planning. A suitable quality is essential in order to ensure that decisions based on it are technically the best. There are different components to describe this quality. One of them is thematic accuracy, as is established by the international standard ISO 19157 [1], which includes the following so-called data quality elements: classification correctness, non-quantitative attribute correctness, and quantitative attribute accuracy. Classification correctness is usually represented by means of the so-called confusion matrix (also referred to as misclassification matrix or error matrix), which is one of the data quality measures included in [1]. In [2], it is recommended to always report the raw confusion matrix, so that the user of the data can derive any metric suitable for their needs.

In this setting, the Kappa coefficient [3] has been widely used for thematic accuracy assessment. It summarizes, in a single value, all the data included in the confusion matrix. It has also been included in [1] as a data quality measure for classification correctness. Since it was introduced as a measure of agreement, not for accuracy assessment, it can be seen by using simple numerical examples that Kappa is not an appropriate coefficient for accuracy assessment [4]. In consequence, given two independent classifications, it is not appropriate to compare both Kappa coefficients in order to assess the similarity of the two respective confusion matrices.

We propose an alternative procedure to evaluate whether two confusion matrices represent the same accuracy level. This proposal takes into account a multinomial distribution for the matrices, and uses a measure based on the squared Hellinger distance to evaluate the equality of both multinomial distributions. The context is presented in Section 2, the basic statements of the proposal are given in Section 3, in Section 4, the method is applied over a set of predefined matrices which are perturbed to explore how the p-value evolves, and finally, Section 5 includes a numerical example.

2. Description of the Context

Suppose that $k$ categories $C_1,C_2,\dots ,C_k$ are given (i.e., land-cover categories, etc.) and n sample units from the categories $C_i$ are observed for $i=1,\dots ,k$. In a general way, we will consider the n sample units are drawn according with a simple random sampling. Note that for particular application contexts, other sampling schemes may be preferred, and some corrections should be done in the data analysis. All sample units were classified into categories through a certain classification method, and such classification is summarized in a contingency table called confusion matrix. The $\left(i,j\right)$ element $n_{ij}$ represents the number of samples that actually belong to $C_j$, and are classified into $C_i$ for $i,j=1,\dots ,k$. In this way, the columns and rows of the contingency table correspond, respectively, to reference (index j) and classified (index i) data (

Table 1. Structure of a confusion matrix with $k$ categories.

Classified Data	Reference Data
	C1	C2	C3	C4
C1	$n_{11}$	$n_{12}$	…	$n_{1k}$
C2	$n_{21}$	$n_{22}$	…	$n_{2k}$
C3	…	…	…	…
C4	$n_{k1}$	$n_{k2}$	…	$n_{kk}$

). So, the elements in the diagonal are correctly classified items, and the off-diagonal elements contain the number of confusions, namely, the errors due to omissions and commissions.

Two widely adopted indices for thematic accuracy controls upon confusion matrices are overall accuracy (OA) and the Kappa coefficient (ĸ) (see [5] or [6]). OA is the ratio between the number of elements that are correctly classified and the total number of elements in the matrix

$$OA=\frac{1}{n}{\sum }_{i=1}^k{n}_{ii},$$

(1)

where $n={\sum }_{i,j=1}^k{n}_{ij}$ is the total number of sample units. The Kappa coefficient is a measure based on the difference between the agreement indicated by OA, and the chance agreement estimated by the marginal values as

$$\kappa =\frac{OA-P_c}{1-P_c},$$

(2)

where $P_c=\frac{1}{n^2}{\sum }_{i=1}^k{n}_{+i}{n}_{i+}$, $n_{+i}$ and $n_{i+}$ being the sum of each column and row, respectively.

Both indices are global, and do not allow for a category-wise control. Some authors have criticized its use ([7,8,9], among many others).

Along this line, it is possible to determine if two independent OA or ĸ values, associated with two confusion matrices, are significantly different. Therefore, two analysts, two classification strategies, the same analyst over time, etc. can be compared. The corresponding null hypothesis under consideration can be expressed as $H_0:O{A}_1-O{A}_2=0$ or $H_0:{\kappa }_1-{\kappa }_2=0$, where $O{A}_1,O{A}_2,{\kappa }_1$ and ${\kappa }_2$ are the OA and Kappa coefficient for both confusion matrices. However, not rejecting the null hypothesis does not mean that the confusion matrices are similar, because many different matrices could obtain the same value of OA or ĸ.

In the case of the Kappa coefficient, [4] have shown that evaluating the significant difference between classifications by means of the difference of the corresponding Kappa coefficient is not appropriate. They proved this fact with simple numeral examples, and the main reason is the origin of the Kappa coefficient as a measure of agreement (in which context, the invariance property is essentially required), and not as a measure of accuracy assessment. Such invariance is not welcome because the main interest is how reference data are correctly classified (fixed number $n_{+i}$ of samples in each category $C_j$), not how classified data contain the correct data ($n_{i+}$ not fixed).

3. Proposal to Test the Similarity of Two Confusion Matrices

In statistics, homogeneity is a generic term used when certain statistical properties can be assumed to be the same. The prior section has shown that the difference in the OA and ĸ values has been used as a similarity measure of two confusion matrices. In this section, we propose an alternative which takes advantage of the underlying sampling model and deals with a confusion matrix as a multinomial distributed random vector. This way, the similarity between confusion matrices can be stated as the equality (or homogeneity) of both underlying multinomial distributions. The proposal considers the individual cell values instead of aggregated information from such matrices, which is the case of OA and ĸ. Therefore, equality between the multinomial distributions will hereafter mean that both matrices are similar.

Several distance measures can be considered for discriminating between multinomial distributions. Among them, it can be highlighted that the family of phi-divergences introduced by Csiszár in 1963 (see [10] (p. 1787)) has been extensively used in testing statistical hypotheses involving multinomial distributions. Examples in goodness-of-fit tests, homogeneity of two multinomial distributions and in model selection can be found in [11,12,13], among many others.

From this family, we will use the squared Hellinger distance (SHD). Under the premise that a confusion matrix can be modelled as a multinomial distribution, with frequent values of zero, this choice allows us to take advantage of two things: first, the good statistical properties of the family of phi-divergences, and second, the fact that SHD is well defined, even if zero values are observed.

Therefore, in what follows, each confusion matrix is considered as a random vector, X and Y, which are independent and whose values have been grouped into $M=k\times k$ classes, or equivalently, taking values in $\mathsf{{\rm Y}}=\left(1,\dots ,M\right)$ with probabilities $P=\left(P_1,P_2,\dots ,P_M\right)$ and $Q=\left(Q_1,Q_2,\dots ,Q_M\right)$, respectively. The idea of equality is expressed by means of the following null hypothesis

$$H_0:P=Q.$$

(3)

The Hellinger distance (HD) is a probabilistic analog of the Euclidean distance. For two discrete probability distributions, $P$ and $Q$, their Hellinger distance $HD\left(P,Q\right)$ is defined as

$$HD\left(P,Q\right)=\frac{1}{\sqrt{2}}\sqrt{{\sum }_{i=1}^M{\left(\sqrt{P_i}-\sqrt{Q_i}\right)}^2},$$

(4)

where the $\sqrt{2}$ in the definition is for ensuring that $HD\left(P,Q\right)\le 1$ (see [14]). Therefore, the value of this similarity measure is in the range $\left[0,1\right]$.

Let $\left(X_1,\dots ,X_n\right)$ and $\left(Y_1,\dots ,Y_m\right)$ be two independent random samples from X and Y, with sizes n and m, respectively. Let ${\widehat{P}}_i=p_i,{\widehat{Q}}_i=q_i,i=1,\dots ,M$ be the observed relative frequencies which are the maximum likelihood estimators of $P_i$ and $Q_i$, $i=1,\dots ,M$, respectively. For testing $H_0$, we consider the following test function based on SHD:

$$\mathsf{\Psi }=\{\begin{array}{cc}1& \mathrm{if}{T}_{n,m}\ge t_{n,m,\alpha }\\ 0& \mathrm{otherwise}\end{array},$$

(5)

where $T_{n,m}=\frac{4\mathrm{nm}}{\mathrm{n}+\mathrm{m}}{\sum }_{i=1}^M{\left(\sqrt{p_i}-\sqrt{q_i}\right)}^2$ and $t_{n,m,\alpha }$ is the 1-α percentile of the null distribution of $T_{n,m}$. A reasonable test for testing $H_0$ should reject the null hypothesis for large values of $T_{n,m}$. To decide when to reject $H_0$, that is, to calculate $t_{n,m,\alpha }$ or, equivalently, to calculate the p-value of the observed value of the test statistic, $p=P\left[T_{n,m}\ge T_{obs}\right]$, $T_{obs}$ being the observed value of the test statistic $T_{n,m}$, we need to know the null distribution of $T_{n,m}$, which is clearly unknown. Therefore, it has to be approximated. One option is to approximate the null distribution of $T_{n,m}$ by means of its asymptotic null distribution. The following theorem states this fact.

Theorem 1.

Given the maximum likelihood estimators of P and Q, say${\widehat{P}}_i=p_i,{\widehat{Q}}_i=q_i,i=1,\dots ,M$, under the null hypothesis that P = Q, we have

$$\frac{4nm}{n+m}{\sum }_{i=1}^M{\left(\sqrt{p_i}-\sqrt{q_i}\right)}^2\stackrel{\mathcal{L}}{\to }{\chi }_{M-1}^2,$$

(6)

if $\frac{n}{n+m}\to \lambda >0$ as $n,m\to \infty$. Note that $\left(\stackrel{\mathcal{L}}{\to }\right)$ means convergence in distribution.

Proof. 

The SHD can be seen as a particular case of a f-dissimilarity between populations [10]. According to notation in ([10], p. 303, Equation (4.1)) given the probability vectors associated with two multinomial distributions P and Q, the test statistic $T_{n,m}$ is based on $D_f\left(P,Q\right)={\sum }_{i=1}^{M}f\left(P_i,Q_i\right)$, where $f\left(P_i,Q_i\right)={\left(\sqrt{P_i}-\sqrt{Q_i}\right)}^2$.

The results follows from the corollary 3.1.b) in [10], because f(1) = 0 and the value of the only eigenvalue of matrix HD_λ is $\beta =\frac{{\left(n+m\right)}^2}{2nm}$. Note that $H=\left(\begin{array}{cc}1/2& -1/2\\ -1/2& 1/2\end{array}\right)$ and $D_{\lambda }=\left(\begin{array}{cc}1/\lambda & 0\\ 0& 1/\left(1-\lambda \right)\end{array}\right)$. ☐

Asymptotically, the null distribution of $T_{n,m}$ is a chi-square distribution with M − 1 degrees of freedom. However, for small and moderate sample sizes, the behavior of this approximation is rather poor (see for example [15,16]). To overcome this problem, we approximate the null distribution of the test statistic by means of a bootstrap estimator.

Let $X_1^{*},X_2^{*},\dots ,X_n^{*}$ and $Y_1^{*},Y_2^{*},\dots ,Y_m^{*}$ be two independent samples of sizes n and m, from the multinomial distribution with parameter p₀, where ${\widehat{p}}_0$ is an estimator of the common parameter under $H_0$ given by

$${\widehat{p}}_{0,i}=\frac{n{p}_i+m{q}_i}{n+m},i=1,\dots ,M,$$

(7)

and given ${\widehat{P}}_i^{*},{\widehat{Q}}_i^{*}$ the relative frequencies for the bootstrap samples, $T_{n,m}^{*}$ stands for the bootstrap value of $T_{n,m}$, which is obtained by replacing ${\widehat{P}}_i,{\widehat{Q}}_i$ with ${\widehat{P}}_i^{*},{\widehat{Q}}_i^{*}$, for i = 1,2, ..., M. The next result gives the weak limit of the conditional distribution of $T_{n,m}^{*}$ given the data. P* denotes the conditional probability law given the data.

Theorem 2.

If$n,m\to \infty$with$\frac{n}{n+m}\to \lambda >0$, then

$$su{p}_x\left|P^{*}\left[T_{n,m}^{*}\le x\right]-P\left[{\chi }_{M-1}^2\le x\right]\right|\to 0,a.s.$$

(8)

Proof. 

The proof of the theorem follows the same steps as the one of Theorem 1 in [16]. ☐

As a consequence, the null distribution of $T_{n,m}$ is consistently estimated by its bootstrap estimator.

In order to evaluate the goodness of the bootstrap approximation to the null distribution of the test statistic T_n,m, a simulation experiment was carried out in [17].

4. Analysis of the Test over Predefined Matrices

From Section 3, we have a test statistic based on the SHD, and we can obtain the p-value in order to decide whether to reject $H_0$, that is to say, to consider two confusion matrices as similar or not, or equivalently, two multinomial distributions as homogeneous or not. With the aim of exploring how this p-value evolves when differences appear between two matrices, we considered applying the method to a predefined confusion matrix and introducing perturbations. From each perturbation, we obtain a perturbed matrix and computed the p-value.

Not one but three predefined confusion matrices were considered, in order to take into account different values of OA. Four categories ($k$ = 4) and balanced (equal) diagonal values were considered, where OA is 0.95 (matrix CM₉₅), 0.80 (matrix CM₈₀), and 0.50 (matrix CM₅₀). The matrices were set at relative values, that is to say that they were divided by $n$, and therefore, $OA={\sum }_{i=1}^4{x}_{ii}$.

For the sake of simplicity, we delimited the scope of the analysis. A context was supposed in which the analyst is mainly worried about the number of features that are correctly classified, therefore ignoring how the off-diagonal values are distributed. The proposed method, based on the underlying multinomial model, can be easily adapted to this context. The grouping (sum) of the off-diagonal values (

Table 2. Predesigned relative confusion matrix. Cell values in the diagonal (d) are 0.2375 for matrix CM₉₅, 0.2 for matrix CM₈₀, and 0.125 for matrix CM₅₀. The sum of the off-diagonal values (in gray) is 0.05 for matrix CM₉₅, 0.2 for matrix CM₈₀, and 0.5 for matrix CM₅₀.

Classified Data	Reference Data
	C1	C2	C3	C4
C1	d
C2		d
C3			d
C4				d

) implies that the size of the vector that represents the matrix is $k+1$, not $k\times k$. For matrix CM₉₅, CM₈₀ and CM₅₀ the vectors are, respectively:

$$\begin{gathered} V_{95}=\left(0.2375,0.2375,0.2375,0.2375,0.05\right), \\ {V}_{80}=\left(0.2,0.2,0.2,0.2,0.2\right), \\ {V}_{50}=\left(0.125,0.125,0.125,0.125,0.5\right), \end{gathered}$$

(9)

where the last components of the vectors are $1-OA$.

Given that the number of perturbed matrices can be infinite, we explored perturbations ($x^{\prime }$) introduced in the range (0 ± 0.10) for each diagonal value, with 0.02 per step, that modify OA in the range (0 ± 0.40). All combinations from this exploration provide a total of perturbed matrices between 9495 (CM₉₅) and 14,640 (CM₅₀). The number of perturbed matrices is different for each matrix due to the restriction given by $OA\le 1$.

In order to analyze the results, we first considered a significant situation, that where the perturbations compensate for one another and OA remains the same (therefore, the fifth element of the vector is also unchanged). In this case, the number of perturbed matrices is reduced to 890 in all three confusion matrices. If an analyst used the OA value to test the similarity of any of them in relation to the predefined matrix, the hypothesis that they are similar would not be rejected. The same conclusion would be obtained if ĸ were used, and the off-diagonal values tend to be symmetrical. Nevertheless, the perturbations could be such that the assumption of similarity may be compromised.

From the application of the proposed test, the bootstrap p-value associated with the null hypothesis of Equation (3) was obtained for each underlying multinomial distribution from each perturbed matrix. All computations were performed using programs written in the R language [18]. In Figure 1 the p-values are represented for each matrix (CM₉₅, CM₈₀, and CM₅₀), where the x-axis is the sum of the absolute values of the perturbations $Sum={\sum }_{i=1}^4\left|{x^{\prime }}_{ii}\right|$

From Figure 1, there becomes apparent some similarities between the three charts. They start with p-values concentrated around 1.0, because of the small perturbations that were introduced into the matrix. They also end with a small range in p-values when $Sum$ is high, which makes sense because the null hypothesis should be strongly rejected. The range is wider for medium values of $Sum$. This means that the result of the test depends largely on how the perturbations are distributed, although their sum is zero (OA remains the same). Lower p-values are obtained if the values of the perturbations are heterogeneous. For example, for CM₅₀ and $Sum=0.20$, the maximum and minimum p-value is 0.031 and 0.418 for a vector of perturbations of $x_1^{\prime }=\left(0.0,0.1,0.0,-0.1\right)$ and $x_2^{\prime }=\left(-0.06,0.04,0.06,-0.04\right)$, respectively.

However, there are differences between the charts in Figure 1. If we take matrix CM₉₅, it can be said that the null hypothesis that the underlying multinomial distributions are equal is not rejected in any of the 890 perturbed matrices (at significance level 5%). All the p-values are higher than 0.07. Therefore, all the perturbed matrices are similar to CM₉₅. If we take matrix CM₈₀, there are few changes in relation to matrix CM₉₅, but some (not many) p-values in the range of 0.025–0.07 can be found when $Sum$ is 0.36 or 0.40. In matrix CM₅₀, the situation changes substantially. The p-values decrease faster in the chart, and low p-values (<0.05) can be found when $Sum\ge 0.20$. Moreover, when $Sum\ge 0.28$ the rejection of the null hypothesis is clear, since nearly all the p-values are lower than 0.05. This result is logical, since the same perturbation represents a greater change when the diagonal value is lower.

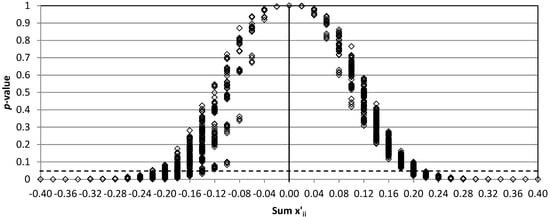
Another situation that can be considered is that in which the entire diagonal improves or worsens. That is to say that in a single perturbed matrix, there are no perturbations of different sign, but they are all positive or all negative. In contrast to the former case, the fifth component of the vector does not remain the same. Figure 2 shows the p-values for CM₉₅, CM₈₀, and CM₅₀. The x-axis is the sum of the values of the perturbations $Sum={\sum }_{i=1}^4{x^{\prime }}_{ii}$, which is positive if OA improves, or negative if OA worsens. The number of perturbed matrices when OA improves is different for each matrix due to the restriction given by $OA\le 1$. This restriction affects particularly CM₉₅ (only 14 perturbed matrices) and C₈₀ (580), but not the matrix CM₅₀ (1295).

Similarly to Figure 1, in Figure 2, the charts start with p-values concentrated around 1.0 when the perturbations are low, but it is noted that the p-values drop more quickly than in Figure 1. It is obvious that the change in the value of OA here supposes a great difference. As has been explained, the statistic $T_{n,m}$ is based on the SHD. As a consequence, it is sensitive to a change in any of the components of the vector, either the first four components (diagonal values) or the fifth component (off-diagonal grouped values).

Focusing on a clear rejection of the null hypothesis (most p-values around 0.05 or lower), this occurs for CM₉₅ when $Sum\le -0.14$, for CM₈₀ when $Sum\ge 0.14$ or $Sum\le -0.20$, and for CM₅₀ when $Sum\ge -0.22$ or $Sum\le -0.22$. In the case of CM₅₀, there are isolated cases of rejection in wide range of p-values when $-0.14\le Sum\le -0.20$. This wider range means that the results of the test depend to a large extent on how the perturbations are distributed to obtain a same value of $Sum$. Other trends that can be appreciated in the p-values from Figure 2 are they drop faster for matrix CM₉₅, CM₈₀ and CM₅₀, in this order, which can be interpreted as a higher sensibility when OA is high, and the range is also broader when OA worsens, which can be interpreted as a higher sensibility for a worsening than for an improvement.

5. Applied Example

In this section, a full example is performed by taking two matrices from [6]. Matrix P (

Table 3. Confusion matrix P.

Classified Data	Reference Data
	C1	C2	C3	C4
C1	65	4	22	24
C2	6	81	5	8
C3	0	11	85	19
C4	4	7	3	90

) has four categories ($k$ = 4) and was derived from an unsupervised classification with sample size $n=434$ from a Landsat Thematic Mapper image with OA₁ = 0.74 and ĸ₁ = 0.65. Matrix Q (

Table 4. Confusion matrix Q.

Classified Data	Reference Data
	C1	C2	C3	C4
C1	45	4	12	24
C2	6	91	5	8
C3	0	8	55	9
C4	4	7	3	55

) was derived from the same image and classification approach, but provided by a different analyst and sample size $m=336$, with OA₂ = 0.73 and ĸ₂ = 0.64. The p-value for a two-sided test of the null hypothesis $H_0:{\kappa }_1-{\kappa }_2=0$ is 0.758, therefore, the hypothesis that both Kappa coefficients are equal should not be rejected, but this does not necessarily mean that the matrices are similar.

As an alternative to that employed in [6] with the Kappa coefficient, the HD between both matrices, 0.096, can be easily obtained. Applying the proposal from Section 3, it can be known whether this value is high enough to consider that the matrices are not similar. The calculation process involves the following steps:

• Take the observed relative frequencies ${\widehat{p}}_i$ and ${\widehat{q}}_i$, corresponding to the matrices to be compared by columns ($p_1,\dots ,p_{16}$) = (0.1497, 0.0138, 0, 0.0092, 0.0092, 0.1866, 0.0253, 0.0161, 0.0506, 0.0115, 0.1958, 0.0069, 0.0552, 0.0184, 0.04377, 0.2073) and ($q_1,\dots ,q_{16}$) = (0.1339, 0.0178, 0, 0.0119, 0.0119, 0.2708, 0.0238, 0.0208, 0.0357, 0.0148, 0.1636, 0.0089, 0.0714, 0.0238, 0.0267, 0.1636). Obtain the observed value of the test statistic from the initial samples, $T_{obs}$ as $T_{obs}=\frac{4·434·336}{434+336}{\sum }_{i=1}^{16}{\left(\sqrt{{\widehat{p}}_i}-\sqrt{{\widehat{q}}_i}\right)}^2=13.8682$.
• Repeat for $b=1,\dots ,B$, B = 10,000 times:
  Generate 2B independent bootstrap samples, $\left(X_1^{*},X_2^{*},\dots ,X_n^{*}\right)$ and $\left(Y_1^{*},Y_2^{*},\dots ,Y_m^{*}\right)$ from the multinomial distribution $M\left(n+m,p_{0,1},p_{0,2},\dots ,p_{0,16}\right)$, where $p_{0,i}=\frac{n{p}_i+m{q}_i}{n+m},i=1,\dots ,16.$
  Calculate $T_{n,m}^{*}$, $b=1,\dots ,B$ for each couple of samples.
• Approximate the p-value by means of $\widehat{p}=\frac{Card\left\{b:T_{n,m}^{*}\ge T_{obs}\right\}}{B}$, whose value is p = 0.573.

As a result, the hypothesis that both distributions are equal (Equation (3)) would not be rejected, and in consequence, both confusion matrices exhibit a similar level of accuracy. Taking into account that OA hardly changes between both matrices, and that the changes are mainly concentrated in the diagonal values, there is a chart from Section 4 which represents a case similar to this example. It is the chart for CM₈₀ in Figure 1. In this example, we have a value of $Sum=0.016+0.084+0.032+0.044=0.176$, but we can see that not until values of $Sum$ are near to 0.4 does the p-value approach 0.05.

To reinforce our proposal, we applied on the diagonal of matrix P the vector of relative perturbations $x^{\prime }=\left(0.1,0.1,-0.1,-0.1\right)$ ($Sum=0.4$). Matrix R (

Table 5. Confusion matrix R.

Classified Data	Reference Data
	C1	C2	C3	C4
C1	84	3	17	19
C2	5	96	4	6
C3	0	9	32	15
C4	3	5	2	36

) is the perturbed matrix which is obtained when $m=336$ (the sample size of matrix Q). ĸ is almost equal in both matrices P (ĸ₁ = 0.65) and R (ĸ₃ = 0.64), while OA remains the same. Nevertheless, a p-value of 0.002 ($T_{obs}=43.74$) is obtained from our proposed method, thus, the hypothesis that both distributions are equal is rejected, and the confusion matrices are, therefore, not similar.

6. Conclusions

A new proposal for testing the similarity of two confusion matrices has been proposed. The test considers the individual cell values in the matrices and not aggregated information, in contrast to the tests based on global indices, like overall accuracy (OA) or the Kappa coefficient (ĸ). It takes into account a multinomial distribution for the matrices and uses the Hellinger distance, which can be applied even if values of zero are present in the matrices. The inconvenience that the null distribution of the test if unknown is overcome by means of a bootstrap approximation, whose goodness has been evaluated. The proposed method is useful for analyses which need to compare classifications results derived from different approaches, mainly classification strategies.

For a better understanding of the behavior of the test, it was applied over three predefined matrices with different values of OA. Perturbations were introduced in each predefined matrix to derive a set of perturbed matrices to be compared with and obtain their p-value. For the sake of simplicity, this analysis was delimited by ignoring how the off-diagonal values are distributed. In order to delimitate the data to be analyzed, the range and step values are fixed for the perturbation. Charts of the p-values are presented in two cases: when OA remains the same and when the entire diagonal improves or worsens. Results indicate that the similarity depends on different aspects. It is remarkable that lower p-values are obtained for a perturbed matrix if the values of the perturbations are heterogeneous. Finally, a numerical example of the proposed method is shown.

A full analysis, without grouping the off-diagonal values, remains an open challenging question. Future research includes the application of the method to individual categories, since the hypothesis of an underlying multinomial model is applicable to a single row or column in the confusion matrix. This means that attention could be focused on the producer’s accuracy or the user’s accuracy of any of the categories. The proposal could also be useful for land-change studies; in this case, the test would indicate whether trends are maintained over time or not.