Identifying Modes of Driving Railway Trains from GPS Trajectory Data: An Ensemble Classifier-Based Approach

Abstract

Recognizing Modes of Driving Railway Trains (MDRT) can help to solve railway freight transportation problems in driver behavior research, auto-driving system design and capacity utilization optimization. Previous studies have focused on analyses and applications of MDRT, but there is currently no approach to automatically and effectively identify MDRT in the context of big data. In this study, we propose an integrated approach including data preprocessing, feature extraction, classifiers modeling, training and parameter tuning, and model evaluation to infer MDRT using GPS data. The highlights of this study are as follows: First, we propose methods for extracting Driving Segmented Standard Deviation Features (DSSDF) combined with classical features for the purpose of improving identification performances. Second, we find the most suitable classifier for identifying MDRT based on a comparison of performances of K-Nearest Neighbor, Support Vector Machines, AdaBoost, Random Forest, Gradient Boosting Decision Tree, and XGBoost. From the real-data experiment, we conclude that: (i) The ensemble classifier XGBoost produces the best performance with an accuracy of 92.70%; (ii) The group of DSSDF plays an important role in identifying MDRT with an accuracy improvement of 11.2% (using XGBoost). The proposed approach has been applied in capacity utilization optimization and new driver training for the Baoshen Railway.

1. Introduction

1.1. Background

With the increasing demands of diversification and individuation, quality improvements in railway freight transportation services have received an unprecedented amount of attention from operators of railway systems. From a planning perspective, quality railway freight transportation services must be built on precise information or knowledge that reflects the characteristics of the railway system [1,2]. For this reason, data mining has become one of the most important areas in the field of railway research. In these repositories of information or knowledge, the operators eagerly want to know the Modes of Driving Railway Trains (MDRT) [3].

MDRT are the results of driving autonomy. For the purpose of ensuring the robustness of railway systems, operators of railways give autonomy to drivers in the driving processes (This phenomenon even exists in the highly information-influenced High-speed Railway System of China). Under these circumstances, drivers are able to drive the trains according to their experience and basic constraints. Although robustness is ensured, the resulting driving diversity makes railway operations unpredictable since different types of driving modes have different impacts on the efficiency, feasibility, etc. of the railway system [3,4,5,6]. For example, MDRT existing in sections (the connecting parts of adjacent stations) make the running time multivariate, even in the same running plan. If operators have little understanding of MDRT (e.g., setting running time as a constant value instead of a multivariate dataset with different contexts), the resulting plans are inaccurate and remain largely unimplemented.

Although a good understanding of MDRT can contribute to the study of driver behavior habits [3,7,8,9], auto-driving system design [3], and capacity utilization optimization [10,11], building a MDRT set is difficult in the context of big data; traditional methods have certain limitations in terms of scale and continuous learning. This paper is motivated by finding an approach to identifying MDRT automatically. Once the train has completed a portion of the work, its trajectory data will be immediately identified and stored. After a certain period of accumulation, the operator can analyze the MDRT in terms of proportion and internal characteristics. The information obtained can be used for multivariate running time calculations (for planning) or driver driving strategy extraction (for new driver training).

In China, locomotives now have built-in GPS devices with the deployment of a set of railway controlling systems (e.g., Train Operation Dispatching Command System (TDCS), and Central Traffic Control (CTC), etc.). Benefiting from this development of railway information systems, we can use GPS trajectory data as proxies to identify MDRT [12]. Recognizing train modes from GPS trajectory data has many advantages, such as being low cost [13], having few spatiotemporal limitations [14], abundant information [12,13,14], and maturing techniques [15,16,17,18]. This paper focuses on finding a proper approach (including data preprocessing, feature extraction, classifiers modeling, training and parameter tuning, and model evaluation) to identify modes of driving railway trains from GPS trajectory data.

1.2. Related Works

In existing studies, the analyses and applications of concepts similar to MDRT are hot spots in railway data mining [3,7,8,9,10,11]. A multi-phase analyzing framework [3] was built to support many complex railway studies such as large-scale micro-simulation [7] and timetable optimizations [9]. However, these studies focused on the applications of MDRT, and there was a lack of an approach to automatically and effectively identify MDRT in a big data context. Inspired by a relatively new area called transportation mode detection, we will propose a data-mining-based approach to fill this gap.

Transportation mode detection is actually a group of applications of supervised-learning classification methods [19]. A technical framework for researching detection includes four components [12,13,14,19,20,21,22,23,24,25]: (i) Data preprocessing; (ii) Feature extraction and selection; (iii) Classifier identifications; (iv) Evaluations and analyses. A proper combination of methods in these four components determines the quality of identification.

A set of discriminative features plays a vital role in identifying modes. In existing studies, global features [19,21,25,26,27,28,29], local features [12,30], time-domain features [26], frequency-domain features [25,26] and specific features [19,28,31,32,33] were extracted through corresponding methods. Among these features, global features focus on describing whole characteristics of trajectory parameters (e.g., speed, acceleration, etc.) including average values (i.e., mean, absolute mean, median, mode), variance, standard deviation, percentiles, skewness, and kurtosis [21] Conversely, local features focus on describing local characteristics of trajectory parameters. For example, Deng et al. [30] proposed a random forest based method to split the trajectory into segments and obtain features including the mean, standard deviation, and slope from the interval part of the trajectory. In addition, feature sinuosity and deviation, which are extracted from each parameter profile of segment data by a profile decomposition algorithm, were proposed by Dodge et al. [12]. The combination of global features and local features has shown a high level of performance (only 0.0923 misclassification rate) in the research [21].

Moreover, from the point of view of signal analysis, time-domain and frequency-domain features were used in mode detections [25,26]. Two time-domain features, zero-crossing rate and number of peaks extracted from the time-domain, were proposed by Elhoushi et al. [26]. As time domain features are easily affected by noise and interference, the current research has focused more on the frequency domain. Frequency-domain features were obtained through DFT (Discrete Fourier Transform) [25], Short-time Fourier Transform (STFT) [26] or Fast Orthogonal Search (FOS) [26]. The results of these studies show that features in the time domain and frequency domain could help to improve accuracy.

In addition, some specific features were proposed for the purposes of improving accuracy of classification, such as average rail location closeness [19], estimated horizontal accuracy uncertainty [20] and average proximity to bus, tram, or train network [28]. The design of a specific features extracting method should be based on characteristics of transportation options. A good combination of the features mentioned above could help improve accuracy of detection.

As to classifiers, many studies have introduced different classifiers into transportation mode detection, such as Decision Tree [14,19,24,26,34], K-Nearest-Neighbor (KNN) [21,34,35], Support Vector Machines (SVM) [12,14,21,34], Artificial Neural Network (ANN) [20,28,33], Fuzzy Logic [13,28], Hidden Markov Models [25,27], and Bayesian Network [19,36,37]. In addition, ensemble classifiers have become a hotspot in the field of transportation mode detections since ensemble classifiers are a combination set of weak learners, which are superior to a single stronger learner [21,38]. Representative ensemble classifiers include XGBoost [39,40], Random Forest (RF) [19,21,30,34], Adaboost [41,42,43]. Another advantage of using ensemble classifiers is that these methods can conduct feature selection, which performed better than the PCA method [21].

Although prior studies achieved a great deal, our goal faces certain challenges; the most significant one is as follows: The existing studies focused on detecting modes from different transportation options. However, our study aims to identify different driving modes in one method of transportation, where the commonness and characteristics of modes are much more complex than those in existing studies. Thus, for the best performance in identifying MDRT, we want the following: (i) A method to extract new features according to railway characteristics; (ii) the most suitable classifier based on performance comparisons of different classifiers.

The proposed approach has been applied in capacity utilization optimization and new driver training of Baoshen railway: (i) the approach constructed a MDRT collection where obtained a multivariate parameter set of running time, so that operators can make distinct plan for different situations; (ii) new drivers can learn different modes and enhance their ability to cope in different situations.

The remainder of this paper is organized as follows: In Section 2, methods of data preprocessing, feature extraction, classifiers modeling, training and parameter tuning, and model evaluation are elaborated in detail. Among these, one of the highlights of this study is that we propose a method for extracting DSSDF combined with classical features for the purpose of improving performance identification. In Section 3, a real-data experiment is conducted, where we fulfill the following tasks: (i) Finding the optimal value of $n_s$, i.e., determining the most suitable extraction method for DSSDF; (ii) Evaluating performances of classifiers by different indicators and finding the most suitable classifier for identifying MDRT; (iii) Evaluating and comparing performances of different combinations of features and classifiers. In Section 4, discussions and conclusions about the experiment, as well as key points for future research, are presented.

2. Methodologies

In this paper, we propose an integrated approach to identify MDRT using GPS data. The main modules of our identification methodologies are shown in Figure 1 and include data preprocessing (discussed in Section 2.1), feature extraction (discussed in Section 2.2), classifiers modeling (discussed in Section 2.3), training and parameter tuning (discussed in Section 2.3), and model evaluation (discussed in Section 2.4). Raw GPS data were first preprocessed (including data cleaning and representation) into data segments, and then four groups of features were extracted before using the ensemble classifiers (AdaBoost, Random Forest, Gradient Boosting Decision Tree, and eXtreme Gradient Boosting) and single classifiers (K-Nearest Neighbor and Support Vector Machine) to identify MDRT. In order to obtain more reliable, stable and accurate models, techniques such as k-fold cross validation and Bayesian optimization were utilized. In addition, an evaluation system was built to represent the performances of features and classifiers. Each step is detailed in the following sections.

2.1. Preprocessing

To achieve a better performance, two data preprocessing techniques were employed in this study. First, we removed the duplicate data in the dataset as some GPS points were recorded more than once due to recording errors on the GPS device. Second, according to common sense, we removed some outlier trajectories that were deemed abnormal. For instance, if the average speed of a trajectory exceeds the designed speed, we identified it as an abnormal trajectory and removed it from the dataset.

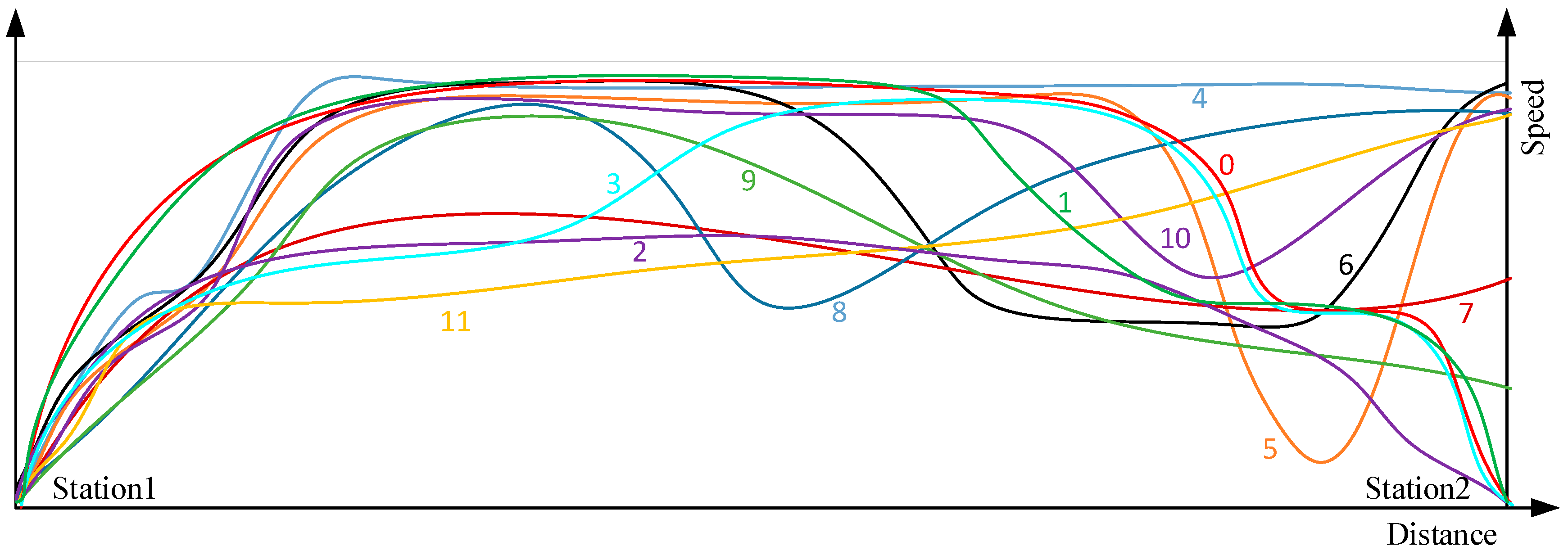
2.1.1. Modes of Driving Railway Train

MDRT are utilized in the field of railway transportation, which is a relatively niche area as compared to existing areas of transportation mode detection. To obtain a more intuitive understanding, Figure 2 is used to illustrate MDRT by trajectories of parameter speed/distance.

Figure 2 shows 12 different modes in MDRT as examples, where the horizontal axis represents distance (measured from the starting station) and the vertical axis represents speed (km/h). These distinct modes are summarized from the actual production processes, which carry information of actual driving habits, reactions to signals and device characteristics. For example, mode 11 is a type of driving that starts from a station, does not speed up to the maximum speed, and passes by the next station by the main track. The details of other modes will be illustrated in Section 3.1. Compared to existing transportation modes, MDRT are more inclined to describe differences and commence at the level of microcosmic driving operation. Thus, the number of modes in MDRT is much more than that of existing mode detections.

These modes are difficult to identify. In the actual production process, operators once used the running time to distinguish MDRT. However, this method is inefficient; many modes are very close in running time. In addition, the inner phases of these modes are complex. For example, mode 8 has two unfixed-location parts of acceleration, which need to be labeled manually. For this reason, methods based on driving phase analyses [3,7,9] in studies could not be used to identify MDRT directly; the traditional method requires a large amount of manual processing, which will restrict pattern recognition under the condition of large data size.

To improve the accuracy of identification of MDRT, we propose a method to extract specific features named Driving Segmented Standard Deviation Features (DSSDF). The idea of extracting DSSDF is from the measures of driving deviations from running plans. From Figure 2, we find two groups of modes: 0–3 stop in both Station 1 and Station 2 (stop-stop). 4–11 stop only in Station1 and pass Station2 (stop-pass). We call these two stop strategies Running plan 1 and Running plan 2, respectively. From the aspect of planning, each running plan corresponds to an idea driving trajectory called Planed Traction Curve (PTC). The proposed features are designed depending on the difference between PTC and MDRS. The details of extracting DSSDF are shown in Section 2.2.2.

2.1.2. Representation and Segments of Trajectory Data

We proposed a three-level representation framework to formulate trajectory data for our study, which contains not only a set of notations but also clear definitions for the inner-relationship between elements according to mode identification. In this framework, tracks are the most primitive forms of GPS trajectory data submitted from GPS sensors. Segments are the data the proposed identifications focus on. In addition, trips are the connections between tracks and segments. We use Figure 3 to illustrate the three-level (track-trip-segment [13,14]) framework for representing trajectory data.

As to the track, it is in large volume and continuous [25] since the GPS sensors in locomotives work ubiquitously. A track is a sequence of GPS points denoted by $track=\left\{P_1,P_2,\cdots ,P_m\right\}$, where GPS point $P_i$ is formatted as $lat,lon,t,v,h,acc$, where: $lat$ represents the latitude; $lon$ represents longitude; $t$ represents the timestamp of the sensor data submitting; $v$ represents the current ground speed of the device; $h$ represents the direction of travel; and $acc$ represents the accuracy level of the latitude and longitude coordinates. Distance, speed, and acceleration can be obtained using the Haversine formula [36]. In the context of railway freight transportation, the track is the whole GPS trajectory of train movements including running in sections, operating in station, and repaired in depot. A track is too large-scale and complex to be analyzed, and therefore, decompositions of trajectory data are necessary.

After decomposing, we obtain components of the track: trips and activities [13]. We define $track=\left\{trips,activities\right\}$. Trips by railway are the GPS sub-trajectories between two terminal stations corresponding to moving tasks (e.g., an operation line on timetable), and activities are the connections between trips (activities are corresponding to tasks in terminal stations). The key of detecting trips is finding activities. In the view of GPS data, if without signal loss, activities are defined as GPS points whose speeds are close to zero [18] or bundles of GPS points that are very close to each other [44,45] or a large change in the direction of the trajectory. Otherwise, if there are single losses (e.g., at an underground station, etc.), activities are defined as silence intervals, where no GPS points are summited. Therefore, there are three criteria for detection of activities in situations with or without signal loss, from aspects of density, speed-satisfied-time or time difference between two consecutive GPS points [13,14].

As to what constitutes a segment, it is defined as a subset of trip. In the railway context, segments correspond to data in sections (between two adjacent stations). We denote segments as $Se=\left\{P_a,P_{a+1}\cdots P_b\right\}=\left\{d_1,d_2,\cdots d_N\right\}$, where $b-a+1=N$ and $N$ is the number of data points in a segment trajectory. The threshold based rule [19] and single loss based rule [13,19,46] are utilized to generate segments. To differentiate the stops in stations and the stops in signal range outside stations, we preset space ranges for each station. If the rules above are activated in the range, the train stops in stations. Otherwise, the train stops at signals. To describe the pattern recognition method more straightforwardly, in the remainder of this study, we also call segments data samples.

Based on segments, parameters (or profiles) such as speed, acceleration, and turning angle can be obtained. These parameters are key carriers of knowledge that could characterize the movement behavior and physics of the driving. Each parameter from a segment can be expressed as a time series $X=\left\{x_1,x_2,\cdots x_N\right\}$. In this study, we used two parameters, speed and acceleration, for extracting features, which is discussed in the following Section 2.2.

2.2. Feature Extraction

Feature extraction plays an important part in Feature engineering, which have great impacts on the performance of classifiers. In this subsection, we first presented classical extracted features including: Global Statistical Features (GSF) and Local Statistical Features (LSF), as well as Time-Domain and Frequency-Domain Features (TDFDF). Then, we proposed a new group of features named Driving Segmented Standard Deviation Features (DSSDF). DSSDF are based on railway transportation characteristics, which are designed for improving identification accuracy. The following explains each group of features in detail.

2.2.1. Classical Features

GSF [21,24,29] refer to descriptive statistics for data samples, which makes the samples more comparable. LSF [12] is extracted by profile decomposition and reveals more detail in movement behavior. TDFDF can represent characteristics from time-domain analysis and frequency-domain analysis [25,26]. We illustrate these features in

Table 1. Features of Global Statistical Features (GSF), Local Statistical Features (LSF) and Time-Domain and Frequency-Domain Features (TDFDF).

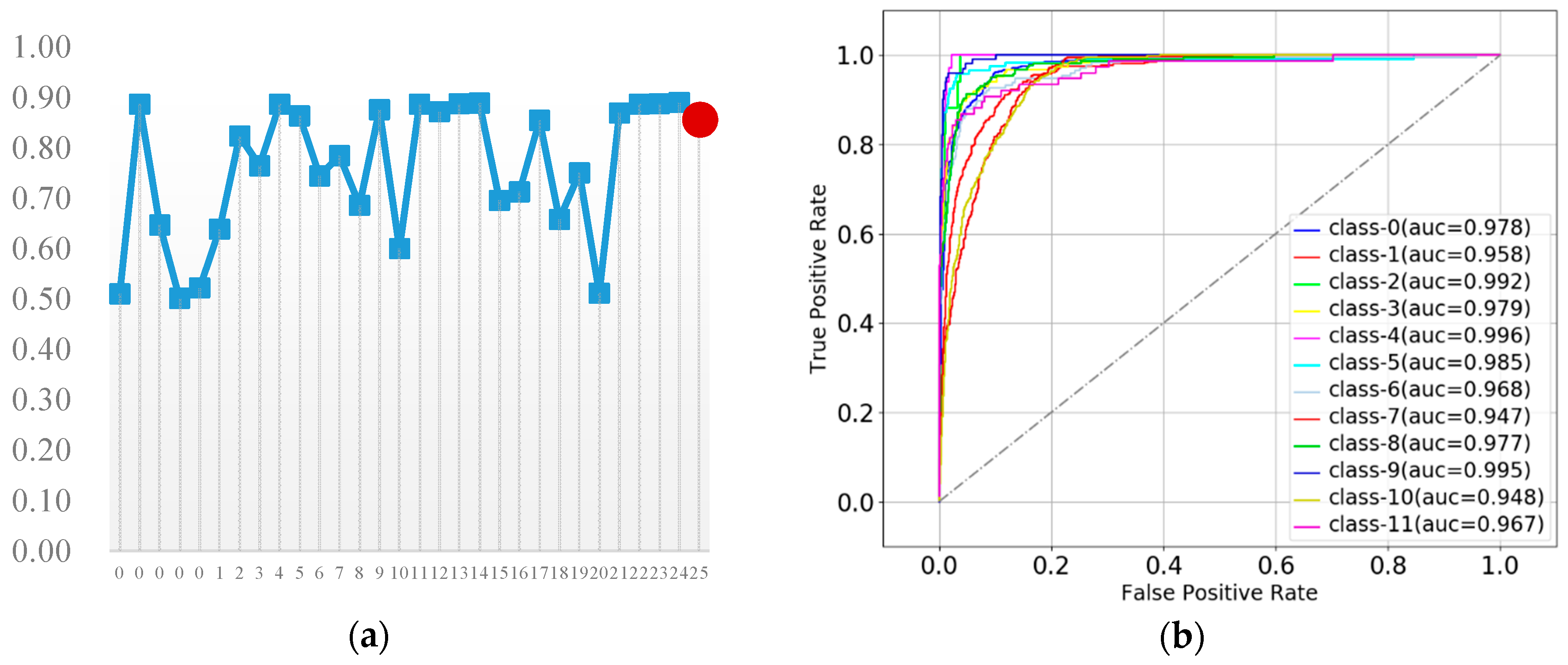
ID	G-Name (ID) 1	Name	Notation	R 2
1	GSF (1)	Mean	$u=\sum y_i/N$	[21,29]
2		Standard deviation	$\sigma =\sqrt{\frac{1}{N}{\displaystyle \sum }_i{\left(x_i-u\right)}^2}$
3		Mode	$mo=Mode\left(X\right)$
4		Median	$me=Median\left(X\right)$
5		Max 3 values Min 3 values	$ma3=Ma{x}_3\left(X\right)$ $mi3=Mi{n}_3\left(X\right)$3
6		Value Range	$vr=Ma{x}_1\left(X\right)-Mi{n}_1\left(X\right)$3
7		Percentile tuple	$perc=\left(per{c}_{25},per{c}_{75}\right)$4
8		Interquartile Range	$\left|perc\right|=per{c}_{75}-per{c}_{25}$4
9		Skewness	$s=\frac{N}{\left(N-1\right)\left(N-2\right)}{\left(\raisebox{1ex}{${{\displaystyle \sum }}_{i=1}^N\left(x_i-u\right)$}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.\right)}^3$
10		Kurtosis	$k=\frac{1}{N}{\left(\raisebox{1ex}{${{\displaystyle \sum }}_{i=1}^N\left(x_i-u\right)$}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.\right)}^4-3$
11		Coefficient of variation	$cv=\sigma /u$
12		Autocorrelation coefficient	$auto=c_1/c_0$ $c_k=\frac{1}{N}{\displaystyle \sum }_{i=1}^{N-k}\left(x_i-u\right)\left(x_{i+k}-u\right)$
13		Stop rate	$sr=\left|p_s\right|/dis$	[24]
14		Velocity change rate	$vcr=\frac{1}{dis}{\displaystyle \sum }_{i=2}^{N}I\left\{\left(x_i-x_{i-1}\right)\ge {\xi }_s\right\}$5
15		Trajectory length	$dis=d\left(X\right)$
16	LSF (2)	Mean length of each decomposition class	$l{u}_{0-3}=\frac{1}{nx{s}_{0-3}}{\displaystyle \sum }_{i=1}^{nx{s}_{0-3}}Len\left(x{s}_i^{0-3}\right)$6	[12]
17		Length standard deviation of each decomposition class	$l{\sigma }_{0-3}=\sqrt{\frac{1}{nx{s}_{0-3}}{\displaystyle \sum }_i{\left(Len\left(x{s}_i^{0-3}\right)-l{u}_{0-3}\right)}^2}$6
18		Proportion of each decomposition class	$l{p}_{0-3}=\frac{1}{N}{\displaystyle \sum }_{i=1}^{nx{s}_{0-3}}Len\left(x{s}_i^{0-3}\right)$6
19		Change times	$ct=\sum nx{s}_{0-3}-1$6
20	TDFDF (3)	Median crossover rate	$mcr=\frac{1}{N-1}{\displaystyle \sum }_{i=1}^{N-1}I\left\{\left(x_i-me\right)\times \left(x_{i-1}-me\right)<0\right\}$5	[25,26]
21		Number of peaks	$peak={\displaystyle \sum }_{i=1}^{N-2}I\left\{sign\left(x_i-x_{i-1}\right)>sign\left(x_{i+1}-x_i\right)\right\}$5 $sign\left(a\right)=\{\begin{array}{c}+1\left(a>0\right)\\ 0\left(a=0\right)\\ -1\left(a<0\right)\end{array}$
22		Short-time Fourier transform	$stf{t}^k={\displaystyle \sum }_{\forall i}{x}_i{w}_i{e}^{-j\frac{2\pi ki}{N}}$ $w_i=\{\begin{array}{c}1(0<i\le N-1)\\ 0otherwise\end{array}$

¹ Group Name (ID); ² References; ³ $Ma{x}_k\left(X\right)$ and $Mi{n}_k\left(X\right)$ are the maximal and minimal k values of points in $X$; ⁴ $per{c}_k$ is the kth percentile of $X$; ⁵ $I\left\{x\right\}$ is the indicator function; ⁶ $nx{s}_{0-3}$ represents the number of decomposition segments of classes $0-3$. $x{s}_i^{0-3}$ represents the ith decomposition segments. $Len\left(x{s}_i^{0-3}\right)$ calculates the length of decomposition $x{s}_i^{0-3}$.

.

2.2.2. Driving Segmented Standard Deviation Features (DSSDF)

Although the classical features were proved efficient in the field of transportation mode detection [21], these features still cannot effectively represent MDRT; modes in MDRT are differentiated by microscopic driving details (e.g., some modes have two acceleration phases, and some modes have two breaking phases, etc.). Specific features with rich information are needed in this study. Thus, we designed DSSDF, which measures deviations between modes and each Planed Traction Curve (PTC) of running plans (as discussed in Section 2.1.1) to improve the quality of identification of MDRT.

As a complex system, railway requires many plans or benchmarks to ensure the efficiency and feasibility of operation. In terms of train driving, the PTC is the most important benchmark (PTC is the ideal driving curve designed by the railway design department by means of an experience summary or Newtonian mechanics calculation [5]). Trajectories in each mode would obey a certain distribution in parts or whole scales. If we measure the differences between a trajectory and the PTC by a certain way, the identifications might obtain more information and thus be more accurate.

Driving Segmented Standard Deviation Features $ssd\left(s_i,p_j\right)$ measures the differences between a sub-segment and the sub-PTC corresponding to the same distance sub-range $s_i$ of running plan $p_j$.

$$\begin{gathered} ssd\left(s_i,p_j\right)=DTW\left(X_{\left(s_i\right)},PT{C}_{\left(s_i,p_j\right)}\right) \\ {{\displaystyle \bigcup }}_i{X}_{\left(s_i\right)}=X,{{\displaystyle \bigcup }}_{i}PT{C}_{\left(s_i,p_j\right)}=PT{C}_{p_j},\mathrm{and}{\displaystyle \bigcup }{s}_i=S \end{gathered}$$

(1)

where $X_{\left(s_i\right)}$ is the sub-segment and $S$ is the distance range corresponding to a target parameter. $s_i$ is the ith ($0\le i<n_s$, $n_s$ represents the number of sub-segments) sub-range of the distance range $S$. $PT{C}_{\left(s_i,p_j\right)}$ is the sub-PTC of $PT{C}_{p_j}$. $PT{C}_{p_j}$ is the PTC of running plan $p_j$. ($0\le j<n_p$, $n_p$ represents the number of running plans). $DTW\left(T_{\left(s_i\right)},PT{C}_{\left(s_i,p_j\right)}\right)$ is a function measuring similarity between $X_{\left(s_i\right)}$ and $PT{C}_{\left(s_i,p_j\right)}$ by the method of Dynamic Time Warping (DTW). The details of DTW can be found in Keogh et al. [47]. The number of PTCs depends only on existing running plans, which can be found in railway plans.

We illustrate the measurements of $ssd\left(s_i,p_j\right)$ with 4-folds ($n_s=4$) and 1 PTC in Figure 4. In this illustration, two parameter trajectories, speed and time, are taken into account. From the aspect of distance range, trajectories and PTCs are divided into 4 sub-ranges (distance sub-ranges 1, 2, 3, 4). Therefore, we extract 8 DSSDF from this example (e.g., in distance sub-range 1, there are two features calculated by $DTW\left(T{1}_{\left(1\right)},PT{C}_{\left(1,1\right)}\right)$ corresponding to origin-cube curve and blue-cube curve as well as $DTW\left(T1t_{\left(1\right)},PTC{t}_{\left(1,1\right)}\right)$ corresponding to yellow-triangle curve and gray-triangle curve) and so on for the other 6 DSSDF. If there is more than one PTC (multiple running plans), differences between a trajectory and any PTC should be measured.

If we just set $n_s=1$, and only 2 DSSDF could be extracted, the result might be inaccurate. Conversely, if we set $n_s$ too large, the calculation cost might be very high. As a key control parameter, the number of sub-segments $n_s$ plays an important part in identifications of MDRT. A proper value of $n_s$ should be found before training classifiers.

As to the criteria of determining the sub-segment, we used signal ranges as the basic units for starting a new sub-segment. In addition, we used a greedy search method that assumes that drivers have more details about driving when leaving and entering stations than when cruising in the middle of a section to generate sub-segments. After enter $n_s$, this search method begins by setting the signal range nearest to the arrival station as a new sub-segment; after that, set the signal range nearest the departure station. In addition, set the second nearest signal range to the arrival station as the third sub-segment. This iteration does not stop until $n_s$ is achieved. Although this method is rough, its efficiency and interpretability are acceptable in practical applications. The determination process of $n_s$ will be discussed in Section 3.3.

2.2.3. Features Summary

A summary of the features discussed above is shown in

Table 2. Feature Summary.

ID	Descriptors	Feature Description	Number
1	GSF	$u$, $\sigma$, $mo$, $me$, $ma3$(3), $mi3$(3), $vr$, $perc$(2), $\left|perc\right|$, $s$, $k$, $cv$, $auto$. For each parameter (2).	$18\times 2=36$
		$sr$, $vcr$, $dis$.	3
2	LSF	$lu$(4), $l\sigma$(4), $lp$(4), $ct$. For each parameter (2).	$\left(4+4+4+1\right)\times 2=26$
3	TDFDF	$mcr$, $peak$, $stft$. For each parameter (2).	$3\times 2=6$
4	DSSDF	$ssd$ ($n_s$). For each parameter (2).	$n_s\times n_p\times 2=2·n_p·n_s$
	SUM		$\left(36+3\right)+26+6+2n_s$ $=71+2·n_p·n_s$

. In Figure 5, we plotted the distribution of six example-features (of 12 modes) mentioned above. However, we found it difficult to differentiate between the different modes using only one feature. Nevertheless, these features can provide useful information in identifying MDRT when they are combined.

2.3. Classifiers Modeling and Parameter Tuning

2.3.1. Classifiers Modeling

In this study, Ensemble classifiers (AdaBoost [48,49], Random Forest (RF) [50], Gradient Boosting Decision Tree (GBDT) [51,52], and eXtreme Gradient Boosting (XGBoost) [39,40]) and single classifiers (K-Nearest Neighbor (KNN) [21,34,35,53] and Support Vector Machine (SVM) [54,55]) were modeled to identify MDRT. The details can be found in their respective references.

As to the implementations of classifiers, the KNN, SVM, AdaBoost, RF, and GBDT models were implemented in the Python software along with “scikit-learn” package. In addition, the XGBoost model was implemented in the Python software along with “XGBoost” package.

2.3.2. Parameter Tuning

In machine learning, parameter tuning (also called hyperparameter optimization) is the problem of choosing a set of optimal hyperparameters for a learning algorithm [38,56]. Grid search [57,58], Random search [59,60], Bayesian optimization [61,62,63,64], and Gradient-based optimization [65] are four existing methods of tuning parameters. In practice, Bayesian optimization has been shown to obtain better results in fewer evaluations compared to grid search and random search due to the ability to reason with respect to the quality of experiments before they are run [61,62,63,64]. Therefore, we chose Bayesian optimization to conduct parameter tuning. The details of Bayesian optimization can be found in references [61,62,63,64].

The tuning parameters of each classifier and the setting of parameter ranges for parameter tuning are shown in

Table 3. Parameter Ranges for Parameter Tuning.

Classifier	Parameter Range	Notes
KNN	“n_neighbors”: (1, 15)	n_neighbors (int): Number of neighbors to get.
SVM	“C”: (0.001, 100) “gamma”: (0.0001, 0.1)	C (float): Penalty parameter C of the error term. gamma (float): Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
Ada	“n_estimators”: (10, 250) “learning_rate”: (0.001, 0.1)	n_estimators (int): The maximum number of estimators at which boosting is terminated. learning_rate (float): Learning rate shrinks the contribution of each classifier by ‘learning_rate’. There is a trade-off between “learning_rate” and “n_estimators”.
RF	“n_estimators”: (10, 200) “min_samples_split”: (2, 15) “max_features”: (0.1, 0.999)	n_estimators (int): number of trees in the forest. min_samples_split (int or float): The minimum number (int) or percentage (float) of samples required to split an internal node. max_features (int or float): The number or percentage of features to consider when looking for the best split.
GBDT	“n_estimators”: (10, 250) “learning_rate”: (0.1, 0.999) “subsample”: (0.1, 0.9)	n_estimators (int): The number of boosting stages to perform. learning_rate (float): learning rate shrinks the contribution of each tree by ‘learning_rate’. subsample (float): The fraction of samples to be used for fitting the individual base learners.
XGBoost	“min_child_weight”: (1, 10) “colsample_bytree”: (0.1, 1) “max_depth”: (5, 10) “subsample”: (0.5, 1) “gamma”: (0, 1) “alpha”: (0, 1) “eta”: (0.001, 0.1)	min_child_weight (int): Minimum sum of instance weight (Hessian) needed in a child. colsample_bytree (float): Subsample ratio of columns when constructing each tree. max_depth (int): Maximum tree depth for base learners. subsample (float): Subsample ratio of the training instance. gamma (float): Minimum loss reduction required to make a further partition on a leaf node of the tree. alpha (float): L1 regularization term on weights eta (float): Boosting learning rate.

.

2.4. Evaluation Methods and Cross-Validation

2.4.1. Evaluation Indicators

An appropriate evaluation framework could help to estimate performance. Basically, samples in classification problems are divided into four categories: true positives; true negatives; false positives; and false negatives. These four categories are shown in Figure 6 as (3), (4), (5), and (6), respectively. Based on these four categories, an evaluation system is established. The arrangement of the indicators in Figure 6 portrays the relationship between them. For example, indicator Recall (10) is calculated from condition positive (1) and true positive (3). Thus it is arranged in row 3 column 1. Indicators in this evaluation system were widely used in existing studies to represent performance [19,21,25,27,28].

In this study, we used PPV, TPR, F₁-score, ACC, confusion matrix and Receiver Operating Characteristic curve (ROC, whose x-axis is FPR and y-axis is TPR, in Figure 6), which are marked blue in Figure 6 to evaluate performances of proposed features and classifiers.

2.4.2. K-Fold Cross-Validation

K-fold cross validation is a technique used to obtain more reliable, stable and accurate models in machine learning. In k-fold cross validation, the original samples are randomly partitioned into k equal parts; of the k parts, a single part is used as the validation dataset, and the remaining k-1 subparts are used as the training dataset to construct the model. This procedure is repeated k times, where a different validation dataset is chosen each time, before the final accuracy of the model is equal to the average accuracy obtained each time. All samples are used for both training and validation, and each sample is used for validation exactly once [21]. For example, a dataset has 10 samples. If we use five-fold cross validation to train a model, this dataset will be divided into 5 parts (each with 2 samples), named 1–5. The training process has 5 rounds. In the first round, part 1 is used as the validation dataset, and parts 2–4 are used as the training dataset to construct the model. In the remaining rounds, parts 2–4 are used as validation dataset, respectively. The final accuracy of the model is equal to the average accuracy obtained each round.

The k-fold cross-validation was embedded in the classifier training processes of our experiment, which can guide parameter tuning processes by estimated generalization performance [60].

3. Results and Discussion

3.1. Experiment Data

A dataset of trajectories over a period (of seven years from January 2009 to January 2013) from a section (Dongsheng–Aobaogou) in Baoshen Railway, Inner Mongolia, China was collected for validating the performance of the models (shown in Figure 7). This dataset contains 20,349 trajectories (approximately 13.94 trajectories per day) produced by 103 locomotives. Almost all the trajectories were recorded densely; i.e., the locomotives use an event-based recording mechanism to record trajectories. That is, if an event occurs (e.g., speed change, gear change), the locomotive submit one record (one data point) to the database.

In this experiment, 12 modes (the representative trajectories are shown in Figure 7b) were identified, and 2 PTCs (i.e., PTC i and PTC ii) corresponding to two running plans (shown in Figure 7c) are used to extract DSSDF. Modes 0–3 stop in both stations (stop-stop). 4–11 stop only in departure station and pass arrival station (stop-pass). The details of these 12 modes are summarized as follows: (1) Mode 0 tries to conduct PTC i; (2) mode 1 slows down in advance; (3) mode 2 slowly moves forward, and the speed does not increase to the speed limit; (4) mode 3 first moves forward at low speed and then accelerates to the speed limit; (5) model 4 tries to conduct PTC ii and passes through the main track; (6) mode 5 passes the station after a large proportion of deceleration; (7) mode 6 slows down a little in advance and passes the station; (8) mode 7 slowly moves forward, and the speed does not increase to the speed limit. In addition, it then passes the station; (9) mode 8 accelerates to the speed limit and starts to decelerate and then re-accelerates and passes the main track; (10) mode 9 accelerates to the speed limit and starts to decelerate and passes at low speed; (11) mode 10 passes the station through a side line; (12) mode 11 slowly accelerates and then passes through the main track.

In this dataset, 1/3 of trajectories were labeled with their modes in each segment. The dataset was separated into a training set (consisting of 70% of the data) and a testing set (30% of the data). The distribution of the number of different categories is shown in

Table 4. The distribution of MDRT in this experiment.

Mode ID	Trajectory Number	Mode ID	Trajectory Number
0	1218	6	441
1	1029	7	1050
2	42	8	546
3	462	9	252
4	84	10	1176
5	294	11	189
		SUM	6783

. As the distribution of the different categories was unbalanced, it was unreasonable to base our evaluation on accuracy alone, despite this being commonly done in the previous literature. Furthermore, it was difficult to evaluate the performance of the model based on a single measure as these measures are sometimes the same. Thus, in our study, different evaluation elements were used, including PPV, TPR, F₁-Score, ROC curve and confusion matrix. We used accuracy (ACC), which is obtained from five-fold Cross-Validation, to tune the parameters (by Bayesian optimization) [21].

3.2. Experiment Scheme

We extracted four groups of features from 6783 trajectories, including GSF (indexed by 1), LSF (indexed by 2), TDFDF (indexed by 3), and DSSDF (indexed by 4), and then used six types of classifiers (KNN, SVM, Ada, RF, GBDT, and XGBoost) to identify MDRT. In this experiment, we need to fulfill the following tasks: (i) Finding the optimal value of $n_s$, i.e., determining the most suitable extraction method for DSSDF; (ii) Evaluating performances of classifiers by different indicators; (iii) Evaluating and comparing performances of different combinations of features and classifiers.

As to task (i), we extracted DSSDF and used XGBoost to determine the optimal value of $n_s$ for the purpose of improving performance identification in the following tests. A candidate set of $n_s$ $\left\{1,2,3,4,5,6\right\}$ was used to extract a set of DSSDF and fed to XGBoost. A curve of indicator ACC was presented for selecting the optimal value of $n_s$. In the processes of trainings with different features, Bayesian optimization and five-fold cross-validation were used to tune parameters so that the XGBoost classifier was in a good situation. The optimal value of $n_s$ would be used in the following trainings.

As to task (ii), we analyzed the performances of six classifiers including two types of single classifiers and four types of ensemble classifiers aggregated with the complete feature group combinations (i.e., $\left\{\mathrm{GSF},\mathrm{LSF},\mathrm{TDFDF},\mathrm{DSSDF}\right\}$, denoted by “1234”) by indicators ROC(AUC), ACC, PPV, TPR, F₁-score. Two single classifiers formed the control group as a basis for measuring the performances of the ensemble classifiers. Bayesian Optimization and five-fold cross-validation were used to tune the parameters of each classifier.

As to task (iii), we evaluated different combinations of the six classifiers and feature groups (i.e., the non-empty power set of set $\left\{\mathrm{GSF},\mathrm{LSF},\mathrm{TDFDF},\mathrm{DSSDF}\right\}$) by indicator ACC to analyze matching relationships between features and classifiers. In addition, the efficiency of DSSDF was evaluated quantitatively here. Bayesian Optimization and five-fold cross-validation were used to tune parameters.

As to parameter tuning, we used the Bayesian Optimization method in the Python software along with the “Bayesian-Optimization” package. The parameters were set as: “n_iter”: 25 and “init_points”: 5, which means the tuning has an initialization with 5 parameter points and 25 iterations. When tuning parameters, “int” type parameters were converted to “real” type fed to Gaussian Process of Bayesian optimization and were converted back to “int” type fed to classifiers.

3.3. Determination the Optimal Value of $n_s$

As discussed in Section 2.2, the extractions of DSSDF are controlled by parameter $n_s$. In this subsection, we conducted an experiment that fed different DSSDF with different $n_s$ to XGBoost and then selected the optimal $n_s$ according to identification performance (evaluated by indicator ACC).

We measured different DSSDF from the $n_s$ collection $\left\{1,2,3,4,5,6\right\}$ (in this section, there are 6 signal ranges) and then trained XGBoost (tuning parameters by Bayesian Optimization with indicator ACC). The Results are shown in Figure 8. We find that 4 is the best value of $n_s$.

3.4. Classifiers Performance Evaluations

3.4.1. K-Nearest Neighbor

Figure 9a and

Table 5. Parameter Tuning Process of KNN Classifier.

I 1	n_n(int) 2	ACC	I 1	n_n(int) 2	ACC	I 1	n_n(int) 2	ACC
0	5.91 (5)	74.1%	6	13.97 (13)	65.6%	16	1.69 (1)	60.1%
0	2.06 (2)	68.3%	7	4.76 (4)	68.6%	17	5.28 (5)	74.1%
0	10.50 (10)	66.8%	8	11.64 (11)	66.1%	18	5.18 (5)	74.1%
0	3.83 (3)	69.4%	9	6.72 (6)	68.1%	19	5.75 (5)	74.1%
0	7.68 (7)	68.0%	10	5.43 (5)	74.1%	20	5.74 (5)	74.1%
1	15.00 (15)	65.9%	11	8.41 (8)	67.5%	21	6.25 (6)	68.1%
2	12.83 (12)	65.6%	12	9.83 (9)	67.5%	22	5.00 (5)	74.1%
3	7.74 (7)	68.0%	13	4.25 (4)	68.6%	23	5.62 (5)	74.1%
4	1.00 (1)	60.1%	14	14.53 (14)	65.4%	24	5.18 (5)	74.1%
5	9.10 (9)	67.5%	15	12.23 (12)	65.6%	25	5.75 (5)	74.1%

¹ Iteration; ² n_neighbors (the value converted to type “int”).

show the changes in ACC in the process of parameter tuning, which was obtained using Bayesian optimization and five-fold cross-validation. From Table 5, we can see that the highest ACC was achieved when K was 5.43, 5.28, 5.18, 5.75 5.74, 5.00 (5), and the value was 74.1%. The ROC curve is plotted in Figure 9b, and the confusion matrix is presented in

Table 6. The Confusion Matrix of the KNN Classifier.

KNN		A
		0	1	2	3	4	5	6	7	8	9	10	11	PPV
P	0	80.7	14.6	11.8	4.9	2.9	0.0	4.0	0.7	0.5	0.0	1.9	13.2	77.7
	1	10.5	75.5	11.8	22.7	2.9	6.8	5.7	0.7	0.9	0.0	0.4	1.3
	2	0.6	0.5	76.5	0.5	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
	3	1.8	7.3	0.0	68.6	0.0	0.0	0.6	0.5	0.9	2.0	0.2	1.3
	4	0.0	0.0	0.0	0.0	67.6	0.8	0.0	0.0	0.0	0.0	0.0	0.0
	5	0.2	0.0	0.0	0.0	8.8	72.9	2.3	0.0	0.9	3.0	0.0	0.0
	6	1.0	0.7	0.0	0.0	2.9	6.8	60.2	1.0	8.3	2.0	3.8	3.9
	7	1.4	0.2	0.0	0.0	0.0	2.5	1.7	69.5	3.2	1.0	14.9	10.5
	8	0.4	0.5	0.0	2.7	14.7	5.9	10.2	2.4	76.6	4.0	2.1	3.9
	9	0.0	0.0	0.0	0.0	0.0	2.5	3.4	0.0	0.0	87.1	0.0	0.0
	10	2.9	0.7	0.0	0.0	0.0	1.7	9.7	25.0	7.8	1.0	76.6	5.3
	11	0.4	0.0	0.0	0.5	0.0	0.0	2.3	0.2	0.9	0.0	0.0	60.5
	TPR	72.9												F1: 74.9

. The weighted mean of AUC was 0.85. The F₁-score was 74.9%. The PPV was 77.7%. The TPR was 72.9%. These indicators show the poor performance of KNN, which led to the conclusion that this classifier is not suitable for differentiating MDRT.

3.4.2. Support Vector Machines

Figure 10a and

Table 7. Parameter Tuning Process of SVM Classifier.

I 1	C	Gamma	ACC	I 1	C	Gamma	ACC	I 1	C	Gamma	ACC
0	43.936	0.03	50.9%	6	0.001	0.03	74.3%	16	0.002	0.08	71.2%
0	5.636	0.09	88.6%	7	99.999	0.10	78.4%	17	99.996	0.04	85.4%
0	7.577	0.07	64.6%	8	0.007	0.03	68.5%	18	0.004	0.07	65.7%
0	43.207	0.08	50.0%	9	0.004	0.03	87.5%	19	100.000	0.00	75.0%
0	79.405	0.04	52.1%	10	100.000	0.09	59.9%	20	100.000	0.00	51.1%
1	99.999	0.09	63.8%	11	0.002	0.02	88.6%	21	0.005	0.04	86.8%
2	0.001	0.04	82.2%	12	0.008	0.07	87.1%	22	0.001	0.07	88.6%
3	99.999	0.07	76.4%	13	0.004	0.07	88.7%	23	0.002	0.07	88.7%
4	0.004	0.10	88.6%	14	0.003	0.01	88.8%	24	0.001	0.01	88.9%
5	99.996	0.09	86.3%	15	0.002	0.08	69.5%	25	0.003	0.06	86.2%

¹ Iteration.

show the changes in ACC in the process of parameter tuning, which was obtained using Bayesian optimization and five-fold cross-validation. From Table 7, we can see that the highest ACC was achieved when “C” was 0.001 and “gamma” was 0.01, and the corresponding value was 88.9%. The ROC curve is plotted in Figure 10b, and the confusion matrix is presented in

Table 8. The Confusion Matrix of the SVM Classifier.

SVM		A
		0	1	2	3	4	5	6	7	8	9	10	11	PPV
P	0	92.2	6.8	0.0	2.7	0.0	0.0	2.8	1.0	0.0	0.0	0.4	3.9	88.0
	1	5.7	88.1	5.9	5.9	2.9	1.7	2.3	1.0	0.9	1.0	0.4	0.0
	2	0.2	0.0	88.2	0.5	8.8	0.0	0.0	0.0	0.0	0.0	0.0	0.0
	3	0.2	3.4	5.9	88.1	0.0	0.8	0.0	0.2	0.0	0.0	0.2	1.3
	4	0.0	0.0	0.0	0.0	85.3	2.5	2.3	0.0	0.0	0.0	0.0	0.0
	5	0.0	0.0	0.0	0.0	2.9	90.7	0.0	0.0	0.9	3.0	0.0	0.0
	6	0.6	0.2	0.0	0.0	0.0	0.0	86.4	1.0	1.4	1.0	1.3	0.0
	7	0.2	0.2	0.0	0.0	0.0	0.0	1.7	86.9	0.9	0.0	7.7	1.3
	8	0.0	0.2	0.0	0.5	0.0	1.7	1.1	0.7	92.2	2.0	1.9	7.9
	9	0.0	0.0	0.0	0.5	0.0	2.5	0.6	0.0	0.0	91.1	0.0	1.3
	10	0.6	0.5	0.0	0.0	0.0	0.0	2.8	9.3	3.2	0.0	88.1	1.3
	11	0.2	0.5	0.0	1.6	0.0	0.0	0.0	0.0	0.5	2.0	0.0	82.9
	TPR	88.5												F1: 88.2

. The weighted mean of AUC was 0.97. The F₁-score was 88.2%. The PPV was 88.0%. The TPR was 88.5%. These indicators show that although the SVM model performed better than the KNN model, it still cannot effectively identify MDRT.

3.4.3. AbaBoost

Figure 11a and

Table 9. Parameter Tuning Process of AdaBoost Classifier.

I 1	n_e(int) 2	l_r 3	ACC	I	n_e(int)	l_r	ACC	I	n_e(int)	l_r	ACC
0	130.42 (130)	0.07	82.5%	6	78.22 (78)	0.00	81.2%	16	160.28 (160)	0.00	75.9%
0	89.48 (89)	0.06	83.8%	7	94.43 (94)	0.00	75.4%	17	183.11 (183)	0.00	79.3%
0	216.15 (216)	0.07	82.2%	8	192.64 (192)	0.10	81.6%	18	18.81 (18)	0.10	81.4%
0	230.86 (230)	0.08	82.3%	9	29.19 (29)	0.10	80.1%	19	84.10 (84)	0.10	81.1%
0	233.10 (233)	0.02	84.3%	10	150.89 (150)	0.10	81.0%	20	65.29 (65)	0.10	80.9%
1	10.00 (10)	0.01	75.6%	11	119.18 (119)	0.10	81.1%	21	71.37 (71)	0.10	80.4%
2	250.00 (250)	0.05	81.3%	12	204.05 (204)	0.00	80.0%	22	113.07 (113)	0.00	75.6%
3	171.39 (171)	0.00	75.2%	13	39.52 (39)	0.10	81.1%	23	125.01 (125)	0.00	75.7%
4	50.67 (50)	0.00	75.3%	14	140.94 (140)	0.00	75.8%	24	210.52 (210)	0.10	81.4%
5	108.26 (108)	0.00	82.1%	15	242.32 (242)	0.10	82.0%	25	58.44 (58)	0.10	81.8%

¹ Iteration; ² n_estimators (the value converted to type “int”); ³ learning_rate.

show the changes in ACC in the process of parameter tuning, which was obtained using Bayesian optimization and five-fold cross-validation. From Table 9, we can see that the highest ACC was achieved when “n_estimators” was 233.10 (233) and “learning_rate” was 0.02, and the corresponding value was 84.3%. The ROC curve is plotted in Figure 11b, and the confusion matrix is presented in

Table 10. The Confusion Matrix of the AdaBoost Classifier.

Ada		A
		0	1	2	3	4	5	6	7	8	9	10	11	PPV
P	0	96.5	11.2	5.9	5.9	0.0	0.8	5.1	2.9	0.9	0.0	4.7	7.9	91.5
	1	1.8	85.9	11.8	16.8	8.8	11.0	5.1	1.0	9.2	16.8	0.2	14.5
	2	0.0	0.0	82.4	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
	3	0.0	0.5	0.0	76.2	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
	4	0.0	0.0	0.0	0.0	82.4	0.0	0.0	0.0	0.0	0.0	0.0	0.0
	5	0.0	0.0	0.0	0.0	0.0	72.0	0.0	0.0	0.0	0.0	0.0	0.0
	6	0.0	0.0	0.0	0.0	8.8	3.4	80.7	0.0	4.6	1.0	0.0	0.0
	7	0.0	0.0	0.0	0.0	0.0	0.0	0.0	75.7	0.0	0.0	1.3	2.6
	8	0.0	0.2	0.0	0.0	0.0	11.9	4.5	0.0	78.4	8.9	0.4	3.9
	9	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	73.3	0.0	0.0
	10	1.6	2.2	0.0	1.1	0.0	0.8	4.5	20.5	6.9	0.0	93.4	2.6
	11	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	68.4
	TPR	79.6												F1: 84.4

. The weighted mean of AUC was 0.95. The F₁-score was 84.4%. The PPV was 91.5%. The TPR was 79.6%. These indicators show that the AdaBoost is weaker than the SVM model when identifying MDRT.

3.4.4. Random Forest

Figure 12a and

Table 11. Parameter Tuning Process of Random Forest Classifier.

I 1	n_e(int) 2	m_s 3	m_f 4	ACC	I 1	n_e(int) 2	m_s	m_f	ACC
0	109.17 (109)	14.51	0.66	88.8%	11	60.86 (60)	2.00	0.10	86.2%
0	128.93 (128)	11.59	0.16	88.9%	12	188.44 (188)	8.18	0.11	88.1%
0	82.95 (82)	7.90	0.76	88.1%	13	10.00 (10)	2.00	1.00	85.5%
0	173.56 (173)	3.06	0.55	90.2%	14	163.27 (163)	8.70	0.11	86.9%
0	151.51 (151)	9.24	0.40	90.9%	15	70.61 (70)	15.00	1.00	87.4%
1	199.83 (199)	14.90	0.40	88.9%	16	118.81 (118)	4.19	1.00	88.3%
2	158.00 (158)	2.04	0.40	88.7%	17	188.43 (188)	2.26	0.99	88.2%
3	10.00 (10)	15.00	0.40	79.7%	18	94.25 (94)	14.94	0.99	88.2%
4	170.47 (170)	14.97	0.40	88.3%	19	144.86 (144)	8.30	1.00	87.9%
5	51.23 (51)	15.00	0.40	85.2%	20	81.62 (81)	14.96	0.12	86.8%
6	199.98 (199)	2.05	0.40	89.6%	21	182.48 (182)	14.97	0.10	87.1%
7	138.00 (138)	2.03	0.40	87.7%	22	29.87 (29)	15.00	1.00	86.6%
8	29.14 (29)	2.00	0.40	82.8%	23	75.74 (75)	2.00	1.00	87.4%
9	144.82 (144)	14.97	0.40	87.1%	24	120.71 (120)	14.92	0.16	88.9%
10	104.86 (104)	2.00	0.40	87.7%	25	199.81 (199)	8.60	0.97	88.5%

¹ Iteration; ² n_estimators (the value converted to type “int”); ³ min_samples_split; ⁴ max_features.

show the changes in ACC in the process of parameter tuning, which was obtained using Bayesian optimization and five-fold cross-validation. From Table 11, we can see that the highest ACC was achieved when “n_estimators” was 151.51 (151), “min_samples_split” was 9.24 and “max_features” was 0.40, and the corresponding value was 90.9%. The ROC curve is plotted in Figure 12b, and the confusion matrix is presented in

Table 12. The Confusion Matrix of the Random Forest Classifier.

RF		A
		0	1	2	3	4	5	6	7	8	9	10	11	PPV
P	0	94.7	5.6	5.9	2.2	0.0	0.8	2.3	0.0	0.9	0.0	1.3	7.9	93.7
	1	3.9	90.5	11.8	10.3	2.9	2.5	2.8	0.2	0.5	0.0	0.0	1.3
	2	0.0	0.0	76.5	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
	3	0.4	1.5	0.0	87.6	0.0	0.0	0.0	0.0	0.0	1.0	0.0	1.3
	4	0.0	0.2	0.0	0.0	82.4	0.0	0.0	0.0	0.0	0.0	0.0	0.0
	5	0.2	0.0	0.0	0.0	11.8	93.2	1.1	0.0	2.3	0.0	0.0	1.3
	6	0.2	0.2	0.0	0.0	0.0	1.7	88.1	0.0	1.8	0.0	0.4	5.3
	7	0.4	0.7	0.0	0.0	0.0	0.0	0.6	92.6	0.9	0.0	7.0	5.3
	8	0.0	0.5	0.0	0.0	0.0	0.8	1.7	0.0	89.4	0.0	0.4	3.9
	9	0.0	0.0	5.9	0.0	2.9	0.8	0.0	0.0	0.5	99.0	0.0	0.0
	10	0.2	0.7	0.0	0.0	0.0	0.0	3.4	7.1	3.2	0.0	90.9	1.3
	11	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.5	0.0	0.0	72.4
	TPR	88.8												F1: 90.9

. The weighted mean of AUC was 0.98. The F₁-score was 90.9%. The PPV was 93.7%. The TPR was 88.8%. These indicators show that the RF has remarkably outperformed the KNN, SVM and Aba models. However, from the confusion matrix, we find that when identifying class2, the RF is weaker than the other classifiers. It still cannot effectively identify MDRT.

3.4.5. Gradient Boosting Decision Tree

Figure 13a and

Table 13. Parameter Tuning Process of GBDT Classifier.

I 1	n_e(int) 2	l_r 3	Subsample	ACC	I 1	n_e(int) 2	l_r	Subsample	ACC
0	218.76 (218)	0.96	0.35	25.3%	11	113.85 (113)	0.10	0.10	64.8%
0	240.10 (240)	0.82	0.77	34.9%	12	30.64 (30)	0.10	0.10	70.4%
0	123.81 (123)	0.37	0.88	81.9%	13	176.71 (176)	1.00	0.10	34.9%
0	17.96 (17)	0.68	0.56	71.3%	14	151.52 (151)	0.10	0.90	85.4%
0	137.47 (137)	0.76	0.18	38.0%	15	187.40 (187)	0.10	0.10	59.4%
1	72.03 (72)	0.10	0.10	69.2%	16	207.85 (207)	0.10	0.90	85.9%
2	99.14 (99)	1.00	0.10	24.4%	17	156.08 (156)	1.00	0.10	32.7%
3	44.94 (44)	1.00	0.90	30.3%	18	145.83 (145)	1.00	0.90	22.5%
4	181.32 (181)	0.10	0.90	86.2%	19	229.98 (229)	0.10	0.10	53.2%
5	164.68 (164)	1.00	0.90	24.1%	20	129.97 (129)	0.10	0.10	31.7%
6	196.56 (196)	1.00	0.10	32.3%	21	37.08 (37)	1.00	0.90	25.2%
7	10.00 (10)	0.10	0.10	72.9%	22	24.64 (24)	1.00	0.90	24.5%
8	250.00 (250)	0.10	0.10	27.2%	23	52.90 (52)	0.10	0.10	69.0%
9	61.47 (61)	1.00	0.90	23.5%	24	106.94 (106)	1.00	0.90	27.3%
10	82.64 (82)	1.00	0.90	26.2%	25	119.00 (119)	1.00	0.90	22.5%

¹ Iteration; ² n_estimators (the value converted to type “int”); ³ learning_rate.

show the changes in ACC in the process of parameter tuning, which was obtained using Bayesian optimization and five-fold cross-validation. From Table 13, we can see that the highest ACC was achieved when “n_estimators” was 181.32 (181), “learning_rate” was 0.10 and “subsample” was 0.90, and the corresponding value was 86.9%. The ROC curve is plotted in Figure 13b, and the confusion matrix is presented in

Table 14. The Confusion Matrix of the GBDT Classifier.

GBDT		A
		0	1	2	3	4	5	6	7	8	9	10	11	PPV
P	0	92.4	8.3	5.9	3.8	2.9	0.0	1.1	0.2	0.0	0.0	1.1	6.6	88.5
	1	6.0	86.4	17.6	9.2	2.9	0.8	0.0	0.0	0.5	1.0	0.0	0.0
	2	0.0	0.2	58.8	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
	3	0.2	1.5	11.8	84.9	0.0	0.0	0.6	0.0	0.9	4.0	0.0	0.0
	4	0.0	0.2	0.0	0.0	88.2	0.8	0.0	0.0	0.0	1.0	0.0	0.0
	5	0.0	0.0	0.0	0.0	5.9	90.7	2.3	0.0	1.8	3.0	0.0	0.0
	6	0.4	0.5	0.0	0.0	0.0	1.7	80.1	0.5	3.2	1.0	1.3	3.9
	7	0.4	1.7	0.0	0.5	0.0	0.8	2.3	86.4	2.3	0.0	12.8	6.6
	8	0.0	0.5	0.0	0.5	0.0	2.5	7.4	0.5	88.5	4.0	1.1	1.3
	9	0.0	0.0	5.9	0.5	0.0	1.7	0.0	0.0	0.5	85.1	0.0	2.6
	10	0.6	0.5	0.0	0.0	0.0	0.8	5.7	12.4	2.3	1.0	83.8	9.2
	11	0.0	0.2	0.0	0.5	0.0	0.0	0.6	0.0	0.0	0.0	0.0	69.7
	TPR	82.8												F1: 85.1

. The weighted mean of AUC was 0.97. The F₁-score was 85.1%. The PPV was 88.5%. The TPR was 82.8%. The results imply a small improvement over the KNN model, but GBDT is weaker than SVM and RF model.

3.4.6. Extreme Gradient Boosting

Figure 14a and

Table 15. Parameter Tuning Process of XGBoost Classifier.

I 1	m_c_w(int) 2	c_b 3	m_d(int) 4	Subsample	Gamma	Alpha	eta	ACC
0	4.25 (4)	0.16	9.03 (9)	0.50	0.77	0.66	0.01	61.9%
0	7.57 (7)	0.54	8.77 (8)	0.72	0.31	0.34	0.04	91.7%
0	9.37 (9)	0.30	9.79 (9)	0.68	0.95	0.42	0.05	91.1%
0	9.77 (9)	0.43	6.35 (6)	0.75	0.20	0.57	0.02	91.5%
0	8.61 (8)	0.86	5.66 (5)	0.84	0.17	0.12	0.08	91.2%
1	10.00 (10)	1.00	10.00 (10)	1.00	0.00	1.00	0.10	60.8%
2	10.00 (10)	0.10	10.00 (10)	0.50	0.00	0.00	0.00	69.9%
3	1.00 (1)	1.00	5.00 (5)	1.00	1.00	1.00	0.10	92.1%
4	6.01 (6)	0.10	5.00 (5)	1.00	1.00	1.00	0.10	88.7%
5	8.46 (8)	1.00	7.31 (7)	0.50	1.00	1.00	0.00	65.0%
6	1.00 (1)	1.00	10.00 (10)	1.00	0.00	0.00	0.10	92.6%
7	1.00 (1)	0.10	5.00 (5)	1.00	0.00	0.00	0.10	87.6%
8	6.02 (6)	1.00	10.00 (10)	1.00	1.00	0.00	0.10	91.8%
9	1.00 (1)	0.10	10.00 (10)	1.00	1.00	1.00	0.10	88.7%
10	10.00 (10)	0.10	5.00 (5)	1.00	1.00	0.00	0.10	88.7%
11	1.00 (1)	1.00	7.46 (7)	1.00	0.00	1.00	0.10	72.6%
12	6.91 (6)	0.10	10.00 (10)	1.00	0.00	1.00	0.10	86.5%
13	1.00 (1)	1.00	7.54 (7)	1.00	1.00	0.00	0.10	92.5%
14	3.91 (3)	1.00	5.00 (5)	1.00	0.00	0.00	0.10	91.8%
15	10.00 (10)	1.00	8.12 (8)	1.00	1.00	0.00	0.10	92.2%
16	10.00 (10)	1.00	5.00 (5)	1.00	0.00	1.00	0.10	91.3%
17	9.23 (9)	0.10	8.51 (8)	1.00	1.00	1.00	0.10	88.4%
18	1.00 (1)	1.00	10.00 (10)	0.50	1.00	1.00	0.00	89.9%
19	8.29 (8)	1.00	10.00 (10)	1.00	1.00	1.00	0.00	85.6%
20	6.18 (6)	0.10	5.00 (5)	0.50	0.00	0.00	0.10	86.4%
21	2.72 (2)	0.10	5.00 (5)	0.50	1.00	1.00	0.10	88.6%
22	5.34 (5)	1.00	7.52 (7)	1.00	0.00	0.00	0.10	91.8%
23	1.00 (1)	0.10	8.99 (8)	0.50	0.00	0.00	0.10	85.5%
24	3.55 (3)	1.00	10.00 (10)	1.00	0.00	0.00	0.10	92.7%
25	1.00 (1)	1.00	5.00 (5)	0.50	0.00	1.00	0.10	90.8%

¹ Iteration; ² min_child_weight (the value converted to type “int”); ³ colsample_bytree; ⁴ max_depth (the value converted to type “int”).

show the changes in ACC in the process of parameter tuning, which was obtained using Bayesian optimization and five-fold cross-validation. From Table 15, we can see that the highest ACC was achieved when “min_child_weight” was 3.55 (3), “colsample_bytree” was 1.00, “max_depth” was 10.00 (10), “subsample” was 1.00, “gamma” was 0, “alpha” was 0 and “eta” was 0.10, and the value was 92.7%. The ROC curve is plotted in Figure 14b, and the confusion matrix is presented in

Table 16. The Confusion Matrix of the XGBoost Model.

XGB		A
		0	1	2	3	4	5	6	7	8	9	10	11	PPV
P	0	95.1	4.9	0.0	1.6	0.0	0.0	0.6	0.2	0.0	0.0	1.7	2.6	92.5
	1	4.1	93.2	11.8	5.9	0.0	0.0	1.1	0.2	0.9	0.0	0.0	0.0
	2	0.0	0.0	76.5	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
	3	0.0	1.2	5.9	91.9	0.0	0.0	0.0	0.0	0.0	1.0	0.0	0.0
	4	0.0	0.0	0.0	0.0	85.3	2.5	0.0	0.0	0.0	0.0	0.0	0.0
	5	0.0	0.0	0.0	0.0	8.8	95.8	1.1	0.0	0.9	0.0	0.2	0.0
	6	0.0	0.0	0.0	0.0	0.0	0.0	90.9	0.0	2.8	0.0	0.6	1.3
	7	0.2	0.2	0.0	0.0	0.0	0.0	1.1	93.1	0.5	0.0	5.5	3.9
	8	0.0	0.2	0.0	0.0	5.9	0.8	2.3	0.0	92.7	2.0	0.9	2.6
	9	0.0	0.0	5.9	0.5	0.0	0.8	0.0	0.0	0.0	97.0	0.0	0.0
	10	0.6	0.2	0.0	0.0	0.0	0.0	2.8	6.4	2.3	0.0	91.1	3.9
	11	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	85.5
	TPR	90.0												F1: 91.2

. The weighted mean of AUC was 0.99. The F₁-score was 91.2%. The PPV was 92.5%. The TPR was 90.0%. The confusion matrix also shows that although XGBoost outperformed other classifiers when identifying modes 0, 1, 3, etc., it is not good at identifying mode 2 with only 76.5% accuracy (much less than the figure of 88.2% achieved by SVM). SVM might be better at dealing with small samples (mode 2 has only 42 labeled trajectories) than XGboost. Overall, these indicators show that the XGBoost classifier has remarkably outperformed the other classifiers when identifying MDRT.

3.5. The Comparison of Features and Classifiers

We tested different combinations of features and classifiers by ACC, which is shown in Figure 15 and

Table 17. Impacts of Features and Classifiers on ACC.

	KNN	SVM	Adaboost	RF	DBGT	XGBoost
1	32.50	56.30	48.30	50.50	58.80	57.90	Combinations
2	20.70	21.40	24.40	40.00	24.00	25.00
3	29.70	46.00	32.80	35.00	33.00	33.90
4	48.50	60.20	47.40	63.60	61.10	62.20
12	34.40	59.00	49.60	81.10	70.10	78.70
13	36.10	60.00	51.30	83.40	69.00	81.00
14	47.10	70.30	64.90	82.50	88.10	82.10
23	30.20	29.50	33.80	37.00	36.10	36.00
24	53.60	58.70	51.50	67.60	65.20	66.00
34	63.10	68.00	52.90	73.30	70.00	73.70
123	36.10	49.50	52.40	81.90	67.70	81.50
134	48.50	57.00	66.00	88.60	89.60	80.20
124	45.30	70.30	65.40	91.60	87.70	90.20
234	55.00	74.20	52.00	74.60	71.60	75.00
1234	74.13	88.91	84.30	90.94	86.22	92.70
	Classifiers

. From this comparison, we can conclude the following: (i) In general, combinations of feature groups perform better than a single feature group; (ii) Different classifiers have their own most suitable feature combinations; (iii) Overall, XGBoost is the most suitable classifier for identifying MDRT with features GSF, LSF, TDFDF, and DSSDF; (iv) The DSSDF (4) is important since all the best performances of different classifiers are related to it; (v) By comparing the results of “123” (XGBoost) and “1234” (XGBoost), we find that DSSDF results in an accuracy improvement of 11.2%.

Features in DSSDF are important mainly because the modes in MDRT mainly differ in the details of microscopic driving. It is difficult to capture these in general statistical methods. With PTCs as benchmarks, the differences between different modes can be demonstrated by segmentation and DTW calculations.

The XGBoost has a complete theoretical system that makes the modeling and tuning process clearer. At the same time, the construction process of its tree structure is more accurate and robust. These advantages make it better in this study.

4. Conclusions

An approach including data preprocessing, feature extraction, classifiers modeling, training and parameter tuning, and model evaluation was developed to infer Modes of Driving Railway Trains (MDRT) using only GPS data. To obtain better performance, we proposed four groups of features with corresponding extraction methods and used different classifiers including four ensemble classifiers and two single classifiers to identify MDRT. The experiment revealed the following: (i) Combinations of feature groups make sense when identifying MDRT, and proposed Driving Segmented Standard Deviation Features play an important role in improving identification performance with an accuracy improvement of 11.2% (using XGBoost); (ii) In general, combinations of feature groups perform better than a single feature group; (iii) Different classifiers have their own most suitable feature combinations; (iv) The XGBoost classifier is the best according to the evaluation indicators, with the highest accuracy (92.70%) from five-fold cross-validation and Bayesian optimization.

The research results of this paper have strong application value in the field of railway transportation. First, in the field of driver behavior habits, further analysis of the internal characteristics of the MDRT can give operators a large deal of micro-decision-support information, such as the driving strategy structure adopted by the driver after the delay, and the proportion of different driving behaviors in the face of signal constraints [3]. The information can help to correct parameters of planning and is of great significance for further optimizing the railway transportation plans [8]. Second, in the field of automatic driving, MDRT can provide the auto-driving system with a decision-making basis for different conditions in accordance with historical reality, reduce the optimization calculation scale and improve the feasibility of the driving scheme. Finally, in the field of capacity utilization optimization, combined with the random occupancy time model, the research results of this paper can be combined with micro-simulation models [3,7,9] and conflict detection systems [10,11] in order to improve the efficiency and feasibility of the optimization process.

In this paper, we used single classifiers and ensemble classifiers to identify MDRS. Testing more classifiers (deep learning and Bayesian network, etc.) is one part of our future work. In addition, analyzing the internal characteristics of MDRT is an important basic of implementing MDRT, which is planned for further work. How to explain the ensemble model more intuitively is also a part of our future work. Another aspect of the research that must be addressed is how to use fusion data to identify MDRS. The utilization of fusion data might improve accuracy of identification. On one hand, we need to strengthen the relevance of our research to existing railway data fusion systems [3,7,8,9,10,11]. On the other hand, approaches to collecting fusion data from other sensors in locomotives need to be mastered.