1. Introduction
Examining quantitatively the precision of historical maps has become possible because of the development of GIS, and scientific findings have therein been accumulated [
1]. In previous studies, the accuracy of the surveying and drawing in historical maps was discussed on the basis of the positional gaps that occurred when historical maps were identified on the projection coordinate system for various current maps [
2,
3]. In other words, geospatial analyses were conducted to examine what georeferences made historical maps match with current maps [
4].
If the precision of historical maps can be verified scientifically, we can advance geographical studies analyzing the distribution patterns of the features and reproducing the landscape and communities from that time. In previous studies in this field, the following outcomes are noted: (1) the study of the transformation of the urban spatial structures of castle towns in the Edo era by measuring the transition of the land-use [
5], (2) the study of constructing a system with a 3D comparison between the scene in the 1940s and that in the current age in Kyoto [
6], and (3) the study of analyzing the landscape of Tokyo in the 1830s with 3D visualization [
7]. It is essential to develop these previous investigations further. The reconstruction of old landscapes and the reproduction of the traditional communities are evolving as primary research themes for the historical GIS of the next generation.
When comparing many maps prepared in different ages, it is required that the same projection method is commonly used for all of them [
8]. In reality, projection method differs from one map to another. There are many maps in which the projection method is unknown. Therefore, previous studies have focused on exploring the spatiotemporal changes from the past to the present, by merely applying georeference to historical maps without thoroughly examining the precision of those historical maps themselves [
9,
10]. To investigate the survey condition in the late Edo era, it is crucial to not only explore the map precision but also to examine the factors of the spatial distortion based on the traditional methodology.
Based on the points above, the purpose of this study is to explore the distortion of INŌ’s maps quantitatively and then to delineate the factors of spatial distortion by focusing on the geodetic datum, projection method, surveying method, and surroundings, among other factors.
2. Materials and Methods
Historical maps are generally divided into two categories: 1) the maps drawn pictorially without implementing the survey, and 2) the maps with actual surveying (surveyed drawings). In light of the purpose of this study, the latter is preferable. The oldest maps surveyed for the whole of Japan are the so-called “INŌ’s maps.” There are various types of INŌ’s maps such as small-scale (approximately 1:432,000) maps which cover the whole land of Japan with three pieces; medium-scale (approximately 1:216,000) maps which include the entire territory of Japan with eight pieces; large-scale (approximately 1:36,000) maps which are divided into 214 parts corresponding to each area; and INŌ’s Tokyo map (approximately 1:6000) which covers the wider Tokyo area. Surveying by Tadataka Inō was conducted from 1800 to 1816. The maps covering the whole of Japan were completed in 1821. The surveying method used by Tadataka Inō was “traverse, “as shown in
Figure 1. He drove a stake into the place used for the reference and measured the distance to the next site using an iron chain. Then, he stepped in the direction of the next stake in a straight line and measured the course of the same object (such as the summit of a distant mountain) seen from the stakes at both ends of the straight line. The slope distance was measured with a simple wooden theodolite. Also, he performed an astronomical observation for the latitude to correct the measurement results [
11].
In this study, we selected INŌ’s Tokyo map. The reasons were as follows: (1) INŌ’s maps are the oldest surveyed drawings in Japan, and show the most past surveying technology; (2) there are few studies on the precision of INŌ’s Tokyo map compared with other INŌ’s maps [
12]; and (3) comparative analysis between them is possible, as there are many different historical maps of Edo (Tokyo) [
3,
7].
INŌ’s Tokyo map was completed in 1817 after the other INŌ maps were made from 1815 to 1816. This map was prepared using the highest level of surveying technology available at that age. INŌ’s survey diary shows that INŌ’s Tokyo map was not a merging of local surveys, but somewhat preliminary surveys conducted by connecting suburbs [
13]. In INŌ’s Tokyo map, the surveyed and non-surveyed lines were discriminated against using different colors (
Figure 2). The original of INŌ’s Tokyo map was destroyed by a fire in the Meiji era. All of the existing maps are copies. Careful attention was paid when creating replication [
14]. The painter was recruited by the central government.
INŌ’s Tokyo map consisted of two pieces, one each for the northern and southern areas. There is less information on the north of part of INŌ’s Tokyo map, and it is difficult to obtain reference points with regards to it. Thus, this study selected only the southern part of the map as the target of the analysis. For processing INŌ’s Tokyo map on GIS, we used the original drawings being collected in the literature [
15] (by the Geospatial Information Authority of Japan, 196 cm (H) and 314 cm (W)). The resolution was set to 250 to 750 dpi.
The scale of INŌ’s Tokyo map is approximately 1:6000. It is necessary to compare with present maps with a similar scale to achieve the goal of this study. In Japan, there are 1:5000 large-scale national maps (Horizontal Mercator projection by the plane orthogonal angle coordinate system) and 1:10,000 topographical maps (Universal Transverse Mercator drawing). The geodetic datum for these maps assumes the Earth as an ellipsoid. In Japan, in the first half of the 1800s when INŌ’s maps were prepared, the Earth was considered as a sphere, as in INŌ’s maps [
16], although it was already known by draftsmen that the Earth was a spheroid, as shown in Astronomia of Sterrekunde [
8,
11]. So far, various discussions have been made about the projection method used for INŌ’s maps [
16,
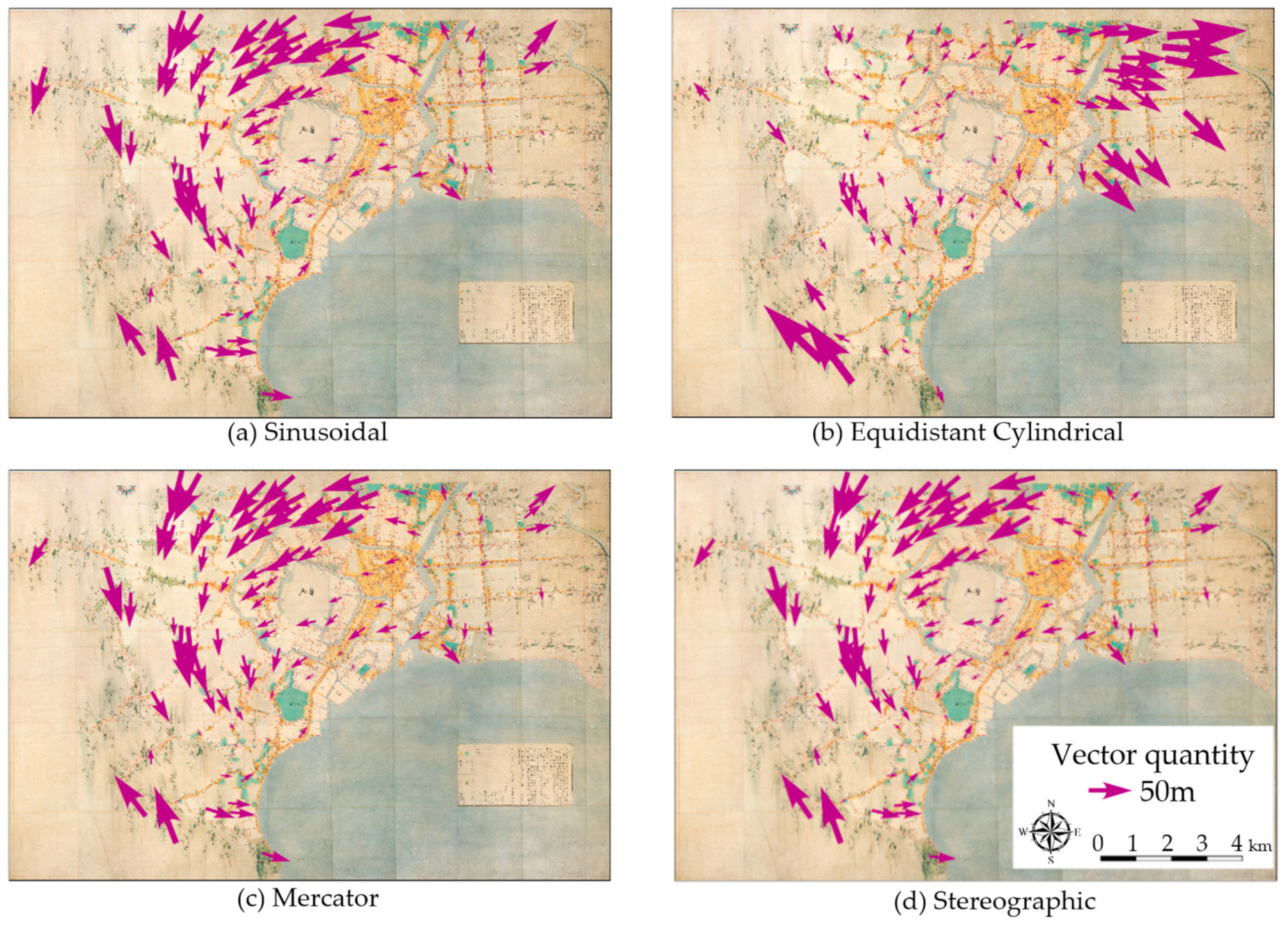
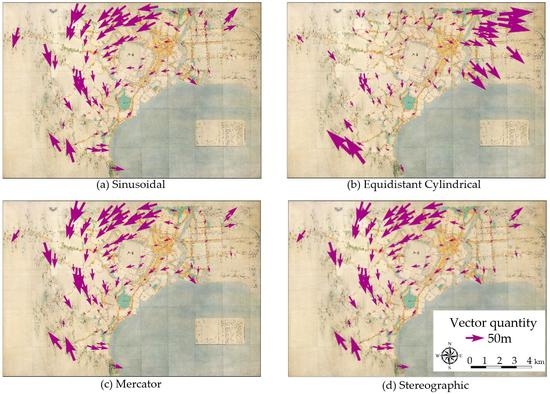
17]. In this study, we considered a total of four projection methods, including the sinusoidal projection (ESRI: 53008) and equidistant cylindrical projection (ESRI: 53002), as used in the previous studies, and adding the mercator projection (ESRI: 53004) and stereographic projection (ESRI: 53026), which are widely used for projecting large-scale maps. We attempted to explore the projection method being the most similar to that of modern maps.
Each projection method has the different characteristics. Sinusoidal projection is a projection where the central meridian and parallels orthogonal to it are expressed equidistantly, and the distortion increases moving from the central meridian and equator [
18]. In the equidistant cylindrical projection, the meridians are expressed equidistantly. If the parameters are changed, it can be considered that the projection assumes the longitude and latitude as the
x and
y coordinates on the map, as they are similar to the longitude-latitude coordinate system [
18]. Mercator projection is a regular cylindrical projection. The distortion of the high latitude region is larger than that of the low latitude region [
19]. Stereographic projection is also a general regular projection [
19]. However, unlike the mercator projection, the meridians and parallels are circles. The distortion increases as it moves further from the center.
In this study, the precision of the maps was verified by the following procedures. First, INŌ’s Tokyo map was overlayed on each present map by the four projection methods. Then, the control point (CP) was set on the map, and the distortion at each point was measured. In previous studies, the root mean square (RMS) residue obtained by applying an affine transformation—one of the georeference formulas—was used frequently as the evaluation method [
20]. The affine transformation does not maintain the aspect ratio of the figure. However, the affine transformation itself distorts the figure. In this study, we used the absolute value of the Euclidean distance between a coordinate (
x,
y) on historical maps, and the coordinate (
x’,
y’) on the present maps as the reference for evaluation, without performing affine transformation, and paying attention to the gaps in the historical maps themselves. For the present maps, the zoom level of the GSI (Geospatial Information Authority of Japan) maps was adopted [
19,
21], and the positional gap between INŌ’s Tokyo map and the GSI map was extracted by ArcGIS 10.4.
As for the parameters for projection, based on the discussions in previous studies [
17], the central meridian was set to 139.7567 for the sinusoidal projection, mercator projection, and stereographic projection. In the equidistant cylindrical projection and mercator projection, the standard parallel was set to 35.6851, in addition to the central meridian, as with the sinusoidal projection. In the stereographic projection, the latitude of origin was set to 35.6851. All of them passed through the Imperial Palace.
The exact scale of INŌ’s Tokyo map is unknown (the scale of the original map is said to be 1:6000). Thus a process to unify the scale with the present maps was conducted first. To be concrete, INŌ’s Tokyo map was transformed by setting the four points at the corner of the roads, extending to the front of temples and shrines located in the peripheral area of the map as necessary CPs (
Figure 3), as it is often the case that historical road structures are maintained around temples and shrines. The corner of the road extending to a temple or shrine rather than the temple or shrine itself was selected as a basic CP. That is because (1) a temple or shrine is a feature with a certain area, and it is difficult to set the basic CP as a point in it, and (2) roads are based on actual surveys, whereas the temples and shrines are drawn pictorially without surveying. A similarity conversion enables the scale reduction, turning, and moving of data.
As a result of the similarity transformation, we can show that INŌ’s Tokyo map was turned slightly counterclockwise, and the azimuth of the map was somewhat deviating from due north. Then, we paid attention to the center of each intersection of the road, and selected 100 points from the current position being identified as a local CP in INŌ’s Tokyo map (
Figure 4). For the locations of the local CPs, we selected roads with many paths and corners and roads along the temples and shrines. It was highly probable that the routes of these roads have not changed from those in that age, unlike the wide and straight roads.
In the georeference function of ArcGIS, an automatic adjustment of the image is the default setting, and errors become less in the later stage of the constellation of CPs. We made efforts so that the distortion could be grasped precisely based on an absolute scale while suppressing the effect of georeferencing to a minimum level.
4. Discussion
Longitude was not shown in any of INŌ’s maps including INŌ’s Tokyo map. It was because Tadataka Inō was interested in measuring the distance of latitude by one degree and using the measurement of time, which is indispensable for longitude, making it difficult [
16]. The reason why previous studies insisted INŌ’s maps were made by sinusoidal projection was that the meridians were measured by the calculation formula, which was the same as that of the sinusoidal projection [
11]. On the basis of the later reviews (in and after 1974), because no description of sinusoidal projection was found in the historical materials related to INŌ’s maps, and because meridians are drawn in the form of straight lines, it is hard to say that INŌ’s maps were drawn by taking into consideration of sinusoidal projection [
17]. In recent years, regarding INŌ’s maps, more attention has been paid to the map compilation process, rather than the meridian calculation method or projection method. For INŌ’s maps, the survey results were drawn on a rough sketch first. Next, the rough sketch was reduced in size and matched with other sketches. Then it was checked against the astronomical observation result to prepare a map. In other words, we can say that rough sketches drawn as a plane were applied to the map of a wider area.
If INŌ’s Tokyo map was made as a plane according to the study result of [
17], the meridians and parallels should be orthogonal. Because the distance in latitude was exact, the distance in longitude caused a gap. The projection method meeting this condition was the equidistant cylindrical projection (
Figure 5b). The authors of [
17] suggested the possibility that INŌ’s maps were made by an equidistant cylindrical projection, inspired by Kaisei Nihon Yochi Rotei Zenzu. By fully utilizing GIS, our study showed that INŌ’s maps were more likely to the equidistant cylindrical projection.
Geographical conditions including the surrounding environment and landscape, also influenced the actual surveying. When we paid attention to the urban structure of Edo, we found that samurai residences and townsman residences were accumulated in a sphere with a radius of approximately 4 km around the Imperial Palace (old Edo-jo Castle), and the scene of the farm village opened beyond the range of 4 km [
23]. The large-scale paddy (rice) field was distributed widely from the northern part to the eastern part of Edo. On the other hand, farmland excelled from the northern part to the western part of Edo [
23]. The reason why the surveying precision was lower in the area around Kameido, was that large-scale wetlands and paddy (rice) fields were spreading there (
Figure 7). On the other hand, in the area around Shinjuku located outside the urban fringe, the surveying was rather easy because farmland was dominant there. This area was along Koshu way, on which Tadataka Inō seems to have walked repeatedly. Naturally, the spatial distortion was smaller there (
Figure 8).
Some previous studies have pointed out that the altitude influenced spatial distortion [
24]. However, we considered that the factor hindering surveying was inclination rather than altitude, as we must fully utilize the trigonometric function to calculate the plane distance on a slope, and thus calculation becomes complex. We investigated the actual status by calculating the angle of inclination and by applying a spatial join (nearest-neighbor-joining by one-to-one) with CPs on the present maps, using the 5 m mesh digital altitude model (DEM) of the base map information that was made by aerial laser surveying. As a result, we found a high correlation between the positional gaps and the angle of inclination in the area around Roppongi. However, because differences in altitude are not so significant in Tokyo, no clear correlation was observed between the inclination and the size of the gap. There were places with high precision in Shinagawa and Yotsuya, even if the inclination was prominent.
Lastly, regarding the spatial pattern of distortion, we examined historical maps of Tokyo which were prepared almost at the same time as INŌ’s Tokyo map, and we compared various analyses by the previous studies [
3,
7]. The research of [
3] was Edozu Seihokan, an Edo map published in 1693, whereas the research of [
7] was the Tenpo Kaisei Oedo Ōezu, an Edo map published in 1843.
The location where the direction of the gap matched between this study and the previous studies [
3,
7] was the west side of the Imperial Palace (the area around Yotsuya). In both maps, we confirmed gaps in the western direction. The area around Yotsuya was overestimated in both maps. When looking into INŌ’s Tokyo map, there were blank areas on the west side of the Imperial Palace than on the east side. Blank areas include those of unsurveyed, as well as privately-owned places where surveying was impossible. When looking into the explanatory notes in INŌ’s Tokyo map, we recognize that many samurai residences were located in these blank areas. It was overestimated because this area had an image of a “not well-known place.” It is well-known in the field of behavioral geography that people tend to widely underestimate the spatial distance in familiar places and overestimate the spatial distance in unfamiliar places [
25]. Also, in INŌ’s Tokyo map and the map of preceding studies [
3,
7], it is indicated that distortion excelled in the area around the samurai residences.
5. Conclusions
This study, using INŌ’s Tokyo map prepared in 1817, discussed the spatial distortion of the positions of the features in the map quantitatively, by conducting the overlay analysis with present maps. We explored the factors of spatial distortion by considering the geodetic datum, the projection method, the surveying method of that age, and further miscellaneous geographical conditions.
As a result of the analysis, the distance gap between INŌ’s Tokyo map and the present map was found to be only 30 m. We can say that INŌ’s Tokyo map was made with considerably high precision for a map of the later Edo era. The projection method for INŌ’s Tokyo map was quite similar to the equidistant cylindrical projection.
As for the projection method, INŌ’s Tokyo map matched well with the map displayed by the equidistant cylindrical projection. There are areas with a remarkable spatial distortion in INŌ’s Tokyo map. The surrounding environment at the time of performing the surveying, as well as the geographical conditions such as land-use, was the main factor causing spatial distortions. The precision of maps was influenced by not only factors in physical geography such as the natural conditions of the land and landscape, but also the anthropogeographic factors such as the route of the roads, the distribution of the samurai residences, and the several times of surveying. These findings are only hypothetical at present, and advanced analysis utilizing GIS is required. These remain a future subject of research.