Regionalization and Partitioning of Soil Health Indicators for Nigeria Using Spatially Contiguous Clustering for Economic and Social-Cultural Developments
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Dataset Description
2.3. Imputation of Missing Values and Spatial Variability of Soil Health Indicators
2.4. Regionalization with REDCAP
- Spatial clustering of the datasets with contiguity constraints, which results in spatially contiguous trees and;
- Partitioning the trees in Step 1 to obtain regions. This involves optimizing an objective function, such as the heterogeneity of all soil variables or the homogeneity of the derived regions.
2.5. Markov Chain Monte Carlo (MCMC) Bayesian Change-Point Analyses
3. Results and Discussion
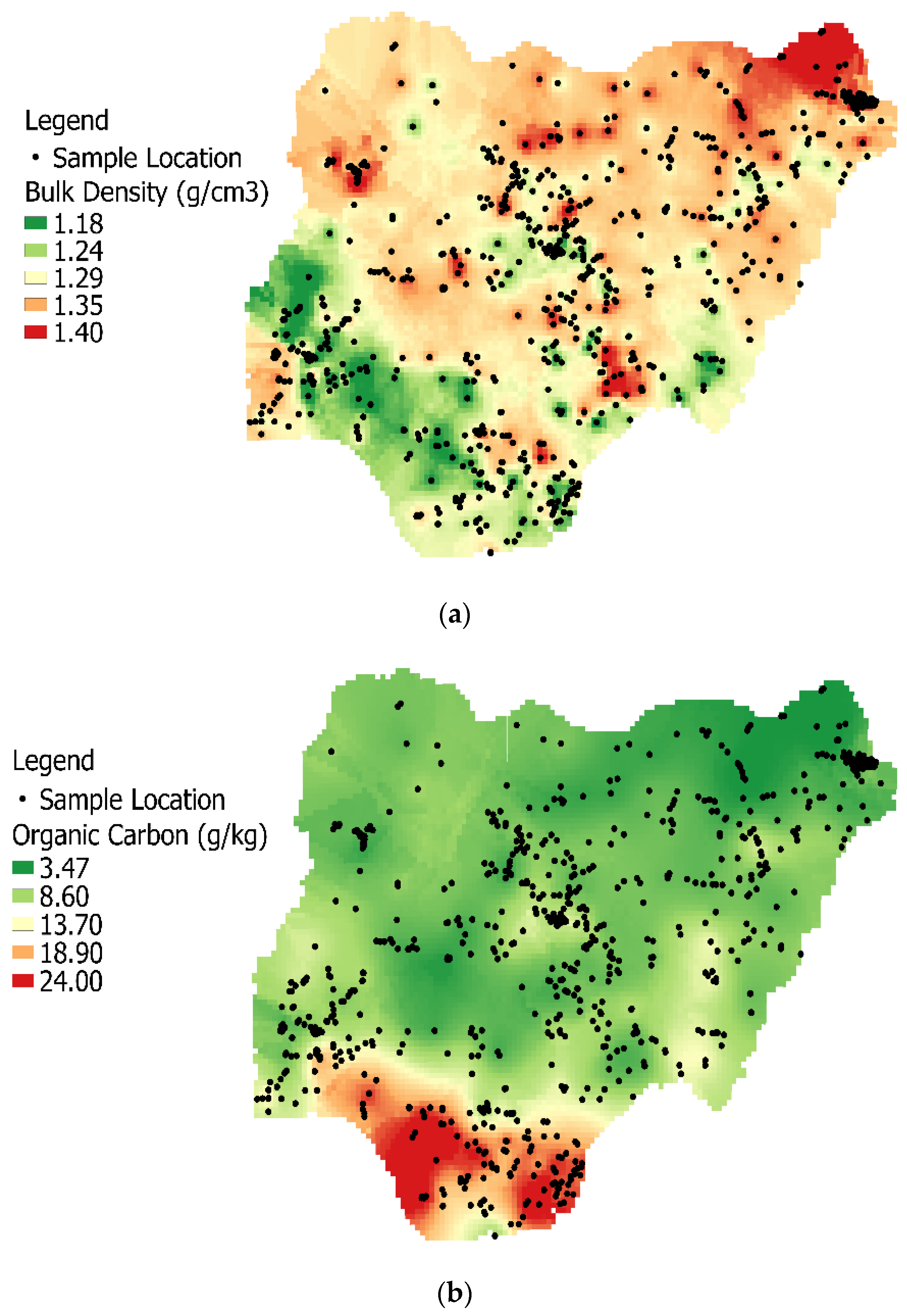
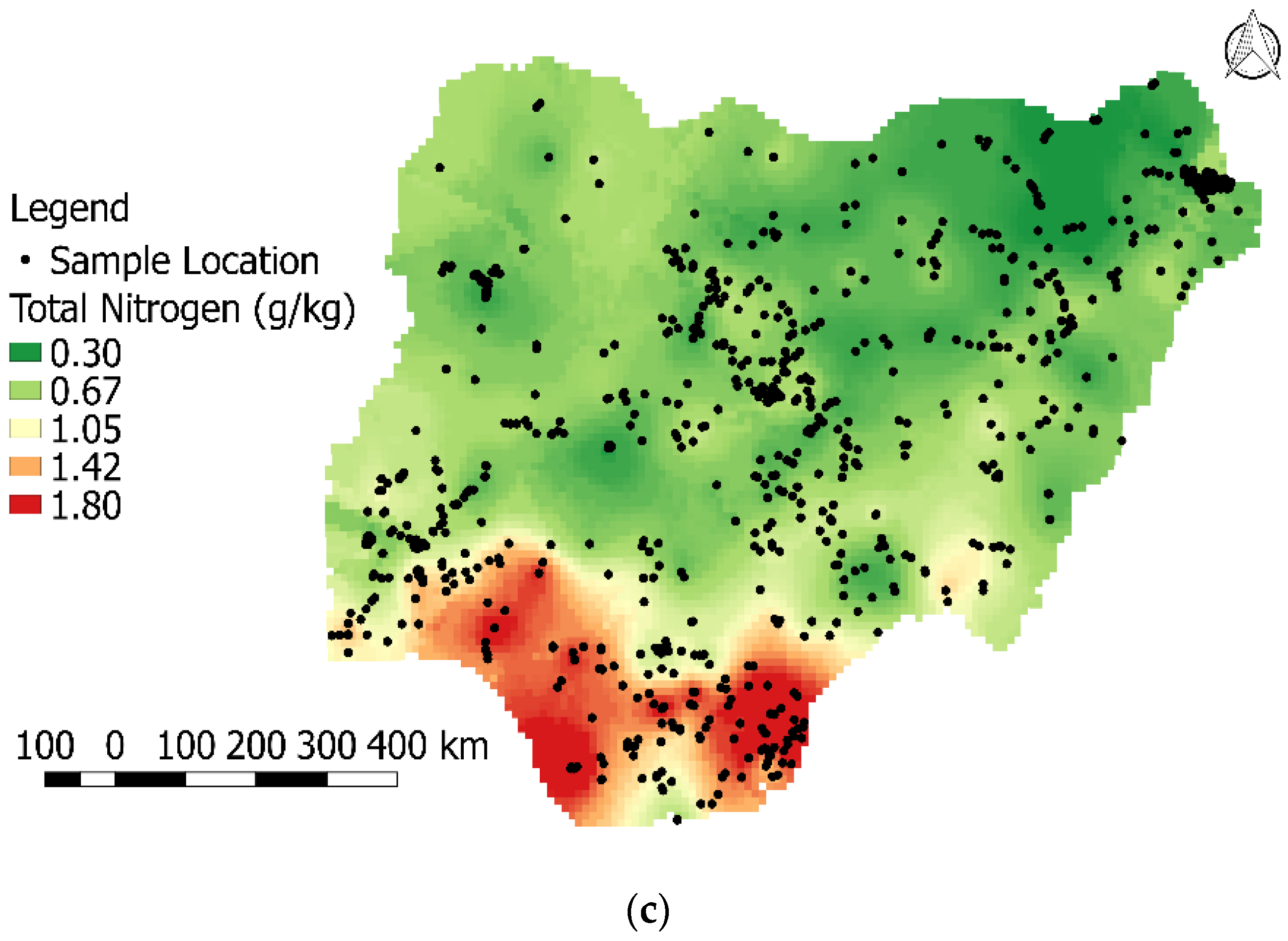
3.1. Imputation and Spatial Variability of Soil Health Properties
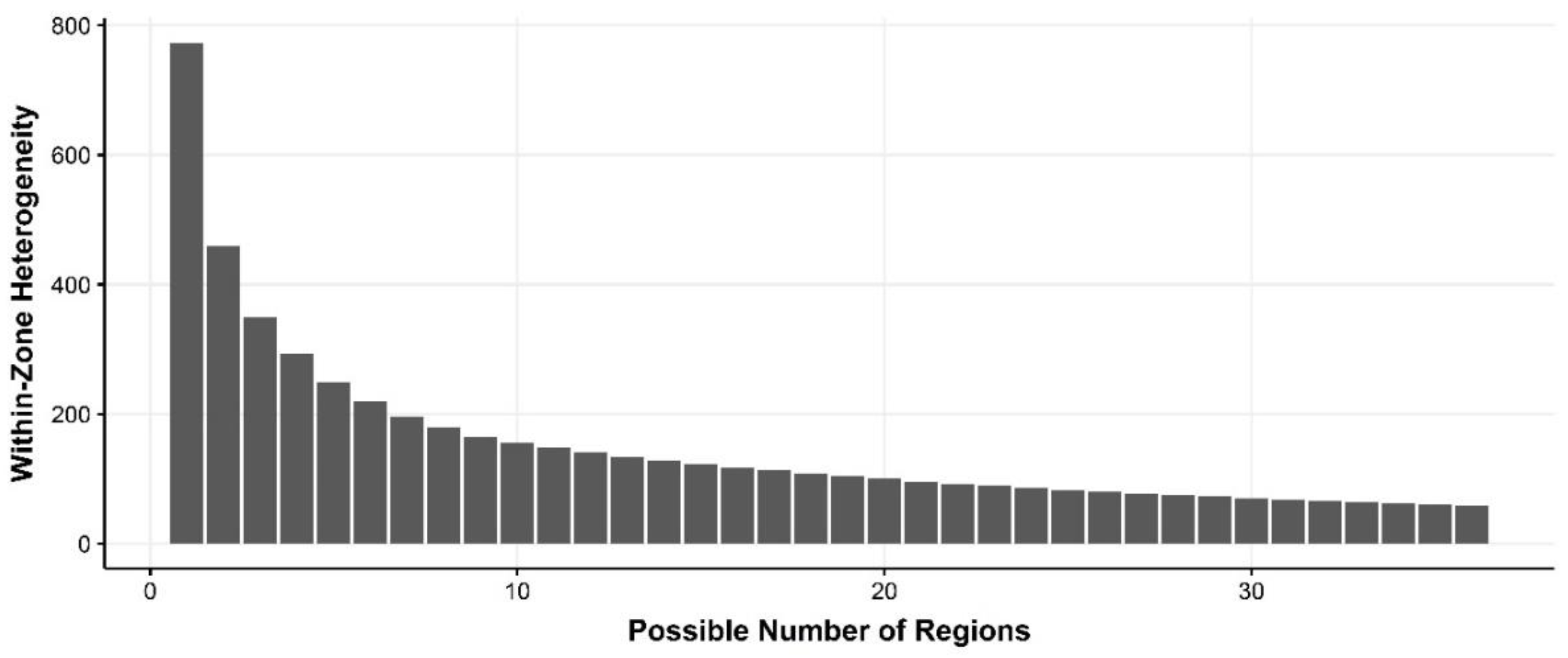
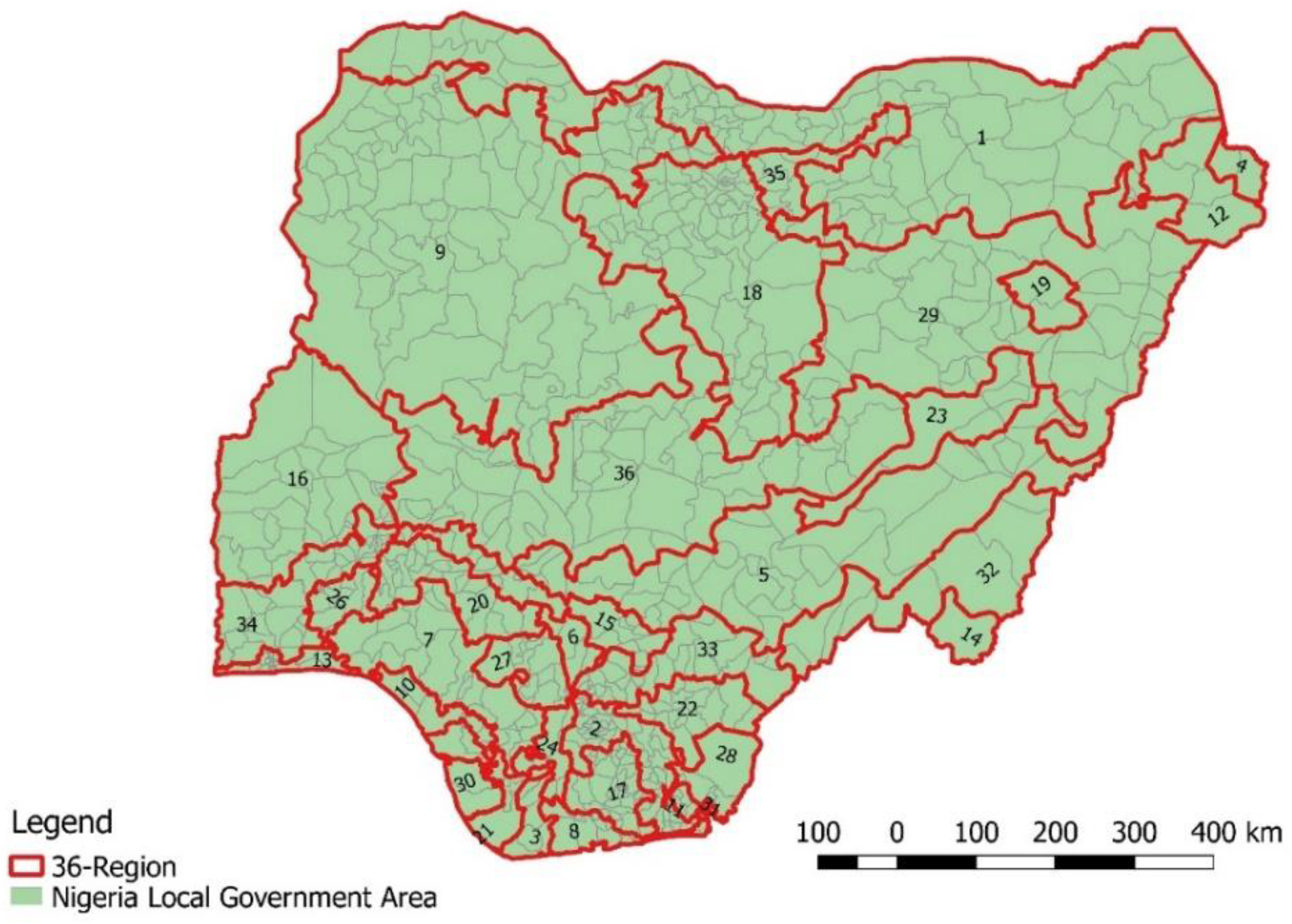
3.2. Soil Heterogeneities and Possible Number of Regional Divisions
3.3. Optimal Management Scenario and Socioeconomic Implications for Nigeria
4. Conclusions
- The random forest method of data imputation improved the spatial relationship (cross-correlation) between the SHIs. A very low imputation error (NRMSE = 1.2%) for all three variables was observed suggesting that this method can be used in multivariate analysis of missing geospatial variables;
- BD had the lowest CV, indicating a relatively uniform spatial distribution or homogeneity across Nigeria. It also signified little or no effect of external factors or human influence on the BD values. Measuring spatial variability, displayed as variograms of the SHIs, revealed that OC had the highest variability of the three SHIs. The spatially interpolated surface indicated spatial dependency of the three variables was high across Nigeria;
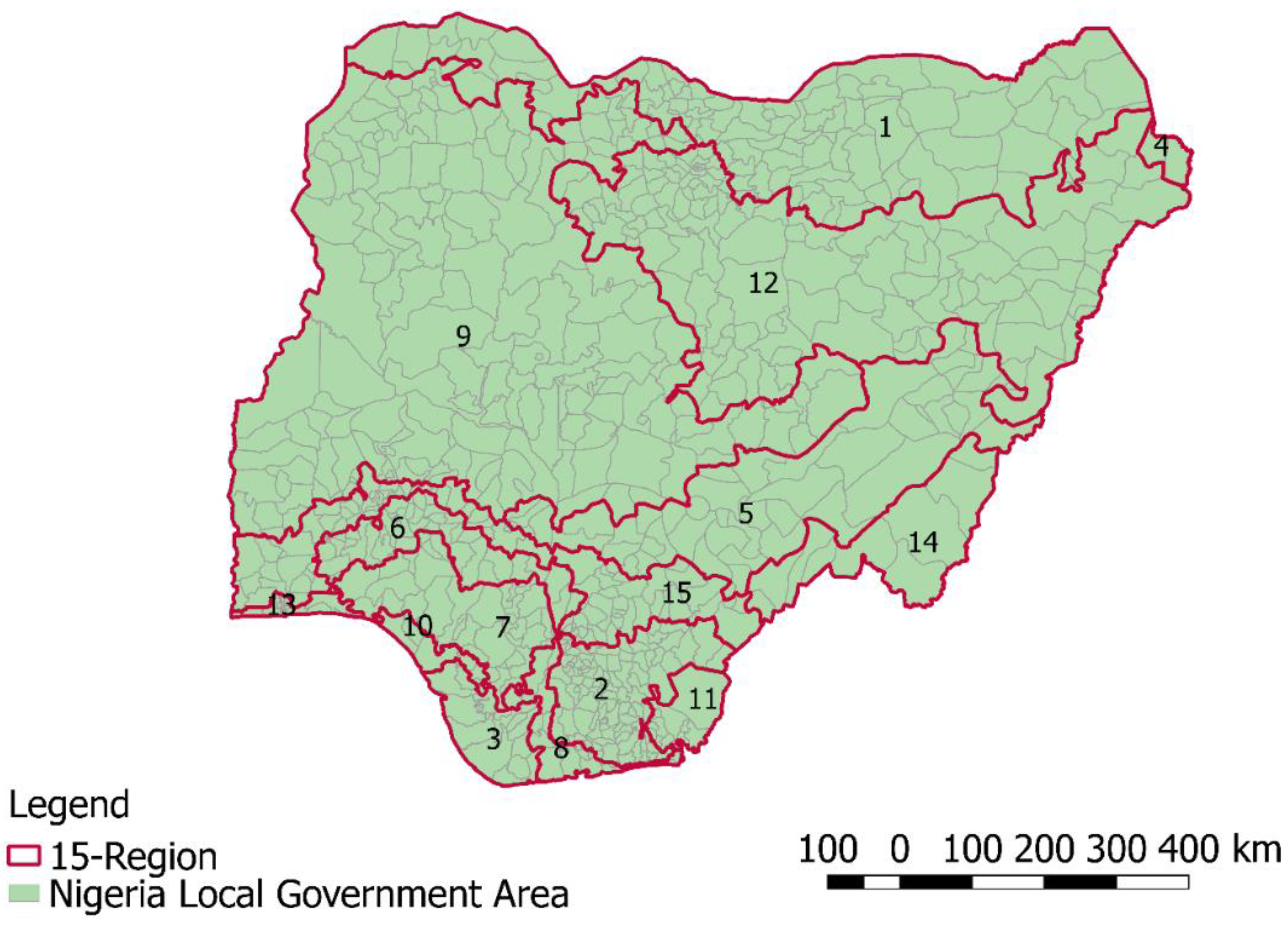
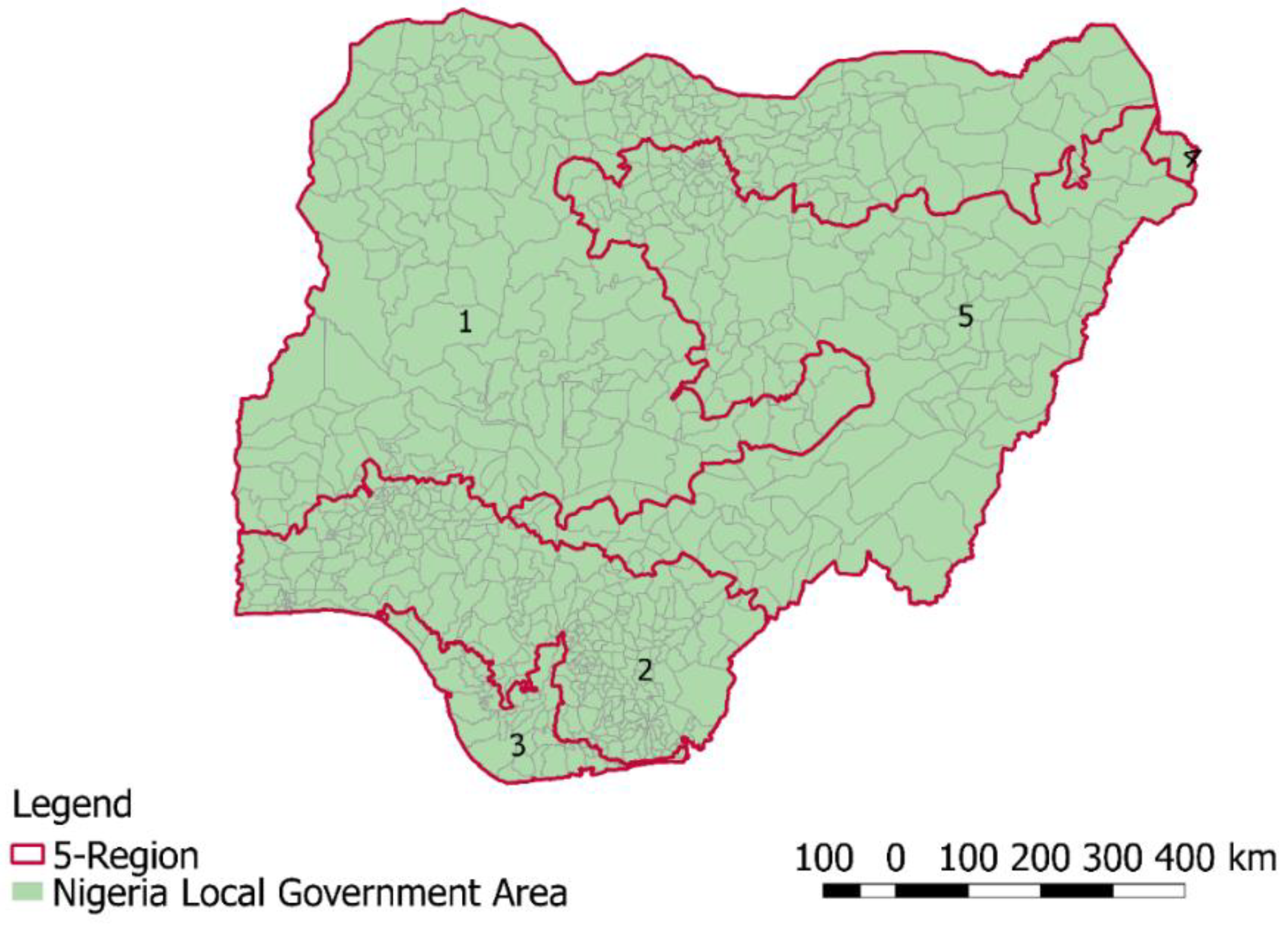
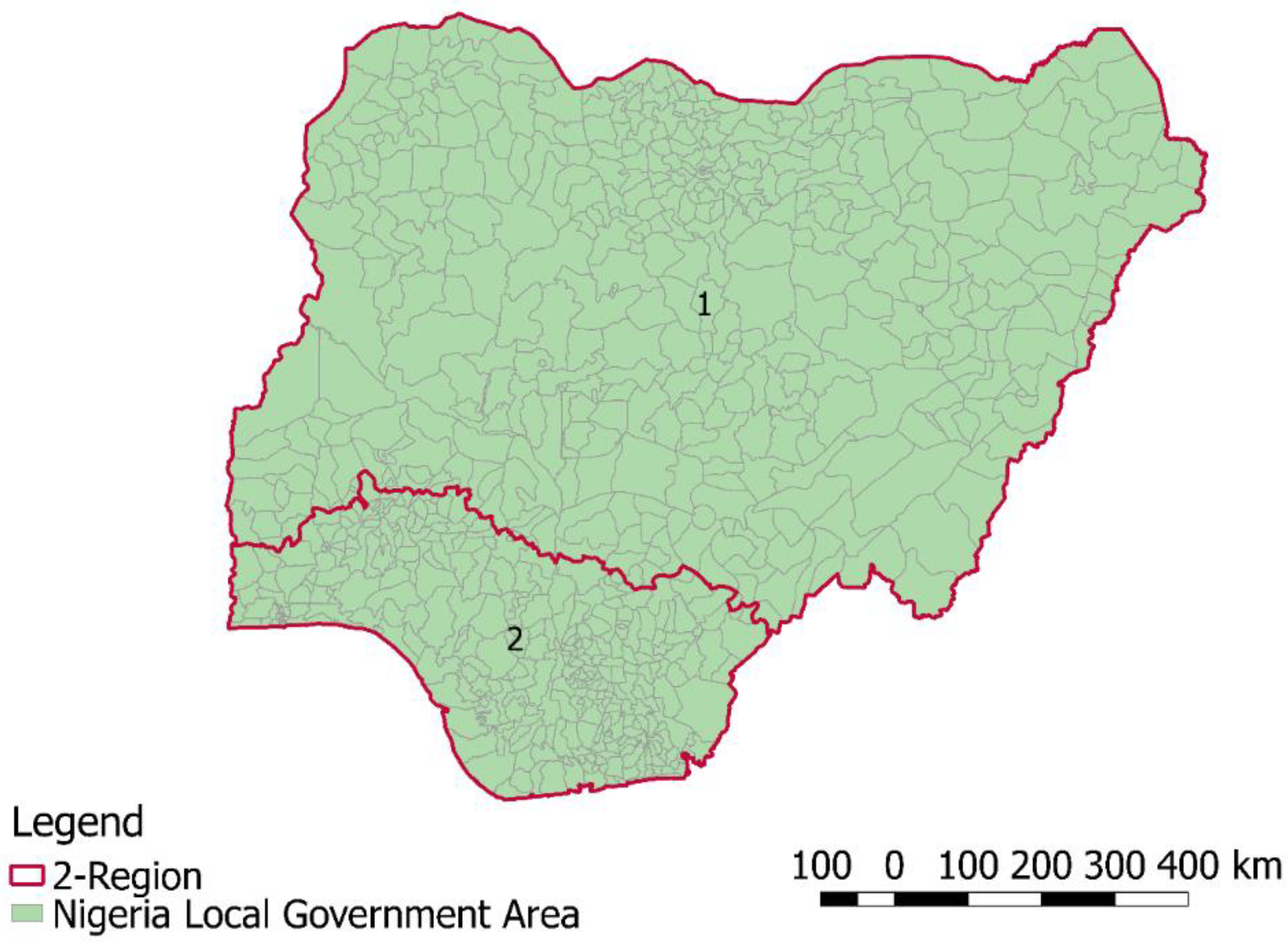
- Corresponding averages of the interpolated values were extracted based on the 774 LGAs. This study involved partitioning the LGAs as spatial objects into a number of spatially contiguous regions, and during the process optimized an objective function using REDCAP. Three divisions (two, five, and 15 regions scenarios) were selected as being optimal based on the WZH of the soil properties. The MCMC change-point technique was applied to the WZH to validate the optimal number of regions;
- In summary, this study provides a knowledge base to improve understanding of soil spatial variability and heterogeneities (or homogeneities). The findings could facilitate agricultural programs that combine or merge state and local governments that share the same soil health properties, rather than making agricultural management decisions based on geopolitical, racial, or ethnoreligious factors. This study may also aid decision-making bodies such as the UN FAO, IFAD, and the World Bank in their efforts to alleviate poverty, meet future food needs, mitigate the impacts of climate change, and provide financial funding through precise sustainable agriculture and intervention in developing countries such as Nigeria.
Funding
Acknowledgments
Conflicts of Interest
References
- Paustian, K.; Lehmann, J.; Ogle, S.; David Reay, D.; Robertson, G.; Smith, P.P. Climate-smart soils. Nature 2016, 532, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Doran, J.W. Soil health and global sustainability: Translating science into practice. Agric. Ecosyst. Environ. 2002, 88, 119–127. [Google Scholar] [CrossRef]
- Ball, B.C.; Hargreaves, P.R.; Watson, A.C. A framework of connections between soil and people can help improve sustainability of the food system and soil functions. Ambio 2018, 47, 269–283. [Google Scholar] [CrossRef] [PubMed]
- CAB International. CAB Abstract Hot Topics: Soil Health and Sustainability. Available online: https://www.cabi.org/Uploads/CABI/publishing/promotional-materials/insert/Hot%20Topics%20Soil%20Health%20And%20Sustainability%20Hr%202.pdf (accessed on 22 July 2019).
- Bouma, J.; McBratney, A.B. Framing soils as an actor when dealing with wicked environmental problems. Geoderma 2013, 200–201, 130–139. [Google Scholar] [CrossRef]
- McBratney, A.; Field, D. Securing our soil. Soil Sci. Plant Nutr. 2015, 61, 587–591. [Google Scholar] [CrossRef]
- World Bank. Population Growth (Annual %). Available online: https://data.worldbank.org/indicator/SP.POP.GROW?locations=NG (accessed on 22 July 2019).
- Rockström, J.; Falkenmark, M. Agriculture: Increase water harvesting in Africa. Nature 2015, 519, 283–285. [Google Scholar] [CrossRef]
- Voice of America. Nigeria’s Population Projected to Double by 2050. 2019. Available online: https://www.voanews.com/a/nigeria-population/4872735.html (accessed on 22 July 2019).
- FAO. Soil Fertility Management in Support of Food Security in Sub-Saharan Africa. 2011. Available online: ftp://ftp.fao.org/agl/agll/docs/foodsec.pdf (accessed on 22 July 2019).
- Rasul, G. Managing the food, water, and energy nexus for achieving the Sustainable Development Goals in South Asia. Environ. Dev. 2016, 18, 14–25. [Google Scholar] [CrossRef]
- Tacoli, C.; Thanh, H.X.; Owusu, M.; Kigen, L.; Padgham, J. The Role of Local Government in Urban Food Security. IIED Briefing. Available online: http://pubs.iied.org/17171IIED (accessed on 22 July 2019).
- FAO. Implications of Economic Policy for Food Security: A Training Manual. Available online: http://www.fao.org/3/X3936E/X3936E07.htm (accessed on 22 July 2019).
- Leenaars, J.G.B. Africa Soil Profiles Database, Version 1.1. A Compilation of Geo-Referenced and Standardized Legacy Soil Profile Data for Sub Saharan Africa (with Dataset); ISRIC Report 2013/03; Africa Soil Information Service (AfSIS) Project; ISRIC—World Soil Information: Wageningen, The Netherlands, 2019. [Google Scholar]
- Breiman, L. Random forests. Mach Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Shah, A.; Bartlett, D.J.W.; Carpenter, J.; Nicholas, O.; Hemingway, H. Comparison of Random Forest and Parametric Imputation Models for Imputing Missing Data Using MICE: A CALIBER Study. Am. J. Epidemiol. 2014, 179, 764–774. [Google Scholar] [CrossRef]
- Tang, F.; Ishwaranm, H. Random Forest Missing Data Algorithms. Stat. Anal. Data Min. ASA Data Sci. J. 2017, 10, 363–377. [Google Scholar] [CrossRef]
- Stekhoven, D.J.; Buehlmann, P. MissForest—Nonparametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Manual–Setting Up, Using, and Understanding Random Forests V4.0. Available online: https://www.stat.berkeley.edu/breiman (accessed on 22 July 2019).
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University Press: New York, NY, USA, 1991. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Boluwade, A.; Madramootoo, C. A Assessment of Uncertainty in Soil Test Phosphorus using Kriging Techniques and Sequential Gaussian Simulation: Implications for Water Quality Management in Southern Quebec. Water Qual. Res. J. Can. 2000, 48, 344–357. [Google Scholar] [CrossRef]
- Boluwade, A.; Madramootoo, C.A. Geostatistical independent simulation of spatially correlated soil variables. Comput. Geosci. 2015. [Google Scholar] [CrossRef]
- Bivand, R.S.; Pebesma, E.J.; Gómez-Rubio, V. Applied Spatial Data Analysis with R; Springer: New York, NY, USA, 2008. [Google Scholar]
- Boluwade, A.; Madramootoo, C.A.; Aghil, Y. Application of Unsupervised Clustering Techniques for Management Zone Delineation: A Case Study of Variable Rate Irrigation in Southern Alberta, Canada. J. Irrig. Drain. 2015. [Google Scholar] [CrossRef]
- Haining, R.P.; Wise, S.M.; Blake, M. Constructing regions for small area analysis: Health service delivery and colorectal cancer. J. Public Health Med. 1994, 16, 429–438. [Google Scholar] [CrossRef]
- Openshaw, S.; Wymer, C. Classifying and regionalizing census data. In Census Users Handbook; GeoInformation International: Cambridge, UK, 1995; pp. 239–268. [Google Scholar]
- Guo, D. Regionalization with dynamically constrained agglomerative clustering and partitioning (REDCAP). Int. J. Geogr. Inf. Sci. 2008, 801–823. [Google Scholar] [CrossRef]
- Fovell, R.G.; Fovell, M.-Y.C. Climate zones of the conterminous United States Defined Using Cluster Analysis. J. Clim. 1993, 6, 2103–2135. [Google Scholar] [CrossRef]
- Handcock, R.; Csillag, F. Spatio-temporal analysis using a multiscale hierarchical ecoregionalization. Photogramm. Eng. Remote Sens. 2004, 70, 101–110. [Google Scholar] [CrossRef]
- Erdman, C.; Emerson, J.W. A fast Bayesian change point analysis for the segmentation of microarray data. Bioinformatics 2008, 24, 2143–2148. [Google Scholar] [CrossRef]
- AssunÇão, R.M.; Neves, M.C.; Câmara, G.; Da Costa Freitas, C. Efficient regionalization techniques for socio-economic geographical units using minimum spanning trees. Int. J. Geogr. Inf. Sci. 2006, 20, 797–811. [Google Scholar] [CrossRef]
- World Bank. Poverty & Equity Data Portal. Available online: http://povertydata.worldbank.org/poverty/country/NGA (accessed on 22 July 2019).
- World Bank Nigeria’s Booming Population Requires More and Better Jobs. Available online: https://www.worldbank.org/en/news/press-release/2016/03/15/nigerias-booming-population-requires-more-and-better-jobs (accessed on 22 July 2019).
- Harpstead, M.I. The Classification of some Nigeria Soils. Soil Sci. 1973, 116, 437–443. [Google Scholar] [CrossRef]
- Agboola, A.A. Planning for crop production without planning for soil fertility evaluation and management. In Proceedings of the 4th Annual Conference of Soil Science Society of Nigeria, Makurdi, Benue State, Nigeria, 19–23 October 1986; Chaude, V.O., Ed.; pp. 32–45. [Google Scholar]
- Osunade, M.A. Identification of crop soils by small farmers of south-western Nigeria. J. Environ. Manag. 1992, 35, 193–203. [Google Scholar] [CrossRef]
- Ojuola, O. Status Soil Management, Nigeria. Global Partnership Workshop. Managing Living Soils. FAO Headquarters. Available online: http://www.fao.org/fileadmin/user_upload/GSP/docs/WS_managinglivingsoils/Status_Soil_Management_Nigeria_Ojuola.pdf (accessed on 22 July 2019).
- Leenaars, J.G.B.; Oostrum, A.J.M.; Gonzalez, M.R. Africa Soil Profiles Database. Version 1.2 A Compilation of Georeferenced and Standardised Legacy Soil Profile Data for Sub-Saharan Africa (with Dataset). ISRIC Report 2014/01. Wageningen. Available online: https://www.isric.org/sites/default/files/isric_report_2014_01.pdf (accessed on 22 July 2019).
- Edwards, J.H.; Wood, C.W.; Thurlow, D.L.; Ruf, M.E. Tillage and crop rotation effects on fertility status of a Hapludalf soil. Soil Sci. Soc. Am. J. 1999, 56, 1577–1582. [Google Scholar] [CrossRef]
- Oba, S.; Sato, M.A.; Takemasa, I.; Monden, M.; Matsubara, K.I.; Ishii, S. A Bayesian missing value estimation method for gene expression profile data. Bioinformatics 2003, 19, 2088–2096. [Google Scholar] [CrossRef] [PubMed]
- Chilès, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Hijmans, R.J.; van Etten, J. Raster: Geographic Analysis and Modeling with Raster Data. R Package Version 2.0-12. Available online: http://CRAN.R-project.org/package=raster (accessed on 22 July 2019).
- Wong, D.W.S.; Wang, F. Spatial Analysis Methods. In Comprehensive Geographical Information Systems; Huang, B., Ed.; Elsevier Science: Amsterdam, The Netherlands, 2017; pp. 125–147. [Google Scholar]
- Benassi, F.; Deva, M.; Zindato, D. Graph Regionalization with Clustering and Partitioning: An Application for Daily Commuting Flows in Albania. MPRA Paper No. 73946. Available online: https://mpra.ub.uni-muenchen.de/73946/ (accessed on 22 July 2019).
- Barry, D.; Hartigan, J.A. A Bayesian analysis for change point problems. J. Am. Stat. Assoc. 1993, 35, 309–319. [Google Scholar]
- Boluwade, A.; Zhao, K.-Y.; Stadnyk, T.A.; Rasmussen, P. Towards Validation of the Canadian Precipitation Analysis (CaPA) for Hydrologic Modeling Applications in the Canadian Prairies. J. Hydrol. 2018. [Google Scholar] [CrossRef]
- FAO. Smallholders’ Data Portrait. Available online: www.fao.org/family-farming/data-sources/dataportrait/farm-size/en (accessed on 22 July 2019).
- Goidts, E.; van Wesemael, B.; Crucifix, M. Magnitude and sources of uncertainties in soil organic carbon (SOC) stock assessments at various scales. Eur. J. Soil Sci. 2009, 60, 723–739. [Google Scholar] [CrossRef]
- Xiong, Z.; Li, S.; Yao, L.; Liu, G.; Zhang, Q.; Liu, W. Topography and land use effects on spatial variability of soil denitrification and related soil properties in riparian wetlands. Ecol. Eng. 2015, 83, 437–443. [Google Scholar] [CrossRef]
- Jones, D.L.; Willett, V.B. Experimental evaluation of methods to quantify dissolved organic nitrogen (DON) and dissolved organic carbon (DOC) in soil. Soil Biol. Biochem. 2006, 38, 991–999. [Google Scholar] [CrossRef]
- World Bank. 3rd National Fadama Development Project (FADAMA III). 2019. Available online: http://projects.worldbank.org/P096572/third-national-fadama-development-project-fadama-iii?lang=en&tab=documents&subTab=projectDocuments (accessed on 22 July 2019).
- IFAD-Adaptation for Smallholder Agriculture Programme (ASAP). Climate Change Adaptation and Agribusiness Support Programme (CasP) in the Savannah Belt of Nigeria. Available online: https://www.ifad.org/en/web/knowledge/publication/asset/39573568 (accessed on 22 July 2019).

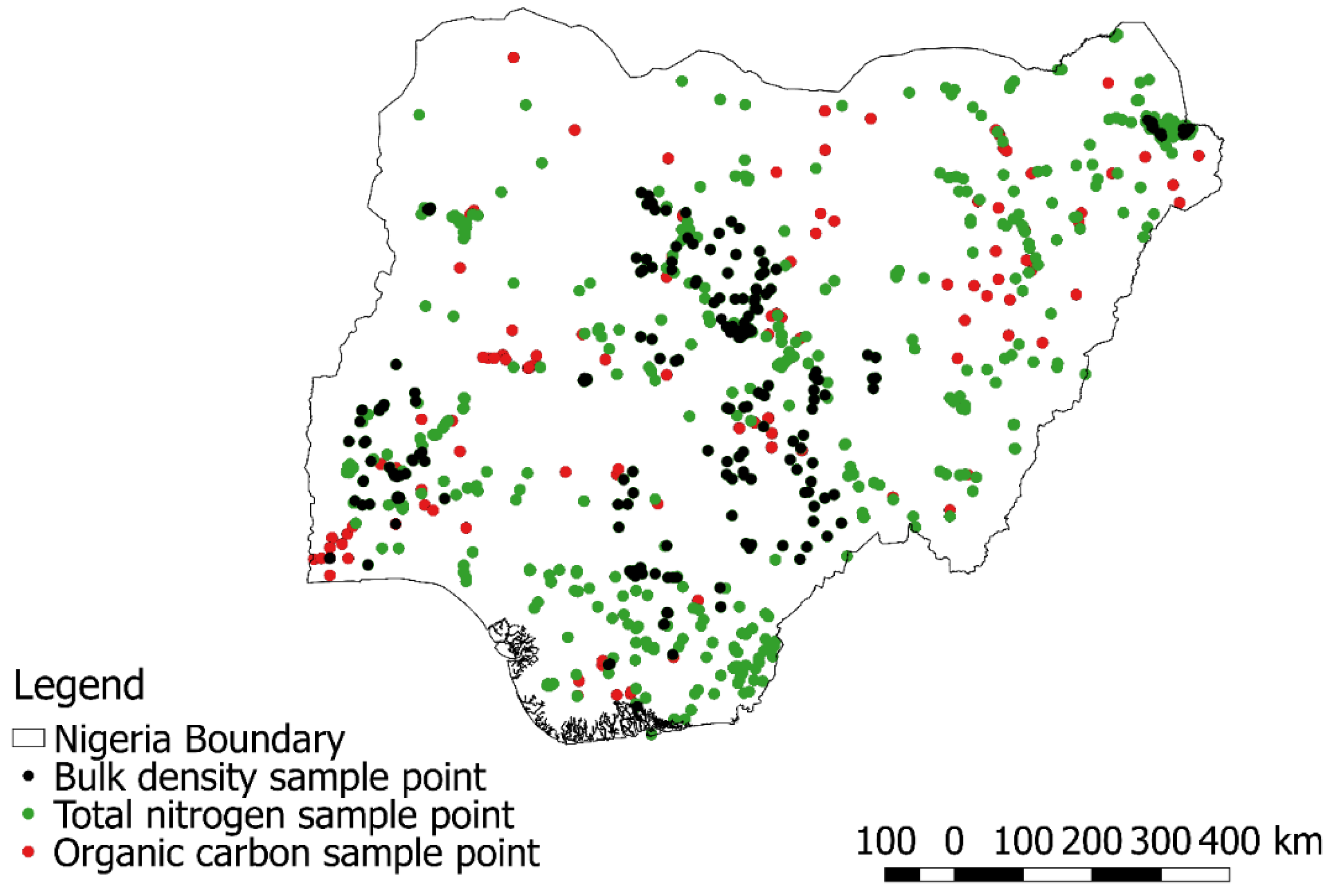

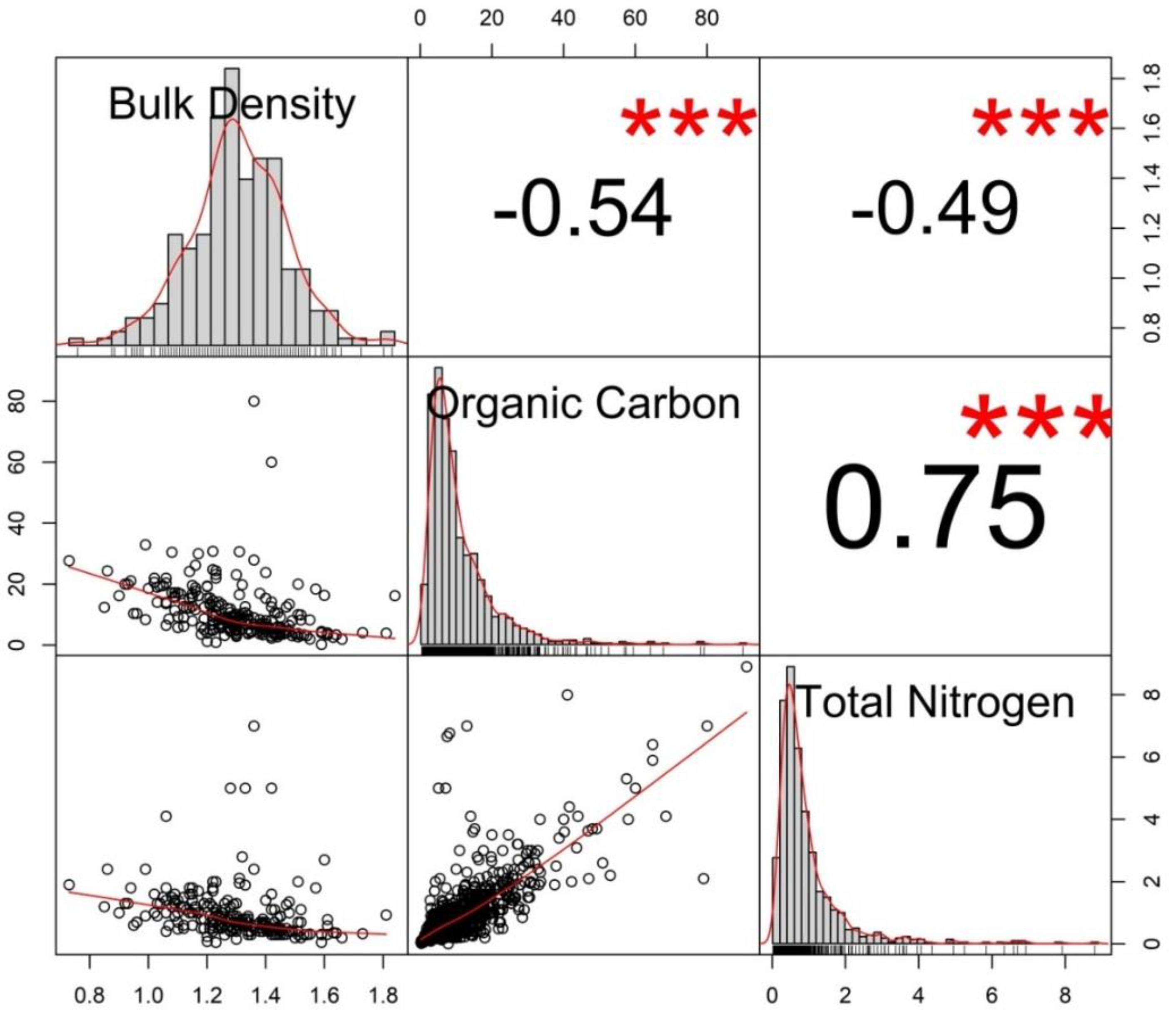
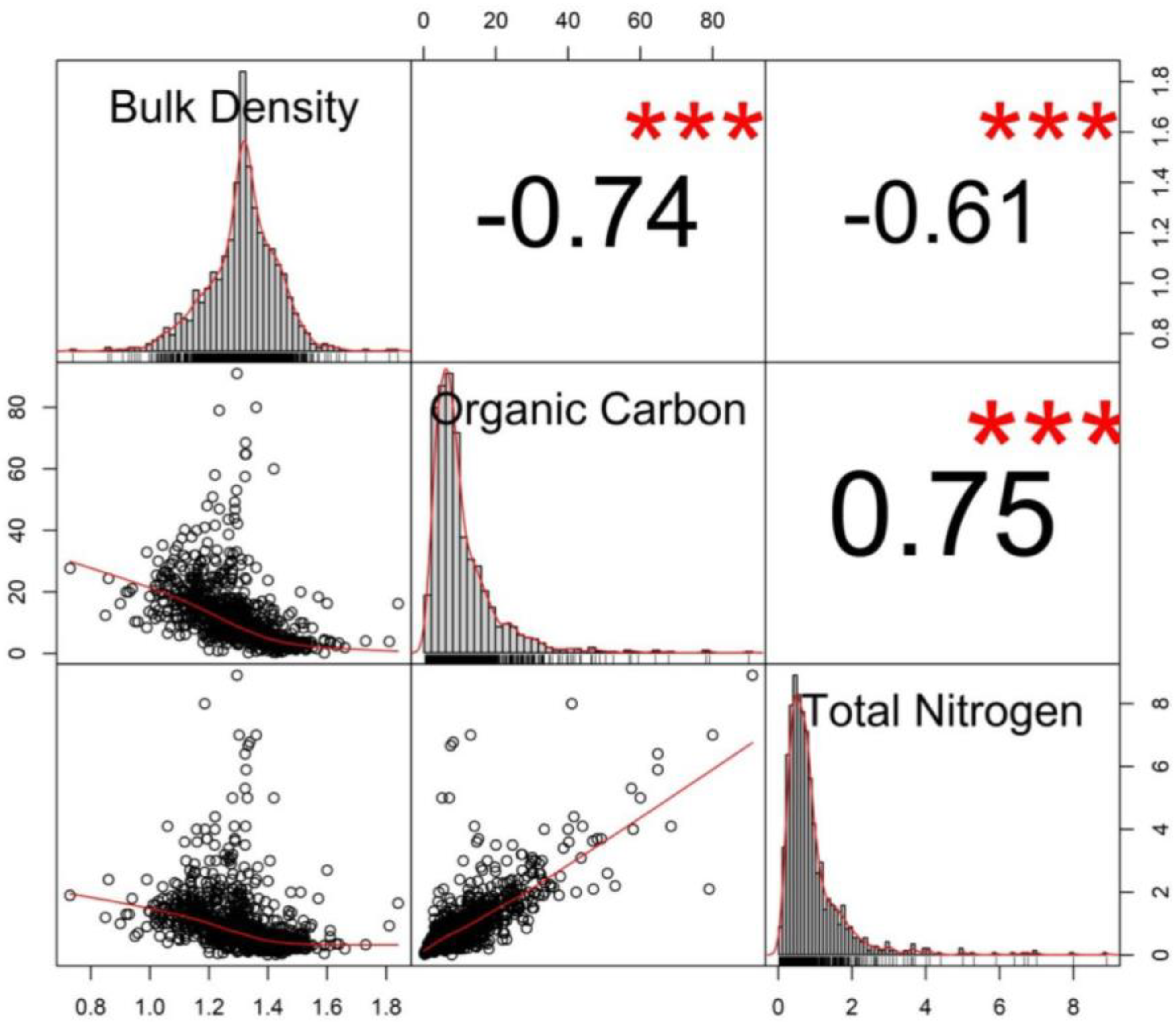
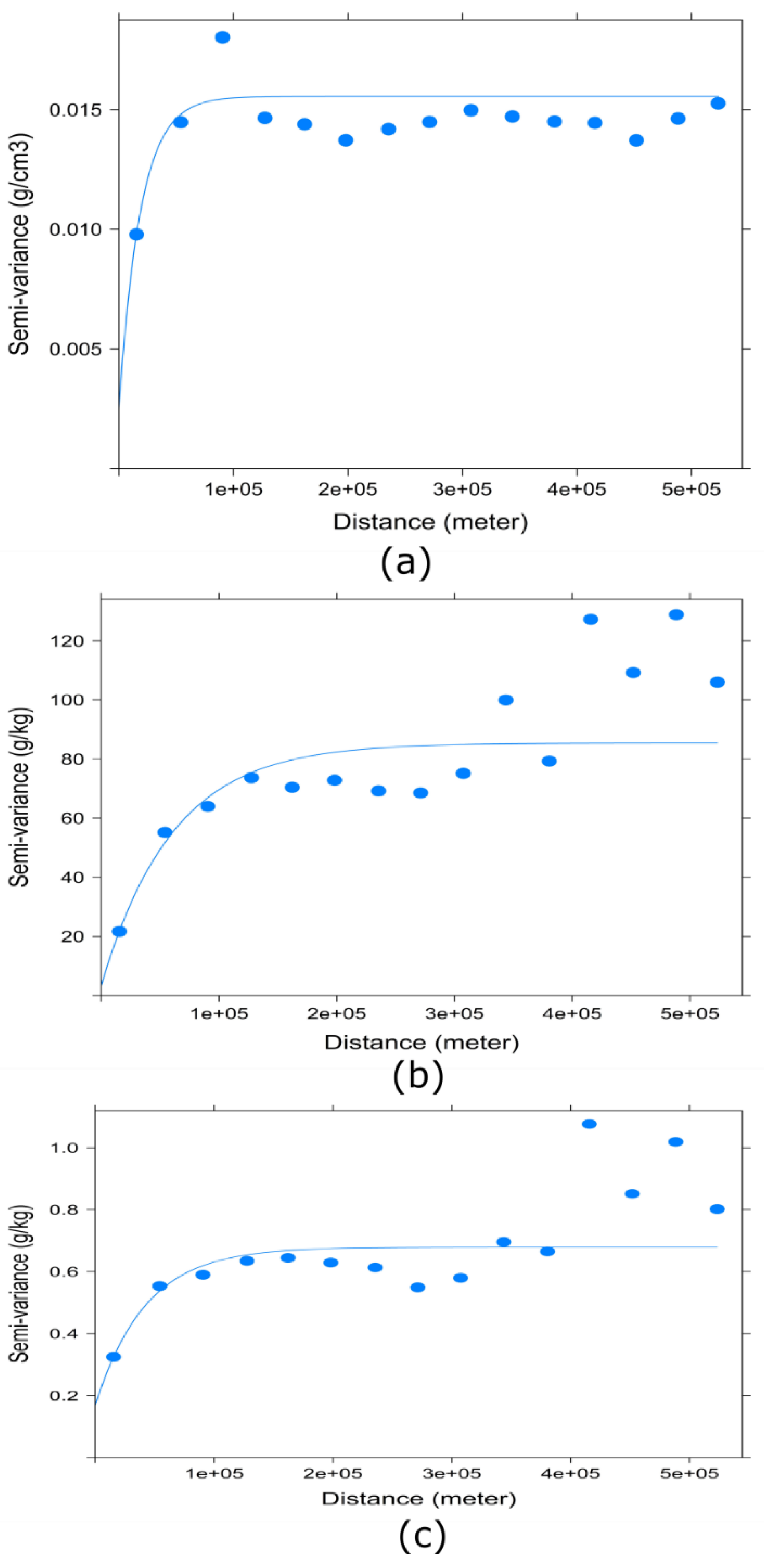

| Variable | Available Measured Samples | Number of Missing Samples | Percentage of Missing Values (%) |
|---|---|---|---|
| Bulk density | 251 | 949 | 79 |
| Soil organic content | 918 | 282 | 23 |
| Total nitrogen | 1088 | 112 | 9 |
| Bulk Density (g/cm3) | Organic Carbon (g/kg) | Total Nitrogen (g/kg) | |
|---|---|---|---|
| Mean | 1.31 | 10.52 | 0.92 |
| Standard deviation | 0.12 | 9.45 | 0.88 |
| Sample variance | 0.01 | 89.32 | 0.77 |
| Coefficient of variation (%) | 9.10 | 89.44 | 95.65 |
| Minimum | 0.73 | 0.20 | 0.01 |
| Maximum | 1.84 | 91.00 | 8.90 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boluwade, A. Regionalization and Partitioning of Soil Health Indicators for Nigeria Using Spatially Contiguous Clustering for Economic and Social-Cultural Developments. ISPRS Int. J. Geo-Inf. 2019, 8, 458. https://doi.org/10.3390/ijgi8100458
Boluwade A. Regionalization and Partitioning of Soil Health Indicators for Nigeria Using Spatially Contiguous Clustering for Economic and Social-Cultural Developments. ISPRS International Journal of Geo-Information. 2019; 8(10):458. https://doi.org/10.3390/ijgi8100458
Chicago/Turabian StyleBoluwade, Alaba. 2019. "Regionalization and Partitioning of Soil Health Indicators for Nigeria Using Spatially Contiguous Clustering for Economic and Social-Cultural Developments" ISPRS International Journal of Geo-Information 8, no. 10: 458. https://doi.org/10.3390/ijgi8100458
APA StyleBoluwade, A. (2019). Regionalization and Partitioning of Soil Health Indicators for Nigeria Using Spatially Contiguous Clustering for Economic and Social-Cultural Developments. ISPRS International Journal of Geo-Information, 8(10), 458. https://doi.org/10.3390/ijgi8100458





