Non-Temporal Point Cloud Analysis for Surface Damage in Civil Structures
Abstract
:1. Introduction
1.1. Damage Detection Based on Geometrical Features
1.2. Damage Detection Based on Color and Intensity Information
1.3. Detection Based on Geometrical Features, Color Information, and Intensity Data
1.4. Knowledge Gap
1.5. Research Motivation and Scope
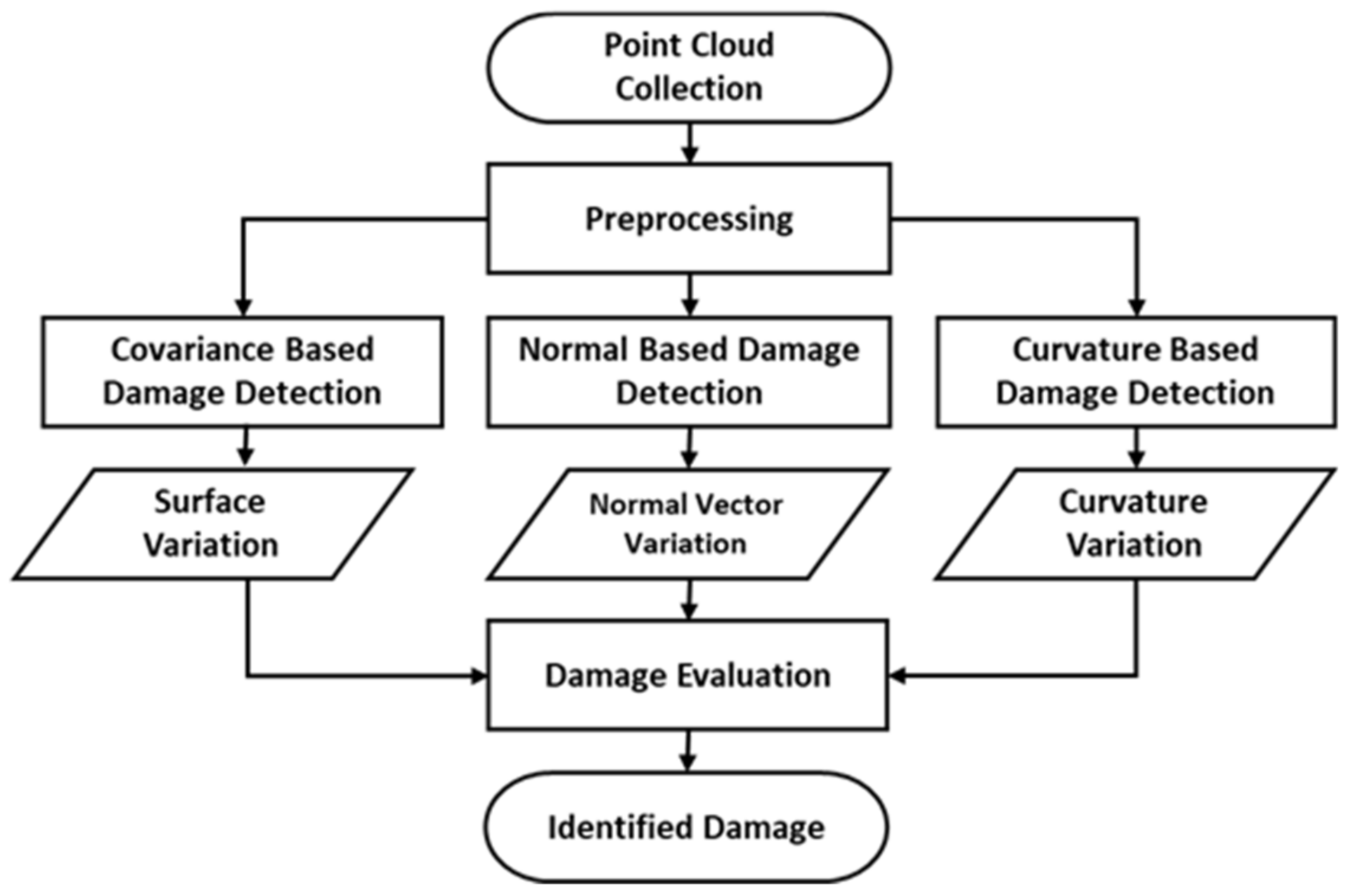
2. Methodology
2.1. Overview and Synthetic Datasets
2.2. Preprocessing Step
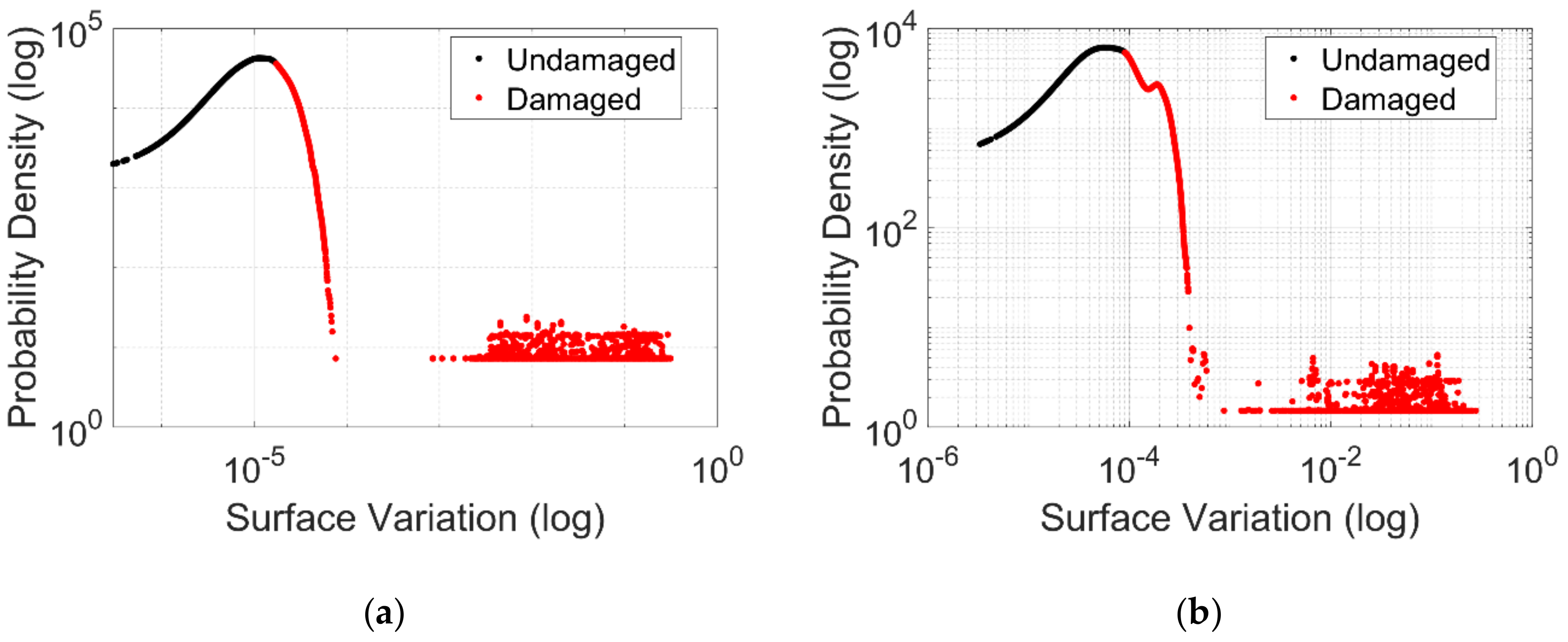
2.3. Surface Variation-Based Damage Detection
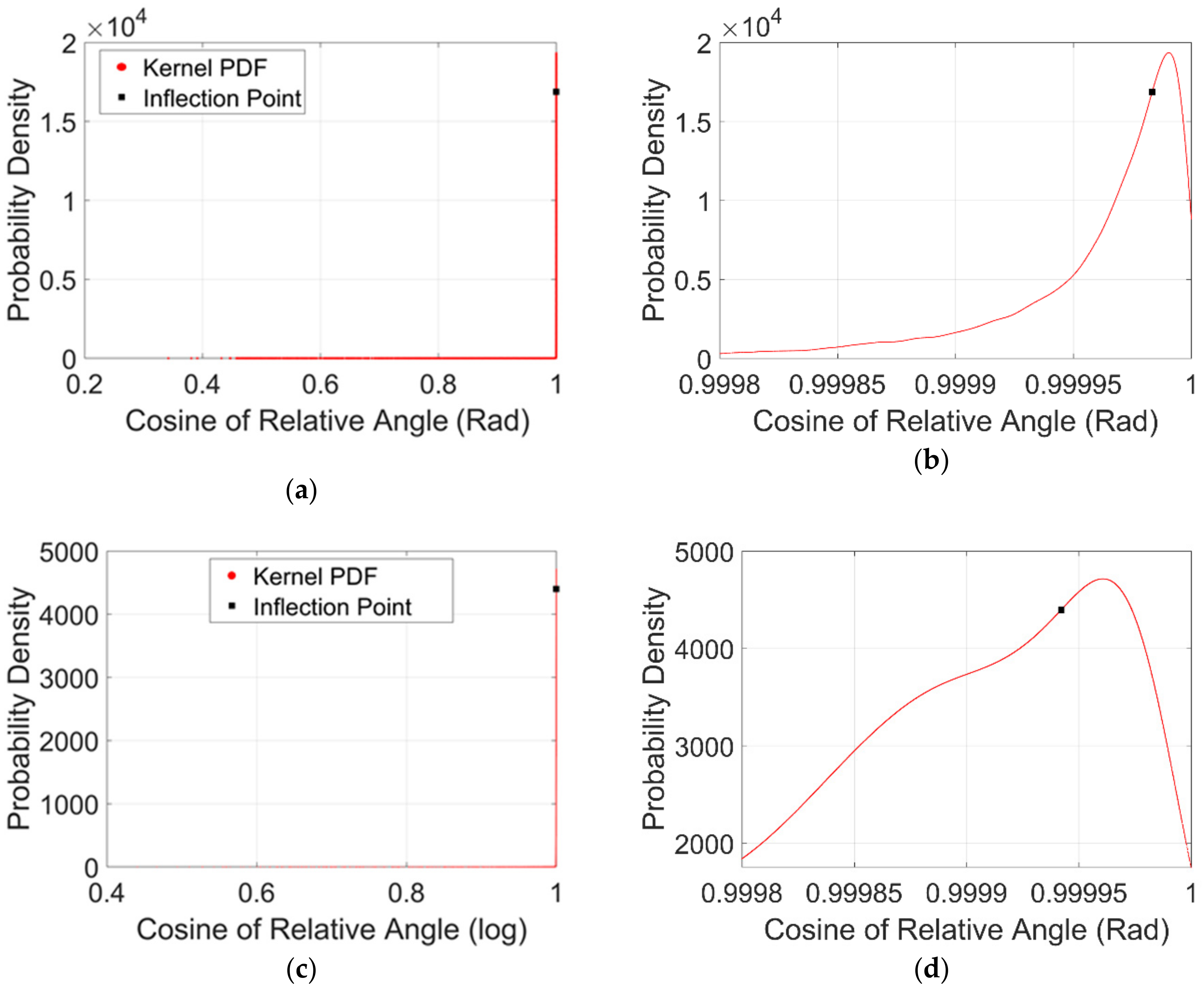
2.4. Normal Vector-Based Damage Detection
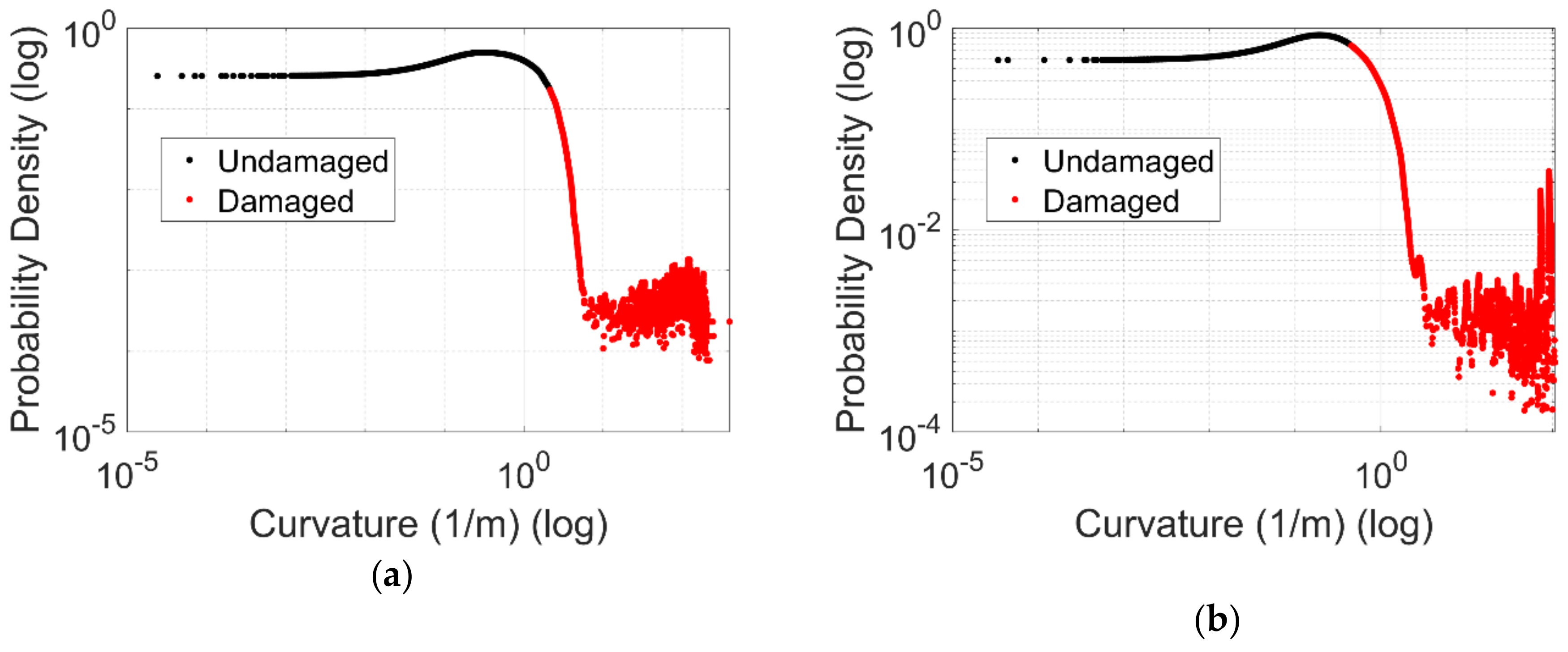
2.5. Curvature-Based Damage Detection
2.6. Damage Detection Evaluation Step
3. Discussion on Input Parameters
4. Case Study Application to Planar and Nonplanar Structures
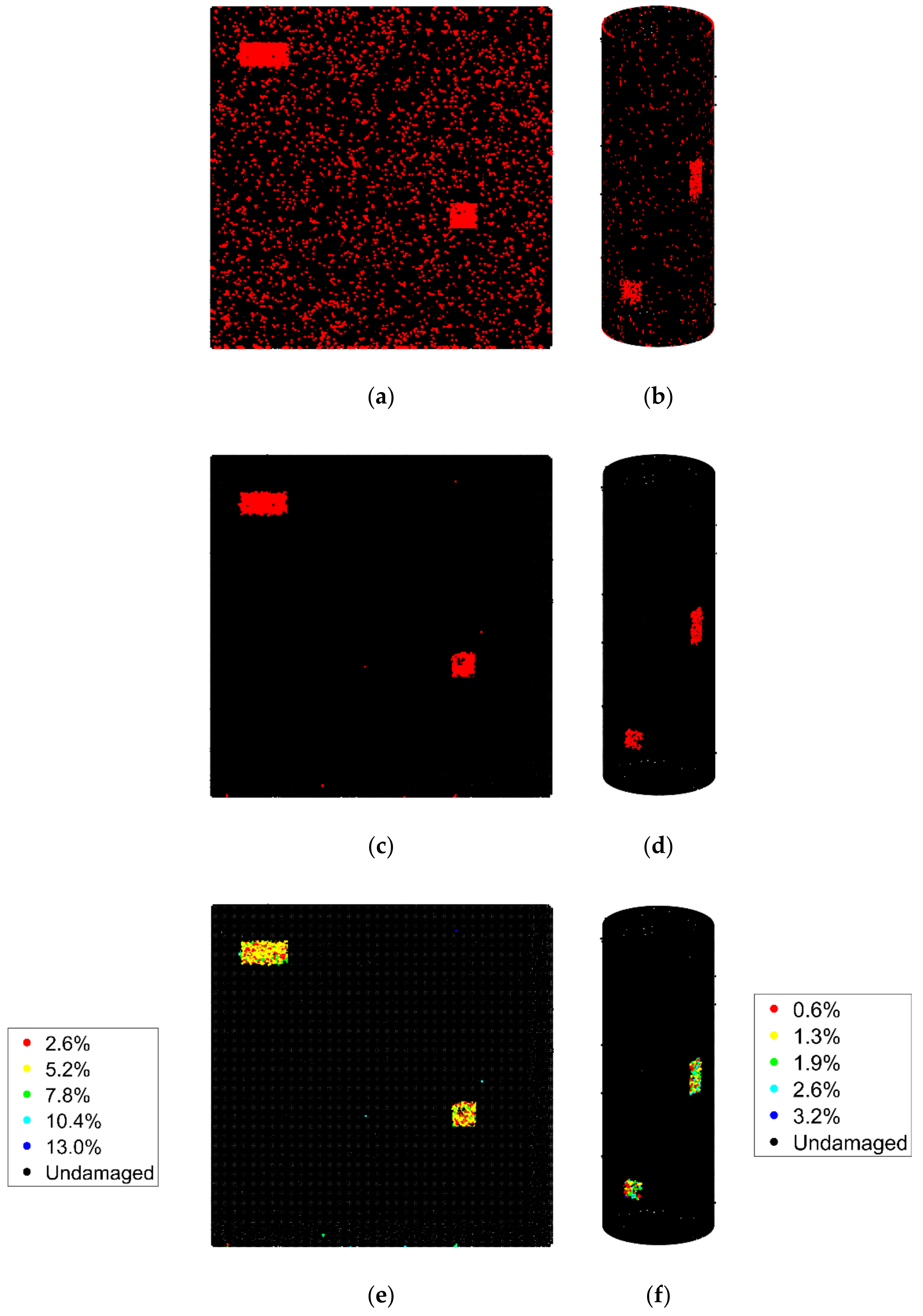
4.1. Planar Case Study: Concrete Specimen
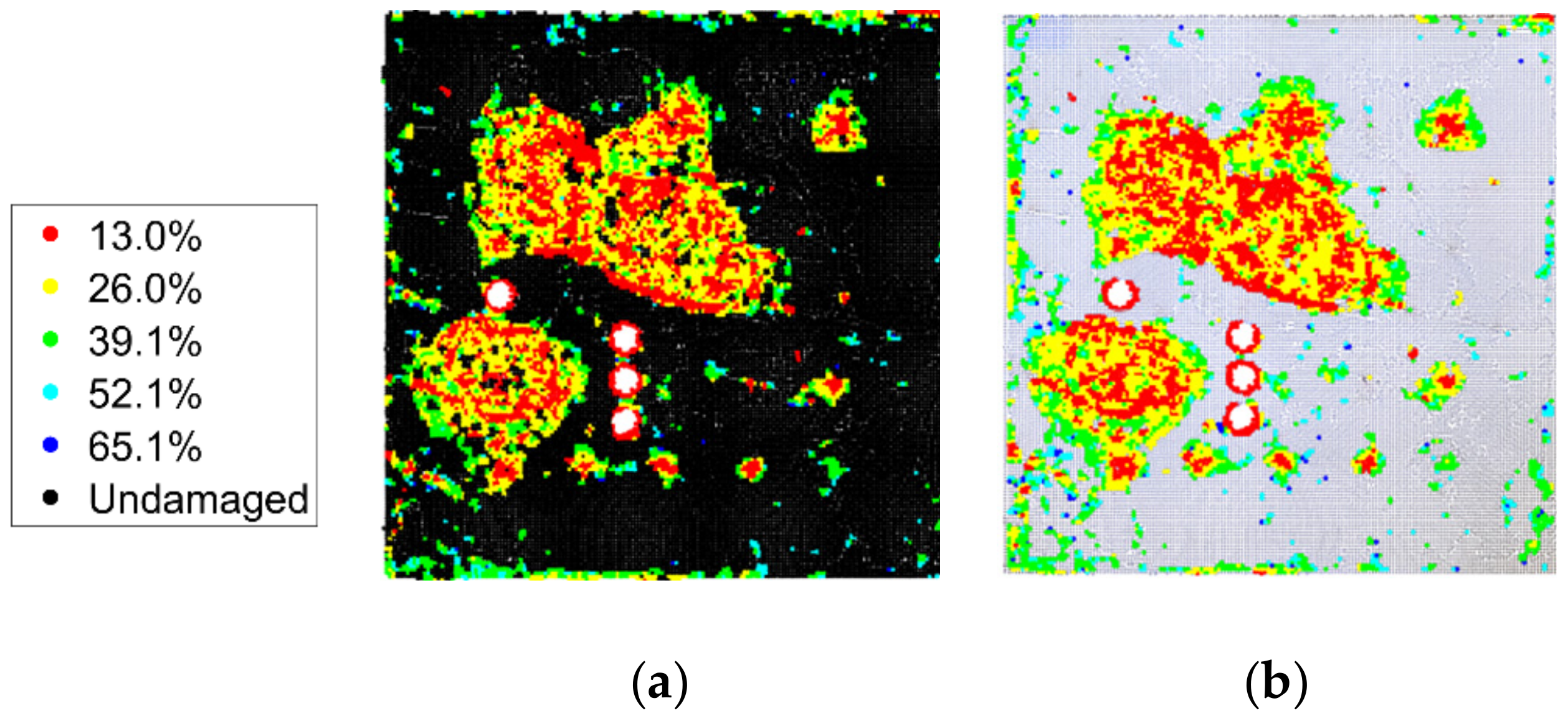
4.2. Nonplanar Case Study: Silo Structure
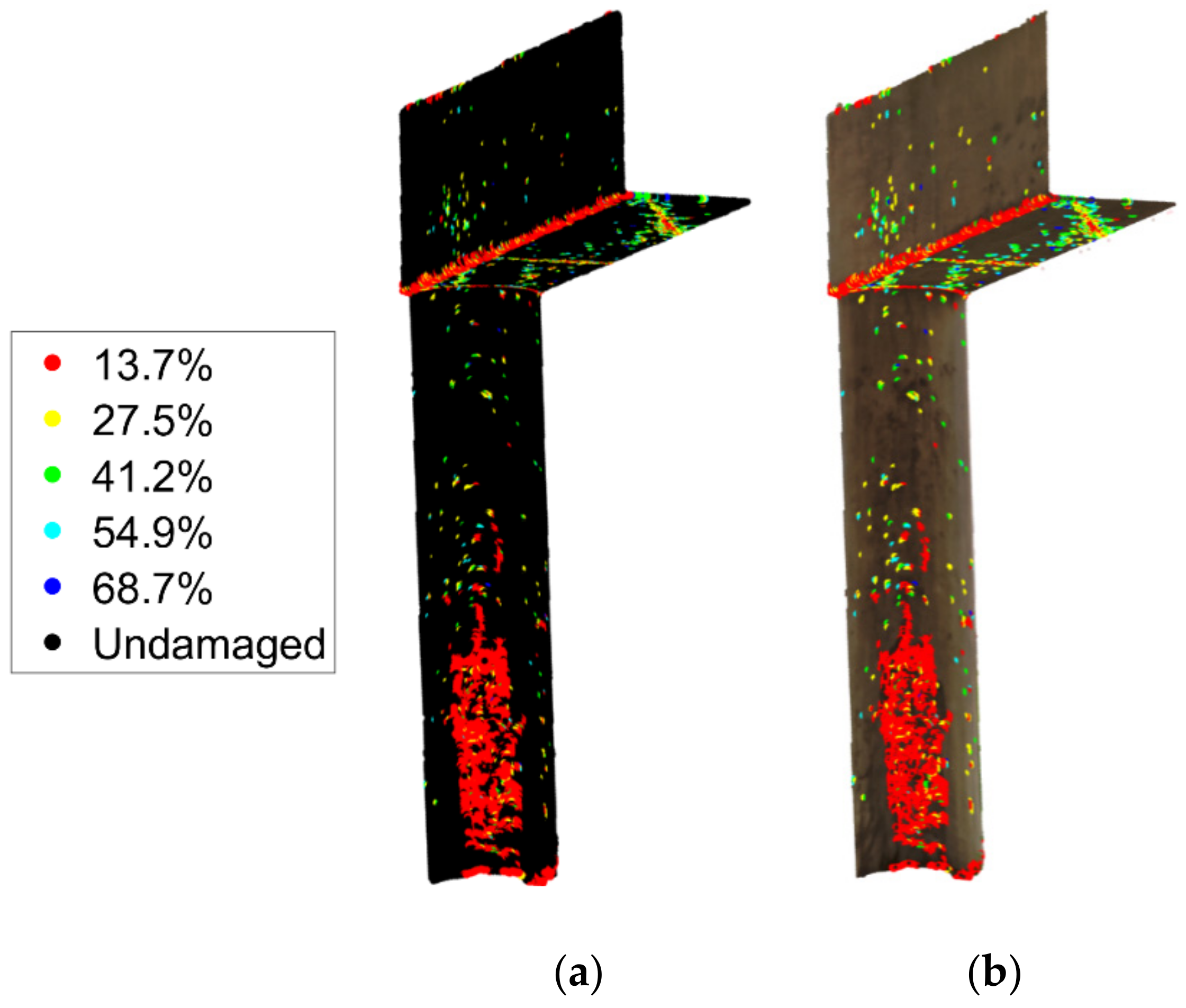
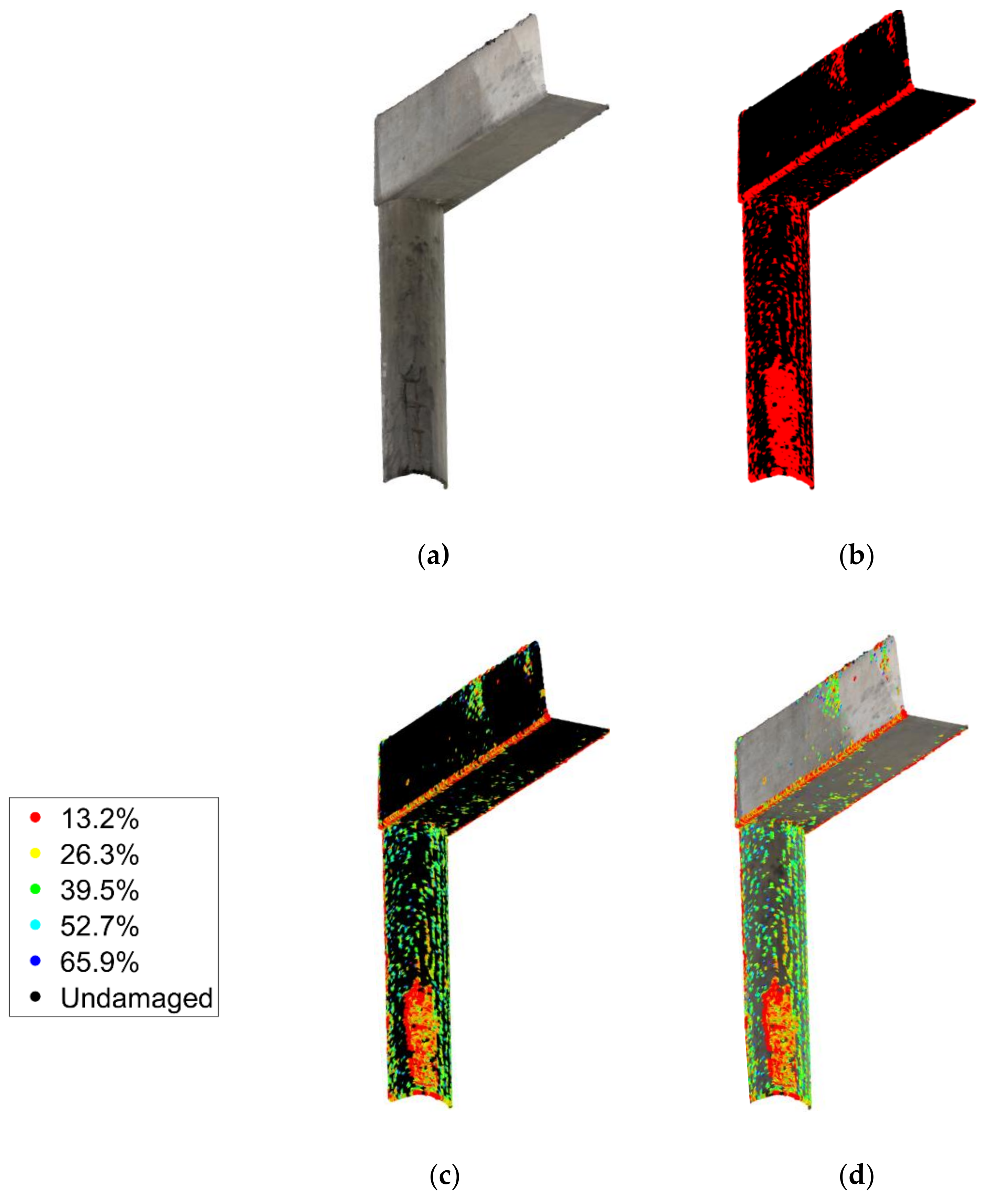
4.3. Complex Geometry Case Study: Bridge Bent Cap
4.4. Complex Geometry Case Study: Bridge Bent Cap via an SfM Point Cloud
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Park, H.S.; Lee, H.M.; Adeli, H.; Lee, I. A new approach for health monitoring of structures: Terrestrial laser scanning. Comput. Aided Civ. Infrastruct. Eng. 2007, 22, 19–30. [Google Scholar] [CrossRef]
- Sohn, H.; Worden, K.; Farrar, C.R. Statistical damage classification under changing environmental and operational conditions. J. Intell. Mater. Syst. Struct. 2002, 13, 561–574. [Google Scholar] [CrossRef]
- Hackmann, G.; Guo, W.; Yan, G.; Sun, Z.; Lu, C.; Dyke, S. Cyber-physical codesign of distributed structural health monitoring with wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2013, 25, 63–72. [Google Scholar] [CrossRef]
- Hao, S. I-35W bridge collapse. J. Bridge Eng. 2009, 15, 608–614. [Google Scholar] [CrossRef]
- Hartle, R.A.; Ryan, T.W.; Mann, E.; Danovich, L.J.; Sosko, W.B.; Bouscher, J.W.; Baker, M., Jr. Bridge Inspector’s Reference Manual: Volume 1 and Volume 2; Federal Highway Administration: Washington, DC, USA, 2002.
- Zulifqar, A.; Cabieses, M.; Mikhail, A.; Khan, N. Design of a Bridge Inspection System (BIS) to Reduce Time and Cost; George Mason University: Fairfax, VA, USA, 2014. [Google Scholar]
- Chaiyasarn, K.; Kim, T.-K.; Viola, F.; Cipolla, R.; Soga, K. Distortion-free image mosaicing for tunnel inspection based on robust cylindrical surface estimation through structure from motion. J. Comput. Civ. Eng. 2015, 30, 04015045. [Google Scholar] [CrossRef]
- Mosalam, K.M.; Takhirov, S.M.; Park, S. Applications of laser scanning to structures in laboratory tests and field surveys. Struct. Control Health Monit. 2014, 21, 115–134. [Google Scholar] [CrossRef]
- Bose, S.; Nozari, A.; Mohammadi, M.E.; Stavridis, A.; Babak, M.; Wood, R.; Gillins, D.; Barbosa, A. Structural assessment of a school building in Sankhu, Nepal damaged due to torsional response during the 2015 Gorkha earthquake. In Dynamics of Civil Structures; Springer: Berlin/Heidelberg, Germany, 2016; Volume 2, pp. 31–41. [Google Scholar]
- Yu, H.; Mohammed, M.A.; Mohammadi, M.E.; Moaveni, B.; Barbosa, A.R.; Stavridis, A.; Wood, R.L. Structural identification of an 18-story RC building in Nepal using post-earthquake ambient vibration and lidar data. Front. Built Environ. 2017, 3, 11. [Google Scholar] [CrossRef]
- Wittich, C.E.; Hutchinson, T.C.; Wood, R.L.; Seracini, M.; Kuester, F. Characterization of full-scale, human-form, culturally important statues: Case study. J. Comput. Civ. Eng. 2015, 30, 05015001. [Google Scholar] [CrossRef]
- Olsen, M.J. In situ change analysis and monitoring through terrestrial laser scanning. J. Comput. Civ. Eng. 2013, 29, 04014040. [Google Scholar] [CrossRef]
- Torok, M.M.; Golparvar-Fard, M.; Kochersberger, K.B. Image-based automated 3D crack detection for post-disaster building assessment. J. Comput. Civ. Eng. 2013, 28, A4014004. [Google Scholar] [CrossRef]
- Kim, M.-K.; Sohn, H.; Chang, C.-C. Localization and quantification of concrete spalling defects using terrestrial laser scanning. J. Comput. Civ. Eng. 2014, 29, 04014086. [Google Scholar] [CrossRef]
- Pauly, M.; Gross, M.; Kobbelt, L.P. Efficient simplification of point-sampled surfaces. In Proceedings of the IEEE Visualization, VIS 2002, Boston, MA, USA, 27 October–1 November 2002; pp. 163–170. [Google Scholar]
- Turkan, Y.; Hong, J.; Laflamme, S.; Puri, N. Adaptive wavelet neural network for terrestrial laser scanner-based crack detection. Autom. Constr. 2018, 94, 191–202. [Google Scholar] [CrossRef]
- Kashani, A.G.; Graettinger, A.J. Cluster-Based Roof Covering Damage Detection in Ground-Based Lidar Data. Autom. Constr. 2015, 58, 19–27. [Google Scholar] [CrossRef]
- Kashani, A.G.; Olsen, M.J.; Graettinger, A.J. Laser scanning intensity analysis for automated building wind damage detection. Comput. Civ. Eng. 2015 2015, 199–205. [Google Scholar] [CrossRef]
- Hou, T.C.; Liu, J.W.; Liu, Y.W. Algorithmic clustering of LiDAR point cloud data for textural damage identifications of structural elements. Measurement 2017, 108, 77–90. [Google Scholar] [CrossRef]
- Olsen, M.J.; Kuester, F.; Chang, B.J.; Hutchinson, T.C. Terrestrial laser scanning-based structural damage assessment. J. Comput. Civ. Eng. 2009, 24, 264–272. [Google Scholar] [CrossRef]
- Valença, J.; Puente, I.; Júlio, E.; González-Jorge, H.; Arias-Sánchez, P. Assessment of cracks on concrete bridges using image processing supported by laser scanning survey. Constr. Build. Mater. 2017, 146, 668–678. [Google Scholar] [CrossRef]
- Erkal, B.G.; Hajjar, J.F. Laser-based surface damage detection and quantification using predicted surface properties. Autom. Constr. 2017, 83, 285–302. [Google Scholar] [CrossRef]
- Vetrivel, A.; Gerke, M.; Kerle, N.; Nex, F.; Vosselman, G. Disaster damage detection through synergistic use of deep learning and 3D point cloud features derived from very high resolution oblique aerial images, and multiple-kernel-learning. ISPRS J. Photogramm. Remote Sens. 2018, 140, 45–59. [Google Scholar] [CrossRef]
- Ding, Q.; Chen, W.; King, B.; Liu, Y.X.; Liu, G.X. Combination of overlap-driven adjustment and Phong model for LiDAR intensity correction. ISPRS J. Photogramm. Remote Sens. 2013, 75, 40–47. [Google Scholar] [CrossRef]
- Nasrollahi, M.; Bolourian, N.; Hammad, A. Concrete surface defect detection using deep neural network based on lidar scanning. In Proceedings of the CSCE Annual Conference, Laval, Greater Montreal, QC, Canada, 12–15 June 2019. [Google Scholar]
- Kashani, A.G.; Olsen, M.J.; Parrish, C.E.; Wilson, N. A Review of LIDAR Radiometric Processing: From Ad Hoc Intensity Correction to Rigorous Radiometric Calibration. Sensors 2015, 15, 28099–28128. [Google Scholar] [CrossRef] [PubMed]
- Weinmann, M.; Jutzi, B.; Mallet, C. Semantic 3D scene interpretation: A framework combining optimal neighborhood size selection with relevant features. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 181. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Fast Semantic Segmentation of 3D Point Clouds with Strongly Varying Density. Int. Arch. Photogramm. 2016, 3, 177–184. [Google Scholar] [CrossRef]
- Mohammadi, M.E. Point Cloud Analysis for Surface Defects in Civil Structures. Ph.D. Thesis, Department of Civil Engineering, University of Nebraska-Lincoln, Lincoln, NE, USA, 2019. [Google Scholar]
- Kitago, M.; Gopi, M. Efficient and Prioritized Point Subsampling for CSRBF Compression. In Proceedings of the Symposium on Point Based Graphics, Boston, MA, USA, 29–30 July 2006; pp. 121–128. [Google Scholar]
- Rusu, R.B.; Marton, Z.C.; Blodow, N.; Dolha, M.; Beetz, M. Towards 3D Point cloud based object maps for household environments. Robot. Auton. Syst. 2008, 56, 927–941. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional Binary Search Trees Used for Associative Searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- De Berg, M.; Cheong, O.; Van Kerveld, M.; Overmars, M. Computational Geometry: Algorithms and Applications; Springer: Berlin, Germany, 2008. [Google Scholar]
- Ang, A.H.S.; Tang, W.H. Probability Concepts in Engineering Planning and Design, Volume 2: Decision, Risk, and Reliability; John Wiley & Sons, Inc.: New York, NY, USA, 1984. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Shalizi, C. Advanced Data Analysis from an Elementary Point of View; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Jin, S.S.; Lewis, R.R.; West, D. A comparison of algorithms for vertex normal computation. Vis. Comput. 2005, 21, 71–82. [Google Scholar] [CrossRef]
- Gander, W.; Golub, G.H.; Strebel, R. Least-Squares Fitting of Circles and Ellipses. Bit 1994, 34, 558–578. [Google Scholar] [CrossRef]
- Grinspun, E.; Desbrun, M.; Polthier, K.; Schröder, P.; Stern, A. Discrete differential geometry: An applied introduction. ACM Siggraph Course 2006, 7, 1–139. [Google Scholar]
- Wood, R.L.; Liao, Y.; Mohammadi, M.E.; Wipf, J. Design Procedures of Retrofitted Bridge Rail; University of Nebraska-Lincoln: Lincoln, NE, USA, 2016. [Google Scholar]
- Dogangun, A.; Karaca, Z.; Durmus, A.; Sezen, H. Cause of Damage and Failures in Silo Structures. J. Perform. Constr. Facil. 2009, 23, 65–71. [Google Scholar] [CrossRef]
- Wood, R.L.; Mohammadi, M.E. LiDAR scanning with supplementary UAV captured images for structural inspections. In Proceedings of the International Lidar Mapping Forum, Denver, CO, USA, 23–25 February 2015. [Google Scholar]
- Sanz-Ablanedo, E.; Chandler, J.H.; Rodriguez-Perez, J.R.; Ordonez, C. Accuracy of Unmanned Aerial Vehicle (UAV) and SfM Photogrammetry Survey as a Function of the Number and Location of Ground Control Points Used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef] [Green Version]










| Method | Accuracy | FPR | Precision | Recall | F1 |
|---|---|---|---|---|---|
| SV | 59% | 43% | 12% | 100% | 22% |
| NVG | 55% | 47% | 11% | 100% | 21% |
| CV | 63% | 37% | 11% | 79% | 20% |
| Evaluation Step | 89% | 11% | 35% | 90% | 52% |
| Reevaluation Step | 98% | 0% | 98% | 67% | 80% |
| Method | Accuracy | FPR | Precision | Recall | F1 |
|---|---|---|---|---|---|
| SV | 78% | 23% | 4% | 100% | 8% |
| NVL | 41% | 59% | 2% | 100% | 3% |
| CV | 91% | 09% | 9% | 97% | 17% |
| Evaluation Step | 96% | 04% | 19% | 93% | 31% |
| Reevaluation Step | 99% | 00% | 100% | 63% | 77% |
| Region | Measured Length (cm) | Detected Length (cm) | Percent Difference (%) |
|---|---|---|---|
| D1 | 67 | 68 | 1.4 |
| D2 | 117 | 120 | 2.5 |
| D3 | 25 | 24 | −4.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadi, M.E.; Wood, R.L.; Wittich, C.E. Non-Temporal Point Cloud Analysis for Surface Damage in Civil Structures. ISPRS Int. J. Geo-Inf. 2019, 8, 527. https://doi.org/10.3390/ijgi8120527
Mohammadi ME, Wood RL, Wittich CE. Non-Temporal Point Cloud Analysis for Surface Damage in Civil Structures. ISPRS International Journal of Geo-Information. 2019; 8(12):527. https://doi.org/10.3390/ijgi8120527
Chicago/Turabian StyleMohammadi, Mohammad Ebrahim, Richard L. Wood, and Christine E. Wittich. 2019. "Non-Temporal Point Cloud Analysis for Surface Damage in Civil Structures" ISPRS International Journal of Geo-Information 8, no. 12: 527. https://doi.org/10.3390/ijgi8120527
APA StyleMohammadi, M. E., Wood, R. L., & Wittich, C. E. (2019). Non-Temporal Point Cloud Analysis for Surface Damage in Civil Structures. ISPRS International Journal of Geo-Information, 8(12), 527. https://doi.org/10.3390/ijgi8120527





