Abstract
The low-cost, indoor-feasibility, and non-intrusive characteristic of passive infrared sensors (PIR sensors) makes it widely used in human motion detection, but the limitation of its object identification ability makes it difficult to further analyze in the field of Geographic Information System (GIS). We present a template matching approach based on geometric algebra (GA) that can recover the semantics of different human motion patterns through the binary activation data of PIR sensor networks. A 5-neighborhood model was first designed to represent the azimuth of the sensor network and establish the motion template generation method based on GA coding. Full sets of 36 human motion templates were generated and then classified into eight categories. According to human behavior characteristics, we combined the sub-sequences of activation data to generate all possible semantic sequences by using a matrix-free searching strategy with a spatiotemporal constraint window. The sub-sequences were used to perform the matching operation with the generation-templates. Experiments were conducted using Mitsubishi Electric Research Laboratories (MERL) motion datasets. The results suggest that the sequences of human motion patterns could be efficiently extracted in different observation periods. The extracted sequences of human motion patterns agreed well with the event logs under various circumstances. The verification based on the environment and architectural space shows that the accuracy of the result of our method was up to 96.75%.
1. Introduction
The analysis of trajectory semantics and motion patterns is crucial to human behavior research, and extensive research is already being conducted on the extraction of human motion patterns by modern observation technologies such as video surveillance, mobile location tracking, GPS receivers, and sensor networks [1,2,3,4,5,6]. As one of the most widely used sensors, passive infrared (PIR) sensors provide cheap, non-invasive, power-efficient, and long-term observations [7,8]. Unlike other passive motion sensors such as cameras, PIR sensor measurements are qualitative and record only the Boolean activation state of sensors, which means that information of the object under observation is concealed. With this “privacy-protection” feature, PIR sensors can be used in privacy-sensitive environments.
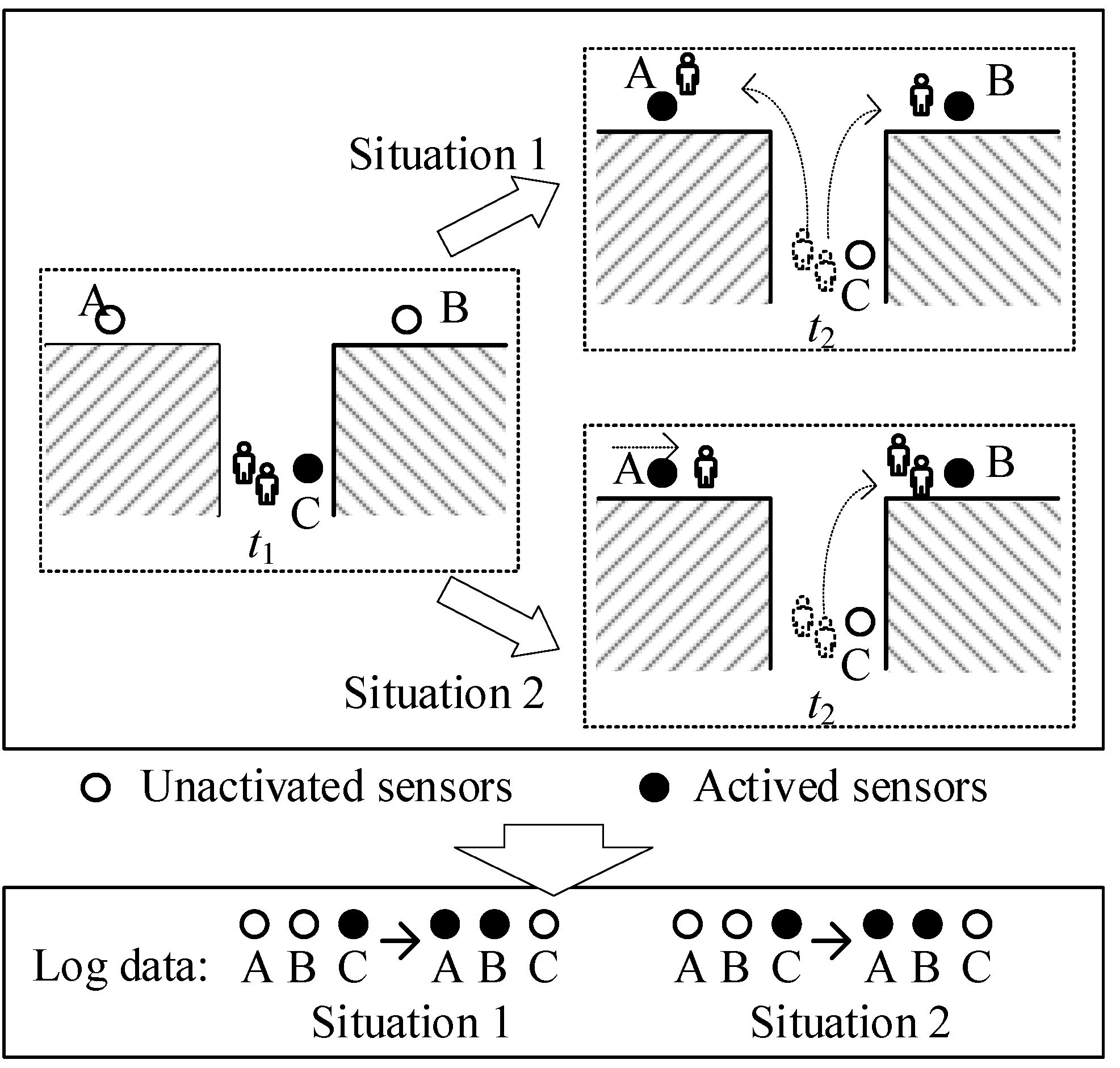
However, the PIR sensors can acquire only limited target information and azimuth information, which hinders their application to the recovery of accurate motion of every object. Taking Figure 1 as an example, different human trajectory patterns can lead to the same activation data sequences, due to the binary activation properties of PIR. Therefore, the motions recorded for multiple people by different sensors at the same time are difficult to recover. Nevertheless, PIR sensor networks contain rich embedded human motion information derived from spatial PIR sensors, which is especially the case when it is considered in a reasonably selected time window, like a day, a week, or a month [9].
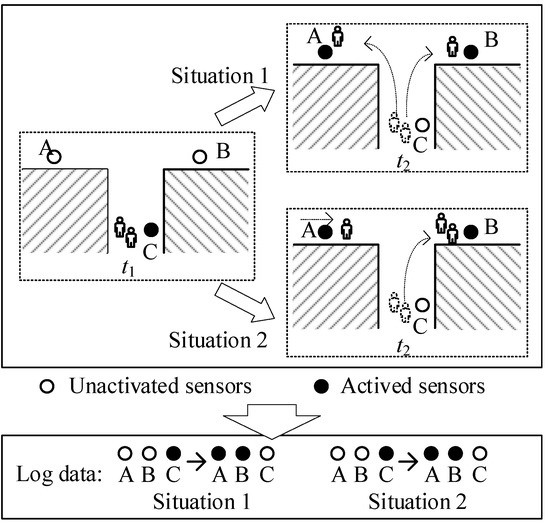
Figure 1.
Uncertainties from Boolean activation. The different two situations can lead to the same log data. First, two people pass from position C to A and B separately; second, two people pass from C to B, and an additional person arrives A at .
The embedded human motion information can also be called as human motion patterns, which was widely used in crowd detection, movement direction detection, and indoor location/activity recognition [8,10,11,12,13].
Typical approaches to separate different human motion patterns from the PIR log data are the geometric and statistical methods [14,15]. For geometric methods, geometric sensor locations and target motion characteristics were used to build a probabilistic model, and target numbers were recovered using feature-extracting methods such as cluster or particle filters [16]. These approaches illustrate the theoretical boundary conditions on whether the human motion pattern can be classified using binary activation data. However, most of these methods have been analyzed only theoretically because numerous challenges arise when PIR sensing is applied to complex scenes (e.g., a floor of an office building with different rooms and channels) due to the complex spatiotemporal constraints. The initial work is to use geometric algebra and matrix products to recover the target motions in complex scenes. With the assumptions of more detailed sensing capabilities, complex scenes can extract possible motion directions and limited trajectory types [9]. However, the accuracy of the trajectory recovery remains low. In addition, the matrix-based computation and the computational complexities of the methods are high, which avoids the large-scale application for PIR sensor networks.
Template matching methods, which are commonly applied in the signal processing or image analysis, have the potential to bridge the gap between the binary sensor activation data and identifiable human motion patterns. Template matching defines feasible patterns in a template and reveals both local and global patterns by matching the original data with these pattern templates [17,18,19,20]. Nevertheless, unlike template matching methods widely used in signal processing and image analysis, the location of the sensors and log data are hard to represent as structured data. Thus, as far as we know, there are no formal template matching methods for extracting human motion patterns from PIR networks. The lack of a key mathematical theory is the key issue of such template matching.
Here, we developed a generation template matching (GTM) paradigm with geometric algebra (GA) to solve the problem of recovering qualitative motion patterns from PIR sensor data. In our approach, the motion templates that classify different human motion patterns, were generated by GA coding and the outer product of the 5-neighborhood model. With the consideration of the PIR sensor network and uncertainties of motions, spatial and temporal constraints were embedded into the data selection step, trying to recover all possible trajectories. A template-matching algorithm was also developed to calculate the relationships between the template and the overall sensor activation data, and this is to recover human motion pattern sequences. Finally, we evaluated our method based on MERL (Mitsubishi Electric Research Labs) datasets.
The paper is organized as follows: the formal definition of the problem and the basic idea is described in Section 2. The methods including the GTM algorithm of human behavioral semantics are described in detail in Section 3. The case study and performance analysis are given in Section 4. The conclusions are given in Section 5.
2. Materials and Methods
This section describes the main problems in human motion pattern analysis and the basic idea for extracting trajectory semantics using the GTM algorithm.
2.1. Problem Definition and Basic Idea
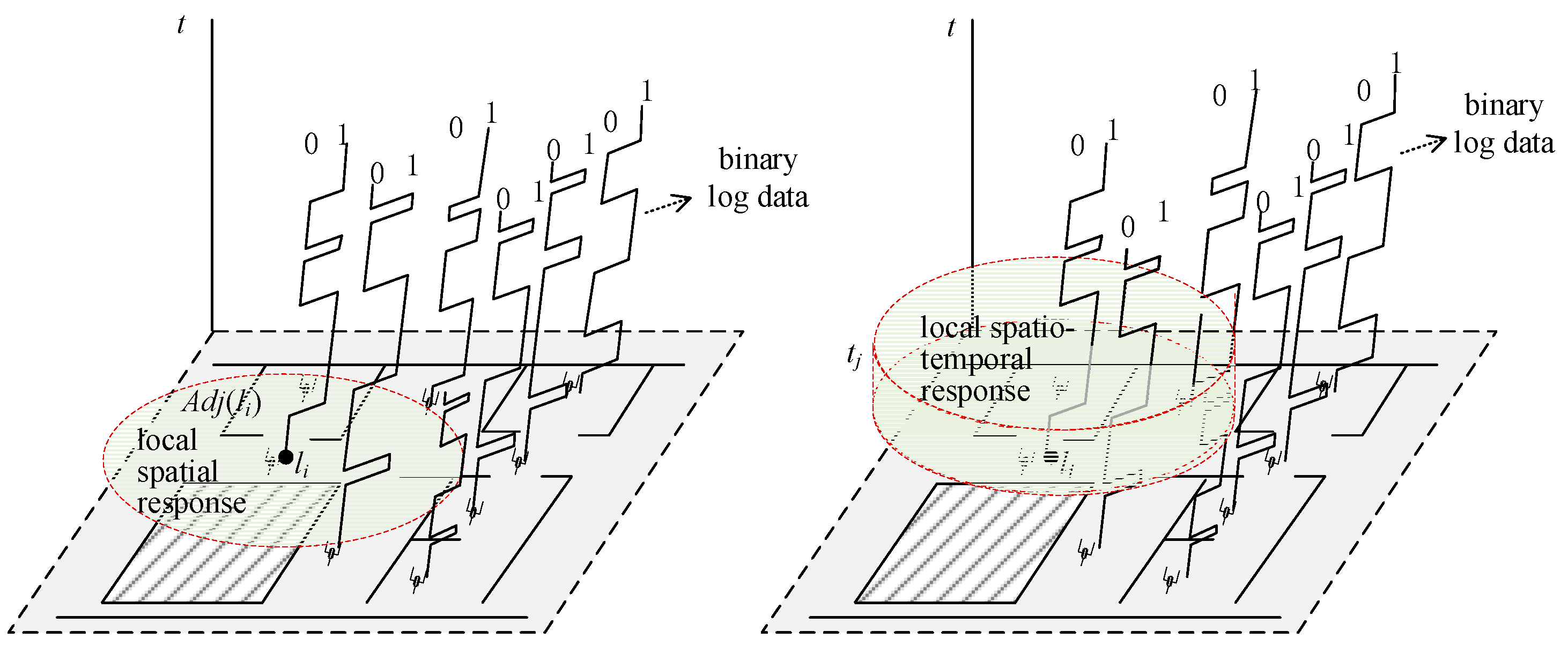
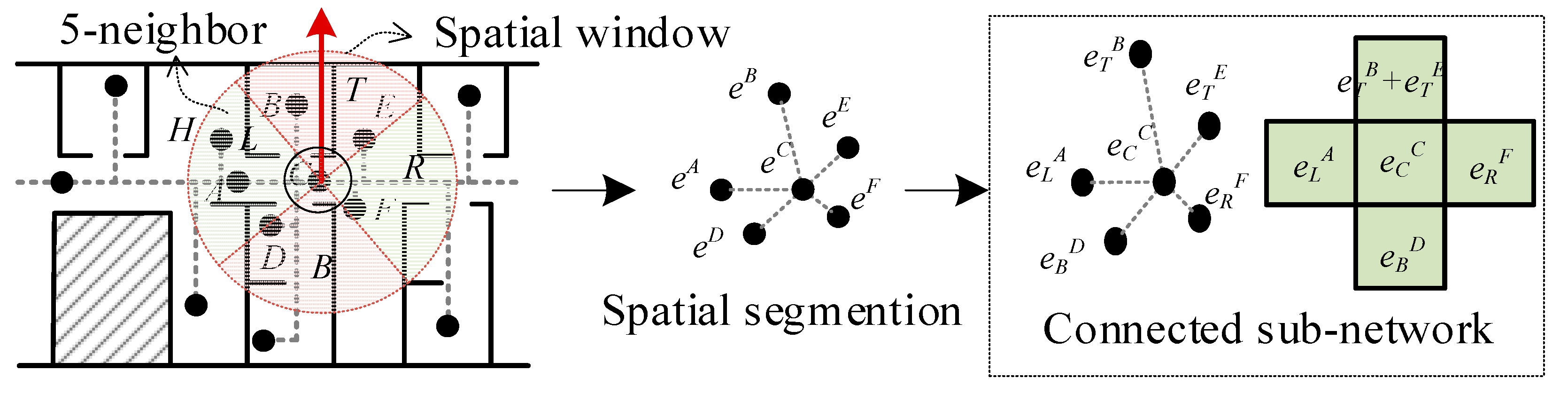
In order to constrain the linkage between different sensors, PIR sensors are commonly installed in closed spaces. The observed states of the PIR sensor at each time are encoded into a binary set as , where 1 indicates that the corresponding sensor is active, and 0 indicates otherwise. For large sensor networks with hundreds or thousands of sensors deployed, the combination of all global states may grow significantly. To avoid the computational exploration, the local response of the sensor network should first be considered (Figure 2).
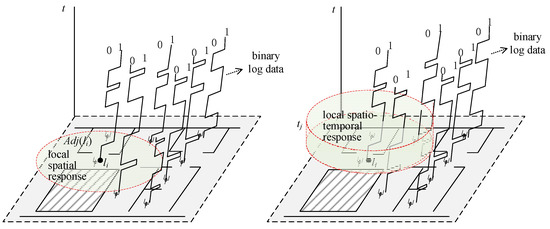
Figure 2.
The local spatial response and local spatial-temporal response.
As shown in Figure 2, considering the spatially constrained by the neighborhood of specific sensors, we define the local spatial sensor response as follows:
Definition 1.
Local spatial response of sensor:
Given the observation time series, the state series of the sensor located atcan be represented as a global temporal binary response vector. Considering the adjacent PIR sensor set, a local spatial response sequence can be defined as a binary matrix, where. Since the motions occur at a limited time, the spatiotemporal response is also defined.
Definition 2.
Local spatio-temporal response of sensor:
For the PIR sensorat observed time, a spatiotemporal response sequence with two-tuples can be defined as, wheredenotes the time span fromto,denotes the time span fromto, andis a user-specified maximum time span threshold (or time interval).
It is evident that the spatiotemporal responses are composed of observed states including those before and after the current time. Then, we can extract the sensor setsandactivated before and after the current time with the constraints thatand.
To extract the patterns from the local spatiotemporal response of the sensor and match them with the human trajectory semantics, extracting some of the constant response patterns from the sensor activation data is important. Since complex trajectory can be combined from several simple structures, we defined these fundamental structures as a meta response pattern.
Definition 3.
Meta response pattern:
According to the spatiotemporal response of sensor, the meta response pattern is defined as the minimum response sequence composed of the active sensors in the previous and next states:
The objective of motion pattern recovery is refining the meta response pattern set and convert the bool data of the PIR response into the final motion semantics. This process can be divided into two parts: (1) defining a reasonable motion semantic set and (2) constructing the mapping from the meta sensor response pattern to the motion semantics. However, this two-step method may lead to a new problem between the infinite meta response patterns, which is theoretically true when infinite sensors are used, and the motion semantics are limited.
Therefore, we introduced the template method to filter the meta response patterns into a finite motion template set. Given the motion template set , according to the above definitions, we can formally define the template matching method as follows:
where ⨂ is the filtering and matching operator, which is similar to the convolution approach in the image data analysis. denotes the similarity of the motion template and the spatiotemporal response of sensor at time . For all of the templates , if can be matched and filtered with the meta response pattern , the template matching results can get the maximum value, and this means that the motion semantic of people has the same motion semantic as . The overall solution can then be decomposed into three different steps: (1) The definition of the template set; (2) the definition of the filter method to refine the unstructured PIR log data into structured GA coding; and (3) the definition of the template matching operator ⨂.
2.2. Basic Idea
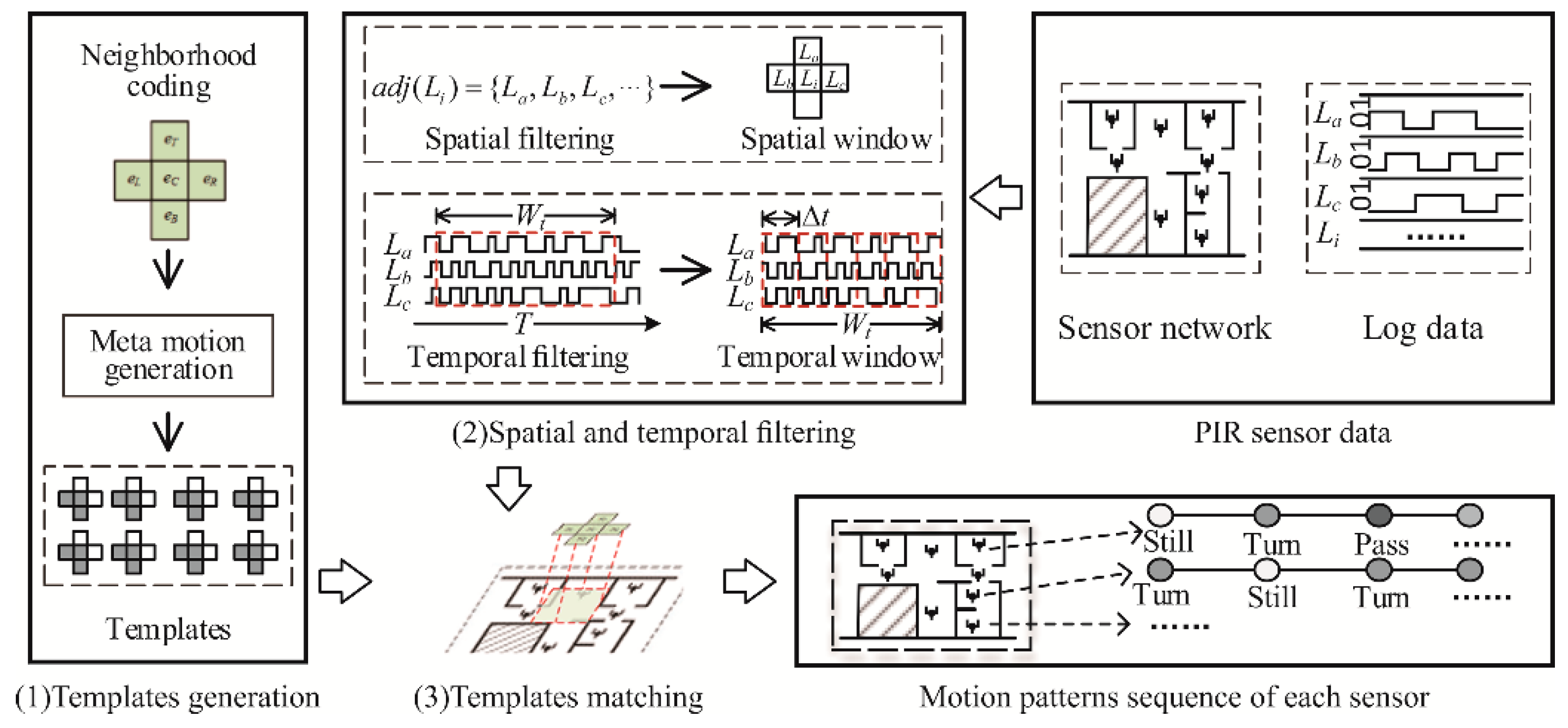
Focusing more on qualitative motion patterns, we attempted to embed both the spatial and temporal meaning in the template. To reduce the uncertainty of response combinations, which are composed of mixtures of semantically meaningful or meaningless codes, we refined the mixed response by a temporal-neighborhood window. As shown in Figure 3, the framework of our method comprises three parts.
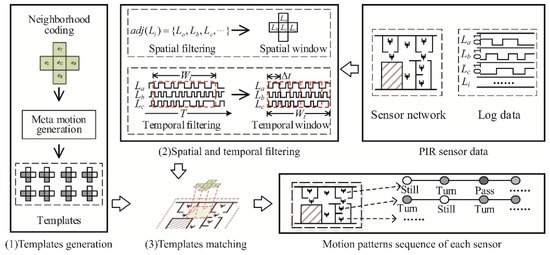
Figure 3.
Flow chart of the generation-template matching approach showing three steps.
2.2.1. Template Generation
In the template-matching method, the structure of the template directly affects the performance and efficiency of the trajectory semantics extraction. As there are various semantic sets with different spatial cognition and partition granularity, the predefined human motion patterns may be so limited that additional human motion patterns cannot be classified. The numerous template types also make the algorithm computationally expensive. To make it simple enough, we considered the motion pattern in both the spatial and temporal domains and used the 5-neighborhood model to represent the direction of motion including center, top, right, bottom, and left. In the temporal domain, the motion process is represented by the meta response pattern . GA coding of the 5-neighborhood model was used and then the outer product was introduced to generate the GA expression of the meta response pattern [21]. Thus, the local templates can be used to generate all possible trajectory types (template) in a local spatial and temporal range, which can be used to recover all the trajectory semantics.
2.2.2. Spatial and Temporal Filtering
In our approach, motion patterns should be defined by the template, and human motion types should be matched and filtered by sensor log data. Template matching is a local computation process satisfying both local and global constraints. Unlike the template matching widely used in signal processing and image analysis, the location of the sensors and the log data are unstructured. The trajectories’ distribution in space–time is irregular, and the data types of trajectory and sensor log data are not unique.
In the PIR sensor networks, the topological and directional relations between different sensors can be seen as a key indicator of the spatial structure. The templates focus on a single sensor and its adjacency reproduce the entire possible motion trajectory. Therefore, we can map the irregular sensor logs to the topology of the network to regulate both the sensor log data and the template. In the work by Yu (2016), they used a global matrix-based approach to model the network and trajectory topologies, which have lots of redundancy. Here, we used the outer product in a local region to achieve the trajectory filtering.
It is important to define an appropriate spatio-temporal window to participate in template matching. Here, a well-defined time window should first be defined to segment the duration time of the log data into small intervals, thus we can form the meta response pattern. Consequently, the meta response pattern actually means the motion state of the behavior trajectory and is expressed as a GA blade, which contributes to the implementation of template matching. To reduce the uncertainty of the meta response patterns, an accuracy correction step is raised here. Since the behavior trajectory of a target remains stable during a reasonably selected time window (e.g., a day, a week, or a month), we can collect the entire possible behavior trajectory and only retain those occurring at a frequency of 50% and higher. Thus, in a small given local area and stable time window, the status of possible human motions is limited and fixed.
2.2.3. Template Matching
Similar to the convolution operation in signal processing or image analysis, the template matching uses certain operators to compute the similarity or relations between the template and the local region of original data. The difference with the convolution operation is that the template matching of PIR sensors is required to compute the similarities between the template and local spatial-temporal regions across different active sensors. Since the meta response pattern and the template have already been converted into GA blades, the similarity can also be implemented by the inner product, which is always used to calculate the relationship of blades in GA [21,22]. The inner product can distinguish if the two blades are consistent, in addition, it can also work when the blades are in reverse arrangement.
With the generated template, the computation of PIR sensor logs can be limited to a local window to distinguish more complete human motion types. By combining the generation-template paradigm and the matching method, it is possible to increase the accuracy of the PIR data analysis and obtain stable motion patterns.
3. Methods
3.1. Templates with the Neighborhood Model
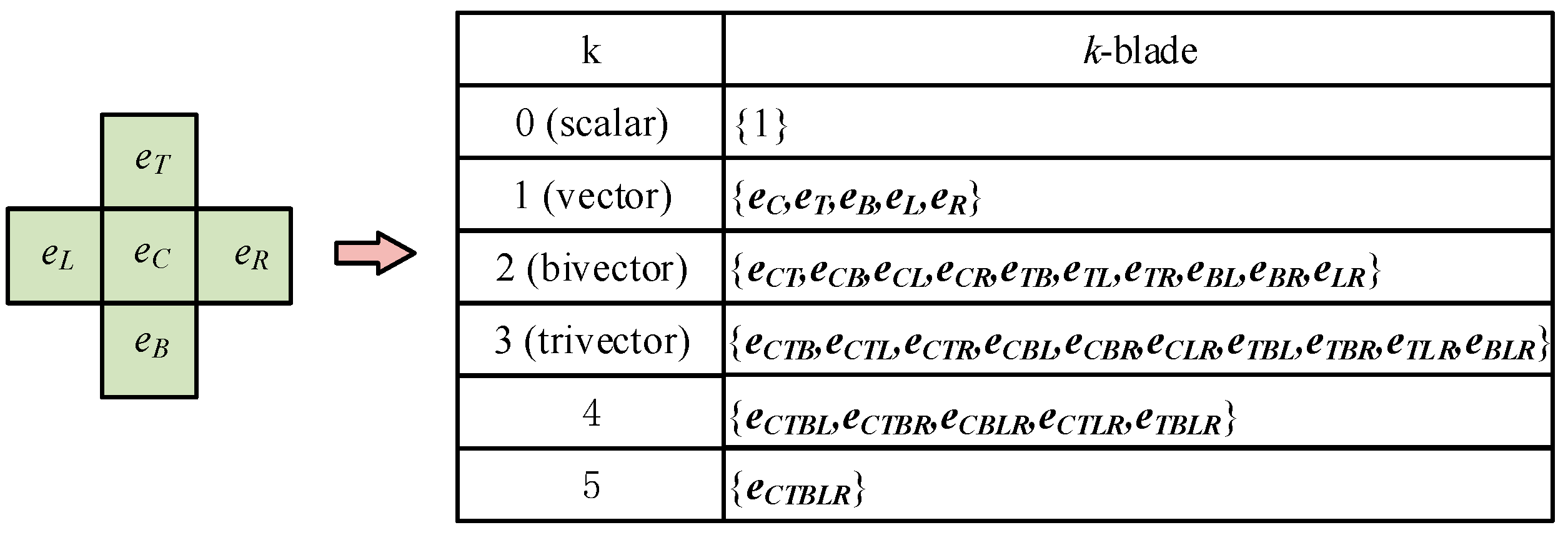
The key point of the template-matching method is defining the templates and determining the completeness of the retrieved motion patterns. In order to define reasonable templates, the selection of neighborhood and the expression of motion behavior under the neighborhood are considered. Adjacent PIR sensors of the selected sensor are built based on the topology of the sensor network. The area of the motion can then be retrieved according to this local unit. Meanwhile, the direction for the clear motion semantics is also important. Thus, we introduced the 5-neighborhood model, expressed as , which indicates the center, top, right, bottom, and left, respectively. Then, the key point is to express the 5-neighborhood model algebraically.
Geometric algebra is an ideal tool for expressing multi-dimensional algebra, and this can be used to synchronize spatial construction and computation [21,23,24,25]. For any given positive integer n, the GA space is constructed as a set of base vectors . The element can be calculated by arbitrary through the outer product [22]. Such an element in the GA space can be expressed as:
Since the blade structure can not only record node information, but also embed the node order, the GA coding can be used to define the templates. As for the specific predefined set , it can be represented by the GA space . Each element in such a set corresponds to the orthogonal base vector in . Then, the k-blade structure within the 5-neighborhood model can be used to code the distinct combinations of sensor nodes as Figure 4, which are active at different directions in a continuous period.
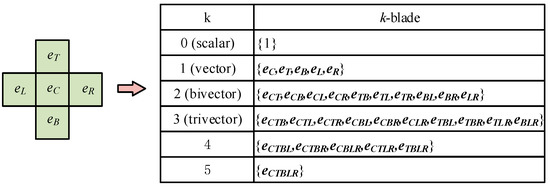
Figure 4.
Neighborhood coding by .
However, not all correspond to the actual motion. For example, , one type of , is invalid for expressing motion in the network. Thus, in order to obtain all meaningful that can be used as standard motion codes in the templates, further filtering is required.
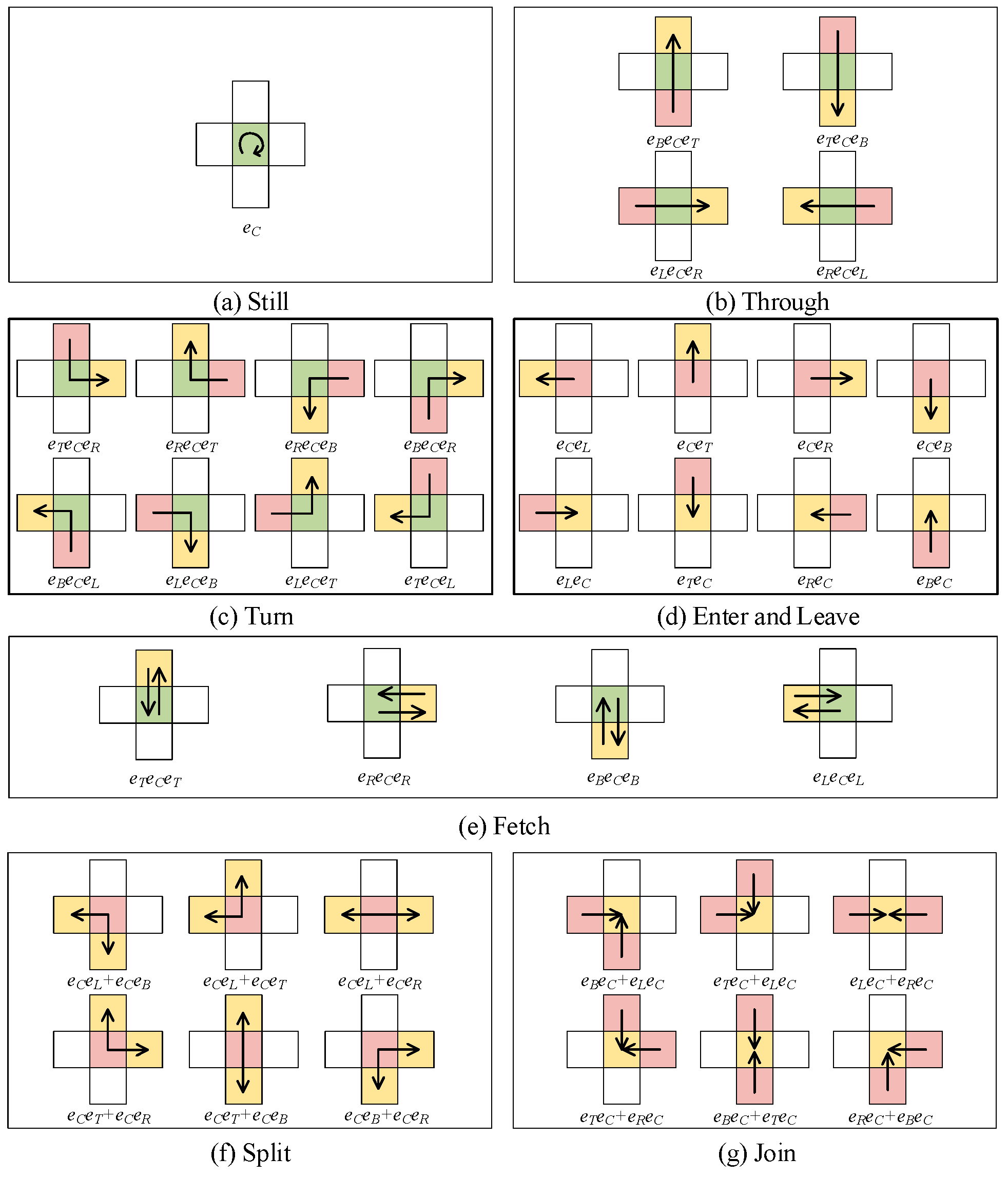
We defined all motions from the center node of the 5-neighborhood model. According to the definition of the meta response pattern, all the meaningful orders of sensor nodes can be expressed as three continuous sets, . Given a response sequential , it can be encoded in GA space as , where means the node is located to the bottom of the center node . The corresponding motion can be regarded as the single body and easily encoded as .
According to the above rules of motion encoding, we can easily extract all possible motions in the 5-neighborhood. As shown in Figure 5, eight types of motion templates (including Still, Through, Turn, Enter, Leave, Fetch, Split, and Join) are proposed and the detailed motion codes are also given. Such templates provide the paradigm for the extraction of meta response pattern and motion semantics from the original trajectory.
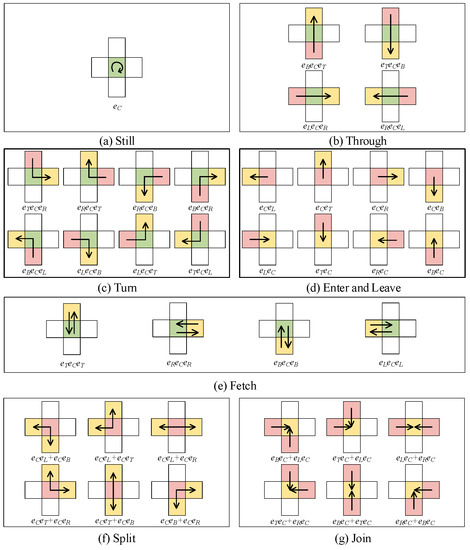
Figure 5.
Templates of trajectory semantics.
3.2. Spatial and Temporal Constraint Window
For the arranged PIR sensor system, templates can provide a unified extraction paradigm, but it is difficult to apply directly them to the real PIR network without an effective spatial-temporal window. Here, we introduce the spatial-temporal constraint window to preprocess the PIR sensor data.
3.2.1. Spatial Constraint Window
For the given PIR sensor network, all sensor nodes are clearly represented by the GA-based network graph, which can provide a precondition for additional spatial constraints in the PIR sensor network (Figure 6). Based on the 5-neighbor model of templates, it is necessary to find all neighbors of the whole sensor nodes to build the same spatial structure. As shown in Figure 6, any sensor node in the sensor network is treated as the center node individually to obtain its neighbors in four directions (Top, Left, Bottom, and Right). The four directions are divided according to their angles with the center node, which is defined in detail as:
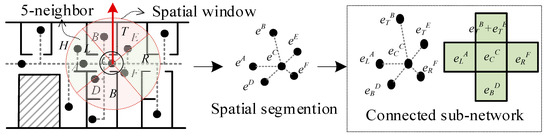
Figure 6.
Spatial constraint window based on the 5-neighbor model.
For each region separated by angle θ, only adjacent sensors are selected as the neighbor, this selection also depends on whether this node and the center node are sufficiently close for continuous movement detection. The result is defined as a connected sub-network, having the same structure with the 5-neighborhood model.
3.2.2. Temporal Constraint Window
Spatial constraints segment the PIR sensor network into sub-networks that correspond to the templates. However, for the sensor log data themselves , the activation response sequences are continuously recorded over time. Thus, the temporal constraint is needed to segment the continuous sensor log data.
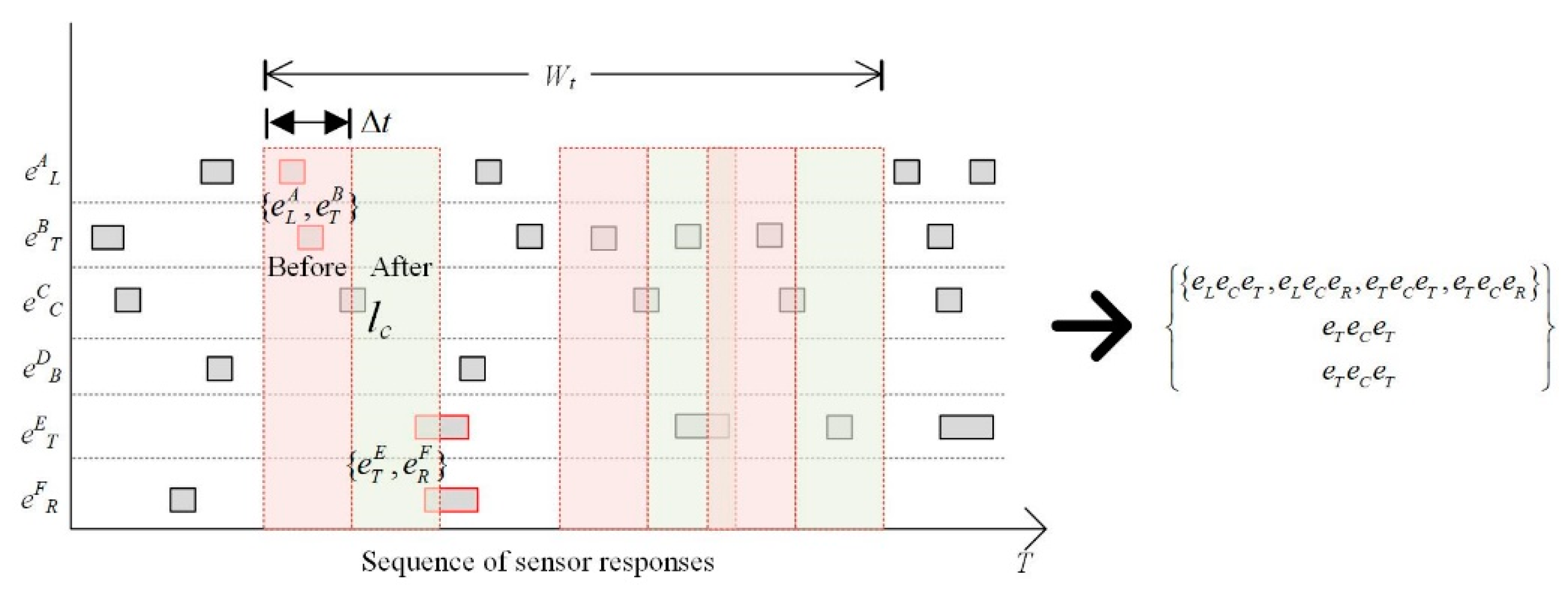
First, in the 5-neighborhood model, the GA codes of sensor nodes can be used to signify the response state. Then, the activated sensor sequences can be expressed as in Figure 7. We introduced the time interval, which decides whether the sensor node is activated adjacently by time. is a parameter related to human motion and sensor settings. Assuming to be the normal walking speed (1.3 m/s) of an adult, to be the sensor detection radius, and to be the feasible distance between two sensors, the time interval is calculated as:
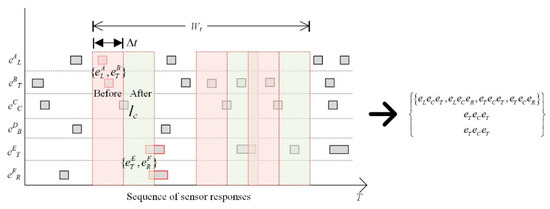
Figure 7.
Spatial constraint window based on the 5-neighbor model.
Since motion detection based on a single sequence may lead to uncertainties of the trajectory (as shown in Figure 1), here we introduce the duration window , in which all sequences including the center sensor are collected, and only trajectory semantics occurring at high frequency (e.g., 50%) are retained. As shown in Figure 7, every time window that contains sensor will be analyzed in duration window , even when two windows overlap. Taking the center sensor as the split line, the response sequence of can be divided into previous and next response sequences. Taking the first time window in Figure 7 as an example, two types of response sequences including the previous response sequence and next response sequence are divided by the center sensor node . Then, six trajectory semantics were evaluated, where occurred three times and met the 50% frequency condition. According to the templates of trajectory semantics, for sensor and the duration window , the trajectory semantic was ‘Fetch’.
3.3. Meta Response Pattern Generation
We refer to the 5-neighborhood templates to generate possible trajectory semantics according to the sensor network topology and sensor log data. As the sensor network is segmented by the spatial and temporal constraints into sub-networks, and the continuous sensor activation response sequence is divided into two response sequence sets, we proposed the following gradual generation method to obtain the GA expression of all possible trajectories.
First, in the front and back response sequences, the common situation of sensor nodes were considered. As all response sequences are coded on the basis of GA and the 5-neighborhood model, the response sequence was used to represent the previous and next response sequences, which are named as and , respectively. There are three common types of response states based on the number of sensor nodes in the and :
- and are both empty, which means only the center sensor node responds;
- and both have response sensor nodes;
- Either or is empty.
Among these three types, type (1) is easy to handle because it means that there is no other motion at that time. Types (2) and (3) are much more difficult because more possible combinations exist. Therefore, the encoding method is used to signify all combinations as GA expressions. Given the representations of and , , , all possible combinations, , constructed by the outer product are formulated as:
The above formula represents general GA forms of sensor responses. In particular, when (meaning that there are multi-targets in both and ), the trajectory is uncertain due to the diversity of combinations. In our method, all possible trajectories were generated in order to avoid the loss of trajectory semantics.
Second, after the generation, it was obvious that not all of the GA expressions are meaningful from the viewpoint of motion. Therefore, template matching was applied to obtain the similarity calculation of response sequences and template. So far, the combinations of both sensor response sequences and templates have been represented as GA expressions. Based on the quantified expressions of GA, the matching processes can be easily implemented by the inner product.
3.4. Template Matching of Meta Response Pattern and Template
According to the original definition of the inner product, for the given base vector , there exist when ; and when . Therefore, the template matching operator ⨂ in Equation (1) can be defined as:
As two forms of templates exist, the matching operator is divided into two situations. When is a blade, the inner product is enough, but if it is a (like split and join, which composed with two blades), the inner product must be divided by two. The value range of the matching operator is [0, 1], and only when the result equals to 1, the obtains the best math of .
3.5. Generation-Template Matching Algorithm
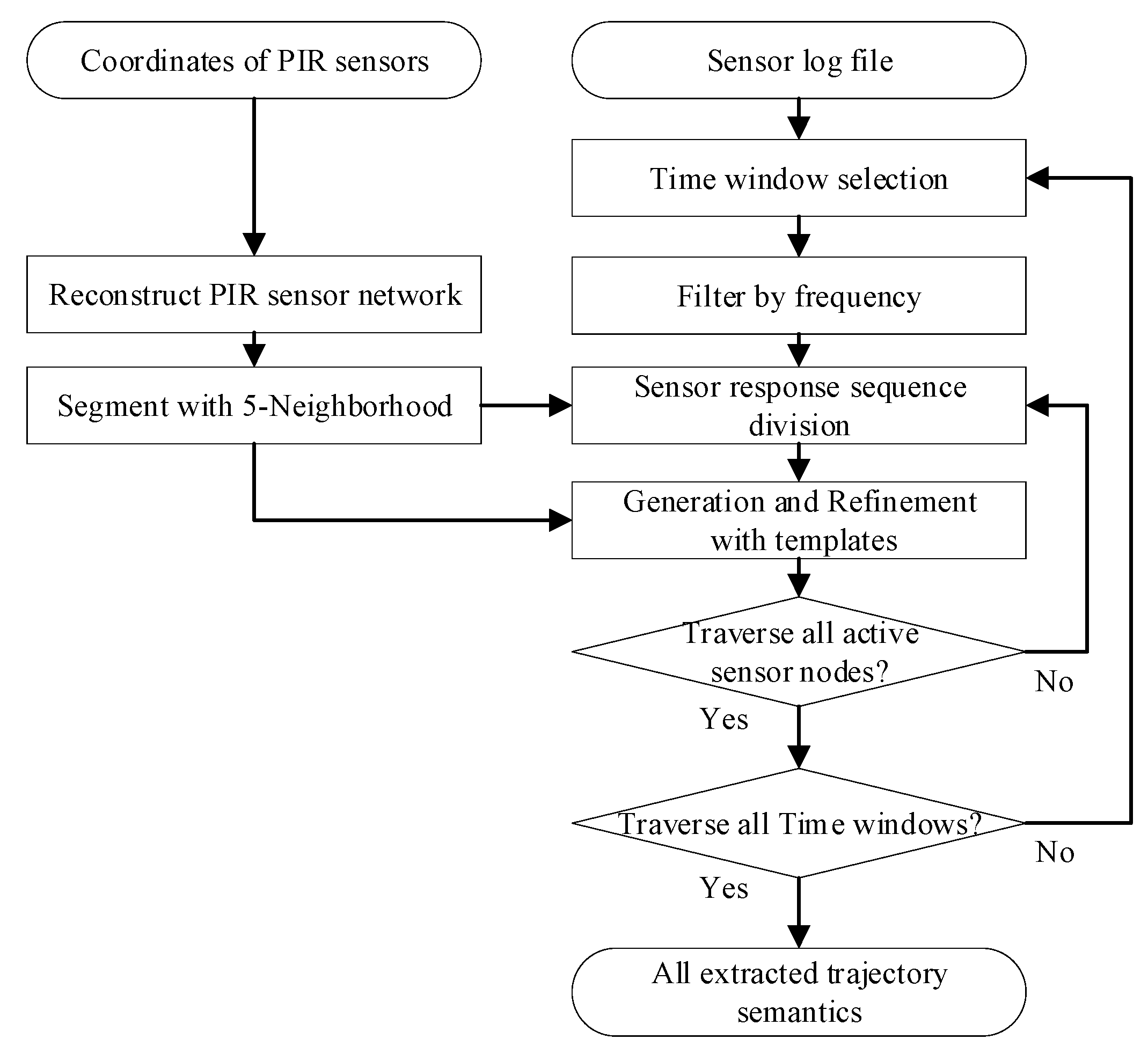
Based on all definitions in the above-mentioned four sections, a generation-template matching algorithm can be developed according to the sensor activation log, and it can help to extract all possible trajectory semantics.
The algorithm starts with the sensor network data, and then the whole network is segmented into sub-networks with the spatial constraint. The generation process is executed over each time window in duration window . After applying a 50% frequency filter, the stable sensor activation response sequences of the sub-networks were divided into and before being combined with the center node and then encoded to obtain possible GA expressions. The pre-defined templates traverse each node to match the GA codes with those defined in the templates, which is mainly to achieve meaningful coding. Finally, the retrieved GA codes are translated into corresponding motion semantics, and the whole algorithm process is completed, as illustrated in Figure 8.
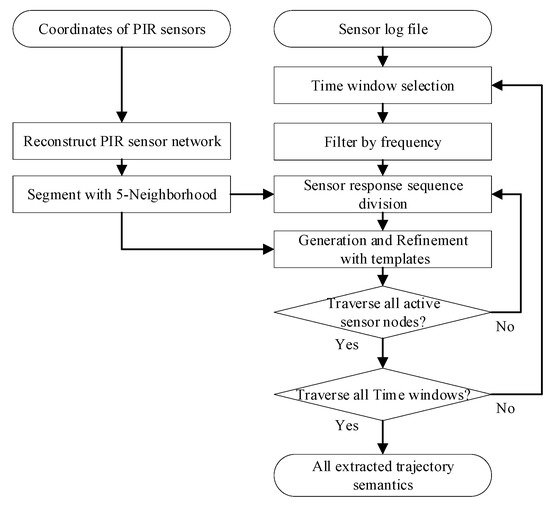
Figure 8.
Flow chart of the process of the generation-template matching algorithm.
In order to satisfy the requirements of the generation-template matching algorithm, we built an operator library as shown in Table 1. It mainly includes four parts: a network reconfiguration operator set, spatial constraint operator set, time constraint operator set, and generation and matching operator set. Among them, the network reconfiguration operator set mainly rebuilds topological relationships based on the sensor position, obtains the sensor network map, and establishes the adjacency matrix by sensor position. The spatially constrained operator set mainly segments the entire network into sub-networks. The time constraint operator set divides the sensor activation response sequences into front and back response sequences; the generation and matching operator set is used to generate all possible trajectories, and it is matched by templates to obtain the motion patterns.

Table 1.
Operator database of the generation-template matching algorithm.
Through the construction of the above four kinds of operator sets, the generation-template matching algorithm can be implemented, from the original response data to the final trajectory semantics. The pseudo-code of the complete algorithm is shown in Algorithm 1.
| Algorithm 1. Pseudo code of the generation and matching algorithm. |
| Input: Basic parameters, Coordinate set of sensors C, Sensor activation log Data, Time division step Δt |
| Output: semantic set of trajectory ST |
| Function Explanation: The functions used in the pseudo-code are explained with reference to Table 1. TC means all the sensor nodes after coordination conversion; Aj means the set of nodes adjacent to TC; M means the adjacency matrix; E denotes adjacent domain coding; T denotes the total time; W denotes the duration time window; GA_code represents the code sequence with the combination of Front_seq and Back_seq; Templates mean the pre-defined 5-neighborhood motion templates. |
| 1: TC = DataCoordTrans(C); |
| 2: for i←0 to Count of TC do |
| 3: Aji←DataFindAdj(TCi); |
| 4: for each element e in Aji |
| 5: if (AdjJudgeCon(e, TCi)) |
| 6: M←IniAdjMatrix(e, TCi); |
| 7: End if |
| 8: End for |
| 9: End for |
| 10: for i←0 to Count of TC do |
| 11: M5i←DataNeighScreen(TCi, M); |
| 12: E5i,←DataNeighCode(M5i); |
| 13: for j←0 to T/W |
| 14: E5 i,j←FreqFilter(E5 i,j) ; |
| 15: Front_seq←DataDivSeq(Data, E5 i,j, Wj, Δt).Front; |
| 16: Back_seq←DataDivSeq(Data, E5 i,j, Wj, Δt).Back; |
| 17: GA_code←DataSemGenerate (Front_seq, Back_seq); |
| 18: End for |
| 19: End for |
| 20: Motion_Pattern←DataSemMatch(GA_code, Templates); |
4. Case Study
4.1. Data and Analysis Environment
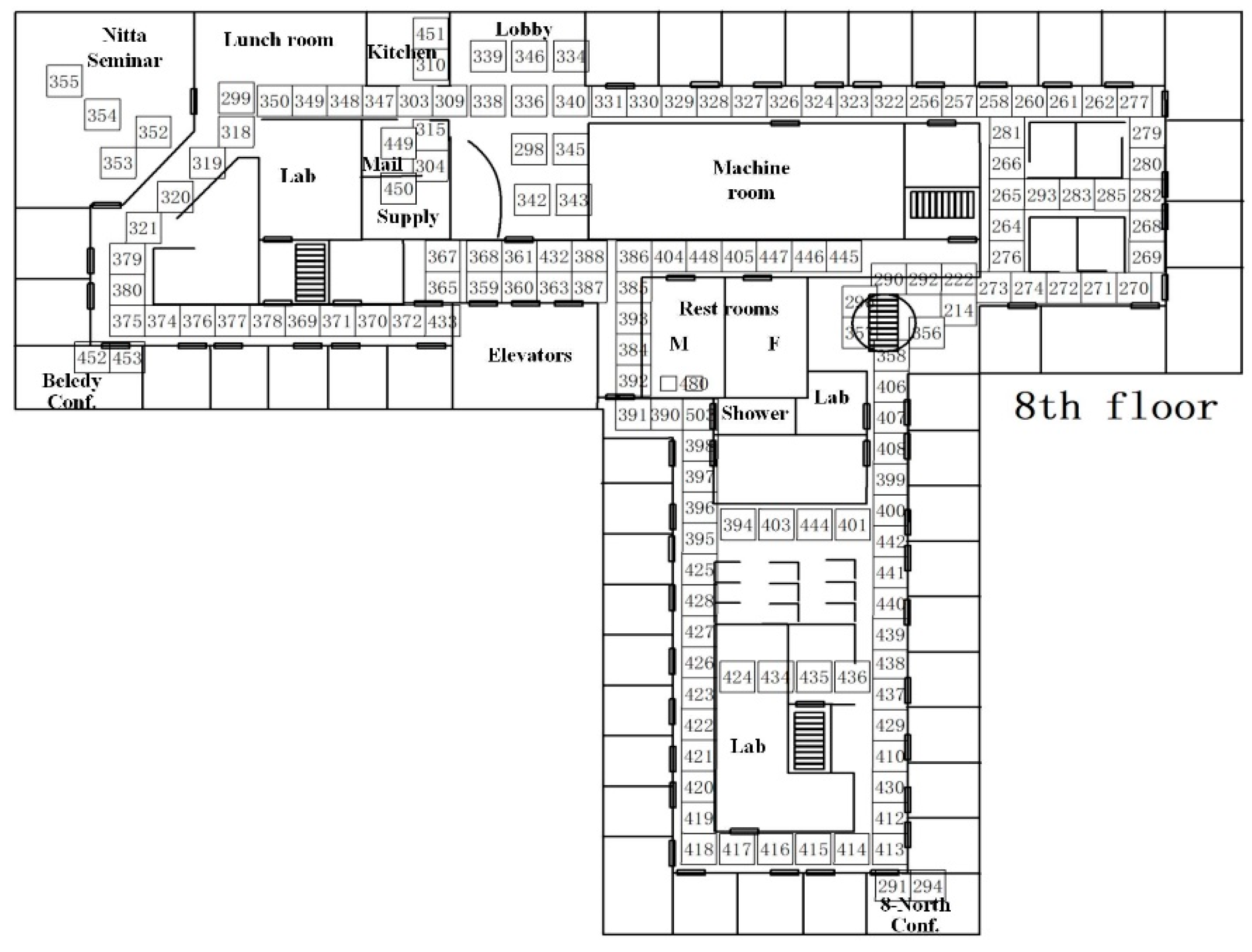
We used the Mitsubishi Electric Research Laboratories (MERL) data to test our algorithm [26]. All 157 PIR sensors were located on the eighth floor of the laboratory building (Figure 9). Each sensor was closely placed at the indoor passage and had no blind spot at any passage. The feasible distance between the two sensors was 4.4 meters, and the sensor detection radius was 1.1 meters. The sensor data log was up to one year, from 21 March 2006 to 24 March 2007 and included sensor ID, start time, end time, and validity test, etc. A one-year event log for the lab such as climate data, meeting, and place data was also included.
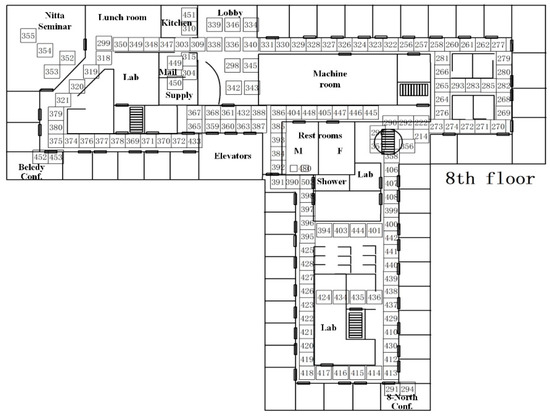
Figure 9.
Spatial distribution of sensor data and the indoor floor plan of the Mitsubishi Electric Research Laboratories.
The case system was developed based on the API provided by the Clifford Algebra based Unified Spatial-Temporal Analysis system and features its own independent analysis and visualization interface [9]. The sensor data log in the case were stored in the PostgreSQL v9.6 database, but they are accessed, managed, and analyzed by the case system. The case system had functions such as topology reconstruction of sensor network, sensor 5-neighborhood coding, and generation matching of motion behavior, through which trajectory semantics can be extracted dynamically.
4.2. Analysis and Verification
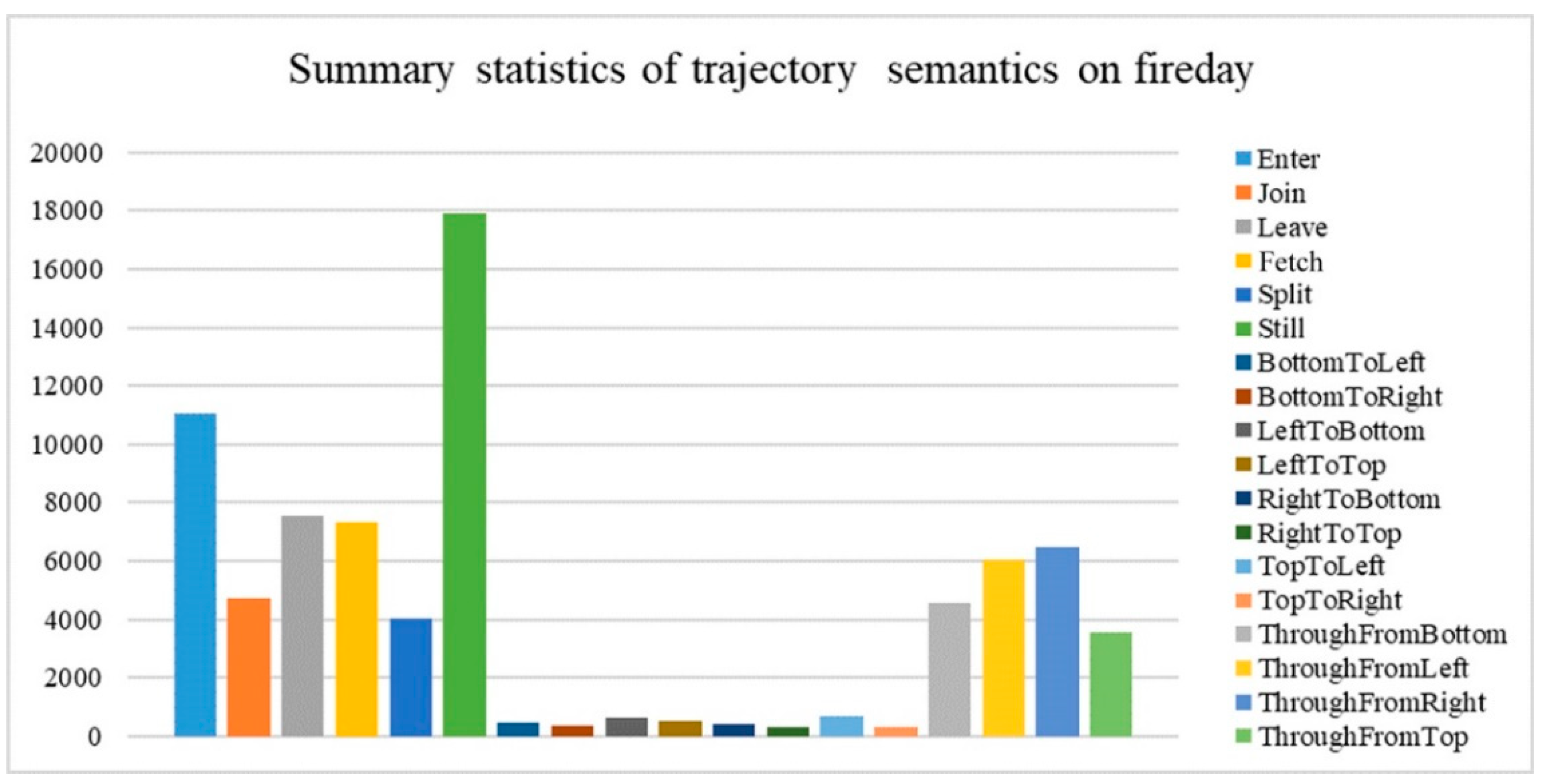
In order to obtain the possible behavioral pattern of the trajectory semantics extracted from sensor activation response sequences, and to verify their correspondence with real human behavior, we selected a day (20 April 2006) with special events from the sensor event log as a typical case. At 12:50 on this day, a fire alert simulation was conducted on the eighth floor of MERL. The fire alarm prompted people occupying indoor spaces to exit from the building. After the evacuation, there was a blank period of sensor activation, which provided a favorable situation for comparing and verifying the target behavior. A total of 76,959 trajectory semantics were extracted on 20 April 2006, and the results are presented in Figure 10.
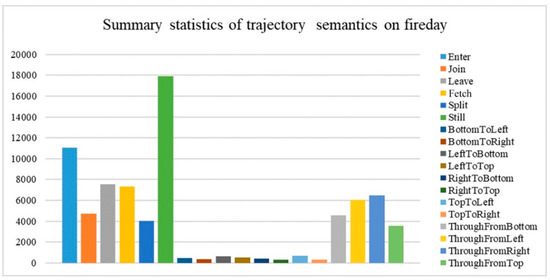
Figure 10.
Summary statistics of the full day semantic trajectory.
Figure 10 shows that the entire trajectory semantics can be divided into three levels. The first level included standing, entering, and leaving, which occurred the most frequently on that day. The second level included crossing, merging, and splitting, and the third level included turning, which was not that frequent because of restricted movement in the indoor space. Considering the motion characteristics of the indoor crowd, the trajectory semantics of standing, entering, and crossing, which reflect daily indoor motion, were all consistent characteristics of a person’s daily behavior.
4.2.1. Verification Based on the Environment
The MERI monitoring data do not contain real records of human movement, therefore, the quantitative accuracy evaluation of semantic trajectory could not be evaluated. We verified the correctness of the algorithm by considering the consistency of the spatial structure and semantic particularity of the scene. People’s moving semantics will be restrained by the environment and architectural space. For example, in a long gallery, only the passing through semantics (enter, leave) can generally appear. In order to verify the correctness of the method, the results were verified by the architectural space. First, the environment of each sensor can be divided into four types including I type, L type, T type, and Cross type, and this division is done according to the path topology and the characteristics of the architectural space. On the other hand, we could also obtain the proposed environment types by the trajectory semantic results based on the behavior features when people went through the sensors. Finally, the accuracy of this method could be obtained by comparing the environment types based on the trajectory semantic results with the actual environment types.
Since the division of environment types here was based on the number of turns, there were a total of eight turning semantics including BottomToLeft (or LeftToBottom), BottomToRight (or RightToBottom), TopToRight (or RightToTop), and TopToLeft (or LeftToTop). As shown in Table 2, the mapping table from trajectory semantics to environment types was constructed.

Table 2.
Mapping table from trajectory semantics to environment types.
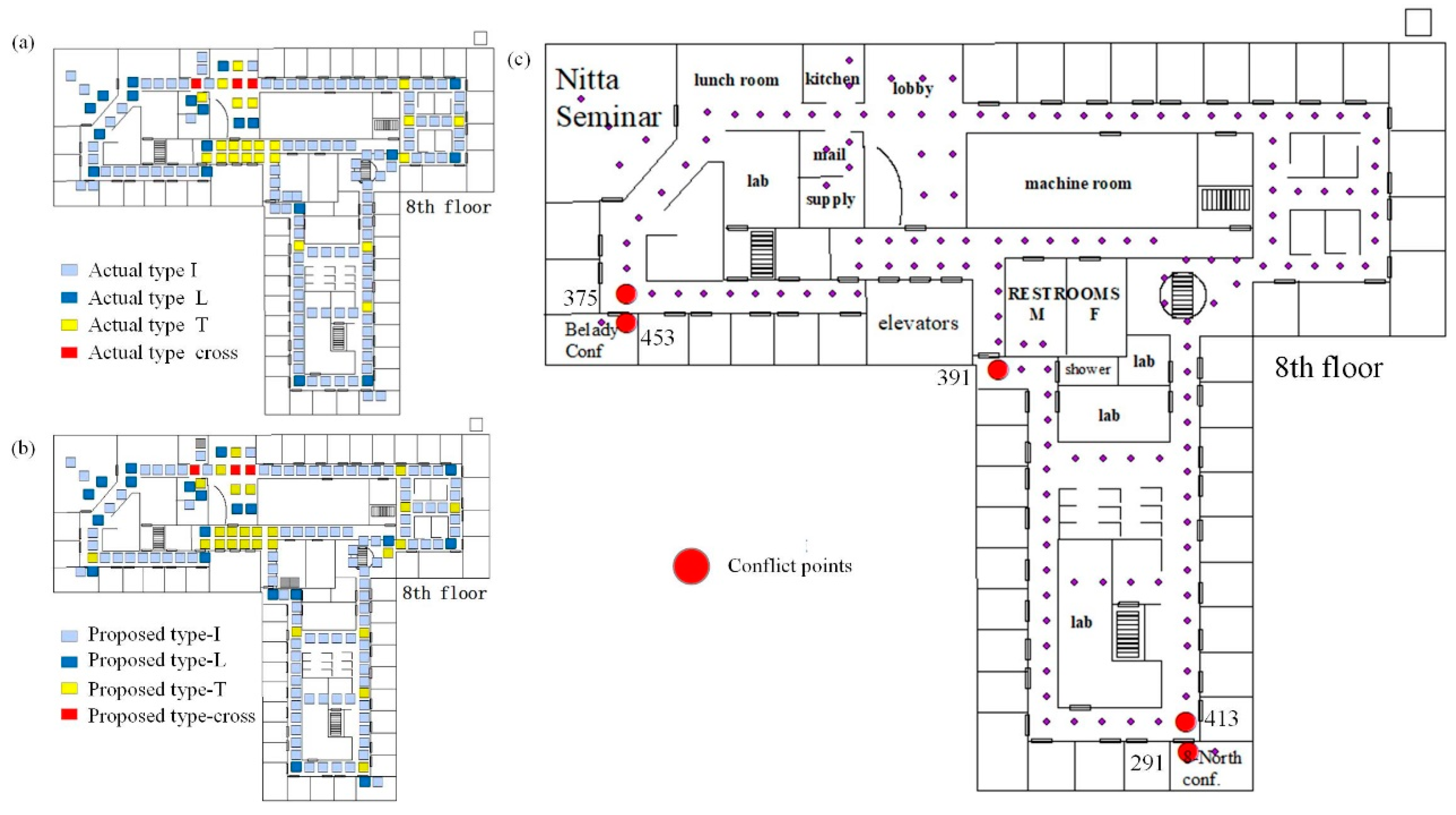
The analysis results are shown in Figure 11. The comparison shows that 149 nodes in the analysis result of this method were consistent with the original environment types, while the other five nodes were inconsistent. The verification based on the environment and architectural space shows that the accuracy of the result of our method was up to 96.75%. We set up the confusion matrix as shown in Table 3. There were 157 samples in the experiment, among which three were invalid (the three sensors did not respond during the selected sample period). From the confusion matrix, we calculated that the Kappa coefficient was equal to 0.918.
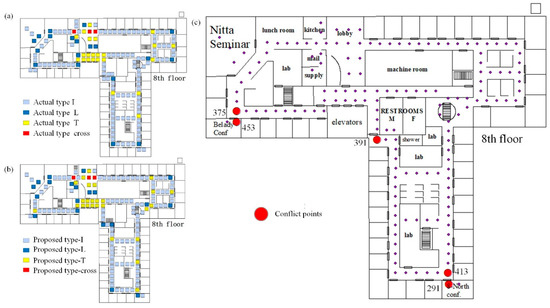
Figure 11.
The comparison of the actual environment types and the proposed types. (a) The actual environment types; (b) the proposed environment types; (c) the node in the result that are inconsistent with the actual environment type.

Table 3.
Confusion matrix for the environment type classification.
Further analysis of the nodes with inconsistent results (Figure 11c) showed that all five nodes were in the location where the door may be in a long-open state (for example, sensor nodes 375, 453, 291, 413 were arranged next to the door of the conference room, while sensor node 391 was arranged next to the door of restroom), which many change the path topology. The analysis showed that the results of this paper were still accurate for the calculation of trajectory semantics.
4.2.2. Verification Based on the Event
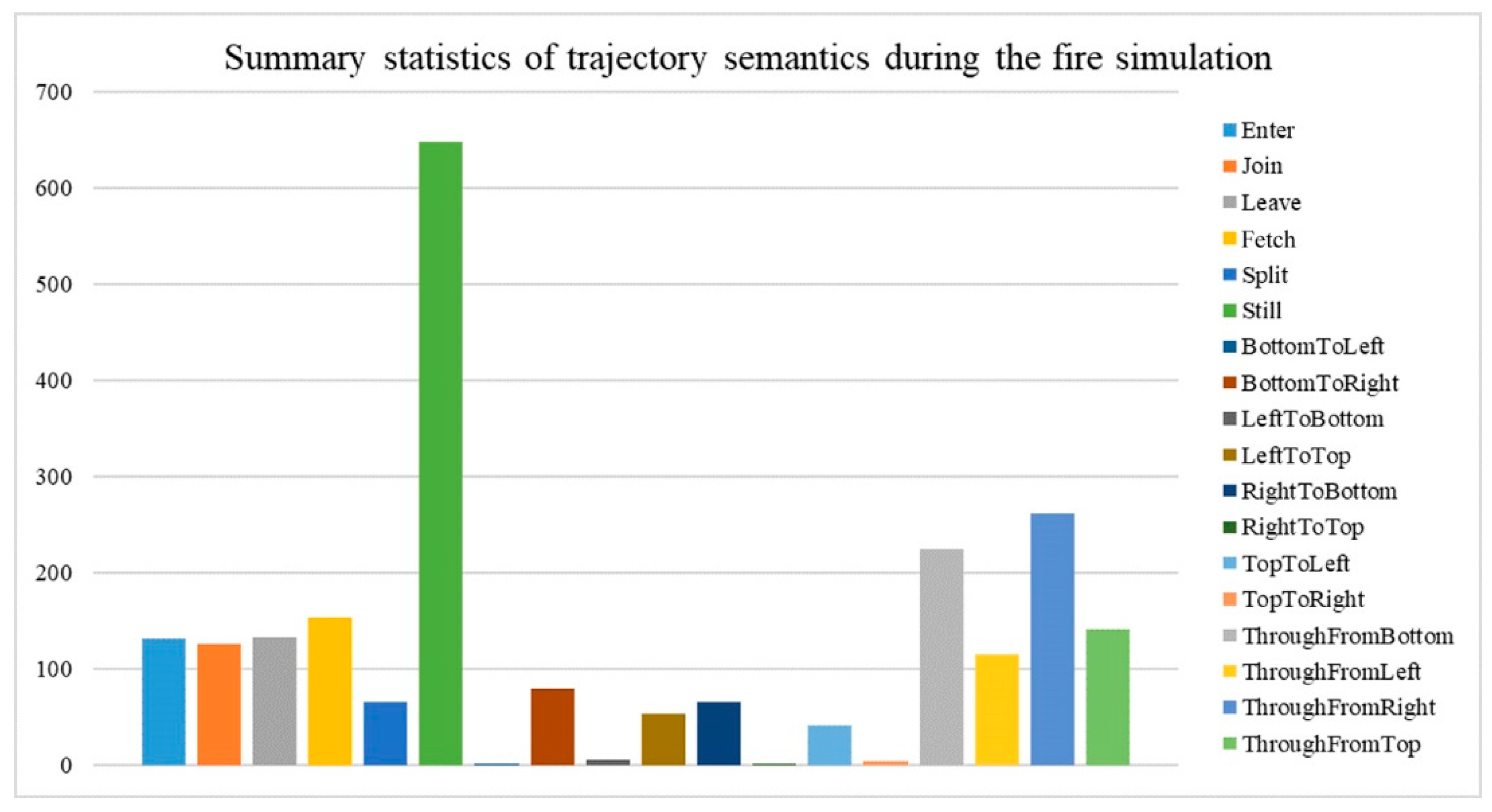
People’s moving semantics can also be affected by some emergency events like fire alarms. In order to further verify the correlation between trajectory semantics and the fire event, we selected particular time periods during the event for separate analysis. The sensor data log recorded a blank period after 12:58, suggesting that the fire simulation period occurred between 12:50 and 12:58. A total of 2247 trajectory semantics were extracted, as shown in Figure 12. The figure shows that the trajectory semantics of ‘Still’ and ‘Through’ occupied the major share. The semantic ‘Through’ may depict the process of evacuation, while the semantic ‘Still’ may show possible congestion at passages or exits.
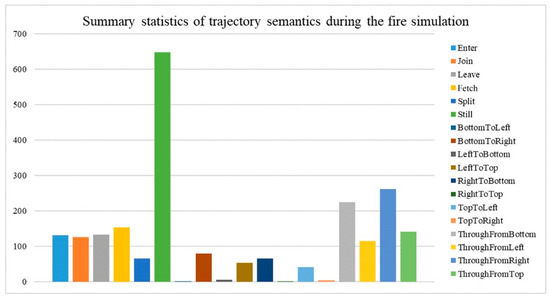
Figure 12.
Summary statistics of trajectory semantics during a fire simulation.
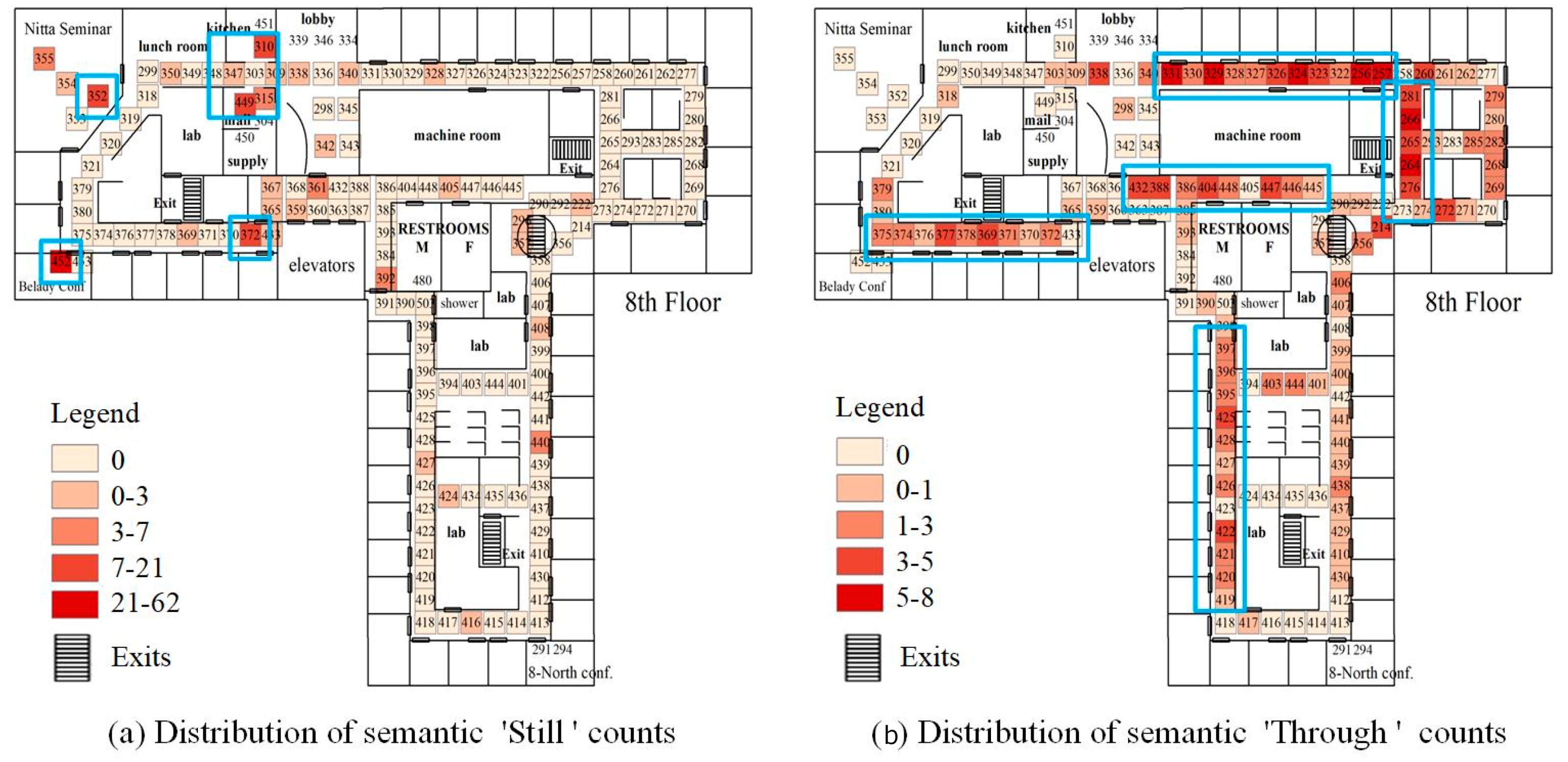
Then, we visualized these two semantics to further confirm their distribution indoors. In Figure 13a, the semantic ‘Still’ mostly occurred at nodes 310, 449, 372, 352, and 452 (marked by blue box). All these nodes are obviously located near the exit of two large conference rooms and lunch room, as shown in the floor plan of the eighth floor, many people occupied the area at noon and may experience a jam from the rooms to the exit. In Figure 13b, the semantic ‘Through’ is dense at upper sensor nodes 375–433, nodes 331-257, nodes 432–445, nodes 281–276, and nodes 397–419 (marked by blue box), which were near the four exits. However, the count of semantic ‘Through’ near the “Still” event nodes (node 352, 310, 449) were quite low, the possible reason is that during the evacuation process, the jam took place and people moved slowly until they reached the exits. The slow movement cannot be recognized as the semantic ‘Through’. The uniform distribution of the semantic ‘Through’ counts also indicates a smooth evacuation. In addition, the distribution of sensor nodes in the lounge also reflects human behavior patterns. The trajectory semantics extending from the exit to the left and right sides reflect an orderly and direct crowd motion, a motion that goes to the left and the right after the activation of the fire alarm. This reveals that the crowd is well organized during the evacuation.
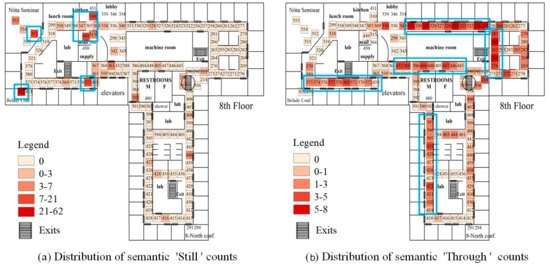
Figure 13.
Visualization of two semantics during fire simulation. (a) Distribution of semantic ‘Still’ count, (b) Distribution of semantic ‘Through’ counts.
According to the analysis of the fire simulation, the trajectory semantics extraction has good correspondence with the event, which could not only reflect human motion under special events, but also reveal some hidden human behavioral pattern restrained by the environment and architectural space.
4.3. Algorithm Efficiency
The computational complexity of the generation-template matching algorithm can be mainly attributed to the constraints and the extraction. Suppose the number of all sensor nodes is , then the algorithm complexity in neighborhood searching is . Additionally, suppose the number of extraction according to the total time is , the complexity of extraction process is , drawing the conclusion that the entire algorithm complexity is , which is equal to .
Since there is no similar algorithm for extracting trajectory semantics from PIR sensor networks, the efficiency comparison was mainly performed between different node sizes and time scales. The computing time only included the processes of generation and matching. The specifications of the system environment are as follows: Intel Xeon E5645 (2.4 G) CPU, 48.00 GB RAM, and Windows Server 2008 R2 operating system. In terms of the node size, the efficiency of extracting 1000 trajectory semantics from 10, 50, and 100 sensor nodes was considered. The results are shown in Table 4. With the increasing sensor nodes, more operations such as neighborhood establishment and parameter storage were required, which slightly increased the time and memory consumption. Nevertheless, the stability of the algorithm remained excellent with the expansion of node size.

Table 4.
Comparison of the efficiency of different node sizes.
For evaluating efficiency, we selected three times nodes, one hour, one day, and one week, when all 157 sensors responded frequently, as our detection time. The results in Table 5 show that the computation complexity and memory usage were relatively stable. With the increase in time span, the number of records was up to 355,702 during one week. The extraction of sensor response data from the one week dataset consumed approximately 155.18 s and 357.7 MB.

Table 5.
Efficiency comparison of different time spans (started in 12:00 on April 20, 2006).
5. Conclusions and Discussion
In this paper, the advantages of the representation and operation of GA for PIR data processing could be fully utilized. Generation-templates with the 5-neighborhood model including eight different types of motion semantics were first defined to provide a standard paradigm for extraction. Then, spatial and temporal constraints were introduced to segment the entire sensor network and sensor log data. Such constraints could simplify the objects for processing and enable the semantic extraction to focus on single sensor nodes. The generation-template matching algorithm was introduced to extract all trajectories and matched them with the templates. With our method, eight types of detailed trajectories could be obtained from the PIR sensor network. Then, these trajectories were further analyzed to determine human behavior patterns. The case study showed that the sequences of human motion patterns could be efficiently extracted in different observation periods. The results agreed well with the event logs under various circumstances.
PIR sensor data are a set of discrete activation response sequences, which seemingly do not have any semantics. Nevertheless, the relationship between the activation responses can be determined through data mining under constraints. Geometric algebra provides a solid mathematical foundation for expressing both the sensor network and motion pattern templates. The spatial and temporal constraints segment the PIR sensor activation response sequences into sub-sequences and can be expressed as GA codes by the outer product. The GA expression of the response sequences are in accordance with the motion pattern templates and can be further used in semantic extraction and analysis. Therefore, the process of trajectory semantics extraction is converted into encoding and matching. Compared to previous methods, our method completely avoids complex matrix calculations and supports more types of motion semantics, facilitated by the generated coding paradigm. Therefore, it avoids the computational complexity problem of high-dimensional GA computation, and makes it possible for large-scale applications.
In our method, the moving semantics were extracted by spatial and temporal filtering, therefore the result was sensitive with the setting of a spatial and temporal window. Although we set the default walking speed (1.3 m/s), according to the general situation of adults, in different passable conditions, the speed may change. For example, in the case of a jammed situation, a person’s walking speed decreases, which may generate ‘Still’ semantics. In future work, the moving semantics should be further studied in different scenarios, and the neighborhood semantics can also be used to improve the result. Here, we only used the 5-neighborhood model to extract a total number of 36 human motion template. However, the extension to a more complex human behavior template, which means using high-order grades or multivector to form the template, is direct. In this way, the methods can be extended as a generalized method to filter semantical meaningful human motions from the binary PIR sensor network log data. Based on the unified construction and computation operator of GA, our method provides a template system with both geometry and motion features. Using this method, complex calculations of response sequences can be converted into simple local data processing, similar to image convolution. Further integration of our method with real-time access of data under the Internet of Things can lead to a feasible method for timely sensor data analysis. Overall, it provides an opportunity to further explore human motion patterns based on PIR sensors.
Author Contributions
Conceptualization, Zhaoyuan Yu, Shengjun Xiao, and Linwang Yuan; Methodology, Zhaoyuan Yu, Linwang Yuan, and Shengjun Xiao; Validation, Dongshuang Li, Zhaoyuan Yu, and Shengjun Xiao; Formal Analysis, Chunye Zhou, Shengjun Xiao, and Wen Luo; Resources, Zhaoyuan Yu and Linwang Yuan; Data Curation, Wen Luo and Chunye Zhou; Writing—Original Draft Preparation, Zhaoyuan Yu, Shengjun Xiao, and Dongshuang Li; Supervision, Linwang Yuan; Project Administration, Zhaoyuan Yu.
Funding
This research was funded by the National Key R&D Program of China, grant number 2016YFB0502301, National Science Fund for Distinguished Young Scholars of China, grant number 41625004 and the National Natural Science Foundation of China, grant number 41971404, 41571379 and The APC was funded by 41571379.
Acknowledgments
We acknowledge MERL in providing the PIR sensor data. We also thank formal students Linyao Feng, Shuai Yuan, and Jianjian Wang for their helpful work on data processing and comments on this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- D’Apuzzo, N. Surface measurement and tracking of human body parts from multi-image video sequences. ISPRS J. Photogramm. Remote Sens. 2002, 56, 360–375. [Google Scholar] [CrossRef]
- Guo, S.; Xiong, H.; Zheng, X.; Zhou, Y. Activity Recognition and Semantic Description for Indoor Mobile Localization. Sensors 2017, 17, 649. [Google Scholar] [CrossRef] [PubMed]
- Kulshrestha, T.; Saxena, D.; Niyogi, R.; Raychoudhury, V.; Misra, M. SmartITS: Smartphone-based Identification and Tracking using Seamless Indoor-Outdoor Localization. J. Netw. Comput. Appl. 2017, 98, 97–113. [Google Scholar] [CrossRef]
- Pittet, S.; Renaudin, V.; Merminod, B.; Kasser, M. UWB and MEMS Based Indoor Navigation. J. Navig. 2008, 61, 369–384. [Google Scholar] [CrossRef]
- Dodge, S.; Weibel, R.; Forootan, E. Revealing the physics of movement: Comparing the similarity of movement characteristics of different types of moving objects. Comput. Environ. Urban Syst. 2009, 33, 419–434. [Google Scholar] [CrossRef]
- Laube, P.; Dennis, T.; Forer, P.; Walker, M. Movement beyond the snapshot—Dynamic analysis of geospatial lifelines. Comput. Environ. Urban Syst. 2007, 31, 481–501. [Google Scholar] [CrossRef]
- Jin, X.; Sarkar, S.; Ray, A.; Gupta, S.; Damarla, T. Target Detection and Classification Using Seismic and PIR Sensors. IEEE Sens. J. 2012, 12, 1709–1718. [Google Scholar] [CrossRef]
- Yang, D.; Xu, B.; Rao, K.; Sheng, W. Passive Infrared (PIR)-Based Indoor Position Tracking for Smart Homes Using Accessibility Maps and A-Star Algorithm. Sensors 2018, 18, 332. [Google Scholar] [CrossRef]
- Yu, Z.; Luo, W.; Yuan, L.; Hu, Y.; Zhu, A. Geometric Algebra Model for Geometry-oriented Topological Relation Computation. Trans. GIS 2016, 20, 259–279. [Google Scholar] [CrossRef]
- Zappi, P.; Farella, E.; Benini, L. Tracking Motion Direction and Distance with Pyroelectric IR Sensors. IEEE Sens. J. 2010, 10, 1486–1494. [Google Scholar] [CrossRef]
- Agarwal, R.; Kumar, S.; Hegde, R.M. Algorithms for Crowd Surveillance Using Passive Acoustic Sensors Over a Multimodal Sensor Network. IEEE Sens. J. 2015, 15, 1920–1930. [Google Scholar] [CrossRef]
- Kim, H.H.; Ha, K.N.; Lee, S.; Lee, K.C. Resident Location-Recognition Algorithm Using a Bayesian Classifier in the PIR Sensor-Based Indoor Location-Aware System. IEEE Trans. Syst. Man Cybern. Part C 2009, 39, 240–245. [Google Scholar]
- Luo, X.; Guan, Q.; Tan, H.; Gao, L.; Wang, Z.; Luo, X. Simultaneous Indoor Tracking and Activity Recognition Using Pyroelectric Infrared Sensors. Sensors 2017, 17, 1738. [Google Scholar] [CrossRef] [PubMed]
- Shrivastava, N.; Mudumbai, R.; Madhow, U.; Suri, S. Target Tracking with Binary Proximity Sensors. ACM Trans. Sens. Netw. 2009, 5, 30:1–33. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, M. Credit-Based Multiple Human Location for Passive Binary Pyroelectric Infrared Sensor Tracking System: Free from Region Partition and Classifier. IEEE Sens. J. 2016, 17, 37–45. [Google Scholar] [CrossRef]
- Yang, B.; Wei, Q.; Zhang, M. Multiple Human Location in a Distributed Binary Pyroelectric Infrared Sensor Network. Infrared Phys. Technol. 2017, 85, 216–224. [Google Scholar] [CrossRef]
- Belongie, S.; Malik, J.; Puzicha, J. Shape Matching and Object Recognition Using Shape Contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Davis, J.W.; Bobick, A.F. The recognition of human movement using temporal templates. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 257–267. [Google Scholar]
- Gesto-Diaz, M.; Tombari, F.; Gonzalez-Aguilera, D.; Lopez-Fernandez, L.; Rodriguez-Gonzalvez, P. Feature matching evaluation for multimodal correspondence. ISPRS J. Photogramm. Remote Sens. 2017, 129, 179–188. [Google Scholar] [CrossRef]
- Wang, M.; Cui, Q.; Sun, Y.; Wang, Q. Photovoltaic panel extraction from very high-resolution aerial imagery using region–line primitive association analysis and template matching. ISPRS J. Photogramm. Remote Sens. 2018, 141, 100–111. [Google Scholar] [CrossRef]
- Yuan, L.; Yu, Z.; Luo, W.; Zhang, J.; Hu, Y. Clifford algebra method for network expression, computation, and algorithm construction. Math. Methods Appl. Sci. 2014, 37, 1428–1435. [Google Scholar] [CrossRef]
- Dorst, L.; Fontijne, D.H.F.; Mann, S. Geometric Algebra for Computer Science: An Object-Oriented Approach to Geometry; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2007. [Google Scholar]
- Hitzer, E.; Nitta, T.; Kuroe, Y. Applications of Clifford’s Geometric Algebra. Adv. Appl. Clifford Algebras 2013, 23, 377–404. [Google Scholar] [CrossRef]
- Yu, Z.; Yuan, L.; Luo, W.; Feng, L.; Lv, G. Spatio-Temporal Constrained Human Trajectory Generation from the PIR Motion Detector Sensor Network Data: A Geometric Algebra Approach. Sensors 2016, 16, 43. [Google Scholar] [CrossRef]
- Yuan, L.; Yu, Z.; Luo, W.; Yi, L.; Lü, G. Geometric Algebra for Multidimension-Unified Geographical Information System. Adv. Appl. Clifford Algebras 2013, 23, 497–518. [Google Scholar] [CrossRef]
- Wren, C.R.; Ivanov, Y.A.; Leigh, D.; Westhues, J. The MERL motion detector dataset. In Proceedings of the Workshop on Massive Datasets, Nagoya, Japan, 15 November 2007; pp. 10–14. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).