Author Contributions
Conceptualization, Kelvin Wong, Ehsan Javanmardi, Mahdi Javanmardi and Shunsuke Kamijo; Data curation, Kelvin Wong, Ehsan Javanmardi and Mahdi Javanmardi; Formal analysis, Kelvin Wong; Funding acquisition, Kelvin Wong and Shunsuke Kamijo; Investigation, Kelvin Wong; Methodology, Kelvin Wong; Project administration, Kelvin Wong and Shunsuke Kamijo; Resources, Kelvin Wong; Software, Kelvin Wong; Supervision, Kelvin Wong and Shunsuke Kamijo; Validation, Kelvin Wong; Visualization, Kelvin Wong; Writing—original draft, Kelvin Wong; Writing—review & editing, Kelvin Wong.
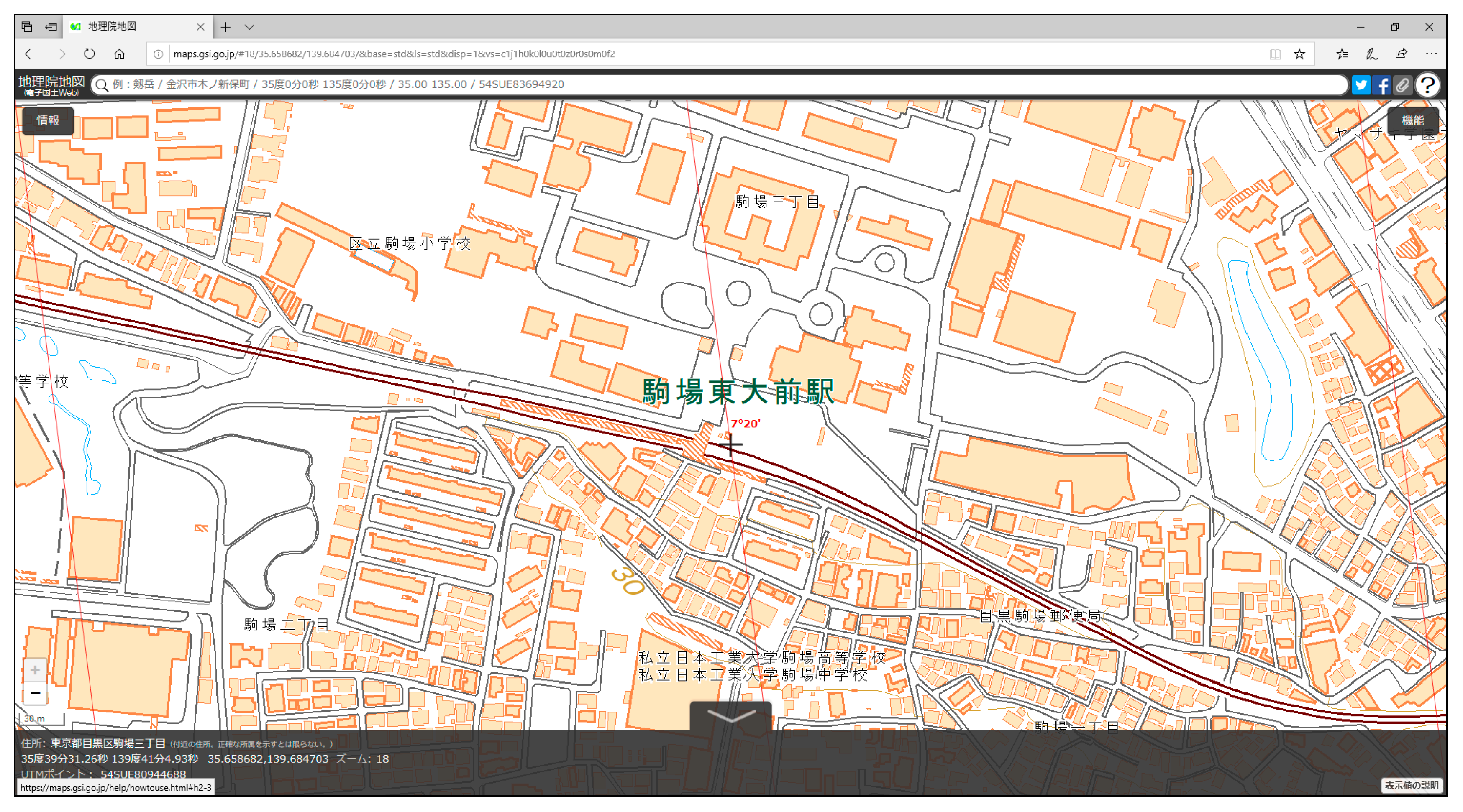
Figure 1.
Excerpt of GSI 1:25,000 base map, as viewed on the GSI web map portal.
Figure 1.
Excerpt of GSI 1:25,000 base map, as viewed on the GSI web map portal.
Figure 2.
Excerpt of OSM [left] and Geospatial Information Authority of Japan (GSI) base map [right]. Note the inconsistency in completeness for OSM, in contrast to the GSI data.
Figure 2.
Excerpt of OSM [left] and Geospatial Information Authority of Japan (GSI) base map [right]. Note the inconsistency in completeness for OSM, in contrast to the GSI data.
Figure 3.
The generation of view lines and view polygons. (a) 360 view lines generated, each 20 meter in length, at 1° interval. (b) View lines clipped by building footprints. (c) View polygon generated from the minimum bounding convex hull of the clipped view lines.
Figure 3.
The generation of view lines and view polygons. (a) 360 view lines generated, each 20 meter in length, at 1° interval. (b) View lines clipped by building footprints. (c) View polygon generated from the minimum bounding convex hull of the clipped view lines.
Figure 4.
Calculating angular dispersion. The measure describes the dispersion of intersection points (red circles) in relation to the sample point in the center (black circle).
Figure 4.
Calculating angular dispersion. The measure describes the dispersion of intersection points (red circles) in relation to the sample point in the center (black circle).
Figure 5.
Two different view polygons and their respective area, perimeter and compactness.
Figure 5.
Two different view polygons and their respective area, perimeter and compactness.
Figure 6.
Five experiment paths (I, II, III, IV, V) in Shinjuku, Tokyo, Japan, as viewed in Google Earth.
Figure 6.
Five experiment paths (I, II, III, IV, V) in Shinjuku, Tokyo, Japan, as viewed in Google Earth.
Figure 7.
Map showing the completed barriers (point/line/polygon) layer, completed trees layer, GSI building footprints, GSI road and curb edge, and experiment paths I, III, IV, and V.
Figure 7.
Map showing the completed barriers (point/line/polygon) layer, completed trees layer, GSI building footprints, GSI road and curb edge, and experiment paths I, III, IV, and V.
Figure 8.
Map showing the completed barriers (point/line/polygon) layer, completed trees layer, GSI building footprints, GSI road and curb edge, and experiment path II.
Figure 8.
Map showing the completed barriers (point/line/polygon) layer, completed trees layer, GSI building footprints, GSI road and curb edge, and experiment path II.
Figure 9.
Maps showing the different data layers in each of the eight models as described in
Table 4.
Figure 9.
Maps showing the different data layers in each of the eight models as described in
Table 4.
Figure 10.
Predicted (red) vs. actual (black) value of localization error, sorted by actual value (Model 8, test data).
Figure 10.
Predicted (red) vs. actual (black) value of localization error, sorted by actual value (Model 8, test data).
Figure 11.
Residual plot of predicted values against the actual value (Model 8, test data). The table shows the minimum, mean and maximum residual, as grouped by the actual value.
Figure 11.
Residual plot of predicted values against the actual value (Model 8, test data). The table shows the minimum, mean and maximum residual, as grouped by the actual value.
Table 1.
Coverage of OSM tags in Japan 2017 [
18].
Table 1.
Coverage of OSM tags in Japan 2017 [
18].
| Tag | Count (Actual) | Count (OSM) | Coverage |
|---|
| School | 36,024 | 45,568 | 126.5% 1 |
| Fire department | 5604 | 5028 | 89.7% |
| Police station | 15,034 | 13,152 | 87.5% |
| Post office | 24,052 | 20,795 | 86.5% |
| Traffic lights | 191,770 | 108,498 | 56.6% |
| Convenience store | 55,176 | 30,710 | 55.7% |
| Bank | 13,595 | 7077 | 52.1% |
| Gas station | 32,333 | 8944 | 27.7% |
| Pharmacy | 58,326 | 7842 | 13.4% |
| Shrine | 88,281 | 10,292 | 11.7% |
| Temple | 85,045 | 9610 | 11.3% |
| Post box | 181,523 | 7522 | 4.1% |
| Vending machine | 3,648,600 | 10,311 | 0.3% |
Table 2.
Summary of all paths.
Table 2.
Summary of all paths.
| Path | Length | Description |
|---|
| I | 1.16 km | The path begins through a narrow and dense shopping area populated with buildings two to four stories tall. The middle and final third of the path consists of wide roads (two to three lanes), with hedges and trees along the roadside and central reservation, passing by several skyscrapers. |
| II | 0.73 km | A long straight path passing through a residential area. The path begins by passing under a railway bridge. After, residential buildings can be found on the left. On the right, there are no buildings. Instead, there is a metal fence separating the road and the Shinjuku Gyoen National Garden. |
| III | 0.27 km | The shortest of the five paths. This straight path passes between a number of skyscrapers. While the drivable portion of the road is narrow, the pavements are wide and are populated with bollards, trees and lamp posts. |
| IV | 0.65 km | This path is fully contained with the same narrow and dense shopping area found at the beginning of Path I. |
| V | 0.79 km | This long straight path starts in the narrow and dense shopping area from Paths I & IV, before opening to wider, multi-lane roads for the remaining 4/5th of the path. The path passes by a number of skyscrapers in the latter portion, as well as passing under four bridges. |
| Total | 3.60 km | |
Table 3.
OSM tags and feature count in the study area.
Table 3.
OSM tags and feature count in the study area.
| OSM Tags | Feature Count | OSM Tags | Feature Count |
|---|
| aeroway | 11 | natural | 811 |
| amenity | 2468 | office | 47 |
| barrier | 735 | place | 8 |
| boundary | 18 | power | 21 |
| building | 12,434 | public transport | 161 |
| craft | 2 | railway | 553 |
| emergency | 14 | route | 99 |
| highway | 5407 | shop | 645 |
| historic | 21 | tourism | 199 |
| landuse | 230 | unknown | 690 |
| leisure | 143 | waterway | 5 |
| man made | 18 | | |
Table 4.
Combination of data layers and the performance (accuracy) of the predictive models.
Table 4.
Combination of data layers and the performance (accuracy) of the predictive models.
| Data | Models |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| Buildings | OSM Buildings | ● | | ● | ● | ● | | | |
| GSI Buildings | | ● | | | | ● | ● | ● |
| Barriers | OSM Polygon barriers | | | ● | ● | | | | |
| OSM Line barriers | | | ● | ● | | | | |
| OSM Point barriers | | | ● | ● | | | | |
| Completed Polygon barriers | | | | | ● | ● | | ● |
| Completed Line barriers | | | | | ● | ● | | ● |
| Completed Point barriers | | | | | ● | ● | | ● |
| Curb | GSI road and curb edge | | | | | | | ● | ● |
| Trees | OSM Natural Points | | | | ● | | | | |
| Completed Natural Points | | | | | ● | ● | | ● |
| Number of factors | 7 | 7 | 13 | 15 | 15 | 15 | 9 | 17 |
| R2 (adjusted) | 0.26 | 0.28 | 0.39 | 0.40 | 0.68 | 0.67 | 0.50 | 0.65 |
| RMSE [cm] | 7.47 | 6.60 | 6.79 | 6.76 | 4.96 | 4.50 | 5.51 | 4.59 |
| MAE [cm] | 4.19 | 4.08 | 3.51 | 3.48 | 2.66 | 2.61 | 3.09 | 2.59 |
| Percentile rank (5 cm) [%] | 75.1 | 72.6 | 81.5 | 81.5 | 88.3 | 87.1 | 84.4 | 87.4 |
| Percentile rank (2.5 cm) [%] | 48.6 | 47.2 | 59.7 | 60.0 | 68.4 | 68.8 | 62.9 | 69.8 |
| Percentile rank (1 cm) [%] | 24.6 | 22.3 | 32.8 | 32.1 | 35.4 | 36.2 | 32.5 | 36.9 |
Table 5.
Factor importance of the eight predictive models. The two most important factors in each model are emphasized in bold.
Table 5.
Factor importance of the eight predictive models. The two most important factors in each model are emphasized in bold.
| Factors | Models |
|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| Feature count | Buildings | 0.12 | 0.15 | 0.07 | 0.07 | 0.04 | 0.07 | 0.08 | 0.06 |
| Polygon barriers | - | - | 0.10 | 0.10 | 0.18 | 0.15 | - | 0.07 |
| Line barriers | - | - | 0.10 | 0.10 | 0.11 | 0.08 | - | 0.05 |
| Point barriers | - | - | 0.00 | 0.00 | 0.04 | 0.05 | - | 0.03 |
| Natural point (trees) | - | - | - | 0.01 | 0.08 | 0.12 | - | 0.06 |
| Road and curb edge | - | - | - | - | - | - | 0.38 | 0.27 |
| Angular dispersion | Buildings | 0.17 | 0.14 | 0.09 | 0.09 | 0.05 | 0.04 | 0.06 | 0.03 |
| Polygon barriers | - | - | 0.12 | 0.12 | 0.07 | 0.06 | - | 0.07 |
| Line barriers | - | - | 0.17 | 0.17 | 0.08 | 0.08 | - | 0.04 |
| Point barriers | - | - | 0.00 | 0.00 | 0.08 | 0.08 | - | 0.04 |
| Natural point (trees) | - | - | - | 0.01 | 0.05 | 0.02 | - | 0.02 |
| Road and curb edge | - | - | - | - | - | - | 0.20 | 0.09 |
| Other | View line mean length | 0.17 | 0.14 | 0.09 | 0.08 | 0.05 | 0.05 | 0.05 | 0.03 |
| View polygon area | 0.11 | 0.09 | 0.06 | 0.05 | 0.04 | 0.03 | 0.03 | 0.02 |
| View polygon perimeter | 0.15 | 0.17 | 0.07 | 0.07 | 0.04 | 0.05 | 0.11 | 0.07 |
| View polygon compactness | 0.11 | 0.09 | 0.06 | 0.06 | 0.04 | 0.03 | 0.03 | 0.02 |
| Variance of building face dir. | 0.17 | 0.21 | 0.08 | 0.08 | 0.05 | 0.08 | 0.07 | 0.05 |
Table 6.
Model 8 performance after hyperparameter tuning.
Table 6.
Model 8 performance after hyperparameter tuning.
| Performance | Default | Random Search | Grid Search |
|---|
| R2 (adjusted) | 0.65 | 0.66 | 0.66 |
| RMSE [cm] | 4.59 | 4.54 | 4.54 |
| MAE [cm] | 2.59 | 2.54 | 2.54 |
| Percentile rank (5 cm) [%] | 87.4 | 87.5 | 87.5 |
| Percentile rank (2.5 cm) [%] | 69.8 | 71.3 | 71.2 |
| Percentile rank (1 cm) [%] | 36.9 | 38.5 | 38.3 |
Table 7.
Mean number of intersection points with features per path point, split by path. The highest value for each feature is highlighted in bold.
Table 7.
Mean number of intersection points with features per path point, split by path. The highest value for each feature is highlighted in bold.
| Features | Path |
|---|
| I | II | III | IV | V |
|---|
| Buildings | 244.4 | 258.4 | 253.7 | 296.0 | 222.6 |
| Polygon barriers | 4981.5 | 261.2 | 2069.2 | 1158.4 | 4011.2 |
| Line barriers | 42.0 | 169.6 | 13.5 | 29.2 | 30.2 |
| Point barriers | 4.6 | 2.6 | 4.1 | 5.3 | 4.8 |
| Natural point (trees) | 2.4 | 3.5 | 13.6 | 4.7 | 3.2 |
| Road and curb edge | 263.3 | 327.4 | 333.5 | 306.4 | 245.2 |
| Path length [km] | 1.2 | 0.7 | 0.3 | 0.7 | 0.8 |
| Path points | 1096 | 715 | 270 | 631 | 753 |
Table 8.
Result of training and testing individual paths, based on model 8.
Table 8.
Result of training and testing individual paths, based on model 8.
| Performance | Path |
|---|
| I | II | III | IV | V |
|---|
| Number of factors | 17 | 17 | 17 | 17 | 17 |
| R2 (adjusted) | 0.60 | 0.75 | 0.53 | 0.51 | 0.79 |
| RMSE [cm] | 0.03 | 0.05 | 0.03 | 0.51 | 0.03 |
| MAE [cm] | 0.02 | 0.03 | 0.02 | 0.03 | 0.02 |
| Percentile rank (5 cm) [%] | 92.0 | 88.7 | 94.1 | 86.7 | 91.8 |
| Percentile rank (2.5 cm) [%] | 70.1 | 72.9 | 66.2 | 69.0 | 79.1 |
| Percentile rank (1 cm) [%] | 34.3 | 39.6 | 32.4 | 29.1 | 47.3 |
Table 9.
Factor importance, individual paths. The two most important factors for each path are emphasized in bold.
Table 9.
Factor importance, individual paths. The two most important factors for each path are emphasized in bold.
| Factors | Path |
|---|
| I | II | III | IV | V |
|---|
| Feature count | Buildings | 0.02 | 0.06 | 0.02 | 0.05 | 0.01 |
| Polygon barriers | 0.05 | 0.00 | 0.05 | 0.03 | 0.09 |
| Line barriers | 0.07 | 0.04 | 0.28 | 0.14 | 0.03 |
| Point barriers | 0.03 | 0.04 | 0.01 | 0.02 | 0.03 |
| Natural point (trees) | 0.03 | 0.08 | 0.02 | 0.04 | 0.01 |
| Road and curb edge | 0.34 | 0.10 | 0.28 | 0.03 | 0.47 |
| Angular dispersion | Buildings | 0.02 | 0.03 | 0.01 | 0.04 | 0.04 |
| Polygon barriers | 0.05 | 0.01 | 0.02 | 0.12 | 0.05 |
| Line barriers | 0.03 | 0.02 | 0.14 | 0.03 | 0.09 |
| Point barriers | 0.08 | 0.02 | 0.03 | 0.10 | 0.04 |
| Natural point (trees) | 0.03 | 0.09 | 0.01 | 0.04 | 0.01 |
| Road and curb edge | 0.12 | 0.20 | 0.02 | 0.04 | 0.07 |
| Other | View line mean length | 0.02 | 0.03 | 0.01 | 0.05 | 0.02 |
| View polygon area | 0.01 | 0.01 | 0.01 | 0.03 | 0.01 |
| View polygon perimeter | 0.04 | 0.03 | 0.07 | 0.08 | 0.02 |
| View polygon compactness | 0.01 | 0.01 | 0.01 | 0.03 | 0.01 |
| Variance of building face dir. | 0.03 | 0.23 | 0.01 | 0.13 | 0.02 |
Table 10.
Comparison with other models.
Table 10.
Comparison with other models.
| Author | Model | R2 | RMSE [cm] |
|---|
| Javanmardi et al. [28] | 2.0 m grid size | 0.770 | 9.0 |
| | 5.0 m grid size | 0.551 | 20.6 |
| Our models | Model 5 | 0.677 | 5.0 |
| | Model 8 | 0.654 | 4.6 |
Table 11.
Distribution of actual localization error, by count (Model 8).
Table 11.
Distribution of actual localization error, by count (Model 8).
| Localization Error | All | Test | Training |
|---|
| 0.0 ≤ x < 0.2 | 3179 | 797 | 2382 |
| 0.2 ≤ x < 0.4 | 207 | 53 | 154 |
| 0.4 ≤ x < 0.6 | 28 | 6 | 22 |
| 0.6 ≤ x | 15 | 2 | 13 |
| Total | 3429 | 858 | 2571 |
| Localization error higher than 25 cm | 129 | 29 | 100 |