A Novel Underwater Simultaneous Localization and Mapping Online Algorithm Based on Neural Network
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Positioning Principle of the Beacon of the Low-Frequency Magnetic Field
2.2. Description of the Artificial Neural Network
2.3. Optimization of MLP-ANN
2.3.1. Data Preprocessing
2.3.2. Training
2.4. Description of the Proposed AMB-SLAM Algorithm
2.4.1. State Equation
2.4.2. Observation Equation
2.4.3. Updating
3. Experimental Results and Discussion
3.1. Data Sets
3.2. Optimal MLP-ANN Configuration
3.3. AMB-SLAM Loop Map Simulation Setups
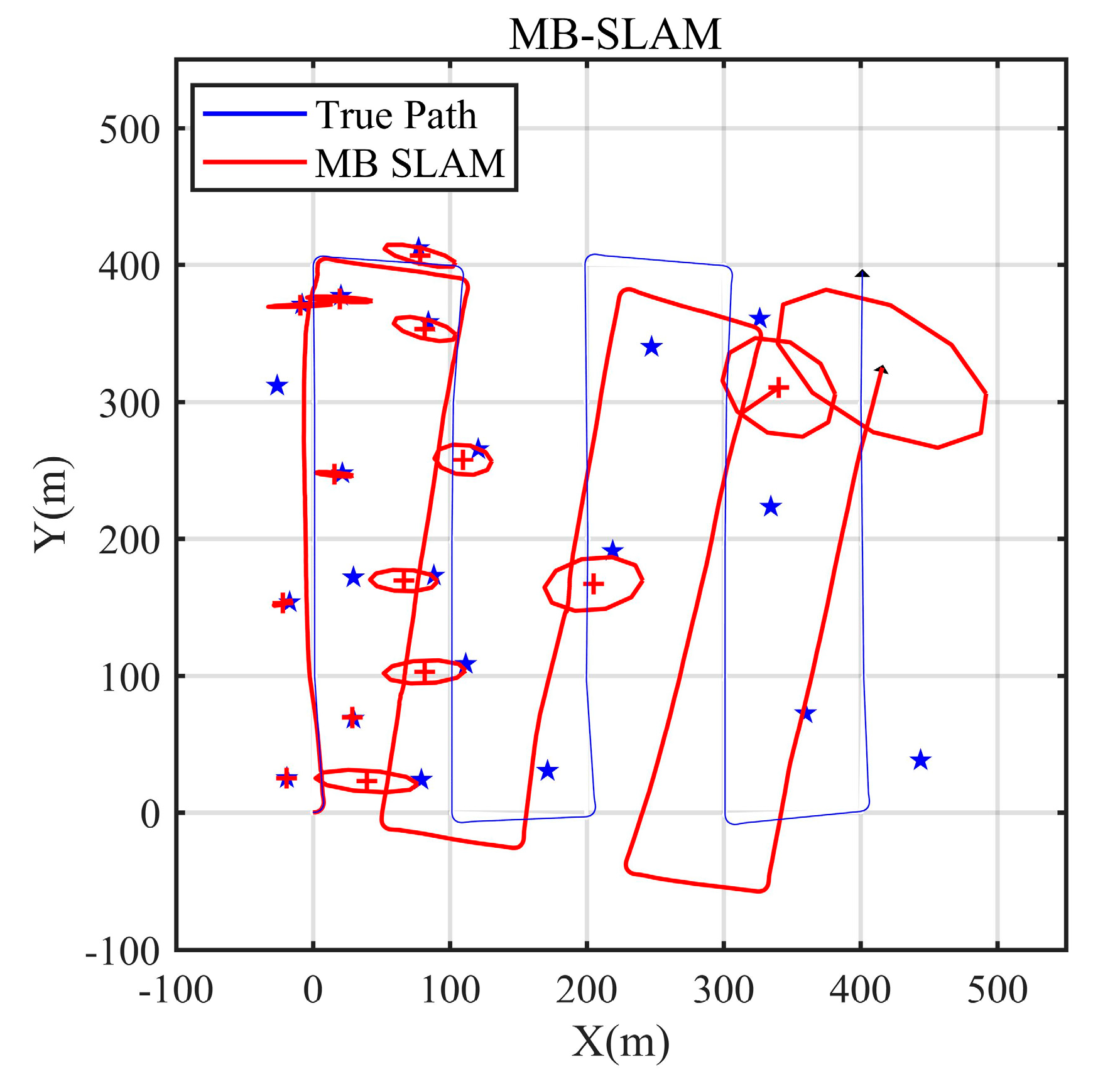
3.4. AMB-SLAM Simulation Results and Discussion
4. Conclusions and Future Work
4.1. Conclusions
4.2. Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV Navigation and localization: A review. IEEE J. Ocean. Eng. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Antonelli, G. Underwater Robots, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–350. [Google Scholar]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Tipsuwan, Y.; Hoonsuwan, P. Design and implementation of an AUV for petroleum pipeline inspection. In Proceedings of the 2015 7th International Conference on Information Technology and Electrical Engineering (ICITEE), Chiang Mai, Thailand, 29–30 October 2015; pp. 382–387. [Google Scholar]
- Roh, H.; Joe, H.; Yu, S. Simultaneous wide area scan purpose AUV with tethered multi-agent (SWAN). In Proceedings of the 2016 IEEE/OES Autonomous Underwater Vehicles (AUV), Tokyo, Japan, 6–9 November 2016; pp. 10–13. [Google Scholar]
- Anderson, B.; Crowell, J. Workhorse AUV-A cost-sensible new autonomous underwater vehicle for surveys/soundings, search & rescue, and research. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005; pp. 1–6. [Google Scholar]
- Matos, A.; Martins, A.; Dias, A.; Ferreira, B.; Almeida, J.M.; Ferreira, H.; Amaral, G.; Figueiredo, A.; Almeida, R.; Silva, F. Multiple robot operations for maritime search and rescue in euRathlon 2015 competition. In Proceedings of the OCEANS 2016, Shanghai, China, 10–13 April 2016; pp. 1–7. [Google Scholar]
- Murphy, R.R.; Dreger, K.L.; Newsome, S.; Rodocker, J.; Slaughter, B.; Smith, R.; Steimle, E.; Kimura, T.; Makabe, K.; Kon, K.; et al. Marine heterogeneous multirobot systems at the great Eastern Japan Tsunami recovery. J. Field Robot. 2012, 29, 819–831. [Google Scholar] [CrossRef]
- Yoerger, D.R.; Jakuba, M.; Bradley, A.M.; Bingham, B. Techniques for deep sea near bottom survey using an autonomous underwater vehicle. In Springer Trac Adv Ro, 1st ed.; Thrun, S., Brooks, R., Durrant-Whyte, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 28, pp. 416–429. [Google Scholar]
- Jakuba, M.V.; Roman, C.N.; Singh, H.; Murphy, C.; Kunz, C.; Willis, C.; Sato, T.; Sohn, R.A. Long-baseline acoustic navigation for under-ice autonomous underwater vehicle operations. J. Field Robot. 2008, 25, 861–879. [Google Scholar] [CrossRef]
- Kunz, C.; Murphy, C.; Singh, H.; Pontbriand, C.; Sohn, R.A.; Singh, S.; Sato, T.; Roman, C.; Nakamura, K.-i.; Jakuba, M.; et al. Toward extraplanetary under-ice exploration: Robotic steps in the Arctic. J. Field Robot. 2009, 26, 411–429. [Google Scholar] [CrossRef]
- Eustice, R.M.; Singh, H.; Leonard, J.J. Exactly sparse delayed-state filters for view-based SLAM. IEEE Trans. Robot. 2006, 22, 1100–1114. [Google Scholar] [CrossRef]
- Kussat, N.H.; Chadwell, C.D.; Zimmerman, R. Absolute positioning of an autonomous underwater vehicle using GPS and acoustic measurements. IEEE J. Ocean. Eng. 2005, 30, 153–164. [Google Scholar] [CrossRef]
- Vasilescu, I.; Detweiler, C.; Doniec, M.; Gurdan, D.; Sosnowski, S.; Stumpf, J.; Rus, D. AMOUR V: A Hovering Energy Efficient Underwater Robot Capable of Dynamic Payloads. Int. J. Robot. Res. 2010, 29, 547–570. [Google Scholar] [CrossRef]
- LaPointe, C.E.G. Virtual Long Baseline (VLBL) Autonomous Underwater Vehicle Navigation Using a Single Transponder. Bachelor’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2006. [Google Scholar]
- Youngberg, J.W.; Rome, N.Y. Method for Extending GPS to Underwater Applications. U.S. Patent 5119341, 2 June 1992. [Google Scholar]
- Youngberg, J.W. A novel method for extending GPS to underwater applications. Navigation 1991, 38, 263–271. [Google Scholar] [CrossRef]
- Sgorbini, S.; Peirano, A.; Cocito, S.; Morgigni, M. An underwater tracking system for mapping marine communities an application to Posidonia oceanica. Oceanol. Acta 2002, 25, 135–138. [Google Scholar] [CrossRef]
- Thomas, H.G. GIB buoys an interface between space and depths of the oceans. In Proceedings of the 1998 Workshop on Autonomous Underwater Vehicles, Cambridge, MA, USA, 20–21 August 1998; pp. 181–184. [Google Scholar]
- Alcocer, A.; Oliveira, P.; Pascoal, A. Study and implementation of an EKF GIB-based underwater positioning system. Control Eng. Pract. 2007, 15, 689–701. [Google Scholar] [CrossRef]
- Batista, P.; Silvestre, C.; Oliveira, P. GAS tightly coupled LBL/USBL position and velocity filter for underwater vehicles. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 2982–2987. [Google Scholar]
- Batista, P.; Silvestre, C.; Oliveira, P. GES integrated LBL/USBL navigation system for underwater vehicles. In Proceedings of the 51st IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 6609–6614. [Google Scholar]
- Batista, P.; Silvestre, C.; Oliveira, P. Tightly coupled long baseline/ultra-short baseline integrated navigation system. Int. J. Syst. Sci. 2014, 47, 1837–1855. [Google Scholar] [CrossRef]
- Vickery, K. Acoustic positioning systems. New concepts—The future. In Proceedings of the 1998 Workshop on Autonomous Underwater Vehicles, Cambridge, MA, USA, 20–21 August 1998; pp. 103–110. [Google Scholar]
- Whitcomb, L.L.; Yoerger, D.R.; Singh, H.; Howland, J. Combined Doppler/LBL based navigation of underwater vehicles. In Proceedings of the 11th International Symposium on uNmanned Untethered Submersible Technology, Durham, NH, USA, 22–25 August 1999; pp. 1–7. [Google Scholar]
- Spindel, R.; Porter, R.; Marquet, W.; Durham, J. A high-resolution pulse-Doppler underwater acoustic navigation system. IEEE J. Ocean. Eng. 1976, 1, 6–13. [Google Scholar] [CrossRef]
- Panish, R.; Taylor, M. Achieving high navigation accuracy using inertial navigation systems in autonomous underwater vehicles. In Proceedings of the IEEE OCEANS 2011, Santander, Spain, 6–9 June 2011; pp. 1–7. [Google Scholar]
- Fallon, M.F.; Kaess, M.; Johannsson, H.; Leonard, J.J. Efficient AUV navigation fusing acoustic ranging and side-scan sonar. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2398–2405. [Google Scholar]
- Morgado, M.; Oliveira, P.; Silvestre, C.; Vasconcelos, J.F. Embedded vehicle dynamics aiding for USBL/INS underwater navigation system. IEEE Trans. Control Syst. Technol. 2014, 22, 322–330. [Google Scholar] [CrossRef]
- Watanabe, Y.; Ochi, H.; Shimura, T.; Hattori, T. Super short baseline underwater acoustic positioning supported by inertial navigation data using spread spectrum communication for autonomous underwater vehicle and error analysis in deep water. Jpn. J. Appl. Phys. 2009, 48, 1–12. [Google Scholar] [CrossRef]
- Morgado, M.; Oliveira, P.; Silvestre, C. Tightly coupled ultrashort baseline and inertial navigation system for underwater vehicles: An experimental validation. J. Field Robot. 2013, 30, 142–170. [Google Scholar] [CrossRef]
- Morgado, M.; Oliveira, P.; Silvestre, C.; Vasconcelos, J.F. USBL/INS tightly-coupled integration technique for underwater vehicles. In Proceedings of the 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; pp. 1–8. [Google Scholar]
- Choi, W.-S.; Hoang, N.-M.; Jung, J.-H.; Lee, J.-M. Navigation system development of the underwater vehicles using the GPS/INS sensor fusion. In Proceedings of the 7th International Conference on Intelligent Robotics and Applications, Guangzhou, China, 17–20 December 2014; pp. 491–497. [Google Scholar]
- Knight, D.T. Rapid development of tightly-coupled GPS/INS systems. IEEE Aerosp. Electron. Syst. Mag. 1997, 12, 14–18. [Google Scholar] [CrossRef]
- Tal, A.; Klein, I.; Katz, R. Inertial Navigation System/Doppler Velocity Log (INS/DVL) fusion with partial DVL measurements. Sensors 2017, 17, 415. [Google Scholar] [CrossRef]
- Smith, R.; Self, M.; Cheeseman, P. Estimating uncertain spatial relationships in robotics. In Machine Intelligence and Pattern Recognition; Lemmer, J.F., Kanal, L.N., Eds.; North-Holland: Menlo Park, CA, USA, 1988; Volume 5, pp. 435–461. [Google Scholar]
- Smith, R.; Self, M.; Cheeseman, P. A stochastic map for uncertain spatial relationships. In Proceedings of the International Symposium on Robotics Research, Santa Clara, CA, USA, 10–11 August 1988; pp. 467–474. [Google Scholar]
- Durrant-whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–108. [Google Scholar] [CrossRef]
- Pierzchała, M.; Giguère, P.; Astrup, R. Mapping forests using an unmanned ground vehicle with 3D LiDAR and graph-SLAM. Comput. Electron. Agric. 2018, 145, 217–225. [Google Scholar] [CrossRef]
- Kownacki, C. A concept of laser scanner designed to realize 3D obstacle avoidance for a fixed-wing UAV. Robotica 2014, 34, 243–257. [Google Scholar] [CrossRef]
- Munguía, R.; Urzua, S.; Bolea, Y.; Grau, A. Vision-based SLAM system for unmanned aerial vehicles. Sensors 2016, 16, 372. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Li, Y.; Wang, R.; Cong, Z.; Gong, Y. AUV robust bathymetric simultaneous localization and mapping. Ocean Eng. 2018, 166, 336–349. [Google Scholar] [CrossRef]
- Hidalgo, F.; Bräunl, T. Review of underwater SLAM techniques. In Proceedings of the International Conference on Automation, Robotics and Applications, Queenstown, New Zealand, 17–19 February 2015; pp. 306–311. [Google Scholar]
- Woock, P. Survey on suitable 3D features for sonar-based underwater navigation. In Proceedings of the 2012 Oceans, Yeosu, Korea, 21–24 May 2012; pp. 1–6. [Google Scholar]
- Eustice, R.M.; Pizarro, O.; Singh, H. Visually augmented navigation for autonomous underwater vehicles. IEEE J. Ocean. Eng. 2008, 33, 103–122. [Google Scholar] [CrossRef]
- Eustice, R.M.; Singh, H.; Leonard, J.J.; Walter, M.R. Visually mapping the RMS titanic: Conservative covariance estimates for SLAM information filters. Int. J. Robot. Res. 2006, 25, 1223–1242. [Google Scholar] [CrossRef]
- Fairfield, N.; Kantor, G.; Jonak, D.; Wettergreen, D. Autonomous exploration and mapping of flooded sinkholes. Int. J. Robot. Res. 2010, 29, 748–774. [Google Scholar] [CrossRef]
- Fairfield, N.; Kantor, G.; Wettergreen, D. Real-time SLAM with Octree evidence grids for exploration in underwater tunnels. J. Field Robot. 2007, 24, 3–21. [Google Scholar] [CrossRef]
- Maki, T.; Kondo, H.; Ura, T.; Sakamaki, T. Imaging vent fields: SLAM based navigation scheme for an AUV toward large-area seafloor imaging. In Proceedings of the 2008 IEEE/OES Autonomous Underwater Vehicles, Woods Hole, MA, USA, 13–14 October 2008; pp. 1–10. [Google Scholar]
- Barkby, S.; Williams, S.B.; Pizarro, O.; Jakuba, M.V. Bathymetric particle filter SLAM using trajectory maps. Int. J. Robot. Res. 2012, 31, 1409–1430. [Google Scholar] [CrossRef]
- Barkby, S.; Williams, S.B.; Pizarro, O.; Jakuba, M.V. A featureless approach to efficient bathymetric SLAM using distributed particle mapping. J. Field Robot. 2011, 28, 19–39. [Google Scholar] [CrossRef]
- Barkby, S.; Williams, S.; Pizarro, O.; Jakuba, M. An efficient approach to bathymetric SLAM. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 219–224. [Google Scholar]
- Roman, C.; Singh, H. Improved vehicle based multibeam bathymetry using sub-maps and SLAM. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 3662–3669. [Google Scholar]
- Zandara, S.; Ridao, P.; Mallios, A.; Ribas, D. MBpIC-SLAM: Probabilistic surface matching for bathymetry based SLAM. IFAC Proc. Vol. 2012, 45, 126–131. [Google Scholar] [CrossRef]
- Ruiz, I.T.; Raucourt, S.d.; Petillot, Y.; Lane, D.M. Concurrent mapping and localization using sidescan sonar. IEEE J. Ocean. Eng. 2004, 29, 442–456. [Google Scholar] [CrossRef]
- Jaulin, L. A nonlinear set membership approach for the localization and map building of underwater robots. IEEE Trans. Robot. 2009, 25, 88–98. [Google Scholar] [CrossRef]
- Woock, P.; Frey, C. Deep-sea AUV navigation using side-scan sonar images and SLAM. In Proceedings of the OCEANS’10 IEEE SYDNEY, Sydney, Australia, 24–27 May 2010; pp. 1–8. [Google Scholar]
- Aulinas, J.; Lladó, X.; Salvi, J.; Petillot, Y.R. Feature based slam using side-scan salient objects. In Proceedings of the OCEANS 2010 MTS/IEEE SEATTLE, Seattle, WA, USA, 20–23 September 2010; pp. 1–8. [Google Scholar]
- Walter, M.; Hover, F.; Leonard, J. SLAM for ship hull inspection using exactly sparse extended information filters. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 1463–1470. [Google Scholar]
- Shippey, G.; Jonsson, M.; Pihl, J.N.B. Position correction using echoes from a navigation fix for synthetic aperture sonar imaging. IEEE J. Ocean. Eng. 2009, 34, 294–306. [Google Scholar] [CrossRef]
- Newman, P.M.; Leonard, J.J.; Rikoski, R.J. Towards constant-time SLAM on an autonomous underwater vehicle using synthetic aperture sonar. In Proceedings of the 11th International Symposium of Robotics Research; Springer: Berlin/Heidelberg, Germany, 2005; pp. 409–420. [Google Scholar]
- Ribas, D.; Ridao, P.; Tardós, J.D.; Neira, J. Underwater SLAM in man-made structured environments. J. Field Robot. 2008, 25, 898–921. [Google Scholar] [CrossRef]
- Ribas, D.; Ridao, P.; Neira, J.; Tardos, J.D. SLAM using an imaging sonar for partially structured underwater environments. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 5040–5045. [Google Scholar]
- Mallios, A.; Ridao, P.; Hernandez, E.; Ribas, D.; Maurelli, F.; Petillot, Y. Pose-based SLAM with probabilistic scan matching algorithm using a mechanical scanned imaging sonar. In Proceedings of the OCEANS 2009-EUROPE, Bremen, Germany, 11–14 May 2009; pp. 1–6. [Google Scholar]
- Ferreira, F.; Veruggio, G.; Caccia, M.; Bruzzone, G. Real-time optical SLAM-based mosaicking for unmanned underwater vehicles. Intell. Serv. Robot. 2012, 5, 55–71. [Google Scholar] [CrossRef]
- Bleser, G.; Hendeby, G. Using optical flow as lightweight SLAM alternative. In Proceedings of the 2009 8th IEEE International Symposium on Mixed and Augmented Reality, Orlando, FL, USA, 19–22 October 2009; pp. 175–176. [Google Scholar]
- Wang, P.; Chen, C.; Dong, C.; Xu, H.; Tian, F. The analysis method of video camera’s motion based on optical flow and slam. In Proceedings of the 2016 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 11–12 July 2016; pp. 62–66. [Google Scholar]
- Andert, F.; Ammann, N.; Krause, S.; Lorenz, S.; Bratanov, D.; Mejias, L. Optical-aided aircraft navigation using decoupled visual SLAM with range sensor augmentation. J. Intell. Robot. Syst. 2017, 88, 547–565. [Google Scholar] [CrossRef]
- Neira, J.; Tardos, J.D. Data association in stochastic mapping using the joint compatibility test. IEEE Trans. Robot. Autom. 2001, 17, 890–897. [Google Scholar] [CrossRef]
- Davis, C. GPS-like navigation underground. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 1108–1111. [Google Scholar]
- Shanmuganathan, S. Artificial neural network modelling: An introduction. In Artificial Neural Network Modelling; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–14. [Google Scholar]
- Masters, T. Practical Neural Network Recipes in C++, 1st ed.; Academic Press: Cambridge, MA, USA, 1993; pp. 1–493. [Google Scholar]
- Burden, F.R.; Brereton, R.G.; Walsh, P.T. Cross-validatory selection of test and validation sets in multivariate calibration and neural networks as applied to spectroscopy. Analyst 1997, 122, 1015–1022. [Google Scholar] [CrossRef]
- Minns, A.W.; Hall, M.J. Artificial neural networks as rainfall-runoff models. Hydrol. Sci. J. Sci. Hydrol. 1996, 41, 399–417. [Google Scholar] [CrossRef]
- White, H. Learning in artificial neural networks: A statistical perspective. Neural Comput. 1989, 1, 425–464. [Google Scholar] [CrossRef]
- Parisi, R.; Claudio, E.D.D.; Orlandi, G.; Rao, B.D. A generalized learning paradigm exploiting the structure of feedforward neural networks. IEEE Trans. Neural Netw. 1996, 7, 1450–1460. [Google Scholar] [CrossRef] [PubMed]
- Amari, S.; Murata, N.; Muller, K.; Finke, M.; Yang, H.H. Asymptotic statistical theory of overtraining and cross-validation. IEEE Trans. Neural Netw. 1997, 8, 985–996. [Google Scholar] [CrossRef] [PubMed]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Modell. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Bebis, G.; Georgiopoulos, M. Feed-forward neural networks. IEEE Potentials 1994, 13, 27–31. [Google Scholar] [CrossRef]
- Dissanayake, M.W.M.G.; Newman, P.; Clark, S.; Durrant-Whyte, H.F.; Csorba, M. A solution to the simultaneous localization and map building (SLAM) problem. IEEE Trans. Robot. Autom. 2001, 17, 229–241. [Google Scholar] [CrossRef]



















| Team ID | Samples Number |
|---|---|
| 1 | 1–100 |
| 2 | 101–200 |
| 3 | 201–300 |
| 4 | 301–400 |
| 5 | 401–500 |
| 6 | 501–600 |
| 7 | 601–700 |
| 8 | 701–800 |
| 9 | 801–900 |
| 10 | 901–1000 |
| Experiment ID | Train ID | Test ID |
|---|---|---|
| A | 1–9 | 10 |
| B | 1–8, 10 | 9 |
| C | 1–7, 9, 10 | 8 |
| D | 1–6, 8–10 | 7 |
| E | 1–5, 7–10 | 6 |
| F | 1–4, 6–10 | 5 |
| G | 1–3, 5–10 | 4 |
| H | 1, 2, 4–10 | 3 |
| I | 1, 3–10 | 2 |
| J | 2–10 | 1 |
| Experiment ID | Correlation Coefficient of x Direction | Correlation Coefficient of y Direction | Correlation Coefficient of z Direction |
|---|---|---|---|
| A | 0.9553 | 0.8368 | 0.9921 |
| B | 0.9234 | 0.8182 | 0.9768 |
| C | 0.9378 | 0.9648 | 0.9764 |
| D | 0.9736 | 0.9364 | 0.9242 |
| E | 0.7729 | 0.9372 | 0.9012 |
| F | 0.8251 | 0.8374 | 0.8893 |
| G | 0.9824 | 0.9372 | 0.8783 |
| H | 0.9734 | 0.9346 | 0.8940 |
| I | 0.9191 | 0.8237 | 0.9092 |
| J | 0.7732 | 0.6919 | 0.7489 |
| Parameter | Value |
|---|---|
| Wheelbase of vehicle | 2 m |
| Control speed input noise | 3 m/s |
| Control heading input noise | 3° |
| Vehicle speed | 5 m/s |
| Observation noise | 0.1 m/s |
| Maximum steering angle | 30° |
| Frequency of control loops | 40 Hz |
| Observation frequency | 5 Hz |
| Maximum range | 25 m |
| Maximum distance for association | 8 m |
| Augment distance | 28 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, G.; Shao, Q.; Zou, B.; Dai, L.; Zhang, Z.; Mu, Z.; Zhang, Y.; Zhai, J. A Novel Underwater Simultaneous Localization and Mapping Online Algorithm Based on Neural Network. ISPRS Int. J. Geo-Inf. 2020, 9, 5. https://doi.org/10.3390/ijgi9010005
Hou G, Shao Q, Zou B, Dai L, Zhang Z, Mu Z, Zhang Y, Zhai J. A Novel Underwater Simultaneous Localization and Mapping Online Algorithm Based on Neural Network. ISPRS International Journal of Geo-Information. 2020; 9(1):5. https://doi.org/10.3390/ijgi9010005
Chicago/Turabian StyleHou, Guangchao, Qi Shao, Bo Zou, Liwen Dai, Zhe Zhang, Zhehan Mu, Yadong Zhang, and Jingsheng Zhai. 2020. "A Novel Underwater Simultaneous Localization and Mapping Online Algorithm Based on Neural Network" ISPRS International Journal of Geo-Information 9, no. 1: 5. https://doi.org/10.3390/ijgi9010005
APA StyleHou, G., Shao, Q., Zou, B., Dai, L., Zhang, Z., Mu, Z., Zhang, Y., & Zhai, J. (2020). A Novel Underwater Simultaneous Localization and Mapping Online Algorithm Based on Neural Network. ISPRS International Journal of Geo-Information, 9(1), 5. https://doi.org/10.3390/ijgi9010005






