Landslide Susceptibility Assessment Using an Optimized Group Method of Data Handling Model
Abstract
:1. Introduction
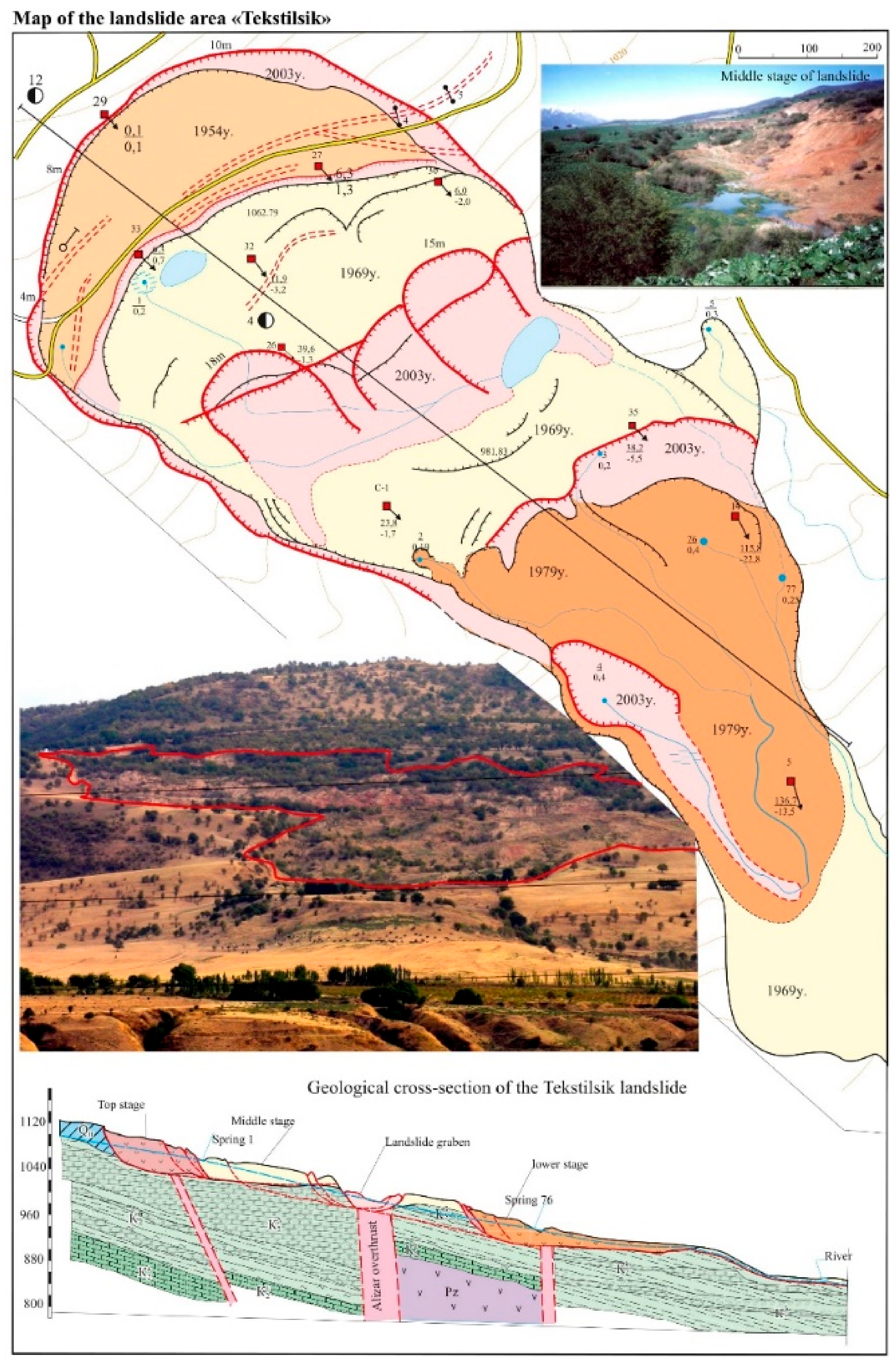
2. Study Area
3. Data and Method
3.1. Historical Landslide Data
3.2. Conditioning Factors
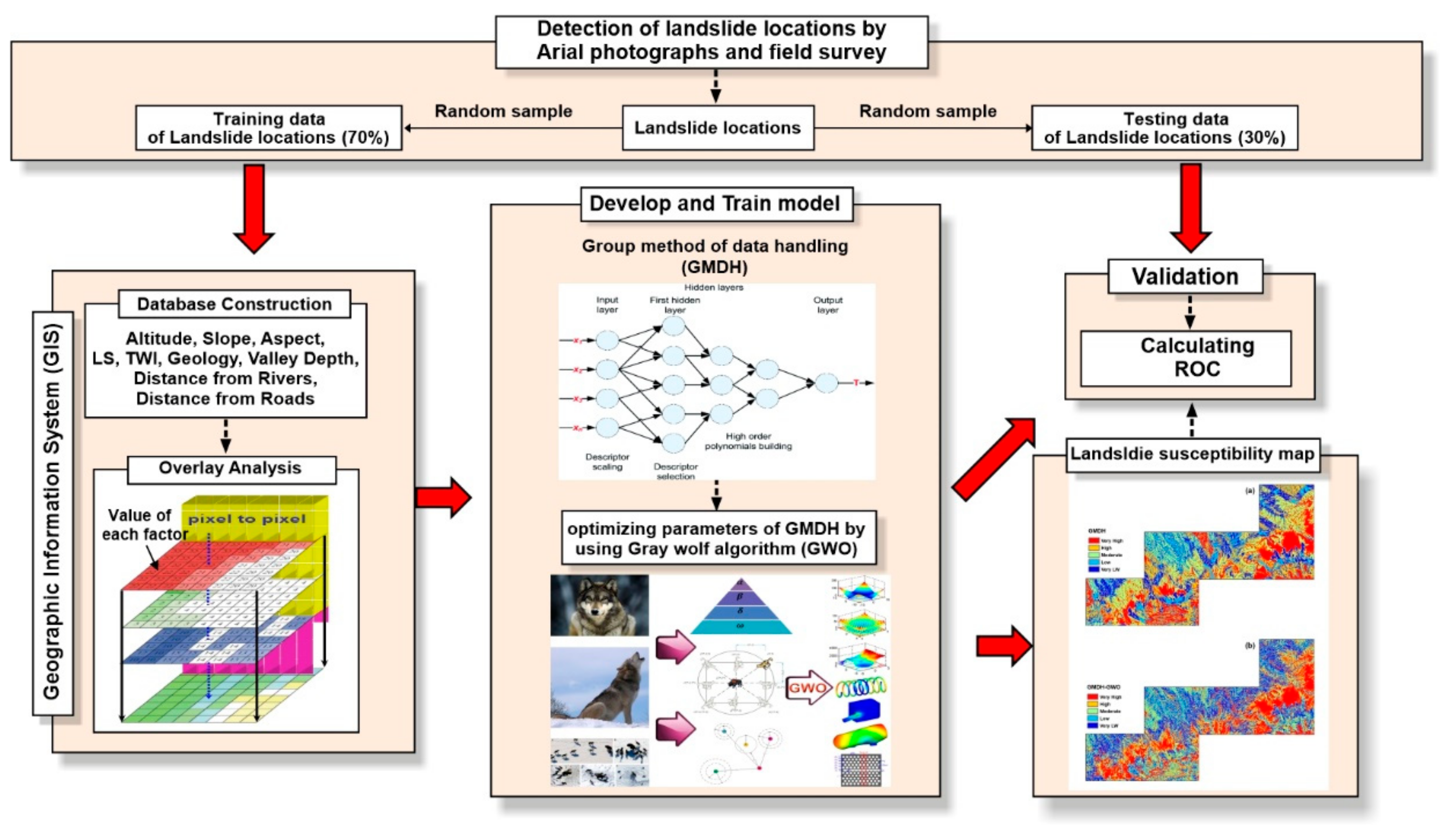
3.3. Method
3.3.1. Group Method of Data Handling (GMDH)
3.3.2. Gray Wolf Optimizer (GWO)
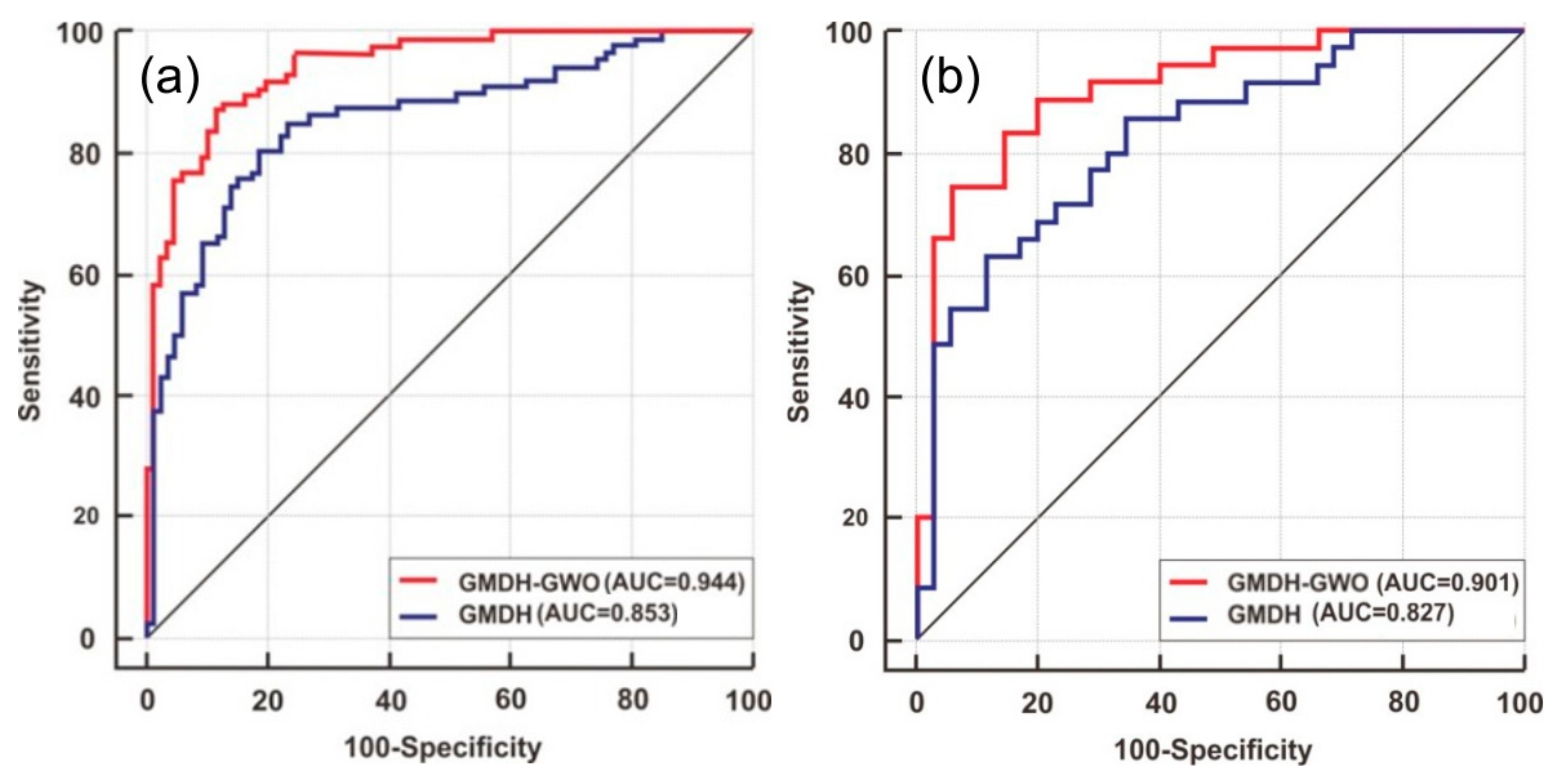
3.4. Model Validation
4. Results and Discussion
4.1. Impact of Conditioning Factor Subclasses on Landslide Probability
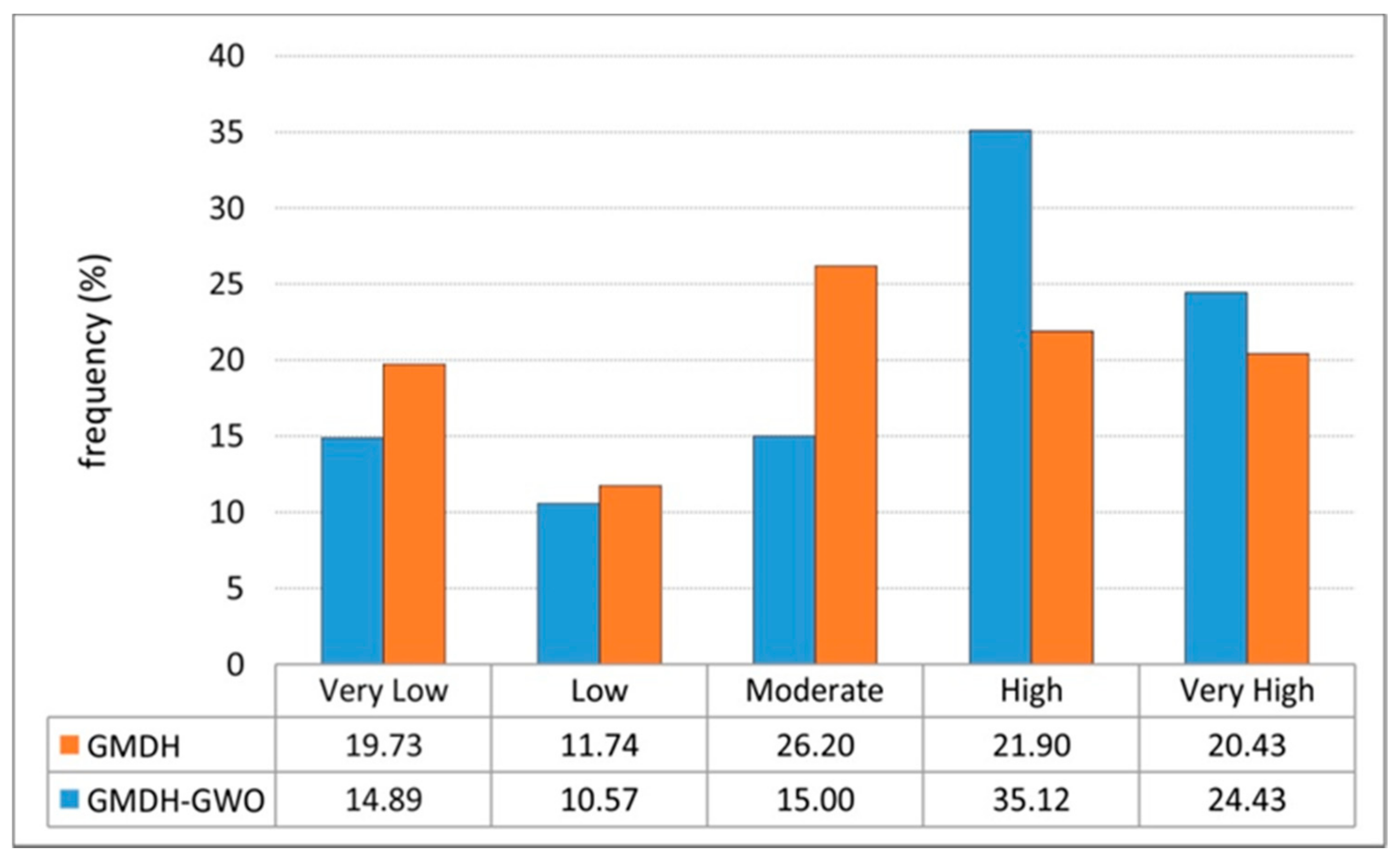
4.2. Landslide Susceptibility Maps
5. Discussion
6. Conclusions
- Landslides were most likely in the study area at altitudes of 1420–1736 m, and with southwest slope aspects, an LS of 3.12–18.94 m, a distance from the river of 65–318 m, a distance from the road of 0–1440 m, a 6–9.7° slope, a TWI of −24 to −145, and a valley depth of 77–144 m.
- The GWO enhanced the predictive power of the standard GMDH model.
- The performance of the GMDH–GWO model was superior to that of the standard GMDH model in the training and testing phases, by 9.6% and 8.5%, respectively.
- The GMDH–GWO and standard GMDH models had 90% and 82% landslide prediction accuracy, respectively.
- The GMDH–GWO model classified 14.89%, 10.57%, 15.00%, 35.12%, and 24.43% of the study area as having very low, low, moderate, high, and very high susceptibility to future landslides.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chakraborty, S.; Pradhan, R. Development of GIS based landslide information system for the region of East Sikkim. Int. J. Comput. Appl. 2012, 49, 5–9. [Google Scholar] [CrossRef]
- Aleotti, P.; Chowdhury, R. Landslide hazard assessment: Summary review and new perspectives. Bull. Eng. Geol. Environ. 1999, 58, 21–44. [Google Scholar] [CrossRef]
- Goetz, S.; Dubayah, R. Advances in remote sensing technology and implications for measuring and monitoring forest carbon stocks and change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Nohani, E.; Moharrami, M.; Sharafi, S.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Lee, S.; Melesse, A.M. Landslide susceptibility mapping using different GIS-based bivariate models. Water 2019, 11, 1402. [Google Scholar] [CrossRef] [Green Version]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pradhan, B.; Pourghasemi, H.R.; Abdullahi, S. Landslide susceptibility assessment at Wadi Jawrah Basin, Jizan region, Saudi Arabia using two bivariate models in GIS. Geosci. J. 2015, 19, 449–469. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Park, H.-J.; Lee, J.H. A novel ensemble bivariate statistical evidential belief function with knowledge-based analytical hierarchy process and multivariate statistical logistic regression for landslide susceptibility mapping. Catena 2014, 114, 21–36. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in GIS: Safarood Basin, Iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Shirzadi, A.; Saro, L.; Joo, O.H.; Chapi, K. A GIS-based logistic regression model in rock-fall susceptibility mapping along a mountainous road: Salavat Abad case study, Kurdistan, Iran. Nat. Hazards 2012, 64, 1639–1656. [Google Scholar] [CrossRef] [Green Version]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and analytical hierarchy process (AHP) to landslide susceptibility mapping at Haraz watershed, Iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Neaupane, K.M.; Piantanakulchai, M. Analytic network process model for landslide hazard zonation. Eng. Geol. 2006, 85, 281–294. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.-H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Najafabadi, R.M.; Ramesht, M.H.; Ghazi, I.; Khajedin, S.J.; Seif, A.; Nohegar, A.; Mahdavi, A. Identification of natural hazards and classification of urban areas by TOPSIS model (case study: Bandar Abbas city, Iran). Geomat. Nat. Hazards Risk 2016, 7, 85–100. [Google Scholar] [CrossRef]
- Khosravi, K.; Sartaj, M.; Tsai, F.T.-C.; Singh, V.P.; Kazakis, N.; Melesse, A.M.; Prakash, I.; Bui, D.T.; Pham, B.T. A comparison study of DRASTIC methods with various objective methods for groundwater vulnerability assessment. Sci. Total Environ. 2018, 642, 1032–1049. [Google Scholar] [CrossRef]
- Khosravi, K.; Shahabi, H.; Pham, B.T.; Adamowski, J.; Shirzadi, A.; Pradhan, B.; Dou, J.; Ly, H.-B.; Gróf, G.; Ho, H.L. A comparative assessment of flood susceptibility modeling using Multi-Criteria Decision-Making Analysis and Machine Learning Methods. J. Hydrol. 2019, 573, 311–323. [Google Scholar] [CrossRef]
- Khosravi, K.; Cooper, J.R.; Daggupati, P.; Pham, B.T.; Bui, D.T. Bedload transport rate prediction: Application of novel hybrid data mining techniques. J. Hydrol. 2020, 585, 124774. [Google Scholar] [CrossRef]
- Ngo, P.T.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Karimnejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2020. [Google Scholar] [CrossRef]
- Lee, S. Landslide susceptibility mapping using an artificial neural network in the Gangneung area, Korea. Int. J. Remote Sens. 2007, 28, 4763–4783. [Google Scholar] [CrossRef]
- Pascale, S.; Parisi, S.; Mancini, A.; Schiattarella, M.; Conforti, M.; Sole, A.; Murgante, B.; Sdao, F. Landslide susceptibility mapping using artificial neural network in the urban area of Senise and San Costantino Albanese (Basilicata, Southern Italy). In Proceedings of the International Conference on Computational Science and Its Applications, Ho Chi Minh City, Vietnam, 24–27 June 2013; pp. 473–488. [Google Scholar]
- Shahri, A.A.; Spross, J.; Johansson, F.; Larsson, S. Landslide susceptibility hazard map in southwest Sweden using artificial neural network. Catena 2019, 183, 104225. [Google Scholar] [CrossRef]
- Choubin, B.; Darabi, H.; Rahmati, O.; Sajedi-Hosseini, F.; Kløve, B. River suspended sediment modelling using the CART model: A comparative study of machine learning techniques. Sci. Total Environ. 2018, 615, 272–281. [Google Scholar] [CrossRef]
- Lee, S.; Panahi, M.; Pourghasemi, H.R.; Shahabi, H.; Alizadeh, M.; Shirzadi, A.; Khosravi, K.; Melesse, A.M.; Yekrangnia, M.; Rezaie, F. Sevucas: A novel gis-based machine learning software for seismic vulnerability assessment. Appl. Sci. 2019, 9, 3495. [Google Scholar] [CrossRef] [Green Version]
- Panahi, M.; Gayen, A.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of landslide susceptibility using hybrid support vector regression (SVR) and the adaptive neuro-fuzzy inference system (ANFIS) with various metaheuristic algorithms. Sci. Total Environ. 2020, 741, 139937. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Varzandeh, M.H.M. A new hybrid model using step-wise weight assessment ratio analysis (SWARA) technique and adaptive neuro-fuzzy inference system (ANFIS) for regional landslide hazard assessment in Iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Polykretis, C.; Chalkias, C.; Ferentinou, M. Adaptive neuro-fuzzy inference system (ANFIS) modeling for landslide susceptibility assessment in a Mediterranean hilly area. Bull. Eng. Geol. Environ. 2019, 78, 1173–1187. [Google Scholar] [CrossRef]
- Bui, D.T.; Khosravi, K.; Tiefenbacher, J.; Nguyen, H.; Kazakis, N. Improving prediction of water quality indices using novel hybrid machine-learning algorithms. Sci. Total Environ. 2020, 721, 137612. [Google Scholar] [CrossRef] [PubMed]
- Ballabio, C.; Sterlacchini, S. Support vector machines for landslide susceptibility mapping: The Staffora River Basin case study, Italy. Math. Geosci. 2012, 44, 47–70. [Google Scholar] [CrossRef]
- Lee, S.; Hong, S.-M.; Jung, H.-S. A support vector machine for landslide susceptibility mapping in Gangwon Province, Korea. Sustainability 2017, 9, 48. [Google Scholar] [CrossRef] [Green Version]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
- Pham, B.T.; Khosravi, K.; Prakash, I. Application and comparison of decision tree-based machine learning methods in landside susceptibility assessment at Pauri Garhwal Area, Uttarakhand, India. Environ. Process. 2017, 4, 711–730. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Khosravi, K.; Chapi, K.; Trinh, P.T.; Ngo, T.Q.; Hosseini, S.V.; Bui, D.T. A comparison of Support Vector Machines and Bayesian algorithms for landslide susceptibility modelling. Geocarto Int. 2019, 34, 1385–1407. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.-X.; Chen, W.; Ahmad, B.B. Landslide susceptibility mapping using J48 Decision Tree with AdaBoost, Bagging and Rotation Forest ensembles in the Guangchang area (China). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Shahabi, H.; Geertsema, M.; Omidvar, E.; Clague, J.J.; Thai Pham, B.; Dou, J.; Talebpour Asl, D.; Bin Ahmad, B. New ensemble models for shallow landslide susceptibility modeling in a semi-arid watershed. Forests 2019, 10, 743. [Google Scholar] [CrossRef] [Green Version]
- Di Napoli, M.; Carotenuto, F.; Cevasco, A.; Confuorto, P.; Di Martire, D.; Firpo, M.; Pepe, G.; Raso, E.; Calcaterra, D. Machine learning ensemble modelling as a tool to improve landslide susceptibility mapping reliability. Landslides 2020, 17, 1897–1914. [Google Scholar] [CrossRef]
- Khodadadi, F.; Entezari, M.; Sasanpour, F. Analysis of Geomorphologic Hazards of Landslide and Flood using VIKOR-AHP and Fr Models in the Alborz Province. Phys. Geogr. Res. Q. 2019, 51, 183–199. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Panahi, M.; Shahabi, H.; Wang, Y.; Shirzadi, A.; Pirasteh, S.; Alesheikh, A.A.; Khosravi, K.; Panahi, S. Spatial prediction of landslide susceptibility using gis-based data mining techniques of anfis with whale optimization algorithm (woa) and grey wolf optimizer (gwo). Appl. Sci. 2019, 9, 3755. [Google Scholar] [CrossRef] [Green Version]
- Ebtehaj, I.; Bonakdari, H. A support vector regression-firefly algorithm-based model for limiting velocity prediction in sewer pipes. Water Sci. Technol. 2016, 73, 2244–2250. [Google Scholar] [CrossRef] [Green Version]
- Shaghaghi, S.; Bonakdari, H.; Gholami, A.; Ebtehaj, I.; Zeinolabedini, M. Comparative analysis of GMDH neural network based on genetic algorithm and particle swarm optimization in stable channel design. Appl. Math. Comput. 2017, 313, 271–286. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Dodangeh, E.; Panahi, M.; Rezaie, F.; Lee, S.; Bui, D.T.; Lee, C.-W.; Pradhan, B. Novel hybrid intelligence models for flood-susceptibility prediction: Meta optimization of the GMDH and SVR models with the genetic algorithm and harmony search. J. Hydrol. 2020, 590, 125423. [Google Scholar] [CrossRef]
- Nguyen, V.V.; Pham, B.T.; Vu, B.T.; Prakash, I.; Jha, S.; Shahabi, H.; Shirzadi, A.; Ba, D.N.; Kumar, R.; Chatterjee, J.M. Hybrid machine learning approaches for landslide susceptibility modeling. Forests 2019, 10, 157. [Google Scholar] [CrossRef] [Green Version]
- Shirzadi, A.; Soliamani, K.; Habibnejhad, M.; Kavian, A.; Chapi, K.; Shahabi, H.; Chen, W.; Khosravi, K.; Thai Pham, B.; Pradhan, B. Novel GIS based machine learning algorithms for shallow landslide susceptibility mapping. Sensors 2018, 18, 3777. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Chen, X.; Peng, J.; Panahi, M.; Lee, S. Landslide susceptibility modeling based on ANFIS with teaching-learning-based optimization and Satin bowerbird optimizer. Geosci. Front. 2020, 12, 93–107. [Google Scholar] [CrossRef]
- Thai Pham, B.; Prakash, I.; Dou, J.; Singh, S.; Trinh, P.; Trung Tran, H.; Minh Le, T.; Tran, V.; Kim Khoi, D.; Shirzadi, A. A novel hybrid approach of landslide susceptibility modeling using rotation forest ensemble and different base classifiers. Geocarto Int. 2018, 14, 1–38. [Google Scholar] [CrossRef]
- Feuillet, T.; Coquin, J.; Mercier, D.; Cossart, E.; Decaulne, A.; Jónsson, H.P.; Sæmundsson, Þ. Focusing on the spatial non-stationarity of landslide predisposing factors in northern Iceland: Do paraglacial factors vary over space? Prog. Phys. Geogr. 2014, 38, 354–377. [Google Scholar] [CrossRef]
- Menking, J.A.; Han, J.; Gasparini, N.M.; Johnson, J.P. The effects of precipitation gradients on river profile evolution on the Big Island of Hawai’i. GSA Bull. 2013, 125, 594–608. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.; Naghibi, S.A.; Pourghasemi, H.R.; Pradhan, B. GIS-based landslide spatial modeling in Ganzhou City, China. Arab. J. Geosci. 2016, 9, 112. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. The group method of data of handling; a rival of the method of stochastic approximation. Sov. Autom. Control 1968, 13, 43–55. [Google Scholar]
- Jiang, Y.; Liu, S.; Peng, L.; Zhao, N. A novel wind speed prediction method based on robust local mean decomposition, group method of data handling and conditional kernel density estimation. Energy Convers. Manag. 2019, 200, 112099. [Google Scholar] [CrossRef]
- Mohebbian, M.R.; Dinh, A.; Wahid, K.; Alam, M.S. Blind, Cuff-less, Calibration-Free and Continuous Blood Pressure Estimation using Optimized Inductive Group Method of Data Handling. Biomed. Signal Process. Control 2020, 57, 101682. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, J.; Zhang, W.; Sun, D. Short-term effects of air pollution on lower respiratory diseases and forecasting by the group method of data handling. Atmos. Environ. 2012, 51, 29–38. [Google Scholar] [CrossRef]
- Rostami, A.; Hemmati-Sarapardeh, A.; Karkevandi-Talkhooncheh, A.; Husein, M.M.; Shamshirband, S.; Rabczuk, T. Modeling heat capacity of ionic liquids using group method of data handling: A hybrid and structure-based approach. Int. J. Heat Mass Transf. 2019, 129, 7–17. [Google Scholar] [CrossRef]
- Stefenon, S.F.; Ribeiro, M.H.D.M.; Nied, A.; Mariani, V.C.; dos Santos Coelho, L.; da Rocha, D.F.M.; Grebogi, R.B.; de Barros Ruano, A.E. Wavelet group method of data handling for fault prediction in electrical power insulators. Int. J. Electr. Power Energy Syst. 2020, 123, 106269. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Barani, G.-A.; Hessami-Kermani, M.-R. Group method of data handling to predict scour depth around vertical piles under regular waves. Sci. Iran. 2013, 20, 406–413. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.; Deep, K. An opposition-based chaotic grey wolf optimizer for global optimisation tasks. J. Exp. Theor. Artif. Intell. 2019, 31, 751–779. [Google Scholar] [CrossRef]
- Tu, Q.; Chen, X.; Liu, X. Hierarchy strengthened grey wolf optimizer for numerical optimization and feature selection. IEEE Access 2019, 7, 78012–78028. [Google Scholar] [CrossRef]
- Niu, M.; Wang, Y.; Sun, S.; Li, Y. A novel hybrid decomposition-and-ensemble model based on CEEMD and GWO for short-term PM2. 5 concentration forecasting. Atmos. Environ. 2016, 134, 168–180. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.; Liang, X.; Tang, M. An exploration-enhanced grey wolf optimizer to solve high-dimensional numerical optimization. Eng. Appl. Artif. Intell. 2018, 68, 63–80. [Google Scholar] [CrossRef]
- Kaveh, A.; Zakian, P. Improved GWO algorithm for optimal design of truss structures. Eng. Comput. 2018, 34, 685–707. [Google Scholar] [CrossRef]
- Luo, K.; Zhao, Q. A binary grey wolf optimizer for the multidimensional knapsack problem. Appl. Soft Comput. 2019, 83, 105645. [Google Scholar] [CrossRef]
- Chung, C.-J.F.; Fabbri, A.G. Validation of spatial prediction models for landslide hazard mapping. Nat. Hazards 2003, 30, 451–472. [Google Scholar] [CrossRef]
- Jaafari, A.; Zenner, E.K.; Pham, B.T. Wildfire spatial pattern analysis in the Zagros Mountains, Iran: A comparative study of decision tree based classifiers. Ecol. Inform. 2018, 43, 200–211. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Akgun, A.; Kıncal, C.; Pradhan, B. Application of remote sensing data and GIS for landslide risk assessment as an environmental threat to Izmir city (west Turkey). Environ. Monit. Assess. 2012, 184, 5453–5470. [Google Scholar] [CrossRef]

| Authors | Models |
|---|---|
| Nohani et al. [4] | FR |
| Youssef et al. [6] | WOE |
| Althuwaynee [7] | EBF |
| Pourghasemi et al. [8] | SE |
| Shirzadi et al. [9] | LR |
| Pourghasemi et al. [10] | AHP |
| Neaupane et al. [11] | ANP |
| Khodadadi et al. [35] | VIKOR |
| Najafabadi et al. [13] | TOPSIS |
| Lee et al. [18]; Pascale et al. [19] and Shahri et al. [20] | ANN |
| Panahi et al. [23]; Dehnavi et al. [24] and Polykretis et al. [25] | ANFIS |
| Dou et al. [29] | RF |
| Chen at al. (2018) [36] | kernel logistic regression |
| Pham et al. [30] | RF, LMT, BFDT, CART |
| Pham et al. [31] | NBT, BN and NB |
| Honge et al. [32] | AdaBoost, Bagging and RF |
| Bui et al. [33] | SVM |
| Napoli et al. [34] | ANN and |
| Ngo et al. [17] | Deep learning (RNN and CNN) |
| No | Year of HGP | Type of HGP | Characteristics of HGP |
|---|---|---|---|
| 1 | 1966 | Suffusion (subsoil erosion) | - |
| 2 | 1969 | Crack | L = up to 500 m |
| 3 | 1973 | Activation of cracks | L = up to 550 m |
| 4 | 1979 | Landslide | 22.5 million m3 |
| 5 | 1981 | Crack | L = up to 70 m |
| 6 | 1987 | Landslide | 6.8 thousand m3 |
| 7 | 1994 | Landslide | 3.0 million m3 |
| 8 | 2003 | Landslide | 1.5 million m3 |
| 9 | 2004 | Crack | L = up to 20 m |
| 10 | 2005 | Crack | L = up to 450 m |
| 11 | 2016 | Crack | L = 7 m |
| 12 | 2017 | Crack | L = up to 60 m |
| Conditioning Factors | Classes | Number of Pixels | Number of Landslide | FR |
|---|---|---|---|---|
| Altitude (m) | 837–1137 | 155,854 | 764 | 0.20 |
| 1137–1275 | 155,708 | 2521 | 0.66 | |
| 1275–1420 | 155,503 | 5056 | 1.32 | |
| 1420–1736 | 155,241 | 7483 | 1.96 | |
| 1736–3201 | 155,068 | 3286 | 0.86 | |
| Slope (degree) | 0–6.09 | 150,709 | 3693 | 0.99 |
| 6.09–9.74 | 152,907 | 4996 | 1.32 | |
| 9.74–13.64 | 155,563 | 4163 | 1.08 | |
| 13.64–19.25 | 160,617 | 3747 | 0.94 | |
| 19.25–62.13 | 152,241 | 2511 | 0.67 | |
| Aspect | Flat | 4567 | 107 | 0.95 |
| North | 133,382 | 3358 | 1.02 | |
| Northeast | 128,344 | 3102 | 0.98 | |
| East | 59,410 | 1598 | 1.09 | |
| Southeast | 42,604 | 752 | 0.71 | |
| South | 58,574 | 1867 | 1.29 | |
| Southwest | 95,198 | 3183 | 1.35 | |
| West | 117,352 | 2619 | 0.90 | |
| Northwest | 132,606 | 2525 | 0.77 | |
| Valley depth | 77.87–144.92 | 154,154 | 2347 | 1.54 |
| 144.92–203.02 | 155,482 | 5901 | 1.36 | |
| 203.02–258.88 | 157,529 | 5271 | 0.97 | |
| 258.88–502.47 | 150,119 | 3581 | 0.51 | |
| TWI | −2.59–−0.59 | 140,906 | 2335 | 0.67 |
| −59–−0.71 | 161,569 | 2845 | 0.72 | |
| −0.71–−1.18 | 164,117 | 3664 | 0.91 | |
| −1.18–−24.98 | 161,011 | 4845 | 1.22 | |
| −24.98–−145.25 | 149,771 | 5422 | 1.47 | |
| −145.25< | 140,906 | 2335 | 0.62 | |
| LS | 0–2.00 | 108,564 | 1730 | 0.65 |
| 2.00–2.30 | 185,629 | 3500 | 0.77 | |
| 2.30–2.60 | 167,555 | 3742 | 0.91 | |
| 2.60–3.12 | 162,271 | 4627 | 1.16 | |
| 3.12–18.94 | 153,355 | 5512 | 1.46 | |
| Distance from Roads (m) | 0–617.19 | 160,972 | 5155 | 1.35 |
| 617.19–1440.12 | 160,514 | 5207 | 1.36 | |
| 1440.12–2365.92 | 160,476 | 5054 | 1.32 | |
| 2365.92–3566.02 | 160,430 | 2918 | 0.76 | |
| 3566.02–8743.62 | 160,370 | 777 | 0.20 | |
| Distance from Rivers (m) | 0–65.90 | 164,916 | 4186 | 1.07 |
| 65.90–164.75 | 160,628 | 4212 | 1.10 | |
| 164.75–318.52 | 162,069 | 4247 | 1.10 | |
| 318.52–593.11 | 158,501 | 3996 | 1.06 | |
| 593.11–2800.80 | 156,534 | 2471 | 0.66 | |
| Geology | C1-2 | 15,330 | 196 | 0.61 |
| J | 91,031 | 53 | 0.03 | |
| K | 60,724 | 584 | 0.46 | |
| N | 415,325 | 7123 | 0.82 | |
| P | 34,984 | 1340 | 1.84 | |
| P1 | 21,524 | 46 | 0.10 | |
| QIaz | 21,784 | 149 | 0.33 | |
| QIIkr | 96,833 | 2769 | 1.37 | |
| QIIIsk | 115,307 | 6289 | 2.62 | |
| QIVam | 23,832 | 560 | 1.13 | |
| other | 21,606 | 0 | 0.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadirhodjaev, A.; Rezaie, F.; Lee, M.-J.; Lee, S. Landslide Susceptibility Assessment Using an Optimized Group Method of Data Handling Model. ISPRS Int. J. Geo-Inf. 2020, 9, 566. https://doi.org/10.3390/ijgi9100566
Kadirhodjaev A, Rezaie F, Lee M-J, Lee S. Landslide Susceptibility Assessment Using an Optimized Group Method of Data Handling Model. ISPRS International Journal of Geo-Information. 2020; 9(10):566. https://doi.org/10.3390/ijgi9100566
Chicago/Turabian StyleKadirhodjaev, Azam, Fatemeh Rezaie, Moung-Jin Lee, and Saro Lee. 2020. "Landslide Susceptibility Assessment Using an Optimized Group Method of Data Handling Model" ISPRS International Journal of Geo-Information 9, no. 10: 566. https://doi.org/10.3390/ijgi9100566
APA StyleKadirhodjaev, A., Rezaie, F., Lee, M.-J., & Lee, S. (2020). Landslide Susceptibility Assessment Using an Optimized Group Method of Data Handling Model. ISPRS International Journal of Geo-Information, 9(10), 566. https://doi.org/10.3390/ijgi9100566








