A Flexible Framework for Covering and Partitioning Problems in Indoor Spaces

Abstract

Utilizing indoor spaces has become important with the progress of localization and positioning technologies. Covering and partitioning problems play an important role in managing, indexing, and analyzing spatial data. In this paper, we propose a multi-stage framework for indoor space partitioning, each stage of which can be flexibly adjusted according to target applications. One of the main features of our framework is the parameterized constraint, which characterizes the properties and restrictions of unit geometries used for the covering and partitioning tasks formulated as the binary linear programs. It enables us to apply the proposed method to various problems by simply changing the constraint parameter. We present basic constraints that are widely used in many covering and partitioning problems regarding the indoor space applications along with several techniques that simplify the computation process. We apply it to particular applications, device placement and route planning problems, in order to give examples of the use of our framework in the perspective on how to design a constraint and how to use the resulting partitions. We also demonstrate the effectiveness with experimental results compared to baseline methods.

1. Motivation

With the progress of indoor location technologies such as indoor positioning [1,2,3,4] and indoor LiDAR sensors [5], the demands for computational analysis in indoor spaces have been rapidly increasing. For example, building safety managers can inspect the building structures to plan escape routes for effective evacuation in an emergency situation [6,7]. Security managers may want to find the optimal position of surveillance cameras to guard an important facility or to detect some suspicious visitors who show unusual behavior [8,9]. One can also analyze the crowd movement in the shopping mall to expose merchandise to customers effectively [10].

In order to respond to these requirements, it is important to analyze, process and manage indoor-related information effectively. The partitioning of the indoor space is one of these essential requirements when given indoor space is complex and large such as subway stations with long corridors, sophisticated shopping malls, or big convention centers. While many indoor applications have been developed based on its own partitioning problems [1,11,12], they are limited by specific assumptions and not universally applicable to other domains. This leads us to the necessity of a unified framework for indoor space partitioning.

In this paper, we present a flexible framework for indoor space partitioning in order to bridge the gaps among different partitioning methods for various applications. We especially focus on two important indoor applications: (i) device placement problem and (ii) route planning problem. However, we emphasize that our framework is not limited to these applications but it can be extended into other applications with proper settings as well.

There are many 2D and 3D models that represent geographical structures including indoor spaces. Computer-Aided Design (CAD) has widely been used for designing products and architectural structures in both 2D and 3D [13,14]. Building floorplans and their 3D geometries have also been designed and managed in CAD formats [13,14]. Building Information Modeling (BIM) format is a widely used model in constructing and managing building structures and processing 3D geometry of architectural structures [15,16]. Industry Foundation Classes (IFC) is a standardized data exchange model for this purpose [17]. CityGML [18] is a standard data exchange model for digital modeling of cities, issued by OGC. Although it mainly handles 3D geometries of city objects such as terrains, roads and buildings, it also provides 2D footprints at a certain Level-of-Detail (LOD) model. IndoorGML [19] is a data exchange model for indoor spaces, which handles geometric and topological structures and semantics for indoor applications. It handles both 2D and 3D geometries of indoor spaces. Regarding the interoperability, the compatibility with these standardized models is also important. In particular, we present the IndoorGML-compatible representation of partitioned spaces. In addition, although these models support 3D geometries, it is also common to consider 2D spaces in many applications in geographical problems [20,21]. So we focus on the covering and partitioning in 2D space in this paper.

Our contributions in this paper are listed as follows:

• a unified framework for the covering and partitioning problems in 2D spaces, which is flexible in the sense that we can obtain suitable partitions for many different problems with proper constraints.
• a binary linear programming formulation for covering and partitioning problems, which effectively find solutions for given requirements.
• a methodology for route planning based on convex partitioning. Our method is not only space efficient but also provides an IndoorGML-compatible representation. We also empirically demonstrate the effectiveness of the routing method with the proposed framework.

The remainder of this paper is organized as follows. In Section 2, we briefly review existing approaches on device placement problems and indoor navigation, which are important applications in indoor spaces. Then we give an overview of the multi-stage structure of the proposed framework for covering and partitioning tasks in Section 3. In Section 4, we look into the detail of a specific stage, named maximal expansion computation, which produces the essential input of the following stage. We address the covering problem and the partitioning problem in Section 5 and Section 6, respectively, in which we give the formulations of the binary linear programming to solve the problems. After presenting experimental results in Section 7, we discuss several issues that should be addressed for the further improvement in Section 8. Section 9 concludes the paper.

2. Related Work

In this section, we review previous studies related to our work. First we give a brief overview on the covering and partitioning problems in order to clarify the contribution of our work (see

Table 1. Problems and constraints covered by previous work.

Problem and Constraints	[22]	[23]	[24]	[25]	[26]	[27]	[28]	Ours
Range Partition	◯							◯
Convex Partition		◯						◯
Visibility Covering			◯	◯				◯
Visibility Partition					◯			◯
Range+Visibility Covering						◯		◯
Partition with Different Contraint							◯	◯
Polygon with Holes	×	◯	×	◯	×	▵	×	◯

). Then we discuss existing work on important indoor applications: device placement problem and route planning problem.

There are many work and variations on the problems of covering and partitioning polygons particularly in the field of computational geometry, and many related problems are known to be NP-hard [29,30,31]. Theoretical studies [22,24] usually deal with simple polygons because polygons with holes complicate the problem significantly. Many covering problems [24,25,28] are related to the visibility problems. However, they do not consider polygon partitions with visibility constraints. Partitioning a polygon into star shape is known to be NP-hard [30] and several algorithms for simple polygons have been presented [26,32]. Partitioning with other constraints such as range [22] and convexity [23] have also been studied. As a generic method, Buchin et al. [28] recently presented a skeleton-based polygon partitioning method that can be easily modified for different constraints but the method is limited to simple polygons without holes. Our method can be used as an off-the-shelf method that can deal with a wide range of problems with a little and simple modification; although it does not guarantee to give the optimal solution, it gives outputs with an acceptable quality as we will discuss later.

2.1. Device Placement Problems

The covering problem is one of fundamental requirements of many applications in indoor spaces. In particular, it is closely related to positioning devices, where each device has a limited effective area and we need to cover the entire indoor space with a smaller number of devices. Locating surveillance cameras is one example. For its simplest version, we may assume we have omni-cameras with an unlimited resolution so that it can observe as long as the line of sight is not disturbed. This problem is called the Art gallery problem, a well-studied problem in the field of computational geometry, which has been shown to be NP-hard even if the locations are restricted on the vertices of the polygon (see [31] for details). For realistic considerations, we may also take other factors into account such as field of view (FOV), pixel resolutions, and perspective distortion (For a comprehensive review, see [33]).

Placing sensors and beacons are also similar problems, as they also share several characteristics of the camera placement problem. Unlike outdoor spaces, signal emitting and processing devices in indoor spaces should consider the permeability and diffraction issues as there are many walls, columns and obstacles that obstruct the line of sight from the device [34]. There are also other issues regarding various device characteristics such as beacons with limited effective ranges and angular restrictions [35], and with different power levels [36].

There are also other variants regarding camera and device placement problems focusing on the target spaces as well as device characteristics. In some applications, surveillance cameras should be able to monitor important areas such as the entrances of the building and the doors of the vault room of the bank. It can be simply addressed by weighting the subregions to be covered according to their importance [37,38], which can also be applied to our framework directly.

2.2. Route Planning Problem

As indoor positioning systems have been advancing with various sensing technologies such as Wifi fingerprinting [1], light sensors [2] and Bluetooth Low Energy (BLE) beacons [3], navigation services in indoor spaces have become feasible.

Indexing indoor spaces for route planning in an efficient way is an important issue for both online service systems and data exchange. Regarding many issues including specific requirements of target applications such as dynamicity, quality assessment and the trade-off between index complexity and accuracy, there are a variety of indexing methods for navigation graphs (see [39]). Xu et al. [40] triangulated the input polygon and established a node for each triangular facet and a link between each pair of adjacent facets if it is not obstructed by indoor objects. Kruminaite et al. [11] considered the temporal dynamicity, which should find paths in peak and off-peak hours differently. They used constrained Delauney triangulation to partition the space and constructed a navigation graph by connecting centroid of adjacent facets. Habibi et al. [41] suggested a binary integer programming formulation for finding a route based on triangulated facets. They presented an objective function combining several factors including the number of facets, area and perimeter length to assess the path quality. They also used the paths connecting the middle of the edge of convex fragments. Mortari et al. [42] also presented a triangulation-based graph constructing method, which has the advantages of both methods based on the medial axis and the visibility graph. Yang et al. [43] proposed a navigation graph construction method based on Poincaré dual graph from combinatorial maps representing the indoor space.

Grid-based methods have also been widely used because of the simplicity and applicability. Lin et al. [44] presented a grid-based route planning method using A* algorithm. They used the adjacency graph representing the topology of subregions to reduce the search space. Frias et al. [45] used a grid-based method (as well as triangulation) to plan the scanning route for the task of capturing the point cloud of indoor spaces.

3. Overview

In this section, we describe the overall architecture of our framework, as illustrated in Figure 1.

We assume that the input space is represented by a polygon, which is a common setting in the literature [43,46]. Although many data models support the representation of curved geometries in their specification, the data usually consist of planar (in 3D) and polygonal (in 2D) components in practice [15]. If there are non-polygonal structures of the building such as curved walls, we can approximate them with line segments [47].

At the highest level, our method starts with splitting the input polygon into small facets and merges them into larger polygons with proper rules. We use the merged polygons as basic units of the next step that deals with the covering and partitioning problems. Each step of Figure 1 is explained below.

3.1. Edge Segmentation and Triangulation

For each boundary edge of an indoor space polygon, we split it into short segments. More specifically, given a threshold length $\theta$, we split an edge of length l into d segments where $d=\lceil l/\theta \rceil$. For example, if $\theta =5$, an edge with length 13 would be split into three line segments because $\lceil 13/5\rceil =3$. Determining the optimal value of $\theta$ depends on the target task. Among the example settings in the next section, the convexity is not sensitive to $\theta$ while the range constraint is relatively more sensitive because every triangular facet should be contained in a circle with the given constrained radius centered at the centroid. Heuristically, we can set $\theta$ according to the corridor width, e.g., half the corridor width, which provides an acceptable results without suffering from it.

Using the line segments and their vertices as constraints, we compute its constrained Delaunay triangulation. Note that we constrained only on the boundary of the input polygon, which does not produce any point in the inside of the polygon. It might produce large and long triangles, when the input polygon has a huge empty space such as a large conference hall and excessively wide corridors in its inside. For some particular settings we will discuss below, these large and long-shape triangles may produce undesired results. To avoid this, we may add more constraints such as holes inside of the polygon representing some indoor installations such as columns and quasi-stationary furniture (like tables and chairs). We may intentionally narrow the space reflecting some wall-mounted furniture to make triangles smaller and less long-shaped.

3.2. Expansion

After triangulation, we merge triangulated facets into larger polygons. Starting with a single triangular facet, we expand the region by merging it with adjacent facets. In order to determine the facets to merge, we apply a set of rules that we can control as parameters. These rules and parameters make the proposed framework flexible and more adaptable to different types of applications. By properly setting the rules and parameters, we would be able to apply appropriate a partitioning solution by reflecting the characteristics and requirements of the target applications. For example, we can use the rules of visibility constraint for the surveillance camera placement problem so that each merged polygon contains a point from which the line of sight within the polygon is completely ensured. As a result of the expansion step, a set of expanded regions is produced. Note that they may overlap with each other and we will use them to compute the optimal cover and partition in the next step. The details of this merging step will be described in the next section.

3.3. Covering and Partitioning

Now we use the set of expanded regions computed in the prior step to produce the final result for the covering or partitioning problem. In the covering problem, we are asked to find a subset of the expanded regions whose geometric union covers the entire indoor space. On the other hand, for the partitioning problem, we need to divide the indoor space into disjoint sub-regions, each of which is a subset of an expansion. Since these two problems are fundamentally similar to each other, one might use the output of one problem to compute the solution of the other problem. For example, we can find the partition of a polygon by finding its cover and distributing the shared regions properly to prevent them from overlapping. However, the distributing procedure may become too complicated especially when the resulting regions cross one another so they cut in the middle of other regions, which results in too many candidate partitions. For this reason, we consider the two problems separately by giving their respective solutions in terms of the binary linear programming formulation.

4. Maximal Expansion

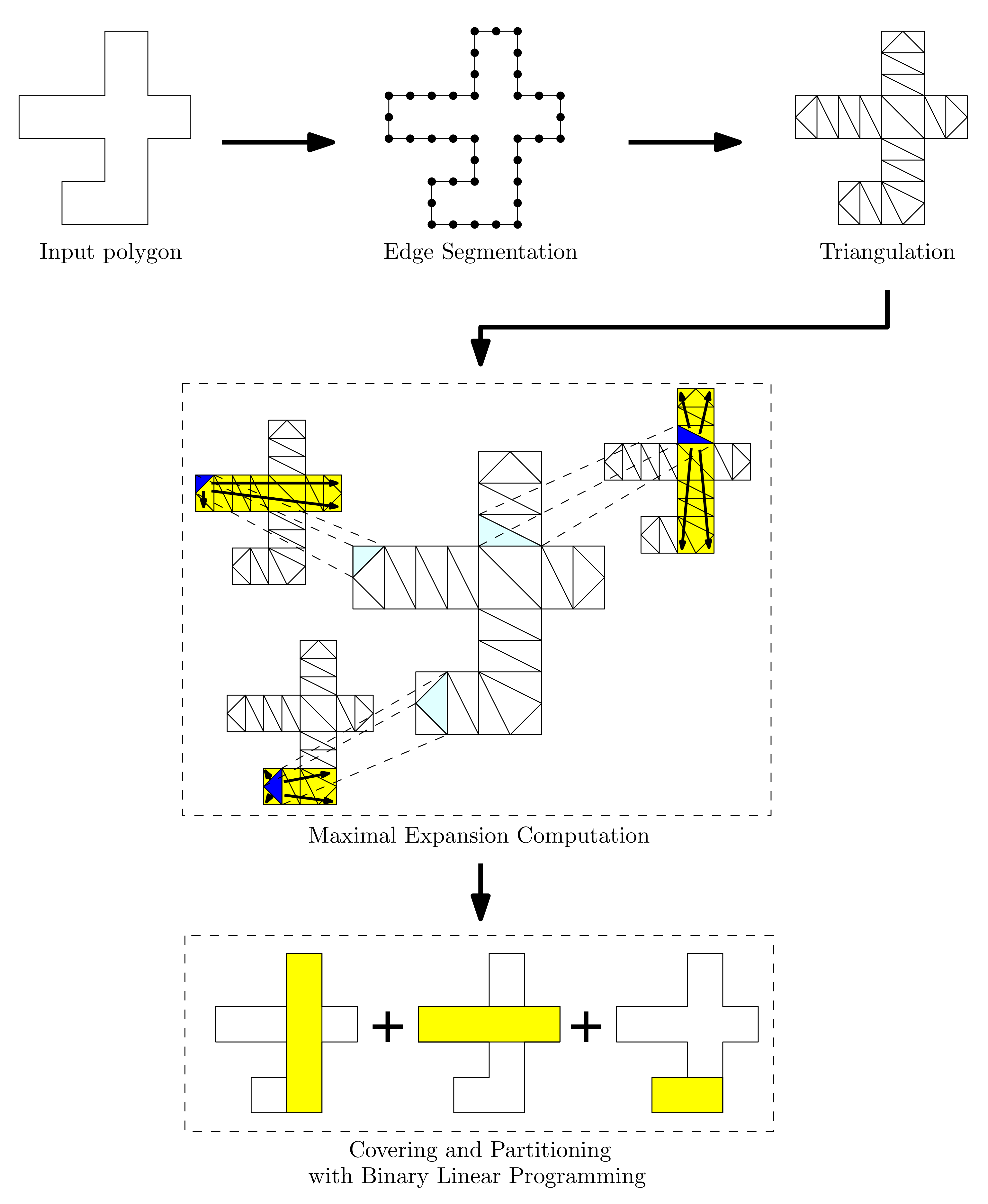
This section is dedicated to describe the notion of expansions, and the procedure to compute them. An expansion is a union of triangulated facets and it plays a role as a unit component of the binary linear programming for the final covering and partitioning task. The flexibility of our framework is based on the fact that we can make a variety of instances of expansions by setting detailed rules in computing expansions and defining a new constraint checking function. In this section, we present a simple expansion computation algorithm and several constraints that can come up in many applications in indoor spaces.

4.1. Computing Expansion

The set of triangular facets produced by constrained Delaunay triangulation is used as basic units in further covering or partitioning steps. We start from a triangular facet to merge with adjacent facets. The initial facet is called a seed facet and the merged polygon of the connected facets an expansion.

Definition 1 (Expansion).

Given a input polygon P triangulated into a set of facets$\mathcal{T}$, a set$X\subset \mathcal{T}$is an expansion from a seed facet$s\in X$if the geometric union of all facets$x\in X$forms a single (connected) polygon.

We compute the maximal expansions with seed facets in this step, and introduce a constraint checking function f in order to determine the maximality of an expansion.

Definition 2 (Maximal Expansion).

An expansion$X\subset \mathcal{T}$of a seed facet$s\in X$is maximal with respect to a constraint checking function$f:\mathcal{T}\times 2^{\mathcal{T}}\times \mathcal{T}\to \{\mathtt{true},\mathtt{false}\}$, if$f(s,X,y)$yields$\mathtt{false}$for all the facets$y\in \mathcal{T}$that are adjacent to some of currently expanded facets$x\in X$.

The computation of a maximal expansion of a seed facet is explained in detail as follows. It is done in an iterative traversal manner on the dual graph, in which each facet is denoted by a node, and two nodes are connected via a link if the corresponding facets share an edge of the facets. The iterative traversal of the graph to compute the maximal expansions is as described in Algorithm 1.

Algorithm 1 Compute maximal expansion

1: procedure Expand(s: seed facet, S: set of facets to cover: f: constraint checking function)

2: Initialize queue C

3: add an element s into queue C

4: $E\leftarrow \varphi$.

5: while $\left|C\right|>0$ do // repeat until queue C is not empty

6:  $x\leftarrow$ remove an element from queue C.

7:  if $f(s,E,t)=\mathtt{true}$ then

8:   $E\leftarrow E\cup \left\{t\right\}$

9:   For any unvisited facet $t^{\prime }$ adjacent to t, add $t^{\prime }$ into queue C

10:  end if

11: end while

12: return E

13: end procedure

This algorithm receives a seed facet as the input. Starting from the seed facet, we expand the region E by including new facets that satisfy the constraint checking function f and are adjacent with the seed facet or one of the facets in the current expansion. We assume that any seed facet satisfies the constraint as itself, i.e., $f(s,\varphi ,s)=\mathtt{true}$ for any $s\in \mathcal{T}$; otherwise the polygon may not be covered completely in some cases. When there is no more facet to include, it returns the currently merged polygon as the maximal expansion. The constraint checking function f takes three arguments: the seed facet, the current expansion, and a facet to newly add. The reason we make the function take its arguments separately is because we can define the constraint checking function in a much efficient way than the case in which the function takes only the merged geometry. If the constraint checking function $f(s,E,t)$ gives false, it means that adding t does not satisfy the condition and we do not include it to the expansion set. We repeat this task until all the adjacent facets are completely processed.

Algorithm 1 iterates all the facets and calls the constraint checking function, it runs in $\mathcal{O}\left(n\phi \right(n\left)\right)$ time where n is the number of facets and $\phi \left(n\right)$ is the time taken by the constraint checking function with at most n facets. For constraints we discuss in this paper, we have $\phi \left(n\right)=\mathcal{O}\left(1\right)$, thus Algorithm 1 runs in linear time.

We compute the maximal expansions for each facet as a seed. Then we can obtain maximal expansions as many as the number of facets. We can use these maximal expansions to get the covers or partitions using the binary linear program, which will be discussed in the next section. However, it takes a quadratic time when we iterate over all the facets as seeds, because it runs in linear time per seed facet. Alternatively, we can use only a subset of facets. We can pick $\rho n$ facets at random for some $0<\rho \le 1$ and compute their maximal expansions. We empirically show the performance of this strategy with respect to $\rho$ in Section 7.

Figure 2 illustrates the process of computing the maximal expansion of a seed facet. Suppose the given constraint is convexity, so the resulting expansion should be a convex polygon. Starting from a seed facet A as depicted in Figure 2a, we add it into the queue. In Figure 2b, two facets are adjacent to A. Since $A\cup B$ is still convex, we include B into the expansion. Again, let us assume that we choose the facet indicated by C in Figure 2c, which leads to the next state as described in Figure 2d. When we choose the facet indicated by D, the resulting expansion would form a polygon described by the thick boundary in Figure 2d, which has a concave vertex as indicated by a red circle. It violates the convexity constraint so we withdraw this selected facet. In Figure 2e, we can see that the facet is removed from the candidate facet queue (as it is not indicated by green). When we repeat this process until the queue is empty, we can obtain the maximal expansion as in Figure 2f.

Note that we can choose another green facet that satisfies the convexity constraint rather than C in Figure 2c. In this case, we may obtain a different maximal expansion. One may be afraid that we may miss some essential maximal expansions that are indispensable to cover the input polygon with the minimum cost. However, if we use a sufficient number of seed facets (possibly, all facets), these essential maximal expansions are likely to be obtained. For example, with the convexity constraint, a maximal expansion can be obtained by starting from any of facets in it. A large maximal expansion, which would be more useful for covering the space, is likely to have a large number of facets therein. It means that this maximal expansion has more seed facets from which it can be expanded. In other words, even if we fail to obtain a particular desired maximal expansion when we start the expansion from a seed facet, we still have a chance to obtain it from other seed facets.

Although we have a random choice for the simplicity here, we can use a particular strategy for the facet choice during the expansion procedure. For example, we can use a deterministic strategy that produces a unique maximal expansion from a seed facet such like choosing a facet sharing a longer edge with the current expansion. While there are many alternative options, we leave the extensive study on expansion strategies as the future work.

4.2. Constraint Design

In this subsection, we discuss the constraint checking function of Algorithm 1 in Section 4.1. As we mentioned, resulting maximal expansions, as well as covering and partitioning results, depend on what constraint is given. Thus it is important to design a constraint that fits the requirement of the target application. As examples, we present three simple constraints in this subsection, which are expected to be frequently used in many applications. We also present some tricks that efficiently evaluate the constraint checking functions, which are illustrated in Figure 3.

4.2.1. Range Constraint

First we design a constraint checking function f for the range constraint. Recall that f takes three arguments: seed facet s, current expansion E, and facet t to add, and checks if it does not violate the given constraint when we add t to E.

Because we have already triangulated the input polygon, t is a triangle, and its two vertices are on the boundary of the current expansion E. It is therefore sufficient to check if the other vertex that resides on the exterior of E within the constrained range r from s. By setting the centroid of the seed facet s as the center of the covered range, we can define the checking function $f_{\mathtt{range}}$ as follows:

$$f_{\mathtt{range}},\mathtt{r}(s,E,t)=\left\{\begin{array}{c}\mathtt{true}\mathrm{i}\mathrm{f}d(s.\mathtt{centroid},v)\le r,\hfill \\ \mathtt{false}\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.$$

(1)

where, v is the vertex of t that resides on E’s exterior, r is the constrained range.

4.2.2. Visibility Constraint

The visibility constraint forces the resulting expansion to be visible from a specific point inside the seed facet. For simplicity, we shall use the centroid of the seed facet for checking the visibility. We need to implement the constraint checking function $f_{\mathtt{vis}}(s,E,t)$ to determine whether $E\cup \left\{t\right\}$ is visible from the centroid c of triangle s.

Recall that E is expanded from s, and one edge of t, say $\overline{uv}$, is on the boundary of E and visible from c. Let us denote by w the other vertex of t. Then we can see that $E\cup \left\{t\right\}$ is visible from c if and only if two segments $\overline{uv}$ and $\overline{cw}$ intersects at a single point.

The resulting function $f_{\mathtt{vis}}$ can be defined as follows:

$$f_{\mathtt{vis}}(s,E,t)=\left\{\begin{array}{c}\mathtt{true}\mathrm{i}\mathrm{f}\overline{uv}\cap \overline{cw}\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t},\hfill \\ \mathtt{false}\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.$$

(2)

where $u,v$ are the vertices on E’s boundary, w is the vertex of t that resides on E’s exterior, and c is s’s centroid.

4.2.3. Convexity Constraint

With the convexity constraint, the resulting expansions are restricted to be convex polygons. When we expand a triangle from the current expansion polygon, two vertices of the triangle are on the boundary of the current expansion polygon. We need to check whether inserting the other vertex of the triangle into the middle of the edge produces concave angles with the resulting polygon. Let $u,v$ be these two vertices shared by the current expansion polygon and the triangle to add, and the other vertex of the triangle is denoted by w. The preceding and succeeding vertices of u and v are denoted by x and y, respectively, as shown in Figure 3c. After adding the triangle to the expansion polygon, the resulting polygon has a sequence of consecutive vertices $x\to u\to w\to v\to y$ ash shown in Figure 2c. To check the convexity, it is sufficient to determine whether $\angle \left(xuw\right)\le {180}^{\circ }$ and $\angle \left(wvy\right)\le {180}^{\circ }$. Now we define the checking function $f_{\mathtt{cvx}}$ for the convexity as follows:

$$f_{\mathtt{cvx}}(s,E,t)=\left\{\begin{array}{c}\mathtt{true} \mathrm{i}\mathrm{f}\angle \left(xuw\right)\le {180}^{\circ } \mathrm{and} \angle \left(wvy\right)\le {180}^{\circ }\hfill \\ \mathtt{false} \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\hfill \end{array}\right.$$

(3)

where u and v are common vertices of E, and w is the other vertex of the triangle t to add, and x (and y) is the preceding (and succeeding) vertex of u (and v, resp.).

5. Covering Problems

In this section, we present the binary linear program for the covering problem. The objective is to cover the input polygon using the expansions we computed in the previous section.

5.1. Problem Definition

We formally define the problem as follow. Recall that we have a set $\mathcal{X}=\left\{X_i\right\}$ of expansions computed in the previous section by expanding adjacent facets from every single seed facet. We can find a combination of expanded regions whose union contains every single facet of the underlying triangulated polygon:

Definition 3 (Cover).

Given a set$\mathcal{X}=\{X_i\subset \mathcal{T}\}$of expansions of a triangulated polygon$\mathcal{T}$, a set$\mathcal{C}\subset \mathcal{X}$is a cover of$\mathcal{T}$if${\bigcup }_{c\in \mathcal{C}}c=\mathcal{T}$.

In the minimum cover problem, we are asked to find a cover with the minimum cardinality;

Definition 4 (Minimum Cover Problem).

Minimum Cover Problem$(\mathcal{T},\mathcal{X})$asks to find a cover$\mathcal{C}$of$\mathcal{T}$under$\mathcal{X}$such that$\left|\mathcal{C}\right|\le |{\mathcal{C}}^{\prime }|$for every cover${\mathcal{C}}^{\prime }$.

In some applications, the number of devices is limited so that we are asked to locate them in order to cover the target space as much as possible. Given a subset $\mathcal{C}$ of the expansion set $\mathcal{X}=\left\{X_i\right\}$, we can measure the corresponding area by summing the area of the triangular facets in its union ${\bigcup }_{c\in \mathcal{C}}c$. With this measure, we can define the maximum coverage problem as follows;

Definition 5 (Maximum Coverage Problem).

Maximum Coverage Problem$(\mathcal{X},m)$asks to find a subset$\mathcal{C}\subset \mathcal{X}$of cardinality of m such that there exists no any size-m subset${\mathcal{C}}^{\prime }\subset \mathcal{X}$that has its corresponding area greater than$\mathcal{C}$’s.

Figure 4 illustrates the minimum cover and maximum coverage problems. Dots indicate facets, and each facet is associated with its maximal expansion with the visibility constraint. In the minimum cover problem, we need to choose the minimum number of facets so as to cover the entire polygon with their maximal expansions. We can choose the two green dots in Figure 4a, each of which is associated with expansions indicated with blue and yellow, respectively. In the maximum coverage problem, the number of seed facets is restricted. In this example, suppose we are allowed to choose only one facet. When we choose the facet indicated with the greed dot in Figure 4b, we can cover 70% of the polygon, which is the desired result.

5.2. Binary Linear Programming Formulations

Now we are ready to present the formulations of two aforementioned problems using the binary linear programming.

Minimum Cover Problem: We define binary variables $b_i$ which indicate an expansion $X_i\in \mathcal{X}$ is chosen. A facet $t\in \mathcal{T}$ is covered by at least one expansion. In other words, for every $t\in \mathcal{T}$, there must be i such that $b_i=1$ and $t\in X_i$. Since we want to minimize the number of expansions, we finally obtain the following binary linear program:

$$\begin{array}{cc}\hfill \mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}& \sum _i{b}_i\hfill \\ \hfill \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& \sum _{i:t\in X_i}{b}_i\ge 1\mathrm{for}\forall t\in \mathcal{T}.\hfill \end{array}$$

(4)

Maximum Coverage Problem: Similarly, binary variables $b_i$ indicate $X_i\in \mathcal{X}$ is chosen. We introduce another set of binary variables $a_j$ to indicate a facet $t_j\in \mathcal{T}$ is covered by at least one $X_i$. We want to maximize the sum of the area of covered facets, and we have the following binary linear program:

$$\begin{array}{cc}\hfill \mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}& \sum _j\mathtt{area}\left(t_j\right)a_j\hfill \\ \hfill \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& \sum _{i:t_j\in X_i}{b}_i\ge a_j\mathrm{for}\forall j\hfill \\ \hfill & \sum _i{b}_i=m\hfill \end{array}$$

(5)

Figure 5 illustrates the formulation. Each facet $t_j$ is associated with the facets $t_{i_k}$ such that the maximal expansion $X_{i_k}$ whose seed facet is $t_{i_k}$ contains the facet $t_j$. In the minimum cover problem, at least one of $t_{i_k}$ should be selected while the number of selected facets be minimized. In the maximum coverage problem, the weighted sum of covered facets should be maximized.

5.3. Covering Example

In this subsection, we give several results of our experiments to show how different results are produced by different settings. We used a floor of a building in our university campus as shown in Figure 6a and its fine-grained triangulation is shown in Figure 6b. We performed the covering task described earlier on this input polygon.

Figure 7a shows the results of the minimum number of covers with different constraints: visibility and range. We applied the binary linear programming to solve the minimum cover problem and the maximum coverage problem defined in the previous subsection. Red dots indicate the centroid of the seed facets that are chosen to cover the input polygon. These points can be used as the actual placement of sensors and surveillance cameras.

Figure 7b shows the maximum coverage with a limited number of devices. Regions colored by gray indicate the uncovered area. This particular problem can be used for such applications like the Wi-Fi access point placement with a limited number of devices, and the surveillance camera placement with a limited number of cameras.

5.4. Application: Device Placement Problem

The device placement problem is a direct application of the covering problem. We need to locate the optimal positions of devices that have a limited effective area. In the minimum cover problem, we need to minimize the number of devices to cover the entire space (input polygon). On the other hand, in the maximum coverage problem, we have a limited number of devices and we are asked to cover the space using them as much as possible. Depending on the characteristics of an effective area of devices, we can design their appropriate constraints.

Table 2. Example constraints with respect to device characteristics.

Device	Characteristics	Constraint
Sensor, beacon, Wi-Fi AP	radius, non-penetrating, diffraction	Range
Camera	omni-directional, unlimited resolution	Visibility
Camera	omni-directional, limited resolution	Visibility + Range
Camera	limited FoV, limited resolution	Visibility + Range + Angle

shows examples of constraints according to the device characteristics. For example, we can use the range constraint we have presented earlier for the devices that can send signals within a limited range and the signals cannot penetrate but can detour walls. For surveillance cameras, we can use the visibility constraint if we do not consider its direction and resolution. Omni-directional cameras with a limited resolution can be modeled with the combination of two constraints, visibility and range. If we take into account the field of view, we may design a new constraint considering the direction and angle.

6. Partitioning Problems

6.1. Problem Definitions

Partitioning is one of the most effective methods to represent the space itself and its related information. Many spatial data structures and methodologies have been proposed for space partitioning. The difference between the covering problem and the partitioning problem is that each facet should be covered by exactly one expansion in the partitioning problem; i.e., no overlap is allowed among selected expansions. While we have computed maximal expansions, merely selecting some maximal expansions that cover the target polygon would result in overlap. To avoid the overlap, we need to properly specify one expansion for each facet if the facet can be covered by multiple numbers of selected expansions.

Figure 8 illustrates the difference between the covering and partitioning problems. In the covering problem, a facet can be covered by more than one expansions. In Figure 8a, two facets at the intersection point of two corridors are covered by two expansions. However, the partition problem does not allow any facet to be covered by more than one expansion. For each of the facets that can be covered by many expansions, we need to decide which single expansion should cover it. This decision of covered expansion may make another expansion separated. Because we shall control the number of partitions with the number of selected seed facets, the isolated part that does not contain the seed facet should not be considered as covered by the disconnected expansion, and the facets therein should be covered by some other expansions. We should consider this connectivity in the partitioning problem, which leads us to the following notion.

Definition 6 (Connected Partial Expansion).

Given an expansion X from a seed facet s, a subset$Y\subset X$is its connected partial expansion if$s\in Y$and the geometric union of facets$y_i\in Y$form a single polygon.

We consider the process of deciding the covered expansion of a facet as taking a subset of each of selected expansions, so that each subsetted expansion is connected and contains its seed facet. For example, if we have a facet with its maximal expansion X as in Figure 9a, the region indicated with A in Figure 9b is its connected partial expansion. If we use A to cover the polygon, the remaining part of the original maximal expansion should be covered by connected partial expansions of other expansions. B is not a connected partial expansion of X because it does not contain the seed facet, which is represented by a green dot in Figure 9a. $A\cup B$ is not X’s connected partial expansion because it is not connected.

Now we can consider a partition which is obtained by choosing some expansions, and subsetting them so that each of these disjoint facet sets has the corresponding seed facet and its connected facets:

Definition 7 (Induced Partition).

Given a set$\mathcal{X}$of expansions of a triangulated polygon$\mathcal{T}$, a set$\mathcal{Y}=\{Y_1,\cdots ,Y_m\}$is said to be induced partition if$Y_i\cap Y_j=\varphi$for all$i\ne j$and${\bigcup }_i{Y}_i=\mathcal{T}$.

Based on this definition, we can define the minimum partition problem and the maximum coverage problem as the following:

Definition 8 (Minimum Partition Problem).

Minimum Partition Problem$(\mathcal{T},\mathcal{X})$asks to find an induced partition$\mathcal{Y}$of$\mathcal{X}$with the minimum cardinality.

Definition 9 (Maximum Coverage Partition Problem).

Maximum Coverage Partition Problem$(\mathcal{X},m)$asks to find an induced partition$\mathcal{Y}$of$\mathcal{X}$such that$\left|\mathcal{Y}\right|=m$and there does not exists an induced partition${\mathcal{Y}}^{\prime }$of size m such that$\mathtt{area}\left(\mathcal{Y}\right)<\mathtt{area}\left({\mathcal{Y}}^{\prime }\right)$, where$\mathtt{area}(·)$is the sum of the area of the facets in the set.

6.2. Binary Linear Program for General Cases

We first present the binary linear program that can be used without any restriction under the proposed framework. Thereafter, we propose a simpler formulation for a special case where expansions have a special property called acyclicity in the following subsection.

Let $b_j^{\left(i\right)}$ be binary variables indicating a facet $t_j\in \mathcal{T}$ is covered by an expansion $X_i\in \mathcal{X}$. $b_i^{\left(i\right)}$ is a seed facet with its corresponding expansion, and it can be 1 by itself. For other variables $b_k^{\left(i\right)}$ for $k\ne i$, its value can be set to 1 only if there exists j such that $t_j$ is an adjacent facet to $t_k$ and $b_j^{\left(i\right)}=1$. It works as like we expand the regions from the seed facet into its adjacent facets repeatedly again. To describe this, let $w_{j,k}^{\left(i\right)}$ be also binary variables to indicate whether facet $t_j$ can affect its adjacent $t_k$ on the expansion $X_i$; in other words, for any $k\ne i$, $b_k^{\left(i\right)}$ can be 1 only if $b_j^{\left(i\right)}=1$ and $w_{j,k}^{\left(i\right)}=1$.

$$\begin{array}{cc}\hfill \mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}& \sum _i{b}_i^{\left(i\right)}\hfill \\ \hfill \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& \sum _i{b}_j^{\left(i\right)}=1for\forall j\hfill \\ \hfill & w_{j,k}^{\left(i\right)}\le b_j^{\left(i\right)}for\forall i,j,\forall (j,k)\in A\left(j\right)\hfill \\ \hfill & \sum _{(j,k)\in A\left(k\right)}{w}_{j,k}^{\left(i\right)}\ge b_k^{\left(i\right)}for\forall k,i\ne k\hfill \\ \hfill & \sum _j{x}_{j,k}^{\left(i\right)}+y_{k,j}^{\left(i\right)}<2-ϵfor\forall i,k\hfill \\ \hfill & x_{j,k}^{\left(i\right)}+y_{k,j}^{\left(i\right)}=2w_{j,k}^{\left(i\right)}for\forall i,j,k\hfill \end{array}$$

(6)

where $A\left(k\right)$ is the set of all pairs $(j,k)$ such that $t_j$ and $t_k$ are adjacent facets.

Figure 10 illustrates the presented binary linear program. Each facet $t_j$ has a variable $b_j^{\left(i\right)}$’ if it can be covered by a maximal expansion whose seed facet is $t_i$. For adjacent facets $t_j$ and $t_k$, variable $w_{k,j}^{\left(i\right)}$ is associated with an edge from $t_k$ to $t_j$. It can be set only if $b_k^{\left(i\right)}$ is set, and $b_j^{\left(i\right)}$ can be set only if at least one variables for its incoming edges is set.

The first constraint $({\sum }_i{b}_j^{\left(i\right)}=1)$ forces each facet to belong to exactly one expansion so that the chosen expansions form a partition of the input polygon. The second constraint $(w_{j,k}^{\left(i\right)}\le b_j^{\left(i\right)})$ is about outgoing edge; $w_{j,k}^{\left(i\right)}$ can be set to 1 only if $b_j^{\left(i\right)}$ so that $b_j^{\left(i\right)}$’s values can propagate along only the activated variables. The third one $({\sum }_{(j,k)\in A\left(k\right)}{w}_{j,k}^{\left(i\right)}\ge b_k^{\left(i\right)})$ is a constraint on incoming edges of non-seed facets. $b_k^{\left(i\right)}$ can be set to 1 only if at least one of its incoming edge are activated. The last two constraints (${\sum }_j{x}_{j,k}^{\left(i\right)}+y_{k,j}^{\left(i\right)}<2-ϵ$ and $x_{j,k}^{\left(i\right)}+y_{k,j}^{\left(i\right)}=2w_{j,k}^{\left(i\right)}$) are to prevent cycles of the flow formed by $w_{j,k}^{\left(i\right)}$. Without these constraints, when $w_{j,k}^{\left(i\right)}$ forms a cycle, it does not violate the above constraints (except the cycle checking ones) even if the seed facet is disconnected from the cycle, which may produce an undesired partition.

Although this binary linear programming theoretically can find the solution for the minimum partition problem, it takes too much cost especially with the constraints for the cycle elimination. If it is guaranteed that there are no cycles in the expansion, we can simplify the formulation further.

6.3. Simpler Binary Linear Program for Special Cases: Acyclic Expansion

Before developing a solution for the cases having no cycles in the expansions, let us start from its underlying graph formed by the adjacency of the triangulated facets that comprise an expansion.

Definition 10 (Adjacency Graph).

The adjacency graph$G_i$of an expansion$X_i$is a planar graph whose node set is$X_i$, and links are established between two nodes$t_j$and$t_k$if the corresponding facets of the two nodes share an edge.

Definition 11 (Acyclic Expansion).

An expansion$X_i$is said to be acyclic if its adjacency graph is a tree.

Recall that we constrained only on the boundary of the input polygon when it is triangulated. Thus all the vertices of triangulated facets are located on the boundary of the input polygon. This leads us to the fact that, for a simple polygon without holes, the adjacency graph of its triangulation is a tree. Since an expansion $X_i$ is a subset of the triangulated facets, its adjacency graph is essentially a subtree of the tree of the entire polygon, which naturally leads to us to the following:

Example 1 (Simple Polygon).

Any expansion of a simple polygon is acyclic.

Even if the input polygon has holes inside it, the vertices of triangulated facets are still located on the exterior or interior boundaries, not inside the polygon. The constraint (e.g., convexity and visibility) used in obtaining the expansions can make them acyclic. For example, when we compute the expansions with the visibility constraint mentioned in (2), the resulting adjacent graph cannot have a cycle. Once a node branches into more than one child nodes, there must be a boundary of the polygon at the intersection. This means the line of sight from the centroid of the seed facet is blocked by this boundary, and the branched paths cannot be joined anymore.

Example 2 (Visibility Constraint).

Any expansion with the visibility constraint is acyclic.

Since the convexity constraint is a stronger constraint than the visibility, it is also applied to it as well.

Example 3 (Convexity Constraint).

Any expansion with the convexity constraint is acyclic.

Let $X_i\in \mathcal{X}$ be a maximal expansion from a facet $t_i\in \mathcal{T}$. Let us assume that all the given expansions are acyclic. Then the adjacency graph of expansion is represented as a tree. Letting $t_i$ be the root of the tree derived from $X_i$, we can define the edge set $E_i$ of this rooted tree:

$$E_i=\{(j,k):t_j\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{f}{t}_k\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{o}\mathrm{f}{X}_i\}.$$

(7)

Now we are ready to formulate the binary linear program for the partition problems.

Minimum Partition Problem: Let $b_j^{\left(i\right)}$ be binary variables indicating $t_j$ is activated for the expansion $X_i$. This activation is propagated along the edges $E_i$. The seed facet $t_i$ is the root node and it does not have any incoming edges; thus $b_i^{\left(i\right)}$ can be activated by itself. The remainder facets in the expansion $X_i$ can be activated only if its parent facet on the rooted tree formed by $E_i$ is activated. Each facet should be activated only for one expansion. Now we have the following formulation:

$$\begin{array}{cc}\hfill \mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}& \sum _i{b}_i^{\left(i\right)}\hfill \\ \hfill \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& \sum _i{b}_j^{\left(i\right)}=1for\forall j\hfill \\ \hfill & b_j^{\left(i\right)}\ge b_k^{\left(i\right)}for\forall i,\forall (j,k)\in E_i\hfill \end{array}$$

(8)

Maximum Coverage Partition Problem: For the maximum coverage partition problem, we can easily derive the formulation by applying small changes from the previous binary linear program. It is obvious to replace the objective function to maximize the sum of the activated facets. For the first constraint (${\sum }_i{b}_j^{\left(i\right)}\le 1$), we replace the equation with an inequality since not all facets have to be activated. Finally, adding the constraint (${\sum }_i{b}_i^{\left(i\right)}\le m$) about the number of partitions completes the formulation:

$$\begin{array}{cc}\hfill \mathrm{M}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}& \sum _{i,j:t_j\in X_i}\mathtt{area}\left(t_j\right)b_j^{\left(i\right)}\hfill \\ \hfill \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}& \sum _i{b}_j^{\left(i\right)}\le 1for\forall j\hfill \\ \hfill & b_j^{\left(i\right)}\ge b_k^{\left(i\right)}for\forall i,\forall (j,k)\in E_i\hfill \\ \hfill & \sum _i{b}_i^{\left(i\right)}\le m\hfill \end{array}$$

(9)

6.4. Partitioning Examples

Figure 11 shows the minimum number of partitions computed by the proposed method. Compared to the minimum cover shown in Figure 7, regions covered by a single seed facet is completely connected. We indicate the selected seed facet by red dots for the range constraint case. Supposing we use this method for the Wi-Fi access point placement, it seems to give a more intuitive description for finding which Wi-Fi access point covers a specific area compared to the simple minimum covering result, which may involve so many discontiguous regions assigned to a single access point. We can observe that the resulting partitioning is likely to represent the actual semantic units of the building such as rooms and corridors.

6.5. Application to Route Planning Problem

6.5.1. Route Planning with Convex Partition

We present a method to find the path on a polygon decomposed into convex partitions. Although the resulting path is not the optimal shortest path, it is a compromising method for representing the underlying graph structure for pathfinding in a space-efficient way without a significant sacrifice of its optimality as we will empirically show in Section 7.

The basic idea is simple. We find the shortest path in the partition level, then we compute the actual path. This hierarchical pathfinding strategy is widely used, particularly for game AIs although their specific details are different. We use the following strategy for locating the actual path: moving forward to the closest point to the next cell. Figure 12 illustrates this procedure. This is based on the fact that the shortest path between any two points in a convex polygon is the straight line. One may want to use the centroid of cells for the actual path, but merely connecting the centroids of neighboring cells on the path found from the adjacency graph would not guarantee that the line segments of the actual path are contained in the input polygon. In addition, at the beginning and the end of the resulting path, connecting actual start/target points to the centroid of the first and last cells along the path may cause an unnecessarily long path. Although our proposed method to compute the actual path can be improved further, we present its simplest version and leave a further discussion in the future work.

The procedure for the detailed task is described in Algorithm 2. Let us assume we are given a set $\Pi$ of convex polygons and query points s and t representing the start and destination points, respectively. At the first stage, we construct the graph $G=(V,E)$ where the set V of nodes represents partitioned polygons, and the set E of links indicates their adjacency. Then we find the shortest path on this graph. Let u and v be the corresponding nodes to the partitions $s\in P_u$ and $t\in P_v$. The shortest path on the graph gives us the sequence $(u=w_1,w_2,\cdots ,w_n=v)$ of nodes, which means the partitions $\left(P_{w_i}\right)$ the resulting path should pass through. Now we compute the exact path $(s=p_1,p_2,\cdots ,p_n,p_{n+1}=t)$ in terms of geometric points. The invariant in computing the exact path is that $p_i$ belongs to the i-th partition $P_{w_i}$ at step i. We calculate the point $p_{i+1}$ to reach to the next partition $P_{w_{i+1}}$. This point $p_{i+1}$ is a point on the intersection of two partitions $P_{w_i}$ and $P_{w_{i+1}}$, which is a line segment, and we can simply obtain this point by calculating the nearest point on the line segment from $p_i$. Because these both points $p_i$ and $p_{i+1}$ are inside of convex polygon $P_{w_i}$, the segment connecting the two points is naturally inside of $P_{w_i}$. At the final step, we have $p_n$ on the boundary of $P_{w_n}$, which also contains the destination point t. Connecting two points $p_n$ and t completes the resulting path.

Algorithm 2 Finding a Path on Convex-Decomposed Polygon

1: procedure Find($\Pi$: Convex Partition of a polygon, s: Starting Point, t: Destination)

2: Compute G regarding the adjacency of polygons in the partition $\Pi$.

3: Find nodes u and v corresponding to s and t, respectively.

4: Find the shortest path $(u=w_1,w_2,\cdots ,w_n=v)$ on G.

5: $p\leftarrow s$

6: $R\leftarrow$[ ]

7: for $i\in \{1,\cdots ,n-1\}$ do

8:  $l\leftarrow P_{w_i}\cap P_{w_{i+1}}$

9:  Find the nearest point q on l from p.

10:  R.add(Line($p,q$))

11:  $p\leftarrow q$.

12: end for

13: R.add(Line($p,t$))

14: return R

15: end procedure)

Let $\Pi$ be the set of m convex polygons decomposed by the partitioning task. When we compute the adjacency graph G from $\Pi$ in Line 2, we can determine the adjacency of two partitions (cells) by checking if they share any vertex. Using a hash table keyed with the vertex index, it takes $\mathcal{O}\left(v\right)$ time where v is the sum of the number of vertices of partitioned polygons. Finding the corresponding nodes in Line 3 also takes $\mathcal{O}\left(v\right)$ time because we can perform a point-in-polygon query in linear time to the number of vertices of a polygon. We denote by $f(\Pi )$ the time taken in finding the shortest path in the adjacency graph induced from $\Pi$. If we use the Dijkstra algorithm to find the shortest path, $f(\Pi )=\mathcal{O}(mlgm)$, because the time complexity of Dijkstra algorithm is $\mathcal{O}(e+mlgm)$ where e and m are the number of edges and vertices of the given graph, and $e\le 3v-6$ due to the planarity. For each iteration of the loop, the actual path computation runs in $\mathcal{O}\left(n\right)$ time where n is the path length on the adjacency graph. Because $n=O\left(m\right)$, the loop part runs in $\mathcal{O}\left(m\right)$ time. Putting this all together, Algorithm 2 takes $\mathcal{O}(v+mlgm)$ where m is the number of polygons in $\Pi$ and v is the sum of the number of vertices over polygons in $\Pi$.

6.5.2. IndoorGML Compatibility

As an international standard published by Open Geospatial Consortium, IndoorGML provides a well-defined data exchange model for indoor spaces [19]. It adopts the space model as a set of non-overlapping subspaces, which are essentially partitions of the underlying space. Each geometric or semantic partition is modeled as a cellular space named CellSpace, and CellSpaceBoundary represents a boundary geometry such as doors and windows of a CellSpace. As its Poincaré dual space, IndoorGML also describe the topological information using the graph structure with State for nodes and Transition for links.

The proposed pathfinding method based on the convexity partitioning is compatible with IndoorGML while other indexing methods usually represent the navigation graphs separately from the CellSpace geometry. As a matter of fact, any partitioned space with other constraints such as range and visibility can be represented in the same way although their applicability is unclear.

Table 3. Corresponding concepts between proposedpathfinding method and IndoorGML.

Components	IndoorGML
Partition (Polygon)	CellSpace
Intersection of Adjacent Polygons	CellSpaceBoundary
Node in Partition-level Graph	State
Link in Partition-level Graph	Transition

shows the correspondence between the partition-based index for pathfinding and the IndoorGML concepts.

Figure 13 shows an example of representing the partitioned spaces using IndoorGML. For each semantic cellular spaces, we can subspace it into convex subregions. Each of the subregions is represented as a CellSpace, and their shared boundaries are to be CellSpaceBoundarys. The nodes and edges in the adjacency graph of the partitions correspond to States and Transitions in terms of IndoorGML concepts. In order to make the association between the newly created partitioned space and the underlying building space, we establish InterLayerConnections between the original State and the States of its partitioned subregions.

7. Experimental Results

We conducted experiments with various settings to assess the effectiveness of our framework in a quantitative way. We performed the covering and partitioning tasks with our framework using synthetically generated data, and compared them to several baseline methods.

7.1. Settings

For assessing the effectiveness of the proposed method in a quantitative way, we constructed three different types of synthetic datasets as described in Figure 14.

Remind that the covering and partitioning problems are NP-hard problems in general so it is infeasible to obtain the optimal solution. These synthetic data sets are designed for the purpose with which we can simply get intuitive solutions that are at least promising as baselines. The first type is a single long corridor as shown in Figure 14a; a corridor consists of a small number of short axis-aligned segments. The second type has additional short sub-corridors along with a long main corridor as shown in Figure 14b. The third type has a hall at the center and several corridors extended radially as shown in Figure 14c. We generated them with the following procedure. For type 1, we generated 5–8 random connected axis-aligned segments of length ranged from 9 m to 60 m, then we applied a buffering operation with 1.5 m, which produces a long 3 m wide hallway. For type 2, we generated 3 random connected axis-aligned segments of length ranged from 6 m to 60 m. Then we generated segments of length ranged from 6 m to 12 m as branches perpendicular to the main segment. Then we applied buffering operations on them in the same way. For type 3, we generated a circle of radius of 6 m, and simplified it into line segments. Then we generated a 1 m wide branches of length ranged from 15 m to 30 m that extends from the center of the circle radially. We generated 100 instances for each type and conducted the experiments so that we can measure the performance by averaging over them. We stored them in a json format described as follows:

{’vertices’: [[1.5,52.5],[-40.2,52.5],[-40.2,89.7],[-6.6,89.7],[-6.6,57.9],

        [19.2,57.9],[19.2,60.9],[-3.6,60.9],[-3.6,92.7],[-43.2,92.7],

        [-43.2,49.5],[-1.5,49.5],[-1.5,-1.5],[1.5,-1.5]],

’segments’: [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6],[6,7],[7,8],[8,9],[10,11],

       [11,12],[12,13],[13,0]],

’holes’:[]}

All the algorithms are implemented in Python 3. We used Shapely package for handling the geometry such as the synthetic data generation. We used triangle package for the constrained Delaunay triangulation. We used CBC(COIN-OR branch and Cut) as the binary linear program solver provided by pulp library to find the solution of the formula described in Section 5 and Section 6. Each of four stages is implemented as a separate module and the output of the module of a stage is consumed as the input of the module of its next stage, which comprises a pipeline of the whole framework. Each module takes its own arguments for the specific settings so that we can combine them flexibly according to the desired tasks. We conducted several experiments on various settings regarding the device placement problem for the assessment of the performance of the covering task. We also ran an experiment on the route planning problem as an application of the partitioning task.

7.2. Seed Sampling

We first conduct an experiment on seed sampling discussed in Section 4. Because we do not need to compute maximal expansions from unnecessarily many seed facets to cover the input polygon, we may choose an alternative strategy that chooses a part of facets to be the seeds. The experiment in this subsection shows how the covering performance is affected by the ratio of the portion of seed facets. First, we perform the minimum cover task with all facets as seeds to determine the minimum number k of expansions to cover the input solution using our framework. We choose $\rho n$ seed facets where $0<\rho \le 1$ is a parameter and n is the number of all facets, and compute the maximal expansions of the selected seed facets. If we use only portion of seed facets (with their maximal expansions), it is not guaranteed that all the facets can be covered by at least one of the maximal expansions of selected seed facets. Although we may use some heuristics to avoid the uncovered facets, e.g., using heuristic algorithms for the hitting set problem, we use the simplest strategy that randomly chooses the seed facets. Rather, we perform the maximum coverage task with k covers with the selected seed facets. The result shows how much it can cover the input polygon with a small portion of seed facets compared to the best solution the framework can give.

Table 4. Coverage performance with respect to the seed facet ratio.

Dataset	Constraint	$\mathit{\rho }$
		0.1	0.2	0.3
1	Range	0.949	0.985	0.993
	Convexity	0.994	0.999	0.999
	Visibility	0.897	0.956	0.985
2	Range	0.967	0.991	0.997
	Convexity	0.936	0.996	0.999
	Visibility	0.946	0.982	0.993
3	Range	0.934	0.978	0.990
	Convexity	0.928	0.985	0.995
	Visibility	0.659	0.756	0.800

shows the experimental results. The values indicate the ratio of the covered area with k covers with sampled seeds to the total area of the input polygon. For example, when we perform the maximum coverage task on dataset 1 with the range coverage with using 10% of the facets as seeds, we can cover 94.9% of the input polygon at average. For the cases with the visibility constraint in dataset 3, we can see relatively lower coverages. In dataset 3, there is a large hall at the center. The triangular facets in the center are important to cover the entire polygon because a seed facet in a branch has visibility only through that branch, and it cannot expand to the center. If some of the facets at the center are missing in the random choice of seed facets, it would reduce the coverage as a result. Nevertheless, we can observe that 90% of the input polygons can be covered only with 10% of the facets to be chosen as seeds in other settings, which means we can reduce the time for computing the maximal expansions. The time for solving the binary linear program can also be reduced because of the number of parameters for the program formula decrease. While we checked only the random choice, a better strategy of choosing seed facets should be addressed in the future work.

7.3. Device Placement Problems

We consider a covering problem with a radius constraint such as the sensor placement problem. The target space is almost linearly extended so we can expect a near-optimal number of sensors with radius r to cover the space to be $\lceil l/2r\rceil$ where l is the length of the corridor, as we covers the line of the central axis of the polygon with circles of radius r. It can be approximated by using the perimeter p of the input polygon and the corridor width w: $l\approx (p-2w)/2$. Note that the baseline is not actually optimal because we consider only the central axis of the input polygon. Rather, we use this baseline in order to simply estimate the number of required covers.

Table 5. Experiments on the minimum cover with a range constraint ($l\approx 2183.5$, $w=30$).

Radius r	Baseline($\lceil \mathit{l}/2\mathit{r}\rceil$)	Number of Covers Produced
50	22.34	26.40
100	11.44	11.60
200	5.92	5.41

shows the number of covers produced by the proposed method. When r is small, we need a larger number of covers than the baseline. This is because an actual solution should cover not only the central axis but also the whole polygon area. When r becomes larger, we need a smaller number of covers as a cover at a corner may envelop a larger portion of the central axis than merely $2r$.

We can also consider the visibility constraint such as the art gallery problem. It is known that $\lfloor n/3\rfloor$ guards are sufficient in this problem [48], but the optimal number of guards has been shown to be NP-Hard as we mentioned. However, in this data set, we can think of a simple solution by placing a guard at several corners so that each guard can cover two short segments. As the number of segments can be computed using the number of vertices of the input polygon $(n-2)/2$, the number of guards would be $(n-2)/4$, where n is the number of vertices. As shown in

Table 6. Experiments on the minimum cover with a visibility constraint.

Dataset	n	Upper bound($\lfloor \mathit{n}/3\rfloor$)	Baseline	Number of Covers Produced
Type 1	14.78	4.67	3.43	3.43
Type 2	52.95	17.36	10.96	10.91
Type 3	28.16	9.04	1.00	1.63

, we could obtained the optimal number of guards to cover the input polygons of type 1.

With the second dataset, which has a number of sub-corridors along with a main long corridor, guards should be placed properly in order to cover all the sub-corridors. If none of two sub-corridors are visible from each other, we need as many guards as the number of sub-corridors. As shown in Table 6, we observe that a little bit less number of guards are needed compared to the baseline. This is because one guard can cover two sub-corridors in some cases, especially when they are located at a corner.

For the third dataset, which has a star-shaped structure, we need only one guard at the center of the hall. However, we used the centroid of the seed facet for checking the constraints during the computation of the maximal expansions, which actually restricts the feasible guard positions so that we may not be able to place the guard properly. It causes that only one guard is not sufficient to cover the whole input space in some cases as we can see from Table 6. We may improve our placement strategy rather than choosing the centroid of the seed facet, but we will leave it as future work. We measured the average coverage with respect to the number of guards increases as shown in

Table 7. Experiments on the maximum cover with a visibility constraint.

Number of Covers	Coverage
1	0.890
2	0.992
3	0.999

. We could observe that one guard can cover 89% of the input polygon even though we need more guards due to the limited placement of the guard to the centroid. However, we can also observe that one additional guard can cover more than 99% of the area of the input polygons at average.

To show the performance compared to the optimal solution further, we conducted additional comparative experiments with a recent existing work [25] dedicated to the Art Gallery problem. This approach gives the optimal solution and they provide several testbench datasets. We used datasets of random orthogonal polygons and random simple polygons, each of which contains 30 instances of random polygons with various numbers of vertices. In

Table 8. Comparison with the optimal solution.

Dataset	n	Optimal [25]	Ratio	Difference
Ortho	20	2.967	1.052	0.133
	40	5.800	1.052	0.267
	60	9.067	1.074	0.633
	80	11.567	1.071	0.800
	100	14.633	1.086	1.233
Random	20	3.067	1.228	0.633
	40	5.700	1.213	1.167
	60	8.100	1.204	1.567
	80	10.800	1.201	2.133
	100	13.167	1.226	2.900

, we listed the optimal solution (the minimum number of guards) obtained by [25]’s work, and the performance of covering result computed by our framework in terms of average ratio and average difference to the optimal solution. For orthogonal polygons with 100 vertices, our results used 8% more guards in terms of ratio to the optimal solution, and 1.233 more guards in terms of the absolute number of guards. We observe that our framework performs better for orthogonal polygons than simple polygons, which is actually common in many indoor spaces. For random simple polygons, which are not natural for real-world cases, our framework uses about 20% more guards to cover the entire polygon. Nevertheless, when we perform the linear regression on the number of vertices and the number of additional guards, we use 0.0275 additional guards with respect to the number of vertices, which we consider to be quite acceptable. Note that our framework is not dedicated to this particular problem, thus the purpose of this experiment is to show how our method can be applied to this problem without significantly sacrificing the solution quality.

7.4. Route Planning Problem

In this subsection, we demonstrate the effectiveness of the proposed route planning method. The emphasis of this experiment is on the fact that the proposed method can store the network information for indoor navigation efficiently without degradation of the quality of the route planning tasks.

We generated 1000 random point pairs in each of input polygons, and searched the path between the query points. We assessed the resulting path by considering two measures. The path length is an essential measure because it is desirable in many applications for the path to be the shortest. In robot navigation, the number of turns is also an important measure because turning a robot involves additional operation consuming time and energy. We also measured the number of nodes and edges of the underlying network that is used to search the routes. We compared the results of the proposed method with the grid-based network, which are widely used for the pathfinding tasks in the literature [39,44,45], as well as the shortest path in the input polygons. For the grid-based network, we placed nodes on a rectangular grid and established the edges to 8 neighbors for each node. We used two grid sizes $g=0.5$ m and $g=1.0$ m.

Table 9. Experimental results on the route planning task.

Method	Dataset
	Type 1		Type 2		Type 3
	Length	Turns	Length	Turns	Length	Turns
Shortest	673.48	1.95	330.97	1.59	181.60	0.84
Grid-based Network $(g=0.5)$	691.53	4.94	347.18	5.74	196.57	8.79
Grid-based Network $(g=1.0)$	703.52	6.28	353.90	5.36	201.57	6.39
Proposed Method	683.96	2.03	339.10	1.93	188.25	1.64

shows the comparative evaluation of the resulting paths. The proposed method using the convex partition achieved a better performance than the grid-based method in terms of both the path length and the number of turns. The average path length of the proposed was longer but no more than 4% of the optimal shortest path.

Table 10. Average graph size for the route planning task.

Method	Dataset
	Type 1		Type 2		Type 3
	Nodes	Edges	Nodes	Edges	Nodes	Edges
Shortest	5.39	8.78	24.61	286.10	11.59	103.9
Grid-based Network $(g=0.5)$	2420.08	18,315.22	2430.39	17,044.82	1793.16	12,836.6
Grid-based Network $(g=1.0)$	637.15	3780.88	589.92	1769.84	448.67	2842.82
Proposed Method	6.39	10.78	14.60	28.30	9.86	24.68

shows the graph size for each method. As we can expect, the grid-based network consumes an excessively large space, as we they need a lot of nodes and edges. The proposed method needs only a convex partition and its connectivity, which is more efficient in terms of the graph size.

8. Discussion

There are several issues that can be computationally improved. Although we have presented an improved formulation under a certain condition, the binary linear programming itself may be costly when we handle a huge volume of data. For the scalability, we may develop an efficient algorithm for the covering and partitioning stage. The pivotal point of the seed facet used in the expansion computation stage can be improved so that we can achieve a better performance in covering and partitioning tasks; for example, we may use an arbitrary point in the seed facet rather than fixing at its centroid as in this study. Future work should also include a comprehensive study on designing proper constraints for particular real-world applications regarding covering and partitioning problems.

We may also consider semantics, especially in partitioning tasks. Many indoor applications are based on services that provide semantic information. Regarding these applications, we should consider these semantics rather than performing our partitioning framework directly to the entire space. For example, we can perform the partitioning task for individual spaces separately with different parameters if we can split the space into semantic units manually. We may weight triangular facets in order to indicate some important point-of-interests (POI) for specific applications. In the route planning problem, semantics play an important role in navigation as well [49]. For human pedestrians, destinations are not likely to be an exact coordinate but some places having particular semantics like shops, gates, restrooms, or elevators. We can consider these aspects in developing and evaluating our framework in the future.

9. Conclusions

The covering and partitioning problems are important in analyzing and managing indoor spaces. In this paper, we have presented a flexible framework that can be applied to these problems effectively. Our contributions can be summarized as follows:

• We have proposed a framework for addressing covering and partitioning problems, which are related to many indoor applications. The framework consists of three stages, which are fine-grained triangulation, expansion computation, and covering/partitioning.
• In the expansion computation stage, we can use an appropriate constraint designed for the target application, which is what we mean by flexible as the proposed method is not too specific to a single individual application. We presented several constraints with an efficient computation method, which can be used for many well-known indoor applications.
• We proposed binary linear programming formulations for the covering and partitioning stage. Especially, we introduced the notion of acyclic expansion, and we presented a simplified binary linear programming formulation for the partitioning problem under this particular condition.
• As a usecase of the partitioning method, we presented the route planning problem with convex partition. We also presented how to represent the resulting partition and their connectivity for navigation in the format of IndoorGML, which is an international standard for representing indoor spaces.
• With experimental results, we demonstrated that our framework can be used as an off-the-shelf method for various covering and partitioning problems by showing that it computed acceptable solutions compared to the other methods even though they are not guaranteed to be optimal.

We also found several issues that can be improved, which we discussed in the earlier section. We will improve the framework in these perspectives in the future work.