Three-Dimensional (3D) Parametric Modeling and Organization for Web-Based Visualization of City-Scale Pipe Network
Abstract
:1. Introduction
2. Pipeline Modeling and Organization
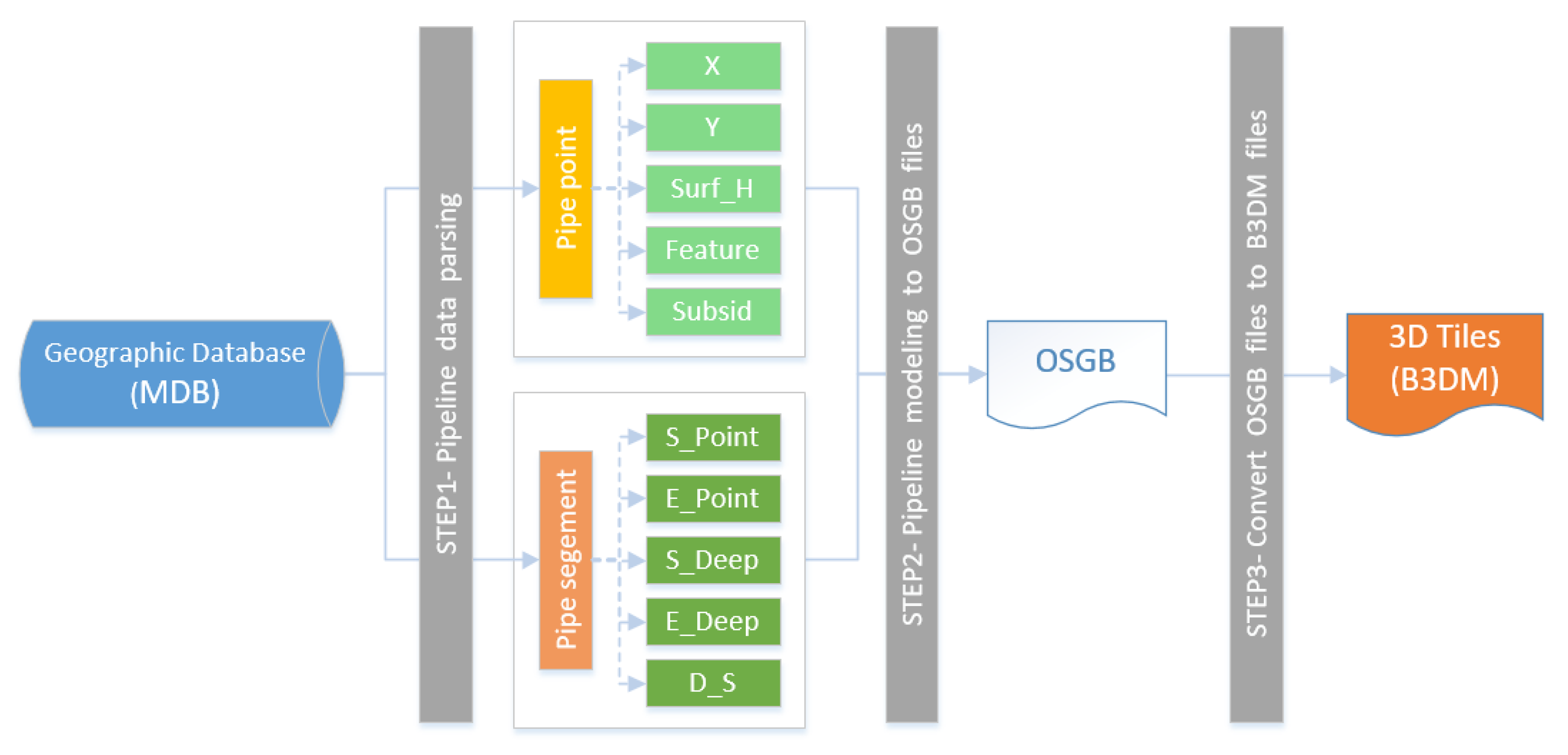
2.1. Workflow
2.2. Pipe Network Data Structure
2.3. Parametric Modeling of Pipe Segment
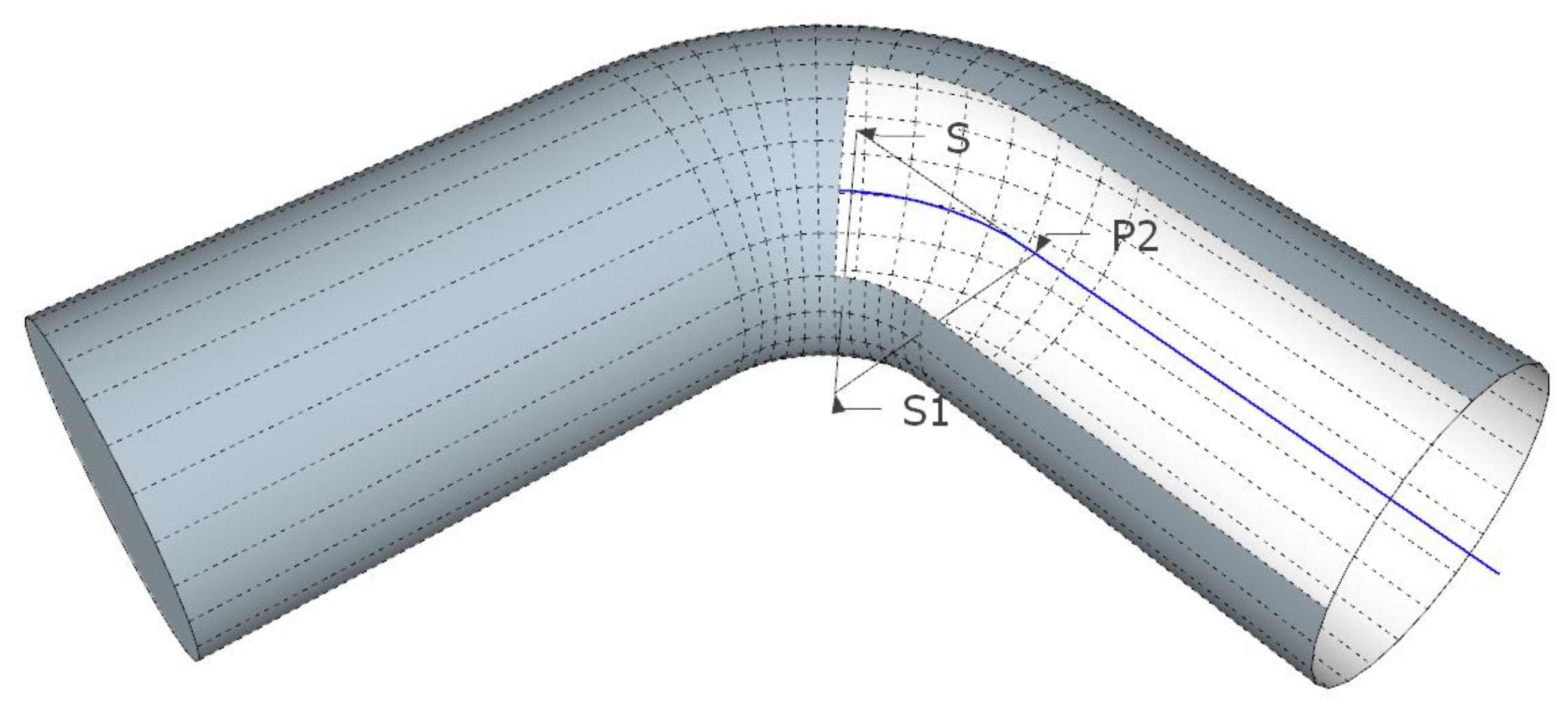
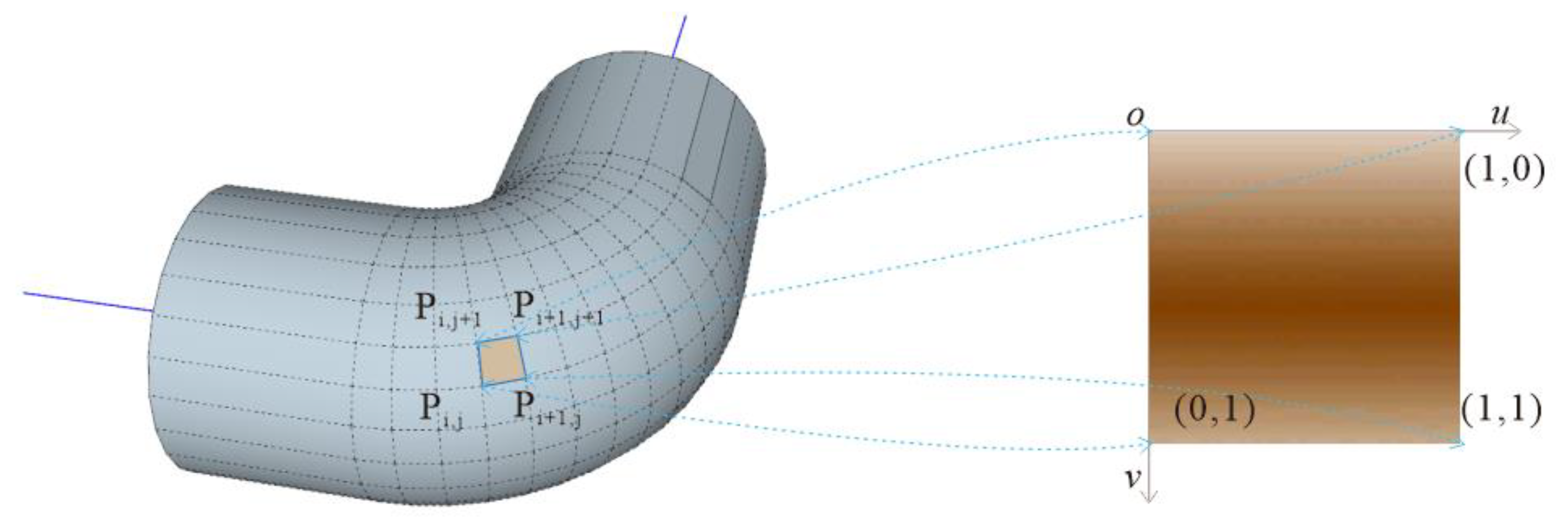
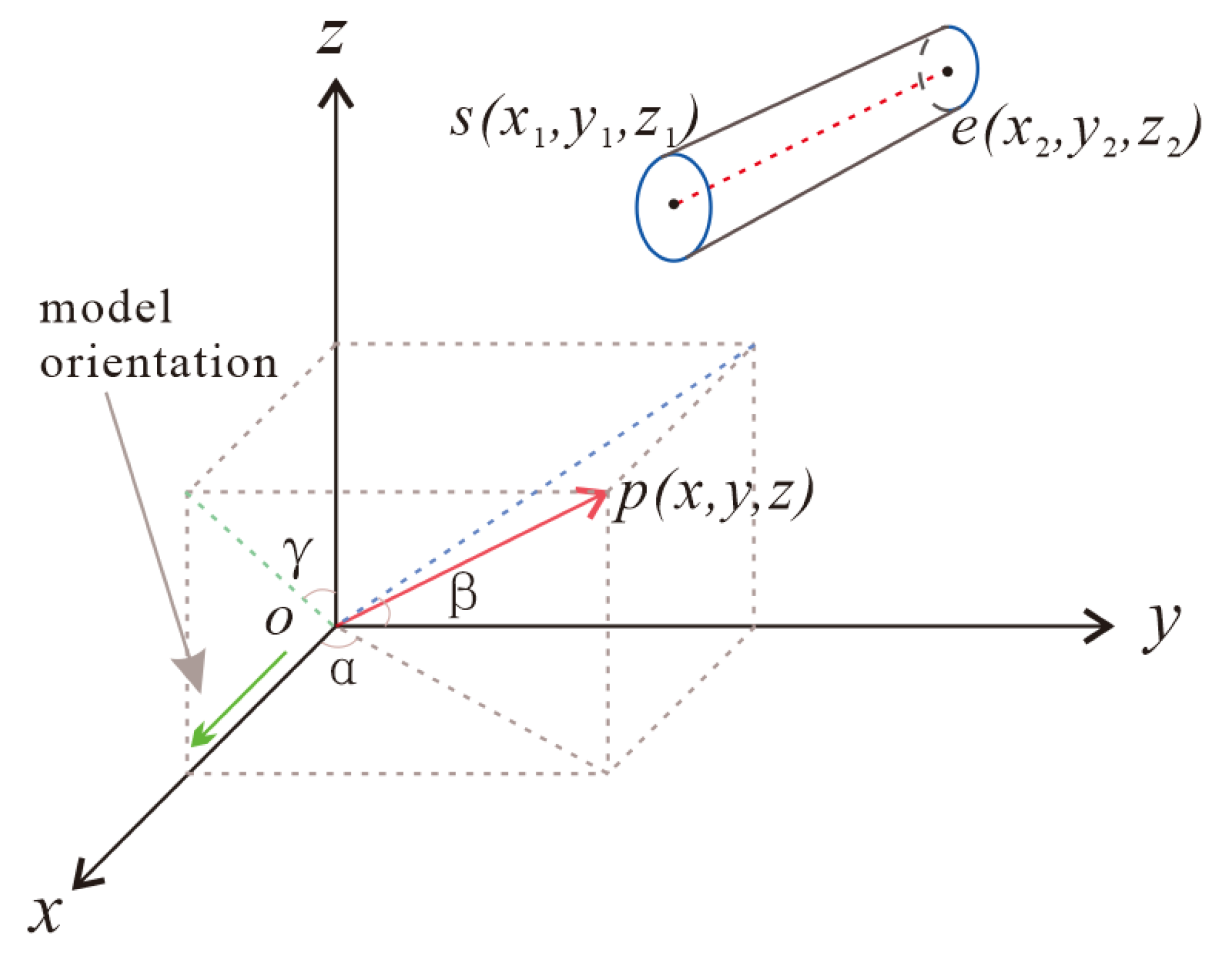
2.3.1. Pipe Segment Mesh Construction
- (1)
- Obtaining the coordinates of the start and end points as well as the diameter of the pipe segment;
- (2)
- Calculating the coordinates of each vertex in the spatial coordinate system: three vertices are used to form a triangle, and all the triangles are spliced together to form the geometry of the pipe segment.
2.3.2. Dynamic Texture Mapping
2.4. Parametric Modeling of Pipe-Point
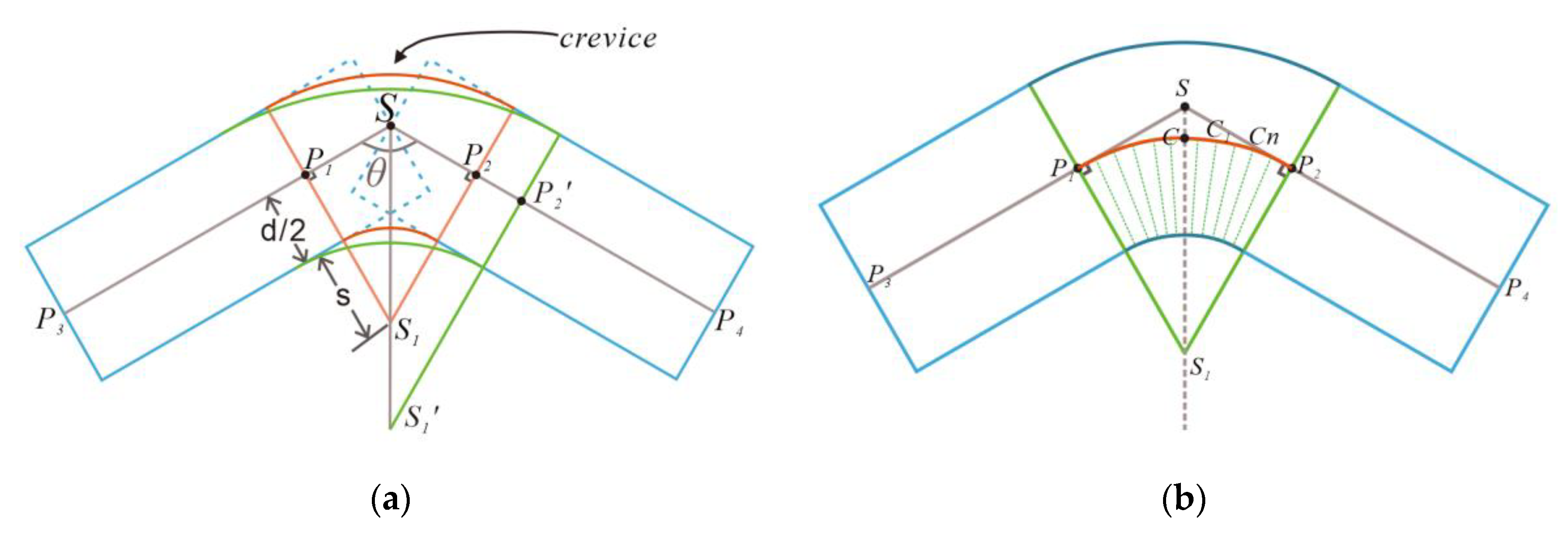
2.4.1. Feature Point Processing
2.4.2. Connection Point Processing
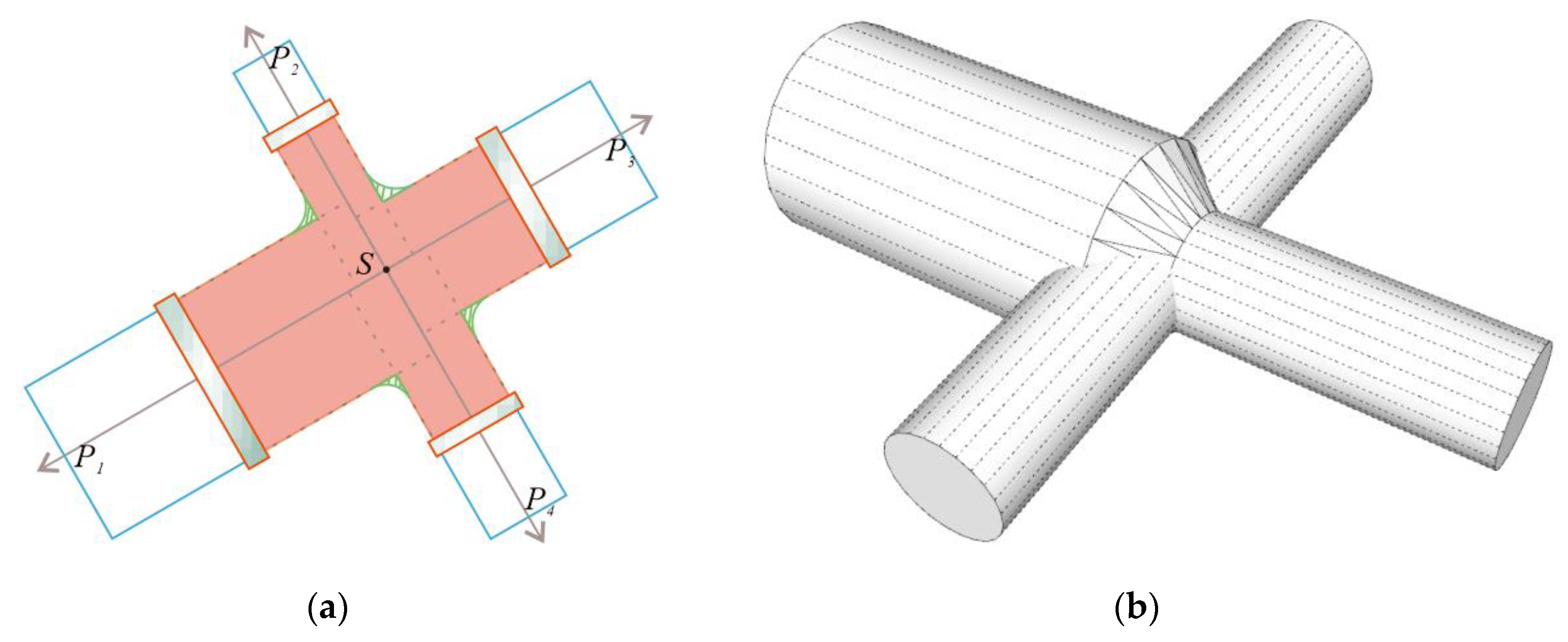
2.4.3. Multi-Directional Point Processing
2.5. City-Scale Pipe Model Organization
2.5.1. Data Organization for Pipe Model in 3D Tiles
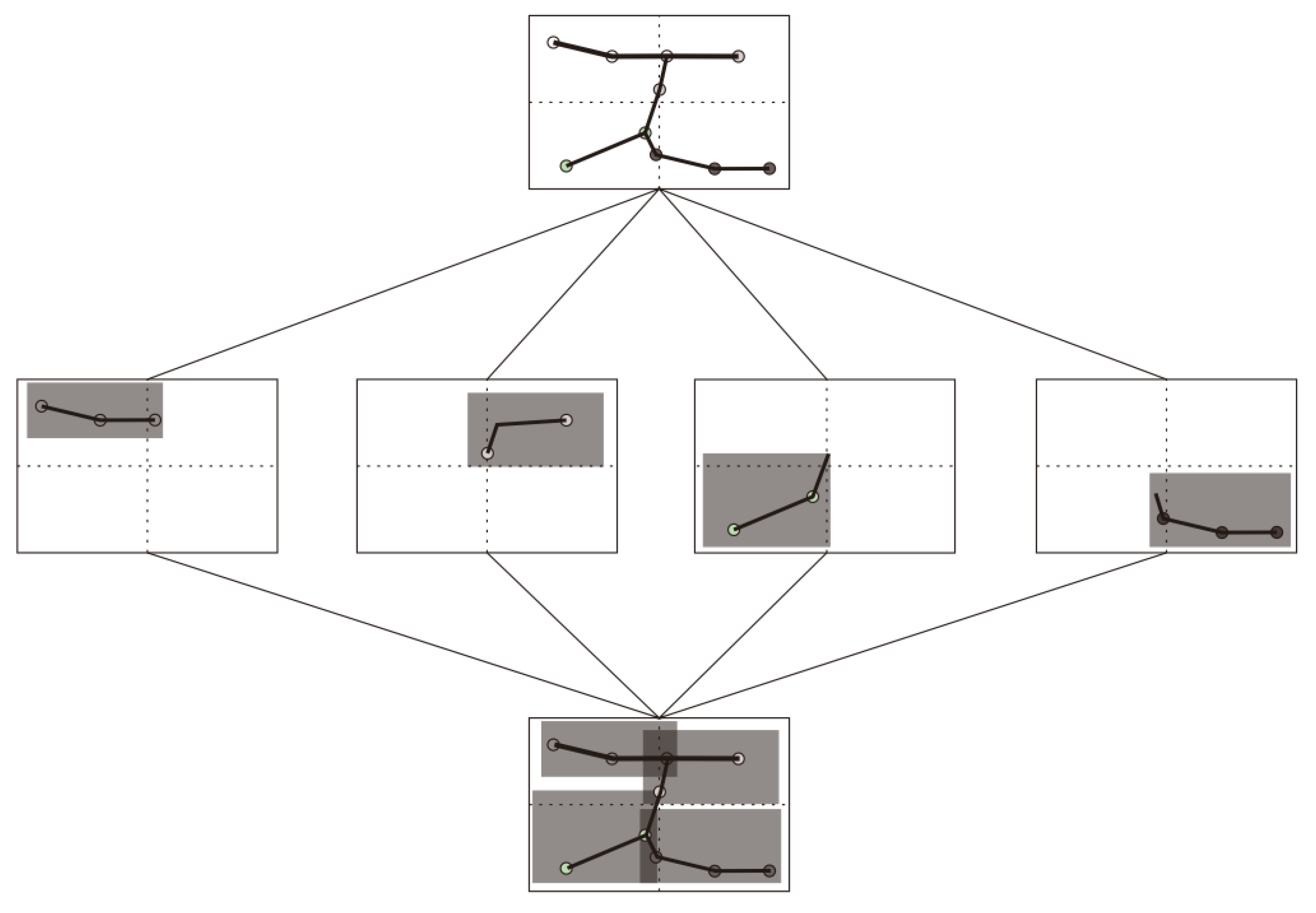
2.5.2. Splitting Pipe Models into 3D Tiles
3. Experiment and Analysis
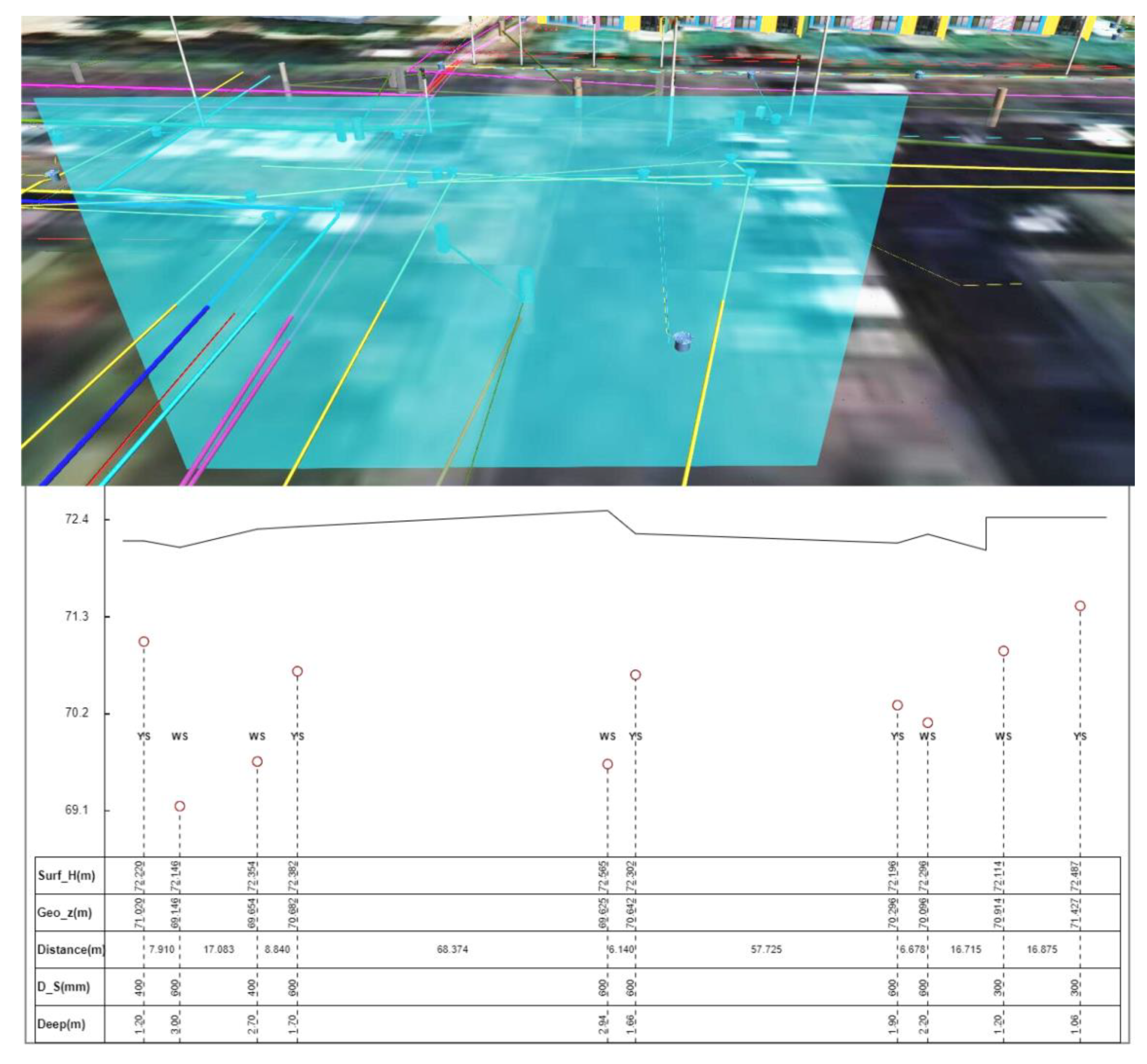
3.1. Experimental Data
3.2. Performance
4. Conclusions and Future Work
- (1)
- Pipe GIS data, including pipe segments and points, can be quickly and automatically processed into a 3D pipe model;
- (2)
- The pipe model is organized as a loose quadtree structure that can satisfy the visualization of city-scale underground pipe networks on a virtual globe.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mendez, E.; Schall, G.; Havemann, S.; Junghanns, S.; Fellner, D.; Schmalstieg, D. Generating semantic 3D models of underground infrastructure. IEEE Comput. Graph. Appl. 2008, 28, 48–57. [Google Scholar] [CrossRef]
- Balogun, A.L.; Matori, A.N.; Lawal, D.U. Geovisualization of sub-surface pipelines: A 3D approach. Mod. Appl. Sci. 2011, 5, 158. [Google Scholar] [CrossRef]
- Urban Underground Pipeline Survey. Available online: http://www.mohurd.gov.cn/wjfb/201605/t20160510_227405.html (accessed on 10 March 2020).
- Döner, F.; Thompson, R.; Stoter, J.; Lemmen, C.; Ploeger, H.; van Oosterom, P.; Zlatanova, S. Solutions for 4D cadastre—with a case study on utility networks. Int. J. Geogr. Inf. Sci. 2011, 25, 1173–1189. [Google Scholar] [CrossRef]
- Hijazi, I.H.; Ehlers, M.; Zlatanova, S. Nibu: A new approach to representing and analysing interior utility networks within 3D geo-information systems. Int. J. Digit. Earth 2012, 5, 22–42. [Google Scholar] [CrossRef]
- Li, S.; Cai, H.; Kamat, V.R. Uncertainty-aware geospatial system for mapping and visualizing underground utilities. Autom. Constr. 2015, 53, 105–119. [Google Scholar] [CrossRef]
- Peng, J.; Peng, F. Le A GIS-based evaluation method of underground space resources for urban spatial planning: Part 1 methodology. Tunn. Undergr. Space Technol. 2018, 74, 82–95. [Google Scholar] [CrossRef]
- Hou, Z.; Gu, Q. An improved method for drawing point of underground pipeline in AutoCAD. J. Geomat. 2011, 4, 43–44. [Google Scholar]
- Liu, H.Y.; Small, J.C.; Carter, J.P. Full 3D modelling for effects of tunnelling on existing support systems in the Sydney region. Tunn. Undergr. Space Technol. 2008, 23, 399–420. [Google Scholar] [CrossRef]
- Du, Y.; Zlatanova, S. An approach for 3D visualization of pipelines. In Innovations in 3D Geo Information Systems; Springer: Berlin/Heidelberg, Germnay, 2006; pp. 501–507. ISBN 354036997X. [Google Scholar]
- Becker, T.; Nagel, C.; Kolbe, T.H. Semantic 3D modeling of multi-utility networks in cities for analysis and 3D visualization. In Progress and New Trends in 3D Geoinformation Sciences; Pouliot, J., Daniel, S., Hubert, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 41–62. [Google Scholar]
- Gröger, G.; Plümer, L. CityGML—Interoperable semantic 3D city models. ISPRS J. Photogramm. Remote Sens. 2012, 71, 12–33. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, N.; Shao, J.; Deng, G. GPU ray casting method for visualizing 3D pipelines in a virtual globe. Int. J. Digit. Earth 2019, 12, 428–441. [Google Scholar] [CrossRef]
- Clarke, R.J. Planning and mapping of underground space—An overview. Tunn. Undergr. Space Technol. 2000, 15, 271–286. [Google Scholar] [CrossRef]
- Hunter, J.; Brooking, C.; Reading, L.; Vink, S. A Web-based system enabling the integration, analysis, and 3D sub-surface visualization of groundwater monitoring data and geological models. Int. J. Digit. Earth 2016, 9, 197–214. [Google Scholar] [CrossRef]
- Resch, B.; Wohlfahrt, R.; Wosniok, C. Web-based 4D visualization of marine geo-data using WebGL. Cartogr. Geogr. Inf. Sci. 2014, 41, 235–247. [Google Scholar] [CrossRef] [Green Version]
- Cesium. Available online: https://cesiumjs.org/about/ (accessed on 29 March 2020).
- 3D Tiles. Available online: https://cesium.com/blog/2015/08/10/introducing-3d-tiles/ (accessed on 9 June 2020).
- 3D Tiles Specification. Available online: https://github.com/AnalyticalGraphicsInc/3d-tiles/tree/master/specification#tileset-json (accessed on 9 June 2020).
- Chen, Y.; Shooraj, E.; Rajabifard, A.; Sabri, S. From IFC to 3D tiles: An integrated open-source solution for visualising BIMs on cesium. ISPRS Int. J. Geo Inf. 2018, 7, 393. [Google Scholar] [CrossRef] [Green Version]
- Jurado, J.M.; Ortega, L.; Graciano, A.; Feito, F.R. Web-based GIS application for real-time interaction of underground infrastructure through virtual reality. In Proceedings of the GIS: Proceedings of the ACM International Symposium on Advances in Geographic Information Systems, Redondo Beach, CA, USA, 1–10 November 2017. [Google Scholar]
- Wang, S.; Sun, Y.; Sun, Y.; Guan, Y.; Feng, Z.; Lu, H.; Cai, W.; Long, L. A hybrid framework for high-performance modeling of three-dimensional pipe networks. ISPRS Int. J. Geo Inf. 2019, 8, 441. [Google Scholar] [CrossRef] [Green Version]
- China, M. Of H. and U.-R.D. of the P.R. of Technical Specification for Urban Underground Pipeline Detection. Available online: http://www.mohurd.gov.cn/wjfb/201905/t20190506_240463.html (accessed on 9 June 2020).
- Weinhaus, F.M.; Devarajan, V. Texture mapping 3D models of real-world scenes. ACM Comput. Surv. 1997, 29, 325–365. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Guo, H.; Annoni, A.; Bian, L.; De Bie, K.; Campbell, F.; Craglia, M.; Ehlers, M.; Van Genderen, J.; Jackson, D.; et al. Next-generation digital earth. Proc. Natl. Acad. Sci. USA 2012, 109, 11088–11094. [Google Scholar] [CrossRef] [Green Version]
- Khronos Group Inc. glTF Overview. Available online: https://www.khronos.org/gltf/ (accessed on 6 June 2020).
- Keysers, J. Review of Digital Globes 2015; Australia and New Zealand Cooperative Research Centre for Spatial Information: Melbourne, Australia, 2015; ISBN 0994301901. [Google Scholar]
- Zinsmaier, M.; Brandes, U.; Deussen, O.; Strobelt, H. Interactive level-of-detail rendering of large graphs. IEEE Trans. Vis. Comput. Graph. 2012, 18, 2486–2495. [Google Scholar] [CrossRef]
- Ebdon, D. SPANS-A quadtree-based GIS. Comput. Geosci. 1992, 18, 471–475. [Google Scholar] [CrossRef]
- Wang, R.; Qian, X. OpenSceneGraph 3.0: Beginner’s Guide; Packt Publishing Ltd.: Birmingham, UK, 2010; ISBN 1849512833. [Google Scholar]
- Silc, J.; Robic, B.; Ungerer, T. Asynchrony in parallel computing: From dataflow to multithreading. J. Parallel Distrib. Comput. Pract. 1998, 1, 3–30. [Google Scholar]
- Li, X.; Yeh, A.G.O. Modelling sustainable urban development by the integration of constrained cellular automata and GIS. Int. J. Geogr. Inf. Sci. 2000, 14, 131–152. [Google Scholar] [CrossRef]






| ID | Field Name | Meaning | Comment |
|---|---|---|---|
| 1 | Exp_No | No. of pipe point | |
| 2 | X | X coordinate | Surveying coordinate systems |
| 3 | Y | Y coordinate | Surveying coordinate systems |
| 4 | Surf_H | Ground elevation | |
| 5 | Feature | Feature of pipe point | |
| 6 | Subsid | Subsidiary type of pipe point | |
| 7 | Angle | Rotate angle of subsidiary | |
| 8 | Offset | Offset of eccentric well |
| ID | Field Name | Meaning | Comment |
|---|---|---|---|
| 1 | S_Point | No. of start point | |
| 2 | E_Point | No. of end point | |
| 3 | S_Deep | Depth of start point | |
| 4 | E_Deep | Depth of end point | |
| 5 | D_S | Diameter of segment | Like D300 or 300 * 600 |
| 6 | Material | Material of pipe segment | Like polyethylene or nodular cast iron |
| Type | Water Supply | Drainage | Gas | Heating | Communications | Television | Electricity |
|---|---|---|---|---|---|---|---|
| Number of pipe points | 55,295 | 15,777 | 20,793 | 15,491 | 1032 | 128 | 1196 |
| Length of pipeline (km) | 1191.9 | 459.3 | 472.2 | 976.2 | 23.4 | 4.4 | 22.9 |
| Pipeline Type | OSGB Size | B3DM Size | Generation Time | Conversion Time |
|---|---|---|---|---|
| Water supply | 787 MB | 508 MB | 213 s | 182 s |
| Drainage | 149 MB | 136 MB | 45 s | 37 s |
| Gas | 146 MB | 126 MB | 42 s | 35 s |
| Heating | 273 MB | 213 MB | 89 s | 58 s |
| Communications | 10 MB | 17 MB | 4 s | 5 s |
| Television | 6 MB | 5 MB | 2 s | 4 s |
| Electricity | 65 MB | 46 MB | 23 s | 21 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Guo, J.; Zhang, X. Three-Dimensional (3D) Parametric Modeling and Organization for Web-Based Visualization of City-Scale Pipe Network. ISPRS Int. J. Geo-Inf. 2020, 9, 623. https://doi.org/10.3390/ijgi9110623
Hu Z, Guo J, Zhang X. Three-Dimensional (3D) Parametric Modeling and Organization for Web-Based Visualization of City-Scale Pipe Network. ISPRS International Journal of Geo-Information. 2020; 9(11):623. https://doi.org/10.3390/ijgi9110623
Chicago/Turabian StyleHu, Zihe, Jing Guo, and Xuequan Zhang. 2020. "Three-Dimensional (3D) Parametric Modeling and Organization for Web-Based Visualization of City-Scale Pipe Network" ISPRS International Journal of Geo-Information 9, no. 11: 623. https://doi.org/10.3390/ijgi9110623
APA StyleHu, Z., Guo, J., & Zhang, X. (2020). Three-Dimensional (3D) Parametric Modeling and Organization for Web-Based Visualization of City-Scale Pipe Network. ISPRS International Journal of Geo-Information, 9(11), 623. https://doi.org/10.3390/ijgi9110623




