Near Relation-Based Indoor Positioning Method under Sparse Wi-Fi Fingerprints

Abstract

Indoor positioning is of great importance in the era of mobile computing. Currently, considerable focus has been on RSS-based locations because they can provide position information without additional equipment. However, this method suffers from two challenges: (1) fingerprint ambiguity and (2) labour-intensive fingerprint collection. To overcome these drawbacks, we provide a near relation-based indoor positioning method under a sparse Wi-Fi fingerprint. To effectively obtain the fingerprint database, certain interpolation methods are used to enrich sparse Wi-Fi fingerprints. A near relation boundary is provided, and Wi-Fi fingerprints are constrained to this region to reduce fingerprint ambiguity, which can also improve the efficiency of fingerprint matching. Extensive experiments show that the kriging interpolation method performs well, and a positioning accuracy of 2.86 m can be achieved with a near relation under a 1 m interpolation density.

1. Introduction

With the increasing popularity of mobile and pervasive computing, location services based on indoor positioning have attracted considerable attention due to their wide applications in living, production, commerce, and public services [1,2]. Recent years have witnessed considerable work in indoor positioning. Single source location (e.g., received signal strength, radio frequency identification, ultra-wideband and visible light) and multi-source location-based indoor positioning strategies are differentiated by inference techniques such as the time of arrival, the time difference of arrival and the angle of arrival [3,4,5,6]. RSS-based localization has attracted considerable attention and is regarded as one of the most promising solutions for indoor positioning because it can provide position information without additional hardware and deployment investment [7,8].

RSS-based localization mainly contains two stages: offline and online [9,10,11]. During the offline stage, the RSS fingerprint dataset mapping the relationship between signal fingerprints and spatial locations is established. Then, in the online stage, the location is estimated by matching the online RSS fingerprint collection with an offline fingerprint dataset [12,13]. However, the RSS-based method faces many challenges: (1) fingerprint ambiguity due to the multi-path reflection of RSS in indoor complex environments, which results in two different locations that may have similar RSS fingerprints and low positioning accuracy [14]; (2) fingerprint collection is labour intensive and time consuming [2]; and (3) low efficiency in fingerprint database matching [14].

To overcome the drawbacks of traditional RSS-based indoor positioning methods, certain interpolation methods are provided to enrich sparse Wi-Fi fingerprints, which reduce the labour of fingerprint collection. A near relation is provided to constrain the Wi-Fi fingerprint matching space, which not only reduces fingerprint ambiguity but also improves matching efficiency.

The contributions of our paper are as follows:

(1)

We identify the opportunity for a near relation for resolving fingerprint ambiguity. To the best of our knowledge, this is the first work combining spatial relationships in locality descriptions with fingerprints.

(2)

A near relation-based indoor positioning under a sparse Wi-Fi fingerprinting scheme is provided, which is a new interactive indoor positioning method. Some interpolation methods are adopted to encrypt sparse Wi-Fi fingerprinting. A near relation region is provided to narrow the searching space of fingerprinting and resolve fingerprinting ambiguity.

(3)

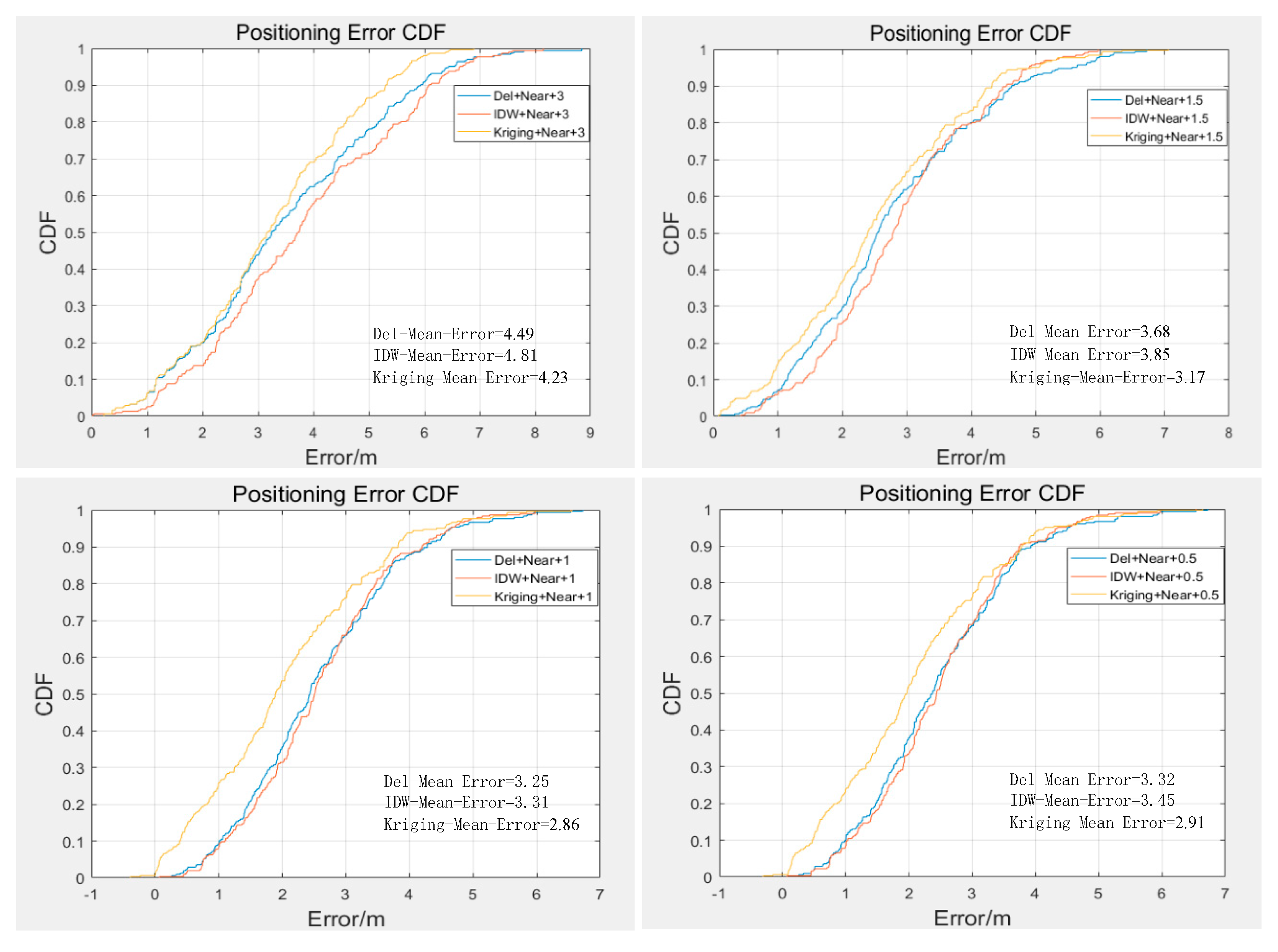
To evaluate our method, extensive experiments are conducted. The results demonstrate that the kriging interpolation method performs better than other interpolation methods, and a positioning accuracy of 3.8 m is achievable with a near relation constraint under a 1 m interpolation density.

The remainder of this paper is organized as follows. The related works are provided in Section 2. Section 3 describes the system overview and method. Section 4 presents the related experiments. Section 5 summarizes this work and discusses future research directions.

2. Related Works

The literature on fingerprinting-based indoor localization is extensive and rich. The major reason for fingerprint ambiguity comes from two aspects: position ambiguity and RSS ambiguity (Han et al., 2015). RSS ambiguity refers to the locations of two reference points being geographically close to one another, but the fingerprints at these reference points are distinct. Position ambiguity references fingerprints that are close, but the locations are geographically distant. The ambiguity of fingerprints can be reduced by adding fingerprint dimensions [15] and using scene information [16] or pedestrian dead-reckoning (PDR) [17] to narrow the fingerprint database. Li [15] extended the fingerprint dimension from one point to multiple points to avoid the ambiguity of RSS. A multidimensional dynamic time warping (MD-DTW) algorithm was provided for matching. Liu [16] used a smartphone camera as an “eye” to recognize the environment. With scene information constrained, the searching range of the fingerprint database was narrowed, and RSS ambiguities decreased. Chen [17] used pedestrian dead-reckoning (PDR) to track user movements and restricted fingerprints to a circle centre at the PDR positioning result. Additionally, the clustering method can also mitigate the ambiguity issue. Bulut [18] applied a k-means clustering approach to enhance the neighbouring point selection. Hu [19] used a clustering method based on semi-supervised affinity propagation to identify and remove isolated points. Lee [20] provided a novel support vector machine based clustering approach to remove estimation outliers.

The construction and maintenance of a sufficient fingerprint database are laborious and problematic. It is possible to reduce the laborious nature of fingerprint construction in three ways: simultaneous localization and mapping (SLAM), crowdsourcing and interpolation. SLAM collects Wi-Fi fingerprints by taking advantage of the simultaneous accurate positioning of the reference point and indoor mapping [21]. The crowdsourcing method provides fingerprints of reference points by many volunteers according to a certain mechanism [22]. The interpolation method can encrypt fingerprint-based sparse fingerprint databases [23,24]. Voronoi tessellation [23], inverse distance weighting (IDW) [25,26,27], Delaunay-based [28] and kriging interpolation are well known interpolation methods. Lee [25] refined the propagation model for each cell of the target area tessellated by a higher-order Voronoi diagram. This method can more accurately account for the signal fading caused by walls and obstacles, but the location of the access point (AP) must be obtained in advance. The basic idea of IDW is to provide weight for the data points based on their distance to the estimated point. The closer the known data point is to the estimated point, the more weight it has [29]. The Delaunay-based interpolation method is linear and contains two parts: interpolation and extrapolation [30]. The kriging interpolation method is a geostatistical method for optimal spatial prediction at unobserved locations, and it has certain advantages over some other spatial interpolation methods [31]. Kram [32] added a mixed model to a kriging interpolation method for Wi-Fi signal propagation. Zuo [33] adopted a kriging-based interpolation method to efficiently generate a missing iBeacon fingerprint database where some regions were inaccessible.

Near relations in locality descriptions can provide locality clues and are a potential information source that can be used for indoor positioning. For example, the locality description “I am near McDonald’s” can determine the approximate location region by near relation in the locality description. The near relation modelling method depends on the spatial scale and application scenario [34,35,36]. Liu [37] argued that the near relation is inversely proportional to the distance in certain areas. Gong [38,39] provided a mixed probability function based on Euclidean distance and a stolen area for near point relations but no practical feature application. Wang [40,41] developed near relations for polygons and used it for indoor positioning together with qualitative and quantitative distance. However, one near relation in a locality description can determine a region but cannot meet positioning requirements. Therefore, how to position using one near relation in locality description is worth studying and will be solved in our paper.

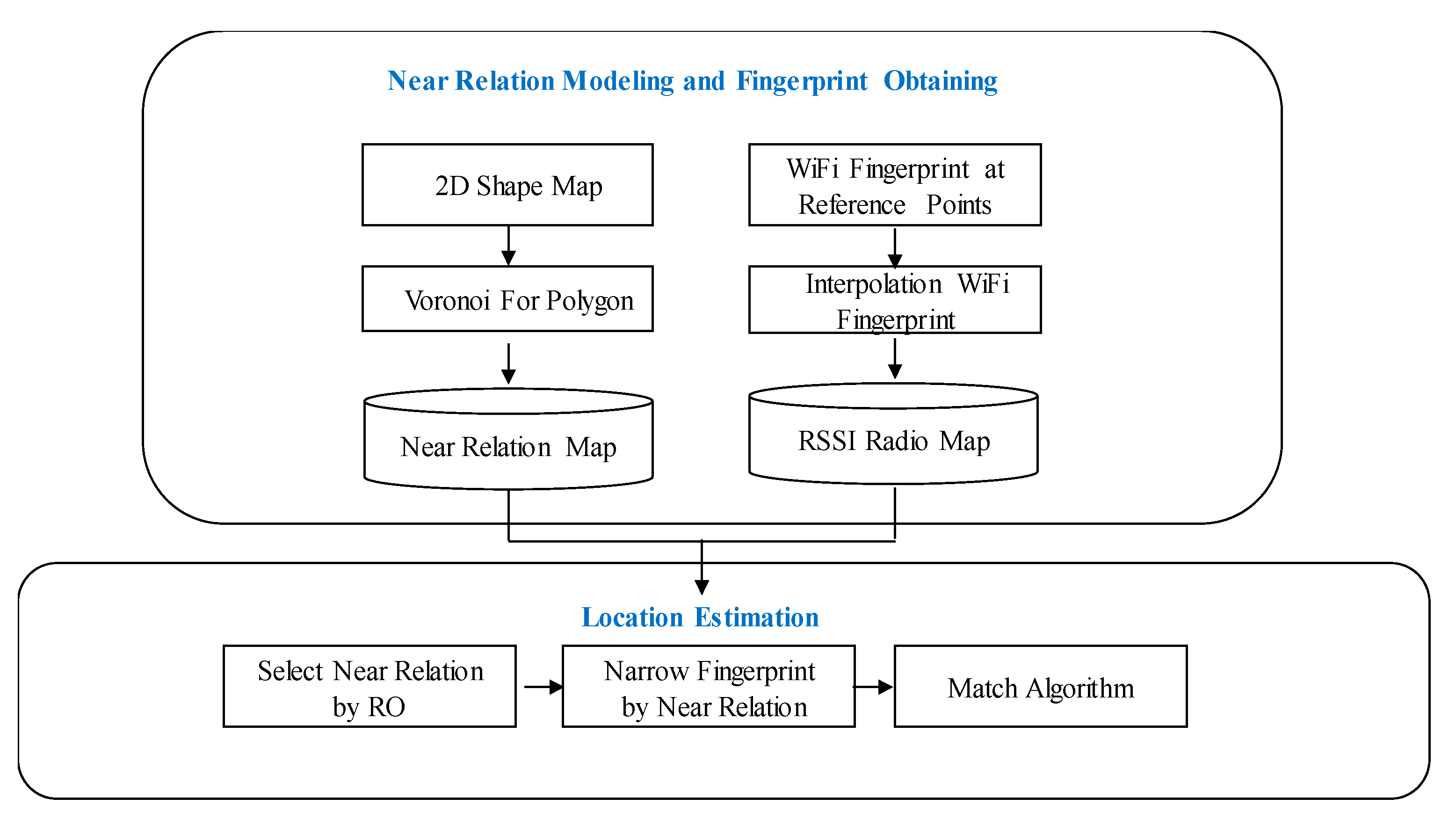
3. System Overview and Method

3.1. System Overview

Generally, there are reference objects (ROs) and their related spatial relations (SRs; i.e., topology, direction and distance) and target objects (TO) in a place description. Reference object (RO) refers to any feature with a name in a place description. A TO is a place that is to be described or located. Take the place description “I am near LaoFX” as an example. The RO (reference object) is LaoFX, and the spatial relation is a near relation. The TO refers to my location, which is the positioning. Additionally, ROs are indoor polygons due to the scale.

The architecture of the proposed system contains two stages (Figure 1). Stage 1: Near relation modelling and fingerprint obtaining. The near relation boundary and a fingerprint database based on the interpolation method are built. Stage 2: Location estimation. The near relation for the RO (reference object) is selected to narrow the search space of fingerprinting to the position.

3.2. Method

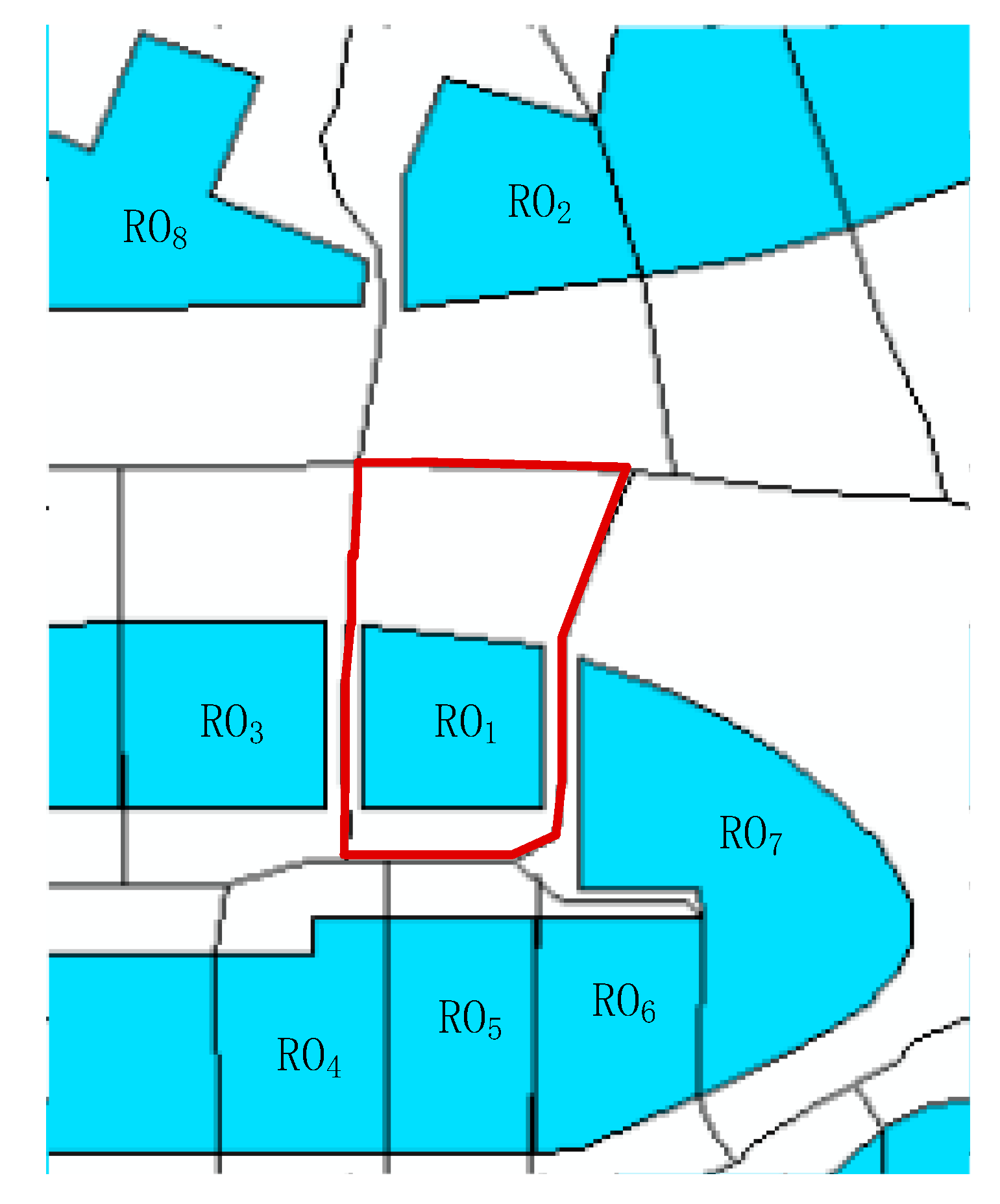
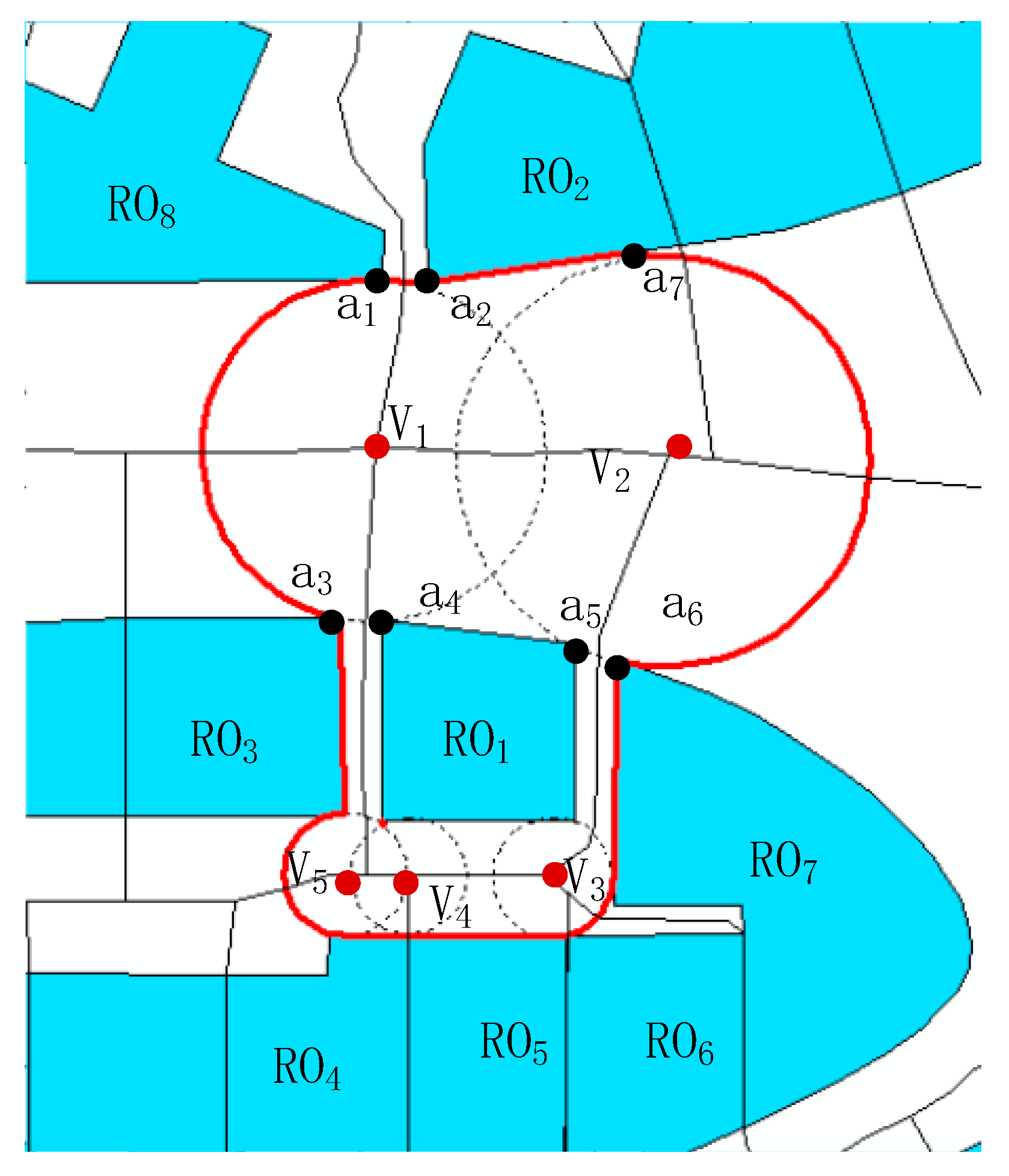
3.2.1. Near Relation Boundary

Definition 1.

Voronoi region of RO: Let R (RO₁, RO₂……RO_i) be a set of shape polygon entities in the 2-D Euclidean plane E² and d(p,RO_i) be the Euclidean distance between point p and RO_i. The minimum distance between p and RO_i is denoted with d_min(p,RO_i). The Voronoi region of RO_i is denoted with Vor(RO_i). As shown in Figure 2, the red solid region is the Voronoi region of RO₁:

$$Vor\left(R{O}_i\right)=\left\{p\right|d_{min}\left(p,R{O}_i\right)<d_{min}\left(p,R{O}_j\right),p\in E^2,i\ne j\}$$

(1)

Definition 2.

Neighbours of RO: Two entities neighbour to each other if the Voronoi regions of them share a common edge. As shown in Figure 2, the neighbours of RO₁ are denoted with neighbours (RO₁) = {RO₂, RO₃, RO₄, RO₅, RO₇, RO₈}.

Definition 3.

Near boundary of RO: The near boundary of RO refers to the region of a site inserted into and neighbours of RO.

The process of obtaining a near boundary of RO₁ is as follows (Figure 3). For ROs in space (as shown in Figure 3), RO₁ is neighbour to RO₂, RO₃, RO₄, RO₅, RO₇ and RO₈. The vertices of the Voronoi polygon of RO₁ are v₁, v₂, v₃, v₄ and v₅. The vertex v₁ is the common vertex of RO₁, RO₂, RO₃ and RO₈. The nearest points of RO₁, RO₂ and RO₇ to v₂ are a₅, a₆ and a_7, respectively. The circumcircle of triangulation with vertices a₅, a₆ and a₇ is drawn and arcs a₆a₇ between RO₂ and RO₇ are obtained. Other arcs between ROs are obtained, and the arcs are connected with segments of ROs (e.g., segment of RO₂ a₂a₇) to form a closed cycle. The red solid region is the near boundary of RO_1.

3.2.2. Kriging Interpolation Method

The kriging algorithm can predict a value at an unobserved location based on known data, which assumes that the nearby points are more similar than those that are far away. In this paper, the workflow of the kriging interpolation of the RSS is depicted in Figure 4. The experimental semi-variogram model fitting and best linear unbiased estimator are the key steps of the kriging interpolation method.

(1) 

Semi-variogram model fitting

Semi-variance is an important step in kriging interpolation, which describes the spatial correlations between observations. The theoretical semi-variance can be defined as Equation (2):

$$r\left(h\right)=\frac{1}{2}Var\left[z\left(u_i\right)-z\left(u_j\right)\right]$$

(2)

where h is the distance between u_i and u_j, and var is the variance. $z\left(u_i\right)$ is the RSS value of point u_i. For real data, the experimental semi-variance is shown in Equation (3):

$$\widehat{r}\left(h\right)=\frac{1}{2N\left(h\right)}{{\displaystyle \sum }}_{i=1}^{N\left(h\right)}{\left[z\left(u_i\right)-z\left(u_j\right)\right]}^2$$

(3)

where $N\left(h\right)$ is the number of pairs of sample points separated by $h$. As shown in Figure 5, the experimental semi-variogram and theoretical semi-variogram can be drawn based on $r$ and $h$.

In Figure 5, when $h$, i.e., Range(D), increases to a specific range, $r$ is stable, namely, still C. The parameters D and C determine the theoretical model. In this paper, we used the Gaussian model (Equation (4)):

$$r\left(h\right)=C[1-exp(-\frac{h^2}{D^2})]$$

(4)

(2) 

Best linear unbiased estimate

Once the experimental semi-variogram is obtained, values at unknown locations can be estimated based on known data points. The kriging estimator satisfies the best linear unbiased estimate (BLUE), as shown in Equation (5):

$$\widehat{z}\left(u_0\right)={{\displaystyle \sum }}_{i=1}^n{\lambda }_{i}z\left(u_i\right)$$

(5)

where $u_0$ is the unknown location, $z\left(u_i\right)$ is the known measurement at location $u_i$, and n is the number of known measurements. ${\lambda }_i$ is the kriging weight of $z\left(u_i\right)$, which can be estimated by Equation (6). ${\lambda }_{ij}$ is the semi-variogram value between $z\left(u_i\right)$ and $z\left(u_j\right)$:

$$\left[\begin{array}{c}{\lambda }_1\\ ⋮\\ {\lambda }_n\end{array}\right]={\left[\begin{array}{ccc}{r}_{11}& \cdots & r_{1n}\\ ⋮& \ddots & ⋮\\ r_{n1}& \cdots & r_{nn}\end{array}\right]}^{-1}\left[\begin{array}{c}{r}_{10}\\ ⋮\\ r_{n0}\end{array}\right]$$

(6)

Then, Equation (5) satisfies the unbiased constraint (Equation (7)) and has the minimum variance (Equation (8)):

$$E{\left[\widehat{z}\left(u_0\right)-z\left(u_0\right)\right]}^2=0$$

(7)

$$min\left\{Var\left[\widehat{z}\left(u_0\right)-z\left(u_0\right)\right]\right\}$$

(8)

3.2.3. Match Algorithm

The fingerprint matching algorithm we used was the weighted K-nearest neighbours (e.g., WKNN) [24,25]. The WKNN method is used to select K RPs which has the minimal signal strength distance as the user’s estimated position, which is calculated as follows:

$$d_j=\sqrt{{{\displaystyle \sum }}_{i=1}^N\left|rss\left(pos,i\right)-RSS\left(j,i\right)\right|}$$

(9)

where rss(pos,i) is the received signal strength of the i_th AP at user position pos; RSS(j,i) is the received signal strength of the i_th AP at the j_th RP, and the N is the total number of APs. The weighting value of each RP is determined by Equation (10):

$$W_j=\frac{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d_j$}\right.}{{{\displaystyle \sum }}_{j=1}^K\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d_j$}\right.}$$

(10)

where K is the total number of the selected RPs. The user position is estimated by Equation (11):

$$\left(\mathrm{X},\mathrm{Y}\right)={{\displaystyle \sum }}_{j=1}^K\left[W_j\times \left(X_j,Y_j\right)\right]$$

(11)

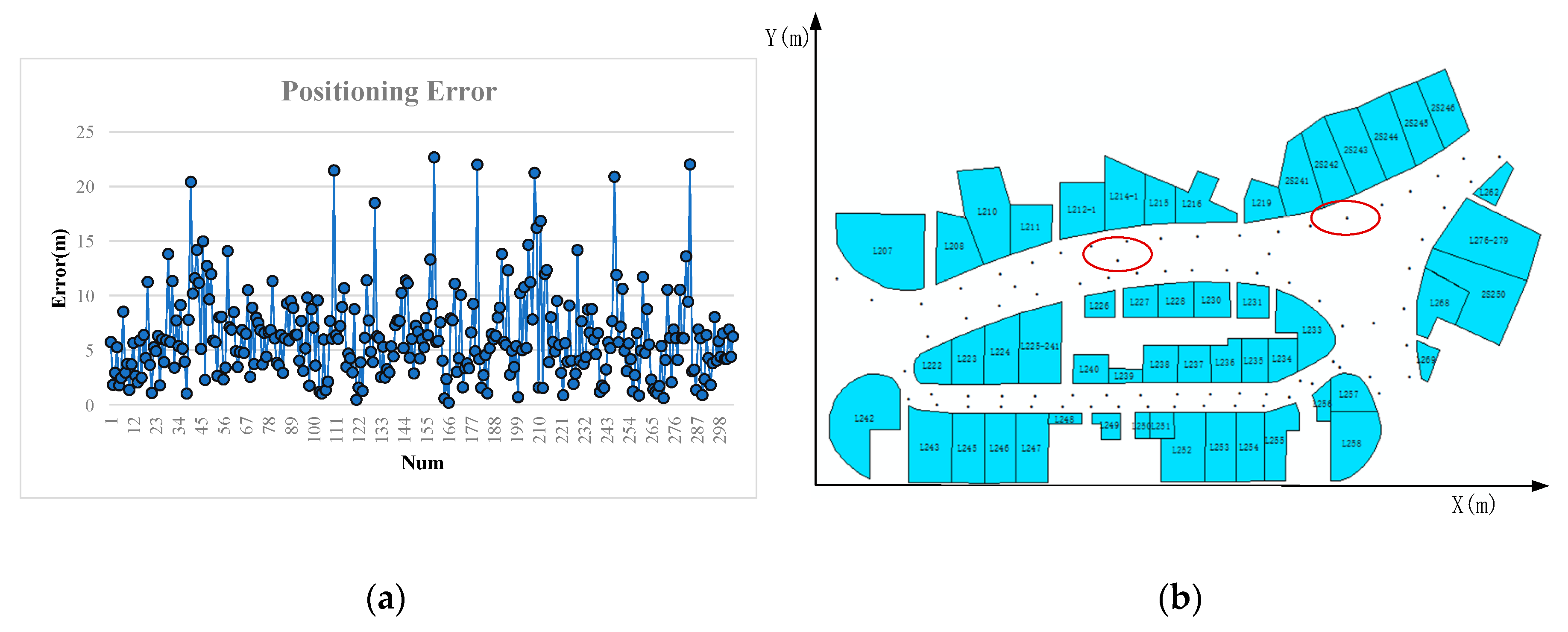
4. Experiment and Evaluation

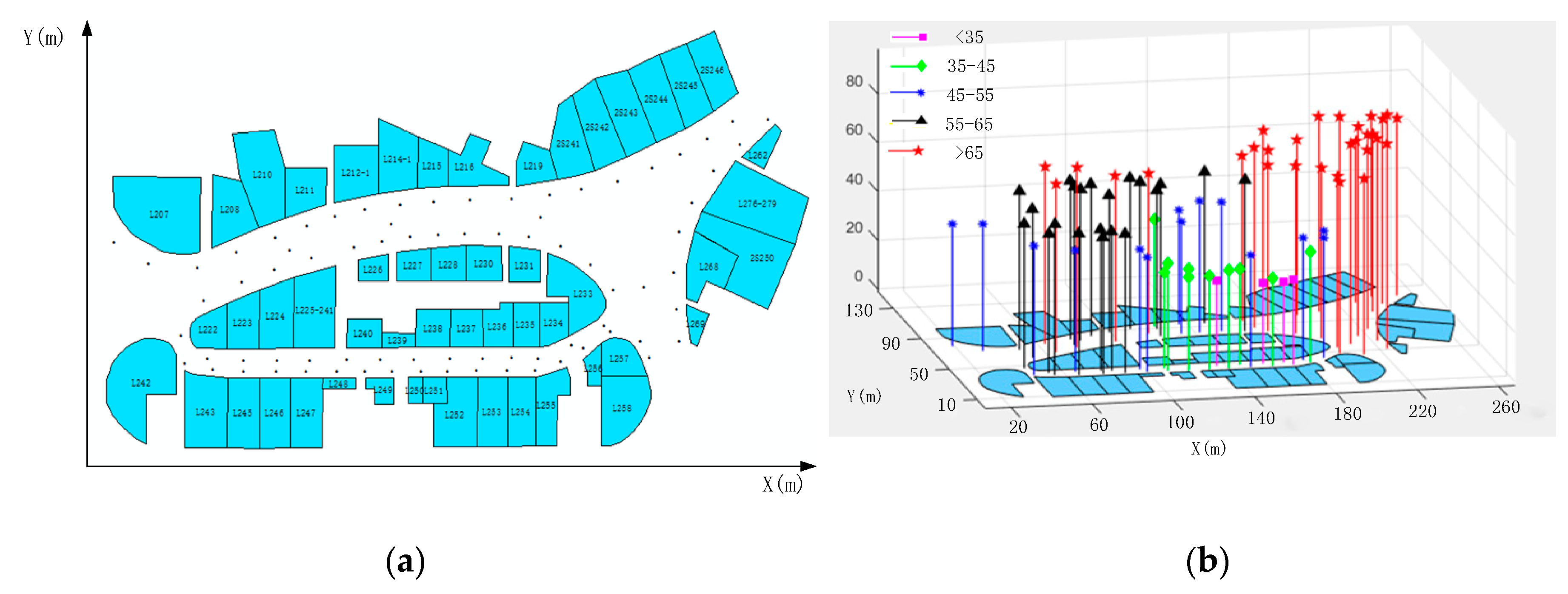
4.1. Experiment Steps

The experiments were conducted on the first floor of a shopping mall with a 120 m × 245 m area. Figure 6 shows the indoor test environment, which was taken during the morning. There were approximately 85 access points (APs). Almost each shop had one AP. In this experiment, only RSS values stronger than −90 dBm were considered. Additionally, the parameter K in WKNN was set to be 3.

The distance between each reference point (RP) was 6 m. As shown in Figure 7a, there were 55 RPs. The Wi-Fi RSSs were collected by an Honour KIW-AL10 smartphone, and the signal sampling frequency was 1 Hz. When collecting the signal, we held the smartphone on our chest and in a fixed orientation. For each RSS, the RSS collection at each RP lasted for 2 min to prevent signal instability. The number of APs’ distribution in the test environment is shown in Figure 7b. The x and y axes indicate the relative coordinates, and the z axis shows the number of APs.

The near boundary for ROs in the test environment is shown in Figure 8. The red line region in Figure 8a is the near boundary of L207. Figure 8b shows all the near boundaries of the ROs.

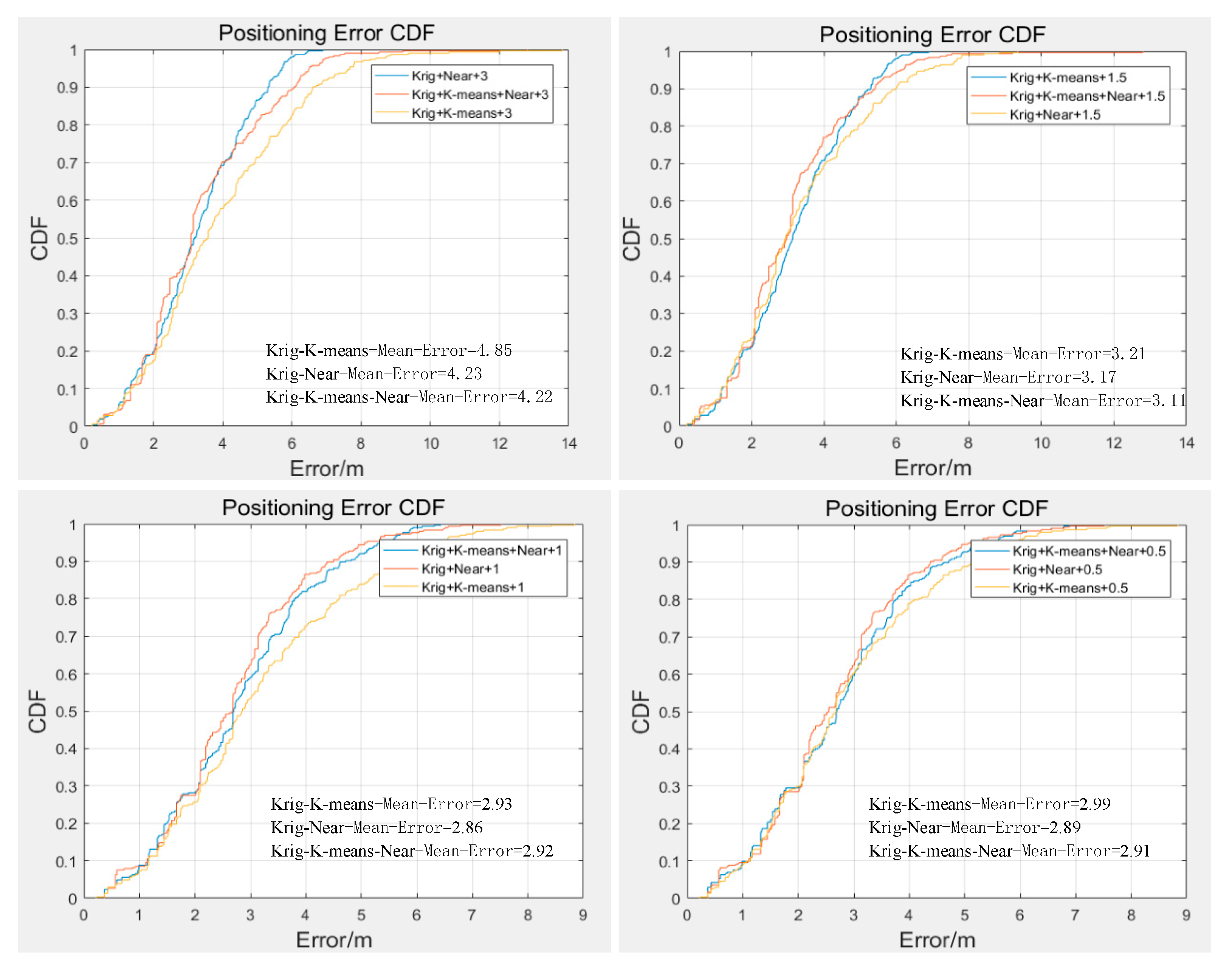
4.2. Localization Results and Evaluation

Some participants were selected to walk around during the test experiment and asked to select near ROs to describe their location. The selected ROs, participants’ locations and the corresponding Wi-Fi fingerprints were recorded. The participants included seven males and nine females, and their ages ranged from 20 to 48. Their locations are evenly distributed and shown in Figure 9.

As shown in Figure 10, when the distance of the reference point was 6 m, the mean positioning error was 10.3 m. It is obvious that there were many large error points. The large positioning error was from fingerprint ambiguity, and the location of the ambiguous fingerprints is shown in Figure 10b with a red circle.

In addition to the kriging interpolation method, IDW and Delaunay-based interpolation methods are commonly used. To further verify our method, we fully compared them.

Figure 11 shows the positioning error with the different interpolation methods and interpolation density without a near relation. The related positioning errors are listed in

Table 1. Positioning error statistics without near relation.

	Max-Error	Min-Error	Mean-Error
IDW + 3 m	25.76	0.46	6.38
IDW + 1.5 m	22.25	0.16	5.31
Dela + 3 m	25.36	0.51	6.06
Dela + 1.5 m	24.36	0.4	4.81
Krig + 3 m	24.4	0.46	5.94
Krig + 1.5 m	18.31	0.18	4.31

. The mean error of IDW + 3 m, IDW + 1.5 m, Dela + 3 m, Dela + 1.5 m, Krig + 3 m, Krig + 1.5 m were 6.38, 5.31, 6.06, 4.81, 5.94 and 4.31 m, respectively. IDW, Dela and Krig denote the IDW, Delaunay and kriging interpolation methods, respectively, and 3 and 1.5 m represent the interpolation density. In other words, IDW+3 m represents the IDW interpolation method and 3 m the interpolation density.

Figure 12 shows the positioning error with different interpolation methods and interpolation densities considering the near relation (i.e., using the near relation boundary as constraint). The related positioning errors are listed in

Table 2. Positioning error statistics considering the near relation.

	Max-Error	Min-Error	Mean-Error
Near + IDW + 3 m	8.15	0.19	4.81
Near + IDW + 1.5 m	5.97	0.42	3.85
Near + Dela + 3 m	8.8	0.22	4.49
Near + Dela + 1.5 m	6.72	0.07	3.68
Near + Krig + 3 m	6.89	0.22	4.23
Near + Krig + 1.5 m	6.03	0.26	3.17

. The mean error of Near + IDW + 3 m, Near + IDW + 1.5 m, Near + Dela + 3 m, Near + Dela + 1.5 m, Near + Krig + 3 m, Near + Krig + 1.5 m were 4.81, 3.85, 4.49, 3.68, 4.23, and 3.17 m, respectively. Near + IDW + 3 m represents the IDW interpolation method and 3 m interpolation density considering the near relation.

Figure 13 shows the cumulative distribution function (CDF) of different interpolation methods under different interpolation densities (i.e., 3, 1.5, 1 and 0.5 m) considering the near relation. It is obvious that the positioning accuracy of the kriging interpolation method performed better than the other interpolation methods. As the interpolation density increased, the mean positioning accuracy no longer improved when the interpolation density increased to 1 m. Its mean positioning accuracy was approximately 2.86 m, and around 80% fewer errors than 3.12 m.

To investigate the effect of the value of k, eight different values (the integers from 3 to 10) of k were tested. In the experiment, we used the kriging interpolation method and the interpolation density was 1 m. As can be seen in

Table 3. Positioning error of the different K values.

K	Mean-Error(m)	Min-Error(m)	Max-Error(m)
3	2.86	0.46	4.86
4	2.89	0.56	4.91
5	3.12	0.91	5.21
6	3.34	0.83	5.13
7	3.41	0.77	5.43
8	3.76	0.81	4.91
9	3.69	0.69	4.88
10	3.71	0.57	4.97

, the average positioning error would increase as k increases from 4 to 8. The results show that the proposed method can achieve good positioning accuracy when k is set to be 3 or 4. Since the positioning accuracy is very similar for k being 3 and 4, k is simply set to be 3.

There are many large positioning errors when positioning with different interpolation methods and interpolation densities considering the near relation. The large positioning error occurs for three reasons: (1) the selection of a reference object (RO) with a near relation is arbitrary. The near relation is a relative concept, and people may not select the nearest RO. Additionally, there may be other factors (e.g., personal preferences) that influence people’s selections. (2) The kriging method performs better than other interpolation methods. However, the fingerprints obtained by interpolation methods are estimation values, not real values. (3) Furthermore, the collection of sparse Wi-Fi fingerprints is ambiguous, which makes the interpolated fingerprint ambiguous.

Additionally, the clustering method (i.e., K-means) can also mitigate the Wi-Fi fingerprints ambiguity issue. To further discuss our method, three sets of experiments (i.e., Krig + K-means, Krig + Near, Krig + K-means + Near) with different interpolation densities (i.e., 0.5, 1, 1.5, 3 m) were conducted. Krig + K-means + Near represents the kriging interpolation method and the K-means clustering method considering the near relation. Figure 14 shows the corresponding cumulative distribution function (CDF). Compared with Krig + K-means and Krig + Near method, the later performs better. The reasons can be as follows: (1) the interpolated Wi-Fi fingerprint is only approximate and not true. The K-means clustering method can only weaken the abnormal fingerprints, but not eliminate them completely. (2) The input of our method is the near relation boundary and Wi-Fi fingerprints. The positioning accuracy depends on them both. However, the positioning accuracy of Krig + the K-means method only rely on the quality of Wi-Fi fingerprints. The positioning accuracy of Krig + Near and Krig + K-means + Near method are almost the same, but the later method is complex.

5. Conclusions

A user-friendly indoor location-based service is envisioned. Voice interactive indoor positioning is a future development direction. In this paper, we developed a near relation-based indoor positioning method that combined near relations in locality descriptions with fingerprint signals and is a new interactive indoor positioning model. Certain common interpolation methods are used to encrypt sparse Wi-Fi fingerprints. The interpolated fingerprint is restricted to the near boundary, which cannot only narrow the search space of the fingerprint but also decrease the RSS ambiguities. The experiment shows that the kriging interpolation method performs well, and a positioning accuracy of 2.86 m can be achieved with a near relation constraint under a 1 m interpolation density.

The near boundary provided in this paper is raster-based, which has low efficiency. In practical applications, the near boundary should be generated in advance and placed on the server. Additionally, the near relation is a probability function, which is based on stolen-area and Euclidean distance [38]. The stolen area is the area that is part of the Voronoi region of the original RO but now belongs to the Voronoi region of a new sit, when it is inserted into the existing Voronoi diagram of ROs. It can deeply integrate with other position signals (e.g., geomagnetic) through particle filtering. However, this paper only uses near boundaries to solve fingerprint ambiguity. In general, studying other near boundary generation methods and deeply integrating them with other positioning signals will be considered in our future works.