Application of AHP to Road Selection

Abstract

The analytic hierarchy process (AHP), a decision-making method, allows the relative prioritization and assessment of alternatives under multiple criteria contexts. This method is also well suited for road selection. The method for road selection based on AHP involves four steps: (i) Points of Interest (POIs), the point-like representations of the facilities and habitations in maps, are used to describe and build the contextual characteristic indicator of roads; (ii) form an AHP model of roads with topological, geometrical, and contextual characteristic indicators to calculate their importance; (iii) select roads based on their importance and the adaptive thresholds of their constituent density partitions; and (iv) maintain the global connectivity of the selected network. The generalized result at a scale of 1:200,000 by AHP-based methods better preserved the structure of the original road network compared with other methods. Our method also gives preference to roads with relatively significant contextual characteristics without interfering with the structure of the road network. Furthermore, the result of our method largely agrees with that of the manual method.

1. Introduction

The automatic generalization of geographic information is still a challenge in the field of cartography. Road selection is one of the main operations in topographic map generalization. It aims to maintain global and local patterns [1,2] and connectivity [3,4,5] of the original road network while reducing the level of detail in the road network. According to the representation mode of road networks, road selection methods can be broadly categorized into mesh-based methods, line-based methods, and combined line-mesh methods [6].

Mesh-based methods indirectly select roads by aggregating the meshes enclosed by road segments in terms of certain constraints (for example, the mesh area is less than the pre-defined threshold) [7,8,9,10,11]. The density pattern and connectivity of the road network can be better retained through these methods [10]. However, this method is not applicable to networks that are unable to construct areas and seldom takes into account the topological characteristics of roads.

Line-based methods are the most commonly used methods in road selection. They are realized by directly deleting roads in a ranked order [1,2,3,4,12,13,14,15,16,17,18,19,20,21,22,23,24]. In this group of methods, much attention is paid to topological relationships. For example, guided by graph theory, road networks are manipulated as connected graphs to perform road selection. Some conceptions like shortest path [12], minimum-spanning-tree [3], and centrality [4] are included to guide road selection. However, the centrality approach is unable to maintain the density distribution of original road networks and neglects some factors in actual road networks, such as roundabouts, dead ends, etc. Weiss and Weibel [13] developed some extensions in response to the aforementioned problems, realizing desirable selection results at small scales.

Line-mesh combination methods achieve selection by successively aggregating meshes and selecting the line features attached to those meshes. These combination methods focus on the individual meshes or lines in road networks, thus performing better than separate methods at medium scales [6,25]. However, different results might be produced by using different combination strategies of lines and meshes. Hence, this method needs to be further explored [26].

Compared with other map features, roads, as a linear feature, have noticeable characteristics in their connectivity and continuity. Fractured and disconnected networks can easily be generated by selection based on road segments. To avert this drawback, Thomson and Richardson proposed the concept of “strokes” based on the good continuation principle of perceptual grouping [15]. In this method, several neighboring road segments are grouped into a stroke, which is then treated as a unit in the selection process. This concatenation mode is widely used in line-based methods and line-mesh methods due to its superiority in maintaining the longitudinal hierarchy and geometric features of the original network. In addition, with the development of volunteered geographic information (VGI), methods that employ big data have come into being, thus widening the clues and perspectives of road selection studies. Points of Interest (POIs)have been adapted in recent years to regulate road selection. Xu et al. developed parameters such as POI density and the ratio of significant POIs around a road to reflect the contextual characteristics of roads [22]. However, this method is insufficient to distinguish the relative importance of different categories of POIs. For transportation purposes, Yu et al. added constraints between strokes by using taxi trajectory data [27]. Benz proposed the concept of POI accessibility. He argued that the paths to POIs should be retained in the selection process to enhance the practicality of the generalized results [25]. In addition, some objective weighting methods, such as Criteria Importance Though Intercriteria Correlation (CRITIC) [17,26,28], entropy [24], and coefficient of variation [22], were introduced to regulate the influence of different indicators on road selection. These methods have a strong mathematical basis, and are able to avoid different selection results caused by differences in cartographic experience. However, the determined weights often fail to reflect the actual importance of the indicators in the road selection environment. For instance, betweenness centrality should be given a higher weight in small-scale generalization due to its ability to identify the main hubs in a network [13]. While a road’s frequency of usage, type, width, length, and degree centrality also play a vital role in generalization at medium scales, these indicators contain local information about roads and reflect the relations between roads and their neighboring facilities. Hence, these methods lead to the weights of indicators being inconsistent with cartographic experience. In this regard, the analytic hierarchy process (AHP) [29], a multiple criteria decision-making tool, was introduced into road selection.

In the AHP model, superior alternatives can be identified. AHP has been applied to almost all fields involving decision-making, since its invention [30]. Rather than pursuing complex mathematical methods, AHP employs pairwise matrices and their associated right-eigenvectors to generate appropriate priority sequences of alternatives [29]. AHP is tolerant of different math tools, like linear programming, fuzzy logic, etc., whose merits can thus be extracted to achieve a desired outcome. Further, AHP organically combines qualitative and quantitative methods and decomposes a decision into a multi-level hierarchical structure. In this way, decision makers’ thinking processes are systematized and simplified. Both cartographic experience and the relations between indicator values can be incorporated into the evaluation system.

This is the first application of AHP in road selection. As a line-based method, our method is suitable for small-scale generalization. In addition, the surrounding habitations and facilities of a road can influence the importance of roads. In this regard, apart from summarizing structural characteristic indicators, an indicator reflecting the contextual characteristics of roads is built by scoring different categories of POIs. The importance values of strokes can be calculated in the AHP model, and the result of AHP serves as the fundamental basis for road selection. This method fully captures the attribute information of roads and conducts the road evaluation process in a structured and organized manner, which can be easily accepted. AHP delves deeper into the nature of road evaluation, multiple indicators, and the internal relations of roads.

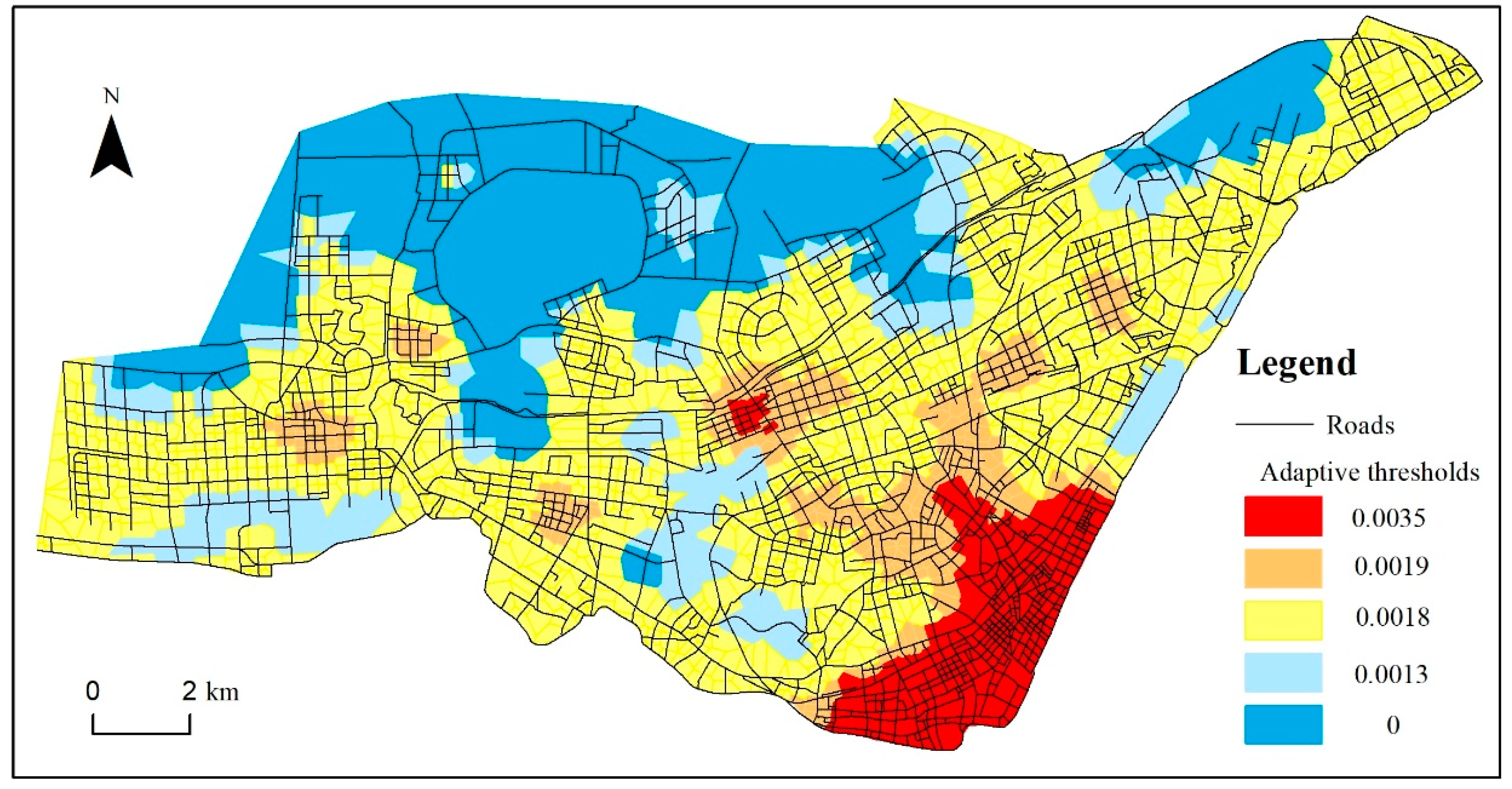
The remainder of this paper is organized as follows. Section 2 begins with an introduction to AHP. In Section 3, a road evaluation strategy based on AHP is proposed. Section 4 offers a density maintenance solution based on adaptive thresholds. Section 5 elaborates the detailed selection process as well as a connectivity maintenance algorithm. In Section 6, attention is turned to validations of the proposed approach. Finally, some conclusions are made in Section 7.

2. Basic Theory of AHP

AHP offers the concept of hierarchy when handling problems related to a number of criteria and alternatives. In this model, factors involved in the corresponding level are compared in a pairwise manner, and a numeric scale is designed to calibrate the subsequent results. AHP usually employs the following subsections.

2.1. Structuring the Target Problem in a Hierarchy

Broaden the problem into a hierarchical structure composed of following levels: a goal, criteria, sub-criteria and alternatives. In the AHP model, the goal of the problem forms the top level. The intermediate levels constitute the criteria and sub-criteria. The bottom level comprises the decision-making alternatives.

2.2. Computing the Weight Vector of the Criteria

Suppose a total of $m$ criteria participate in pairwise comparison. An$m\times m$ matrix $A$ is constructed. Each $a_{ij}$ entry in matrix $A$ represents the relative importance of the $i$th criterion with respect to the $j$th criterion, which is characterized by: ① $a_{ij}·a_{ji}=1$; ② $a_{ii}=1$ ③ $a_{ij}>0$. $a_{ij}$ is determined numerically according to the ratio-scale ranging from 1 to 9. It covers the entire comparison spectrum, as shown in

Table 1. Numerical scale of relative importance.

Numerical Scale	Interpretation
1	Equally important
3	Weakly important
5	Moderately important
7	Very important
9	Extremely important
2, 4, 6, 8	In between their two neighbors

. Finally, perform a calculation to find the maximum eigenvalue ${\lambda }_{max}$ and its corresponding eigenvector $w$ of matrix $A$:

$$Aw={\lambda }_{max}w, w={\left(w_1,w_2,\dots ,w_m\right)}^T$$

(1)

where $w_m$ represents the priority weight of the $m$th criterion.

Then, calculate the consistency index $CI$ and the consistency ratio $CR$ using Formulaes (2) and (3) to verify the effectiveness of the comparison matrix $A$.

$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

(2)

$$CR=CI/RI$$

(3)

where $n$ is the order of matrix $A$, $RI$ is mean random consistency index and can be determined by

Table 2. Mean random consistency index$RI$.

$\mathit{n}$	1	2	3	4	5	6	7	8	9
RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45

. If $CR$ < 0.1, the comparison matrix conforms to the consistency standard.

2.3. Computing the Score Matrix of Alternatives

Given $n$ alternatives altogether, compare each alternative, whose results are calibrated on the numerical scale in Table 1 to develop an $n\times n$ matrix $B^{\left(j\right)}$ with respect to the $j$th criterion,$j=1,\dots ,m$. Each entry $b_{ih}^{\left(j\right)}$ in matrix $B^{\left(j\right)}$ stands for the relative importance of the $i$th alternative compared with the $h$th alternatives under the $j$th criterion. Find the maximum eigenvalue and its corresponding eigenvector $s^{\left(j\right)}$ of matrix $B^{\left(j\right)}$. Finally, the weight vectors $s^{\left(j\right)}$ are grouped into the score matrix $S$:

$$S=\left[s^{\left(1\right)},\dots ,s^{\left(m\right)}\right]$$

(4)

2.4. Computing the Global Alternative Scores

The global scores $V$ are finally obtained by multiplying the score matrix S and the weight vector $W$.

$$V=S·W$$

(5)

The priority of the $i$th alternative depends on the entry$v_i$ of $V$.

3. Road Importance Evaluation Strategy Based on AHP

3.1. Road Network Maps

As shown in Figure 1, the experimental dataset was collected from the road network from Hankou District, Wuhan City, China, at a scale of 1:5000 and contains a total of 2815 segments. A total of 65,650 POIs inside road buffers were fetched from the open platform of Amap (http://lbs.amap.com/) by a Python crawler. Amap is a Chinese supplier of digital map content, navigation, and location services solutions., so the aforementioned website is in Chinese.

The roads in the map present a discernable distribution pattern. The roads in the lower-right corner are more densely distributed and surrounded by more POIs. These roads constitute the commercial center of the district. The roads and POIs in the upper areas are relatively sparse and represent the sub-urban areas.

3.2. Linegraph and Structural Characteristic Indicators of the Road Network

In road selection studies, when using graph theoretic principles, there are two kinds of common representations of road networks: one is to present roads as edges and road intersections as nodes, and the other is to map a road network onto a line graph, with roads as nodes and road intersections as edges.

The line graph can be defined by a simple unweighted graph $D=\langle N,E\rangle$, where $N$ and $E$ are the number of nodes and connected edges, respectively. The advantage of a line graph is that it is able to depict the connecting relationships between roads, the status of roads in a network, and the local and global efficiency of road networks clearly [31]. Hence, a line graph aids in the in-depth analysis of the structural characteristics and overall morphology of a road network [32].

The practice of treating strokes, sets of road segments, as the selection unit has been widely accepted in previous research. Strokes are usually generated in terms of the semantic consistency or deflection angle threshold between neighboring road segments. Some studies have argued that a deflection angle threshold within a range of 40°~60° is optimal [33]. However, Weiss and Weibel [13] used a series of hierarchical angle thresholds according to road classes. This solution generated more reasonable stroke networks. Due to the lack of road class information, we adapted the standard method of setting the deflection angle to 45° to generate strokes.

Figure 2 shows an example to illustrate the methods mentioned above. To the left is a stroke network generated based on a deflection angle of 45°, while to the right is the corresponding line graph.

Geometrical characteristics and topological relations are the most fundamental and important attributes of roads and the key factors that affect the function of road networks. The relevant information for these attributes is inherent in road networks. Thus, they are highly practical to reflect the importance of roads [19]. Derived from a line graph, centrality indicators are used to measure the topological characteristics of roads, which can be mathematically summarized as degree centrality, betweenness centrality, and closeness centrality [4]. As a global indicator, betweenness centrality measures to what extent a road lies in between the paths connecting other roads and has the advantage of revealing the hierarchical importance of roads [13]. In this algorithm, the shortest distances from a given node to all other nodes within a network need to be calculated. So betweenness centrality is computationally expensive in practice. Although $DC$,$P$, and $L$ measure the importance of a stroke from a local perspective, they potentially identify the status of a stroke from the aspect of a structure. Closeness centrality measures to what extent a road is close to the center of a network, without representing the structural characteristics of roads. Thus, betweenness centrality and degree centrality are included in our approach. Since it is not guaranteed that a road with significant topological properties will function well in the network, the length of the stroke is introduced to measure the geometric characteristics of roads.

3.3. Contextual Characteristic Indicator of Roads

In addition to the structural characteristics of roads, it is also necessary to consider the surrounding habitations and facilities. Roads surrounded by key facilities tend to be more significant. Conversely, if the habitations and facilities around a road are sparse and insignificant, its status in the network might be lowered. For example, Wangfujing street in Beijing is not prominent in terms of structural characteristics. However, as a well-known commercial street in Beijing, it enjoys high recognition among people and performs a very important function. Furthermore, map features are constrained by their spatial interactions. The generalization of road networks should not be isolated from other features. Specifically, roads and their neighboring habitations are associated cartographic elements on maps [34,35]. This addition embodies the theory of the cooperative generalization of multiple features. In this regard, consideration should be given to the content of surrounding habitations and facilities to enhance the practicability and scientific rigor of road evaluation. To accomplish this, an indicator is built to define the contextual characteristics of roads assisted by POIs.

3.3.1. POI

A POI is a general term for any geographic entities that can be expressed using points, especially facilities and habitations. POI data are highly integrated and up to date. As point-like representations of habitations, POIs contain abundant relevant information, which can be used to assist in measuring the effects of contextual facilities on roads. According to existing studies and standard specifications [22,34], POIs within a buffer of 30 m from roads are regarded as habitations and facilities that are able to exert an influence on roads. In addition, due to the different sources of POI datasets, there are diverse POI classification criteria. Our objective is to distinguish differences in the importance of POIs by their classification. From this point of view, an official and unified classification of POIs is required. In this way, POIs are reclassified in line with the national standards for urban land classification (the code for the classification of urban land use and planning standards of development land GB50137-2011). The classification details are listed in

Table 3. Reclassification of Points of Interest (POIs).

First Class Classification	Second Class Classification
Residence Communities	residential areas, villas, etc.
Public Management	government agencies and administrative offices
Public Services	medical care, science and education, life services, etc.
Business Services	catering services, shopping services, financial services, accommodation services, etc.
Industrial	factories
Logistics and warehousing	warehouses, postal services, etc.
Transportation	transport facilities, affiliated facilities of roads, etc.
Public facilities	power supply, sewage treatments, public toilets, etc.
Greenbelts and squares	parks, squares, etc.

.

3.3.2. Building the Contextual Characteristic Indicator

Different categories of POIs have unequal influence on the status of a road. Thus, when measuring the contextual characteristics of strokes, the Delphi method [36] is introduced to score POIs in terms of their categories, thereby differentiating and quantizing the influence of different POIs.

The Delphi method is a widely accepted method used to gather insights from respondents. It aims to discover a complete range of options, potential assumptions and associated judgements and eventually reaches a consensus on a real-world topic. This method conducts a series of questionnaires repeatedly to collect feedback from the respondent group.

When receiving the questionnaires, the experts are required to make judgments of “not significant”, “not very significant”, “generally significant”, “rather significant” or “quite significant” for each category of POIs. According to a 5-point Likert scale, the above five types of judgments are assigned scores of 1 to 5. The attributes of some categories of POIs can be measured with industrial or national standards or via common sense. For example, the shopping service category can be clearly classified into supermarkets, general shopping malls, and small shops according to business scopes. Tourist attractions can be classified into world heritage sites, national attractions, provincial attractions, and other attractions. Medical care can be divided into general hospitals, specialized hospitals, clinics, and pharmacies. Therefore, when making judgments, on the one hand, experts should consider the influence of POIs on the importance of roads. On the other hand, they should distinguish the differences of the attributes and characteristics within one category. Assume that among eight cartographers, the numbers of experts scoring 1 to 5 for the $j$th category of POIs are $N_1^j$, $N_2^j$, $N_3^j$, $N_4^j$ and $N_5^j$, respectively, and the final score of the $j$th category is calculated as:

$$I{P}^j=\left(1\times N_1^j+2\times N_2^j+3\times N_3^j+4\times N_4^j +5\times N_5^j\right)/8$$

(6)

Scores for partial POI categories are shown in

Table 4. Scores of partial POI categories.

First Class Classification	Third Class Classification	Scores
Residence Communities	residential districts	1.25
Public Management	provincial and municipal government agencies	4.75
Public Services	art troupes	1
	general hospitals	4.875
	movie theaters	1.375
	sports venues	1
	national attractions	4.625
	research institutions	3.625
Business Services	supermarkets	4.5
	four-star hotels	2.125
	hostels	1
	office buildings	1
Industrial	mining companies	1.125
Logistics and warehousing	postal offices	1.625
Transportation	railway stations	4.25
	subways	2
Public facilities	public toilets	1
Greenbelts and squares	zoos	2.75

.

Both the number and importance of different categories of POIs alongside a stroke are indispensable parameters to determine the influence of contextual habitations and facilities. Gather the statistics for the number and categories of POIs inside the buffer of the $i$th stroke, and the contextual characteristic indicator can be calculated by the following formula:

$$P_i={\displaystyle \sum }_{j=1}^{n }{N}_i^j\times I{P}^j$$

(7)

where $N_i^j$ is the number of the POIs of the $j$th category inside the buffer of the $i$th stroke, and $I{P}^j$ is the score of the $j$th category. Unlike betweenness centrality, the $P$ measures the local characteristics of a road, so the indicator takes less computation time.

3.4. Stroke Importance Evaluation Based on AHP

In the model of AHP, the elements in the corresponding level are compared in a natural, pairwise manner, and their results are then synthesized to assist decision makers. Not only does this systematic and structured method make full use of attribute information, but it is also in line with human cognition [35]. In this paper, AHP is introduced to compute the priority weights of stokes. The betweenness centrality, degree centrality, contextual characteristic indicator, length (corresponding to $BC$, $DC$, $P$, and $L$, respectively) are integrated in the procedure to measure strokes from the perspective of their geometrical, topological, and contextual characteristics. The AHP model based on stroke importance is shown in Figure 3.

The proposed method is divided into the steps listed below:

Step 1: The values of the $BC$, $DC$, $P$, and $L$ of each stroke are calculated first. These four indicators are regarded as the criteria in AHP. Assume that there are $n$ strokes in the networks, then a matrix$\mathrm{A}$ of $n\times$4 can be constructed:

$$\mathrm{A}=\left(\begin{array}{cc}{\alpha }_1^{\left(BC\right)}& \begin{array}{ccc}{\alpha }_1^{\left(DC\right)}& {\alpha }_1^{\left(P\right)}& {\alpha }_1^{\left(L\right)}\end{array}\\ \begin{array}{c}{\alpha }_2^{\left(BC\right)}\\ {\alpha }_3^{\left(BC\right)}\\ \begin{array}{c}⋮\\ {\alpha }_4^{\left(BC\right)}\end{array}\end{array}& \begin{array}{ccc}\begin{array}{c}{\alpha }_2^{\left(DC\right)}\\ {\alpha }_3^{\left(DC\right)}\\ \begin{array}{c}⋮\\ {\alpha }_4^{\left(DC\right)}\end{array}\end{array}& \begin{array}{c}\begin{array}{c}{\alpha }_2^{\left(P\right)}\\ {\alpha }_3^{\left(P\right)}\end{array}\\ ⋮\\ {\alpha }_4^{\left(P\right)}\end{array}& \begin{array}{c}\begin{array}{c}{\alpha }_2^{\left(L\right)}\\ {\alpha }_3^{\left(L\right)}\end{array}\\ ⋮\\ {\alpha }_4^{\left(L\right)}\end{array}\end{array}\end{array}\right)$$

(8)

Step 2: Calculate the weights of the indicators

The weights of the indicators are determined by evaluating their effects on the importance of the strokes. $BC$ measures the importance of strokes in terms of the global and structural aspects of a network, so $BC$ has a more significant effect on strokes. $DC$,$P,$ and $L$ contain the local information of a stroke, so they are less important compared to $BC$. According to the ratio-scale in AHP (Table 2), the comparison matrix $A$ of the four indicators is shown in

Table 5. Comparison matrix of the indicators.

$\mathit{A}$	$\mathit{B}\mathit{C}$	$\mathit{D}\mathit{C}$	$\mathit{L}$	$\mathit{P}$
$BC$	1	2	2	2
$DC$	1/2	1	1	1
$L$	1/2	1	1	1
$P$	1/2	1	1	1

. The consistency ratio $CR=0$ indicates that comparison matrix$A$ is completely consistent.

Then, calculate the corresponding eigenvector $w$ of matrix $A$ to obtain the weight vector of the indicators: $w=$[0.4, 0.2, 0.2, 0.2].

Step 3: Calculate the score matrix of the strokes

Given $n$ total strokes in a network, construct an $n\times n$ pairwise comparison matrix $B^{\left(j\right)}$, $j=$ 1, 2, 3, 4 with respect to the indicators $BC$,$DC$,$P,$ and $L$, respectively, whose entry $b_{ih}^{\left(j\right)}={\alpha }_i^{\left(j\right)}/{\alpha }_h^{\left(j\right)}$ indicates the relative importance of the $i$th stroke compared to the $h$th stroke under the $j$th criterion. Note that if the $j$th indicator value of the $i$th or the $h$th stroke is 0, then $b_{ih}^{\left(j\right)}=0$. Then, find the maximum eigenvalue and its eigenvector $s^{\left(j\right)}$ of matrix $B^{\left(j\right)}$ according to Section 2. The weight vectors $s^{\left(j\right)}$ are grouped into the score matrix $S=\left[s^{\left(1\right)},\dots ,s^{\left(4\right)}\right]$.

$$B^{\left(j\right)}=\left(\begin{array}{cccc}{\alpha }_1^{\left(j\right)}/{\alpha }_1^{\left(j\right)}& {\alpha }_1^{\left(j\right)}/{\alpha }_2^{\left(j\right)}& \dots & {\alpha }_1^{\left(j\right)}/{\alpha }_n^{\left(j\right)}\\ {\alpha }_2^{\left(j\right)}/{\alpha }_1^{\left(j\right)}& {\alpha }_2^{\left(j\right)}/{\alpha }_2^{\left(j\right)}& \dots & {\alpha }_2^{\left(j\right)}/{\alpha }_{\mathrm{n}}^{\left(j\right)} \\ ⋮& ⋮& ⋮& ⋮\\ {\alpha }_n^{\left(j\right)}/{\alpha }_1^{\left(j\right)}& {\alpha }_n^{\left(j\right)}/{\alpha }_2^{\left(j\right)}& \dots & {\alpha }_{\mathrm{n}}^{\left(j\right)}/{\alpha }_{\mathrm{n}}^{\left(j\right)}\end{array}\right)$$

(9)

Step 4: Multiply score matrix $S$ and the indicator weight vector $W$ to obtain the final scores of the strokes.

4. Adaptive Thresholds Based on Road Density Partition

Since the density distribution of roads on maps is heterogeneous, the selection results should reflect the contrast in the road density of different regions, to avoid the flattening or reversal of the density of a road network [37,38]. In our method, the stroke importance in urban areas tends to be relatively high. Because the values of $BC$ and $P$ of the strokes in cities are higher, more roads in denser areas should be eliminated, while fewer roads should be eliminated in less dense areas in the generalization process. Considering the work of Tian [37] and Weiss and Weibel [13], we included a road density partition method based on Voronoi diagrams. The adaptive thresholds for stroke importance are pre-determined to regulate the selection process.

4.1. Road Density Partition

The basic idea of this method is that road intersections and endpoints are densely distributed in dense regions of the road network, while there are opposite situations in sparse regions. First, Voronoi diagrams of road intersections and endpoints are constructed to partition the entire map. The dense regions of the road network correspond to the clusters of Voronoi units of a small area. Similarly, the sparse regions correspond to the clusters of Voronoi units of a large area. Then, Getis-Ord Gi*, a hot spot analysis tool, is used to extract statistically high-value clustered regions and low-value clustered regions based on the area of the Voronoi units. Finally, the centroid points of the strokes are extracted. Their locations are then used to determine the density regions that the strokes belong to.

4.2. Preset Adaptive Thresholds Based on Road Density Partition

After the determination of the density regions of individual strokes, the adaptive thresholds for stroke importance are assigned to these clustered regions according to the importance values of their corresponding strokes. The principle for setting thresholds is to ensure the reservation of significant roads in each region and to exclude as many insignificant strokes as possible. Denser areas are constrained by more stringent thresholds. A stroke with a lower importance than the threshold is winnowed out when making selective omission decisions. The results of the road density partition and the preset thresholds for our test area are shown in Figure 4.

5. Road Selection Process

5.1. Overall Idea

In the proposed method, four indicators are considered in the selection process, $BC$,$DC$,$P$ and $L$. The values of these indicators are aggregated into AHP to calculate the scores of strokes, which are then used to rank the strokes. This procedure is done in four main steps:

(1)

Extract the indicator values of the strokes: Generate the stroke network by setting the deflection angle as 45° and obtain the length of strokes. Calculate the contextual characteristic information assisted by the POIs inside the stroke buffer. Map the stroke network into a line graph to calculate the centrality indicator values.

(2)

Conduct a density partition using a Voronoi diagram and Getis-Ord Gi* to determine the importance threshold of each stroke.

(3)

Compute the scores of the strokes by the AHP-based method in Section 3.4, and select strokes in the descending order of the calculated scores. If the score of a stroke is higher than its corresponding importance threshold, the stroke is selected. This selection process continues until the total number is higher than the result calculated by the radical law method.

(4)

If the selected road network is disconnected, then the connectivity maintenance process in Section 5.2 is performed to keep the road network globally connected. Figure 5 shows the specific process of the proposed method.

5.2. Connectivity Maintenance

The generated stroke networks that are selected according to the importance ranking might break up into several disconnected parts, which is unacceptable. Some insignificant strokes connecting these disconnected parts should also be retained. Hence, a connectivity maintenance algorithm is proposed to be used in the selected network. We argue that the following principles should be followed when maintaining connectivity: add as few new strokes as possible and give priority to strokes of higher importance. In this regard, we define the weights of edges$E$ in the line graph of a stroke network $D=\langle N,E\rangle$ and generate a spanning tree with the edges of maximum weight to maintain global connectivity.

5.2.1. Define Edge Weights for Line Graph

Edges in an unweighted complex network feature different significance [39]. To calculate the weights of these edges, we consider the importance of their constituent nodes. The edge weight $w_{ij}$ of the two connecting nodes $i$ and $j$ is defined as:

$$w_{ij}=\left\{I_i+I_j\right\}$$

(10)

where$I_i$ and $I_j$ are the scores of the corresponding strokes of nodes $i$ and $j$, respectively. In this way, the line graph of the stroke network is converted into a weighted graph.

5.2.2. Connectivity Maintenance Algorithm

Figure 6a, for example, represents a line graph of the original road network. The black node set $N_s$ represents the selected strokes according the score ranking, while the white nodes represent the rest of the strokes in the original network. One can see that the generated graph is disconnected. The steps to maintain connectivity are as follows:

(1) Calculate the weights of edges $E$ in the original line graph $D=\langle N,E\rangle$ by the formula in Section 5.2.1.

(2) Build a new spanning tree $D_t=\langle N_t,E_t\rangle$, in which $N_t=N$, $E_t$ = 0. Each node in $D_t$ is regarded as a separate tree.

(3) Add the edges selected from $E$ in descending order of weight to $E_t$. The nodes constituting the selected edges ought to belong to different trees, which are then merged into one tree, after selecting the edges.

(4) Repeat step (3) until all nodes are included in one tree, as shown in Figure 6b.

(5) Iteratively determine whether a leaf node in $D_t$ belongs to the selected node set $N_s$; if not, then delete it. This step ends until there are no white leaf nodes in $D_t$ (Figure 6c).

(6) The corresponding strokes of the remaining nodes in $D_t$ are the final result after maintaining connectivity (Figure 6d).

6. Experiments and Results

6.1. Comparison of the Methods with and without AHP

To highlight the effect of AHP, a comparison between the results with AHP, without AHP, and using the CRITIC method was conducted. In order to identify the difference between the three methods in prioritizing strokes, no extra solutions, i.e., adaptive density thresholds and connectivity maintenance, were applied to the optimization results. The stroke importance $I$ in the last two methods was assessed by the following formula:

$$I= w_1\ast BC+ w_2\ast DC+w_3\ast P+ w_4\ast L$$

(11)

In the method without AHP, $w_1$, $w_2$, $w_3$, and $w_4$ are 0.4, 0.2, 0.2, and 0.2, respectively, which are the same as the weights calculated by the first level of AHP. While the $w_1$, $w_2$, $w_3$, and $w_4$ calculated by CRITIC are 0.18, 0.16, 0.46, and 0.2, respectively. All the values of these indicators are normalized with an interval of [0, 1] before calculation.

Figure 7 shows the results at a scale of 1:200,000 for the three methods. Overall, the results in Figure 7a,b are rather similar. However, after zooming into the details, a few differences can be identified. As shown in the pink circles in (a) and (b), without AHP, more strokes in the urban areas are retained, while the strokes in sub-urban are unduly eliminated. However, the strokes with significant geometric characteristics in sub-urban areas are retained with AHP. In Figure 7c, it can be observed that neither the density distribution nor the coverage of the original road network is maintained by the CRITIC method. Too much weight is assigned to the indicator of $P$ and $L$, thus interfering with the structural characteristics of the road network. By comparing the values of the indicators in pairs and then combining the scores of the two layers, AHP achieves a more thorough and clear analysis of the relevant indicators, and accurately understands their internal relationships, thereby obtaining a more reasonable outcome.

In addition to the visual evaluation, we conducted a quantitative evaluation using the Pearson correlation coefficient, which is a linear correlation coefficient ranging from -1 to 1. This coefficient is used to reflect the degree of linear correlation between two variables. The larger the absolute value, the stronger the correlation. The Pearson correlation coefficient has been used to measure the structural similarity of complex networks [23,40]. We calculated the Pearson correlation coefficient of $BC$ between the generalized road networks and the original network to indicate their structural similarity. Assume that $V_u$ and $V_v$ are the node sets of network $u$ and $v$, respectively. Then, the structural similarity between $u$ and $v$ is calculated by the following formula:

$$S_{uv}=\frac{{{\displaystyle \sum }}_{\alpha \in O_{uv}}\left(r_{u\alpha }-\overline{r_u}\right)\left(r_{v\alpha }-\overline{r_v}\right)}{\sqrt{{{\displaystyle \sum }}_{\alpha \in O_{uv}}{\left(r_{u\alpha }-\overline{r_u}\right)}^2}\sqrt{{{\displaystyle \sum }}_{\alpha \in O_{uv}}{\left(r_{v\alpha }-\overline{r_v}\right)}^2}}$$

(12)

where $S_{uv}$ is the similarity measure of network $u$ and $v$;$O_{uv}={\mathsf{\Gamma }}_u{{\displaystyle \cap }}^{ }{\mathsf{\Gamma }}_v$ means that the node set is shared by network $u$ and $v$; and both $r_{u\alpha }$ and $r_{v\alpha }$ are topological measures (that refer to the betweenness centrality in this experiment) used to measure the structural similarity of network $u$ and $v$. $\overline{r_u}$ and $\overline{r_v}$ is the mean of the topological measures of $u$ and $v$, respectively.

Figure 8 shows the statistics of the betweenness centrality of the strokes in the generalized networks and in the original network. By comparing the Pearson correlation coefficient $r$, it can be concluded that our method better preserves the structural characteristics of the original road network.

6.2. Changes after Considering Contextual Characteristics

Figure 9 illustrates the changes in the importance order of the strokes after integrating the contextual characteristic indicator, in which the positive values represent an ascension in the ranking, and not vice versa. This analysis shows that the categories and number of POIs around different strokes varied, and different degrees of changes occurred in their rankings. The rankings of many streets that were insignificant in their contextual characteristics thus improved. These streets are distributed mainly in the business district at the lower-right corner of the map. However, in the suburban areas with a sparse POI distribution, there was a general drop in stroke rankings.

We ranked the strokes in the original network in descending order according to their $BC$ values. The top twelve strokes (rendered in green in Figure 10) did not change significantly before and after the constraint of POIs, and their statistics are listed in

Table 6. Changes in the order of the top twelve-ranked strokes.

Stroke ID	Order without POI	Order with POI	Difference in Order	$\mathit{B}\mathit{C}$	$\mathit{L}$	$\mathit{P}$	$\mathit{D}\mathit{C}$
0	2	2	0	0.15	30,224.67	1849.5	64
13	10	9	1	0.07	7256.21	1063.25	30
37	3	3	0	0.17	17,041.61	1866	53
39	5	4	1	0.10	14,541.79	941.25	35
52	1	1	0	0.21	21,111.06	1945.25	65
104	6	6	0	0.08	7887.87	1407.62	34
163	8	7	1	0.07	12,463.45	1388.88	41
220	4	5	−1	0.08	26,758.73	347.625	22
247	0	0	0	0.24	22,525.28	332.375	46
282	11	12	−1	0.06	7766.20	187.375	25
346	7	8	−1	0.07	9474.87	809.375	29
478	9	11	−2	0.06	11,430.17	67.375	21

. As indicated by their $BC$ values in the table, these strokes have prominent advantages in the topological structure of the original road network. The constraint of POIs did not significantly influence their rankings. Thus, it can be concluded that our method can also preserve the main structure of the road network in the Hankou District.

In addition, we compared the generalized results at a scale of 1:200,000 with and without the constraint of POIs. In this link, we determined the adaptive thresholds for stroke importance and the connectivity maintenance solution. The different strokes are highlighted in Figure 11. One can see that these different strokes feature similar structural characteristics. The strokes rendered in green tend to be surrounded by more POIs compared to strokes rendered in blue. These green strokes play a relatively significant role in people’s travel due to their adjacent POIs, so they should be preferentially retained in generalized maps compared to blue strokes. Therefore, roads with relatively significant contextual characteristics were selected prior to their competitors, thereby yielding a more reasonable result.

6.3. Comparison with Manual Method

Finally, manual selection was conducted by referring to compilation specifications for national scale maps. Experienced cartographers were invited to select strokes according to general principles, to ensure the preservation of significant roads, to maintain the connection between roads and residential areas, and to maintain the characteristics of the plane graphics of road networks. The result of manual selection was treated as the benchmark. The comparison results between manual approach and our approach are shown in Figure 12. The first observation in the comparison maps is that the results of our approach basically agree with those of the manual approach.

Through in-depth discussion with our cartographic experts, we evaluated the generalized results of our method as follows: The general thinning of the road network was acceptable. The road networks in urban and sub-urban areas were properly generalized overall. However, slight thinning was still needed in denser areas (in the orange circles). Some roads (in the pink circles) that reflected significant structural features of the network were pruned. The ‘crisp boundary effect’, the adaptive thresholds, the constraint of POIs, or the lack of road class are potential reasons for these deviations.

To reflect the results more specifically, we adopted the maximum similarity approach to measure the consistency among two results. The similarity results are listed in

Table 7. Statistics of maximum similarity and its related parameters.

Parameters	Values
Total length of roads by manual method /km	560,498.1
Total length of roads by our method /km	534,801
Total length of common roads of two methods /km	522,549.5
Maximum Similarity	0.91
Ratio of common stroke number among two methods to total selected number	0.89

. The statistics indicate that the two results achieve good consistency.

7. Conclusions

The accurate and reasonable evaluation of roads is a prerequisite for road selection. Some weighting methods such as CRITIC, entropy, and coefficient of variation are widely used in line-based methods. The weights of the road indicators assigned by these methods are not consistent with actual cartographic experience. In this regard, we adapted AHP to prioritize our strokes. Among the various road selection methods, line-based methods generally include multiple indicators to determine the priority order of roads, which can be deemed a multi-attribute decision-making problem. Considering the advantages of AHP in handling this kind of problem, a new road selection method is proposed based on AHP. Previous studies tend to solely rely on the indicators summarized by the intrinsic information of road networks. However, if the effects of other features, such as surrounding habitations or facilities, are included and quantitatively described in the selection method, the produced road network might be more in tune with actual needs. Therefore, we established a road evaluation indicator system that considers both the structural and contextual characteristics of roads. In our method, the contextual characteristic indicator is built according to the surrounding POIs of roads, which is then integrated into the model of AHP along with structural characteristic indicators to calculate the importance values of strokes. We also designed another two complementary solutions, namely preset adaptive thresholds and connectivity maintenance, to improve the generalized results.

To evaluate the performance, we carried out visual and quantitative experiments. Some improvements in terms of the structures and contextual characteristics of roads could be identified. The results ofour method achieved higher accuracy than manual selection. Hence, it is feasible to apply AHP to road selection. In addition, the extra computing time produced by the proposed indicator in Section 3.3.2 can be ignored. Thus, this method has the potential to be adopted in road generalization.