Optimal Signal Wavelengths for Underwater Optical Wireless Communication under Sunlight in Stratified Waters
Abstract
:1. Introduction
- Investigated the effect of attenuation on the end-to-end diffused line-of-sight and point-to-point line-of-sight UOWC systems under eight realistic ocean stratification scenarios in order of increasing turbidity, under a “night condition”.
- Investigated the combined effect of signal attenuation and ambient solar radiation on end-to-end diffused line-of-sight and point-to-point line-of-sight UOWC systems under the eight stratification scenarios. This was evaluated for horizontal links and downlinks (transmitter is vertically above the receiver, with the receiver directly facing up in direct view of sunlight) by varying depth and distance.
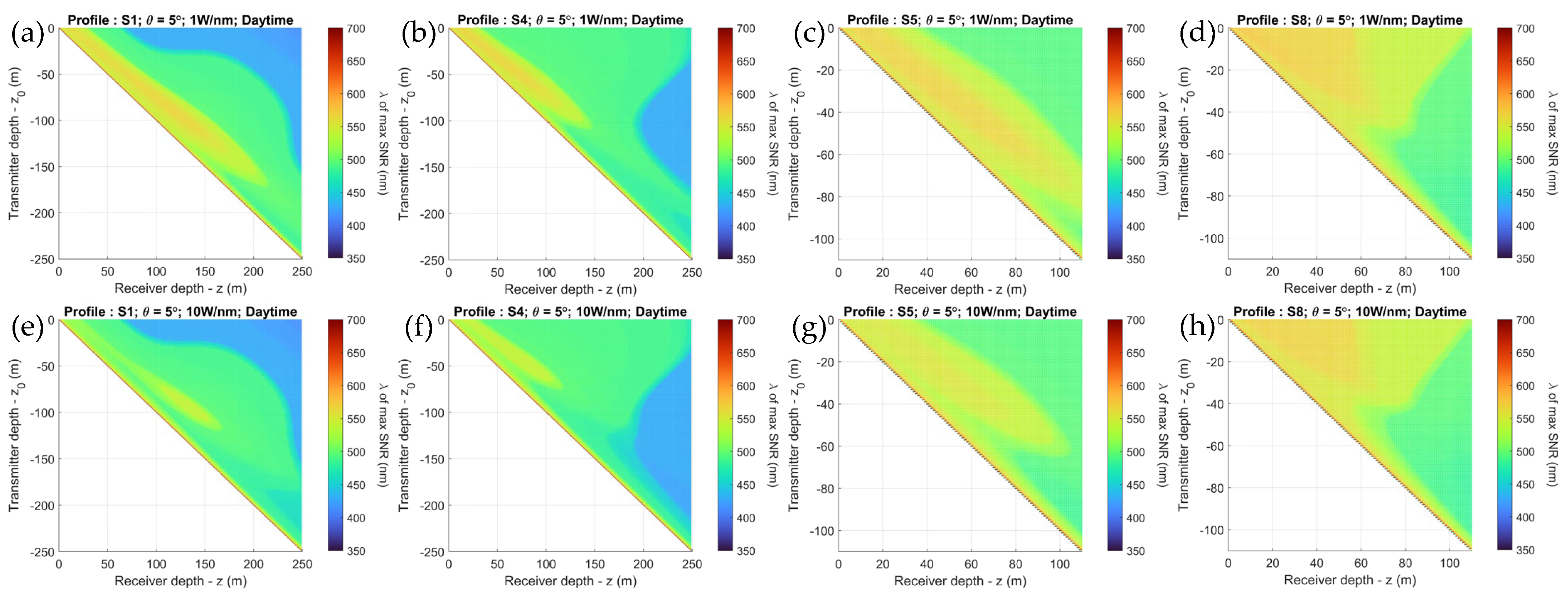
- Shared novel insights on the wavelength preferences for the signal (400–700 nm) for the optimum optical signal-to-noise ratio (O-SNR) under the conditions described above, that seems to be connected to the transmitter and receiver parameters such as transmit power, beam divergence, and the receiver (photodetector) wavelength responsivity curve. The results have been shown with trends discussed for four selected profiles for brevity, in order of increasing turbidity.
- Demonstrated the variability of the maximum achievable link distance with depth based on the O-SNR (0 dB distance) correlated to the signal wavelength that achieves it.
- Shared insights on how these findings may be used to establish cooperative UOWC links for the optimal SNR, based on water profile, depth relative to the deep chlorophyll maximum, link orientation, and distance between the nodes. These findings may be useful for establishing UOWC within individual sites, such as aquaculture farms, or renewable energy sites if the site-specific water quality parameters are known and where the region of the UUV mission or connectivity of the UOWC network would span depths of the euphotic and disphotic zones.
2. Preliminaries
3. Related Works
4. Time-Varying Environmental Influences
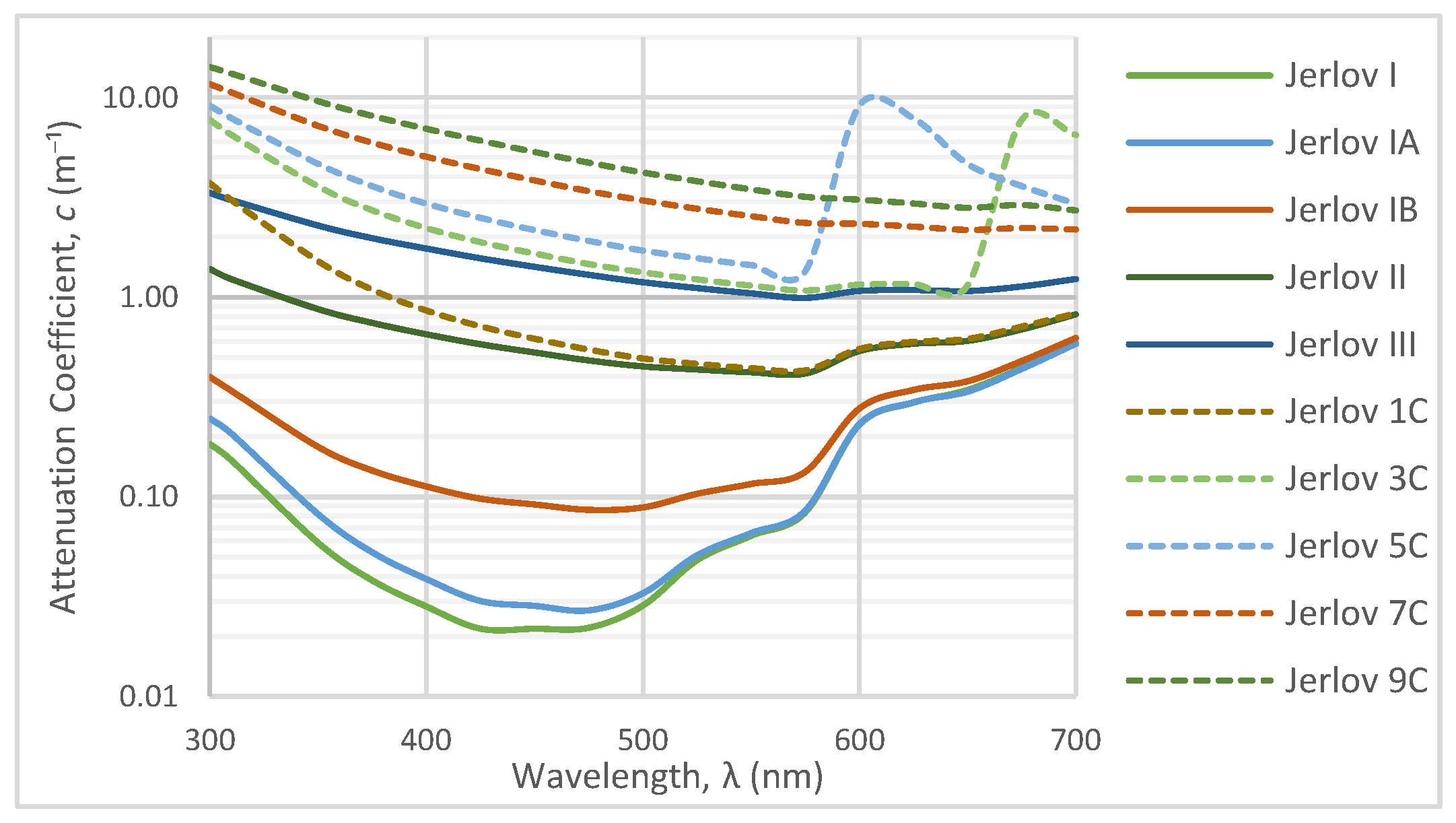
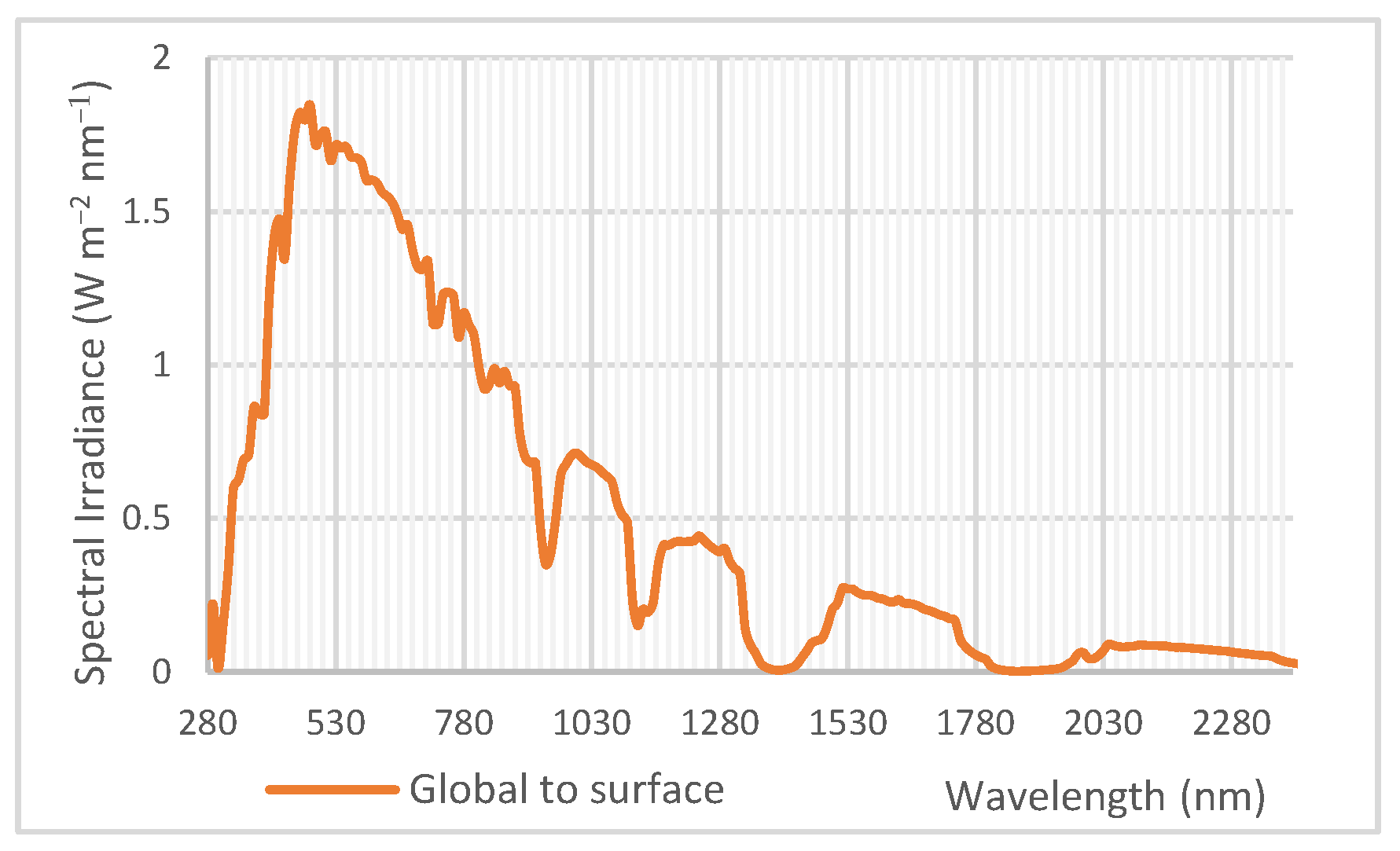
4.1. Downwelling Ambient Light
4.2. Stratified Oceans
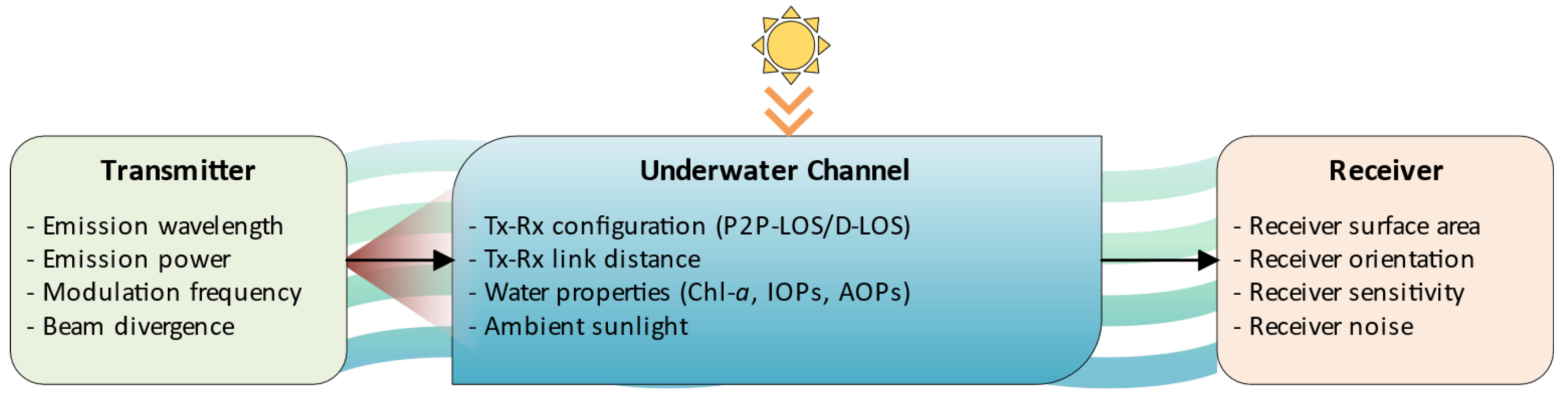
5. System Model
5.1. Haltrin’s Single-Parameter IOP Model Based on Concentration of Chlorophyll-a
5.2. Ambient Noise
5.3. Geometric Propagation Models Common for UOWC
5.4. Optical SNR
6. Simulation and Parameters
6.1. Transmitter and Receiver Parameters
6.2. Downlink and Depth-Variant Horizontal Link
6.3. Simulation
7. Results and Discussion
7.1. Simulation Results with No Sunlight
7.2. Simulation Results with Sunlight
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Class | (mg m™3) | (mg m™2) | (mg m™2) | (mg m™3) | (m) | (m) |
|---|---|---|---|---|---|---|
| S1 | 0.0429 | −0.103 | 11.86 | 0.174 | 114.6 | 415.5 |
| S2 | 0.0805 | −0.261 | 13.86 | 0.237 | 90.6 | 309.5 |
| S3 | 0.0801 | −0.284 | 18.54 | 0.244 | 79.9 | 282.2 |
| S4 | 0.144 | −0.544 | 15.42 | 0.300 | 62.2 | 264.2 |
| S5 | 0.211 | −1.05 | 14.37 | 0.389 | 43.3 | 200.7 |
| S6 | 0.160 | −0.706 | 21.24 | 0.460 | 31 | 226.8 |
| S7 | 0.332 | −1.96 | 20.06 | 0.637 | 20 | 169.1 |
| S8 | 1.014 | −9.09 | 17.48 | 1.31 | 13.9 | 111.5 |
| S9 | 0.555 | 0 | 90.02 | 3.17 | 9.9 | – |
References
- Rayner, R.; Jolly, C.; Gouldman, C. Ocean observing and the blue economy. Front. Mar. Sci. 2019, 6, 330. [Google Scholar] [CrossRef]
- Walsh, D. Exploration and technology—Key building blocks for the new blue economy. In Preparing a Workforce for the New Blue Economy; Elsevier: Amsterdam, The Netherlands, 2021; pp. 3–16. [Google Scholar]
- Graham, A.; Marouchos, A.; Martini, A.; Fischer, A.; Seet, B.-C.; Guihen, D.; Williams, G.; Symonds, J.; Ross, D.; Soutar, J.; et al. Autonomous Marine Systems at Offshore Aquaculture and Energy Sites; 1.20. 002–Final Project Report; Blue Economy CRC: Launceston, Australia, 2020. [Google Scholar]
- Petillot, Y.R.; Antonelli, G.; Casalino, G.; Ferreira, F. Underwater robots: From remotely operated vehicles to intervention-autonomous underwater vehicles. IEEE Robot. Autom. Mag. 2019, 26, 94–101. [Google Scholar] [CrossRef]
- Bogue, R. Underwater robots: A review of technologies and applications. Ind. Robot. Int. J. 2015, 42, 186–191. [Google Scholar] [CrossRef]
- Yang, Y.; Xiao, Y.; Li, T. A survey of autonomous underwater vehicle formation: Performance, formation control, and communication capability. IEEE Commun. Surv. Tutor. 2021, 23, 815–841. [Google Scholar] [CrossRef]
- Khojasteh, D.; Kamali, R. Design and dynamic study of a ROV with application to oil and gas industries of Persian Gulf. Ocean Eng. 2017, 136, 18–30. [Google Scholar] [CrossRef]
- Sahoo, A.; Dwivedy, S.K.; Robi, P. Advancements in the field of autonomous underwater vehicle. Ocean Eng. 2019, 181, 145–160. [Google Scholar] [CrossRef]
- Connor, J.; Champion, B.; Joordens, M.A. Current algorithms, communication methods and designs for underwater swarm robotics: A review. IEEE Sens. J. 2020, 21, 153–169. [Google Scholar] [CrossRef]
- Waduge, T.J.G.; Joordens, M. Fish robotic research platform for swarms. In Proceedings of the 2017 25th International Conference on Systems Engineering (ICSEng), Las Vegas, NV, USA, 22–24 August 2017; pp. 212–217. [Google Scholar]
- Luo, H.; Wang, X.; Bu, F.; Yang, Y.; Ruby, R.; Wu, K. Underwater real-time video transmission via wireless optical channels with swarms of AUVs. IEEE Trans. Veh. Technol. 2023, 19, 1–44. [Google Scholar] [CrossRef]
- Pal, A.; Campagnaro, F.; Ashraf, K.; Rahman, M.R.; Ashok, A.; Guo, H. Communication for underwater sensor networks: A comprehensive summary. ACM Trans. Sens. Netw. 2022, 19, 1–44. [Google Scholar] [CrossRef]
- Meinecke, G.; Ratmeyer, V.; Renken, J. HYBRID-ROV-Development of a new underwater vehicle for high-risk areas. In Proceedings of the OCEANS’11 MTS/IEEE KONA, Waikoloa, HI, USA, 19–22 September 2011; pp. 1–6. [Google Scholar]
- Azis, F.; Aras, M.; Rashid, M.; Othman, M.; Abdullah, S. Problem identification for underwater remotely operated vehicle (ROV): A case study. Procedia Eng. 2012, 41, 554–560. [Google Scholar] [CrossRef]
- Laranjeira, M.; Dune, C.; Hugel, V. Catenary-based visual servoing for tether shape control between underwater vehicles. Ocean Eng. 2020, 200, 107018. [Google Scholar] [CrossRef]
- Armstrong, R.A.; Pizarro, O.; Roman, C. Underwater robotic technology for imaging mesophotic coral ecosystems. In Mesophotic Coral Ecosystems; Springer: Berlin/Heidelberg, Germany, 2019; pp. 973–988. [Google Scholar]
- Kaya, A.; Yauchi, S. An acoustic communication system for subsea robot. In Proceedings of the Proceedings OCEANS, Seattle, WA, USA, 18–21 September 1989; pp. 765–770. [Google Scholar]
- Suzuki, M.; Sasaki, T.; Tsuchiya, T. Digital acoustic image transmission system for deep-sea research submersible. In Proceedings of the OCEANS’92 Proceedings@ m_Mastering the Oceans through Technology, Newport, RI, USA, 26–29 October 1992; pp. 567–570. [Google Scholar]
- Kaushal, H.; Kaddoum, G. Underwater optical wireless communication. IEEE Access 2016, 4, 1518–1547. [Google Scholar] [CrossRef]
- Hoeher, P.A.; Sticklus, J.; Harlakin, A. Underwater optical wireless communications in swarm robotics: A tutorial. IEEE Commun. Surv. Tutor. 2021, 23, 2630–2659. [Google Scholar] [CrossRef]
- Stojanovic, M. Underwater acoustic communications: Design considerations on the physical layer. In Proceedings of the 2008 Fifth Annual Conference on Wireless on Demand Network Systems and Services, Garmisch-Partenkirchen, Germany, 23–25 January 2008; pp. 1–10. [Google Scholar]
- Akyildiz, I.F.; Pompili, D.; Melodia, T. Underwater acoustic sensor networks: Research challenges. Ad Hoc Netw. 2005, 3, 257–279. [Google Scholar] [CrossRef]
- Zeng, Z.; Fu, S.; Zhang, H.; Dong, Y.; Cheng, J. A survey of underwater optical wireless communications. IEEE Commun. Surv. Tutor. 2016, 19, 204–238. [Google Scholar] [CrossRef]
- Saeed, N.; Celik, A.; Al-Naffouri, T.Y.; Alouini, M.-S. Underwater optical wireless communications, networking, and localization: A survey. Ad Hoc Netw. 2019, 94, 101935. [Google Scholar] [CrossRef]
- Dautta, M.; Hasan, M.I. Underwater vehicle communication using electromagnetic fields in shallow seas. In Proceedings of the 2017 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’s Bazar, Bangladesh, 16–18 February 2017; pp. 38–43. [Google Scholar]
- Li, Y.; Wang, S.; Jin, C.; Zhang, Y.; Jiang, T. A survey of underwater magnetic induction communications: Fundamental issues, recent advances, and challenges. IEEE Commun. Surv. Tutor. 2019, 21, 2466–2487. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, M.; Shu, M.; An, J.; Ding, W.; Liu, X.; Wang, S.; Zhao, C.; Yu, H.; Wang, H.; et al. Underwater wireless communication via TENG-generated Maxwell’s displacement current. Nat. Commun. 2022, 13, 1–10. [Google Scholar]
- Li, C.-Y.; Lu, H.-H.; Tsai, W.-S.; Cheng, M.-T.; Ho, C.-M.; Wang, Y.-C.; Yang, Z.-Y.; Chen, D.-Y. 16 Gb/s PAM4 UWOC system based on 488-nm LD with light injection and optoelectronic feedback techniques. Opt. Express 2017, 25, 11598–11605. [Google Scholar] [CrossRef]
- Wu, T.-C.; Chi, Y.-C.; Wang, H.-Y.; Tsai, C.-T.; Lin, G.-R. Blue laser diode enables underwater communication at 12.4 Gbps. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Lu, I.-C.; Liu, Y.-L. 205 Mb/s LED-based underwater optical communication employing OFDM modulation. In Proceedings of the 2018 OCEANS-MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–4. [Google Scholar]
- Lanzagorta, M. Underwater communications. Synth. Lect. Commun. 2012, 5, 1–129. [Google Scholar]
- Jamali, M.V.; Salehi, J.A.; Akhoundi, F. Performance studies of underwater wireless optical communication systems with spatial diversity: MIMO scheme. IEEE Trans. Commun. 2017, 65, 1176–1192. [Google Scholar] [CrossRef]
- Johnson, L.J.; Green, R.J.; Leeson, M.S. Underwater optical wireless communications: Depth dependent variations in attenuation. Appl. Opt. 2013, 52, 7867–7873. [Google Scholar] [CrossRef]
- Uitz, J.; Claustre, H.; Morel, A.; Hooker, S.B. Vertical distribution of phytoplankton communities in open ocean: An assessment based on surface chlorophyll. J. Geophys. Res. Ocean. 2006, 111, 0148–0227. [Google Scholar] [CrossRef]
- Gabriel, C.; Khalighi, M.-A.; Bourennane, S.; Léon, P.; Rigaud, V. Monte-Carlo-based channel characterization for underwater optical communication systems. J. Opt. Commun. Netw. 2013, 5, 1–12. [Google Scholar] [CrossRef]
- Solonenko, M.G.; Mobley, C.D. Inherent optical properties of Jerlov water types. Appl. Opt. 2015, 54, 5392–5401. [Google Scholar] [CrossRef] [PubMed]
- Jerlov, N.G. Optical studies of ocean water. Rept. Swed. Deep-Sea Exped. 1951, 3, 1–59. [Google Scholar]
- Williamson, C.A.; Hollins, R.C. Measured IOPs of Jerlov water types. Appl. Opt. 2022, 61, 9951–9961. [Google Scholar] [CrossRef]
- Sticklus, J.; Hieronymi, M.; Hoeher, P.A. Effects and constraints of optical filtering on ambient light suppression in LED-based underwater communications. Sensors 2018, 18, 3710. [Google Scholar] [CrossRef]
- Giuliano, G.; Laycock, L.; Rowe, D.; Kelly, A.E. Solar rejection in laser based underwater communication systems. Opt. Express 2017, 25, 33066–33077. [Google Scholar] [CrossRef]
- Yap, Y.; Jasman, F.; Marcus, T. Impact of chlorophyll concentration on underwater optical wireless communications. In Proceedings of the 2018 7th International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 19–20 September 2018; pp. 1–6. [Google Scholar]
- Jain, A.; Debnath, B.; Sharma, R. Underwater visible light vertical communication for distinctive chlorophyll. In Proceedings of the 2022 Second International Conference on Advances in Electrical Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 21–22 April 2022; pp. 1–5. [Google Scholar]
- Hudcova, L.; Kovalova, A. Calculation of solar noise in selected underwater depths. In Proceedings of the 2022 32nd International Conference Radioelektronika (RADIOELEKTRONIKA), Kosice, Slovakia, 21–22 April 2022; pp. 1–6. [Google Scholar]
- Elamassie, M.; Uysal, M. Vertical underwater visible light communication links: Channel modeling and performance analysis. IEEE Trans. Wirel. Commun. 2020, 19, 6948–6959. [Google Scholar] [CrossRef]
- Ji, X.; Yin, H.; Jing, L.; Liang, Y.; Wang, J. Modeling and performance analysis of oblique underwater optical communication links considering turbulence effects based on seawater depth layering. Opt. Express 2022, 30, 18874–18888. [Google Scholar] [CrossRef]
- Lou, Y.; Cheng, J.; Nie, D.; Qiao, G. Performance of vertical underwater wireless optical communications with cascaded layered modeling. IEEE Trans. Veh. Technol. 2022, 71, 5651–5655. [Google Scholar] [CrossRef]
- Ijeh, I.C.; Khalighi, M.A.; Hranilovic, S. Parameter optimization for an underwater optical wireless vertical link subject to link misalignments. IEEE J. Ocean. Eng. 2021, 46, 1424–1437. [Google Scholar] [CrossRef]
- Duntley, S.Q. Light in the sea. JOSA 1963, 53, 214–233. [Google Scholar] [CrossRef]
- Tyler, J.E. Radiance Distribution as a Function of Depth in the Submarine Environment; UC San Diego: Scripps Institution of Oceanography: La Jolla, CA, USA, 1958. [Google Scholar]
- Hoejerslev, N.K.; Aas, E. Spectral irradiance, radiance, and polarization in blue western Mediterranean waters. In Proceedings of the Ocean Optics XIII, SPIE 2963, Halifax, NS, Canada, 6 February 1997; pp. 138–147. [Google Scholar]
- Bird, R.E.; Riordan, C. Simple solar spectral model for direct and diffuse irradiance on horizontal and tilted planes at the earth’s surface for cloudless atmospheres. J. Appl. Meteorol. Climatol. 1986, 25, 87–97. [Google Scholar] [CrossRef]
- Solar Spectrum Calculator. Available online: https://www2.pvlighthouse.com.au/calculators/solar%20spectrum%20calculator/solar%20spectrum%20calculator.aspx (accessed on 25 January 2023).
- Miller, S.D.; Turner, R.E. A dynamic lunar spectral irradiance data set for NPOESS/VIIRS day/night band nighttime environmental applications. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2316–2329. [Google Scholar] [CrossRef]
- Ali, M.F.; Jayakody, D.N.K.; Li, Y. Recent trends in underwater visible light communication (UVLC) systems. IEEE Access 2022, 10, 22169–22225. [Google Scholar] [CrossRef]
- Kameda, T.; Matsumura, S. Chlorophyll biomass off Sanriku, northwestern Pacific, estimated by Ocean Color and Temperature Scanner (OCTS) and a vertical distribution model. J. Oceanogr. 1998, 54, 509–516. [Google Scholar] [CrossRef]
- Haltrin, V.I. Chlorophyll-based model of seawater optical properties. Appl. Opt. 1999, 38, 6826–6832. [Google Scholar] [CrossRef]
- Prieur, L.; Sathyendranath, S. An optical classification of coastal and oceanic waters based on the specific spectral absorption curves of phytoplankton pigments, dissolved organic matter, and other particulate materials 1. Limnol. Oceanogr. 1981, 26, 671–689. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Adams, J.T.; Aas, E.; Højerslev, N.K.; Lundgren, B. Comparison of radiance and polarization values observed in the Mediterranean Sea and simulated in a Monte Carlo model. Appl. Opt. 2002, 41, 2724–2733. [Google Scholar] [CrossRef] [PubMed]
- Aas, E.; Højerslev, N.K. Analysis of underwater radiance observations: Apparent optical properties and analytic functions describing the angular radiance distribution. J. Geophys. Res. Ocean. 1999, 104, 8015–8024. [Google Scholar] [CrossRef]
- TE PIN Photodiode (Model PS13-6b TO). Available online: https://www.te.com/usa-en/product-3001225-F.html (accessed on 24 March 2024).
- Xing, F.; Yin, H. Performance analysis for underwater cooperative optical wireless communications in the presence of solar radiation noise. In Proceedings of the 2019 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Dalian, China, 20–23 September 2019; pp. 1–6. [Google Scholar]
- Chaudhary, S.; Sharma, A.; Khichar, S.; Shah, S.; Ullah, R.; Parnianifard, A.; Wuttisittikulkij, L. A salinity-impact analysis of polarization division multiplexing-based underwater optical wireless communication system with high-speed data transmission. J. Sens. Actuator Netw. 2023, 12, 72. [Google Scholar] [CrossRef]
- SMARTS: Simple Model of the Atmospheric Radiative Transfer of Sunshine. Available online: https://www.nrel.gov/grid/solar-resource/smarts.html (accessed on 21 August 2024).
- Gueymard, C. SMARTS2: A Simple Model of the Atmospheric Radiative Transfer of Sunshine: Algorithms and Performance Assessment; Florida Solar Energy Center: Cocoa, FL, USA, 1995; Volume 1. [Google Scholar]
- MODTRAN®. Available online: http://modtran.spectral.com/ (accessed on 21 August 2024).
- Waduge, T.G.; Seet, B.-C.; Vopel, K. Geometric implications of photodiode arrays on received power distribution in mobile underwater optical wireless communication. Sensors 2024, 24, 3490. [Google Scholar] [CrossRef]
- Simpson, J.A.; Hughes, B.L.; Muth, J.F. Smart transmitters and receivers for underwater free-space optical communication. IEEE J. Sel. Areas Commun. 2012, 30, 964–974. [Google Scholar] [CrossRef]






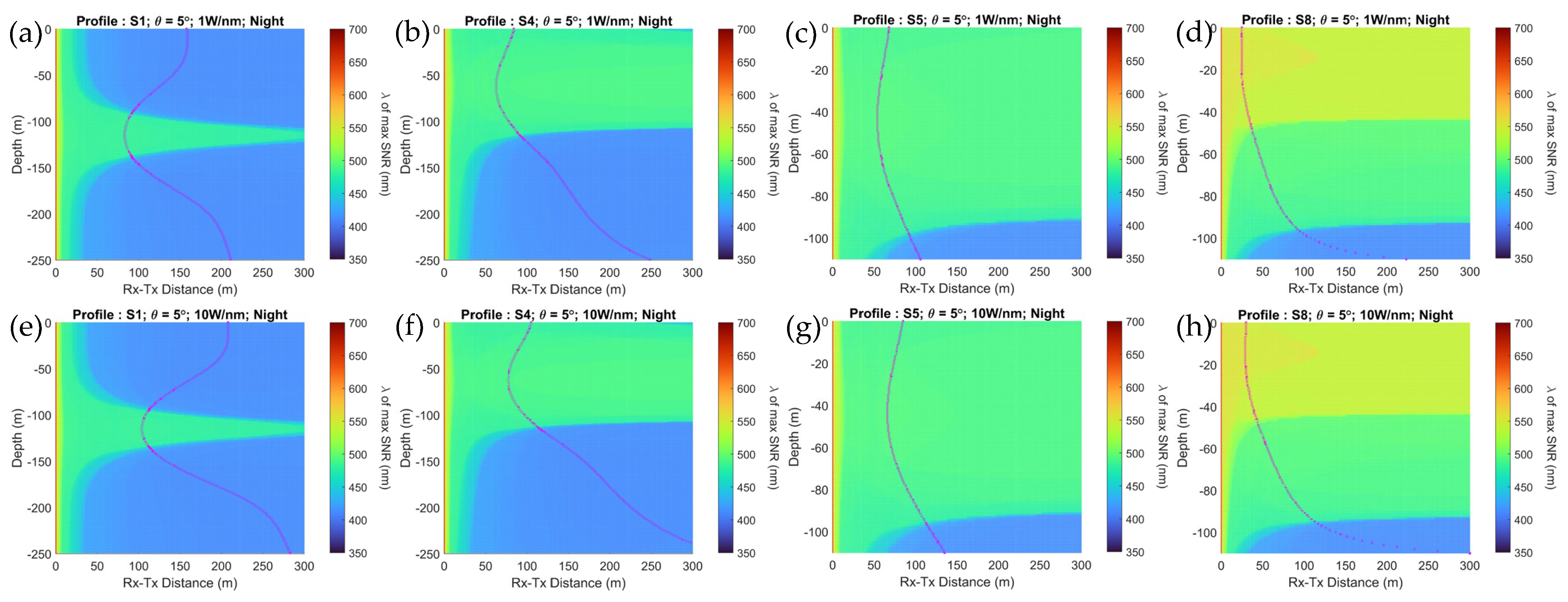
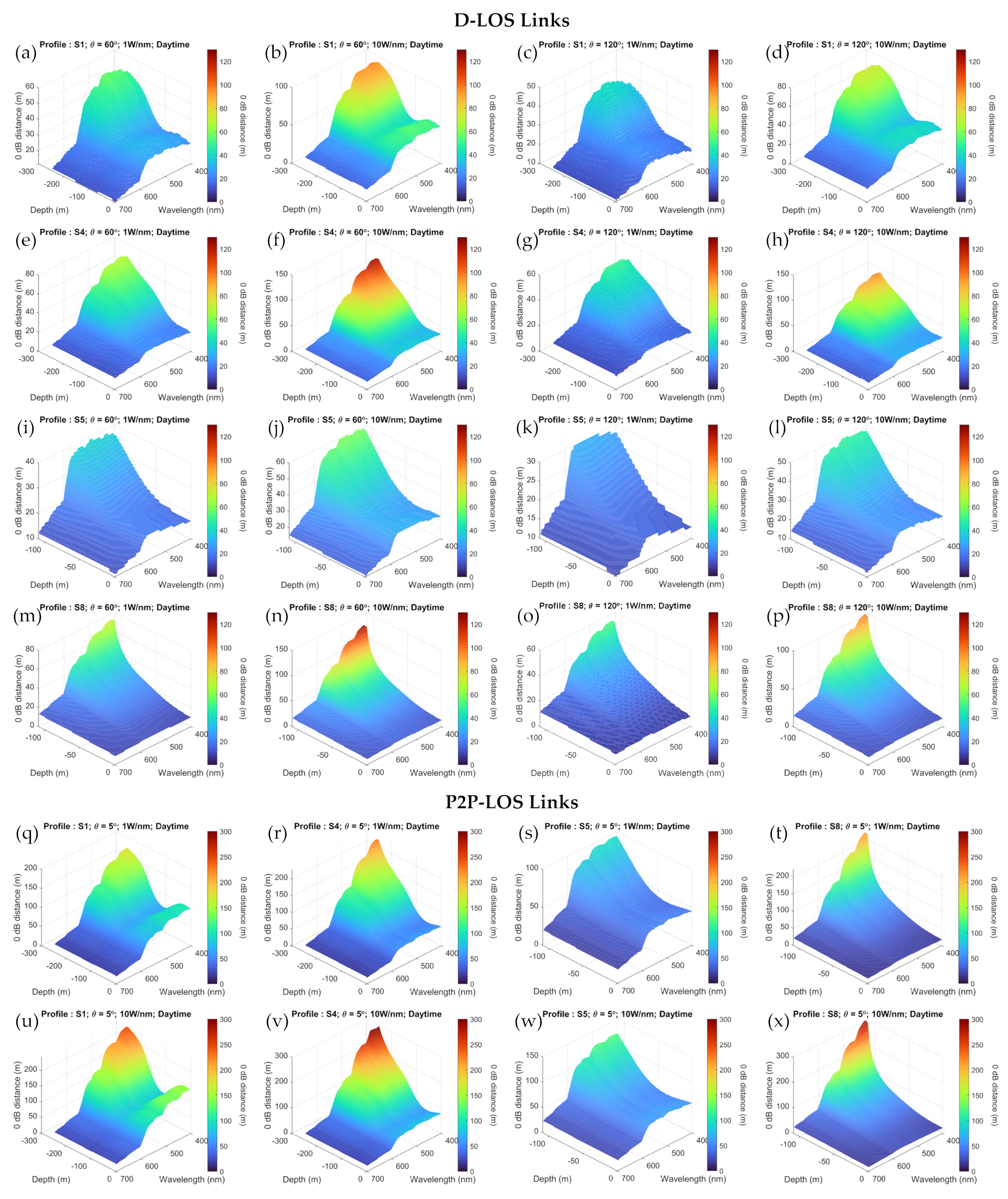
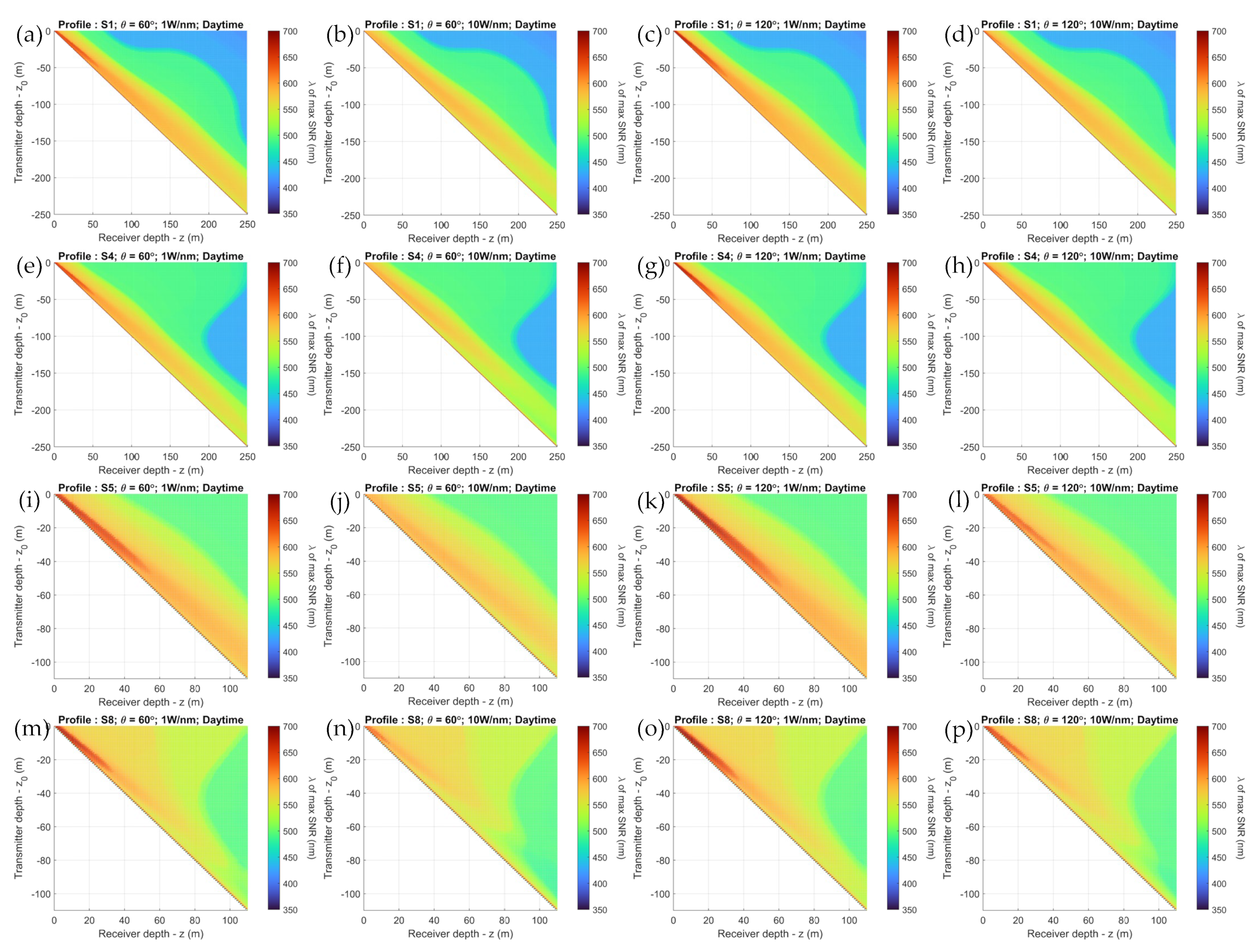
| Literature | Stratified Ocean | Ambient Light | Sensor Network and Mobile UOWC Friendly | Vertical and Horizontal Links | Consider Optical Beam Parameters | SNR Insights for Transmission Wavelength | Realistic Model Assumptions |
| Sticklus et al. [39] | No | Yes | No | No | Yes | Yes | No |
| Giuliano et al. [40] | No | Yes | No | Yes | Yes | Yes | No |
| Johnson et al. [33] | Yes | No | Yes | No | No | No | Yes |
| Yap et al. [41] | Yes | No | Yes | Yes | Yes | No | No |
| Jain et al. [42] | Yes | No | Yes | Yes | Yes | No | No |
| Hudcova and Kovalova [43] | Yes | Yes | Yes | No | No | No | Yes |
| Elamassie and Uysal [44] | Yes | No | Yes | No | Yes | No | Yes |
| Ji et al. [45] | Yes | No | Yes | Yes | Yes | No | Yes |
| Lou et al. [46] | Yes | No | Yes | No | Yes | No | Yes |
| Ijeh et al. [47] | No | No | Yes | Yes | Yes | No | Yes |
| This work | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Class | Cb | s | Cmax | ζmax | Δζ | Zeu | |
| S1 | 0.471 | 0.135 | 1.572 | 0.969 | 0.393 | 0.0910 | 119.1 |
| S2 | 0.533 | 0.172 | 1.194 | 0.921 | 0.435 | 0.151 | 99.9 |
| S3 | 0.428 | 0.138 | 1.015 | 0.905 | 0.630 | 0.185 | 91.0 |
| S4 | 0.57 | 0.173 | 0.766 | 0.814 | 0.586 | 0.250 | 80.2 |
| S5 | 0.611 | 0.214 | 0.676 | 0.663 | 0.539 | 0.338 | 70.3 |
| S6 | 0.390 | 0.109 | 0.788 | 0.521 | 0.681 | 0.410 | 63.4 |
| S7 | 0.569 | 0.183 | 0.608 | 0.452 | 0.744 | 0.578 | 54.4 |
| S8 | 0.835 | 0.298 | 0.382 | 0.512 | 0.625 | 1.206 | 39.8 |
| S9 | 0.188 | 0 | 0.885 | 0.378 | 1.081 | 2.950 | 26.1 |
| Parametar | Typical Value | Unit |
|---|---|---|
| ) | 13 | mm2 |
| ) | 0.25 | nA |
| ) | 70 | ns |
| ) | tan−1 (6.1/4.84) | rad. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waduge, T.G.; Seet, B.-C.; Vopel, K. Optimal Signal Wavelengths for Underwater Optical Wireless Communication under Sunlight in Stratified Waters. J. Sens. Actuator Netw. 2024, 13, 54. https://doi.org/10.3390/jsan13050054
Waduge TG, Seet B-C, Vopel K. Optimal Signal Wavelengths for Underwater Optical Wireless Communication under Sunlight in Stratified Waters. Journal of Sensor and Actuator Networks. 2024; 13(5):54. https://doi.org/10.3390/jsan13050054
Chicago/Turabian StyleWaduge, Tharuka Govinda, Boon-Chong Seet, and Kay Vopel. 2024. "Optimal Signal Wavelengths for Underwater Optical Wireless Communication under Sunlight in Stratified Waters" Journal of Sensor and Actuator Networks 13, no. 5: 54. https://doi.org/10.3390/jsan13050054
APA StyleWaduge, T. G., Seet, B.-C., & Vopel, K. (2024). Optimal Signal Wavelengths for Underwater Optical Wireless Communication under Sunlight in Stratified Waters. Journal of Sensor and Actuator Networks, 13(5), 54. https://doi.org/10.3390/jsan13050054







