Two-Step Lasso Estimation of the Spatial Weights Matrix
Abstract
:1. Introduction
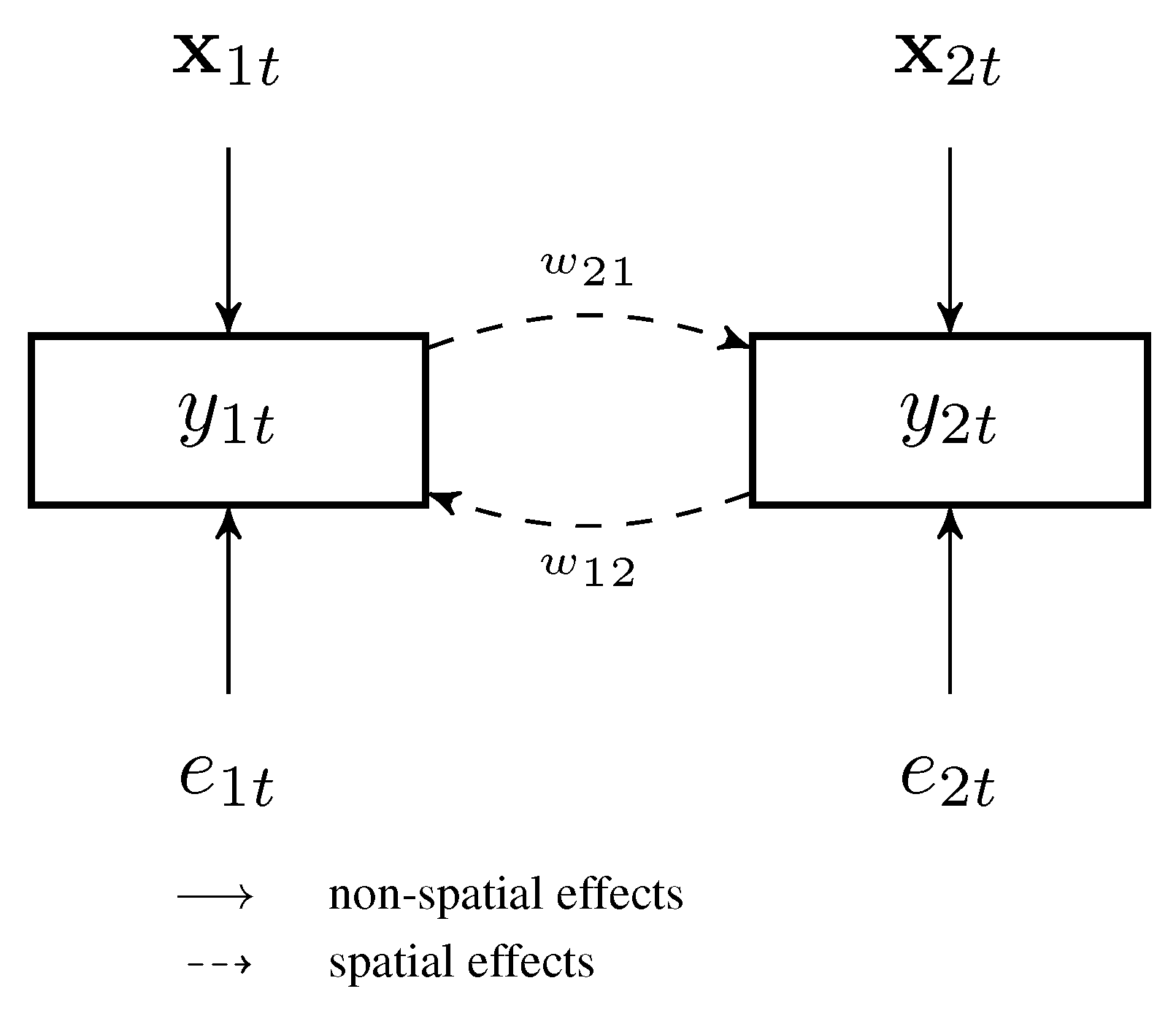
2. Two-Step Lasso Estimator
2.1. First-Step Estimation
2.2. Second-Step Estimation
3. The Spatial Autoregressive Model
3.1. Two-Step Lasso
3.2. Post-Lasso and Thresholded Post-Lasso
4. Monte Carlo Simulation
| N | T | False | False | bias | N | T | False | False | bias | ||||||
| neg. | pos. | mean | median | RMSE | neg. | pos. | mean | median | RMSE | ||||||
| 0.70 | 30 | 50 | 19.23 | 19.01 | 0.04335 | 0.04266 | 0.04335 | 0.70 | 30 | 50 | 8.83 | 11.55 | 0.03649 | 0.03606 | 0.03649 |
| 0.70 | 30 | 100 | 14.62 | 21.22 | 0.03812 | 0.03747 | 0.03812 | 0.70 | 30 | 100 | 5.64 | 11.89 | 0.03090 | 0.03083 | 0.03090 |
| 0.70 | 30 | 500 | 5.30 | 24.82 | 0.02310 | 0.02305 | 0.02310 | 0.70 | 30 | 500 | 2.18 | 12.69 | 0.02029 | 0.02022 | 0.02029 |
| 0.70 | 50 | 50 | 13.96 | 15.13 | 0.02855 | 0.02826 | 0.02855 | 0.70 | 50 | 50 | 4.81 | 9.38 | 0.02453 | 0.02432 | 0.02453 |
| 0.70 | 50 | 100 | 8.86 | 17.58 | 0.02653 | 0.02626 | 0.02653 | 0.70 | 50 | 100 | 1.90 | 10.12 | 0.02187 | 0.02185 | 0.02187 |
| 0.70 | 50 | 500 | 3.14 | 22.13 | 0.01725 | 0.01718 | 0.01725 | 0.70 | 50 | 500 | 0.58 | 10.80 | 0.01519 | 0.01519 | 0.01519 |
| 0.70 | 70 | 50 | 11.93 | 12.35 | 0.02132 | 0.02130 | 0.02132 | 0.70 | 70 | 50 | 3.84 | 7.65 | 0.01829 | 0.01828 | 0.01829 |
| 0.70 | 70 | 100 | 6.09 | 15.36 | 0.02071 | 0.02055 | 0.02071 | 0.70 | 70 | 100 | 0.87 | 8.96 | 0.01746 | 0.01741 | 0.01746 |
| 0.70 | 70 | 500 | 1.89 | 20.39 | 0.01454 | 0.01446 | 0.01454 | 0.70 | 70 | 500 | 0.17 | 9.78 | 0.01277 | 0.01273 | 0.01277 |
| 0.90 | 30 | 50 | 2.07 | 14.99 | 0.02360 | 0.02346 | 0.02360 | 0.90 | 30 | 50 | 0.76 | 9.83 | 0.01823 | 0.01806 | 0.01823 |
| 0.90 | 30 | 100 | 0.97 | 14.92 | 0.02002 | 0.01992 | 0.02002 | 0.90 | 30 | 100 | 0.25 | 7.93 | 0.01267 | 0.01254 | 0.01267 |
| 0.90 | 30 | 500 | 0.18 | 18.35 | 0.01372 | 0.01365 | 0.01372 | 0.90 | 30 | 500 | 0.12 | 7.62 | 0.00794 | 0.00787 | 0.00794 |
| 0.90 | 50 | 50 | 1.03 | 12.69 | 0.01495 | 0.01489 | 0.01495 | 0.90 | 50 | 50 | 0.29 | 9.27 | 0.01364 | 0.01349 | 0.01364 |
| 0.90 | 50 | 100 | 0.29 | 13.11 | 0.01354 | 0.01354 | 0.01354 | 0.90 | 50 | 100 | 0.04 | 7.94 | 0.00947 | 0.00944 | 0.00947 |
| 0.90 | 50 | 500 | 0.03 | 15.24 | 0.00935 | 0.00931 | 0.00935 | 0.90 | 50 | 500 | 0.01 | 6.07 | 0.00513 | 0.00512 | 0.00513 |
| 0.90 | 70 | 50 | 0.52 | 10.37 | 0.01048 | 0.01044 | 0.01048 | 0.90 | 70 | 50 | 0.17 | 7.26 | 0.00931 | 0.00928 | 0.00931 |
| 0.90 | 70 | 100 | 0.15 | 12.17 | 0.01058 | 0.01054 | 0.01058 | 0.90 | 70 | 100 | 0.02 | 8.26 | 0.00854 | 0.00852 | 0.00854 |
| 0.90 | 70 | 500 | 0.01 | 13.60 | 0.00759 | 0.00758 | 0.00759 | 0.90 | 70 | 500 | 0.00 | 5.50 | 0.00409 | 0.00408 | 0.00409 |
| (c) | (d) | ||||||||||||||
| N | T | False | False | bias | N | T | False | False | bias | ||||||
| neg. | pos. | mean | median | RMSE | neg. | pos. | mean | median | RMSE | ||||||
| 0.70 | 30 | 50 | 10.04 | 6.36 | 0.02561 | 0.02523 | 0.02561 | 0.70 | 30 | 50 | – | – | 0.02742 | 0.02444 | 0.02742 |
| 0.70 | 30 | 100 | 6.40 | 6.44 | 0.02165 | 0.02145 | 0.02165 | 0.70 | 30 | 100 | – | – | 0.01915 | 0.01779 | 0.01915 |
| 0.70 | 30 | 500 | 2.36 | 6.60 | 0.01368 | 0.01360 | 0.01368 | 0.70 | 30 | 500 | – | – | 0.00762 | 0.00753 | 0.00762 |
| 0.70 | 50 | 50 | 5.71 | 4.85 | 0.01621 | 0.01609 | 0.01621 | 0.70 | 50 | 50 | – | – | 0.01533 | 0.01462 | 0.01533 |
| 0.70 | 50 | 100 | 2.28 | 5.21 | 0.01434 | 0.01430 | 0.01434 | 0.70 | 50 | 100 | – | – | 0.01135 | 0.01057 | 0.01135 |
| 0.70 | 50 | 500 | 0.65 | 5.36 | 0.00968 | 0.00969 | 0.00968 | 0.70 | 50 | 500 | – | – | 0.00455 | 0.00453 | 0.00455 |
| 0.70 | 70 | 50 | 4.59 | 3.84 | 0.01200 | 0.01197 | 0.01200 | 0.70 | 70 | 50 | – | – | 0.01114 | 0.01055 | 0.01114 |
| 0.70 | 70 | 100 | 1.13 | 4.48 | 0.01114 | 0.01110 | 0.01114 | 0.70 | 70 | 100 | – | – | 0.00816 | 0.00771 | 0.00816 |
| 0.70 | 70 | 500 | 0.20 | 4.69 | 0.00791 | 0.00790 | 0.00791 | 0.70 | 70 | 500 | – | – | 0.00325 | 0.00323 | 0.00325 |
| 0.90 | 30 | 50 | 1.57 | 5.00 | 0.01316 | 0.01298 | 0.01316 | 0.90 | 30 | 50 | – | – | 0.02576 | 0.02358 | 0.02576 |
| 0.90 | 30 | 100 | 0.42 | 3.54 | 0.00923 | 0.00915 | 0.00923 | 0.90 | 30 | 100 | – | – | 0.02039 | 0.01887 | 0.02039 |
| 0.90 | 30 | 500 | 0.13 | 2.35 | 0.00528 | 0.00525 | 0.00528 | 0.90 | 30 | 500 | – | – | 0.01250 | 0.01237 | 0.01250 |
| 0.90 | 50 | 50 | 1.06 | 4.30 | 0.00877 | 0.00871 | 0.00877 | 0.90 | 50 | 50 | – | – | 0.01562 | 0.01418 | 0.01562 |
| 0.90 | 50 | 100 | 0.12 | 3.25 | 0.00620 | 0.00615 | 0.00620 | 0.90 | 50 | 100 | – | – | 0.01216 | 0.01132 | 0.01216 |
| 0.90 | 50 | 500 | 0.01 | 1.54 | 0.00310 | 0.00308 | 0.00310 | 0.90 | 50 | 500 | – | – | 0.00751 | 0.00744 | 0.00751 |
| 0.90 | 70 | 50 | 0.56 | 3.14 | 0.00589 | 0.00584 | 0.00589 | 0.90 | 70 | 50 | – | – | 0.01087 | 0.01020 | 0.01087 |
| 0.90 | 70 | 100 | 0.09 | 3.24 | 0.00513 | 0.00510 | 0.00513 | 0.90 | 70 | 100 | – | – | 0.00860 | 0.00816 | 0.00860 |
| 0.90 | 70 | 500 | 0.00 | 1.21 | 0.00230 | 0.00229 | 0.00230 | 0.90 | 70 | 500 | – | – | 0.00533 | 0.00532 | 0.00533 |
| N | T | False | False | bias | N | T | False | False | bias | ||||||
| neg. | pos. | mean | median | RMSE | neg. | pos. | mean | median | RMSE | ||||||
| 0.50 | 30 | 50 | 41.60 | 19.36 | 0.05258 | 0.04915 | 0.05258 | 0.50 | 30 | 50 | 36.30 | 13.00 | 0.05679 | 0.05388 | 0.05679 |
| 0.50 | 30 | 100 | 32.82 | 20.11 | 0.04119 | 0.03952 | 0.04119 | 0.50 | 30 | 100 | 25.70 | 13.08 | 0.04681 | 0.04572 | 0.04681 |
| 0.50 | 30 | 500 | 7.80 | 18.61 | 0.01904 | 0.01877 | 0.01904 | 0.50 | 30 | 500 | 4.46 | 13.10 | 0.02784 | 0.02779 | 0.02784 |
| 0.50 | 50 | 50 | 39.98 | 15.89 | 0.03820 | 0.03512 | 0.03820 | 0.50 | 50 | 50 | 32.20 | 10.46 | 0.03943 | 0.03689 | 0.03943 |
| 0.50 | 50 | 100 | 30.54 | 16.98 | 0.03055 | 0.02976 | 0.03055 | 0.50 | 50 | 100 | 20.85 | 10.80 | 0.03353 | 0.03326 | 0.03353 |
| 0.50 | 50 | 500 | 7.26 | 17.07 | 0.01497 | 0.01483 | 0.01497 | 0.50 | 50 | 500 | 3.22 | 11.66 | 0.02276 | 0.02274 | 0.02276 |
| 0.50 | 70 | 50 | 40.38 | 12.76 | 0.02885 | 0.02730 | 0.02885 | 0.50 | 70 | 50 | 32.13 | 8.41 | 0.02944 | 0.02814 | 0.02944 |
| 0.50 | 70 | 100 | 28.60 | 14.98 | 0.02477 | 0.02447 | 0.02477 | 0.50 | 70 | 100 | 17.51 | 9.37 | 0.02653 | 0.02642 | 0.02653 |
| 0.50 | 70 | 500 | 6.90 | 15.95 | 0.01290 | 0.01284 | 0.01290 | 0.50 | 70 | 500 | 2.32 | 10.59 | 0.01958 | 0.01956 | 0.01958 |
| (c) | (d) | ||||||||||||||
| N | T | False | False | bias | N | T | False | False | bias | ||||||
| neg. | pos. | mean | median | RMSE | neg. | pos. | mean | median | RMSE | ||||||
| 0.50 | 30 | 50 | 37.53 | 7.81 | 0.03843 | 0.03722 | 0.03843 | 0.50 | 30 | 50 | – | – | 0.01335 | 0.01186 | 0.01335 |
| 0.50 | 30 | 100 | 26.45 | 8.03 | 0.03247 | 0.03218 | 0.03247 | 0.50 | 30 | 100 | – | – | 0.00934 | 0.00861 | 0.00934 |
| 0.50 | 30 | 500 | 4.54 | 7.72 | 0.01811 | 0.01806 | 0.01811 | 0.50 | 30 | 500 | – | – | 0.00351 | 0.00348 | 0.00351 |
| 0.50 | 50 | 50 | 33.53 | 6.00 | 0.02573 | 0.02498 | 0.02573 | 0.50 | 50 | 50 | – | – | 0.00794 | 0.00724 | 0.00794 |
| 0.50 | 50 | 100 | 21.68 | 6.36 | 0.02257 | 0.02252 | 0.02257 | 0.50 | 50 | 100 | – | – | 0.00559 | 0.00524 | 0.00559 |
| 0.50 | 50 | 500 | 3.31 | 6.72 | 0.01441 | 0.01438 | 0.01441 | 0.50 | 50 | 500 | – | – | 0.00210 | 0.00208 | 0.00210 |
| 0.50 | 70 | 50 | 33.43 | 4.72 | 0.01946 | 0.01899 | 0.01946 | 0.50 | 70 | 50 | – | – | 0.00561 | 0.00512 | 0.00561 |
| 0.50 | 70 | 100 | 18.29 | 5.40 | 0.01762 | 0.01758 | 0.01762 | 0.50 | 70 | 100 | – | – | 0.00388 | 0.00371 | 0.00388 |
| 0.50 | 70 | 500 | 2.40 | 5.99 | 0.01224 | 0.01223 | 0.01224 | 0.50 | 70 | 500 | – | – | 0.00149 | 0.00149 | 0.00149 |
4.1. Specification 1

4.2. Specification 2


5. Conclusions
Acknowledgments
Author Contributions
A. Appendix
A.1. Proof of Theorem 1
A.2. Algorithm for Estimating Penalty Loadings
Conflicts of Interest
- 1.See [6] for a similar approach.
- 2.The Lasso has also been applied in the GIS literature, where the focus is on estimation of a spatial model where spatial dependence is a function of geographic distance; see, for example, Huang et al. [10] and Wheeler [11]. Likewise, Seya et al. [12] assume a known spatial weights matrix and apply the Lasso for spatial filtering. Spatial filtering is different from our approach as filtering treats the spatial weights as nuisance parameters whereas we focus on the recovery of the spatial dependence structure.
- 3.We implicitly set the spatial autoregressive parameter, which is commonly employed in spatial models, equal to one, since and the spatial autoregressive parameter are not separately identified [5].
- 4.See [23] for an overview.
- 5.The subscripts “1” and “2” indicate, where appropriate, that the corresponding terms refer to the first and second step, respectively.
- 6.Whether this assumption is reasonable depends on the application. If there is a regime change at a known date, the model can be estimated for each sub-period separately, assuming that parameter stability holds within in each sub-period and that the time dimension is sufficiently large.
- 7.To simplify the exposition, the first and second-step Lasso also applies a penalty to βi and πi,i although we assume ║πi,i║0 = ║βi║0 = K for identification. For better performance in finite samples, we recommend that the coefficients βi and πi,i are not penalized.
- 8.The thresholded Lasso estimators considered in [31] apply the threshold to the Lasso estimates whereas we apply the threshold to the post-Lasso estimates.
- 9.We are grateful to two anonymous referees who suggested useful extensions to our Monte Carlo simulations.
- 10.The Lasso estimations were conducted in R based on the package glmnet by Friedman et al. [50]. The code for the two-step Lasso, two-step post-Lasso and thresholded post-Lasso are available on request.
- 11.We have also considered, among others, and and did not find significant performance differences.
References
- G. Arbia, and B. Fingleton. “New spatial econometric techniques and applications in regional science.” Papers Reg. Sci. 87 (2008): 311–317. [Google Scholar]
- R. Harris, J. Moffat, and V. Kravtsova. “In search of ‘W’.” Spat. Econ. Anal. 6 (2011): 249–270. [Google Scholar]
- L. Corrado, and B. Fingleton. “Where is the economics in spatial econometrics? ” Reg. Sci. 52 (2012): 210–239. [Google Scholar]
- J. Pinkse, M.E. Slade, and C. Brett. “Spatial price competition: A semiparametric approach.” Econometrica 70 (2002): 1111–1153. [Google Scholar]
- A. Bhattacharjee, and C. Jensen-Butler. “Estimation of the spatial weights matrix under structural constraints.” Reg. Sci. Urban Econ. 43 (2013): 617–634. [Google Scholar]
- M. Beenstock, and D. Felsenstein. “Nonparametric estimation of the spatial connectivity matrix using spatial panel data.” Geogr. Anal. 44 (2012): 386–397. [Google Scholar]
- A. Bhattacharjee, and S. Holly. “Structural interactions in spatial panels.” Empir. Econ. 40 (2011): 69–94. [Google Scholar]
- A. Bhattacharjee, and S. Holly. “Understanding interactions in social networks and committees.” Spat. Econ. Anal. 8 (2013): 23–53. [Google Scholar]
- N. Bailey, S. Holly, and M.H. Pesaran. “A two stage approach to spatiotemporal analysis with strong and weak cross-sectional dependence.” J. Appl. Econome., 2014, in press. [Google Scholar]
- H.C. Huang, N.J. Hsu, D.M. Theobald, and F.J. Breidt. “Spatial Lasso with applications to GIS model selection.” J. Comput. Graph. Statist. 19 (2010): 963–983. [Google Scholar]
- D.C. Wheeler. “Simultaneous coefficient penalization and model selection in geographically weighted regression: The geographically weighted lasso.” Environ. Plan. A 41 (2009): 722–742. [Google Scholar]
- H. Seya, D. Murakami, M. Tsutsumi, and Y. Yamagata. “Application of Lasso to the eigenvector selection problem in eigenvector-based spatial filtering.” Geogr. Anal., 2014. [Google Scholar] [CrossRef]
- E. Manresa. Madrid, Spain: CEMFI. “Estimating the structure of social interactions using panel data.” 2014, Unpublished work. [Google Scholar]
- P.C. Souza. London, UK: Department of Statistics, London School of Economics and Political Science. “Estimating networks: Lasso for spatial weights.” 2012, Unpublished work. [Google Scholar]
- C. Lam, and P.C. Souza. London, UK: Department of Statistics, London School of Economics and Political Science. “Regularization for spatial panel time series using adaptive Lasso.” 2013, Unpublished work. [Google Scholar]
- A.D. Cliff, and J.K. Ord. Spatial Autocorrelation: Monographs in Spatial and Environmental Systems Analysis. London, UK: Pion Ltd., 1973. [Google Scholar]
- L. Anselin. Spatial Econometrics: Methods and Models. New York, NY, USA: Springer, 1988. [Google Scholar]
- M. Kapoor, H.H. Kelejian, and I.R. Prucha. “Panel data models with spatially correlated error components.” J. Econom. 140 (2007): 97–130. [Google Scholar]
- L.F. Lee, and J. Yu. “Some recent developments in spatial panel data models.” Reg. Sci. Urban Econ. 40 (2010): 255–271. [Google Scholar]
- L.F. Lee, and J. Yu. “Estimation of spatial autoregressive panel data models with fixed effects.” J. Econom. 154 (2010): 165–185. [Google Scholar]
- L.F. Lee, and J. Yu. “Efficient GMM estimation of spatial dynamic panel data models with fixed effects.” J. Econom. 180 (2014): 174–197. [Google Scholar]
- J. Mutl, and M. Pfaffermayr. “The Hausman test in a Cliff and Ord panel model.” Econom. J. 14 (2011): 48–76. [Google Scholar]
- J. Elhorst. Spatial Econometrics: From Cross-Sectional Data to Spatial Panels. New York, NY, USA: Springer, 2014. [Google Scholar]
- R. Tibshirani. “Regression shrinkage and selection via the Lasso.” J. R. Stat. Soc. Ser. B (Methodological) 58 (1996): 267–288. [Google Scholar]
- H. Akaike. “A new look at the statistical model identification.” IEEE Trans. Autom. Control 19 (1974): 716–723. [Google Scholar]
- G. Schwarz. “Estimating the dimension of a model.” Ann. Stat. 6 (1978): 461–464. [Google Scholar]
- P.J. Bickel, Y. Ritov, and A.B. Tsybakov. “Simultaneous analysis of Lasso and Dantzig selector.” Ann. Stat. 37 (2009): 1705–1732. [Google Scholar]
- P. Bühlmann, and S. van de Geer. Statistics for High-Dimensional Data. New York, NY, USA: Springer, 2011. [Google Scholar]
- P. Zhao, and B. Yu. “On model selection consistency of Lasso.” J. Mach. Learn. Res. 7 (2006): 2541–2563. [Google Scholar]
- A. Belloni, D. Chen, V. Chernozhukov, and C. Hansen. “Sparse models and methods for optimal instruments with an application to eminent domain.” Econometrica 80 (2012): 2369–2429. [Google Scholar]
- A. Belloni, and V. Chernozhukov. “Least squares after model selection in high-dimensional sparse models.” Bernoulli 19 (2013): 521–547. [Google Scholar]
- F. Bunea, A. Tsybakov, and M. Wegkamp. “Sparsity oracle inequalities for the Lasso.” Electron. J. Stat. 1 (2007): 169–194. [Google Scholar]
- M.J. Wainwright. “Sharp thresholds for high-dimensional and noisy sparsity recovery using L1-constrained quadratic programming.” IEEE Trans. Inf. Theor. 55 (2009): 2183–2202. [Google Scholar]
- S. Van de Geer. “High-dimensional generalized linear models and the Lasso.” Ann. Stat. 36 (2008): 614–645. [Google Scholar]
- N. Meinshausen, and B. Yu. “Lasso-type recovery of sparse representations for high-dimensional data.” Ann. Stat. 37 (2009): 246–270. [Google Scholar]
- M.H. Pesaran. “Estimation and inference in large heterogeneous panels with a multifactor error structure.” Econometrica 74 (2006): 967–1012. [Google Scholar]
- M.H. Pesaran, and E. Tosetti. “Large panels with common factors and spatial correlation.” J. Econom. 161 (2011): 182–202. [Google Scholar]
- E. Gautier, and A.B. Tsybakov. Toulouse, France: Toulouse School of Economics. “High-dimensional instrumental variables regression and confidence sets.” 2014, Unpublished work. [Google Scholar]
- E. Candes, and T. Tao. “The Dantzig selector: Statistical estimation when p is much larger than n.” Ann. Stat. 35 (2007): 2313–2351. [Google Scholar]
- J. Fan, and Y. Liao. “Endogeneity in high dimensions.” Ann. Stat. 42 (2014): 872–917. [Google Scholar]
- M. Caner. “Lasso-type Gmm estimator.” Econom. Theor. 25 (2009): 270–290. [Google Scholar]
- W. Lin, R. Feng, and H. Li. “Regularization methods for high-dimensional instrumental variables regression with an application to genetical genomics.” J. Am. Stat. Assoc., 2014. [Google Scholar] [CrossRef]
- A. Belloni, and V. Chernozhukov. “High dimensional sparse econometric models: An introduction.” In Inverse Problems and High-Dimensional Estimation SE - 3. Edited by P. Alquier, E. Gautier and G. Stoltz. Berlin/ Heidelberg, Germany: Springer, 2011, pp. 121–156. [Google Scholar]
- B.Y. Jing, Q.M. Shao, and Q. Wang. “Self-normalized Cramér-type large deviations for independent random variables.” Ann. Probab. 31 (2003): 2167–2215. [Google Scholar]
- A. Belloni, V. Chernozhukov, and C. Hansen. “Inference on treatment effects after selection among high-dimensional controls.” Rev. Econ. Stud. 81 (2014): 608–650. [Google Scholar]
- S. Van de Geer, and P. Bühlmann. “On the conditions used to prove oracle results for the Lasso.” Electron. J. Stat. 3 (2009): 1360–1392. [Google Scholar]
- G. Raskutti, M.J. Wainwright, and B. Yu. “Restricted eigenvalue properties for correlated Gaussian designs.” J. Mach. Learn. Res. 11 (2010): 2241–2259. [Google Scholar]
- H.H. Kelejian, and I.R. Prucha. “A generalized spatial two-stage least squares procedure for estimating a spatial autoregressive model with autoregressive disturbances.” J. Real Estate Financ. Econ. 17 (1998): 99–121. [Google Scholar]
- H.H. Kelejian, and I.R. Prucha. “A generalized moments estimator for the autoregressive parameter in a spatial model.” Int. Econ. Rev. 40 (1999): 509–533. [Google Scholar]
- J. Friedman, T. Hastie, and R. Tibshirani. “Regularization paths for generalized linear models via coordinate descent.” J. Stat. Softw. 33 (2010): 1–22. [Google Scholar]
- R. Lockhart, J. Taylor, R.J. Tibshirani, and R. Tibshirani. “A significance test for the Lasso.” Ann. Stat. 42 (2014): 413–468. [Google Scholar]
- L. Wasserman, and K. Roeder. “High-dimensional variable selection.” Ann. Statist. 37 (2009): 2178–2201. [Google Scholar]
- N. Meinshausen, L. Meier, and P. Bühlmann. “p-Values for high-dimensional regression.” J. Am. Statist. Assoc. 104 (2009): 1671–1681. [Google Scholar]
- J. Fan, and R. Li. “Variable selection via nonconcave penalized likelihood and its oracle properties.” J. Am. Stat. Assoc. 96 (2001): 1348–1360. [Google Scholar]
- K. Knight, and W. Fu. “Asymptotics for Lasso-type estimators.” Ann. Stat. 28 (2000): 1356–1378. [Google Scholar]
- A. Belloni, V. Chernozhukov, and L. Wang. “Square-root lasso: Pivotal recovery of sparse signals via conic programming.” Biometrika 98 (2011): 791–806. [Google Scholar]
- A. Belloni, V. Chernozhukov, and L. Wang. “Pivotal estimation via square-root Lasso in nonparametric regression.” Ann. Stat. 42 (2014): 757–788. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahrens, A.; Bhattacharjee, A. Two-Step Lasso Estimation of the Spatial Weights Matrix. Econometrics 2015, 3, 128-155. https://doi.org/10.3390/econometrics3010128
Ahrens A, Bhattacharjee A. Two-Step Lasso Estimation of the Spatial Weights Matrix. Econometrics. 2015; 3(1):128-155. https://doi.org/10.3390/econometrics3010128
Chicago/Turabian StyleAhrens, Achim, and Arnab Bhattacharjee. 2015. "Two-Step Lasso Estimation of the Spatial Weights Matrix" Econometrics 3, no. 1: 128-155. https://doi.org/10.3390/econometrics3010128
APA StyleAhrens, A., & Bhattacharjee, A. (2015). Two-Step Lasso Estimation of the Spatial Weights Matrix. Econometrics, 3(1), 128-155. https://doi.org/10.3390/econometrics3010128





