Comprehensive Review: Advancements in Rainfall-Runoff Modelling for Flood Mitigation
Abstract
:1. Introduction
2. Overview of Rainfall–Runoff Modelling Approaches
2.1. Conceptual Models
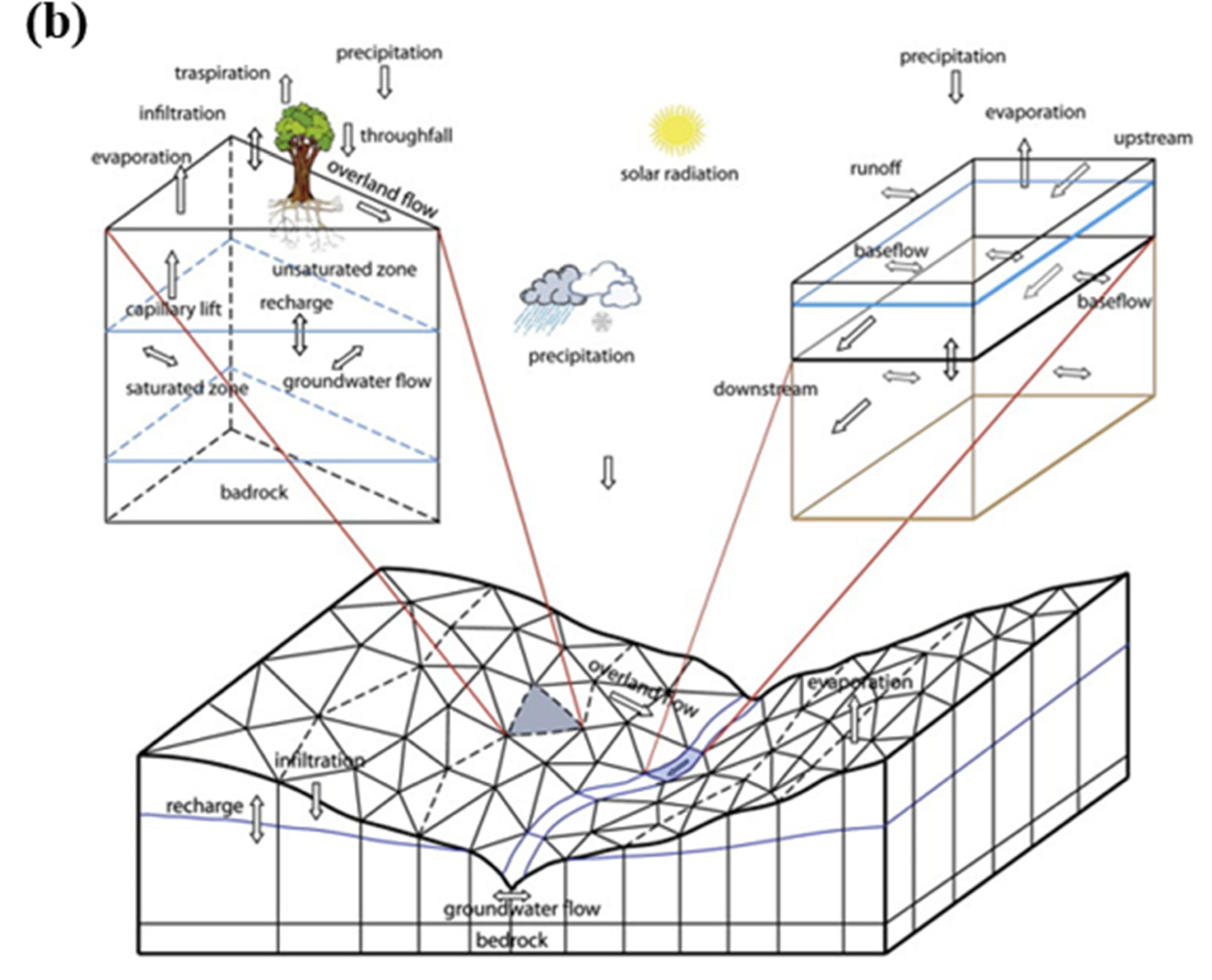
2.2. Physical Process-Based Models
2.3. Empirical Models
3. Machine Learning Methods for Rainfall–Runoff Modelling
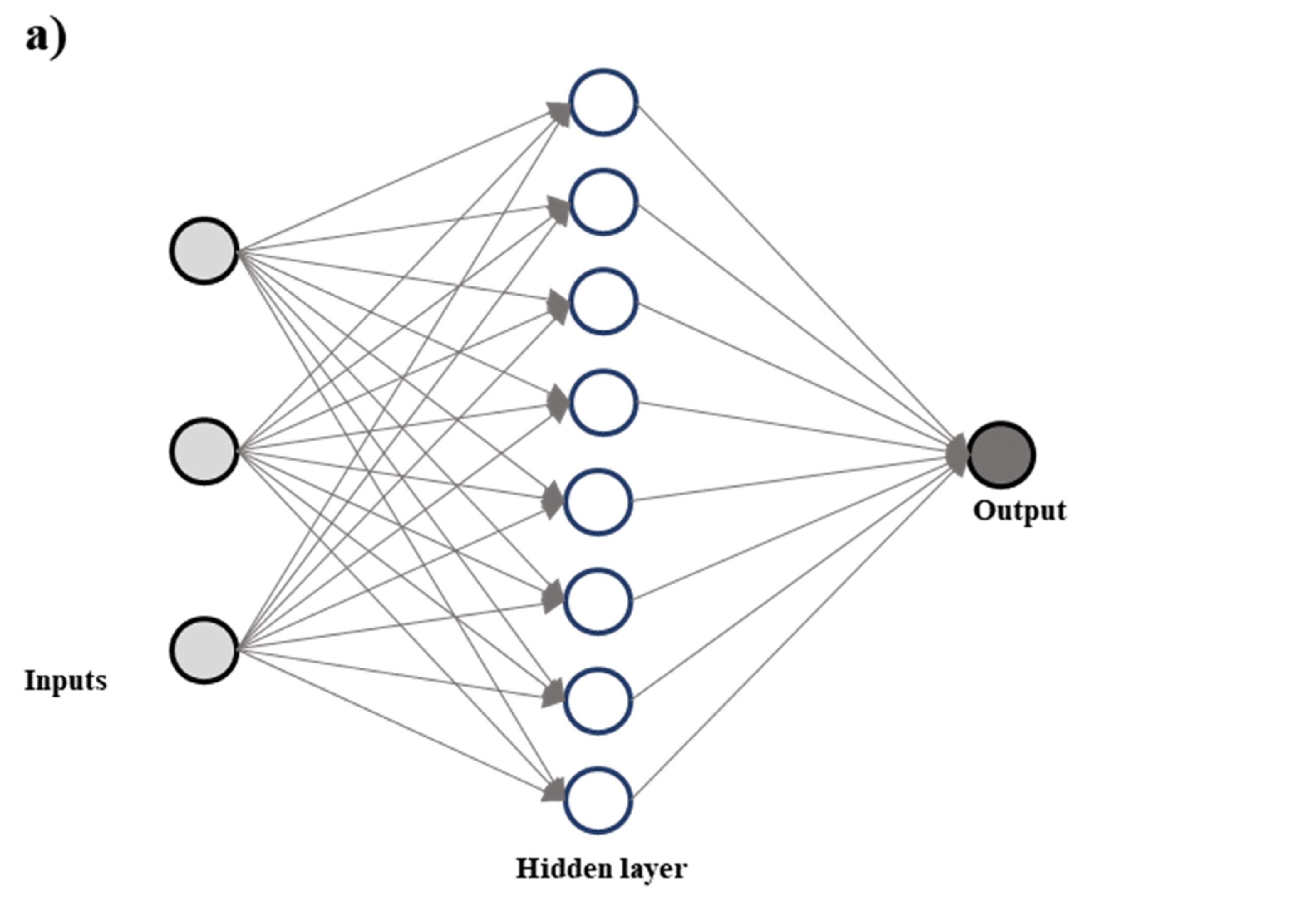
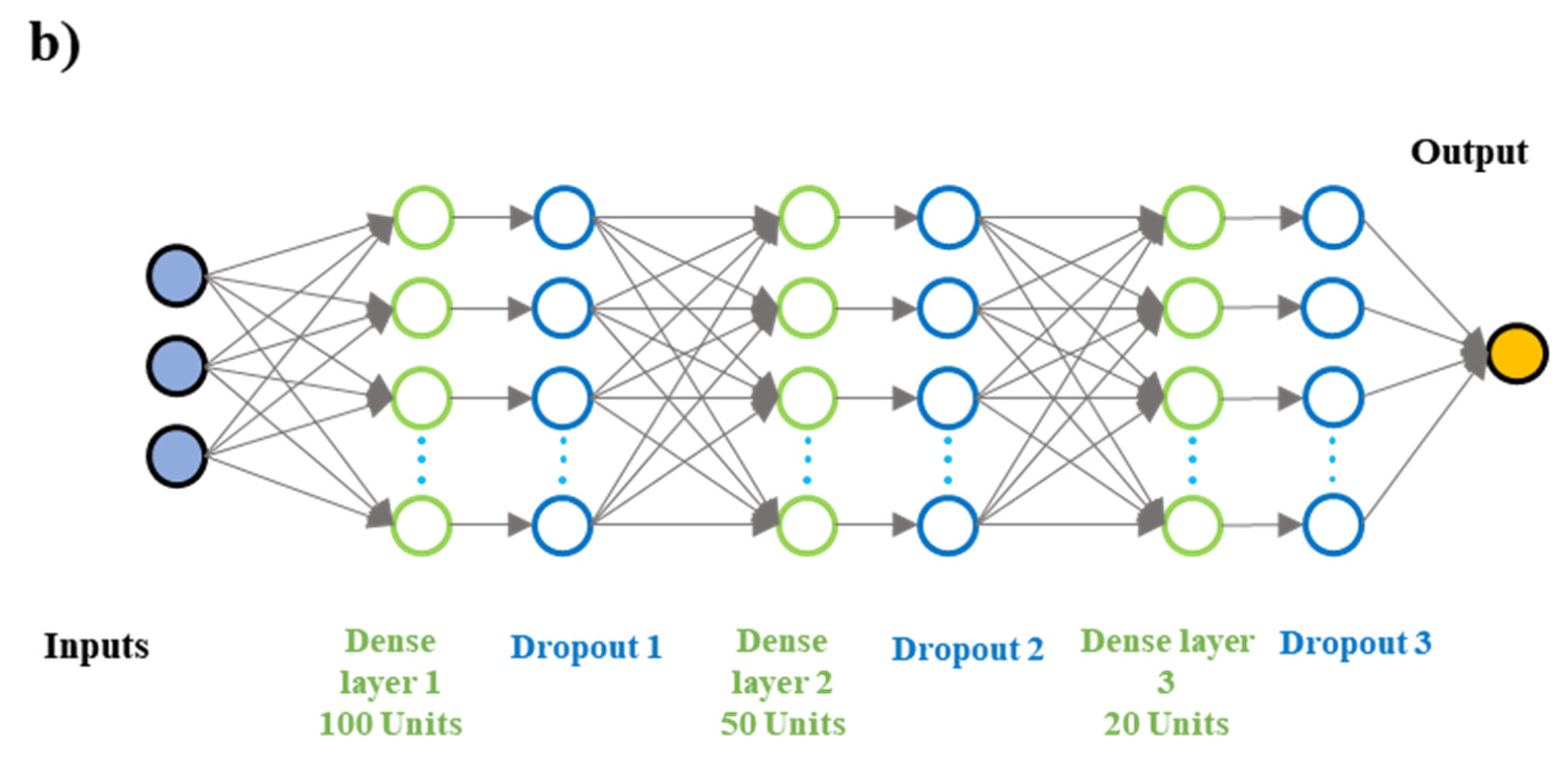
3.1. Artificial Neural Network (ANN)
3.2. Adaptive Neuro-Fuzzy Inference System (ANFIS)
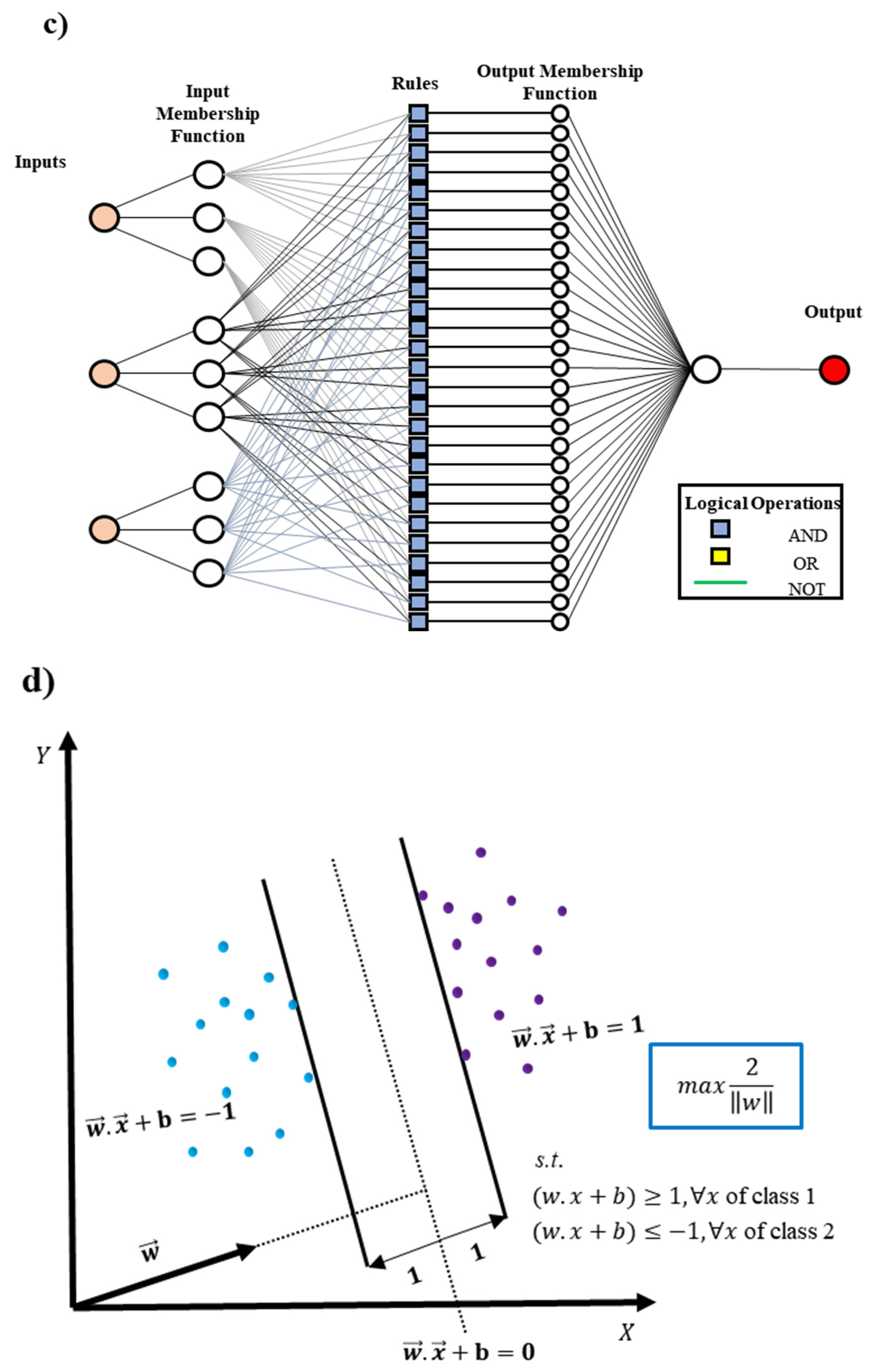
3.3. Support Vector Machine (SVM)
4. Flood Risk Assessment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Linsley, R.K., Jr.; Kohler, M.A.; Paulhus, J.L. Hydrology for Engineers; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Yang, W.-Y.; Li, D.; Sun, T.; Ni, G.-H. Saturation-excess and infiltration-excess runoff on green roofs. Ecol. Eng. 2015, 74, 327–336. [Google Scholar] [CrossRef]
- Kokkonen, T.; Koivusalo, H.; Karvonen, T. A semi-distributed approach to rainfall-runoff modelling—A case study in a snow affected catchment. Environ. Model. Softw. 2001, 16, 481–493. [Google Scholar] [CrossRef]
- Howarth, R.W.; Anderson, D.; Cloern, J.E.; Elfring, C.; Hopkinson, C.S.; Lapointe, B.; Malone, T.; Marcus, N.; McGlathery, K.; Sharpley, A.N. Nutrient pollution of coastal rivers, bays, and seas. Issues Ecol. 2000, 7, 1–16. [Google Scholar]
- Jehanzaib, M.; Shah, S.A.; Yoo, J.; Kim, T.-W. Investigating the impacts of climate change and human activities on hydrological drought using non-stationary approaches. J. Hydrol. 2020, 588, 125052. [Google Scholar] [CrossRef]
- Salvadore, E.; Bronders, J.; Batelaan, O. Hydrological modelling of urbanized catchments: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Xu, C. Hydrologic Models; Uppsala University Department of Earth Sciences Hydrology: Uppsala, Sweden, 2002; Volume 2. [Google Scholar]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A review on hydrological models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Nayak, P.C.; Sudheer, K.; Rangan, D.; Ramasastri, K. A neuro-fuzzy computing technique for modeling hydrological time series. J. Hydrol. 2004, 291, 52–66. [Google Scholar] [CrossRef]
- Vaze, J.; Jordan, P.; Beecham, R.; Frost, A.; Summerell, G. Guidelines for Rainfall–Runoff Modelling: Towards Best Practice Model Application; eWater CRC: Bruce, Australia, 2012. [Google Scholar]
- Bicknell, B.; Imhoff, J.; Kittle, J.; Jobes, T.; Donigian, A. Hydrological Simulation Program–Fortran: HSPF Version 12.2 User’s Manual; United States Environmental Protection Agency, Office of Research and Development, National Exposure Research Laboratory: Athens, GA, USA, 2005. [Google Scholar]
- Singh, V.P. Computer Models of Watershed Hydrology; Water Resources Publications: Littleton, CO, USA, 1995. [Google Scholar]
- Moradkhani, H.; Sorooshian, S. General review of rainfall-runoff modeling: Model calibration, data assimilation, and uncertainty analysis. In Hydrological Modelling and the Water Cycle; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–24. [Google Scholar]
- Anshuka, A.; van Ogtrop, F.F.; Willem Vervoort, R. Drought forecasting through statistical models using standardised precipitation index: A systematic review and meta-regression analysis. Nat. Hazards 2019, 97, 955–977. [Google Scholar] [CrossRef]
- Chen, L.; Young, M.H. Green-Ampt infiltration model for sloping surfaces. Water Resour. Res. 2006, 42, W07420. [Google Scholar] [CrossRef]
- Ponce, V.M.; Hawkins, R.H. Runoff curve number: Has it reached maturity? J. Hydrol. Eng. 1996, 1, 11–19. [Google Scholar] [CrossRef]
- Idowu, T.; Edan, J.; Damuya, S. Estimation of the quantity of surface runoff to determine appropriate location and size of drainage structures in Jimeta Metropolis, Adamawa State, Nigeria. J. Geogr. Earth Sci. 2013, 1, 19–29. [Google Scholar]
- Horton, R.E. The role of infiltration in the hydrologic cycle. Eos Trans. Am. Geophys. Union 1933, 14, 446–460. [Google Scholar] [CrossRef]
- Schulze, R.E. Hydrology and Agrohydrology: A Text to Accompany the ACRU 3.00 Agrohydrological Modelling System; Water Research Commission: Pretoria, South Africa, 1995. [Google Scholar]
- Todini, E. Rainfall-runoff modeling—Past, present and future. J. Hydrol. 1988, 100, 341–352. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen,“SHE”, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Chiew, F.; Stewardson, M.; McMahon, T. Comparison of six rainfall-runoff modelling approaches. J. Hydrol. 1993, 147, 1–36. [Google Scholar] [CrossRef]
- Tsykin, E. Multiple nonlinear statistical models for runoff simulation and prediction. J. Hydrol. 1985, 77, 209–226. [Google Scholar] [CrossRef]
- Crawford, N.H.; Linsley, R.K. Digital Simulation in Hydrology’ Stanford Watershed Model 4; Stanford University: Stanford, CA, USA, 1966. [Google Scholar]
- Burnash, R.J.; Ferral, R.L.; McGuire, R.A. A Generalized Streamflow Simulation System: Conceptual Modeling for Digital Computers; US Department of Commerce, National Weather Service, and State of California: Sacramento, CA, USA, 1973. [Google Scholar]
- Madsen, H. Automatic calibration of a conceptual rainfall–runoff model using multiple objectives. J. Hydrol. 2000, 235, 276–288. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Safari, M.J.S.; Arashloo, S.R.; Mehr, A.D. Rainfall-runoff modeling through regression in the reproducing kernel Hilbert space algorithm. J. Hydrol. 2020, 587, 125014. [Google Scholar] [CrossRef]
- Mohammadi, B.; Ahmadi, F.; Mehdizadeh, S.; Guan, Y.; Pham, Q.B.; Linh, N.T.T.; Tri, D.Q. Developing novel robust models to improve the accuracy of daily streamflow modeling. Water Resour. Manag. 2020, 34, 3387–3409. [Google Scholar] [CrossRef]
- Abdulrazzak, M.; Elfeki, A.; Kamis, A.; Kassab, M.; Alamri, N.; Chaabani, A.; Noor, K. Flash flood risk assessment in urban arid environment: Case study of Taibah and Islamic universities’ campuses, Medina, Kingdom of Saudi Arabia. Geomat. Nat. Hazards Risk 2019, 10, 780–796. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, I. Determining High-Flood-Risk Regions Using Rainfall-Runoff Modeling. In Flood Handbook; CRC Press: Boca Raton, FL, USA, 2022; pp. 447–466. [Google Scholar]
- Giovannettone, J.; Copenhaver, T.; Burns, M.; Choquette, S. A statistical approach to mapping flood susceptibility in the Lower Connecticut River Valley Region. Water Resour. Res. 2018, 54, 7603–7618. [Google Scholar] [CrossRef]
- Qu, Y. An Integrated Hydrological Model Using Semi-Discrete Finite Volume Formulation. Ph.D. Thesis, Pennsylvanian State University, State College, PA, USA, 2004. [Google Scholar]
- Zhang, Y.; Wang, Y.; Zhang, Y.; Luan, Q.; Liu, H. Multi-scenario flash flood hazard assessment based on rainfall–runoff modeling and flood inundation modeling: A case study. Nat. Hazards 2021, 105, 967–981. [Google Scholar] [CrossRef]
- Mushore, T.; Dube, T.; Shoko, C.; Mazvimavi, D.; Masocha, M. Progress in rainfall-runoff modelling–contribution of remote sensing. Trans. R. Soc. S. Afr. 2019, 74, 173–179. [Google Scholar] [CrossRef]
- Jehanzaib, M. Evaluating the Impact of Climate Change and Human Activities on Hydrological Drought Extending towards Drought Propagation in Hydrological Cycle; Hanyang University: Seoul, Korea, 2020. [Google Scholar]
- Lee, J.-Y.; Kim, N.W.; Kim, T.-W.; Jehanzaib, M. Feasible ranges of runoff curve numbers for Korean watersheds based on the interior point optimization algorithm. KSCE J. Civ. Eng. 2019, 23, 5257–5265. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Liang, K.; Liu, C. Comparison of performance of twelve monthly water balance models in different climatic catchments of China. J. Hydrol. 2015, 529, 1030–1040. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Shah, S.A.; Kwon, H.-H.; Kim, T.-W. Investigating the influence of natural events and anthropogenic activities on hydrological drought in South Korea. Terr. Atmos. Ocean. Sci. 2020, 31, 85–96. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Bao, W.; Xiao, Z.; Si, W.; Sun, Y. Application of Regularized Dynamic System Response Curve for Runoff Correction Based on HBV Model: Case Study of Shiquan Catchment, China. J. Hydrol. Eng. 2022, 27, 05022002. [Google Scholar] [CrossRef]
- Hong, N.; Cheng, Q.; Wijesiri, B.; Bandala, E.R.; Goonetilleke, A.; Liu, A. Integrating Tank Model and adsorption/desorption characteristics of filter media to simulate outflow water quantity and quality of a bioretention basin: A case study of biochar-based bioretention basin. J. Environ. Manag. 2022, 304, 114282. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, Z.; Zhao, W. Assessing the impact of climate change on flood events using HEC-HMS and CMIP5. Water Air Soil Pollut. 2019, 230, 1–13. [Google Scholar] [CrossRef]
- Carpenter, T.M.; Georgakakos, K.P. Continuous streamflow simulation with the HRCDHM distributed hydrologic model. J. Hydrol. 2004, 298, 61–79. [Google Scholar] [CrossRef]
- Im, S.; Kim, H.; Kim, C.; Jang, C. Assessing the impacts of land use changes on watershed hydrology using MIKE SHE. Environ. Geol. 2009, 57, 231–239. [Google Scholar] [CrossRef]
- Zakizadeh, F.; Moghaddam Nia, A.; Salajegheh, A.; Sañudo-Fontaneda, L.A.; Alamdari, N. Efficient Urban Runoff Quantity and Quality Modelling Using SWMM Model and Field Data in an Urban Watershed of Tehran Metropolis. Sustainability 2022, 14, 1086. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, M.; Ma, Z.; Zhang, Z.; Yue, S.; Xiao, D.; Zhu, Z.; Wen, Y.; Lü, G. An online participatory system for SWMM-based flood modeling and simulation. Environ. Sci. Pollut. Res. 2022, 29, 7322–7343. [Google Scholar] [CrossRef] [PubMed]
- Amatya, D.; Walega, A.; Callahan, T.; Morrison, A.; Vulava, V.; Hitchcock, D.; Williams, T.; Epps, T. Storm event analysis of four forested catchments on the Atlantic coastal plain using a modified SCS-CN rainfall-runoff model. J. Hydrol. 2022, 608, 127772. [Google Scholar] [CrossRef]
- Dawson, C.; Wilby, R. Hydrological modelling using artificial neural networks. Prog. Phys. Geogr. 2001, 25, 80–108. [Google Scholar] [CrossRef]
- Bahrami, E.; Salarijazi, M.; Nejatian, S. Estimation of flood hydrographs in the ungauged mountainous watershed with Gray synthetic unit hydrograph model. Arab. J. Geosci. 2022, 15, 761. [Google Scholar] [CrossRef]
- Dooge, J. Problems and methods of rainfall-runoff modeling. In Proceedings of the Mathematical Models for Surface Water Hydrology: The Workshop Held at the IBM Scientific Center, Pisa, Italy; London, UK, 9–12 December 1977. [Google Scholar]
- Hasenmueller, E.A.; Criss, R.E. Water balance estimates of evapotranspiration rates in areas with varying land use. In Evapotranspiration—An Overview; IntechOpen: London, UK, 2013; pp. 1–22. [Google Scholar]
- Pandi, D.; Kothandaraman, S.; Kuppusamy, M. Hydrological models: A review. Int. J. Hydrol. Sci. Technol. 2021, 12, 223–242. [Google Scholar] [CrossRef]
- Kling, H.; Gupta, H. On the development of regionalization relationships for lumped watershed models: The impact of ignoring sub-basin scale variability. J. Hydrol. 2009, 373, 337–351. [Google Scholar] [CrossRef]
- Bergstrom, S. The HBV model. In Computer Models of Watershed Hydrology; Water Resources Publications: Littleton, CO, USA, 1995. [Google Scholar]
- Mouelhi, S.; Michel, C.; Perrin, C.; Andréassian, V. Stepwise development of a two-parameter monthly water balance model. J. Hydrol. 2006, 318, 200–214. [Google Scholar] [CrossRef]
- Sugawara, M.; Watanabe, I.; Ozaki, E.; Katsuyama, Y. Tank Model Programs for Personal Computer and the Way to Use; National Research Center for Disaster Prevention: Tsukuba, Japan, 1986. [Google Scholar]
- Thomas, H. Improved Methods for National Water Assessment; Report WR15249270; US Water Resource Council: Washington, DC, USA, 1981. [Google Scholar]
- Chiew, F.; Pitman, A.; McMahon, T. Conceptual catchment scale rainfall-runoff models and AGCM land-surface parameterisation schemes. J. Hydrol. 1996, 179, 137–157. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Vansteenkiste, T.; Tavakoli, M.; Ntegeka, V.; De Smedt, F.; Batelaan, O.; Pereira, F.; Willems, P. Intercomparison of hydrological model structures and calibration approaches in climate scenario impact projections. J. Hydrol. 2014, 519, 743–755. [Google Scholar] [CrossRef]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.-J.; Participants, D. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- El-Nasr, A.A.; Arnold, J.G.; Feyen, J.; Berlamont, J. Modelling the hydrology of a catchment using a distributed and a semi-distributed model. Hydrol. Process. Int. J. 2005, 19, 573–587. [Google Scholar] [CrossRef]
- Troutman, B.M. Errors and parameter estimation in precipitation-runoff modeling: 1. Theory. Water Resour. Res. 1985, 21, 1195–1213. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Vaze, J.; Wang, B. Separating effects of vegetation change and climate variability using hydrological modelling and sensitivity-based approaches. J. Hydrol. 2012, 420, 403–418. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Huber, W.C.; Dickinson, R.; Roesner, L.; Aidrich, J. Storm Water Management Model User’s Manual, Version 4; EPA: Washington, DC, USA, 1988. [Google Scholar]
- Hussain, S.N.; Zwain, H.M.; Nile, B.K. Modeling the effects of land-use and climate change on the performance of stormwater sewer system using SWMM simulation: Case study. J. Water Clim. Chang. 2022, 13, 125–138. [Google Scholar] [CrossRef]
- Mohammed, M.H.; Zwain, H.M.; Hassan, W.H. Modeling the quality of sewage during the leaking of stormwater surface runoff to the sanitary sewer system using SWMM: A case study. AQUA—Water Infrastruct. Ecosyst. Soc. 2022, 71, 86–99. [Google Scholar] [CrossRef]
- Madhuri, R.; Sarath Raja, Y.; Srinivasa Raju, K. Simulation-optimization framework in urban flood management for historic and climate change scenarios. J. Water Clim. Chang. 2022, 13, 1007–1024. [Google Scholar] [CrossRef]
- Wijayarathne, D.B.; Coulibaly, P. Identification of hydrological models for operational flood forecasting in St. John’s, Newfoundland, Canada. J. Hydrol. Reg. Stud. 2020, 27, 100646. [Google Scholar] [CrossRef]
- Calver, A. The Institute of Hydrology distributed model. In Computer Models of Watershed Hydrology; Water Resources Publications: Littleton, CO, USA, 1995; pp. 595–626. [Google Scholar]
- Booker, D.; Woods, R. Comparing and combining physically-based and empirically-based approaches for estimating the hydrology of ungauged catchments. J. Hydrol. 2014, 508, 227–239. [Google Scholar] [CrossRef] [Green Version]
- Haddeland, I.; Clark, D.B.; Franssen, W.; Ludwig, F.; Voß, F.; Arnell, N.W.; Bertrand, N.; Best, M.; Folwell, S.; Gerten, D. Multimodel estimate of the global terrestrial water balance: Setup and first results. J. Hydrometeorol. 2011, 12, 869–884. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Sun, G.; McNulty, S.G.; Zhang, H.; Li, J.; Manliang Zhang, E.; Strauss, P. Evaluation of the mike she model for application in the Loess Lateau, China. J. Am. Water Resour. Assoc. 2008, 44, 1108–1120. [Google Scholar] [CrossRef]
- Yin, D.; Evans, B.; Wang, Q.; Chen, Z.; Jia, H.; Chen, A.S.; Fu, G.; Ahmad, S.; Leng, L. Integrated 1D and 2D model for better assessing runoff quantity control of low impact development facilities on community scale. Sci. Total Environ. 2020, 720, 137630. [Google Scholar] [CrossRef]
- Mobilia, M.; Longobardi, A. Impact of rainfall properties on the performance of hydrological models for green roofs simulation. Water Sci. Technol. 2020, 81, 1375–1387. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; De Marinis, G. Support vector regression for rainfall-runoff modeling in urban drainage: A comparison with the EPA’s storm water management model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Avant, B.; Muche, M. An overview of rainfall-runoff model types. In Proceedings of the iEMSs 2018, 9th International Congress on Environmental Modelling and Software “Modelling for Sustainable Food-Energy-Water Systems”, Fort Collins, CO, USA, 24–28 June 2018. [Google Scholar]
- Pechlivanidis, I.; Jackson, B.; Mcintyre, N.; Wheater, H. Catchment scale hydrological modelling: A review of model types, calibration approaches and uncertainty analysis methods in the context of recent developments in technology and applications. Glob. NEST J. 2011, 13, 193–214. [Google Scholar]
- Niu, W.-J.; Feng, Z.-K.; Zeng, M.; Feng, B.-F.; Min, Y.-W.; Cheng, C.-T.; Zhou, J.-Z. Forecasting reservoir monthly runoff via ensemble empirical mode decomposition and extreme learning machine optimized by an improved gravitational search algorithm. Appl. Soft Comput. 2019, 82, 105589. [Google Scholar] [CrossRef]
- Oppel, H.; Schumann, A.H. Machine learning based identification of dominant controls on runoff dynamics. Hydrol. Process. 2020, 34, 2450–2465. [Google Scholar] [CrossRef]
- Nourani, V.; Gökçekuş, H.; Gichamo, T. Ensemble data-driven rainfall-runoff modeling using multi-source satellite and gauge rainfall data input fusion. Earth Sci. Inform. 2021, 14, 1787–1808. [Google Scholar] [CrossRef]
- Okkan, U.; Ersoy, Z.B.; Kumanlioglu, A.A.; Fistikoglu, O. Embedding machine learning techniques into a conceptual model to improve monthly runoff simulation: A nested hybrid rainfall-runoff modeling. J. Hydrol. 2021, 598, 126433. [Google Scholar] [CrossRef]
- Sang, Y.-F. A review on the applications of wavelet transform in hydrology time series analysis. Atmos. Res. 2013, 122, 8–15. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S. Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm. Agric. Water Manag. 2020, 237, 106145. [Google Scholar] [CrossRef]
- Yang, M.; Wang, H.; Jiang, Y.; Lu, X.; Xu, Z.; Sun, G. Geca proposed ensemble–knn method for improved monthly runoff forecasting. Water Resour. Manag. 2020, 34, 849–863. [Google Scholar] [CrossRef]
- Akbari, M.; Overloop, P.J.v.; Afshar, A. Clustered K nearest neighbor algorithm for daily inflow forecasting. Water Resour. Manag. 2011, 25, 1341–1357. [Google Scholar] [CrossRef] [Green Version]
- Nourani, V.; Tajbakhsh, A.D.; Molajou, A. Data mining based on wavelet and decision tree for rainfall-runoff simulation. Hydrol. Res. 2019, 50, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Zhang, J.; Bao, Z.; Wang, G.; Wang, W.; Yang, Y.; Wang, J. Runoff modeling in ungauged catchments using machine learning algorithm-based model parameters regionalization methodology. Engineering 2022, in press. [CrossRef]
- Samantaray, S.; Sahoo, A. Estimation of runoff through BPNN and SVM in Agalpur Watershed. In Frontiers in Intelligent Computing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 268–275. [Google Scholar]
- Li, B.; Cheng, C. Monthly discharge forecasting using wavelet neural networks with extreme learning machine. Sci. China Technol. Sci. 2014, 57, 2441–2452. [Google Scholar] [CrossRef]
- Jacquin, A.P.; Shamseldin, A.Y. Development of rainfall–runoff models using Takagi–Sugeno fuzzy inference systems. J. Hydrol. 2006, 329, 154–173. [Google Scholar] [CrossRef]
- Aqil, M.; Kita, I.; Yano, A.; Nishiyama, S. Analysis and prediction of flow from local source in a river basin using a Neuro-fuzzy modeling tool. J. Environ. Manag. 2007, 85, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Yokoo, K.; Ishida, K.; Ercan, A.; Tu, T.; Nagasato, T.; Kiyama, M.; Amagasaki, M. Capabilities of deep learning models on learning physical relationships: Case of rainfall-runoff modeling with LSTM. Sci. Total Environ. 2022, 802, 149876. [Google Scholar] [CrossRef] [PubMed]
- Roy, B.; Singh, M.P.; Kaloop, M.R.; Kumar, D.; Hu, J.-W.; Kumar, R.; Hwang, W.-S. Data-Driven Approach for Rainfall-Runoff Modelling Using Equilibrium Optimizer Coupled Extreme Learning Machine and Deep Neural Network. Appl. Sci. 2021, 11, 6238. [Google Scholar] [CrossRef]
- Han, H.; Choi, C.; Jung, J.; Kim, H.S. Deep learning with long short term memory based sequence-to-sequence model for rainfall-runoff simulation. Water 2021, 13, 437. [Google Scholar] [CrossRef]
- Wu, J.S.; Han, J.; Annambhotla, S.; Bryant, S. Artificial neural networks for forecasting watershed runoff and stream flows. J. Hydrol. Eng. 2005, 10, 216–222. [Google Scholar] [CrossRef]
- Mutlu, E.; Chaubey, I.; Hexmoor, H.; Bajwa, S. Comparison of artificial neural network models for hydrologic predictions at multiple gauging stations in an agricultural watershed. Hydrol. Process. Int. J. 2008, 22, 5097–5106. [Google Scholar] [CrossRef]
- Kişi, Ö. Streamflow forecasting using different artificial neural network algorithms. J. Hydrol. Eng. 2007, 12, 532–539. [Google Scholar] [CrossRef]
- Sanikhani, H.; Kisi, O. River flow estimation and forecasting by using two different adaptive neuro-fuzzy approaches. Water Resour. Manag. 2012, 26, 1715–1729. [Google Scholar] [CrossRef]
- Pramanik, N.; Panda, R.K. Application of neural network and adaptive neuro-fuzzy inference systems for river flow prediction. Hydrol. Sci. J. 2009, 54, 247–260. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Bilal Idrees, M.; Kim, D.; Kim, T.-W. Comprehensive Evaluation of Machine Learning Techniques for Hydrological Drought Forecasting. J. Irrig. Drain. Eng. 2021, 147, 04021022. [Google Scholar] [CrossRef]
- Haykin, S.; Network, N. A comprehensive foundation. Neural Netw. 2004, 2, 41. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Jain, A.; Kumar, A.M. Hybrid neural network models for hydrologic time series forecasting. Appl. Soft Comput. 2007, 7, 585–592. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, X.; Wang, F.; Zhang, Y.; Xia, R.; Jin, J. Rainfall-runoff modeling using LSTM-based multi-state-vector sequence-to-sequence model. J. Hydrol. 2021, 598, 126378. [Google Scholar] [CrossRef]
- Jang, J.-S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- El-Shafie, A.; Taha, M.R.; Noureldin, A. A neuro-fuzzy model for inflow forecasting of the Nile river at Aswan high dam. Water Resour. Manag. 2007, 21, 533–556. [Google Scholar] [CrossRef]
- Özger, M. Comparison of fuzzy inference systems for streamflow prediction. Hydrol. Sci. J. 2009, 54, 261–273. [Google Scholar] [CrossRef]
- Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar]
- Bray, M.; Han, D. Identification of support vector machines for runoff modelling. J. Hydroinform. 2004, 6, 265–280. [Google Scholar] [CrossRef] [Green Version]
- He, Z.; Wen, X.; Liu, H.; Du, J. A comparative study of artificial neural network, adaptive neuro fuzzy inference system and support vector machine for forecasting river flow in the semiarid mountain region. J. Hydrol. 2014, 509, 379–386. [Google Scholar] [CrossRef]
- Kim, T.-W.; Jehanzaib, M. Drought risk analysis, forecasting and assessment under climate change. Water 2020, 12, 1862. [Google Scholar] [CrossRef]
- Sood, A.; Muthuwatta, L.; McCartney, M. A SWAT evaluation of the effect of climate change on the hydrology of the Volta River basin. Water Int. 2013, 38, 297–311. [Google Scholar] [CrossRef]
- Mostafazadeh, R.; Sadoddin, A.; Bahremand, A.; Sheikh, V.B.; Garizi, A.Z. Scenario analysis of flood control structures using a multi-criteria decision-making technique in Northeast Iran. Nat. Hazards 2017, 87, 1827–1846. [Google Scholar] [CrossRef]
- Peredo, D.; Ramos, M.-H.; Andréassian, V.; Oudin, L. Investigating hydrological model versatility to simulate extreme flood events. Hydrol. Sci. J. 2022, 67, 628–645. [Google Scholar] [CrossRef]
- Van den Honert, R.C.; McAneney, J. The 2011 Brisbane floods: Causes, impacts and implications. Water 2011, 3, 1149–1173. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, D.; Robertson, D.; Wang, Q.; Pagano, T.; Hapuarachchi, H. Evaluation of numerical weather prediction model precipitation forecasts for short-term streamflow forecasting purpose. Hydrol. Earth Syst. Sci. 2013, 17, 1913–1931. [Google Scholar] [CrossRef] [Green Version]
- Panda, R.K.; Pramanik, N.; Bala, B. Simulation of river stage using artificial neural network and MIKE 11 hydrodynamic model. Comput. Geosci. 2010, 36, 735–745. [Google Scholar] [CrossRef]
- Modaresi, F.; Araghinejad, S.; Ebrahimi, K. A comparative assessment of artificial neural network, generalized regression neural network, least-square support vector regression, and K-nearest neighbor regression for monthly streamflow forecasting in linear and nonlinear conditions. Water Resour. Manag. 2018, 32, 243–258. [Google Scholar] [CrossRef]
- Sankaranarayanan, S.; Prabhakar, M.; Satish, S.; Jain, P.; Ramprasad, A.; Krishnan, A. Flood prediction based on weather parameters using deep learning. J. Water Clim. Chang. 2020, 11, 1766–1783. [Google Scholar] [CrossRef]
- Yang, T.; Sun, F.; Gentine, P.; Liu, W.; Wang, H.; Yin, J.; Du, M.; Liu, C. Evaluation and machine learning improvement of global hydrological model-based flood simulations. Environ. Res. Lett. 2019, 14, 114027. [Google Scholar] [CrossRef]
- Farfán, J.F.; Palacios, K.; Ulloa, J.; Avilés, A. A hybrid neural network-based technique to improve the flow forecasting of physical and data-driven models: Methodology and case studies in Andean watersheds. J. Hydrol. Reg. Stud. 2020, 27, 100652. [Google Scholar] [CrossRef]
- Konapala, G.; Kao, S.-C.; Painter, S.L.; Lu, D. Machine learning assisted hybrid models can improve streamflow simulation in diverse catchments across the conterminous US. Environ. Res. Lett. 2020, 15, 104022. [Google Scholar] [CrossRef]


| Categories | Characteristics | Models | Strengths | Weaknesses | Related Studies |
|---|---|---|---|---|---|
| Conceptual model | 1. Parametric or grey box model. 2. Include semi-empirical equations with a physical basis. 3. Parameters are derived from calibration and field data. 4. Simple and can be easily implemented on computers. 5. Require large hydro-meteorological data. 6. Calibration involves curve fitting and makes physical interpretation difficult. | HBV, GR2M, ABCD, TANK, GR4J, SM | 1. Easy to calibrate, simple model structure. 2. Calibrate with limited data. 3. Need less computation. | 1. Does not consider spatial variability within catchment. 2. Not recommended for large catchments. | [6,39,40,41,42] |
| Physical process-based model | 1. Mechanistic or white box model. 2. Based on spatial distribution, Evaluation of parameters describing physical characteristics. 3. Complex model and requires human expertise and computation capability. 4. Requires data about initial state of model and morphology of catchment. 5. Represents different hydrological processes through mass, momentum, and energy conservation equations | TOPMODEL, SWMM, HEC-HMS, WATFLOOD | 1. Incorporates spatial and temporal variability, very fine scale. 2. Valid for wide range of situations. | 1. Suffer from scale related problems. 2. Large number of parameters and calibration needed; site specific. | [43,44,45,46,47] |
| Empirical or data driven model | 1. Data based or metric model. 2. Involve mathematical equations, derive value from available time series. 3. Little consideration of features and processes of system. 4. Cannot be generated to other catchments. 5. Valid within the boundary of given domain | SCS-CN, ANN, UH | 1. Small number of parameters needed. 2. Limited data requirement. 3. Can be used in Ungauged catchments. | 1. No connection between physical catchment, input data distortion, or Black-box. 2. High computation cost and time. | [8,48,49,50] |
| Model | Advantages | Disadvantages | Related Studies |
|---|---|---|---|
| KNN | 1. Tolerate noise and irrelevant attributes. 2. Capable of identifying past events. | 1. Inability to discover input–output mapping. 2. It does not predict values higher than the range of historical observations. | [88,89] |
| DT | 1. Easy to understand 2. Fast learning and robust to noise | 1. Needs substantial amount of data 2. Tends to overfit if tree length exceeds | [90,91] |
| SVM | 1. Through the regularization parameter, the user can avoid overfitting. 2. Easy to solve complex problems with appropriate Kernel | 1. Selection of kernel function is not easy 2. Fine-tuning of hyperparameters is difficult | [92,93] |
| FRBS | 1. Ability to handle large amount of noisy data from dynamic and nonlinear systems. 2. Fast model development with less computation time. | 1. Attempts to reduce the number of rules generally decreases model generalization ability. 2. Lacks an appropriate set of guidelines for calibrating model parameters in a way that will maximize model interpretability. | [94,95] |
| DLNN | 1. Learn higher-level abstractions from input data. 2. Detects nonlinear interactions and approximates any arbitrary function | 1. High computation cost and time. 2. Very complex black box model structure. | [96,97,98] |
| ANN | 1. Ability to work with inadequate knowledge. 2. Needs less formal statistical training. | 1. Tends to overfit. 2. Time-consuming to train with traditional CPUs. | [99,100,101] |
| ANFIS | 1. Hybrid model with the strength of ANN and fuzzy. 2. Fast convergence rate while training. | 1. Computational complexity rise with an increase in fuzzy rules. 2. Low interpretability of learned information | [102,103] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jehanzaib, M.; Ajmal, M.; Achite, M.; Kim, T.-W. Comprehensive Review: Advancements in Rainfall-Runoff Modelling for Flood Mitigation. Climate 2022, 10, 147. https://doi.org/10.3390/cli10100147
Jehanzaib M, Ajmal M, Achite M, Kim T-W. Comprehensive Review: Advancements in Rainfall-Runoff Modelling for Flood Mitigation. Climate. 2022; 10(10):147. https://doi.org/10.3390/cli10100147
Chicago/Turabian StyleJehanzaib, Muhammad, Muhammad Ajmal, Mohammed Achite, and Tae-Woong Kim. 2022. "Comprehensive Review: Advancements in Rainfall-Runoff Modelling for Flood Mitigation" Climate 10, no. 10: 147. https://doi.org/10.3390/cli10100147
APA StyleJehanzaib, M., Ajmal, M., Achite, M., & Kim, T.-W. (2022). Comprehensive Review: Advancements in Rainfall-Runoff Modelling for Flood Mitigation. Climate, 10(10), 147. https://doi.org/10.3390/cli10100147











