Suitability Assessment of Weather Networks for Wind Data Measurements in the Athabasca Oil Sands Area
Abstract
:1. Introduction
- Evaluation of graphical and quantitative measures on wind data among weather stations to identify the best representative ones for a similarity analysis;
- Calculation of the percentage of similarity in the wind data records using the best measures and integrating the instrumental errors to find the correlations among the weather stations; and
- Determination of optimal weather networks for wind data measurements in the study area based on the estimated percentage of the similarity analysis.
2. Study Area and Data Availability
2.1. Study Area
2.2. Data Availability
3. Methods
3.1. Graphical Measure
3.2. Quantitative Measures
3.2.1. Association-Related Measures
3.2.2. Coincidence-Related Measures
3.2.3. Determination of the Best Representative Measures
3.3. Similarity Analysis
4. Results and Discussion
4.1. Wind Rose Diagram
4.2. Measures of Association
4.3. Measures of Coincidence
4.4. Relationship and Similarity Analysis
4.4.1. Correlation Analysis
4.4.2. Percentage of Similarity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kiranvishnu, K.; Sireesha, K.; Ramprabhakar, J. Comparative Study of Wind Speed Forecasting Techniques. In Proceedings of the 2016 Biennial International Conference on Power and Energy Systems: Towards Sustainable Energy (PESTSE), Bengaluru, India, 21–23 January 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Keevallik, S.; Soomere, T.; Pärg, R.; Žukova, V. Outlook for wind measurement at Estonian automatic weather stations. Proc. Est. Acad. Sci. Eng. 2007, 13, 234–251. [Google Scholar]
- Ahmed, S.A.; Omer, M.A. Surface wind characteristics and wind direction estimation for “Kalar Region/Sulaimani-North Iraq”. J. Univ. Zakho 2013, 1, 882–890. [Google Scholar]
- World Meteorological Organization. Guide to Meteorological Instruments and Methods of Observation, 2010 ed.; WMO-No. 8; World Meteorological Organization (WMO): Geneva, Switzerland, 2010; p. 716. [Google Scholar]
- Cassola, F.; Burlando, M. Wind speed and wind energy forecast through Kalman filtering of Numerical Weather Prediction model output. Appl. Energy 2012, 99, 154–166. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C. Data processing strategies in wind energy forecasting models and applications: A comprehensive review. Appl. Energy 2019, 249, 392–408. [Google Scholar] [CrossRef]
- Rehman, S.; El-Amin, I.M.; Ahmad, F.; Shaahid, S.M.; Al-Shehri, A.M.; Bakhashwain, J.M. Wind power resource assessment for Rafha, Saudi Arabia. Renew. Sustain. Energy Rev. 2007, 11, 937–950. [Google Scholar] [CrossRef]
- Belu, R.; Koracin, D. Statistical and spectral analysis of wind characteristics relevant to wind energy assessment using tower measurements in complex terrain. J. Wind Energy 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Carlotti, P. Urban fluid mechanics: Current issues and trends—Summary of the special symposium on urban fluid mechanics at the ASME 2014 4th joint US-European fluid engineering division summer meeting. Environ. Fluid Mech. 2015, 15, 483–490. [Google Scholar] [CrossRef]
- Allen, B.R.G.; Wright, J.L. Translating wind measurements from weather stations to agricultural crops. J. Hydrol. Eng. 1997, 2, 26–35. [Google Scholar] [CrossRef] [Green Version]
- Desmarteau, D.A.; Ritter, A.M.; Hendley, P.; Guevara, M.W. Impact of wind speed and direction and key meteorological parameters on potential pesticide drift mass loadings from sequential aerial applications. Integr. Environ. Assess. Manag. 2019, 16, 197–210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moscati, M.C.D.L.; Gan, M.A. Rainfall variability in the rainy season of semiarid zone of Northeast Brazil (NEB) and its relation to wind regime Marley. Int. J. Climatol. 2007, 27, 493–512. [Google Scholar] [CrossRef]
- Hand, L.M.; Shepherd, J.M. An investigation of warm-season spatial rainfall variability in Oklahoma City: Possible linkages to urbanization and prevailing wind. J. Appl. Meteorol. Climatol. 2009, 48, 251–269. [Google Scholar] [CrossRef]
- Lledó, L.; Torralba, V.; Soret, A.; Ramon, J.; Doblas-Reyes, F.J. Seasonal forecasts of wind power generation. Renew. Energy 2019, 143, 91–100. [Google Scholar] [CrossRef]
- Marchigiani, R.; Gordy, S.; Cipolla, J.; Stawicki, S.A.; Adams, R.C.; Evans, D.C.; Stehly, C.; Galwankar, S.; Russell, S.; Marco, A.P.; et al. Wind disasters: A comprehensive review of current management strategies. Int. J. Crit. Illn. Inj. Sci. 2013, 3, 130–142. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Wu, B.; He, P.; Gu, W.; Liu, B. Wind disasters adaptation in cities in a changing climate: A systematic review. PLoS ONE 2021, 16, e0248503. [Google Scholar] [CrossRef]
- Horstmann, J.; Borge, J.C.N.; Seemann, J.; Carrasco, R.; Lund, B. Wind, Wave, and Current Retrieval Utilizing X-Band Marine. In Coastal Ocean Observing Systems; Liu, Y., Kerkering, H., Weisberg, R.H., Eds.; Academic Press: Cambridge, MA, USA, 2015; pp. 281–304. ISBN 9780128020616. [Google Scholar]
- Papineau, J.W.; Deacon, L. Fort McMurray and the Canadian Oil Sands: Local Coverage of National Importance. Environ. Commun. 2017, 11, 593–608. [Google Scholar] [CrossRef]
- Ahmed, M.R.; Rahaman, K.R.; Hassan, Q.K. Remote sensing of wildland fire-induced risk assessment at the community level. Sensors 2018, 18, 1570. [Google Scholar] [CrossRef] [Green Version]
- Oil Sands Community Alliance. The Athabasca Oil Sands Area. Available online: https://www.oscaalberta.ca/did-you-know/the-athabasca-oil-sands-area/ (accessed on 24 November 2021).
- Regional Municipality of Wood Buffalo. Envision Wood Buffalo Towards 250k: Fort McMurray—Where We Are Today; Regional Municipality of Wood Buffalo (RMWB): Fort McMurray, AB, Canada, 2008; p. 61. [Google Scholar]
- Alberta Envirvonment and Parks. Oil Sands Monitoring Program: Annual Report for 2017–2018; Environment and Climate Change Canada; Government of Alberta: Edmonton, AB, Canada, 2018; p. 64. [Google Scholar]
- World Meteorological Organization. Manual on the Global Observing System; WMO-No.544; World Meteorological Organization (WMO): Geneva, Switzerland, 2017; Volume I, p. 172. [Google Scholar]
- World Meteorological Organization. Manual on the Global Data-Processing and Forecasting System; WMO-No.485; World Meteorological Organization (WMO): Geneva, Switzerland, 2012; p. 193. [Google Scholar]
- Jammalamadaka, S.R.; Seagupta, A. Topics in Circular Statistics (Multivaria Analysis Vol. 5); World Scientific: Singapore, 2001; ISBN 9810237782. [Google Scholar]
- Mardia, K.V.; Jupp, P.E. Directional Statistics; John Wiley & Sons, Ltd.: West Sussex, UK, 2000; ISBN 0471953334. [Google Scholar]
- Jammalamadaka, S.R.; Lund, U.J. The effect of wind direction on ozone levels: A case study. Environ. Ecol. Stat. 2006, 13, 287–298. [Google Scholar] [CrossRef] [Green Version]
- Mohanakumar, K.; Santosh, K.R.; Mohanan, P.; Vasudevan, K.; Manoj, M.G.; Samson, T.K.; Kottayil, A.; Rakesh, V.; Rebello, R.; Abhilash, S. A versatile 205 MHz stratosphere-troposphere radar at Cochin—scientific applications. Curr. Sci. 2018, 114, 2459–2466. [Google Scholar] [CrossRef]
- Cohen-Zada, A.L.; Maman, S.; Blumberg, D.G. Earth aeolian wind streaks: Comparison to wind data from model and stations. J. Geophys. Res. Planets 2017, 122, 1119–1137. [Google Scholar] [CrossRef]
- Varma, S.A.K.; Srimurali, M.; Varma, S.V.K. Evolution of wind Rose diagrams for RTPP, Kadapa, A.P., India. Int. J. Innov. Res. Dev. 2013, 2, 150–154. [Google Scholar]
- Grange, S.K. Technical Note: Averaging Wind Speeds and Directions; University of Auckland: Auckland, New Zealand, 2014; p. 12. [Google Scholar]
- Ratner, B. The correlation coefficient: Its values range between 1/1, or do they. J. Target. Meas. Anal. Mark. 2009, 17, 139–142. [Google Scholar] [CrossRef] [Green Version]
- Smith, J.; Smith, P. Environmental Modelling. An Introduction; Oxford University Press: Oxford, UK, 2007; ISBN 978019927206. [Google Scholar]
- Anderson, J.; Ash, G.; Wright, H. A Statistical Comparison of Weather Stations in Carberry, Manitoba Canada. In 92nd American Meteorological Society Annual Meeting (22–26 January 2012); American Meteorological Society: Boston, MA, USA, 2012; pp. 1–25. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Deshmukh, D.; Ahmed, M.R.; Dominic, J.A.; Zaghloul, M.S.; Gupta, A.; Achari, G.; Hassan, Q.K. Quantifying relations and similarities of the meteorological parameters among the weather stations in the Alberta Oil Sands region. PLoS ONE 2022, 17, e0261610. [Google Scholar] [CrossRef] [PubMed]
- Alberta Environment and Water. Groundwater Flow Model for the Athabasca Oil Sands, North of Fort MacMurray: Phase 1 Conceptual and Numerical Model Development; Environment and Sustainable Resource Development (ESRD): Edmonton, AB, Canada, 2012; p. 325. [Google Scholar]
- Suncor Energy Inc. Appendix 3: Climate Change in the Oil Sands Region; Voyageur South Project: Fort McMurray, AB, Canada, 2007; p. 134. [Google Scholar]
- Wood Buffalo Environmental Association. WBEA 2000 Annual Report; Wood Buffalo Environmental Association (WBEA): Fort McMurray, AB, Canada, 2000; p. 32. [Google Scholar]
- Government of Canada Canadian Climate Normals. Available online: https://climate.weather.gc.ca/climate_normals/index_e.html (accessed on 29 April 2021).
- Zou, M.; Djokic, S.Z. A review of approaches for the detection and treatment of outliers in processing wind turbine and wind farm measurements. Energies 2020, 13, 4228. [Google Scholar] [CrossRef]
- Government of Alberta Standards and Quality Program. Available online: http://environmentalmonitoring.alberta.ca/resources/standards-and-protocols/ (accessed on 15 December 2020).
- World Meteorological Organization. Guide to Instruments and Methods of Observation, 2018 ed.; WMO-No. 8; World Meteorological Organization (WMO): Geneva, Switzerland, 2018; Volume I, p. 573. [Google Scholar]
- Turgut, E.T.; Usanmaz, Ö. An analysis of vertical profiles of wind and humidity based on long-term radiosonde data in Turkey. Anadolu Univ. J. Sci. Technol. A—Appl. Sci. Eng. 2016, 17, 830. [Google Scholar]
- Mooi, E.; Sarstedt, M. A Concise Guide to Market Research: The Process, Data, and Methods Using IBM SPSS Statistic, 3rd ed.; Springer: Heidelberg, Germany, 2019; ISBN 978-3-662-56706-7. [Google Scholar]
- Golmohammadi, G.; Prasher, S.; Madani, A.; Rudra, R. Evaluating three hydrological distributed watershed models: MIKE-SHE, APEX, SWAT. Hydrology 2014, 1, 20–39. [Google Scholar] [CrossRef] [Green Version]
- Veiga, V.B.; Hassan, Q.K.; He, J. Development of flow forecasting models in the bow river at Calgary, Alberta, Canada. Water 2015, 7, 99–115. [Google Scholar] [CrossRef] [Green Version]
- Anonymous. Coefficient of Determination. Available online: https://www.creativesafetysupply.com/glossary/coefficient-of-determination/ (accessed on 21 April 2021).
- Olabanji, M.F.; Ndarana, T.; Davis, N.; Archer, E. Climate change impact on water availability in the olifants catchment (South Africa) with potential adaptation strategies. Phys. Chem. Earth 2020, 120, 102939. [Google Scholar] [CrossRef]
- Zhong, X.; Dutta, U. Engaging Nash-Sutcliffe Efficiency and Model Efficiency Factor Indicators in Selecting and Validating Effective Light Rail System Operation and Maintenance Cost Models. J. Traffic Transp. Eng. 2015, 3, 255–265. [Google Scholar] [CrossRef] [Green Version]
- Vandeput, N. Forecast KPIs: RMSE, MAE, MAPE & Bias. Available online: https://towardsdatascience.com/forecast-kpi-rmse-mae-mape-bias-cdc5703d242d (accessed on 28 May 2021).
- Ramesh, K.; Anitha, R.; Ramalakshmi, P. Prediction of lead seven day minimum and maximum surface air temperature using neural network and genetic programming. Sains Malays. 2015, 44, 1389–1396. [Google Scholar] [CrossRef]
- Schober, P.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zha, J.; Zhao, D.; Yang, Q. Changes in terrestrial near-surface wind speed and their possible causes: An overview. Clim. Dyn. 2018, 51, 2039–2078. [Google Scholar] [CrossRef] [Green Version]
- Wood Buffalo Environmental Association. WBEA 2019 Annual Report; Wood Buffalo Environmental Association (WBEA): Fort McMurray, AB, Canada, 2020; p. 76. [Google Scholar]
- Ruel, J.C.; Pin, D.; Cooper, K. Effect of topography on wind behaviour in a complex terrain. Forestry 1998, 71, 261–265. [Google Scholar] [CrossRef] [Green Version]
- Jenkins, G. A comparison between two types of widely used weather stations. Weather 2014, 69, 105–110. [Google Scholar] [CrossRef]



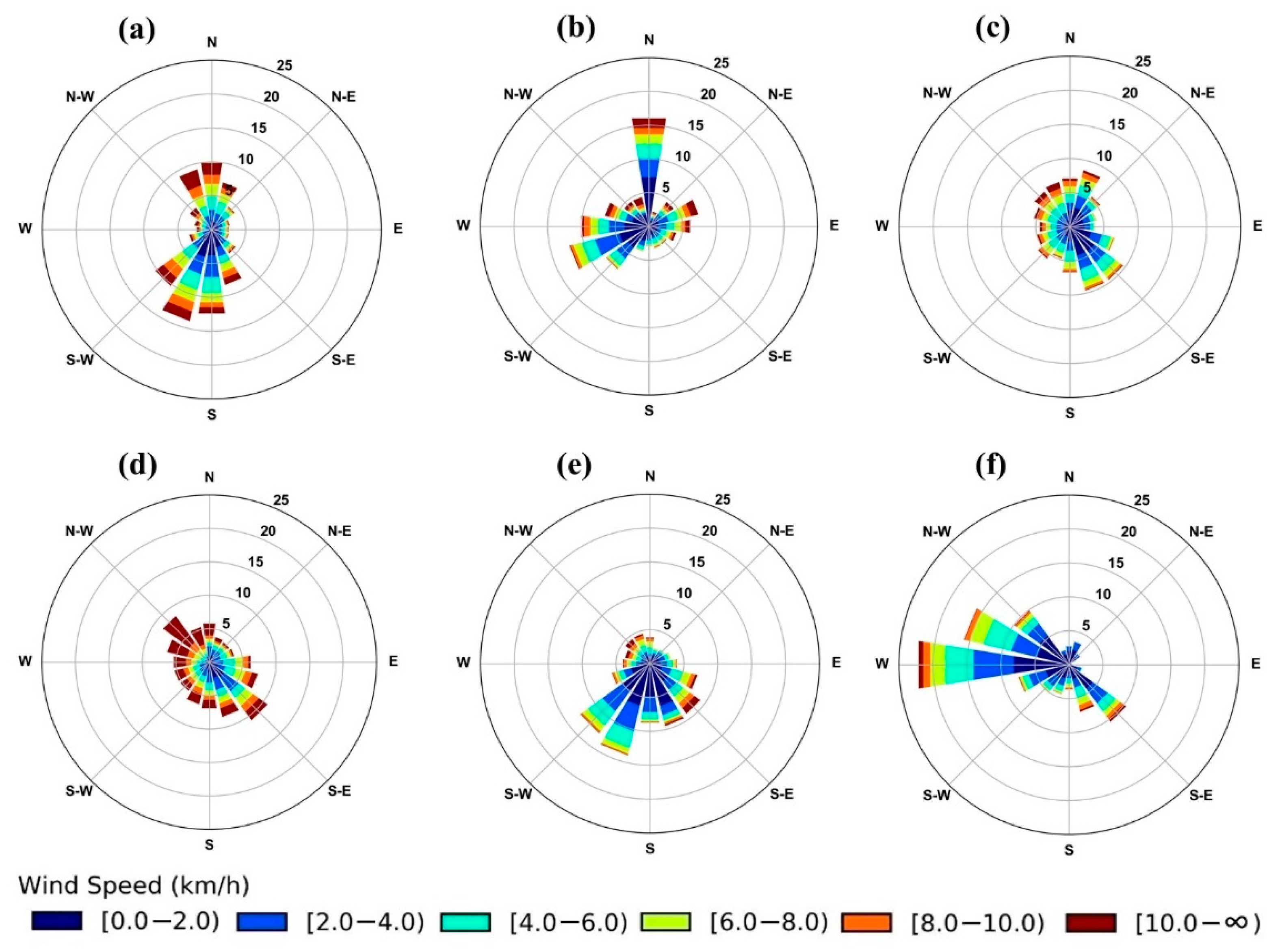

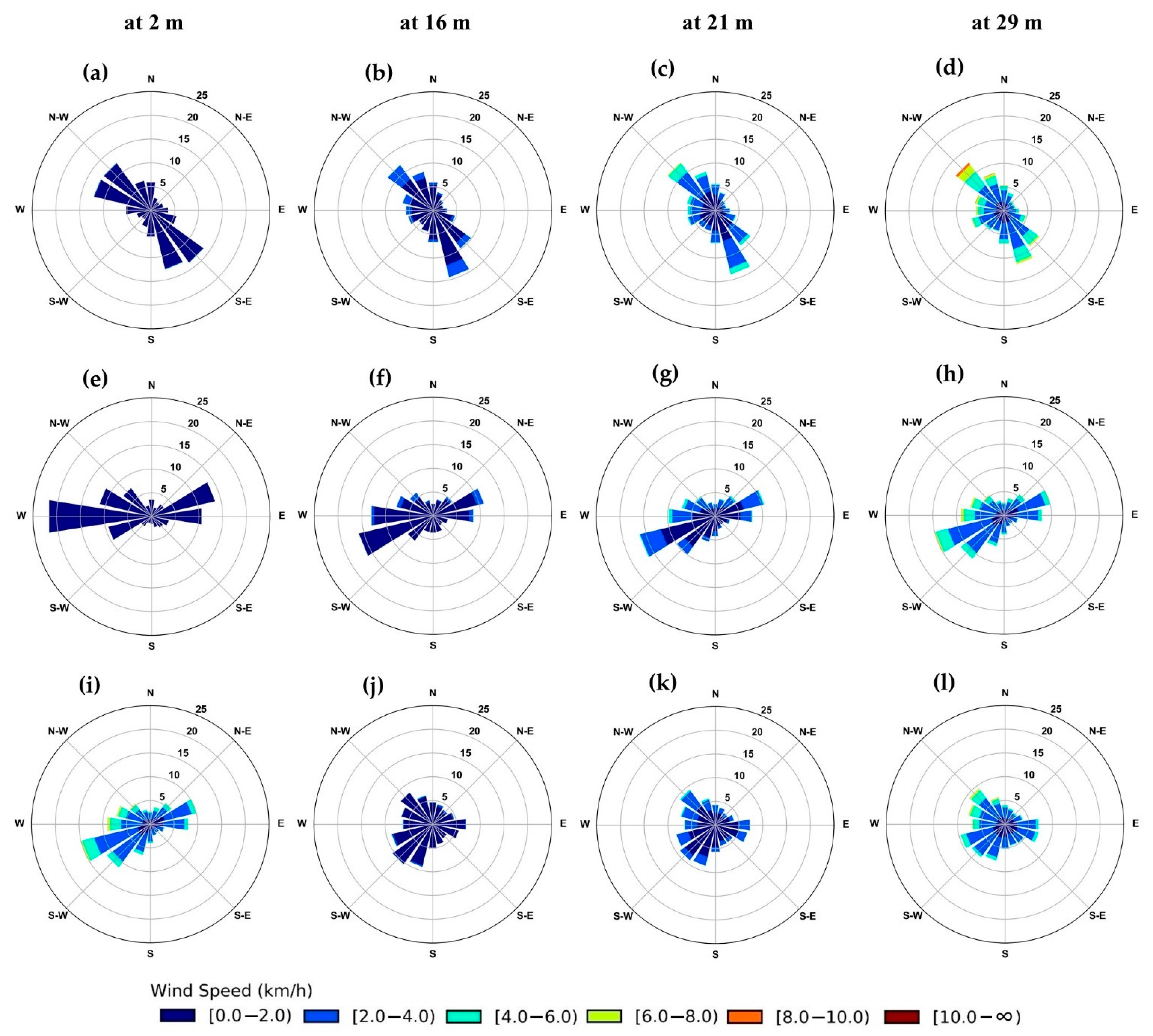


| Network | Weather Station | Data Measurement | Period of Records * | ||
|---|---|---|---|---|---|
| Height (m) | Frequency | From | To | ||
| OSM WQP | C1 | 10 | Daily | 1 January 2009 | 31 March 2017 |
| C2 | 22 December 2008 | ||||
| C3 | 3 November 2010 | ||||
| C4 | 25 July 2011 | ||||
| C5 | 1 November 2011 | ||||
| WBEA ES | JE306 | 2 | Hourly | 3 September 2014 | 1 April 2019 |
| JE308 | 25 March 2014 | ||||
| JE312 | 2 September 2014 | 31 March 2019 | |||
| JE316 | 7 March 2014 | 1 April 2019 | |||
| JE323 | 15 March 2014 | ||||
| R2 | 1 January 2015 | ||||
| WBEA MT | JP104 | 2, 16, 21, and 29 | Hourly | 30 May 2014 | 31 January 2019 |
| JP107 | 29 August 2012 | 1 April 2018 | |||
| JP201 | 27 May 2014 | 31 January 2019 | |||
| JP213 | 18 July 2012 | 1 April 2018 | |||
| JP311 | 30 July 2013 | ||||
| JP316 | 10 October 2012 | ||||
| OSM WQP | WBEA ES | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station Pair | n | u-Component | v-Component | Station Pair | n | u-Component | v-Component | ||||||
| r | AAE | r | AAE | r | AAE | r | AAE | ||||||
| C1 vs. | C2 | 2928 | 0.34 | 3.26 | 0.59 | 4.75 | JE306 vs. | JE308 | 20,628 | 0.49 | 3.90 | 0.58 | 2.45 |
| C3 | 2338 | 0.48 | 3.63 | 0.69 | 2.86 | JE312 | 37,332 | 0.77 | 2.73 | 0.69 | 1.85 | ||
| C4 | 2076 | 0.36 | 2.26 | 0.54 | 2.84 | JE316 | 37,380 | 0.62 | 3.70 | 0.63 | 3.17 | ||
| C5 | 1975 | 0.04 | 3.73 | 0.48 | 4.20 | JE323 | 18,673 | 0.54 | 3.65 | 0.63 | 2.28 | ||
| R2 | 16,846 | 0.50 | 3.76 | 0.37 | 2.65 | ||||||||
| C2 vs. | C3 | 2322 | 0.43 | 4.14 | 0.64 | 5.38 | JE308 vs. | JE312 | 20,576 | 0.51 | 2.55 | 0.66 | 2.01 |
| C4 | 2060 | 0.58 | 2.64 | 0.77 | 3.68 | JE316 | 23,752 | 0.55 | 4.23 | 0.61 | 2.53 | ||
| C5 | 1975 | 0.28 | 3.60 | 0.53 | 4.28 | JE323 | 22,384 | 0.59 | 2.41 | 0.67 | 1.57 | ||
| R2 | 16,469 | 0.33 | 2.64 | 0.35 | 2.99 | ||||||||
| C3 vs. | C4 | 2076 | 0.5 | 3.81 | 0.58 | 3.83 | JE312 vs. | JE316 | 37,166 | 0.69 | 3.35 | 0.77 | 2.83 |
| C5 | 1975 | 0.3 | 4.06 | 0.53 | 5.21 | JE323 | 18,691 | 0.63 | 2.05 | 0.72 | 1.72 | ||
| R2 | 16,723 | 0.48 | 2.57 | 0.42 | 2.40 | ||||||||
| C4 vs. | C5 | 1975 | 0.23 | 3.18 | 0.27 | 4.18 | JE316 vs. | JE323 R2 | 23,089 | 0.71 | 4.09 | 0.61 | 2.58 |
| 16,511 | 0.47 | 4.33 | 0.32 | 4.26 | |||||||||
| JE323 vs. | R2 | 14,985 | 0.55 | 2.07 | 0.52 | 2.43 | |||||||
| Station Pair | 2 m | 16 m | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | u-Component | v-Component | n | u-Component | v-Component | ||||||
| r | AAE | r | AAE | r | AAE | r | AAE | ||||
| JP104 vs. | JP107 | 31,121 | 0.59 | 0.29 | 0.33 | 0.28 | 32,835 | 0.72 | 0.81 | 0.59 | 0.55 |
| JP201 | 39,979 | 0.43 | 0.14 | 0.41 | 0.16 | 39,979 | 0.53 | 0.51 | 0.64 | 0.46 | |
| JP213 | 30,067 | 0.50 | 0.34 | 0.40 | 0.34 | 31,374 | 0.64 | 0.61 | 0.66 | 0.55 | |
| JP311 | 29,855 | 0.52 | 0.17 | 0.48 | 0.34 | 32,394 | 0.71 | 0.41 | 0.60 | 0.56 | |
| JP316 | 28,371 | 0.50 | 0.18 | 0.39 | 0.19 | 31,273 | 0.66 | 0.43 | 0.58 | 0.45 | |
| JP107 vs. | JP201 | 31,486 | 0.45 | 0.34 | 0.49 | 0.26 | 33,230 | 0.58 | 0.98 | 0.52 | 0.66 |
| JP213 | 39,901 | 0.73 | 0.28 | 0.60 | 0.29 | 45,030 | 0.76 | 0.71 | 0.61 | 0.60 | |
| JP311 | 33,622 | 0.62 | 0.31 | 0.50 | 0.34 | 37,775 | 0.69 | 0.89 | 0.53 | 0.67 | |
| JP316 | 33,227 | 0.56 | 0.32 | 0.50 | 0.27 | 42,024 | 0.66 | 0.87 | 0.55 | 0.58 | |
| JP201 vs. | JP213 | 30,376 | 0.43 | 0.36 | 0.57 | 0.30 | 31,758 | 0.55 | 0.68 | 0.67 | 0.55 |
| JP311 | 30,211 | 0.40 | 0.16 | 0.68 | 0.27 | 32,792 | 0.58 | 0.39 | 0.78 | 0.44 | |
| JP316 | 28,479 | 0.35 | 0.18 | 0.58 | 0.19 | 31,535 | 0.47 | 0.49 | 0.67 | 0.49 | |
| JP213 vs. | JP311 | 34,585 | 0.56 | 0.34 | 0.62 | 0.32 | 37,701 | 0.68 | 0.60 | 0.69 | 0.57 |
| JP316 | 35,593 | 0.59 | 0.33 | 0.66 | 0.27 | 41,625 | 0.73 | 0.55 | 0.80 | 0.43 | |
| JP311 vs. | JP316 | 30,732 | 0.59 | 0.15 | 0.63 | 0.29 | 35,552 | 0.71 | 0.37 | 0.78 | 0.43 |
| 21 m | 29 m | ||||||||||
| JP104 vs. | JP107 | 32,842 | 0.81 | 0.94 | 0.56 | 0.86 | 32,834 | 0.74 | 1.32 | 0.64 | 1.11 |
| JP201 | 39,979 | 0.50 | 1.03 | 0.67 | 0.81 | 39,979 | 0.43 | 1.60 | 0.60 | 1.27 | |
| JP213 | 32,750 | 0.72 | 0.96 | 0.67 | 0.94 | 32,504 | 0.65 | 1.37 | 0.55 | 1.08 | |
| JP311 | 32,402 | 0.78 | 0.65 | 0.68 | 1.02 | 32,540 | 0.76 | 1.00 | 0.48 | 1.88 | |
| JP316 | 32,141 | 0.72 | 0.73 | 0.64 | 0.87 | 32,132 | 0.69 | 1.14 | 0.59 | 1.50 | |
| JP107 vs. | JP201 | 33,239 | 0.53 | 1.43 | 0.51 | 1.09 | 33,231 | 0.52 | 1.83 | 0.50 | 1.48 |
| JP213 | 46,868 | 0.77 | 1.00 | 0.62 | 0.96 | 46,620 | 0.77 | 1.33 | 0.63 | 1.38 | |
| JP311 | 37,851 | 0.72 | 1.14 | 0.50 | 1.16 | 37,983 | 0.73 | 1.36 | 0.49 | 1.71 | |
| JP316 | 42,901 | 0.70 | 1.13 | 0.61 | 0.91 | 42,868 | 0.70 | 1.42 | 0.62 | 1.32 | |
| JP201 vs. | JP213 | 33,156 | 0.52 | 1.26 | 0.68 | 0.96 | 32,910 | 0.50 | 1.80 | 0.67 | 1.43 |
| JP311 | 32,804 | 0.51 | 0.87 | 0.77 | 0.85 | 32,942 | 0.49 | 1.35 | 0.76 | 1.32 | |
| JP316 | 32,367 | 0.45 | 0.97 | 0.70 | 0.87 | 32,358 | 0.44 | 1.44 | 0.69 | 1.35 | |
| JP213 vs. | JP311 | 39,391 | 0.70 | 0.99 | 0.70 | 0.97 | 39,277 | 0.72 | 1.35 | 0.69 | 1.46 |
| JP316 | 43,728 | 0.80 | 0.82 | 0.85 | 0.63 | 43,471 | 0.82 | 1.09 | 0.86 | 0.91 | |
| JP311 vs. | JP316 | 36,508 | 0.77 | 0.63 | 0.78 | 0.77 | 36,637 | 0.78 | 0.93 | 0.77 | 1.17 |
| OSM WQP | WBEA ES | WBEA MT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Station Pair | PS (%) | Station Pair | PS (%) | Station Pair | PS (%) | ||||||
| at 10 m | at 2 m | at 2 m | at 16 m | at 21 m | at 29 m | ||||||
| C1 vs. | C2 | 8.57 | JE306 vs. | JE308 | 7.03 | JP104 vs. | JP107 | 10.22 | 15.13 | 19.16 | 14.51 |
| C3 | 16.38 | JE312 | 14.01 | JP201 | 13.31 | 9.79 | 9.78 | 9.76 | |||
| C4 | 11.46 | JE316 | 12.18 | JP213 | 11.00 | 17.71 | 21.34 | 12.12 | |||
| C5 | 8.76 | JE323 | 8.63 | JP311 | 6.94 | 9.00 | 12.35 | 8.03 | |||
| R2 | 4.93 | JP316 | 9.60 | 12.95 | 14.60 | 13.50 | |||||
| C2 vs. | C3 | 8.18 | JE308 vs. | JE312 | 10.72 | JP107 vs. | JP201 | 8.00 | 9.42 | 11.06 | 11.00 |
| C4 | 13.64 | JE316 | 19.39 | JP213 | 20.22 | 20.05 | 21.40 | 20.89 | |||
| C5 | 11.34 | JE323 | 30.53 | JP311 | 10.60 | 11.00 | 10.96 | 10.91 | |||
| R2 | 5.67 | JP316 | 12.70 | 14.47 | 14.61 | 14.38 | |||||
| C3 vs. | C4 | 8.38 | JE312 vs. | JE316 | 10.05 | JP201 vs. | JP213 | 10.69 | 13.36 | 13.55 | 12.89 |
| C5 | 8.15 | JE323 | 16.94 | JP311 | 12.97 | 17.27 | 16.14 | 16.38 | |||
| R2 | 9.19 | JP316 | 10.60 | 15.82 | 15.69 | 14.97 | |||||
| C4 vs. | C5 | 12.10 | JE316 vs. | JE323 | 18.43 | JP213 vs. | JP311 | 12.41 | 15.06 | 15.78 | 16.98 |
| R2 | 3.95 | JP316 | 15.39 | 23.74 | 24.41 | 26.16 | |||||
| JE323 vs. | R2 | 9.90 | JP311 vs. | JP316 | 15.70 | 21.26 | 22.75 | 23.96 | |||
| Station Pair | n | u-Component | v-Component | PS (%) | |||
|---|---|---|---|---|---|---|---|
| r | AAE | r | AAE | ||||
| JP104 vs. | R2 | 15,736 | 0.23 | 1.59 | 0.31 | 2.23 | 6.64 |
| JP316 vs. | JE316 | 28,699 | 0.60 | 4.54 | 0.79 | 3.90 | 4.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deshmukh, D.; Ahmed, M.R.; Dominic, J.A.; Gupta, A.; Achari, G.; Hassan, Q.K. Suitability Assessment of Weather Networks for Wind Data Measurements in the Athabasca Oil Sands Area. Climate 2022, 10, 10. https://doi.org/10.3390/cli10020010
Deshmukh D, Ahmed MR, Dominic JA, Gupta A, Achari G, Hassan QK. Suitability Assessment of Weather Networks for Wind Data Measurements in the Athabasca Oil Sands Area. Climate. 2022; 10(2):10. https://doi.org/10.3390/cli10020010
Chicago/Turabian StyleDeshmukh, Dhananjay, M. Razu Ahmed, John Albino Dominic, Anil Gupta, Gopal Achari, and Quazi K. Hassan. 2022. "Suitability Assessment of Weather Networks for Wind Data Measurements in the Athabasca Oil Sands Area" Climate 10, no. 2: 10. https://doi.org/10.3390/cli10020010
APA StyleDeshmukh, D., Ahmed, M. R., Dominic, J. A., Gupta, A., Achari, G., & Hassan, Q. K. (2022). Suitability Assessment of Weather Networks for Wind Data Measurements in the Athabasca Oil Sands Area. Climate, 10(2), 10. https://doi.org/10.3390/cli10020010







