Observed Zonal Variations of the Relationship between ITCZ Position and Meridional Temperature Contrast
Abstract
:1. Introduction
2. Materials and Methods
3. Results
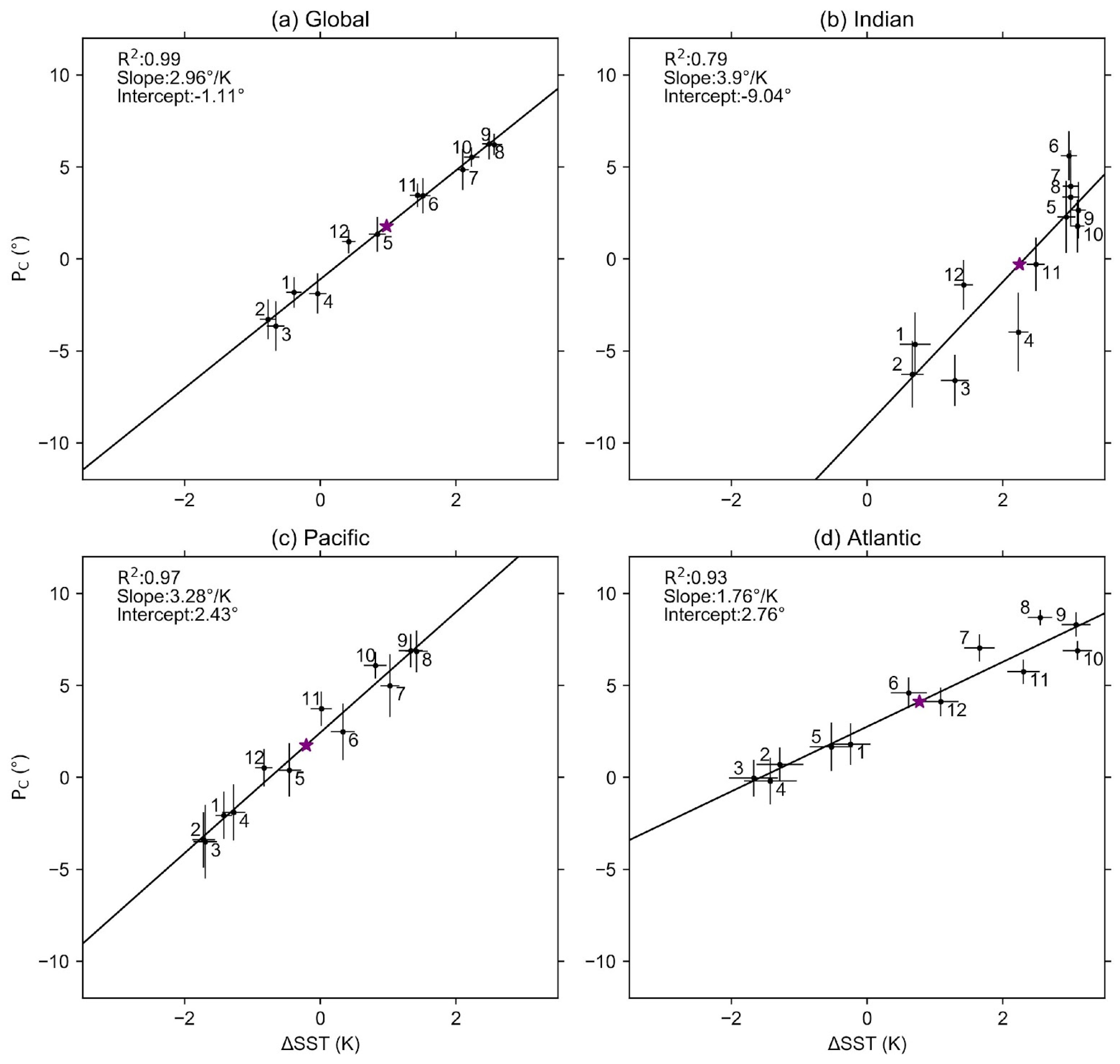
3.1. Basin-Wide Variations
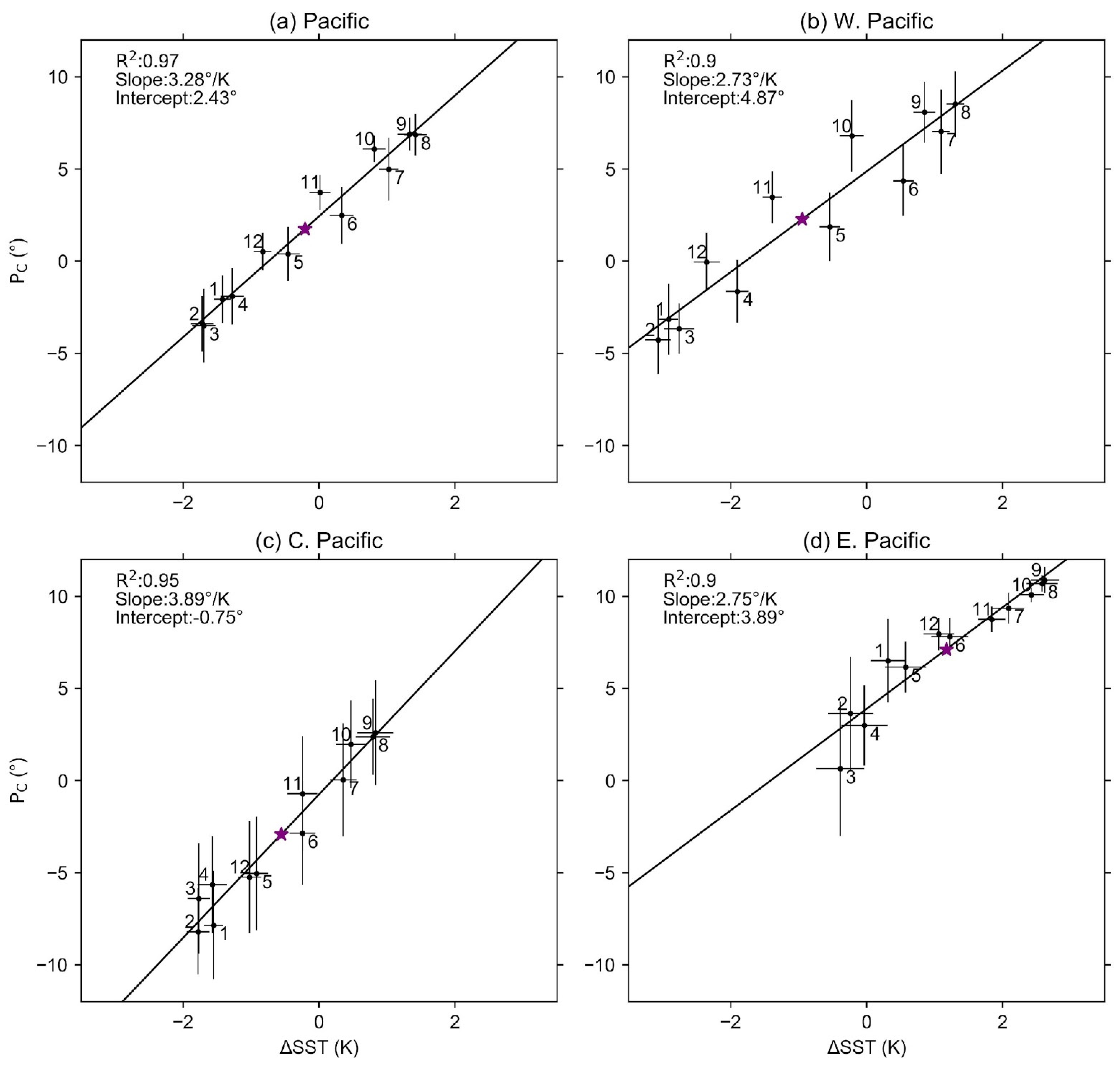
3.2. Longitudinal Variations
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Waliser, D.E.; Gautier, C. A Satellite-Derived Climatology of the ITCZ. J. Clim. 1993, 6, 2162–2174. [Google Scholar] [CrossRef]
- Schneider, T.; Bischoff, T.; Haug, G.H. Migrations and Dynamics of the Intertropical Convergence Zone. Nature 2014, 513, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Frierson, D.M.W.; Hwang, Y.-T.; Fučkar, N.S.; Seager, R.; Kang, S.M.; Donohoe, A.; Maroon, E.A.; Liu, X.; Battisti, D.S. Contribution of Ocean Overturning Circulation to Tropical Rainfall Peak in the Northern Hemisphere. Nat. Geosci. 2013, 6, 940–944. [Google Scholar] [CrossRef] [Green Version]
- Haug, G.H.; Hughen, K.A.; Sigman, D.M.; Peterson, L.C.; Röhl, U. Southward Migration of the Intertropical Convergence Zone Through the Holocene. Science 2001, 293, 1304–1308. [Google Scholar] [CrossRef]
- Koutavas, A.; Lynch-Stieglitz, J. Variability of the Marine ITCZ over the Eastern Pacific during the Past 30,000 Years. In The Hadley Circulation: Present, Past and Future; Diaz, H.F., Bradley, R.S., Eds.; Advances in Global Change Research; Springer: Berlin, Germany, 2004; pp. 347–369. ISBN 978-1-4020-2944-8. [Google Scholar]
- He, J.; Johnson, N.C.; Vecchi, G.A.; Kirtman, B.; Wittenberg, A.T.; Sturm, S. Precipitation Sensitivity to Local Variations in Tropical Sea Surface Temperature. J. Clim. 2018, 31, 9225–9238. [Google Scholar] [CrossRef] [Green Version]
- Neelin, J.D.; Held, I.M. Modeling Tropical Convergence Based on the Moist Static Energy Budget. Mon. Weather. Rev. 1987, 115, 3–12. [Google Scholar] [CrossRef]
- Held, I.M. The Partitioning of the Poleward Energy Transport between the Tropical Ocean and Atmosphere. J. Atmos. Sci. 2001, 58, 943–948. [Google Scholar] [CrossRef] [Green Version]
- Hill, S.A.; Ming, Y.; Held, I.M. Mechanisms of Forced Tropical Meridional Energy Flux Change. J. Clim. 2015, 28, 1725–1742. [Google Scholar] [CrossRef] [Green Version]
- Lindzen, R.S.; Nigam, S. On the Role of Sea Surface Temperature Gradients in Forcing Low-Level Winds and Convergence in the Tropics. J. Atmos. Sci. 1987, 44, 2418–2436. [Google Scholar] [CrossRef] [Green Version]
- Back, L.E.; Bretherton, C.S. On the Relationship between SST Gradients, Boundary Layer Winds, and Convergence over the Tropical Oceans. J. Clim. 2009, 22, 4182–4196. [Google Scholar] [CrossRef]
- Waliser, D.E.; Somerville, R.C.J. Preferred Latitudes of the Intertropical Convergence Zone. J. Atmos. Sci. 1994, 51, 1619–1639. [Google Scholar] [CrossRef] [Green Version]
- Chiang, J.C.H.; Bitz, C.M. Influence of High Latitude Ice Cover on the Marine Intertropical Convergence Zone. Clim. Dyn. 2005, 25, 477–496. [Google Scholar] [CrossRef]
- Kang, S.M.; Held, I.M.; Frierson, D.M.W.; Zhao, M. The Response of the ITCZ to Extratropical Thermal Forcing: Idealized Slab-Ocean Experiments with a GCM. J. Clim. 2008, 21, 3521–3532. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.M.; Frierson, D.M.W.; Held, I.M. The Tropical Response to Extratropical Thermal Forcing in an Idealized GCM: The Importance of Radiative Feedbacks and Convective Parameterization. J. Atmos. Sci. 2009, 66, 2812–2827. [Google Scholar] [CrossRef] [Green Version]
- Bischoff, T.; Schneider, T. Energetic Constraints on the Position of the Intertropical Convergence Zone. J. Clim. 2014, 27, 4937–4951. [Google Scholar] [CrossRef] [Green Version]
- Bischoff, T.; Schneider, T. The Equatorial Energy Balance, ITCZ Position, and Double-ITCZ Bifurcations. J. Clim. 2016, 29, 2997–3013. [Google Scholar] [CrossRef]
- Adam, O.; Bischoff, T.; Schneider, T. Seasonal and Interannual Variations of the Energy Flux Equator and ITCZ. Part I: Zonally Averaged ITCZ Position. J. Clim. 2016, 29, 3219–3230. [Google Scholar] [CrossRef]
- Kang, S.M.; Shin, Y.; Xie, S.-P. Extratropical Forcing and Tropical Rainfall Distribution: Energetics Framework and Ocean Ekman Advection. NPJ Clim. Atmos. Sci. 2018, 1, 20172. [Google Scholar] [CrossRef] [Green Version]
- Byrne, M.P.; Pendergrass, A.G.; Rapp, A.D.; Wodzicki, K.R. Response of the Intertropical Convergence Zone to Climate Change: Location, Width, and Strength. Curr. Clim. Chang. Rep. 2018, 4, 355–370. [Google Scholar] [CrossRef] [Green Version]
- Marshall, J.; Donohoe, A.; Ferreira, D.; McGee, D. The Ocean’s Role in Setting the Mean Position of the Inter-Tropical Convergence Zone. Clim. Dyn. 2014, 42, 1967–1979. [Google Scholar] [CrossRef] [Green Version]
- Adam, O.; Bischoff, T.; Schneider, T. Seasonal and Interannual Variations of the Energy Flux Equator and ITCZ. Part II: Zonally Varying Shifts of the ITCZ. J. Clim. 2016, 29, 7281–7293. [Google Scholar] [CrossRef]
- Keshtgar, B.; Alizadeh-Choobari, O.; Irannejad, P. Seasonal and Interannual Variations of the Intertropical Convergence Zone over the Indian Ocean Based on an Energetic Perspective. Clim. Dyn. 2020, 54, 3627–3639. [Google Scholar] [CrossRef]
- Boos, W.R.; Korty, R.L. Regional Energy Budget Control of the Intertropical Convergence Zone and Application to Mid-Holocene Rainfall. Nat. Geosci. 2016, 9, 892–897. [Google Scholar] [CrossRef] [Green Version]
- Biasutti, M.; Voigt, A.; Boos, W.R.; Braconnot, P.; Hargreaves, J.C.; Harrison, S.P.; Kang, S.M.; Mapes, B.E.; Scheff, J.; Schumacher, C.; et al. Global Energetics and Local Physics as Drivers of Past, Present and Future Monsoons. Nat. Geosci. 2018, 11, 392–400. [Google Scholar] [CrossRef]
- Roberts, W.H.G.; Valdes, P.J.; Singarayer, J.S. Can Energy Fluxes Be Used to Interpret Glacial/Interglacial Precipitation Changes in the Tropics? Geophys. Res. Lett. 2017, 44, 6373–6382. [Google Scholar] [CrossRef] [Green Version]
- McGee, D.; Donohoe, A.; Marshall, J.; Ferreira, D. Changes in ITCZ Location and Cross-Equatorial Heat Transport at the Last Glacial Maximum, Heinrich Stadial 1, and the Mid-Holocene. Earth Planet. Sci. Lett. 2014, 390, 69–79. [Google Scholar] [CrossRef]
- Sachs, J.P.; Sachse, D.; Smittenberg, R.H.; Zhang, Z.; Battisti, D.S.; Golubic, S. Southward Movement of the Pacific Intertropical Convergence Zone AD 1400–1850. Nat. Geosci. 2009, 2, 519–525. [Google Scholar] [CrossRef]
- Arbuszewski, J.A.; de Menocal, P.B.; Cléroux, C.; Bradtmiller, L.; Mix, A. Meridional Shifts of the Atlantic Intertropical Convergence Zone since the Last Glacial Maximum. Nat. Geosci. 2013, 6, 959–962. [Google Scholar] [CrossRef]
- Atwood, A.R.; Donohoe, A.; Battisti, D.S.; Liu, X.; Pausata, F.S.R. Robust Longitudinally Variable Responses of the ITCZ to a Myriad of Climate Forcings. Geophys. Res. Lett. 2020, 47, e2020GL088833. [Google Scholar] [CrossRef]
- Donohoe, A.; Marshall, J.; Ferreira, D.; Mcgee, D. The Relationship between ITCZ Location and Cross-Equatorial Atmospheric Heat Transport: From the Seasonal Cycle to the Last Glacial Maximum. J. Clim. 2012, 26, 3597–3618. [Google Scholar] [CrossRef]
- Donohoe, A.; Marshall, J.; Ferreira, D.; Armour, K.; McGee, D. The Interannual Variability of Tropical Precipitation and Interhemispheric Energy Transport. J. Clim. 2014, 27, 3377–3392. [Google Scholar] [CrossRef]
- Chiang, J.C.H.; Kushnir, Y.; Giannini, A. Deconstructing Atlantic Intertropical Convergence Zone Variability: Influence of the Local Cross-Equatorial Sea Surface Temperature Gradient and Remote Forcing from the Eastern Equatorial Pacific. J. Geophys. Res. Atmos. 2002, 107, ACL-3. [Google Scholar] [CrossRef]
- Xie, S.-P.; Carton, J.A. Tropical Atlantic Variability: Patterns, Mechanisms, and Impacts. In Earth’s Climate; American Geophysical Union (AGU): Washington, DC, USA, 2004; pp. 121–142. ISBN 978-1-118-66594-7. [Google Scholar]
- Weller, E.; Cai, W.; Min, S.-K.; Wu, L.; Ashok, K.; Yamagata, T. More-Frequent Extreme Northward Shifts of Eastern Indian Ocean Tropical Convergence under Greenhouse Warming. Sci. Rep. 2014, 4, 6087. [Google Scholar] [CrossRef] [Green Version]
- Biasutti, M.; Voigt, A. Seasonal and CO2-Induced Shifts of the ITCZ: Testing Energetic Controls in Idealized Simulations with Comprehensive Models. J. Clim. 2020, 33, 2853–2870. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global Analyses of Sea Surface Temperature, Sea Ice, and Night Marine Air Temperature since the Late Nineteenth Century. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Frierson, D.M.W.; Hwang, Y.-T. Extratropical Influence on ITCZ Shifts in Slab Ocean Simulations of Global Warming. J. Clim. 2011, 25, 720–733. [Google Scholar] [CrossRef] [Green Version]
- Yoshimori, M.; Broccoli, A.J. Equilibrium Response of an Atmosphere–Mixed Layer Ocean Model to Different Radiative Forcing Agents: Global and Zonal Mean Response. J. Clim. 2008, 21, 4399–4423. [Google Scholar] [CrossRef]
- Xie, S.-P.; Peng, Q.; Kamae, Y.; Zheng, X.-T.; Tokinaga, H.; Wang, D. Eastern Pacific ITCZ Dipole and ENSO Diversity. J. Clim. 2018, 31, 4449–4462. [Google Scholar] [CrossRef]
- Zhao, B.; Fedorov, A. The Seesaw Response of the Intertropical and South Pacific Convergence Zones to Hemispherically Asymmetric Thermal Forcing. Clim. Dyn. 2020, 54, 1639–1653. [Google Scholar] [CrossRef]
- Wei, H.-H.; Bordoni, S. Energetic Constraints on the ITCZ Position in Idealized Simulations with a Seasonal Cycle. J. Adv. Model. Earth Syst. 2018, 10, 1708–1725. [Google Scholar] [CrossRef]
- Wu, C.R.; Lin, Y.F.; Wang, Y.L.; Keenlyside, N.; Yu, J.Y. An Atlantic-driven rapid circulation change in the North Pacific Ocean during the late 1990s. Sci. Rep. 2019, 9, 14411. [Google Scholar] [CrossRef] [PubMed]
- Ruprich-Robert, Y.; Moreno-Chamarro, E.; Levine, X.; Bellucci, A.; Cassou, C.; Castruccio, F.; Davini, P.; Eade, R.; Gastineau, G.; Hermanson, L.; et al. Impacts of Atlantic multidecadal variability on the tropical Pacific: A multi-model study. NPJ Clim. Atmos. Sci. 2021, 4, 33. [Google Scholar] [CrossRef]
- Hu, S.; Fedorov, A.V. Indian Ocean Warming Can Strengthen the Atlantic Meridional Overturning Circulation. Nat. Clim. Chang. 2019, 9, 747–751. [Google Scholar] [CrossRef]
- Ferster, B.S.; Fedorov, A.V.; Mignot, J.; Guilyardi, E. Sensitivity of the Atlantic meridional overturning circulation and climate to tropical Indian Ocean warming. Clim. Dyn. 2021, 57, 2433–2451. [Google Scholar] [CrossRef]
- Wang, C. Three-ocean interactions and climate variability: A review and perspective. Clim. Dyn. 2019, 53, 5119–5136. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.M.; Hawcroft, M.; Xiang, B.; Hwang, Y.-T.; Cazes, G.; Codron, F.; Crueger, T.; Deser, C.; Hodnebrog, Ø.; Kim, H.; et al. Extratropical-Tropical Interaction Model Intercomparison Project—Protocol and Initial Results. Bull. Am. Meteorol. Soc. 2019, 100, 2589–2606. [Google Scholar]
- Roxy, M.K.; Ritika, K.; Terray, P.; Masson, S. The Curious Case of Indian Ocean Warming. J. Clim. 2014, 27, 8501–8509. [Google Scholar] [CrossRef] [Green Version]
- Back, L.E.; Bretherton, C.S. Geographic Variability in the Export of Moist Static Energy and Vertical Motion Profiles in the Tropical Pacific. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Heaviside, C.; Czaja, A. Deconstructing the Hadley Cell Heat Transport. Q. J. R. Meteorol. Soc. 2013, 139, 2181–2189. [Google Scholar] [CrossRef]
- Green, B.; Marshall, J.; Campin, J.-M. The ‘Sticky’ ITCZ: Ocean-Moderated ITCZ Shifts. Clim. Dyn. 2019, 53, 1–19. [Google Scholar] [CrossRef]
- Green, B.; Marshall, J. Coupling of Trade Winds with Ocean Circulation Damps ITCZ Shifts. J. Clim. 2017, 30, 4395–4411. [Google Scholar] [CrossRef] [Green Version]
- Schneider, T. Feedback of Atmosphere-Ocean Coupling on Shifts of the Intertropical Convergence Zone. Geophys. Res. Lett. 2017, 44, 11–644. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.-P.; Philander, S.G.H. A Coupled Ocean-Atmosphere Model of Relevance to the ITCZ in the Eastern Pacific. Tellus A Dyn. Meteorol. Oceanogr. 1994, 46, 340–350. [Google Scholar] [CrossRef] [Green Version]
- Philander, S.G.H.; Gu, D.; Lambert, G.; Li, T.; Halpern, D.; Lau, N.-C.; Pacanowski, R.C. Why the ITCZ Is Mostly North of the Equator. J. Clim. 1996, 9, 2958–2972. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.M.; Held, I.M. Tropical Precipitation, SSTs and the Surface Energy Budget: A Zonally Symmetric Perspective. Clim. Dyn. 2012, 38, 1917–1924. [Google Scholar] [CrossRef]
- Cvijanovic, I.; Chiang, J.C.H. Global Energy Budget Changes to High Latitude North Atlantic Cooling and the Tropical ITCZ Response. Clim. Dyn. 2013, 40, 1435–1452. [Google Scholar] [CrossRef]
- Adam, O.; Schneider, T.; Brient, F. Regional and Seasonal Variations of the Double-ITCZ Bias in CMIP5 Models. Clim. Dyn. 2018, 51, 101–117. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mischell, E.; Lee, J.-E. Observed Zonal Variations of the Relationship between ITCZ Position and Meridional Temperature Contrast. Climate 2022, 10, 30. https://doi.org/10.3390/cli10030030
Mischell E, Lee J-E. Observed Zonal Variations of the Relationship between ITCZ Position and Meridional Temperature Contrast. Climate. 2022; 10(3):30. https://doi.org/10.3390/cli10030030
Chicago/Turabian StyleMischell, Eric, and Jung-Eun Lee. 2022. "Observed Zonal Variations of the Relationship between ITCZ Position and Meridional Temperature Contrast" Climate 10, no. 3: 30. https://doi.org/10.3390/cli10030030
APA StyleMischell, E., & Lee, J.-E. (2022). Observed Zonal Variations of the Relationship between ITCZ Position and Meridional Temperature Contrast. Climate, 10(3), 30. https://doi.org/10.3390/cli10030030





