Intercomparison of Different Sources of Precipitation Data in the Brazilian Legal Amazon
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Observed Rainfall Data
2.3. Precipitation Obtained from Gridded Analyses
2.4. Precipitation Obtained from Reanalysis
2.5. Precipitation Obtained from Remote Sensing
2.6. Cluster Analysis
2.7. Performance of Gridded Data Compared to In Situ Measurements of Monthly Rainfall
3. Results
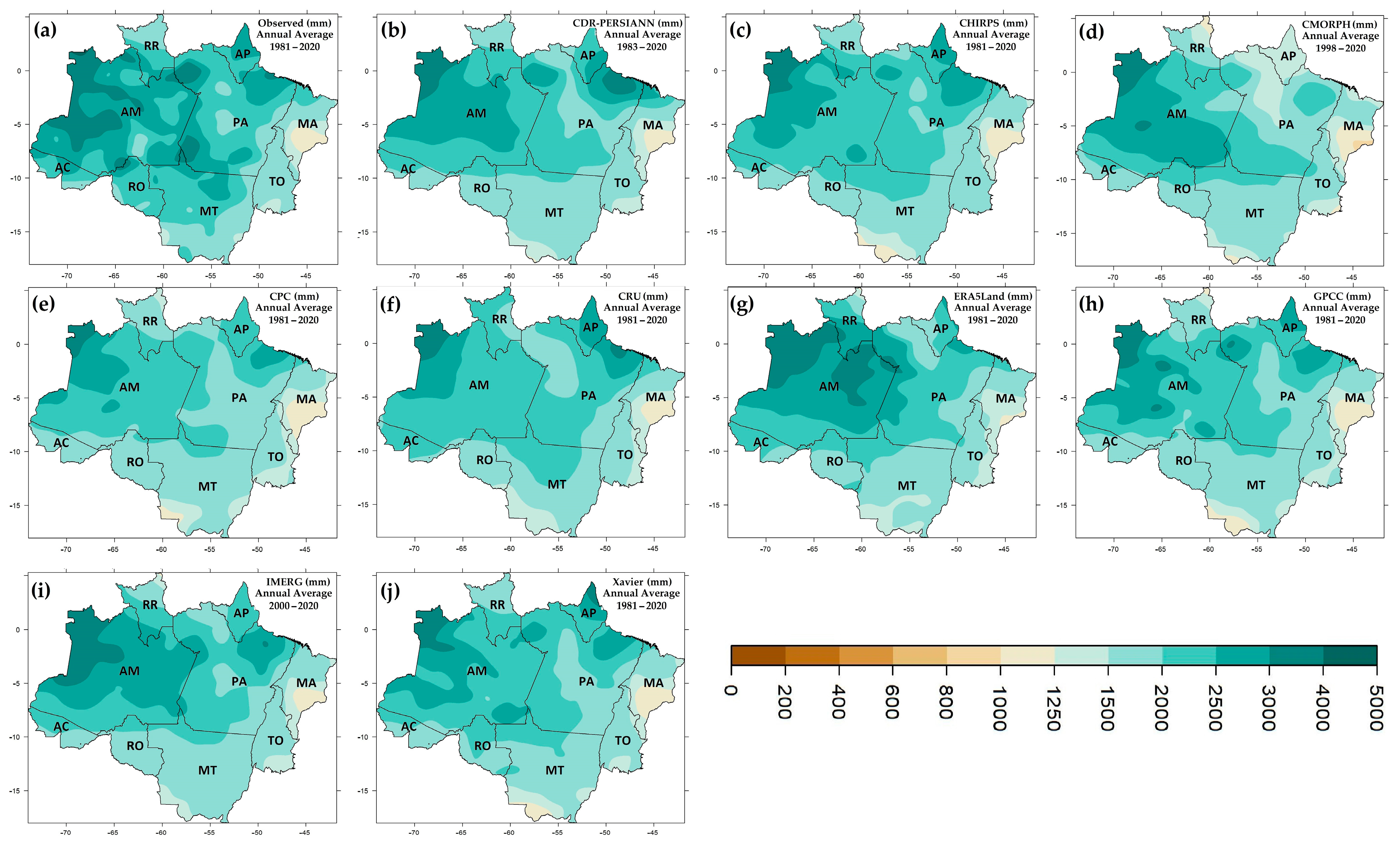
3.1. Description of the Current Climatology
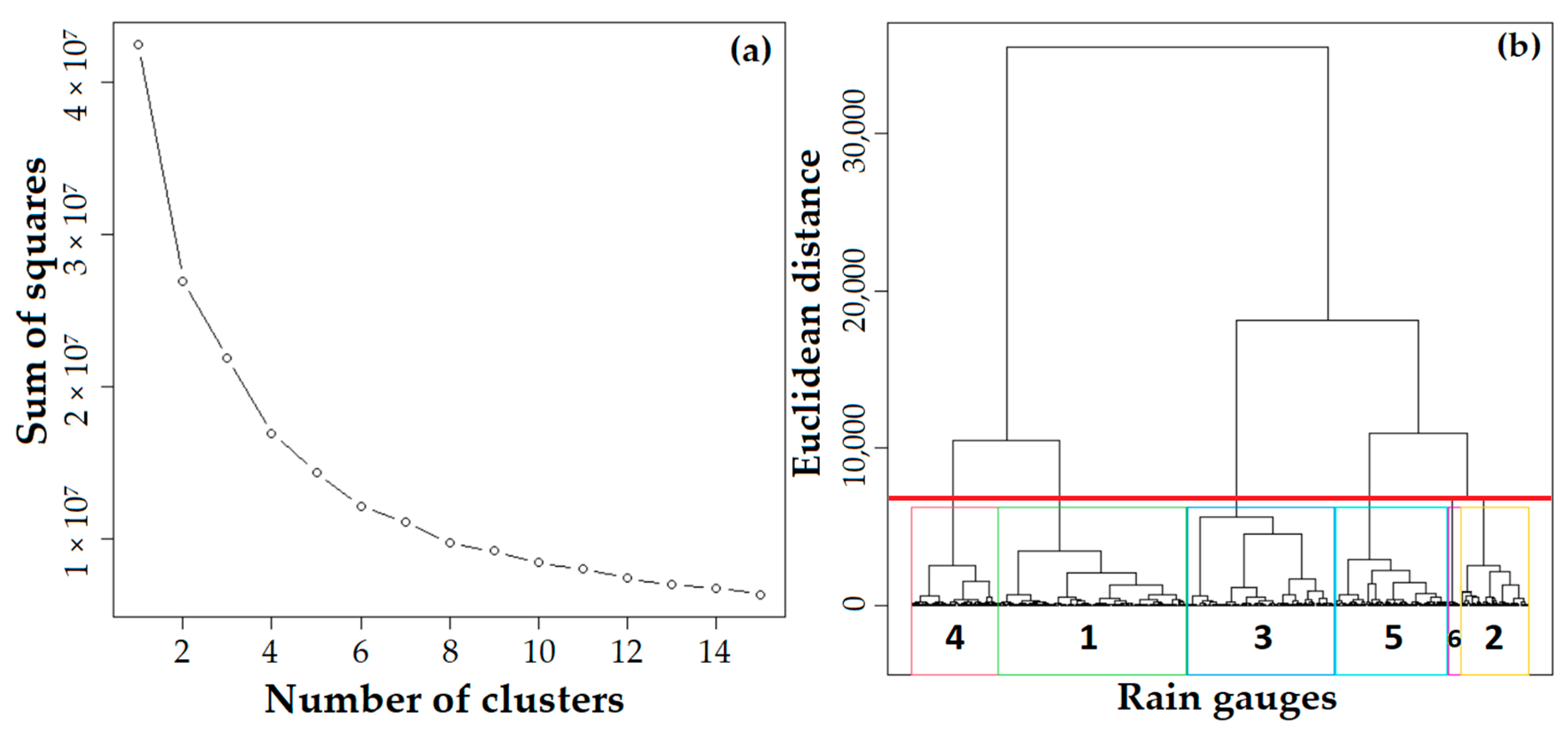
3.2. Cluster Analysis
3.3. Intercomparison between Databases and Observations in BLA—Regional Analysis
3.3.1. Skill Assessment Using Bias
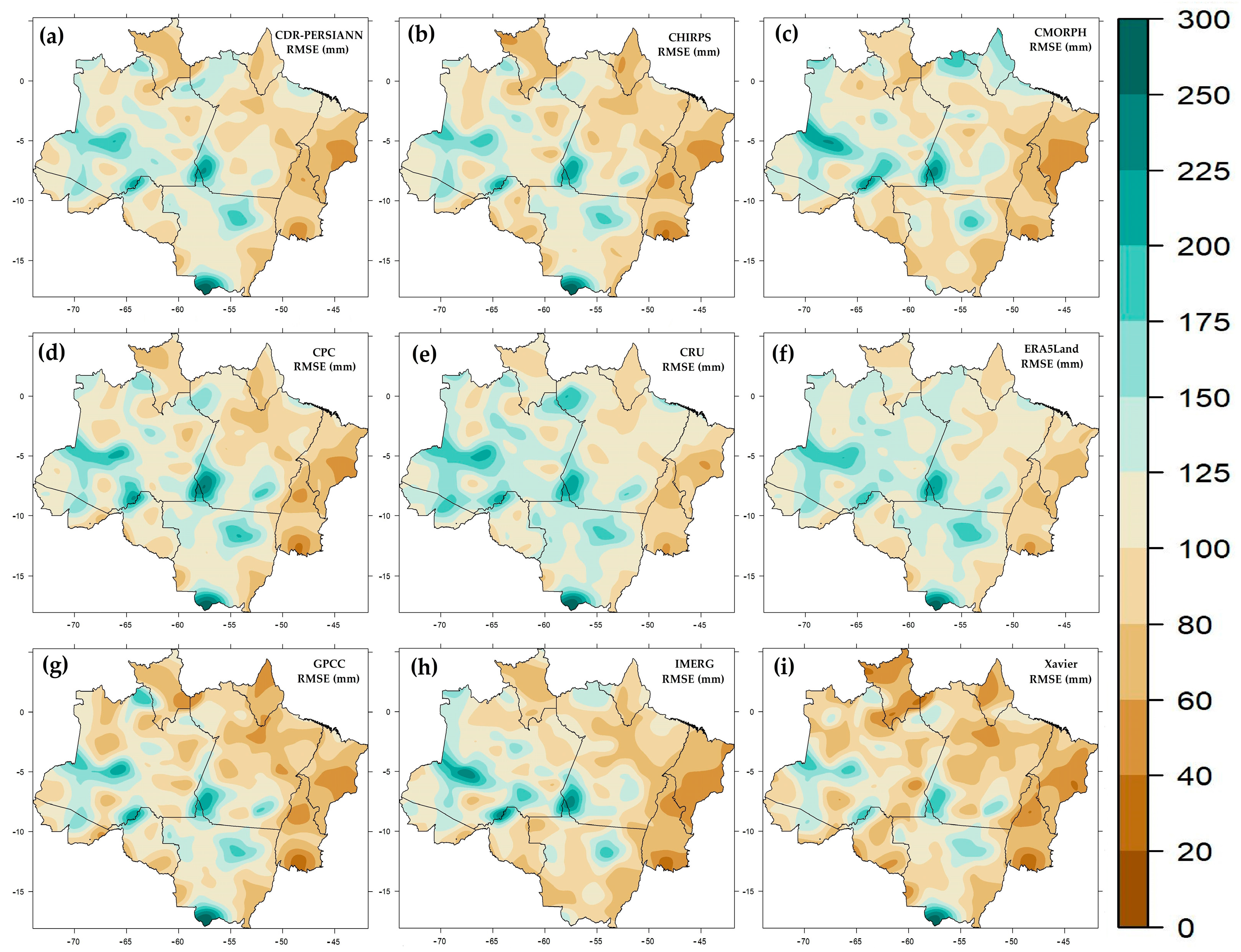
3.3.2. Skill Assessment Using RMSE
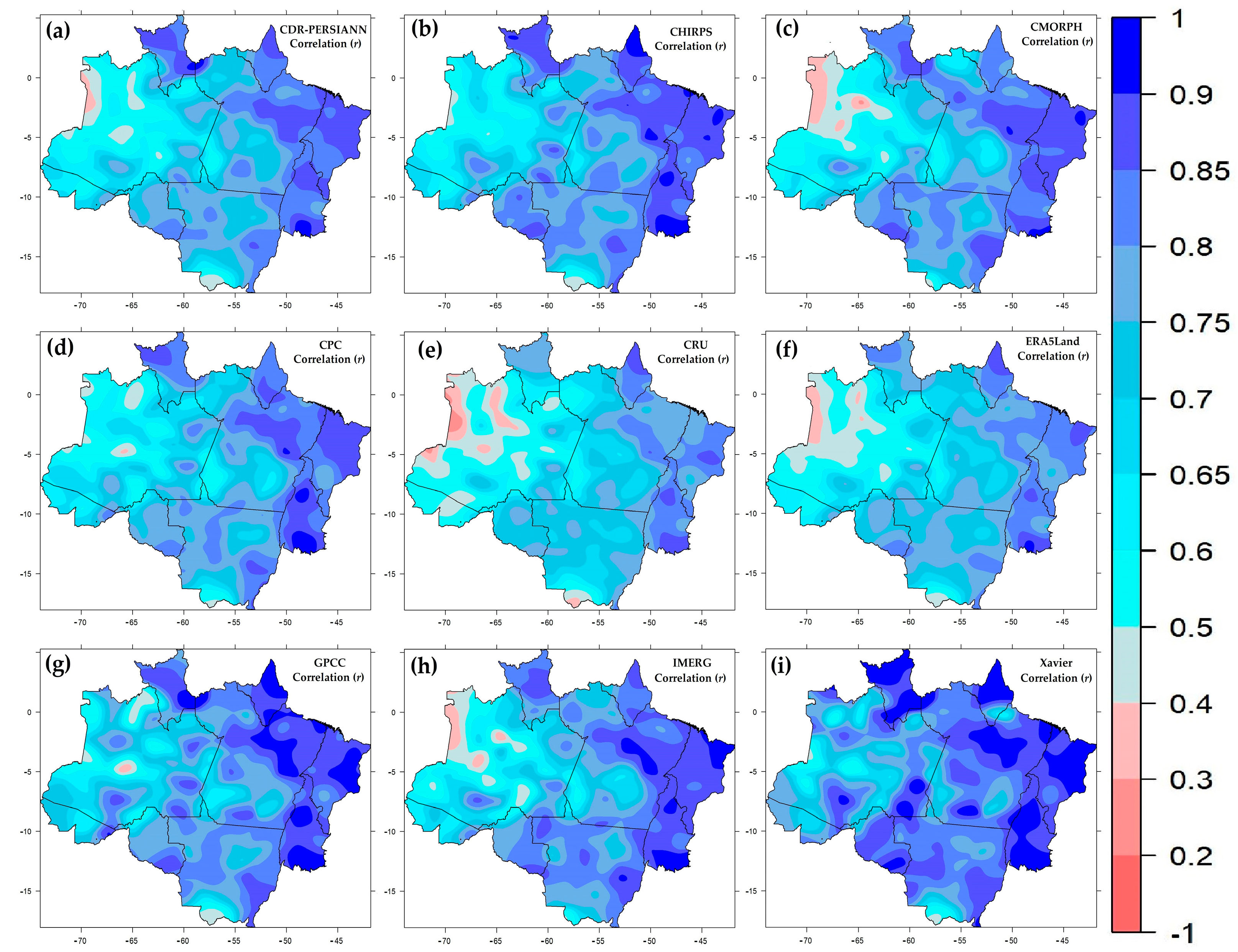
3.3.3. Comparison Using Pearson Correlation
3.4. Intercomparison between Databases and Observations in BLA on a Monthly Scale—Subregional Analysis
4. Discussion
5. Conclusions
- (1)
- The main climatological characteristics of rainfall in the BLA are well represented by the data sources. The spatial distribution and seasonality follow the observed pattern. However, the heterogeneity of the observed patterns is not well captured, especially compared to the observed nuclei of maximum accumulated rainfall, which in the data sources tend to be smoothed out.
- (2)
- The BLA should be divided into six pluviometrically homogeneous regions, which facilitates the analysis of precipitation and the skill of different databases in this vast region of the planet.
- (3)
- There is a tendency to underestimate rainfall in the BLA.
- (4)
- The largest errors between database estimates are concentrated in the northwestern sector of the BLA, and the smallest in the northeastern sector.
- (5)
- Skill rankings based on Taylor diagrams, Pearson’s correlation and RMSE made it possible to better verify the hierarchy of skill between the different data sources compared to the observations for each homogeneous group, where it was possible to observe the good performance, especially of Xavier and CHIRPS.
- (6)
- Based on a skill ranking, we identified, in general, that Xavier, CHIRPS, GPCC and ERA5Land are the four sources that best represent precipitation in the BLA, with CRU and CPC in the last positions.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Villar, J.C.E.; Ronchail, J.; Guyot, J.L.; Cochonneau, G.; Naziano, F.; Lavado, W.; Oliveira, E.; Pombosa, R.; Vauchel, P. Spatio-temporal rainfall variability in the Amazon basin countries (Brazil, Peru, Bolivia, Colombia, and Ecuador). Int. J. Climatol. 2009, 29, 1574–1594. [Google Scholar] [CrossRef]
- Paccini, L.; Espinoza, J.C.; Ronchail, J.; Segura, H. Intra-seasonal rainfall variability in the Amazon basin related to large-scale circulation patterns: A focus on western Amazon–Andes transition region. Int. J. Climatol. 2017, 38, 2386–2399. [Google Scholar] [CrossRef]
- Cohen, J.C.P.; Dias, M.A.F.S.; Nobre, C.A. Environmental conditions associated with amazonian squall lines: A case study. Mon. Weather Rev. 1995, 123, 3163–3174. [Google Scholar] [CrossRef]
- Alcântara, C.; Dias, M.A.F.S.; Souza, E.P.; Cohen, J.C.P. Verification of the role of the low level jets in Amazon squall lines. Atmos. Res. 2011, 100, 36–44. [Google Scholar] [CrossRef]
- Vizy, E.K.; Cook, K.H. Relationship between Amazon and high Andes rainfall. J. Geophys. Res. 2007, 112, 1–14. [Google Scholar] [CrossRef]
- Segura, H.; Espinoza, J.C.; Junquas, C.; Lebel, T.; Vuille, M.; Garreaud, R. Recent changes in the precipitation-driving processes over the southern tropical Andes/western Amazon. Clim. Dyn. 2020, 54, 2613–2631. [Google Scholar] [CrossRef]
- Xu, D.; Agee, E.; Wang, J.; Ivanov, V.Y. Estimation of evapotranspiration of Amazon rainforest using the maximum entropy production method. Geophys. Res. Lett. 2019, 46, 1402–1412. [Google Scholar] [CrossRef]
- O’Connor, J.; Santos, M.J.; Rebel, K.T.; Dekker, S.C. The influence of water table depth on evapotranspiration in the Amazon arc of deforestation. Hydrol. Earth Syst. Sci. 2019, 23, 3917–3931. [Google Scholar] [CrossRef]
- Drumond, A.; Marengo, J.; Ambrizzi, T.; Nieto, R.; Moreira, L.; Gimeno, L. The role of the Amazon Basin moisture in the atmospheric branch of the hydrological cycle: A Lagrangian analysis. Hydrol. Earth Syst. Sci. 2014, 18, 2577–2598. [Google Scholar] [CrossRef]
- Carvalho, L.M.V. Assessing precipitation trends in the Americas with historical data: A review. WIREs Clim. Chang. 2020, 11, e627. [Google Scholar] [CrossRef]
- Lucas, E.W.M.; Sousa, F.A.S.; Silva, F.D.S.; da Rocha Júnior, R.L.; Pinto, D.D.C.; Silva, V.P.R. Trends in climate extreme indices assessed in the Xingu river basin-Brazilian Amazon. Weather Clim. Extrem. 2021, 31, 100306. [Google Scholar] [CrossRef]
- Mishra, A.K. Effect of rain gauge density over the accuracy of rainfall: A case study over Bangalore, India. Springer Plus 2013, 2, 311. [Google Scholar] [CrossRef]
- Xu, H.; Xu, C.-Y.; Chen, H.; Zhang, Z.; Li, L. Assessing the influence of rain gauge density and distribution on hydrological model performance in a humid region of China. J. Hydrol. 2013, 505, 1–12. [Google Scholar] [CrossRef]
- López, M.G.; Wennerstrom, H.; Norden, L.; Seibert, J. Location and density of rain gauges for the estimation of spatial varying precipitation. Geogr. Ann. Ser. A Phys. Geogr. 2015, 97, 167–179. [Google Scholar] [CrossRef]
- Tiwari, S.; Jha, S.K.; Singh, A. Quantification of node importance in rain gauge network: Influence of temporal resolution and rain gauge density. Sci. Rep. 2020, 10, 9761. [Google Scholar] [CrossRef] [PubMed]
- Liebmann, B.; Allured, D. Daily Precipitation Grids for South America. Bull. Am. Meteorol. Soc. 2005, 86, 1567–1570. [Google Scholar] [CrossRef]
- New, M.; Hulme, M.; Jones, P. Representing Twentieth-Century Space Time Climate Variability. Part II: Development of 1901–1996 Monthly Grids of Terrestrial Surface Climate. J. Clim. 2000, 13, 2217–2238. [Google Scholar] [CrossRef]
- Brands, S.; Gutiérrez, J.M.; Herrera, S. On the Use of Reanalysis Data for Downscaling. J. Clim. 2012, 25, 2517–2526. [Google Scholar] [CrossRef]
- Xavier, A.C.; King, C.W.; Scanlon, B.R. Daily gridded meteorological variables in brazil (1980–2013). Int. J. Climatol. 2016, 36, 2644–2659. [Google Scholar] [CrossRef]
- Xie, P.; Arkin, P.A. Global Precipitation: A 17-Year Monthly Analysis Based on Gauge Observations, Satellite Estimates, and Numerical Model Outputs. Bull. Am. Meteorol. Soc. 1997, 78, 2539–2558. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.M.; Bolvin, D.T.; Curtis, S.; Joyce, R.; McGavock, B.; Susskind, J. Global Precipitation at One-Degree Daily Resolution from Multisatellite Observations. J. Hydrometeorol. 2001, 2, 36–50. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.-P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The Version-2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979–Present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Levizzani, V.; Bauer, P.; Turk, F.J. Measuring Precipitation from Space. Advances in Global Change Research; Springer: Dordrecht, The Netherlands; Berlin/Heidelberg, Germany, 2007; 724p. [Google Scholar]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations: A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Tapiador, F.J.; Navarro, A.; Jimenéz, A.; Moreno, R.; García-Ortega, E. Discrepancies with satellite observations in the spatial structure of global precipitation as derived from global climate models. Q. J. R. Meteorol. Soc. 2018, 144, 419–435. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-Year High-Resolution Global Dataset of Meteorological Forcings for Land Surface Modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Veríssimo, A.; Rolla, A.; Vedoveto, M.; Futada, S.M. Áreas Protegidas na Amazônia BRASILEIRA Avanços e Desafios; IMAZON/ISA: Belém, Brazil, 2011; Available online: https://imazon.org.br/areas-protegidas-na-amazonia-brasileira-avancos-e-desafios-2/ (accessed on 23 October 2023).
- Herdies, D.L.; Silva, F.D.d.S.; Gomes, H.B.; Silva, M.C.L.d.; Gomes, H.B.; Costa, R.L.; Lins, M.C.C.; Reis, J.S.d.; Kubota, P.Y.; Souza, D.C.d.; et al. Evaluation of Surface Data Simulation Performance with the Brazilian Global Atmospheric Model (BAM). Atmosphere 2023, 14, 125. [Google Scholar] [CrossRef]
- Costa, R.L.; Gomes, H.B.; Pinto, D.D.C.; da Rocha Júnior, R.L.; dos Santos Silva, F.D.; Gomes, H.B.; da Silva, M.C.L.; Herdies, D.L. Gap Filling and Quality Control Applied to Meteorological Variables Measured in the Northeast Region of Brazil. Atmosphere 2021, 12, 1278. [Google Scholar] [CrossRef]
- Xavier, A.C.; Scanlon, B.R.; King, C.W.; Alves, A.I. New improved Brazilian daily weather gridded data (1961–2020). Int. J. Climatol. 2022, 42, 8390–8404. [Google Scholar] [CrossRef]
- Silva, J.S.; Cabral Júnior, J.B.; Rodrigues, D.T.; Silva, F.D.S. Climatology and significant trends in air temperature in Alagoas, Northeast Brazil. Theor. Appl. Climatol. 2023, 151, 1805–1824. [Google Scholar] [CrossRef]
- da Rocha Júnior, R.L.; dos Santos Silva, F.D.; Lisboa Costa, R.; Barros Gomes, H.; Herdies, D.L.; Rodrigues da Silva, V.d.P.; Candido Xavier, A. Analysis of the Space–Temporal Trends of Wet Conditions in the Different Rainy Seasons of Brazilian Northeast by Quantile Regression and Bootstrap Test. Geosciences 2019, 9, 457. [Google Scholar] [CrossRef]
- Paredes-Trejo, F.; Barbosa, H.A.; dos Santos, C.A.C. Evaluation of the Performance of SM2RAIN-Derived Rainfall Products over Brazil. Remote Sens. 2019, 11, 1113. [Google Scholar] [CrossRef]
- Silva, P.E.; Spyrides, M.H.C.; Barbosa, L.M. Analysis of Climate Extreme Indices in the Northeast Brazil and the Brazilian Amazon in the Period from 1980 to 2013. Anuário Inst. Geociências 2019, 42, 137–148. [Google Scholar] [CrossRef]
- dos Reis, L.C.; Silva, C.M.S.; Silva, C.M.S.; Bezerra, B.G.; Mutti, P.R.; Spyrides, M.H.C.; da Silva, P.E. Analysis of Climate Extreme Indices in the MATOPIBA Region, Brazil. Pure Appl. Geophys. 2020, 177, 4457–4478. [Google Scholar] [CrossRef]
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Glahn, H.R.; Chambers, T.L.; Richardson, W.S.; Perrotti, H.P. Objective Map Analysis for the Local AFOS MOS Program; NOAA Technical Memorandum; National Weather Service TDL 75; Techniques Development Laboratory: Silver Spring, MD, USA, 1985; 34p. [Google Scholar]
- Charba, J.P.; Harrell, A.W., III; Lackner, A.C., III. A Monthly Precipitation Amount Climatology Derived from Published Atlas Maps: Development of a Digital Database; National Oceanic and Atmospheric Administration TDL Office Note 92-7; Techniques Development Laboratory: Silver Spring, MD, USA, 1992; 20p. [Google Scholar]
- Silva, V.B.S.; Kousky, V.E.; Shi, W.; Higgins, R.W. An Improved Gridded Historical Daily Precipitation Analysis for Brazil. J. Hydrometeorol. 2007, 8, 847–861. [Google Scholar] [CrossRef]
- Chen, M.; Shi, W.; Xie, P.; Silva, V.B.S.; Kousky, V.E.; Higgins, R.W.; Janowiak, J.E. Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res.-Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Basheer, M.; Elagib, N.A. Performance of satellite-based and GPCC 7.0 rainfall products in an extremely data-scarce country in the Nile Basin. Atmos. Res. 2016, 215, 128–140. [Google Scholar] [CrossRef]
- Schneider, U.; Ziese, M.; Meyer-Christoffer, A.; Finger, P.; Rustemeier, E.; Becker, A. The new portfolio of global precipitation data products of the Global Precipitation Climatology Centre suitable to assess and quantify the global water cycle and resources. Proc. IAHS 2016, 374, 29–34. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; Dee, D.; Dutra, E.; Muñoz-Sabater, J.; Pappenberger, F.; et al. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef]
- Uppala, S.M.; Kallberg, P.W.; Simmons, A.J.; Andrae, U.; Bechtold, V.C.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez, A.; Kelly, G.A.; et al. The ERA-40 re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Muñoz Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. ESSD Discuss. 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- New, M.; Hulme, M.; Jones, P. Representing Twentieth-Century Space-Time Climate Variability. Part I: Development of a 1961–90 Mean Monthly Terrestrial Climatology. J. Clim. 1999, 12, 829–856. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2013, 115, 15–40. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.O.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and Other Precipitation Products against Gauge Data under Different Topographic and Climatic Conditions in Iran: Preliminary Results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef]
- Liu, Z. Comparison of versions 6 and 7 3-hourly TRMM multi-satellite precipitation analysis (TMPA) research products. Atmos. Res. 2015, 163, 91–101. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Ramsauer, T.; Weib, T.; Marzahn, P. Comparison of the GPM IMERG Final Precipitation Product to RADOLAN Weather Radar Data over the Topographically and Climatically Diverse Germany. Remote Sens. 2018, 10, 2029. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J. Integrated multi-satellitE retrievals for the global precipitation measurement (GPM) mission (IMERG) [Dataset]. Satell. Precip. Meas. 2020, 1, 343–353. [Google Scholar]
- Rozante, J.R.; Gutierrez, E.R.; Fernandes, A.A.; Vila, D.A. Performance of precipitation products obtained from combinations of satellite and surface observations. Int. J. Remote Sens. 2020, 41, 7585–7604. [Google Scholar] [CrossRef]
- Haile, A.T.; Habib, E.; Rientjes, T. Evaluation of the climate prediction center (CPC) morphing technique (CMORPH) rainfall product on hourly time scales over the source of the Blue Nile River. Hydrol. Process. 2013, 27, 1829–1839. [Google Scholar] [CrossRef]
- Xie, P.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. Reprocessed, Bias-Corrected CMORPH Global High-Resolution Precipitation Estimates from 1998. J. Hydrometeorol. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, W.; Wen, J.; Qiu, C.; Sun, W.; Fang, Q.; Xu, M.; Tan, J. Accuracy evaluation of two high-resolution satellite-based rainfall products: TRMM 3B42V7 and CMORPH in Shanghai. Water 2018, 10, 40. [Google Scholar] [CrossRef]
- Bruster-Flores, J.L.; Ortiz-Gómez, R.; Ferriño-Fierro, A.L.; Guerra-Cobián, V.H.; Burgos-Flores, D.; Lizárraga-Mendiola, L.G. Evaluation of Precipitation Estimates CMORPH-CRT on Regions of Mexico with Different Climates. Water 2019, 11, 1722. [Google Scholar] [CrossRef]
- Pingping, X.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. NOAA Climate Data Record (CDR) of CPC Morphing Technique (CMORPH) High Resolution Global Precipitation Estimates, Version 1; National Centers for Environmental Information: Asheville, NC, USA, 2019. [Google Scholar]
- Rossow, W.B.; Tselioudis, G.; Polak, A.; Jakob, C. Tropical climate described as a distribution of weather states indicated by distinct mesoscale cloud property mixtures. Geophys. Res. Lett. 2005, 32, L21812. [Google Scholar] [CrossRef]
- Knapp, K.R. Scientific data stewardship of International Satellite Cloud Climatology Project B1 global geostationary observations. J. Appl. Remote Sens. 2008, 2, 023548. [Google Scholar] [CrossRef]
- Knapp, K.R.; Ansari, S.; Bain, C.L.; Bourassa, M.A.; Dickinson, M.J.; Funk, C.; Helms, C.N.; Hennon, C.C.; Holmes, C.D.; Huffman, G.J.; et al. Globally gridded satellite observations for climate studies. Bull. Am. Meteor. Soc. 2011, 92, 893–907. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Sadeghi, M.; Asanjan, A.A.; Faridzad, M.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Braithwaite, D. PERSIANN-CNN: Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks–Convolutional Neural Networks. J. Hydrometeorol. 2019, 20, 2273–2289. [Google Scholar] [CrossRef]
- Mosaffa, H.; Sadeghi, M.; Hayatbini, N.; Gorooh, V.A.; Asanjan, A.A.; Nguyen, P.; Sorooshian, S. Spatiotemporal Variations of Precipitation over Iran Using the High-Resolution and Nearly Four Decades Satellite-Based PERSIANN-CDR Dataset. Remote Sens. 2020, 12, 1584. [Google Scholar] [CrossRef]
- Wang, J.; Petersen, W.A.; Wolff, D.B. Validation of Satellite-Based Precipitation Products from TRMM to GPM. Remote Sens. 2021, 13, 1745. [Google Scholar] [CrossRef]
- Lyra, G.B.; Oliveira Júnior, J.F.; Zeri, M. Cluster analysis applied to the spatial and temporal variability of monthly rainfall in Alagoas state, Northeast of Brazil. Int. J. Climatol. 2014, 34, 3546–3558. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Brasil Neto, R.M.; Silva, R.M.; Costa, S.G.F. Cluster Analysis Applied to Spatiotemporal Variability of Monthly Precipitation over Paraíba State Using Tropical Rainfall Measuring Mission (TRMM) Data. Remote Sens. 2019, 11, 637. [Google Scholar] [CrossRef]
- Costa, R.L.; de Mello Baptista, G.M.; Barros Gomes, H.; dos Santos Silva, F.D.; da Rocha Júnior, R.L.; de Araújo Salvador, M.; Herdies, D.L. Analysis of climate extremes indices over northeast Brazil from 1961 to 2014. Weather Clim. Extrem. 2020, 28, 100254. [Google Scholar] [CrossRef]
- Mimmack, G.M.; Mason, S.J.; Galpin, J.S. Choice of distance matrices in cluster analysis: Defining regions. J. Clim. 2001, 14, 2790–2797. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Hervada-Sala, C.; Jarauta-Bragulat, E. A program to perform Ward’s clustering method on several regionalized variables. Comput. Geosci. 2004, 30, 881–886. [Google Scholar] [CrossRef]
- Liu, B.; Liu, F.; Wang, C.; Mei, S. Unit commitment considering flexibility and uncertainty of wind power generation. Power Syst. Technol. 2015, 39, 730–736. [Google Scholar]
- Silva, E.H.d.L.; Silva, F.D.d.S.; Junior, R.S.d.S.; Pinto, D.D.C.; Costa, R.L.; Gomes, H.B.; Júnior, J.B.C.; de Freitas, I.G.F.; Herdies, D.L. Performance Assessment of Different Precipitation Databases (Gridded Analyses and Reanalyses) for the New Brazilian Agricultural Frontier: SEALBA. Water 2022, 14, 1473. [Google Scholar] [CrossRef]
- Demirtas, M.; Nance, L.; Barnardet, L.; Lin, Y.; Chuang, H.-Y.; Loughe, A.; Mahoney, J.; Gall, R.; Koch, S. The Developmental Testbed Center Verification System; WRF/MM5 Users’ Workshop; NCAR: Boulder, CO, USA, 2005. [Google Scholar]
- Michot, V.; Vila, D.; Arvor, D.; Corpetti, T.; Ronchail, J.; Funatsu, B.M.; Dubreuil, V. Performance of TRMM TMPA 3B42 V7 in Replicating Daily Precipitation and Regional Precipitation Regimes in the Amazon Basin (1998–2013). Remote Sens. 2018, 10, 1879. [Google Scholar] [CrossRef]
- Rodrigues, D.T.; Silva, C.M.S.; Reis, J.S.; Palharini, R.S.A.; Cabral Júnior, J.B.; Silva, H.J.F.; Mutti, P.R.; Bezerra, B.G.; Gonçalves, W.A. Evaluation of the Integrated Multi-SatellitE Retrievals for the Global Precipitation Measurement (IMERG) Product in the São Francisco Basin (Brazil). Water 2021, 13, 2714. [Google Scholar] [CrossRef]
- Wadoux, A.M.J.-C.; Walvoort, D.J.J.; Brus, D.J. An integrated approach for the evaluation of quantitative soil maps through Taylor and solar diagrams. Geoderma 2022, 405, 115332. [Google Scholar] [CrossRef]
- Sapucci, C.R.; Mayta, V.C.; Dias, P.L.S. Evaluation of diverse-based precipitation data over the Amazon Region. Theor. Appl. Climatol. 2022, 149, 1167–1193. [Google Scholar] [CrossRef]
- Ambrizzi, T.; Ferraz, S.E.T. An objective criterion for determining the South Atlantic Convergence Zone. Front. Environ. Sci. 2015, 3, 23. [Google Scholar] [CrossRef]
- Hastenrath, S.; Heller, L. Dynamics of climatic hazards in Northeast Brazil. Q. J. R. Meteorol. Soc. 1977, 103, 77–92. [Google Scholar] [CrossRef]
- Nobre, P.; Shukla, J. Variation of sea surface temperature, wind stress and rainfall over the tropical Atlantic and South America. J. Clim. 1996, 9, 2464–2479. [Google Scholar] [CrossRef]
- Souza, E.B.; Alves, J.M.B.; Nobre, P. Anomalias de precipitação nos setores norte e leste do Nordeste Brasileiro em associação aos eventos do Padrão de Dipolo observados sobre o Atlântico Tropical. Rev. Bras. Meteorol. 1998, 13, 45–56. [Google Scholar]
- Xavier, T.M.B.S.; Xavier, A.F.S.; Dias, P.L.S.; Dias, M.A.F.S. A Zona de Convergência Intertropical e suas relações com a chuva do Ceará (1964–98). Rev. Bras. Meteorol. 2000, 15, 27–43. [Google Scholar]
- Souza, E.B.; Kayano, M.T.; Ambrizzi, T. The regional precipitation over the eastern Amazon/Northeast Brazil modulated by tropical Pacific and Atlantic SST anomalies on weekly timescale. Rev. Bras. Meteorol. 2004, 19, 113–122. [Google Scholar]
- Wang, H.; Fu, R. The Influence of Amazon Rainfall on the Atlantic ITCZ through Convectively Coupled Kelvin Waves. J. Clim. 2007, 20, 1188–1201. [Google Scholar] [CrossRef]
- Marengo, J.A.; Druyan, L.M.; Hastenrath, S. Observational and modelling studies of Amazonia interannual climate variability. Clim. Chang. 1993, 23, 267–286. [Google Scholar] [CrossRef]
- Penland, C.; Matrosova, L. Prediction of Tropical Atlantic Sea Surface Temperatures Using Linear Inverse Modeling. J. Clim. 1998, 11, 483–496. [Google Scholar] [CrossRef]
- Chérubin, L.M.; Richardson, P.L. Caribbean current variability and the influence of the Amazon and Orinoco freshwater plumes. Deep Sea Res. Part I Oceanogr. Res. Pap. 2007, 54, 1451–1473. [Google Scholar] [CrossRef]
- Yoon, J.H.; Zeng, N. An Atlantic Influence on Amazon Rainfall. Clim. Dyn. 2010, 34, 249–264. [Google Scholar] [CrossRef]
- Paca, V.H.M.; Espinoza-Dávalos, G.E.; Moreira, D.M.; Comair, G. Variability of Trends in Precipitation across the Amazon River Basin Determined from the CHIRPS Precipitation Product and from Station Records. Water 2020, 12, 1244. [Google Scholar] [CrossRef]
- Santos, E.B.; Lucio, P.S.; Santos e Silva, C.M. Precipitation regionalization of the Brazilian Amazon. Atmos. Sci. Lett. 2015, 16, 185–192. [Google Scholar] [CrossRef]
- Villa, P.M.; Moraes, J.R.S.C.; Martorano, L.G.; Martins, S.V.; Rodrigues, A.L.; Gonzáles, B.; Rolim, G.S.; Silva, A.S. Spatio-Temporal variability of precipitation in the Venezuelan region. Rev. Bras. Climatol. 2021, 9, 626–649. [Google Scholar]
- Cavalcante, R.B.L.; Ferreira, D.B.S.; Pontes, P.R.M.; Tedeschi, R.G.; Costa, C.P.W.; Souza, E.B. Evaluation of extreme rainfall indices from CHIRPS precipitation estimates over the Brazilian Amazonia. Atmos. Res. 2020, 238, 104879. [Google Scholar] [CrossRef]
- Funatsu, B.M.; Le Roux, R.; Arvor, D.; Espinoza, J.C.; Claud, C.; Ronchail, J.; Michot, V.; Dubreuil, V. Assessing precipitation extremes (1981–2018) and deep convective activity (2002–2018) in the Amazon region with CHIRPS and AMSU data. Clim. Dyn. 2021, 57, 827–849. [Google Scholar] [CrossRef]
- Barni, P.E.; Barbosa, R.I.; Xaud, H.A.M.; Xaud, M.R.; Fearnside, P.M. Precipitation in northern Amazonia: Spatial distribution in Roraima, Brazil. Soc. Nat. 2020, 32, 439–456. [Google Scholar] [CrossRef]
- Vose, R.S.; Applequist, S.; Squires, M.; Durre, I.; Menne, M.J.; Williams, C.N., Jr.; Fenimore, C.; Gleason, K.; Arndt, D. Improved Historical Temperature and Precipitation Time Series for U.S. Climate Divisions. J. Appl. Meteorol. Climatol. 2014, 53, 1232–1251. [Google Scholar] [CrossRef]
- Medina, F.D.; Zossi, B.S.; Bossolasco, A.; Elias, A.G. Performance of CHIRPS dataset for monthly and annual rainfall-indices in Northern Argentina. Atmos. Res. 2022, 283, 106545. [Google Scholar] [CrossRef]
- Moazami, S.; Najafi, M.R. A comprehensive evaluation of GPM-IMERG V06 and MRMS with hourly ground-based precipitation observations across Canada. J. Hydrol. 2021, 594, 125929. [Google Scholar] [CrossRef]
- Helmi, A.M.; Abdelhamed, M.S. Evaluation of CMORPH, PERSIANN-CDR, CHIRPS V2.0, TMPA 3B42 V7, and GPM IMERG V6 Satellite Precipitation Datasets in Arabian Arid Regions. Water 2023, 15, 92. [Google Scholar] [CrossRef]
- Schneider, U.; Finger, P.; Meyer-Christoffer, A.; Rustemeier, E.; Ziese, M.; Becker, A. 2017. Evaluating the hydrological cycle over land using the newly-corrected precipitation climatology from the Global Precipitation Climatology Centre (GPCC). Atmosphere 2017, 8, 52. [Google Scholar] [CrossRef]
- Sadeghi, M.; Nguyen, P.; Naeini, M.R.; Hsu, K.; Braithwaite, D.; Sorooshian, S. PERSIANN-CCS-CDR, a 3-hourly 0.04° global precipitation climate data record for heavy precipitation studies. Sci. Data 2021, 8, 157. [Google Scholar] [CrossRef] [PubMed]
- Silva Júnior, C.H.L.; Almeida, C.T.; Santos, J.R.N.; Anderson, L.O.; Aragão, L.E.O.C.; Silva, F.B. Spatiotemporal Rainfall Trends in the Brazilian Legal Amazon between the Years 1998 and 2015. Water 2018, 10, 1220. [Google Scholar] [CrossRef]
- Anjum, M.N.; Irfan, M.; Waseem, M.; Leta, M.K.; Niazi, U.M.; Rahman, S.; Ghanim, A.; Mukhtar, M.A.; Nadeem, M.U. Assessment of PERSIANN-CCS, PERSIANN-CDR, SM2RAIN-ASCAT, and CHIRPS-2.0 Rainfall Products over a Semi-Arid Subtropical Climatic Region. Water 2022, 14, 147. [Google Scholar] [CrossRef]
- Fan, J.; Rosenfeld, D.; Zhang, Y.; Giangrande, S.E.; Li, Z.; Machado, L.A.T.; Martin, S.T.; Yang, Y.; Wang, J.; Artaxo, P.; et al. Substantial convection and precipitation enhancements by ultrafine aerosol particles. Science 2018, 359, 411–418. [Google Scholar] [CrossRef] [PubMed]
- Shrivastava, M.; Andreae, M.O.; Artaxo, P.; Barbosa, H.M.L.; Berg, L.K.; Brito, J.; Ching, J.; Easter, R.C.; Fan, J.; Fast, J.D.; et al. Urban pollution greatly enhances formation of natural aerosols over the Amazon rainforest. Nat. Commun. 2019, 10, 1046. [Google Scholar] [CrossRef]
- Pendharkar, J.; Figueroa, S.N.; Vara-Vela, A.; Krishna, R.P.M.; Schuch, D.; Kubota, P.Y.; Alvim, D.S.; Vendrasco, E.P.; Gomes, H.B.; Nobre, P.; et al. Towards Unified Online-Coupled Aerosol Parameterization for the Brazilian Global Atmospheric Model (BAM): Aerosol–Cloud Microphysical–Radiation Interactions. Remote Sens. 2023, 15, 278. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Ribbe, L.; Nauditt, A.; Giraldo-Osorio, J.D.; Thinn, N.X. Temporal and spatial evaluation of satellite rainfall estimates over different regions in Latin-America. Atmos. Res. 2018, 213, 34–50. [Google Scholar] [CrossRef]
- Ceccherini, G.; Ameztoy, I.; Hernandez, C.P.R.; Moreno, C.C. High-resolution precipitation datasets in South America and West Africa based on satellite-derived rainfall, enhanced vegetation index and digital elevation model. Remote Sens. 2015, 7, 6454–6488. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Jujun, H.; Gebregiorgis, A.S.; Xue, X.; Zhang, X. Inter-comparison of high-resolution satellite precipitation products over Central Asia. Remote Sens. 2015, 7, 7181–7211. [Google Scholar] [CrossRef]







| Precipitation Product | Category | Spatial Coverage | Temporal Coverage | Spatial Resolution | Temporal Resolution | Reference |
|---|---|---|---|---|---|---|
| XAV | Gauge-based products | Brazil | 1961–2020 | 0.1° × 0.1° | Daily | [33] |
| CPC | Gauge-based products | Global | 1979–Near Present | 0.5° × 0.5° | Daily | [42] |
| GPCC | Gauge-based products | Global | 1981–Near Present | 0.25° × 0.25° | Daily | [45] |
| CRU | Gauge-based products | Global | 1901–Near Present | 0.5° × 0.5° | Monthly | [46] |
| ERA5Land | Reanalysis products | Global | 1950–Near Present | 0.1° × 0.1° | Hourly | [50] |
| CHIRPS | Satellite-based Products | Quasi-global | 1981–Near Present | 0.05° × 0.05° | Daily | [26] |
| PERSIANN-CDR | Satellite-based Products | Quasi-global | 1983–Near Present | 0.25° × 0.25° | Daily | [70] |
| CMORPH | Satellite-based Products | Quasi-global | 1998–Near Present | 0.5° × 0.5° | Daily | [23] |
| IMERG | Satellite-based Products | Global | 2000–Near Present | 0.1° × 0.1° | Daily | [60] |
| Groups | Station Numbers | Relative Frequency | Average Annual Precipitation (mm) |
|---|---|---|---|
| 1 | 147 | 30.63 | 1843 |
| 2 | 53 | 11,04 | 3055 |
| 3 | 115 | 23.96 | 1704 |
| 4 | 67 | 13.96 | 2630 |
| 5 | 88 | 18.33 | 2477 |
| 6 | 10 | 2.08 | 1899 |
| DJF Quarter | MAM Quarter | JJA Quarter | SON Quarter | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Database | bias | r | RMSE | SDE | bias | r | RMSE | SDE | bias | r | RMSE | SDE | bias | r | RMSE | SDE |
| Xavier | −59 | 0.87 | 77 | 45 | −49 | 0.90 | 65 | 40 | −20 | 0.91 | 33 | 23 | −46 | 0.84 | 62 | 40 |
| CHIRPS | −46 | 0.77 | 96 | 61 | −33 | 0.87 | 72 | 52 | −17 | 0.85 | 41 | 32 | −31 | 0.83 | 58 | 43 |
| GPCC | −75 | 0.78 | 96 | 56 | −73 | 0.71 | 100 | 67 | −41 | 0.79 | 55 | 36 | −56 | 0.78 | 73 | 45 |
| ERA5Land | 2 | 0.73 | 100 | 70 | 10 | 0.82 | 101 | 66 | −24 | 0.73 | 59 | 44 | −12 | 0.69 | 71 | 57 |
| PERSIANN-CDR | −1 | 0.65 | 106 | 79 | −16 | 0.66 | 100 | 78 | −16 | 0.81 | 49 | 38 | −30 | 0.75 | 61 | 49 |
| IMERG | −14 | 0.56 | 114 | 89 | −36 | 0.64 | 99 | 83 | −21 | 0.65 | 60 | 51 | 3 | 0.64 | 69 | 58 |
| CMORPH | −110 | 0.61 | 140 | 77 | −126 | 0.69 | 148 | 75 | −126 | 0.67 | 132 | 46 | 39 | 0.74 | 76 | 51 |
| CRU | −46 | 0.42 | 130 | 92 | −33 | 0.44 | 123 | 100 | −9 | 0.60 | 67 | 51 | −38 | 0.56 | 80 | 62 |
| CPC | −130 | 0.44 | 170 | 108 | −133 | 0.51 | 169 | 106 | −63 | 0.58 | 94 | 67 | −82 | 0.48 | 110 | 72 |
| Annual | ||||
|---|---|---|---|---|
| Database | bias | r | RMSE | SDE |
| Xavier | −166 | 0.85 | 213 | 118 |
| CHIRPS | −118 | 0.77 | 227 | 144 |
| GPCC | −237 | 0.67 | 295 | 163 |
| ERA5Land | −16 | 0.63 | 263 | 175 |
| PERSIANN-CDR | −55 | 0.52 | 268 | 202 |
| IMERG | −58 | 0.47 | 268 | 215 |
| CMORPH | −314 | 0.49 | 395 | 198 |
| CRU | −116 | 0.35 | 310 | 216 |
| CPC | −396 | 0.22 | 515 | 316 |
| Ranking | Score | Group 1 (G1) | Group 2 (G2) | Group 3 (G3) | Group 4 (G4) | Group 5 (G5) | Group 6 (G6) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | XAV | XAV | XAV | XAV | XAV | XAV |
| 2 | 9 | GPC | CHI | CHI | ERA | CHI | CHI |
| 3 | 8 | CHI | ERA | GPC | CHI | GPC | GPC |
| 4 | 7 | ERA | GPC | PER | GPC | PER | PER |
| 5 | 6 | PER | PER | ERA | PER | ERA | IME |
| 6 | 5 | CRU | CRU | IME | IME | IME | ERA |
| 7 | 4 | IME | IME | CMO | CRU | CPC | CPC |
| 8 | 3 | CPC | CPC | CPC | CMO | CMO | CMO |
| 9 | 2 | CMO | CMO | CRU | CPC | CRU | CRU |
| Ranking | Score | Group 1 (G1) | Group 2 (G2) | Group 3 (G3) | Group 4 (G4) | Group 5 (G5) | Group 6 (G6) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | XAV | XAV | XAV | XAV | CHI | XAV |
| 2 | 9 | GPC | CHI | CHI | CHI | XAV | GPC |
| 3 | 8 | CHI | GPC | GPC | ERA | ERA | CHI |
| 4 | 7 | PER | ERA | CMO | GPC | GPC | PER |
| 5 | 6 | ERA | PER | PER | PER | CMO | CMO |
| 6 | 5 | CMO | CMO | ERA | IME | PER | ERA |
| 7 | 4 | CRU | IME | IME | CMO | IME | CRU |
| 8 | 3 | IME | CRU | CRU | CPC | CPC | IME |
| 9 | 2 | CPC | CPC | CPC | CRU | CRU | CPC |
| Ranking | Score | Group 1 (G1) | Group 2 (G2) | Group 3 (G3) | Group 4 (G4) | Group 5 (G5) | Group 6 (G6) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | XAV | ERA | XAV | XAV | CHI | XAV |
| 2 | 9 | CHI | IME | GPC | ERA | XAV | CHI |
| 3 | 8 | GPC | PER | CHI | CHI | GPC | PER |
| 4 | 7 | CRU | CHI | CMO | IME | ERA | IME |
| 5 | 6 | PER | XAV | CRU | PER | IME | GPC |
| 6 | 5 | ERA | GPC | PER | CMO | PER | CRU |
| 7 | 4 | IME | CMO | ERA | CRU | CRU | ERA |
| 8 | 3 | CMO | CRU | IME | GPC | CPC | CMO |
| 9 | 2 | CPC | CPC | CPC | CPC | CMO | CPC |
| Ranking | Score | Group 1 (G1) | Group 2 (G2) | Group 3 (G3) | Group 4 (G4) | Group 5 (G5) | Group 6 (G6) |
|---|---|---|---|---|---|---|---|
| 1 | 10 | CHI | ERA | XAV | ERA | CRU | PER |
| 2 | 9 | CRU | IME | GPC | XAV | IME | IME |
| 3 | 8 | PER | PER | CMO | CMO | CHI | XAV |
| 4 | 7 | CMO | CHI | CRU | CHI | ERA | CHI |
| 5 | 6 | ERA | CMO | CHI | IME | XAV | CRU |
| 6 | 5 | XAV | XAV | ERA | PER | GPC | GPC |
| 7 | 4 | IME | GPC | PER | CRU | PER | CPC |
| 8 | 3 | GPC | CRU | IME | GPC | CPC | ERA |
| 9 | 2 | CPC | CPC | CPC | CPC | CMO | CMO |
| Taylor Diagrams (SDE) | Pearson Correlation (r) | RMSE | bias | Final Result | |||||
|---|---|---|---|---|---|---|---|---|---|
| Data Source | General Score | Data Source | General Score | Data Source | General Score | Data Source | General Score | Data Source | General Score |
| Xavier | 10.0 | Xavier | 9.8 | Xavier | 9.2 | Xavier | 7.2 | Xavier | 9.0 |
| CHIRPS | 8.7 | CHIRPS | 8.8 | CHIRPS | 8.5 | CHIRPS | 7.5 | CHIRPS | 8.4 |
| GPCC | 7.8 | GPCC | 8.0 | GPCC | 6.5 | GPCC | 4.8 | GPCC | 6.8 |
| ERA5Land | 6.8 | ERA5Land | 6.5 | ERA5Land | 6.5 | ERA5Land | 6.8 | ERA5Land | 6.7 |
| PERSIANN | 6.5 | PERSIANN | 6.2 | PERSIANN | 6.3 | PERSIANN | 6.5 | PERSIANN | 6.4 |
| IMERG | 4.8 | CMORPH | 5.5 | IMERG | 6.0 | IMERG | 6.7 | IMERG | 5.8 |
| CRU | 3.3 | IMERG | 3.8 | CMORPH | 4.0 | CRU | 6.5 | CMORPH | 4.4 |
| CPC | 3.2 | CRU | 3.0 | CRU | 4.8 | CPC | 2.5 | CRU | 3.4 |
| CMORPH | 2.8 | CPC | 2.3 | CPC | 2.2 | CMORPH | 5.5 | CPC | 3.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
dos Santos Silva, F.D.; da Costa, C.P.W.; dos Santos Franco, V.; Gomes, H.B.; da Silva, M.C.L.; dos Santos Vanderlei, M.H.G.; Costa, R.L.; da Rocha Júnior, R.L.; Cabral Júnior, J.B.; dos Reis, J.S.; et al. Intercomparison of Different Sources of Precipitation Data in the Brazilian Legal Amazon. Climate 2023, 11, 241. https://doi.org/10.3390/cli11120241
dos Santos Silva FD, da Costa CPW, dos Santos Franco V, Gomes HB, da Silva MCL, dos Santos Vanderlei MHG, Costa RL, da Rocha Júnior RL, Cabral Júnior JB, dos Reis JS, et al. Intercomparison of Different Sources of Precipitation Data in the Brazilian Legal Amazon. Climate. 2023; 11(12):241. https://doi.org/10.3390/cli11120241
Chicago/Turabian Styledos Santos Silva, Fabrício Daniel, Claudia Priscila Wanzeler da Costa, Vânia dos Santos Franco, Helber Barros Gomes, Maria Cristina Lemos da Silva, Mário Henrique Guilherme dos Santos Vanderlei, Rafaela Lisboa Costa, Rodrigo Lins da Rocha Júnior, Jório Bezerra Cabral Júnior, Jean Souza dos Reis, and et al. 2023. "Intercomparison of Different Sources of Precipitation Data in the Brazilian Legal Amazon" Climate 11, no. 12: 241. https://doi.org/10.3390/cli11120241
APA Styledos Santos Silva, F. D., da Costa, C. P. W., dos Santos Franco, V., Gomes, H. B., da Silva, M. C. L., dos Santos Vanderlei, M. H. G., Costa, R. L., da Rocha Júnior, R. L., Cabral Júnior, J. B., dos Reis, J. S., Cavalcante, R. B. L., Tedeschi, R. G., de Jesus da Costa Barreto, N., Nogueira Neto, A. V., dos Santos Jesus, E., & da Silva Ferreira, D. B. (2023). Intercomparison of Different Sources of Precipitation Data in the Brazilian Legal Amazon. Climate, 11(12), 241. https://doi.org/10.3390/cli11120241










