Precipitation Variability for Protected Areas of Primary Forest and Pastureland in Southwestern Amazônia
Abstract
:1. Introduction
2. Materials and Methods
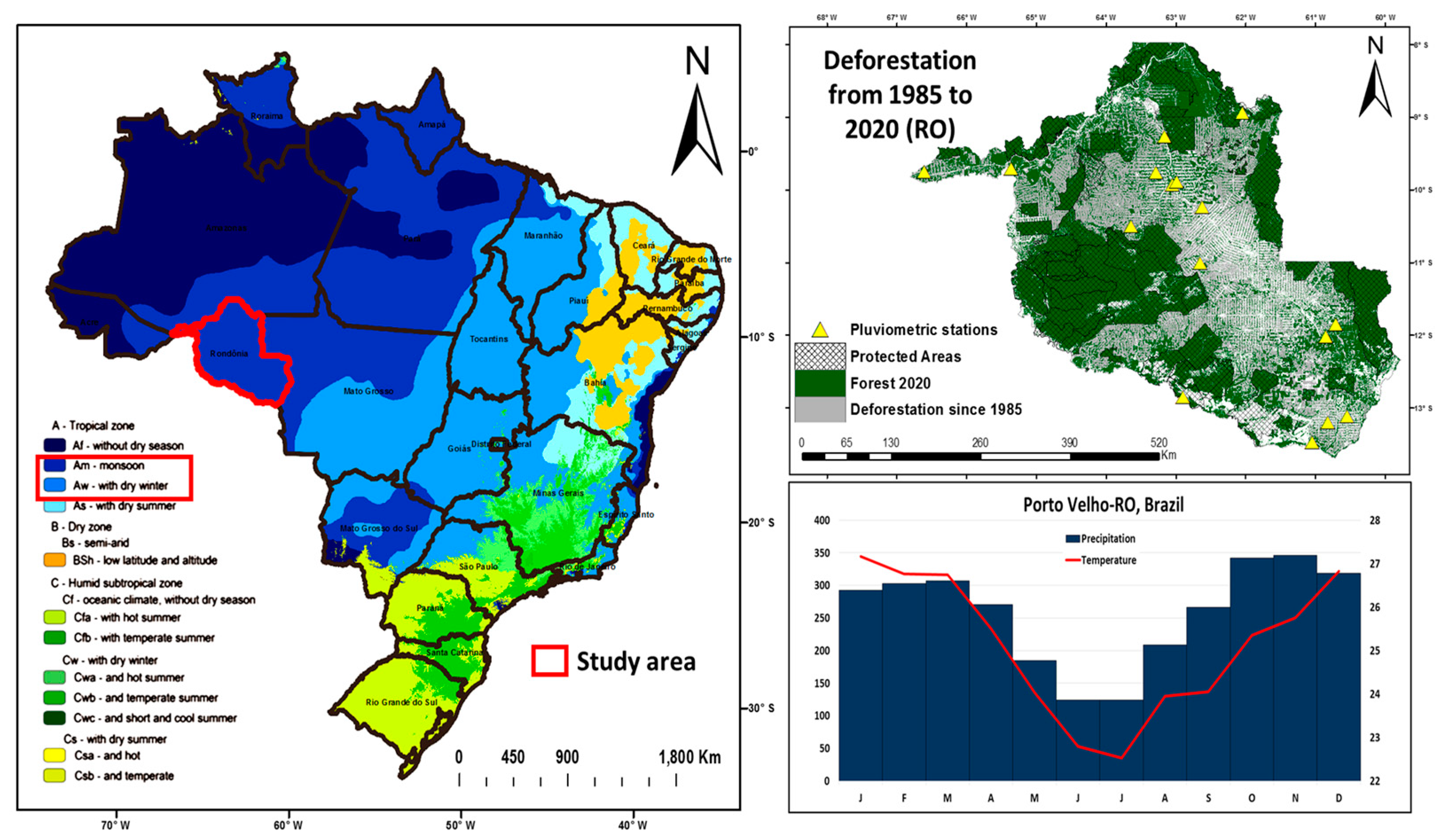
2.1. Study Area Description
2.2. Selection of Rain Gauges
2.3. Collection of CHIRPS Data
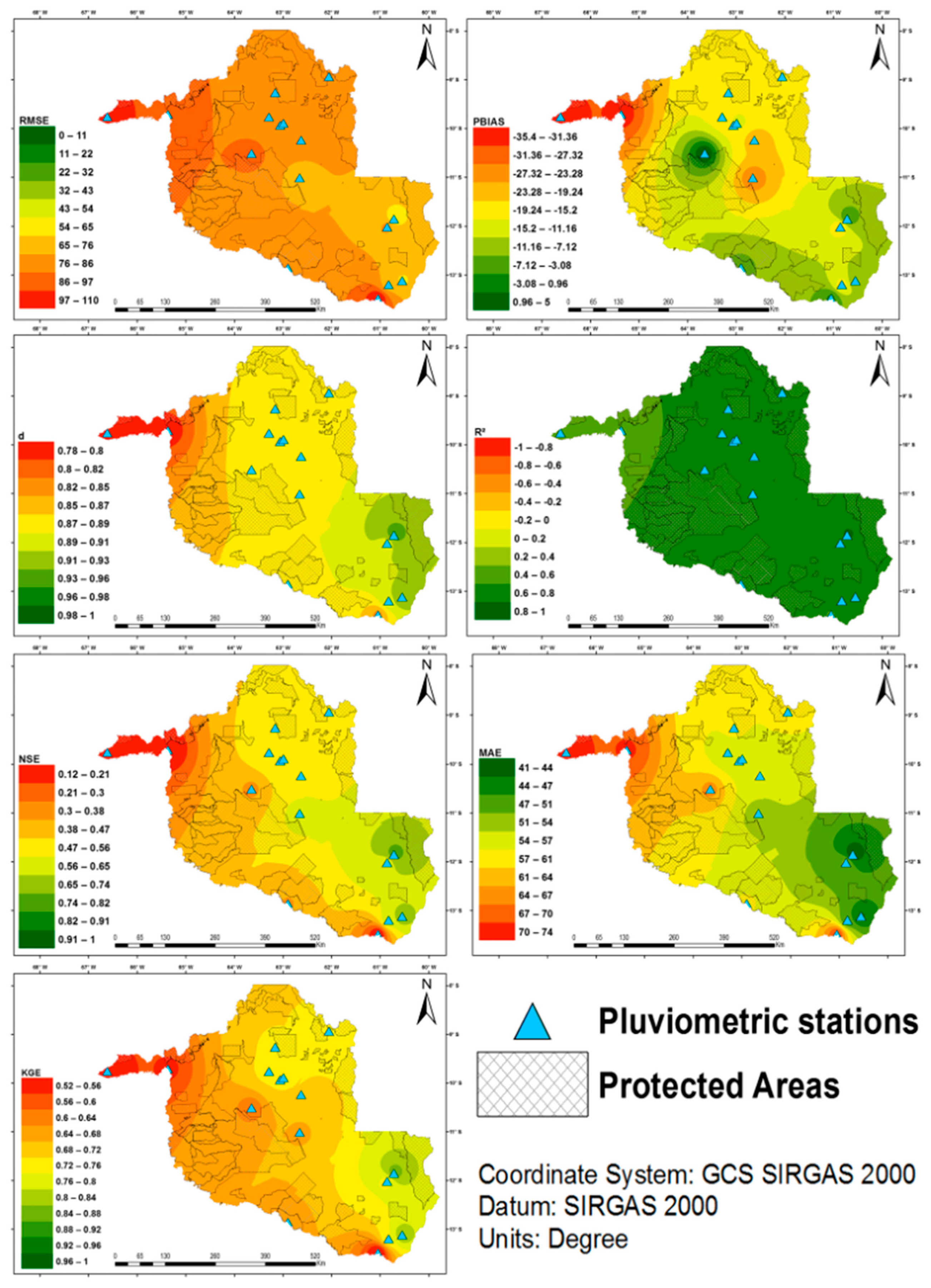
2.4. Metrics for Validating CHIRPS Data
2.5. Historical Analysis of CHIRPS Precipitation Data
2.6. Standard Precipitation Index (SPI–6)
2.7. Mann-Kendall Test
2.8. Sen’s Slope Analysis
2.9. Laplace Trend Test
3. Results
3.1. Validation of CHIRPS Data
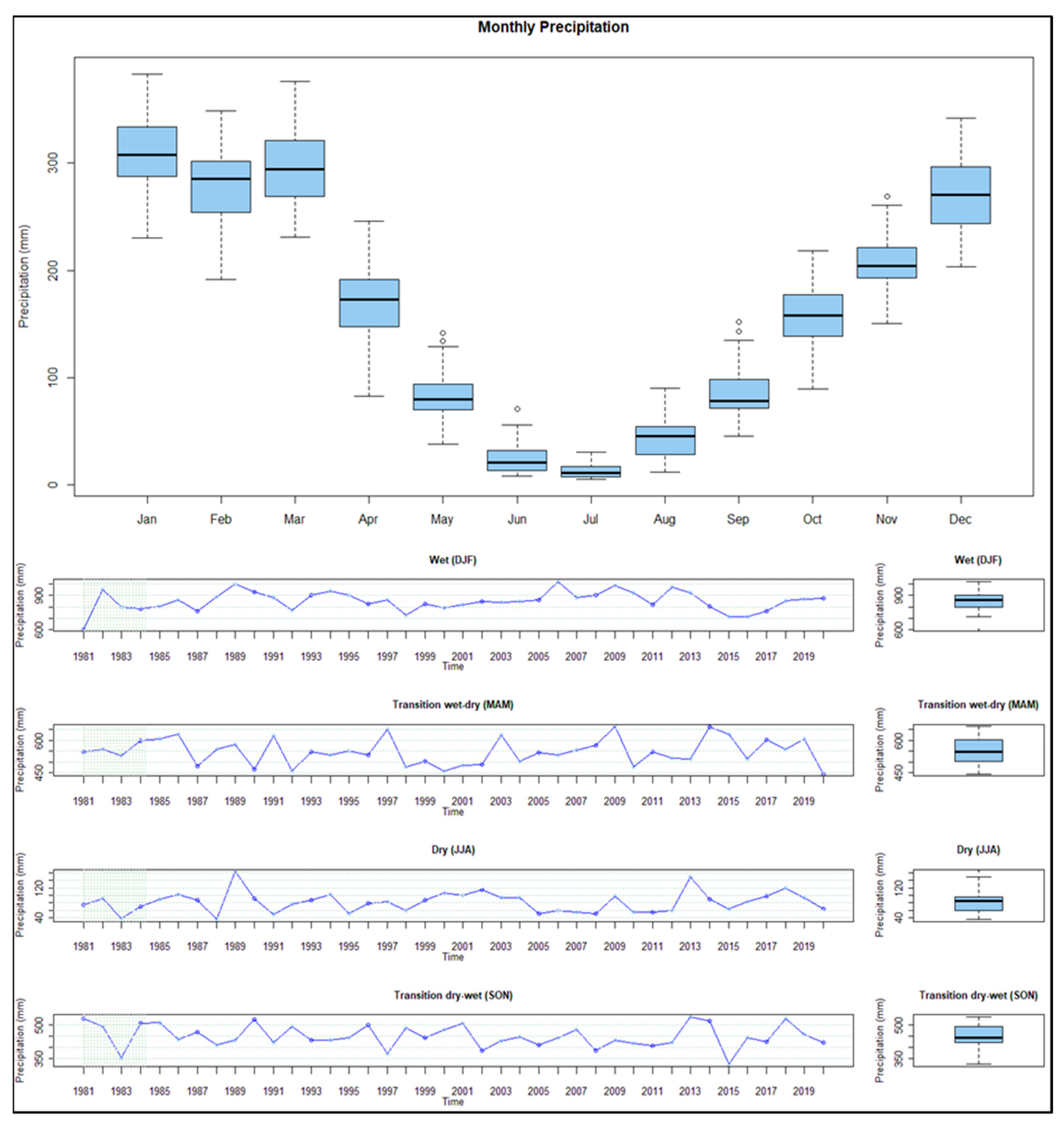
3.2. Monthly Rainfall Distribution and Standardized Precipitation Index (SPI)
3.3. Mann-Kendall and Sen’s Slope Precipitation Trends Analysis for the State of Rondônia
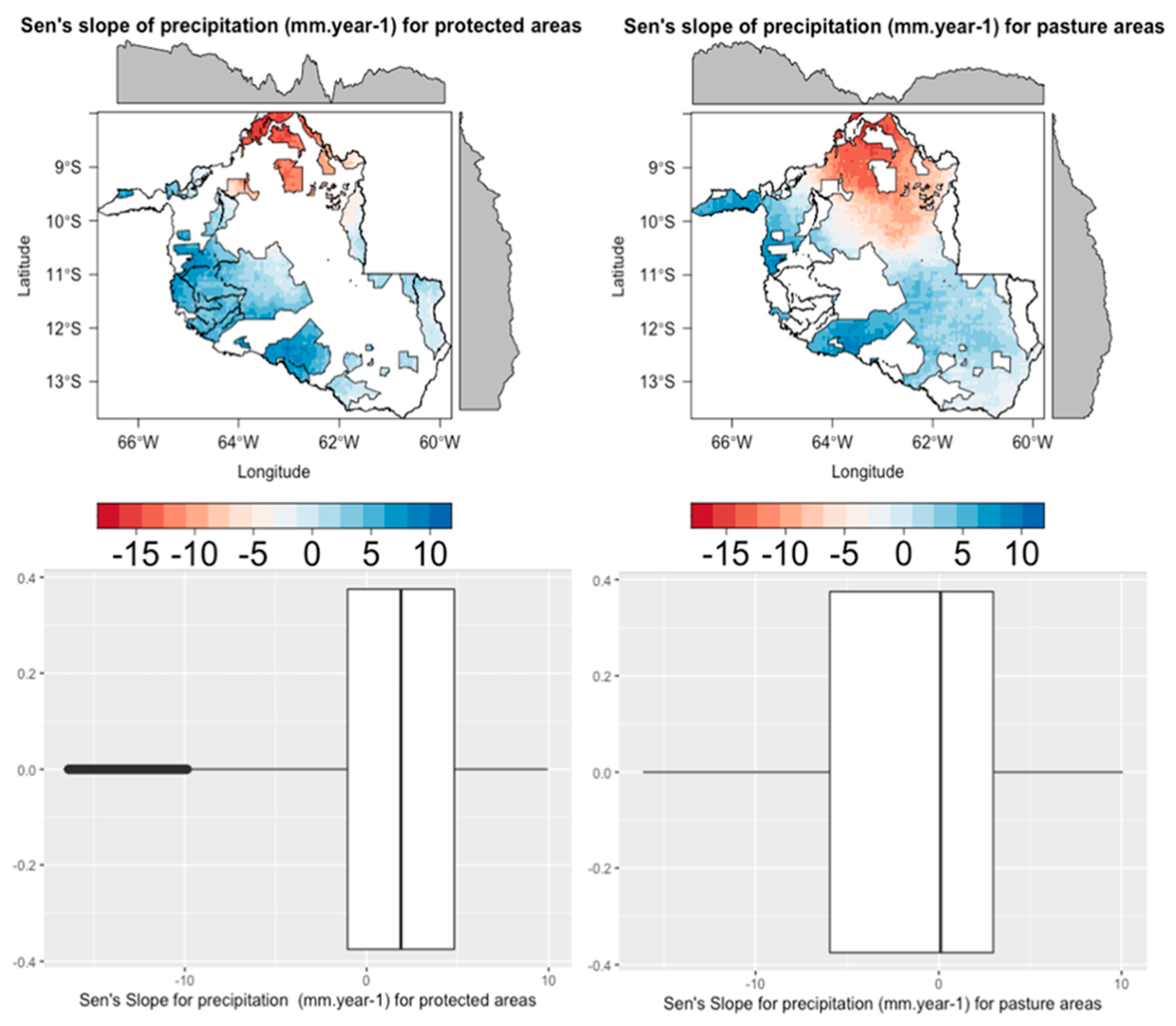
3.4. Spatial Analysis of Precipitation Trends in the State of Rondônia Separated per Dry and Rainy Season for Anthropized and Primary Forest Areas
3.4.1. Spatial Analysis of Precipitation Trends in the State of Rondônia Separated per Dry and Rainy Season for Anthropized and Primary Forest Areas
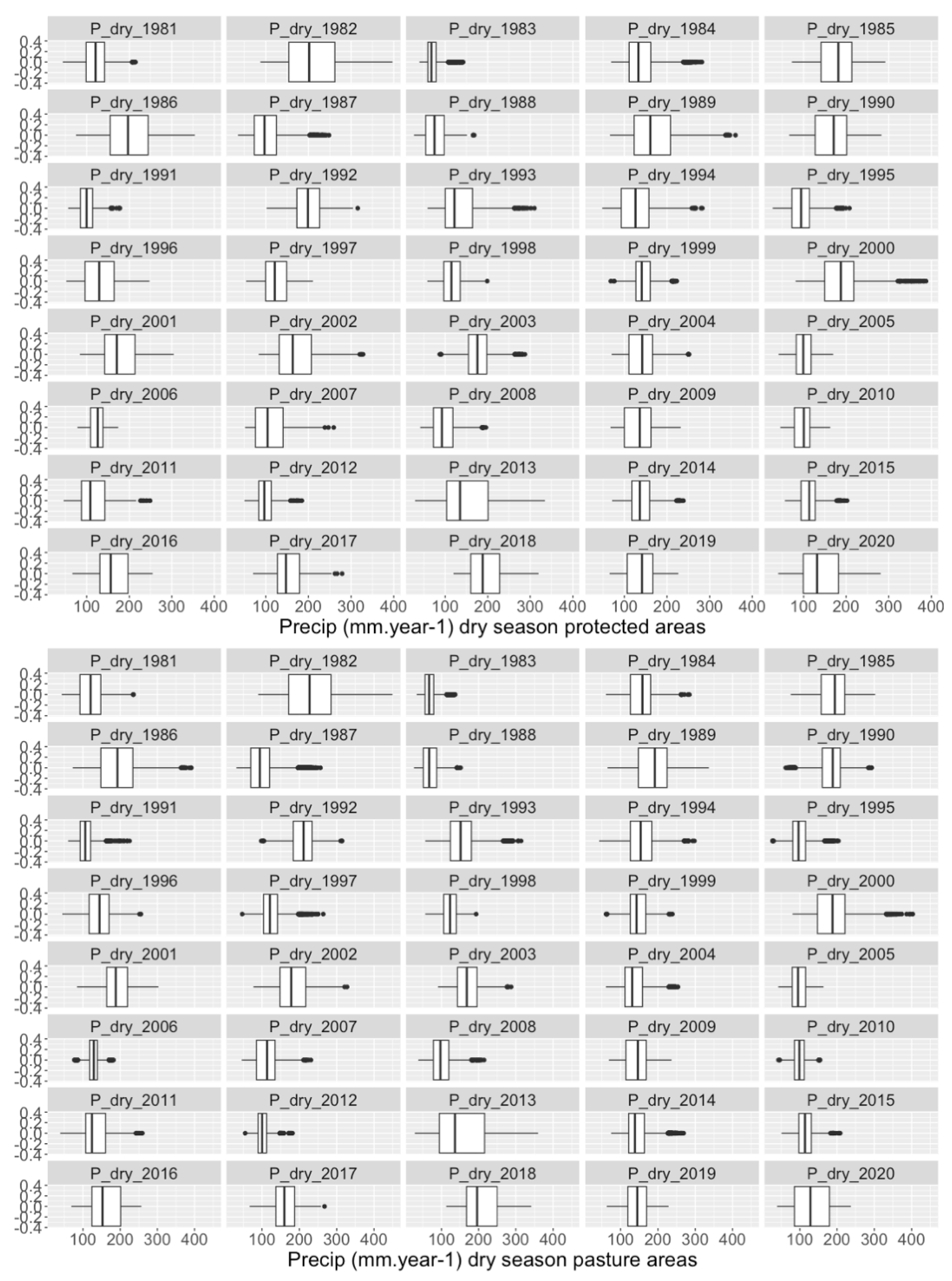
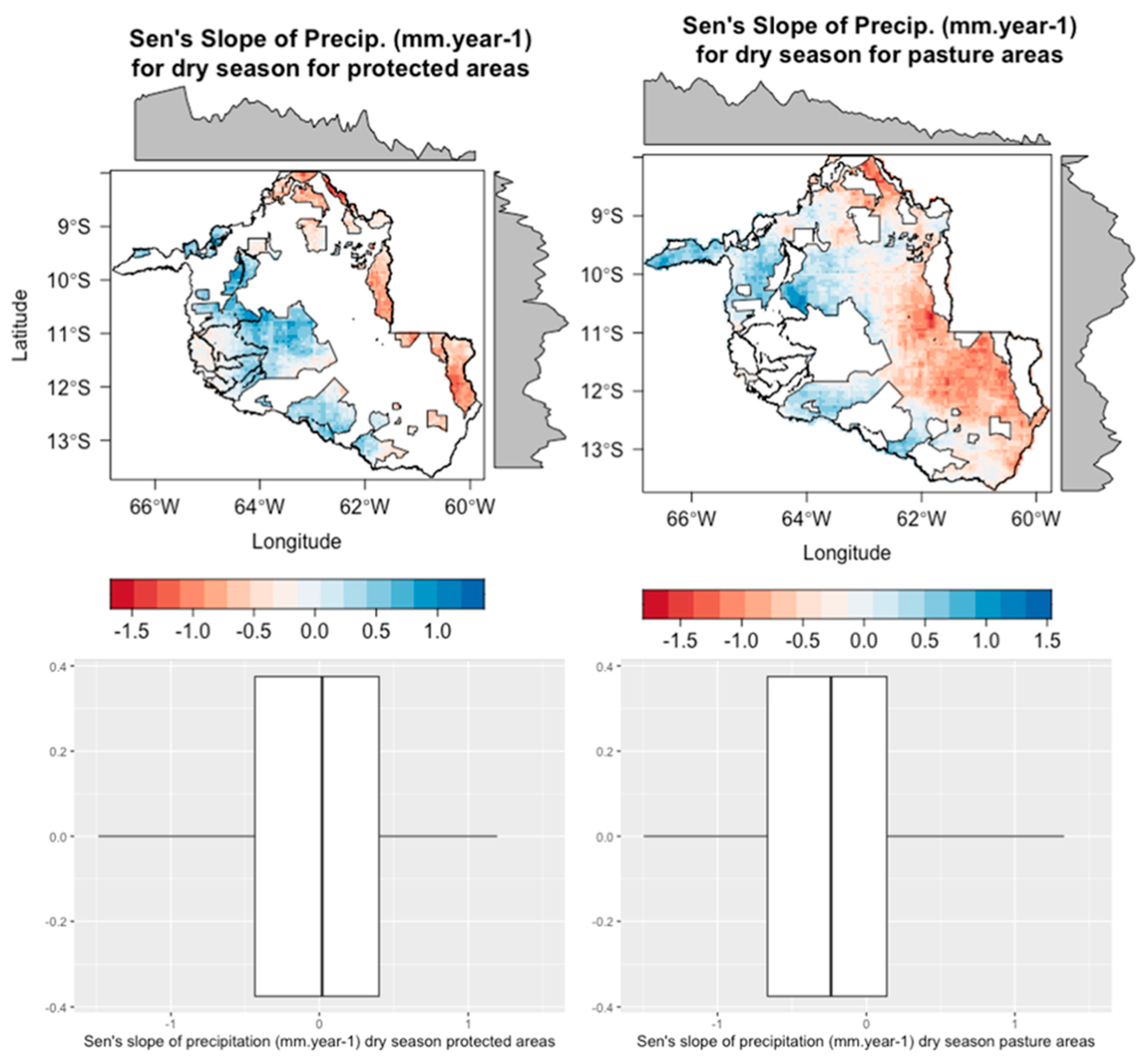
3.4.2. Analysis of Precipitation in the Dry Season for Protected and Pasture Areas
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Ethical Approval
References
- de Moraes Cordeiro, A.L.; Blanco, C.J.C. Assessment of Satellite Products for Filling Rainfall Data Gaps in the Amazon Region. Nat. Resour. Model. 2021, 34, e12298. [Google Scholar] [CrossRef]
- Tian, H.; Melillo, J.M.; Kicklighter, D.W.; McGuire, A.D.; Helfrich, J.V.K.; Moore, B.; Vörösmarty, C.J. Effect of Interannual Climate Variability on Carbon Storage in Amazonian Ecosystems. Nature 1998, 396, 664–667. [Google Scholar] [CrossRef]
- Mu, Y.; Biggs, T.; Shen, S.S. Satellite-based precipitation estimates using a dense rain gauge network over the Southwestern Brazilian Amazon: Implication for identifying trends in dry season rainfall. Atmos. Res. 2021, 261, 105741. [Google Scholar] [CrossRef]
- Sikora de Souza, V.A.; Moreira, D.M.; Rotunno Filho, O.C.; Rudke, A.P. Extreme Rainfall Events in Amazonia: The Madeira River Basin. Remote Sens. Appl. Soc. Environ. 2020, 18, 100316. [Google Scholar] [CrossRef]
- Bier, A.A.; Ferraz, S.E.T. Comparação de Metodologias de Preenchimento de Falhas em Dados Meteorológicos para Estações no Sul do Brasil. Rev. Bras. Meteorol. 2017, 32, 215–226. [Google Scholar] [CrossRef]
- Gimenez, D.F.S.; Nery, J.T. Aplicação das redes neurais artificiais no preenchimento de dados diários de chuva no estado de São Paulo. Desafios Geogr. Física Front. Conhecimento 2017, 1, 1747–1755. [Google Scholar] [CrossRef] [Green Version]
- Machado, L.A.; Assis, W.L. Comparação entre métodos de preenchimento de falhas em séries de dados meteorológicos da bacia hidrográfica do Rio das Velhas (MG). GEOgrafias 2018, 26, 73–90. [Google Scholar] [CrossRef]
- Santos, S.R.Q.D.; Cunha, A.P.M.d.A.; Ribeiro-Neto, G.G. Avaliação De Dados De Precipitação Para O Monitoramento Do Padrão Espaço-Temporal Da Seca No Nordeste Do Brasil. Rev. Bras. Climatol. 2019, 25, 80–100. [Google Scholar] [CrossRef] [Green Version]
- Cavalcante, R.B.L.; da Silva Ferreira, D.B.; Pontes, P.R.M.; Tedeschi, R.G.; da Costa, C.P.W.; de Souza, E.B. Evaluation of Extreme Rainfall Indices from CHIRPS Precipitation Estimates over the Brazilian Amazonia. Atmos. Res. 2020, 238, 104879. [Google Scholar] [CrossRef]
- Haghtalab, N.; Moore, N.; Heerspink, B.P.; Hyndman, D.W. Evaluating Spatial Patterns in Precipitation Trends across the Amazon Basin Driven by Land Cover and Global Scale Forcings. Theor. Appl. Climatol. 2020, 140, 411–427. [Google Scholar] [CrossRef]
- da Franca, R.R. Climatologia das chuvas em Rondônia—Período 1981–2011. Rev. Geogr. 2015, 11, 44–58. [Google Scholar] [CrossRef]
- Haylock, M.R.; Peterson, T.C.; Alves, L.M.; Ambrizzi, T.; Anunciação, Y.M.T.; Baez, J.; Barros, V.R.; Berlato, M.A.; Bidegain, M.; Coronel, G.; et al. Trends in Total and Extreme South American Rainfall in 1960–2000 and Links with Sea Surface Temperature. J. Clim. 2006, 19, 1490–1512. [Google Scholar] [CrossRef]
- Liebmann, B.; Kiladis, G.N.; Marengo José, A.; Ambrizzi, T.; Glick, J.D. Submonthly Convective Variability over South America and the South Atlantic Convergence Zone. J. Clim. 1999, 12, 1877–1891. [Google Scholar] [CrossRef]
- Liebmann, B.; Jones, C.; de Carvalho, L.M.V. Interannual Variability of Daily Extreme Precipitation Events in the State of São Paulo, Brazil. J. Clim. 2001, 14, 208–218. [Google Scholar] [CrossRef]
- Marengo, J.A.; Rusticucci, M.; Penalba, O.; Renom, M. An Intercomparison of Observed and Simulated Extreme Rainfall and Temperature Events during the Last Half of the Twentieth Century: Part 2: Historical Trends. Clim. Chang. 2010, 98, 509–529. [Google Scholar] [CrossRef] [Green Version]
- Marengo, J.A.; Liebmann, B.; Grimm, A.M.; Misra, V.; Silva Dias, P.L.; Cavalcanti, I.F.A.; Carvalho, L.M.V.; Berbery, E.H.; Ambrizzi, T.; Vera, C.S.; et al. Recent Developments on the South American Monsoon System. Int. J. Climatol. 2012, 32, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Rao, V.B.; Franchito, S.H.; Santo, C.M.E.; Gan, M.A. An Update on the Rainfall Characteristics of Brazil: Seasonal Variations and Trends in 1979–2011. Int. J. Climatol. 2016, 36, 291–302. [Google Scholar] [CrossRef]
- Sanches, R.G.; Santos, B.C.D.; Miani, R.S.; Neves, G.Z.d.F.; Silva, M.S.D.; Tech, A.R.B. Analysis of Daily Rainfall in São Carlos/SP, Brazil over 1979-2017 Using Laplace Trend Test. J. Geosci. Environ. Prot. 2020, 8, 104–125. [Google Scholar] [CrossRef]
- De Sousa, A.C.; Candido, L.A.; Andreoli, R.V. Variabilidade Interanual da Precipitação e Fluxo de Umidade Sobre a Amazônia Usando o QTCM. Rev. Bras. Meteorol. 2018, 33, 41–56. [Google Scholar] [CrossRef] [Green Version]
- Sugahara, S.; da Rocha, R.P.; Silveira, R. Non-Stationary Frequency Analysis of Extreme Daily Rainfall in Sao Paulo, Brazil. Int. J. Climatol. 2009, 29, 1339–1349. [Google Scholar] [CrossRef]
- Zilli, M.T.; Carvalho, L.M.V.; Liebmann, B.; Silva Dias, M.A. A Comprehensive Analysis of Trends in Extreme Precipitation over Southeastern Coast of Brazil. Int. J. Climatol. 2017, 37, 2269–2279. [Google Scholar] [CrossRef]
- Coutinho, E.R.; da Silva, R.M.; Madeira, J.G.F.; de Oliveira dos Santos Coutinho, P.R.; Boloy, R.A.M.; Delgado, A.R.S. Application of Artificial Neural Networks (ANNs) in the Gap Filling of Meteorological Time Series. Rev. Bras. Meteorol. 2018, 33, 317–328. [Google Scholar] [CrossRef]
- Costa, J.C.; Pereira, G.; Siqueira, M.E.; Cardozo, F.d.S.; da Silva, V.V. Validação Dos Dados De Precipitação Estimados Pelo Chirps Para O Brasil. Rev. Bras. Climatol. 2019, 24. [Google Scholar] [CrossRef] [Green Version]
- Mu, Y.; Jones, C. An observational analysis of precipitation and deforestation age in the Brazilian Legal Amazon. Atmos. Res. 2022, 271, 106122. [Google Scholar] [CrossRef]
- Cabral Júnior, J.B.; Lucena, R.L. Análises Das Precipitações Pelos Testes Não Paramétricos De Mann-Kendall E Kruskal-Wallis. Mercator 2020, 19, 1–14. [Google Scholar] [CrossRef]
- Souza, E.B.D.; Carmo, A.M.C.; Moares, B.C.; Nacif, A.; Ferreira, D.B.d.S.; Rocha, E.J.P.; Souza, P.J.d.O.P. Seasonal Precipitation Over the Brazilian Legal Amazon: Climate Current and Future Projections Using Regcm4 Model. Rev. Bras. Climatol. 2016, 18. [Google Scholar] [CrossRef] [Green Version]
- Salviano, M.F.; Groppo, J.D.; Pellegrino, G.Q. Análise de Tendências em Dados de Precipitação e Temperatura no Brasil. Rev. Bras. Meteorol. 2016, 31, 64–73. [Google Scholar] [CrossRef] [Green Version]
- Ali, R.; Kuriqi, A.; Abubaker, S.; Kisi, O. Long-Term Trends and Seasonality Detection of the Observed Flow in Yangtze River Using Mann-Kendall and Sen’s Innovative Trend Method. Water 2019, 11, 1855. [Google Scholar] [CrossRef] [Green Version]
- Natividade, U.A.; Garcia, S.R.; Torres, R.R. Tendência dos Índices de Extremos Climáticos Observados e Projetados no Estado de Minas Gerais. Rev. Bras. Meteorol. 2017, 32, 600–614. [Google Scholar] [CrossRef] [Green Version]
- Stabile, M.C.C.; Guimarães, A.L.; Silva, D.S.; Ribeiro, V.; Macedo, M.N.; Coe, M.T.; Pinto, E.; Moutinho, P.; Alencar, A. Solving Brazil’s Land Use Puzzle: Increasing Production and Slowing Amazon Deforestation. Land Use Policy 2020, 91, 104362. [Google Scholar] [CrossRef]
- IBGE—Instituto Brasileiro de Geografia e Estatística. Censo Demográfico 2010; CD 1.09; IBGE: Rio de Janeiro, Brazil, 2010. [Google Scholar]
- De Paula, C.F.S.; Calvo, C.R. Uma problematização acerca do conceito de migração: Apontamentos na produção historiográfica do Estado de Rondônia. Rev. História Perspect. 2017, 30, 56. Available online: https://seer.ufu.br/index.php/historiaperspectivas/article/view/40737 (accessed on 7 December 2022). [CrossRef]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; de Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s Climate Classification Map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef] [PubMed]
- Projeto MapBiomas—Collection 07 of the Annual Series of Land Use and Land Cover Maps in Brazil. Available online: https://mapbiomas.org/download (accessed on 1 February 2022).
- Cavalcanti, I.R.A.; Ferreira, N.J.; Silva, M.G.A.; Dias, M.A.F.S. Tempo e Clima No Brasil; Oficina de Textos: São Paulo, Brazil, 2009. [Google Scholar]
- Dantas, L.G.; de Brito, J.I.B.; de Rodrigues, H.P.; de Araújo Aires, R.; Cabral, D.E.C. Oscilação Decadal do Pacífico e Multidecadal do Atlântico no clima da Amazônia Ocidental. Rev. Bras. Geogr. Física 2012, 5, 600–611. [Google Scholar] [CrossRef]
- Butt, N.; De Oliveira, P.A.; Costa, M. Evidence that deforestation affects the onset of the rainy season in Rondonia, Brazil. J. Geophys. Res. Atmos./Clim. Dyn. 2011, 116, D11120. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [Green Version]
- R Studio Team. RStudio: Integrated Development for R. RStudio; R Studio, PBC: Boston, MA, USA, 2020; Available online: http://www.rstudio.com/ (accessed on 15 January 2021).
- ANA—National Water Agency. ANA Data Acquisition v1.0. 2022. Available online: https://mega.nz/file/BtNBlQAB#t_- (accessed on 12 July 2022).
- Willmott, C.J. On the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation Project. 2021. Available online: http://qgis.osgeo.org (accessed on 10 October 2021).
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Measures; Charles Griffin: London, UK, 1975; Volume 15, p. 202. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Kanoun, K.; de Martini, M.R.B.; de Souza, J.M. A method for software reliability analysis and prediction application to the TROPICO-R switching system. IEEE Trans. Softw. Eng. 1991, 17, 334–344. [Google Scholar] [CrossRef]
- Shrestha, A.B.; Bajracharya, S.R.; Sharma, A.R.; Duo, C.; Kulkarni, A. Observed trends and changes in daily temperature and precipitation extremes over the Koshi river basin 1975–2010. Int. J. Climatol. 2017, 37, 1066–1083. [Google Scholar] [CrossRef]
- Paredes-Trejo, F.J.; Barbosa, H.A.; Lakshmi Kumar, T.V. Validating CHIRPS-Based Satellite Precipitation Estimates in Northeast Brazil. J. Arid. Environ. 2017, 139, 26–40. [Google Scholar] [CrossRef]
- Peixoto, J.P. As Variações Do Clima e O Ambiente—O Homem, O Clima e O Ambiente II; Secretaria de Estado do Ambiente e dos Recursos Naturais: Lisboa, Portugal, 1987. [Google Scholar]
- Zuffo, C.; Franca, R. Caracterização climática de Rondônia e variabilidade do clima em Porto Velho. In IX Simpósio Brasileiro de Climatologia Geográfica; Anais IX SBCG: Fortaleza, Brazil, 2010. [Google Scholar]
- Li, W.; Zhang, P.; Ye, J.; Li, L.; Baker, P.A. Impact of Two Different Types of El Niño Events on the Amazon Climate and Ecosystem Productivity. J. Plant Ecol. 2011, 4, 91–99. [Google Scholar] [CrossRef]
- Panisset, J.S.; Libonati, R.; Gouveia, C.M.P.; Machado-Silva, F.; França, D.A.; França, J.R.A.; Peres, L.F. Contrasting Patterns of the Extreme Drought Episodes of 2005, 2010 and 2015 in the Amazon Basin. Int. J. Climatol. 2018, 38, 1096–1104. [Google Scholar] [CrossRef]
- De Sales, F.; Santiago, T.; Biggs, T.W.; Mullan, K.; Sills, E.O.; Monteverde, C. Impacts of Protected Area Deforestation on Dry-Season Regional Climate in the Brazilian Amazon. J. Geophys. Res. Atmos. 2020, 125, e2020JD033048. [Google Scholar] [CrossRef]
- Lira, B.R.P.; Fernandes, L.L.; Ishihara, J.H. Pluviometric behavior and trends in the Legal Amazon from 1986 to 2015. Theor. Appl. Climatol. 2022, 150, 1353–1367. [Google Scholar] [CrossRef]



| Station Code | Lat | Long | Missing Data (%) | Elevation (m) | Min | Max | CV |
|---|---|---|---|---|---|---|---|
| 862000 | −8.93 | −62.06 | 10 | 80 | 0 | 543.3 | 0.74 |
| 963000 | −9.93 | −63.06 | 8.2 | 114 | 0 | 591.1 | 0.86 |
| 963001 | −9.26 | −63.16 | 2.6 | 98 | 0 | 551.3 | 0.84 |
| 963004 | −9.89 | −62.99 | 5.8 | 113 | 0 | 687 | 0.85 |
| 965001 | −9.70 | −65.36 | 10.8 | 98 | 0 | 652.8 | 0.98 |
| 966000 | −9.76 | −66.61 | 4.5 | 148 | 0 | 532.9 | 0.94 |
| 1062002 | −10.24 | −62.63 | 3.1 | 220 | 0 | 566.1 | 0.88 |
| 1062003 | −11.00 | −62.66 | 10.7 | 251 | 0 | 467.7 | 0.80 |
| 1063000 | −10.51 | −63.65 | 10.1 | 187 | 0 | 724,6 | 0.87 |
| 1063001 | −9.76 | −63.29 | 11.3 | 115 | 0 | 588.2 | 0.82 |
| 1160000 | −12.02 | −60.86 | 5.1 | 264 | 0 | 505.9 | 0.96 |
| 1160001 | −11.85 | −60.72 | 9.6 | 269 | 0 | 634.3 | 0.85 |
| 1262000 | −12.85 | −62.90 | 6.3 | 158 | 0 | 663.7 | 1.04 |
| 1360000 | −13.11 | −60.55 | 11.2 | 419 | 0 | 524.1 | 0.84 |
| 1360001 | −13.20 | −60.82 | 9.2 | 257 | 0 | 658.7 | 0.97 |
| 1360002 | −13.48 | −61.05 | 7.6 | 171 | 0 | 848.4 | 1.17 |
| SPI Values | Categories |
|---|---|
| ≥2 | Extremely wet |
| 1.50 to 1.99 | Severely wet |
| 1.00 to 1.49 | Moderately wet |
| 0.99 to –0.99 | Near normal |
| –1.00 to –1.49 | Moderately dry |
| –1.50 to –1.99 | Severely dry |
| ≤–2 | Extremely dry |
| Station | MAE | RMSE | PBIAS % | NSE | d | R2 | KGE |
|---|---|---|---|---|---|---|---|
| 862000 | 59.03 | 84.33 | −18.2 | 0.56 | 0.88 | 0.66 | 0.73 |
| 963000 | 56.09 | 80.16 | −18.1 | 0.52 | 0.88 | 0.64 | 0.73 |
| 963001 | 58.57 | 84.08 | −17 | 0.52 | 0.88 | 0.63 | 0.73 |
| 963004 | 56.12 | 84.74 | −12.1 | 0.46 | 0.87 | 0.61 | 0.72 |
| 965001 | 71.16 | 95.61 | −33.4 | 0.12 | 0.79 | 0.49 | 0.55 |
| 966000 | 73.8 | 102.65 | −35.4 | 0.16 | 0.78 | 0.48 | 0.52 |
| 1062002 | 54.64 | 77.3 | −22.4 | 0.56 | 0.89 | 0.69 | 0.72 |
| 1062003 | 52.23 | 69.91 | −26.4 | 0.6 | 0.88 | 0.74 | 0.67 |
| 1063000 | 65.24 | 91.47 | 5 | 0.36 | 0.87 | 0.65 | 0.61 |
| 1063001 | 53.7 | 76.03 | −18.1 | 0.55 | 0.89 | 0.67 | 0.74 |
| 1160000 | 51.35 | 78.23 | −19.3 | 0.59 | 0.9 | 0.69 | 0.74 |
| 1160001 | 40.78 | 57.81 | −2.4 | 0.79 | 0.95 | 0.82 | 0.87 |
| 1262000 | 57.52 | 84.94 | −6.1 | 0.38 | 0.87 | 0.61 | 0.66 |
| 1360000 | 43.58 | 62.85 | −7.9 | 0.71 | 0.93 | 0.75 | 0.84 |
| 1360001 | 47.42 | 70.1 | −17.3 | 0.63 | 0.91 | 0.72 | 0.76 |
| 1360002 | 70.9 | 107.9 | −2.2 | 0.11 | 0.84 | 0.59 | 0.49 |
| Year | Protected Areas | Pasture Areas | ||||||
|---|---|---|---|---|---|---|---|---|
| min | med | max | CV | min | med | max | CV | |
| 1983 | 1272 | 1609 | 2262 | 0.12 | 1264 | 1695 | 2285 | 0.11 |
| 1998 | 1325 | 1668 | 2474 | 0.11 | 1316 | 1714 | 2421 | 0.11 |
| 2010 | 1345 | 1778 | 2265 | 0.10 | 1327 | 1845 | 2282 | 0.08 |
| 2015 | 1418 | 1773 | 2046 | 0.07 | 1407 | 1729 | 2045 | 0.8 |
| Month | ZMK | SS (mm.month−1) | p-Value |
|---|---|---|---|
| January | −0.64 | −0.32 | 0.52 |
| February | 0.52 | 0.26 | 0.60 |
| March | 0.52 | 0.34 | 0.60 |
| April | 0 | 1 | 0.001 |
| May | 0.83 | 0.27 | 0.41 |
| June | 0.64 | 0.09 | 0.52 |
| July | −1.1 | −0.07 | 0.27 |
| August | 0.69 | 0.13 | 0.5 |
| September | −0.36 | −0.11 | 0.72 |
| October | 0.71 | 0.3 | 0.48 |
| November | −1.43 | −0.52 | 0.15 |
| December | −0.12 | −0.06 | 0.9 |
| Year | Dry Season | Rainy Season | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Protected Areas | Pasture Areas | Protected Areas | Pasture Areas | |||||||||||||
| min | med | max | CV | min | med | max | CV | min | med | max | CV | min | med | max | CV | |
| 1983 | 39 | 67 | 142 | 0.25 | 33 | 66 | 136 | 0.26 | 547 | 794 | 1230 | 0.15 | 572 | 840 | 1229 | 0.16 |
| 1988 | 58 | 114 | 198 | 0.35 | 26 | 67 | 151 | 0.33 | 585 | 918 | 1321 | 0.13 | 571 | 945 | 1223 | 0.11 |
| 1998 | 26 | 74 | 168 | 0.23 | 56 | 122 | 193 | 0.18 | 530 | 740 | 1020 | 0.12 | 502 | 749 | 1173 | 0.13 |
| 2010 | 45 | 100 | 162 | 0.25 | 42 | 98 | 154 | 0.18 | 689 | 881 | 1255 | 0.13 | 669 | 824 | 1078 | 0.14 |
| 2012 | 50 | 96 | 184 | 0.21 | 54 | 100 | 181 | 0.15 | 580 | 883 | 1172 | 0.16 | 554 | 931 | 1155 | 0.11 |
| 2015 | 56 | 113 | 202 | 0.22 | 50 | 113 | 208 | 0.21 | 521 | 870 | 1050 | 0.16 | 523 | 824 | 1078 | 0.18 |
| 2020 | 40 | 132 | 281 | 0.35 | 39 | 128 | 237 | 0.37 | 630 | 790 | 1030 | 0.08 | 591 | 797 | 1030 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreira, R.M.; dos Santos, B.C.; Sanches, R.G.; Bourscheidt, V.; de Sales, F.; Sieber, S.; de Souza, P.H. Precipitation Variability for Protected Areas of Primary Forest and Pastureland in Southwestern Amazônia. Climate 2023, 11, 27. https://doi.org/10.3390/cli11020027
Moreira RM, dos Santos BC, Sanches RG, Bourscheidt V, de Sales F, Sieber S, de Souza PH. Precipitation Variability for Protected Areas of Primary Forest and Pastureland in Southwestern Amazônia. Climate. 2023; 11(2):27. https://doi.org/10.3390/cli11020027
Chicago/Turabian StyleMoreira, Rodrigo Martins, Bruno César dos Santos, Rafael Grecco Sanches, Vandoir Bourscheidt, Fernando de Sales, Stefan Sieber, and Paulo Henrique de Souza. 2023. "Precipitation Variability for Protected Areas of Primary Forest and Pastureland in Southwestern Amazônia" Climate 11, no. 2: 27. https://doi.org/10.3390/cli11020027
APA StyleMoreira, R. M., dos Santos, B. C., Sanches, R. G., Bourscheidt, V., de Sales, F., Sieber, S., & de Souza, P. H. (2023). Precipitation Variability for Protected Areas of Primary Forest and Pastureland in Southwestern Amazônia. Climate, 11(2), 27. https://doi.org/10.3390/cli11020027








