City-Wise Assessment of Suitable CMIP6 GCM in Simulating Different Urban Meteorological Variables over Major Cities in Indonesia

Abstract

This study evaluates the performance of 6 global climate models (GCMs) from the Coupled Model Intercomparison Project Phase 6 (CMIP6) for simulating temperature, precipitation, wind speed, and relative humidity over 29 cities in Indonesia. Modern-Era Retrospective Analysis for Research Applications (MERRA-2) was considered as reference data to assess the city-wise performance of surface air temperature, precipitation, wind speed, and relative humidity simulated by the CMIP6 GCMs during 1980–2014. Six statistical measures were computed in this process (mean annual, seasonal amplitude, mean annual bias, root mean square error, correlation coefficient, and standard deviation). For 29 cities, the mean annual values of surface air temperature, precipitation, wind speed, and relative humidity obtained from the GCMs range between 290 to 302 K, 100 cm to 450 cm, 1 to 6 m/s, and 70 to 94%, respectively. The correlation coefficient between the GCMs and the surface air temperature (precipitation) reanalysis dataset ranges from 0.3 to 0.85 (−0.14 to 0.77). The correlation coefficient for wind speed (relative humidity) varies from 0.2 to 0.6 and is positive in some cases (0.2 to 0.8). Subsequently, the relative error that combines the statistical measurement results was calculated for each city and meteorological variable. Results show that for surface air temperature and precipitation, the performance of TaiESM was outstanding over the 10 or more cities. In contrast, for wind speed and relative humidity, NOR-MM and MPI-HR were the best over 7 and 19 cities, respectively. For all the meteorological variables, the performance of AWI was found to be worst over all the cities. The outcomes of this study are essential for climate-resilience planning and GCM selection while performing downscaling experiments. It will also be useful for producing updated national climate change projections for each city in Indonesia and providing new insights into the climate system.

1. Introduction

Rising global temperature trends are causing detrimental effects, such as desertification, droughts, floods, extreme heat (precipitation) events, rising sea levels, and extinction of natural habitats, disrupting the balance of ecosystems [1]. The extent of climate change in the upcoming decades will mainly rely on the emissions of greenhouse gases (GHGs). Significant reductions in GHGs are possible ways to keep annual mean surface air temperature growth below 2 °C. However, it has been reported that compared with the pre-industrial era, without significant reductions in GHG emission, the growth in mean global surface air temperature could reach up to 5 °C. Therefore, it is necessary to evaluate how these alterations in future climate will affect society’s resilience and to deliver helpful information for enhancing climate-related risk management. Such global climatic alterations vary according to regions and seasons [2]. Today, many regions of the globe face extreme heat events such as heat islands, droughts, air pollution, more frequent and intense heat waves, and other extreme weather events [3,4,5,6,7]. In the future, these climatic events are expected to significantly impact regional climates, particularly in areas that are already vulnerable to such events.

The most convenient way to examine the alterations in future climate is to utilize the global circulation/climate models (GCMs). GCMs are complex mathematical models of the four key climate system components (atmosphere, land surface, ocean, and sea ice) and their interfaces. GCMs can imitate the past and project the future climatic conditions of the globe by considering several potential emission scenarios [8,9]. The performance of GCMs varies concerning different attributes such as topography, region location, season, etc. To engender the climate model experiments, which are under the coupled model intercomparison project (CMIP), several GCM outputs were collected by the World Climate Research Program (WCRP). Among those modeling experiments, CMIP phase 6 (CMIP6) is the most updated iteration officially launched in 2017 [10].

Compared with CMIP5, the models embedded in the CMIP6 project have higher spatial resolution and some significant enhancement in the physical process [11]. For the researchers, these improvements in CMIP6 opened new doors to assess the climate systems and carry out future projections. The most idealistic approach for projecting future climatic trends is to perform the statistical or dynamical downscaling of the GCMs by coupling the future trend of urbanization and other physical parameters such as vegetation, topography, etc. The CMIP6 provides datasets containing more than 30 GCMs developed by various organizations. Those GCMs datasets included in the CMIP6 project are available for historical and future periods. However, projecting the future tendency of different climatic variables by regionalizing each GCM is a tedious and computationally costly process. Therefore, before regionalizing any GCM, it is necessary to evaluate the performance of GCMs and check their suitability concerning other physical attributes. Subsequently, the physical parameterization schemes and development strategies of each GCM differ, thereby inducing significant perturbations in the outcomes of the climatic variables over the identical region. It makes local scale evaluation of GCMs more crucial.

Previous studies have already examined the performance of CMIP6 GCMs for various climatic variables on a regional scale. Kamworapan et al. [10] evaluated the 13 CMIP6 GCMs for historical simulations of surface air temperature over Thailand and found that CNRM-CM6-1 (MIROC6) was the best (worst) performing model, followed by the CNRM-ESM-2-1 (CanESM5). Andrea et al. [12] assessed the CMIP6 models’ performance in simulating the present-day climate in Brazil to identify the best subset of models and reduce the uncertainties. The outcomes carried out by Andera et al. [12] revealed that the model with the highest ability to simulate monthly rainfall over five Brazilian regions was HadGEM3-GC31-MM, while for monthly temperatures, CMCC-ESM2 was outstanding.

Over a Mediterranean region, after examining the 22 CMIP6 GCMs on a monthly scale, the 8 INM-CM5–0 model was the most successful model for simulating surface air temperature over the region [13]. Lu et al. [14] evaluated future spatiotemporal alterations in surface air temperature over China and noted that the multi-model ensemble mean (MME) underestimates surface air temperature across China.

Additional research by Zhu & Yang [15] stated that most CMIP6 GCMs reasonably simulated the surface air temperature and the spatial precipitation pattern over the Tibetan Plateau, with a correlation coefficient higher than 0.70. In 2021, Shiru & Chung [16] across Nigeria used 13 CMIP6-GCMs to analyze the performance of each GCM in terms of maximum and minimum surface air temperature. Results of this study showed that among these 13 GCMs, CP. IPSL-CM6A-LR was the best suitable model, with a standard deviation (correlation coefficient) of <0.3 °C (>0.8).

Recently, Kamruzzaman et al. [11] assessed the 15 CMIP GCMs to reconstruct the climatological precipitation over Bangladesh. This study calculated eight statistical metrics compared to the reference dataset, and Shannon’s entropy decision analysis was used to finalize the GCMs. Their study noted that among 15 CMIP GCMs, MPI-ESM1-2-LR was the most effective GCM for replicating the precipitation data over Bangladesh. Apart from these studies, numerous other studies have also evaluated the performance of CMIP6 GCMs in simulating various climatic variables over different regions of the world. For instance, the United States [17], Southeast Asia [18], Western North Pacific, and East Asia [19].

Most of the above-cited research adopted the traditional approach that compares the area-averaged values of the climatic variable with the reanalysis dataset. However, in urban climatic studies, precise representation of the climatic variables, especially over the cities, is a primary requirement since urban areas have their own physical and climatic characteristics [20].

For instance, soil type, surface roughness, temperature, and energy balance differ greatly from their surrounding region. These attributes are very sensitive to the model’s various physical and parameterization schemes. However, in the case of the traditional approach, the effect of those characteristics fades due to area averaging. Therefore, the evaluation of the city-wise performance of CMIP6 GCMs is an important step in understanding the impacts of climate change on urban areas. Subsequently, cities are particularly vulnerable to the impacts of climate change, such as heatwaves, flooding, and extreme weather events, which can significantly impact human health, infrastructure, and ecosystems [21,22]. Therefore, it is important to evaluate climate models at the city scale to assess their ability to capture these local impacts and inform climate adaptation and mitigation strategies for urban areas.

Additionally, city-wise evaluation of climate models can help identify areas where further modeling improvements are needed to understand better and predict regional climate variability and change. Decision-makers can use this information to develop effective policies and interventions to address climate risks and build city resilience. Therefore, this study primarily aims to identify the suitable GCM over 29 major cities in Indonesia for a target year’s future typical meteorological year (FTMY) generation.

The present research has been divided into five sections. The first section of the research paper signifies the previous literature, research gaps, and the main motive of the present study. Section 2 contains the details of the study area. Section 3 describes the data and methodology utilized to accomplish the main motive of the study, whereas Section 4 comprises the result and discussion. Section 5 summarizes the essential findings and conclusions of the study.

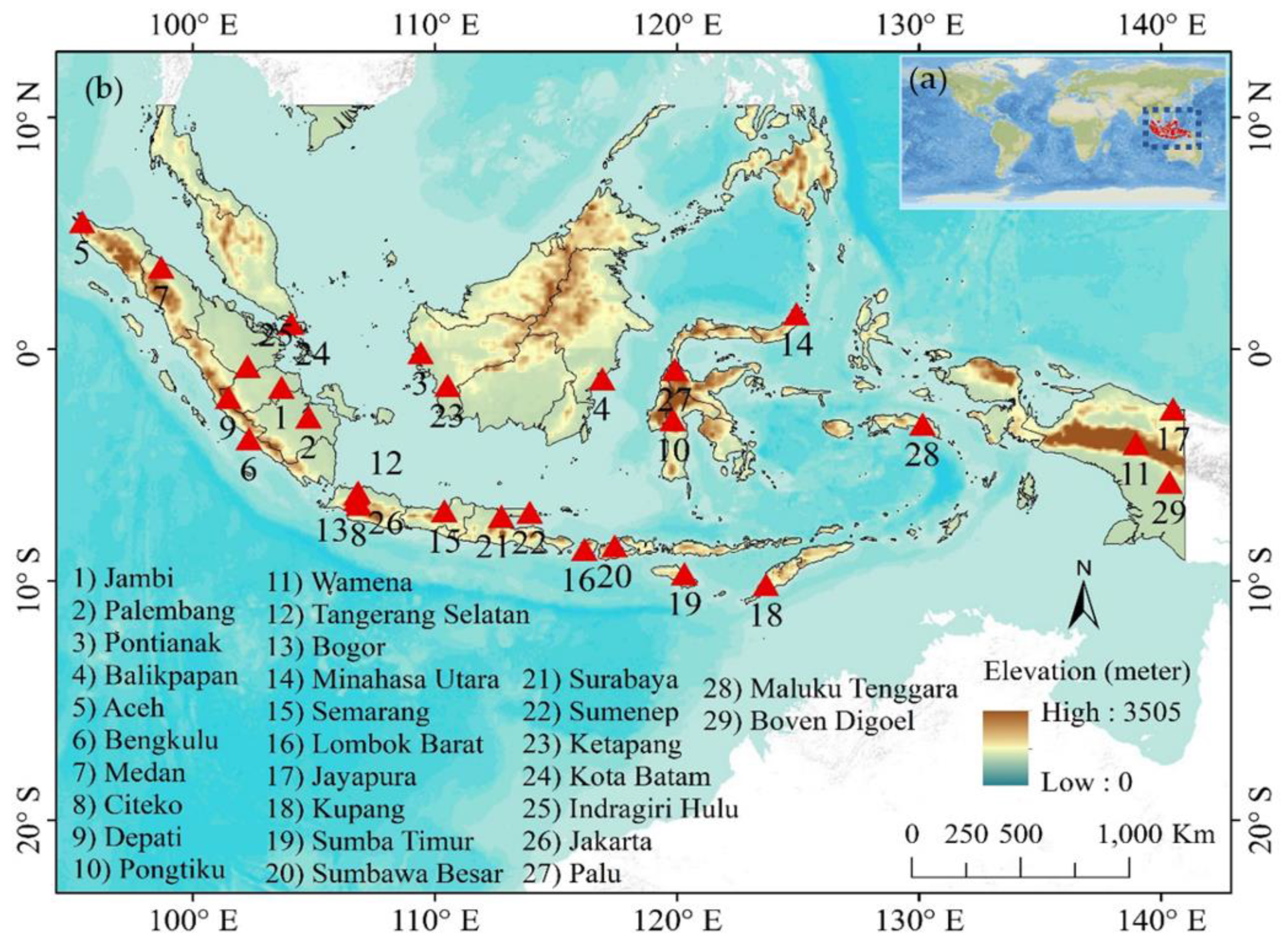
2. Study Area

The present studies have been carried out over 29 different cities in Indonesia (Figure 1). The climate of Indonesia is hot-humid tropical, and the surface air temperature over Indonesia remains almost constant throughout the year. The total area of Indonesia spans between the latitudes 11° S and 6° N and longitudes 95° E and 141° E. It is the world’s largest archipelagic state, extending approximately 5120 km from east to west and 1760 km from north to south.

The elevation of the country varies from 0 m to 3505 m. Being a developing country, it experiences the rapid process of urbanization. Today, around 50% of the Indonesian population lives in cities and towns, and it is expected that by 2045 this percentage will increase by 20% [23]. This forthcoming trend of urbanization can induce significant growth in building energy consumption for cooling, thereby causing the growth of GHG emissions and affecting the region’s climate.

In the world, Indonesia stands in the top three countries regarding climate risk, with exposure to all types of flooding and extreme heat [24]. By 2050, the temperature in Indonesia is projected to increase from 0.8 °C to 1.4 °C. Moreover, projections also show significant growth in annual precipitation by 2050 [25]. However, these projections of temperature rise and precipitation for Indonesia are impeded by the lack of fine-resolution modeling at spatial and temporal scales. Thus, high-resolution, and accurate information about these projections is important to minimize their adverse impacts on society.

3. Data and Method

GCMs are useful for acquiring future and precise information about the climate. However, as discussed in the previous section, each GCM varies concerning the region and other physical conditions. Thus, city-wise evaluation has been performed in this study to identify the most suitable CMIP6 model. It will help to obtain precise information about the forthcoming alterations in the various climatic variables such as surface air temperature, wind speed, precipitation, and relative humidity. A detailed list of selected cities and their respective locations are shown in Figure 1. The general flow of the methodology used is represented in Figure 2. An evaluation has been conducted for identifying an appropriate Global Climate Model (GCM) by comparing various statistical measures between the reference dataset and CMIP GCMs. The bilinear interpolation method was utilized to make the uniform spatial resolution of all the reference and CMIP6 GCMs datasets onto a 1° × 1° grid. Afterward, using retrospective datasets (1980–2014) obtained from the reanalysis product, CMIP6 GCMs were evaluated over the 29 major cities in Indonesia.

3.1. Selection of CMIP6 GCMs

CMIP6 dataset contains several GCMs representing the various climatic variables from the past to the future by considering the various sets of experiments. Therefore, to shortlist the models, the following three criteria are mainly considered: (a) The GCM should contain the historical dataset of four meteorological variables (surface air temperature, precipitation, relative humidity, and wind speed) for the period of 1980–2014, (b) the same model should encompass the aforesaid meteorological dataset for the period of 2015–2100 at six hourly intervals for statistical downscaling, and (c) the model should have a forced dataset from the first realization (r1i1p1f1).

After applying these criteria, six shortlisted CMIP6 GCMs were considered for further evaluation. The details of each shortlisted CMIP6 GCM are given in

Table 1. List of shortlisted six GCMs.

No	GCM ID	Acronym	Spatial Resolution	Period	Institution
1	NorESM2-MM	NOR-MM	1° × 1°	Jan. 1980–Dec. 2014	Norwegian-Climate Centre/Norway
2	NorESM2-LM	NOR-LM	2.5° × 2.5°	Jan. 1980–Dec. 2014	Norwegian-Climate Centre/Norway
3	MPIESM 1-2-HR	MPI-HR	1° × 1°	Jan. 1980–Dec. 2014	Max Planck Institute of Meteorology/Germany
4	MPI-ESM 1-2-LR	MPI-LR	2.5° × 2.5°	Jan. 1980–Dec. 2014	Max Planck Institute of Meteorology/Germany
5	RCEC. TaiESM1	TaiESM	1° × 1°	Jan. 1980–Dec. 2014	Research Centre for Environmental Changes/Taiwan, China
6.	AWI-CM-1-1-MR	AWI	1° × 1°	Jan. 1980–Dec. 2014	The Alfred Wegener Institute/ Germany

. Subsequently, a multi-model ensemble dataset (6-Model Ensemble) was calculated by Equation (1).

$$(6-\mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{E}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{m}\mathrm{b}\mathrm{l}\mathrm{e})=\frac{1}{\mathrm{n}}\sum \mathrm{G}\mathrm{C}\mathrm{M}\mathrm{x}$$

(1)

where, $\mathrm{n}$ = number of shortlisted GCMs and $\mathrm{G}\mathrm{C}\mathrm{M}\mathrm{x}$ = different global climate models obtained from the CMIP6.

Several researchers reported that multi-model ensembles created from multiple CMIP6 GCMs could reduce bias and uncertainties in simulated climatic datasets [26,27,28]. To evaluate the performance of each shortlisted GCM, the monthly mean of surface air temperature, precipitation, wind speed, and relative humidity of each GCM were extracted and compared with the reference reanalysis dataset for the 29 target cities.

3.2. Reanalysis Dataset

Climate reanalysis datasets are mainly developed by integrating ground/satellite observations and model data. It represents the estimates of atmospheric variables such as air temperature, precipitation, wind speed, etc. On a spatial scale, these estimates of various climatic variables are produced for each global location. Reanalysis datasets can extend to several decades on a temporal scale from the present. Thus, reanalysis products are beneficial, especially when the ground dataset for a particular space/time is unavailable.

Therefore, as reference data, this study uses the reanalysis data from the Modern-Era Retrospective Analysis for Research Applications (MERRA), Version 2 [29]. The spatial resolution of the MERRA2 dataset is 0.50° × 0.65°. Further, it was regridded to 1° × 1° to match the spatial resolution of GCMs. Subsequently, using different statistical metrics, MERRA2 was used to evaluate and identify the suitable CMIP6 GCM over the 29 major cities of Indonesia. From Section 3.3, the MERRA2 dataset has been mentioned as a reference dataset.

3.3. The Measure of the Statistical Performance

The meteorological dataset of surface air temperature, precipitation, wind speed, and relative humidity obtained from the six CMIP6 GCMs and MERRA2 were compared with each other over the 29 cities. Generally, statistical measures examine and quantify the differences between model simulations and reference datasets. Each statistical measure has a different ability to reflect the robustness of the model’s performance. During this study, six key statistical measures, (a) correlation coefficient, (b) standard deviation, (c) mean annual, (d) mean annual bias, (e) seasonal amplitude, and (f) root mean square error, have been used to evaluate the performance of six CMIP6 GCMs for surface air temperature, precipitation, wind speed, and relative humidity. The equations used for computing the statistical measures are given in

Table 2. Formulas for different statistical measures.

Statistical Measure	Formula
Correlation Coefficient	$\frac{\sum ({\mathrm{O}}_{\mathrm{i}}-\stackrel{-}{\mathrm{O}})\left(\mathrm{M}-\stackrel{-}{\mathrm{M}}\right)}{\sqrt{\mathsf{\Sigma }{\left(\mathrm{O}\mathrm{i}-\stackrel{-}{\mathrm{O}}\right)}^2}\sqrt{\mathsf{\Sigma }{\left({\mathrm{M}}_{\mathrm{i}}-\stackrel{-}{\mathrm{M}}\right)}^2}}$
Standard Deviation	$\sqrt{\frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left(\mathrm{M}\mathrm{i}-\stackrel{-}{\mathrm{u}}\right)}^2}{\mathrm{n}}}$
Mean Annual	$\frac{{\sum }_{\mathrm{y}=1}^{\mathrm{N}}\mathrm{T}\mathrm{y}}{\mathrm{N}}$
Mean Bias Error	$\frac{1}{\mathrm{n}}\sum \left({\mathrm{M}}_{\mathrm{i}}\right)-\left({\mathrm{O}}_{\mathrm{i}}\right)$
Mean Seasonal Cycle Amplitude	$\left({\mathrm{M}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)-\left({\mathrm{M}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\right)$
Root Mean Square Error	$\frac{\sqrt{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{M}}_{\mathrm{i}}-{\mathrm{O}}_{\mathrm{i}}\right)}^2}}{\mathrm{n}}$

Note: M_i = Model estimated value, O_i = Observed values, n = Total no. of values in dataset, $\stackrel{-}{\mathrm{u}}$ = The mean of the population (observed or Model), M_max = mean warmest/wettest/windiest/most humid month of model for years 1980–2014, M_min = mean coldest/driest/least windy/least humid month of model for years 1980–2014, T_y = Annual surface air temperature/precipitation/relative humidity/wind speed of the year y, N = Total no. of years.

.

3.4. Ranking of the GCM

The unique advantages and disadvantages of the GCMs are illustrated using a variety of statistical indicators. Statistical measurements raise additional concerns for choosing a GCMs with higher credibility for the following reasons: (i) Some statistical metrics may be more significant than others for a specific application, and the overall rankings may differ on which set of statistical metrics is selected. (ii) There may be redundancy in the statistical metrics, given that not all are physically or statistically independent. Therefore, in this study, all the GCMs were ranked by integrating the above statistical measures to overcome those concerns. For the ranking of the GCMs, we have incorporated all the statistical metrics and assigned equal weight to each metric.

For a given model i and metric j, we first defined an error ${\mathrm{E}}_{\mathrm{i},\mathrm{j}}$ as

$${\mathrm{E}}_{\mathrm{i},\mathrm{j}}=\left|{\mathrm{X}}_{\mathrm{o}\mathrm{b}\mathrm{s},\mathrm{j}-}{\mathrm{X}}_{\mathrm{i},\mathrm{j}}\right|$$

(2)

where X_obs and X_i are the observed and simulated ensemble mean metrics, respectively. Application of Equation (2) included correlations (where X_obs necessarily equaled 1). Furthermore, we defined a relative error $E_{\mathrm{i},j}^{\mathrm{*}}$ as

$$E_{\mathrm{i},j}^{\mathrm{*}}=\frac{{\mathrm{E}}_{\mathrm{i},\mathrm{j}}-\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathrm{E}}_{\mathrm{i},\mathrm{j}}\right)}{\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathrm{E}}_{\mathrm{i},\mathrm{j}}\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left({\mathrm{E}}_{\mathrm{i},\mathrm{j}}\right)}$$

(3)

and then summed the relative error across all m metrics

$$E_{\mathrm{i},tot}^{\mathrm{*}}=\sum _{j=1}^m{E}_{\mathrm{i},j}^{\mathrm{*}}$$

(4)

to get the total relative error $E_{\mathrm{i},tot}^{\mathrm{*}}$ per model. Ordering the models by their respective total relative error determined the ranking. The values obtained for $E_{\mathrm{i},tot}^{\mathrm{*}}$ are unitless. Lower values of the $E_{\mathrm{i},tot}^{\mathrm{*}}$ represents the higher suitability of the GCMs, whereas higher values indicate the worse suitability of the GCMs.

4. Results and Discussion

4.1. Surface Air Temperature

The monthly mean surface air temperature dataset obtained from the six GCMs, 6-Model Ensemble, and reference datasets were used to calculate the mean annual surface air temperature of 29 major cities in Indonesia. Figure 3a depicts the city-wise annual surface air temperature for reference reanalysis data, 6-Model Ensemble, and six individual GCMs. The mean annual values of surface air temperature obtained from the reference and GCMs range between 290 to 302 K. Out of 29 cities, the mean annual surface air temperature of 20 cities varies from 292 to 299 K, whereas the mean annual surface air temperature of the nine cities lies between 300 to 302 K. As per reference datasets, among all the cities, the largest mean annual surface air temperature was observed over Sumenep City (301.85 K). The lowest mean annual surface air temperature was noted over Wamena City (292.35 K). The comparison of the mean annual surface air temperature in Sumenep City using the reference dataset showed that the magnitude obtained from MPI-LR was almost identical with a difference of only −0.12 K. The 6-Model Ensemble simulations followed closely behind in similarity with the reference dataset.

In the case of Wamena City, in comparison with the reference dataset, the simulated mean annual surface air temperature obtained from MPI-HR was very similar, with a difference of 0.94 K followed by the TaiESM. However, for the Sumenep and Wamena cities, as compared to reference data, the mean annual surface air temperature obtained from the NOR-LM performed the worst. For the Sumenep and Wamena cities, the mean annual surface air temperature obtained from the NOR-LM was 0.52 and 5.2 K higher than the reference dataset.

Further, in comparison with the reference dataset, for each GCM and 6-Model Ensemble, Figure 3b presents the relative MBE in mean annual surface air temperature over the 29 major cities in Indonesia. The MBE of 6 GCMs and 6-Model Ensemble ranges from −3 to 5 K. In the case of the 6-Model Ensemble, out of 29 cities, 20 (9) cities showed warm (cold) biases. However, for other GCMs, depending upon their tendency, both warm and cold biases have been observed over the specific city. In the case of 6-Model Ensemble, AWI, MPI-HR, MPI-LR, and TaiESM, the coldest biases were observed over the Medan City, while for the NOR-MM and NOR-LM, it was observed over the Digoel and Palu cities, respectively. Wamena City represented the warmest bias according to the AWI, MPI-LR, NOR-LM, and 6-Model Ensemble simulations. However, other GCMs, viz. MPI-HR and TaiESM (NOR-MM) show the warmest bias over the Aceh (Depati) City. In terms of mean bias error, compared to other GCMs, the performance of the 6-Model Ensemble was very poor. Based on the performance of MBE, among the 29 cities, 6-Model Ensemble was suitable only for two cities, whereas TaiESM performed outstanding, which was suitable for the 11 cities. Generally, it has been observed that the GCMs from the same parent institute depict similar performances and tend to have similar biases in terms of magnitude, sign, etc.

Additional investigations represent a similar trend between biases derived from the NOR-MM and NOR-LM (r = 0.84). In contrast, a low agreement (r = 0.48) was noticed among MPI-HR and MPI-LR GCMs. For most cities, the standard deviation of the MBE derived from each GCM ranges between 0–0.7 K, which emphasizes the consistency of the GCMs. To quantify and evaluate the relationship between GCMs and reference data, the correlation coefficient was calculated over the 29 cities.

Figure 3c exhibits the correlation coefficient values of mean surface air temperature for the 29 cities. The correlation coefficient values for the target cities range from 0.3 to 0.85. However, in terms of the correlation coefficient, except for some cities, at least one GCM shows satisfactory performance (r > 0.5) for each city. Among all cities, the correlation coefficient of 52% of cities ranges from 0.5–0.6. At the same time, the correlation coefficient for the other 35% of cities lies between 0.61–0.85. In terms of the correlation coefficient, the worst performance (r < 0.4) of all the GCMs, including the 6-Model Ensemble, was found over the four cities (Digoel, Palu, Jayapura, and Balikpapan). As compared to GCMs, the performance of the 6-Model Ensemble was outstanding. Among the 29 cities, 6-Model Ensemble was suitable for 20 cities, whereas AWI, MPI-HR, and TaiESM were suitable for two cities each, and MPI-LR performed well only for one city. Out of all GCMs, the performance of the NOR-LM model was the worst, which was not suitable for a single city.

Figure 3d demonstrates the values of RMSE over each city computed by comparing each GCM with reference data. Figure 3d depicts that the RMSE values of all GCMs range from 0.4 to 5.4 K. Over most cities, RMSE values derived from all the cities lie between 0.4 to 3.3 K. However, for some cities like Wamena and Depati, RMSE values vary from 1.1 to 5.4 K. Among the target cities, for 13 cities, the 6-Model Ensemble was found to be suitable, followed by the TaiESM, which was suitable over the nine cities. Moreover, AWI, MPI-HR, MPI-LR, NOR-MM, and NORLR were best suited to the two cities.

Figure 3e depicts the mean seasonal cycle amplitude calculated from all the GCMs over the 29 cities. Seasonal amplitude calculated from all the GCMs, including 6-Model Ensemble, shows alterations varying from 1.97 to 8.67 K. Compared to the reference dataset, seasonal amplitude calculated by the other GCMs is underestimated for most of the cities. The trend of mean seasonal amplitude calculated from the reference data has a similar tendency to those derived from the MPI-HR, MPI-LR, NOR-MM, NorLR, and TaiESM. The correlation coefficient between seasonal amplitude computed from the reference dataset and MPI-LR, NOR-MM, NOR-LM, and TaiESM was larger than 0.5. However, the correlation coefficient between the mean seasonal amplitude calculated from the reference dataset and 6-Model Ensemble (AWI) was very low, i.e., −0.12 (0.16).

Compared to the reference dataset, the GCMs bias in seasonal amplitude ranges from −3.42 to 2.73 K. Differences in mean seasonal amplitude derived from the reference and GCMs reveal that, among all the GCMs, the performance of NOR-LM and NOR-MM was outstanding. However, bias in seasonal amplitude also suggests that AWI and 6-Model Ensemble’s performance was very poor for the mean seasonal amplitude.

Figure 3f shows the city-wise variations in the standard deviations of monthly mean surface air temperature computed from the reference and GCMs, including the 6-Model Ensemble datasets. The standard deviation calculated from all the GCMs, 6-Model Ensemble, and reference datasets ranges from 0.26 to 1.95 K. However, the standard deviation value for most cities is restricted below 1 K. Compared to the reference dataset, except MPI-LR and AWI, all other GCMs and 6-Model Ensemble datasets show a similar trend for each city. In all GCMs, the maximum standard deviation value has been observed over Kupang City, whereas the minimum standard deviation values were noted over Minahasa Utara City. Subsequently, during this analysis, it has been noted that over all the cities, the difference between standard deviation derived from reference and GCMs, 6-Model Ensemble dataset is less than 0.

4.2. Precipitation

Figure 4a illustrates the city-wise mean annual precipitation obtained from the reference data, 6-Model Ensemble, and six individual GCMs. The mean annual precipitation from all the sources ranges between 1230 to 3008 mm. Reference data depicts that, among 29 cities mean annual precipitation of 17 cities is more than 2000 mm, whereas, for the remaining 12 cities, it varies from 1230 to 1994 mm. According to the reference dataset, the highest mean annual precipitation (3008 mm/year) was observed over Balikpapan City.

In contrast, the lowest amount of mean annual precipitation (1230 mm/year) was noted over Sumba City. As compared to the reference dataset, for the Balikpapan (Sumba) City, it has been observed that the magnitude of mean annual precipitation trends derived from the MPI-HR and TaiESM (MPI-HR) are quite similar with the reference dataset. In comparison with reference data, for mean annual precipitation NOR-MM (AWI) depicts the utmost difference of 738.55 mm/year (1883 mm/year) for Balikpapan (Sumba) City.

Relative MBE was also calculated over the 29 major cities for mean annual precipitation. MBE in mean annual precipitation derived from the 6 Model-Ensemble and GCMs ranges from −1000 to 2500 mm/year (Figure 4b). For all the cities (except Pongtiku), 6-Model Ensemble shows the cold biases varying from 96.4 to 1513.39 mm/year. In terms of MBE, for over 8 cities, MPI-HR performance was outstanding, while AWI and NOR-MM showed the worst performance, which was appropriate for 1 city each. Moreover, MPI-LR (TaiESM), NOR-LM, and 6-Model Ensemble had the lowest biases over 6, 5, and 2 cities, respectively.

A further correlation analysis was performed for the monthly mean precipitation values obtained from the GCMs, 6-Model Ensemble, and reference data from 1980–2014. Figure 4c illustrates the correlation coefficient values for all the cities. These values of the correlation coefficient vary from −0.14 to 0.77. Regarding the correlation coefficient, the performance of the 6-Model Ensemble is better than other GCMs. In the case of the 6-Model Ensemble, for 22 cities, the correlation coefficient is between 0.3 to 0.7, whereas for the remaining 7 cities, it varies from 0.07 to 0.28. All the GCMs, including 6-Model Ensemble, show the highest (lowest) correlation over Surabaya (Maluku) City.

Subsequently, RMSE was computed to understand the average difference between monthly mean precipitation values simulated by GCMs, 6-Model Ensemble, and actual reference data. Figure 4d represents that RMSE values calculated for mean monthly precipitation vary between 3 to 8 mm/day. As compared to GCMs, 6-Model Ensemble shows the lowest RMSE values over the 21 cities, followed by the TaiESM (MPI-HR) and AWI, which represent the minimum magnitude of RMSE over 3 and 2 cities, respectively.

Figure 4e depicts the mean seasonal cycle amplitude estimated from the mean monthly precipitation dataset obtained from the GCMs, 6-Model Ensemble, and reference dataset. The seasonal cycle amplitude obtained for precipitation ranges from 10 to 30 mm/day for all the cities. According to the reference dataset, the highest (lowest) seasonal amplitude of 30.95 (12.92) mm/day was noted over Boven-Digoel (Sumba) City. For the seasonal amplitude, the performance of NOR-MM was found to be best over 7 cities, followed by the MPI-HR (6 cities) and AWI (5 cities). However, in the case of seasonal cycle amplitude, the performance of NOR-LM was worst.

Figure 4f represents the city-wise variations in standard deviations. For all the cities, the standard deviation values span between 2 to 7 mm/day. According to the reference dataset, the highest standard deviation of 5.65 mm/day was observed over Boven Digoel City. In contrast, the lowest standard deviation of 2.33 mm/day was noted over Wamena City. The GCMs like TaiESM and 6-Model Ensemble well represent the trend of reference standard deviation obtained over each city.

4.3. Relative Humidity

The mean annual relative humidity obtained from different data sources is shown in Figure 5a. For all cities, the mean annual relative humidity derived from the GCMs, 6-Model Ensemble, and reference data varies from 70 to 92%. According to reference data, the highest mean annual relative humidity was observed over Wamena City (91.18%), whereas the lowest was noted over Sumenep City (71.86%). All the GCMs, including 6 Model-Ensemble, for mean annual relative humidity, depict a higher association with reference data (r > 0.7). In the case of Wamena City, in comparison with the reference dataset, the mean annual relative humidity derived from MPI-HR shows a very close value with a difference of 0.005%.

Figure 5b demonstrates the MBE in mean annual relative humidity over each city of Indonesia under the evaluation. The MBE of all GCMs, 6-Model Ensemble ranges from −21.58 to 7.69%. In terms of MBE, NOR-LM was found to be best over 9 cities, followed by the NOR-MM, which performed well over 8 cities. On the other hand, the simulations of MPI-LR and 6-Model Ensemble were suitable for 1 city each. Compared to reference data, the mean annual relative humidity obtained from all GCMs shows negative biases over most cities.

Subsequently, correlation analysis was carried out over each city to quantify the association between simulated and reference monthly mean relative humidity (Figure 5c). The values of the correlation coefficient vary from −0.22 to 0.84. Regarding correlation coefficient, 6-Model Ensemble was best over 19 cities, followed by MPI-HR, Nor-MM, and TaiESM, suitable over 2 cities each. For all the GCMs, including the 6-Model Ensemble, the highest correlation coefficient value was noted over Surabaya City.

RMSE was calculated between reference and GCMs, 6 Model Ensemble datasets for monthly mean relative humidity. Figure 5d depicts the variation of RMSE over the selected cities of Indonesia. It spans from 3.52 to 21.54%. All the GCMs and 6 Model Ensemble show the highest magnitude of RMSE over Wamena City. Concerning RMSE, the performance of 6 Model Ensemble was excellent in 9 cities. However, NOR-MM and TaiESM show their appropriateness over 6 cities each.

Figure 5e represents the mean seasonal cycle amplitude computed for the monthly mean relative humidity drawn from all the data sources. It diverges from 6 to 52.37%. The maximum seasonal cycle amplitude observed from all the GCMs, 6-Model Ensemble, and reference datasets were noted over the Boven Digoel City. Compared to reference data, for Boven Digoel City, the seasonal cycle amplitude derived from the MPI-HR depicts the minimum deviation of 2.6%. The city-wise trend of seasonal cycle amplitude retrieved from all the GCMs (except AWI and NOR-LM) is the same as the trend obtained from the reference data. Concerning the biases obtained in the seasonal cycle amplitude, NOR-LM was found suitable in 9 cities, while MPI-HR symbolized its appropriateness over 7 cities.

City-wise trends in the standard deviation of monthly mean relative humidity are shown in Figure 5f. It spans between 1.18 to 11.32%. As per the reference dataset, the highest standard deviation values were observed over Surabaya (11.32%), whereas the lowest was noted over Indragiri-Hulu City (1.82%). Compared to the reference standard deviation, the simulated standard deviation obtained from NOR-MM, MPI-HR, and NOR-LM were best over 6 cities.

4.4. Wind Speed

Figure 6a illustrates the variation in mean annual wind speed estimated from all the data sources. It fluctuates between 0.44 to 6.66 m/s. Corresponding to reference data, the highest (lowest) mean annual wind speed has been observed over Kupang City (4.46 m/s), which is well replicated in NOR-LM GCM with a discrepancy of fewer than 0.55 m/s. In contrast, the minimum mean annual wind speed was noted over the Boven Digoel City (0.44 m/s), which was well modeled in MPI-HR GCM with a discrepancy of 0.2 m/s. Across all the cities, for mean annual wind speed, the correlation coefficient values among the reference and all the GCMs, including 6-Model Ensemble, were larger than 0.6. It emphasizes that the trend of reference mean annual wind speed dataset is well captured in all the simulated datasets.

Moreover, corresponding to the reference dataset, Figure 6b represents the estimated values of MBE from all the GCMs and 6-Model Ensemble datasets. The MBE of 6 GCMs and 6-Model Ensemble diverges from −1.25 m/s to 4.98 m/s. Among all the GCMs, MPI-HR shows the lowest values of MBE, over half of the total cities. Around all the cities, positive biases have been observed for every GCM and 6-Model Ensemble dataset.

Figure 6c represents the correlation coefficient value calculated between reference and GCMs, 6-Model Ensemble datasets of monthly mean wind speed for all the cities. These values range from −0.38 to 0.72. Figure 6c shows that for 22 cities concerning the reference dataset, there is at least one GCM/6-Model Ensemble whose correlation coefficient value is larger than 0.5. Regarding the correlation coefficient, 6-Model Ensemble was found to be best in over 16 cities, followed by the MPI-HR, which was outstanding over 7 cities.

Figure 6d shows the city-wise disparity in the RMSE values of monthly mean wind speed obtained from the reference and GCMs, 6-Model Ensemble datasets. It differs from 0.26 to 5.22 m/s. Concerning RMSE values only, MPI-HR was found to be the best GCM over 14 cities, followed by TaiESM, which shows its pertinence over 5 cities.

Figure 6e depicts the variation in seasonal cycle amplitude of mean monthly wind speed data. As per reference data, the highest (lowest) seasonal cycle amplitude was observed over Sumbawa (Boven Digoel) City. Unlike the results of other parameters, the performance of AWI was outstanding over 5 cities, while 6-Model Ensemble performed worst, which was not suitable for a single city.

Standard deviation was calculated for the mean monthly wind speed derived from all the data sources to understand and quantify the deviations in the data from its mean. For all the cities, values of standard deviation range from 0.08 to 2.07 m/s. As per the reference dataset, the highest standard deviation was observed over Maluku City (2.074 m/s), while the lowest was noted over Boven Digoel City (0.21 m/s). All the GCMs replicate the city-wise standard deviation trend observed in the reference dataset.

4.5. Ranking of the GCMs

The statistical performance metrics were estimated for surface air temperature, precipitation, relative humidity, and wind speed for all the GCMs, including 6-Model Ensemble. Then after, the relative error was calculated to rank the integrated performance of each GCM and 6-Model Ensemble over 29 cities in Indonesia. Figure 7a–d represents the city-wise list of relative errors, which was further used to finalize the suitability of the GCM and 6-Model Ensemble for the previously mentioned four meteorological parameters. The values of relative error ranged between 0 to 5. Values closer to 0 indicate the higher suitability of the GCMs, whereas values closer to 5 signify the worst performance of the GCMs.

In the case of surface air temperature, Figure 7a depicts city-wise relative error determined for each GCM and 6-Model Ensemble. It reveals that compared to GCMs, the performance of the 6-Model Ensemble is superior to 10 cities, followed by the TaiESM, NOR-MM, NOR-LM, MPI-LR, and MPI-HR, which was suitable over 7, 6, 2, 3, and 1 city, respectively. In contrast, the performance of AWI was the worst one, which was not suitable for a single city. During this evaluation, the highest (lowest) relative error was noted for the AWI (TaiESM) over Jayapura (Sumba) City.

For precipitation, Figure 7b denotes the city-wise score of relative error. Figure 7b implies that TaiESM performs well over 14 cities for precipitation, followed by the 6-Model Ensemble, MPI-HR, and NOR-LM (Nor-MM), which were found to be suitable over 8, 4, and 2 (1) cities, respectively. However, the AWI and MPI-LR were noted as the worst performers for precipitation.

Regarding relative humidity, the statistical assessment of relative error signifies that NOR-LM, MPI-HR, MPI-LR, TaiESM, NOR-MM, and 6-Model Ensemble were shown their appropriateness over 7, 6, 5, 5, 3, and 2 cities of Indonesia, respectively. Nevertheless, the performance of AWI was restricted up to Jambi City (Figure 7c).

In the case of wind speed, MPI-HR was found to be suitable over 19 cities, followed by the NOR-LM and NOR-MM, indicating their suitability over 4 and 2 cities, respectively (Figure 7d). Besides this, all other GCMs showed their appropriateness over 1 city each.

This study found that most of the GCMs can reasonably capture the annual and monthly trends of different meteorological variables for different cities. The city-wise list of suitable GCMs is shown in Figure 8, similar information is given in tabular format (

Table A1. City-wise suitable GCM for different meteorological parameters.

Cities	Surface Air Temperature	Precipitation	Relative Humidity	Wind Speed
Jambi	6-Model Ensemble	TaiESM	AWI	MPI-HR
Palembang	6-Model Ensemble	MPI-HR	6-Model Ensemble	NOR-MM
Pontianak	MPI-LR	NOR-LM	6-Model Ensemble	MPI-HR
Balikpapan	TAIESM	6-Model Ensemble	MPI-LR	MPI-HR
Aceh	NOR-MM	MPI-HR	TaiESM	MPI-HR
Bengkulu	MPI-LR	TaiESM	NOR-MM	MPI-HR
Medan	NOR-LM	6-Model Ensemble	MPI-HR	NOR-MM
Citeko	6-Model Ensemble	TaiESM	NOR-LM	MPI-HR
Depati	MPI-HR	TaiESM	MPI-HR	MPI-HR
Pongtiku	NOR-MM	6-Model Ensemble	TaiESM	MPI-HR
Wamena	NOR-MM	MPI-HR	MPI-HR	AWI
Tangerang Selatan	6-Model Ensemble	TaiESM	NOR-LM	MPI-HR
Bogor	6-Model Ensemble	TaiESM	NOR-LM	MPI-HR
Minahasa Utara	MPI-LR	NOR-MM	NOR-MM	NOR-LM
Semarang	TaiESM	NOR-LM	TaiESM	MPI-HR
Lombok Barat	TaiESM	TaiESM	TaiESM	MPI-HR
Jayapura	NOR-MM	MPI-HR	NOR-MM	MPI-HR
Kupang	TaiESM	6-Model Ensemble	MPI-LR	NOR-LM
Sumba Timur	TaiESM	6-Model Ensemble	NOR-LM	MPI-HR
Sumbawa Besar	TaiESM	TaiESM	TaiESM	MPI-HR
Surabaya	TaiESM	6-Model Ensemble	MPI-HR	NOR-MM
Sumenep	6-Model Ensemble	TaiESM	MPI-HR	NOR-MM
Ketapang	6-Model Ensemble	TaiESM	NOR-LM	MPI-HR
Kota Batam	6-Model Ensemble	6-Model Ensemble	MPI-LR	6-Model Ensemble
Indragiri Hulu	6-Model Ensemble	TaiESM	MPI-LR	MPI-HR
Jakarta	6-Model Ensemble	TaiESM	NOR-LM	MPI-HR
Palu	NOR-LM	TaiESM	MPI-HR	MPI-LR
Maluku Tenggara	NOR-MM	TaiESM	NOR-LM	TaiESM
Boven Digoel	NOR-MM	6-Model Ensemble	MPI-LR	MPI-HR

) in Appendix A. Figure 8 depicts that different GCMs’ performance varies at the city level. These city-level variations in the performance of GCMs may vary due to a combination of factors related to spatial resolution, land surface characteristics, topography, regional climate patterns, model structure, and parameterization. Therefore, it is important to carefully evaluate the performance of different GCMs at the city level to identify which models are most suitable for use in specific locations.

Recently, several studies have been carried out to evaluate the performance of CMIP6 models in Indonesia and surrounding region [30,31]. Kurniadi et al. [32] evaluated the ability of 42 CMIP6 GCMs to simulate extreme precipitation over Indonesia. Overall, the multi-model ensemble mean of the CMIP6 model represents Indonesia’s climatology of both average and extreme rainfall, but performance varies across the individual model. Desmet & Ngo-Duc [33] assessed the performance of 28 CMIP6 models in simulating the climatic variables over the Southeast Asian region. Their study found that for the wind and rainfall simulations, the performance of EC-Earth3 and EC-Earth3-Veg was better, while temperature outputs were more reliable with CNRM-CM6. Pimonsree et al. [34] evaluated the performance of 27GCMs over southeast Asia to simulate the precipitation. Their study revealed that TaiESM is the most suitable model for simulating precipitation over the Southeast Asian region. Even though these studies shed essential light on the GCM’s general performance, the studies mentioned above fail to assess the performance of the GCMs locally.

In the case of Indonesia, it is crucial to realize that due to its varied topography, geology, and other physical aspects, the country’s climate varies significantly from region to region. Therefore, conducting more specialized assessments to evaluate the city-wise performance of CMIP6 models for various meteorological parameters in Indonesia is inevitable. This would entail gathering and examining meteorological data from various Indonesian towns or regions, then contrasting these observations with the results of the CMIP6 models for the same. City-specific evaluations of CMIP6 models would provide more localized and detailed insights into how climate change may impact individual urban areas, which are missing in several earlier studies [16,30,32].

5. Conclusions

This study evaluated the performance of six CMIP6 GCMs in simulating the monthly mean surface air temperature (Tas) over the 29 cities in Indonesia by comparing it with the MERRA2 dataset from 1980–2014. The evaluation of CMIP6 GCMs has been carried out based on six statistical measures. In the further part, city-wise statistical metrics of each GCM were normalized, and equal weights were assigned to calculate the relative error. Finally, based on the relative error, the city-wise performance of each GCM was assessed. The major findings of the study are as follows.

(i)

From 1980–2014, the mean annual surface air temperature varies from 290 K to 302 K for all the cities. The MBE calculated for mean annual surface temperature derived from 6 GCMs and 6-Model Ensemble ranges from −3 to 5 K. In the case of the 6-Model Ensemble, out of 29 cities, 20 (9) cities showed warm (cold) biases. The performance of each GCM alters concerning the city. Among all the GCMs, including 6-Model Ensemble, TaiESM performed best in 14 cities, followed by the 6-Model Ensemble, which performed well over 10 cities. For Indonesian cities, AWI was the worst performing GCM which was not found to be suitable over any of the cities. Except for a few cities, the performance of each GCM in terms of standard deviation and RMSE is very similar. For most cities, the difference between the seasonal amplitude calculated by each GCM, including 6-Model Ensemble, is less than 0.5 K. While in some cities like Jayapura and Sumbawa, this difference has been observed up to 1.5 K.

(ii)

Regarding precipitation, corresponding to mean annual precipitation, 6-Model Ensemble shows the cold biases across all the cities (except Pongtiku). These cold biases range from 96.4 to 1513.39 mm/year. Among all GCMs, for precipitation, the performance of TaiESM was outstanding in 14 cities.

(iii)

Compared to reference data for most cities, the mean annual relative humidity derived from all the GCMs indicates negative biases. In the case of relative humidity, the performance of NOR-LM was better over seven cities.

(iv)

Compared to reference data, very minimal divergence has been noted in the GCM/6-Model Ensemble derived for mean annual wind speed. For wind speed, MPI-HR performed outstandingly in 19 cities.

The outcomes of this study can help urban climate scientists and engineers, urban scientists interested in the Indonesian region choose the city-wise best suitable GCM to be downscaled to a finer spatial resolution for simulating the climate variables.