Artificial Neural Network (ANN)-Based Long-Term Streamflow Forecasting Models Using Climate Indices for Three Tributaries of Goulburn River, Australia
Abstract
1. Introduction
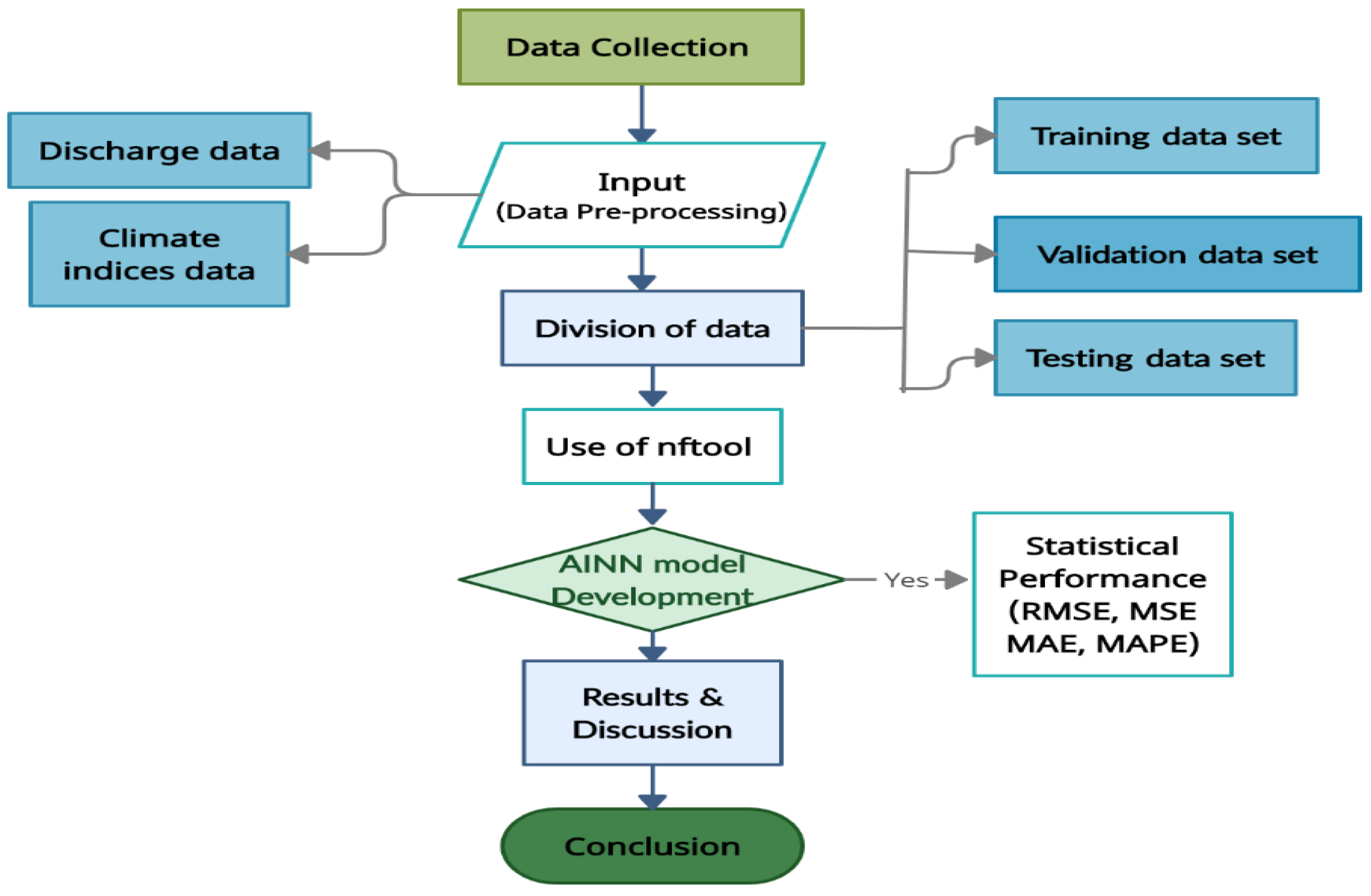
2. Materials and Methods
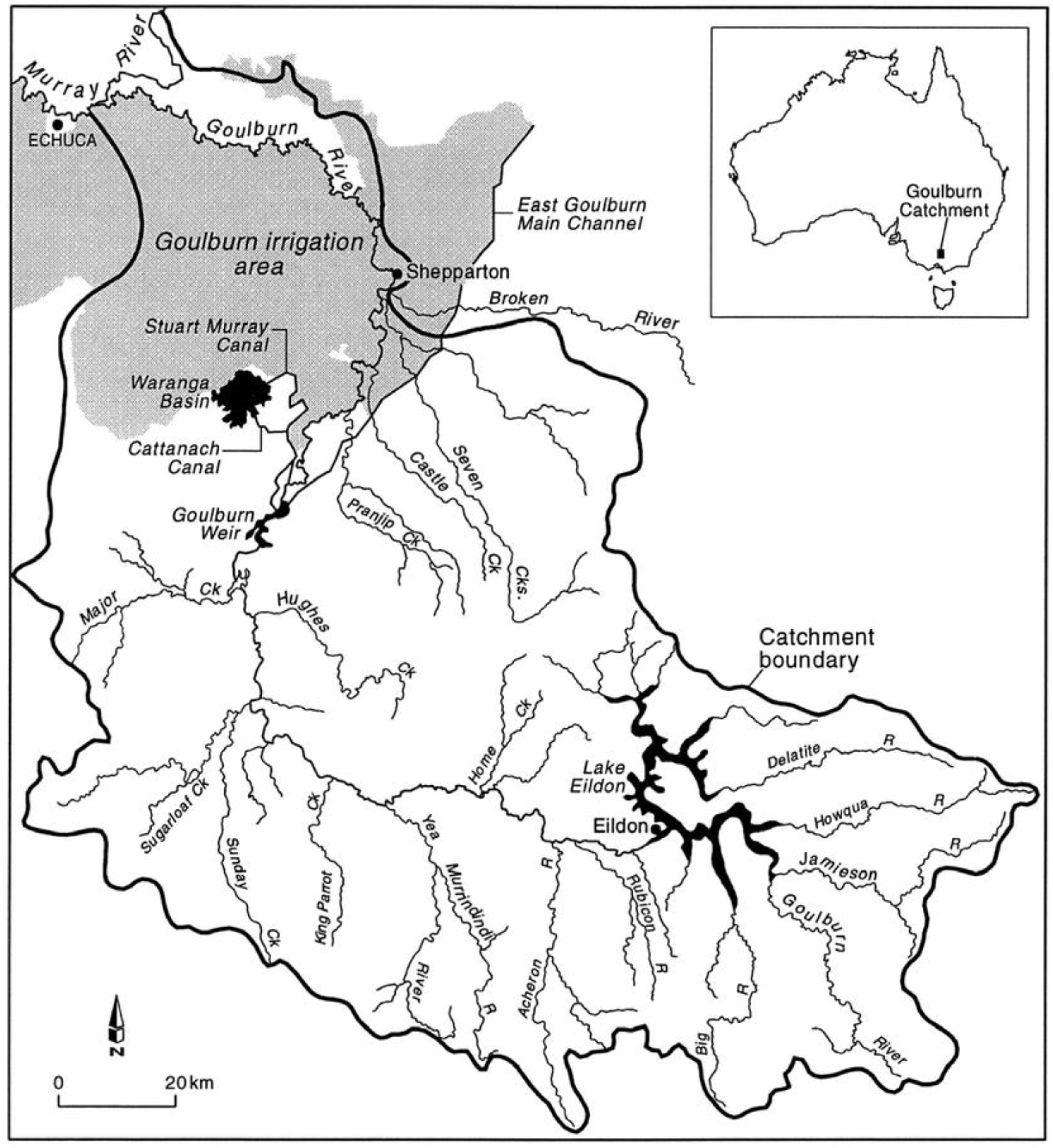
2.1. Study Area
2.2. Data Description
2.3. Artificial Neural Network
2.3.1. Input Selection
2.3.2. Artificial Neural Network Model Structure Development
2.3.3. Artificial Neural Network Model Performance
2.3.4. Statistical Accuracy of Developed Models
3. Results
3.1. Performance of Artificial Neural Network Developed Models
3.2. Statistical Error Assessment of ANN Models
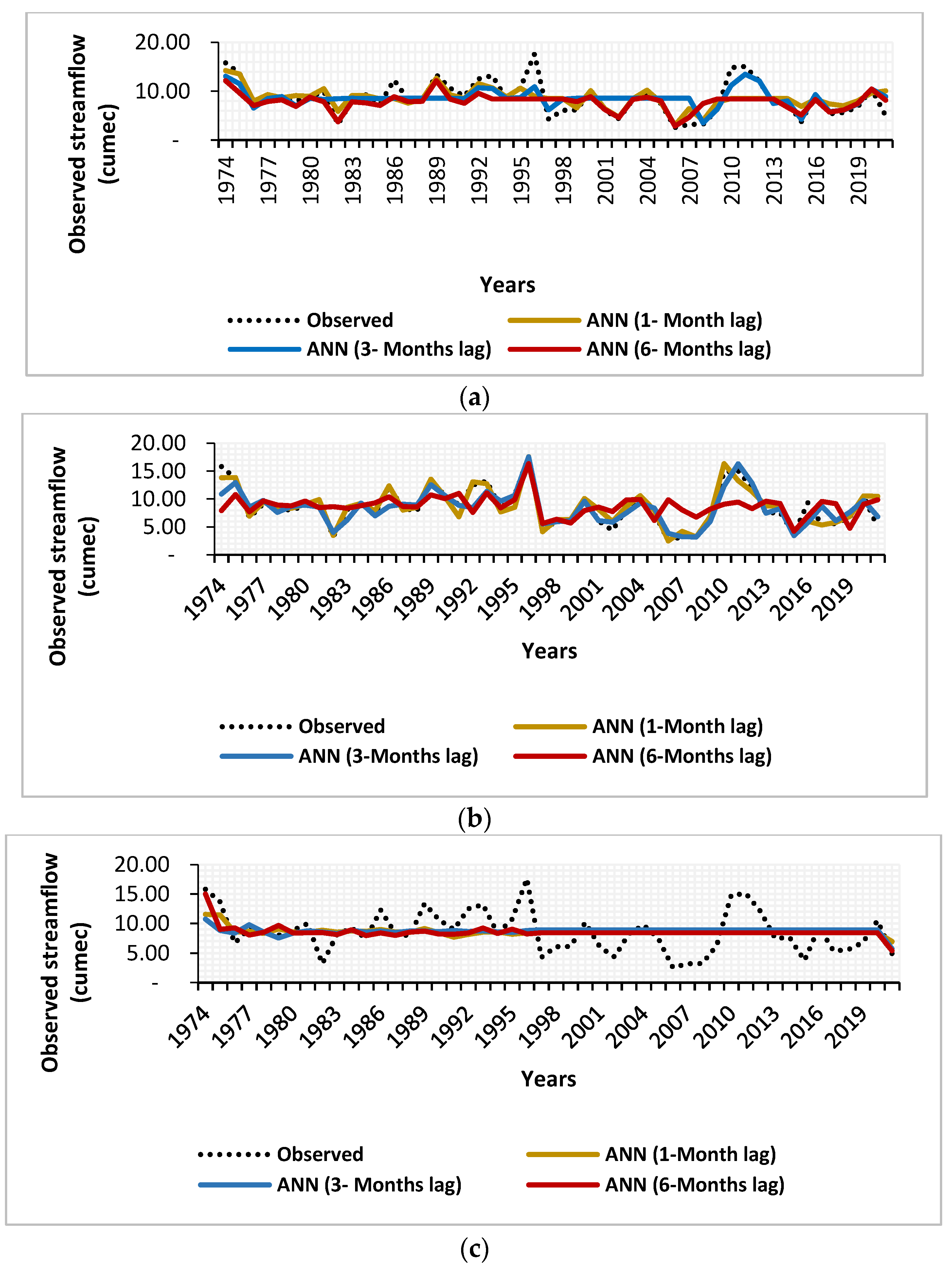
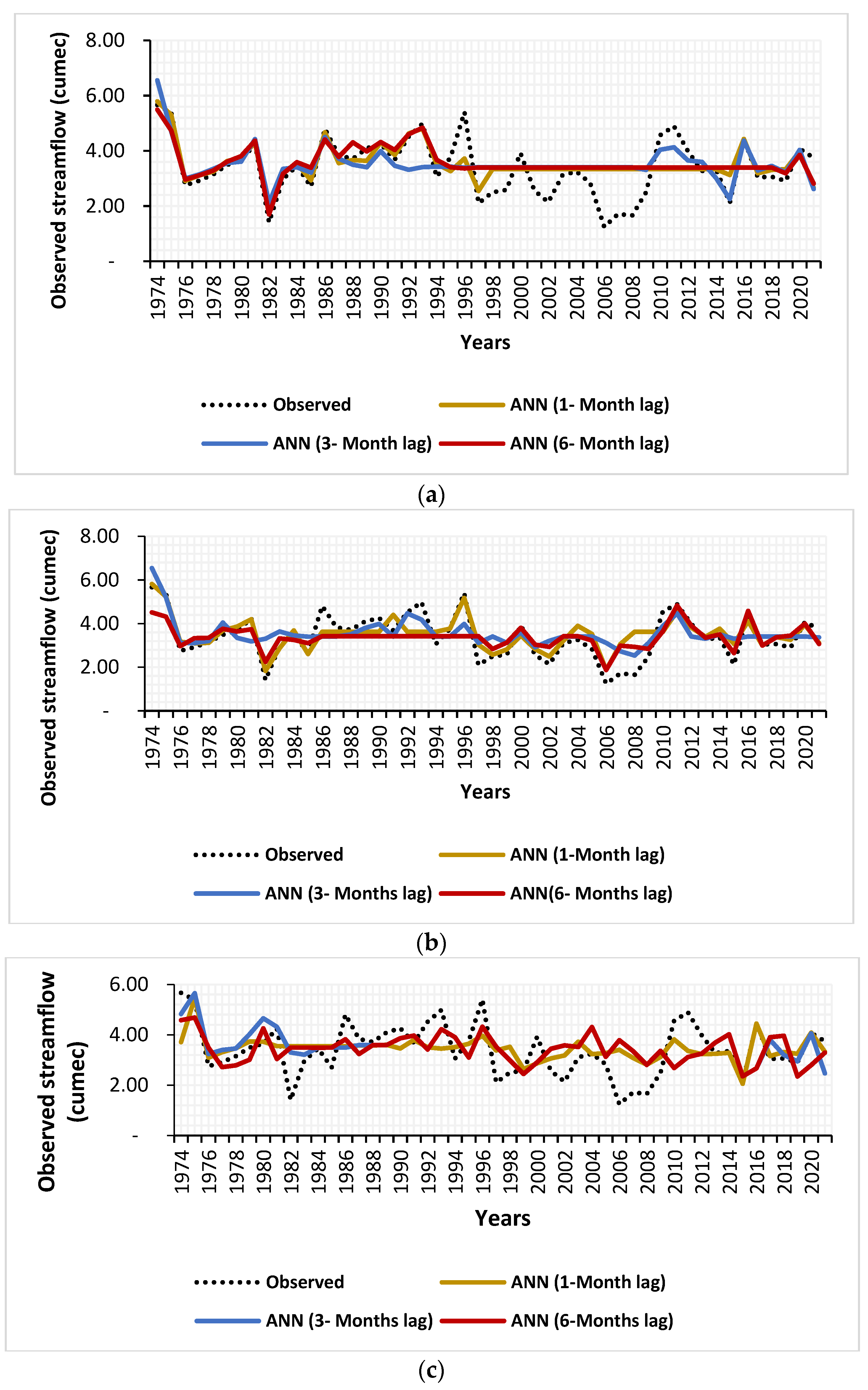
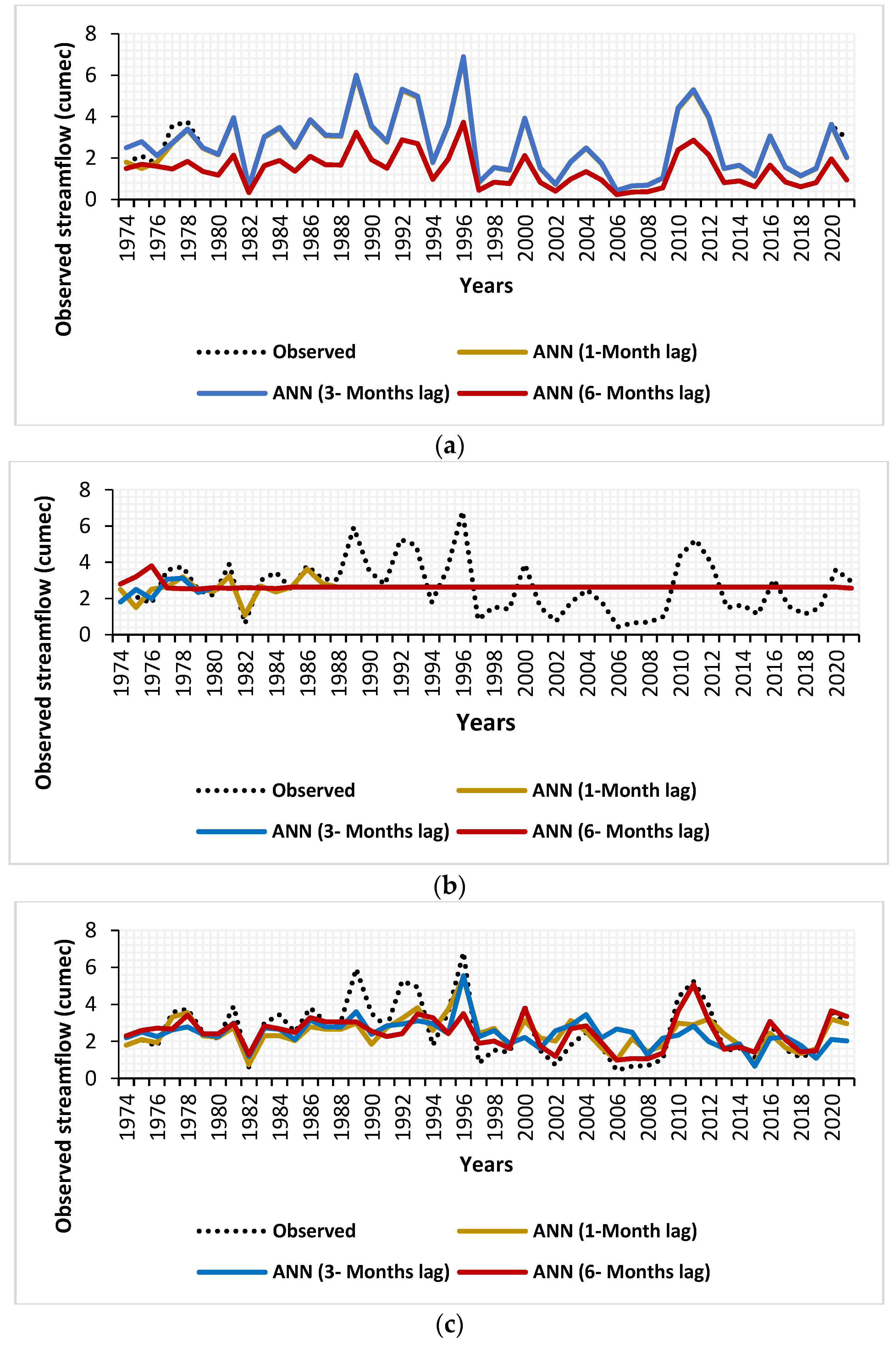
3.3. Time Series Comparison and Discussion
3.4. Discussions
4. Conclusions
- For all the stations, ENSO-based indices are having significant influence on the streamflow and are able to predict streamflow a few months ahead.
- PDO is found to have the least influence on the streamflow of the selected stations.
- IPO shows moderate (regression values 0.4~0.5) influence on the streamflow of the selected stations; however, this was far below the ENSO-based indices.
- Models for both the Acheron River and Rubicon River show the best performance in predicting streamflow up to 6 months in advance. However, dominating combination of indices are different for Acheron River and Rubicon River.
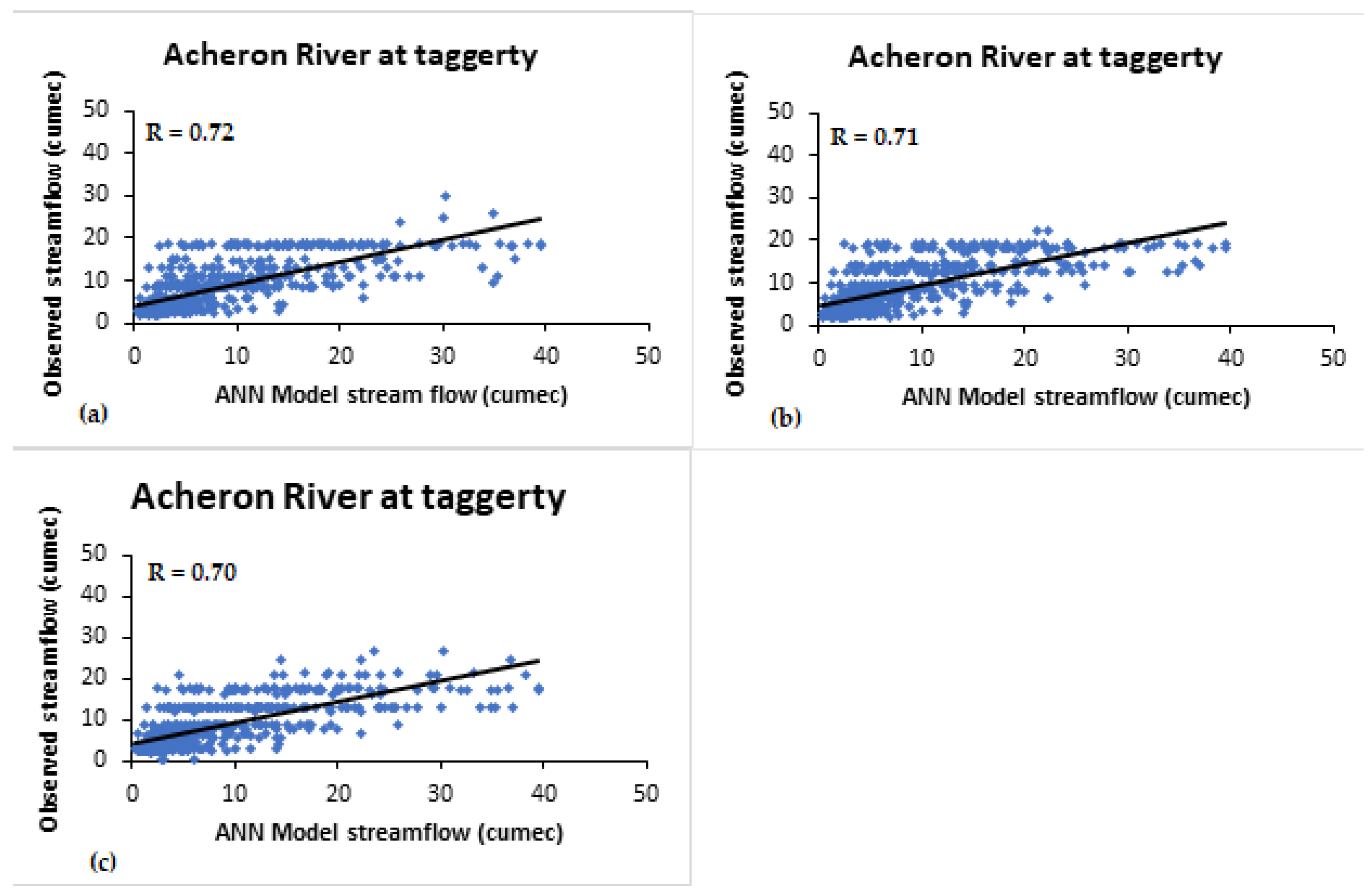
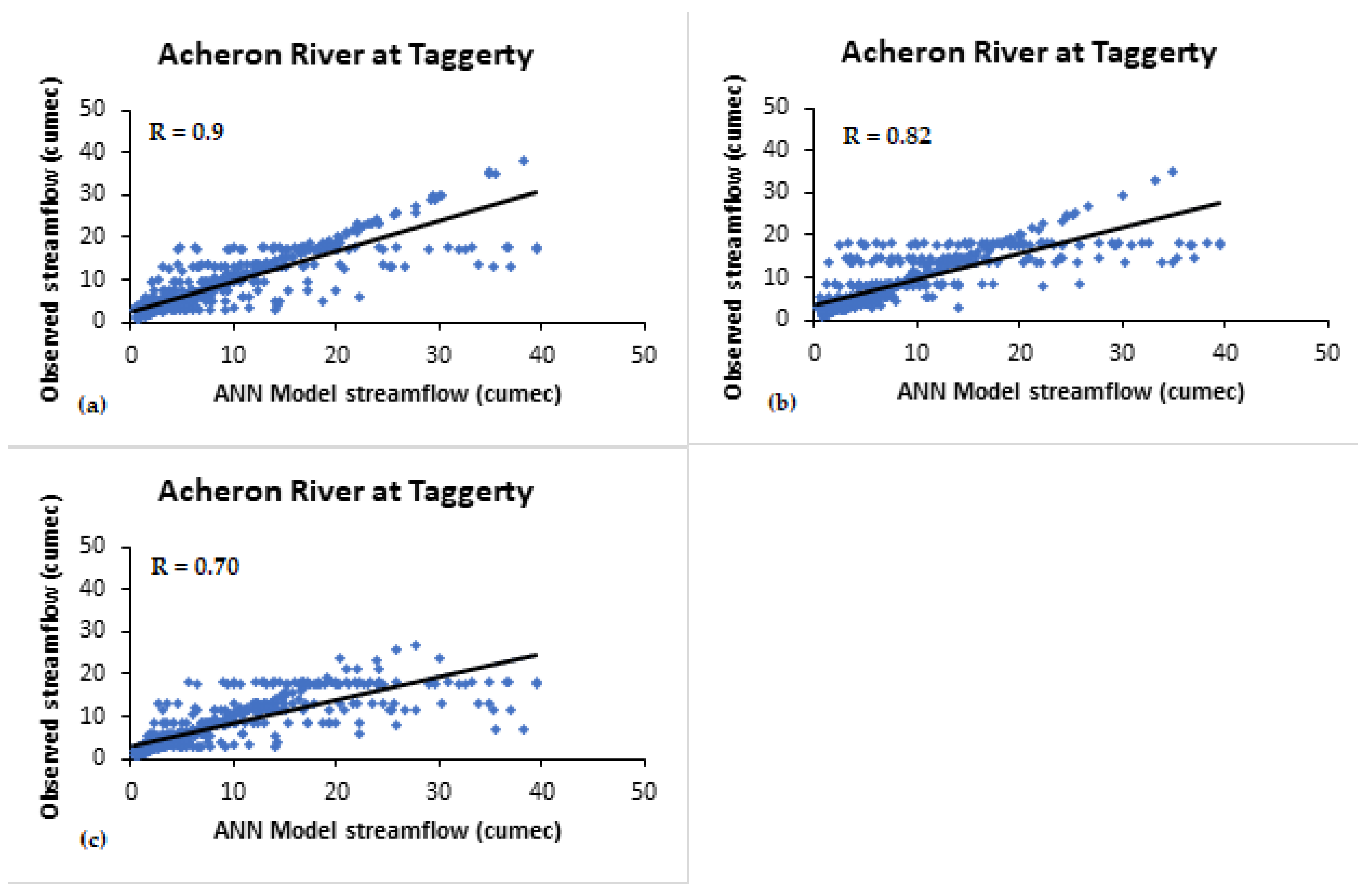
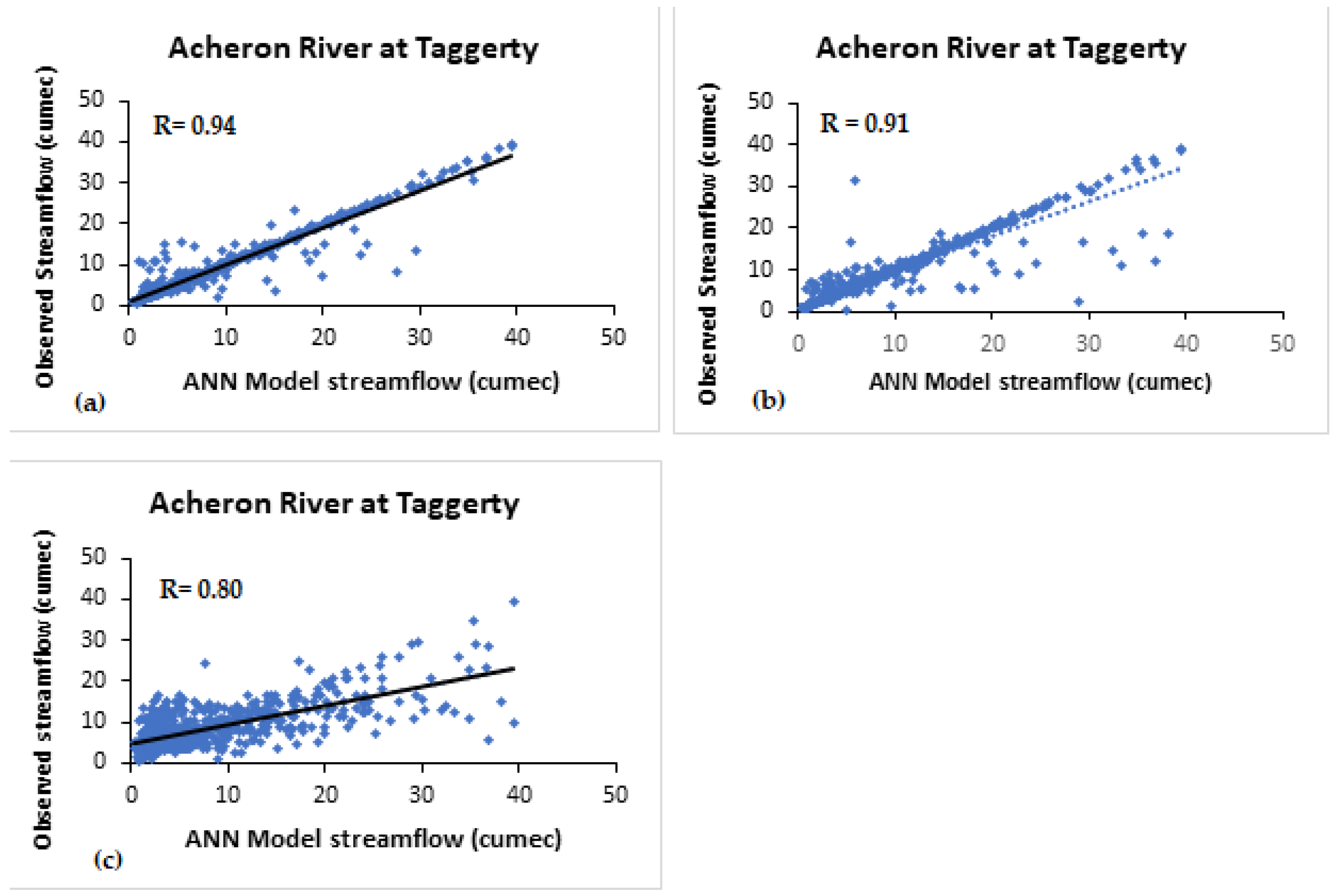
- For Acheron River, Niño3.4 and Niño4 indices were found to be more significant. The correlations between simulated and observed streamflow are 0.90 and 0.94 using Niño3.4 and Niño4, respectively. Corresponding estimation errors are MSE as 0.00 and 0.00, RMSE as 0.00 and 0.00, MAE as 2.03 and 1.06, and MAPE as 37.63 and 17.85, respectively, for one lag month. For 3-month lag, the correlations between predicted and observed streamflow are 0.91 and 0.82 using Niño4 and Niño3.4, respectively.
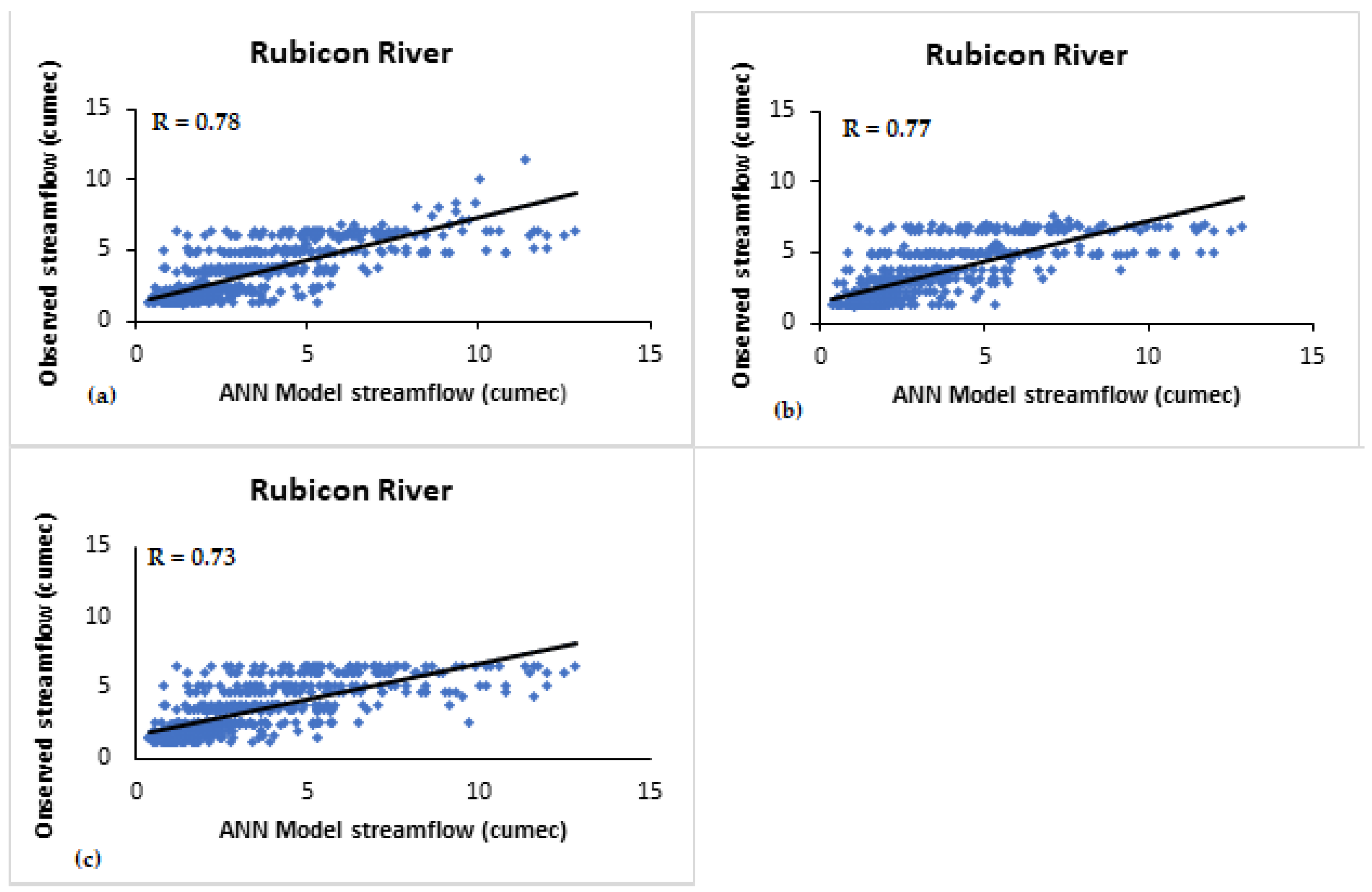
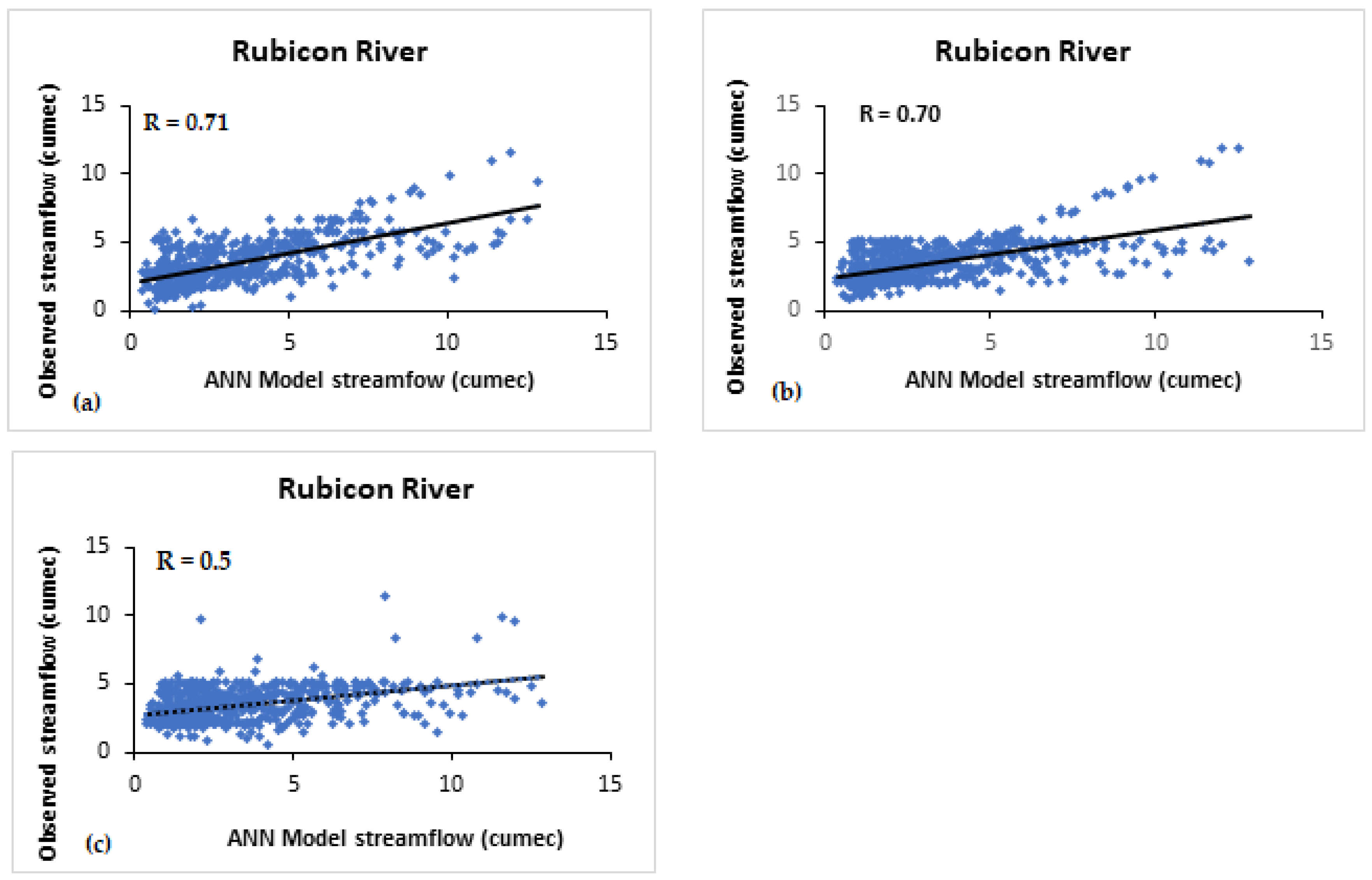
- For Rubicon River, Niño3 and Niño3.4 indices were found to be more significant. The correlations between simulated and observed streamflow are 0.78 and 0.83 using Niño3 and Niño3.4, respectively. Corresponding estimation errors are MSE as 2.4 and 1.91, RMSE as 1.5 and 1.38, MAE as 1.1 and 0.9, and MAPE as 39.76 and 40.67, respectively, for one lag month. For 3-month lag, the correlations between predicted and observed streamflow are 0.77 and 0.73 using Niño3 and Niño3.4, respectively.
- For the predictions 6 months ahead, the Acheron River showed the highest performance, with a regression correlation of 0.8 using Niño3. However, with the Rubicon River model, for 6-month lag a regression correlation of 0.73 was achieved with Niño3 and Niño3.4.
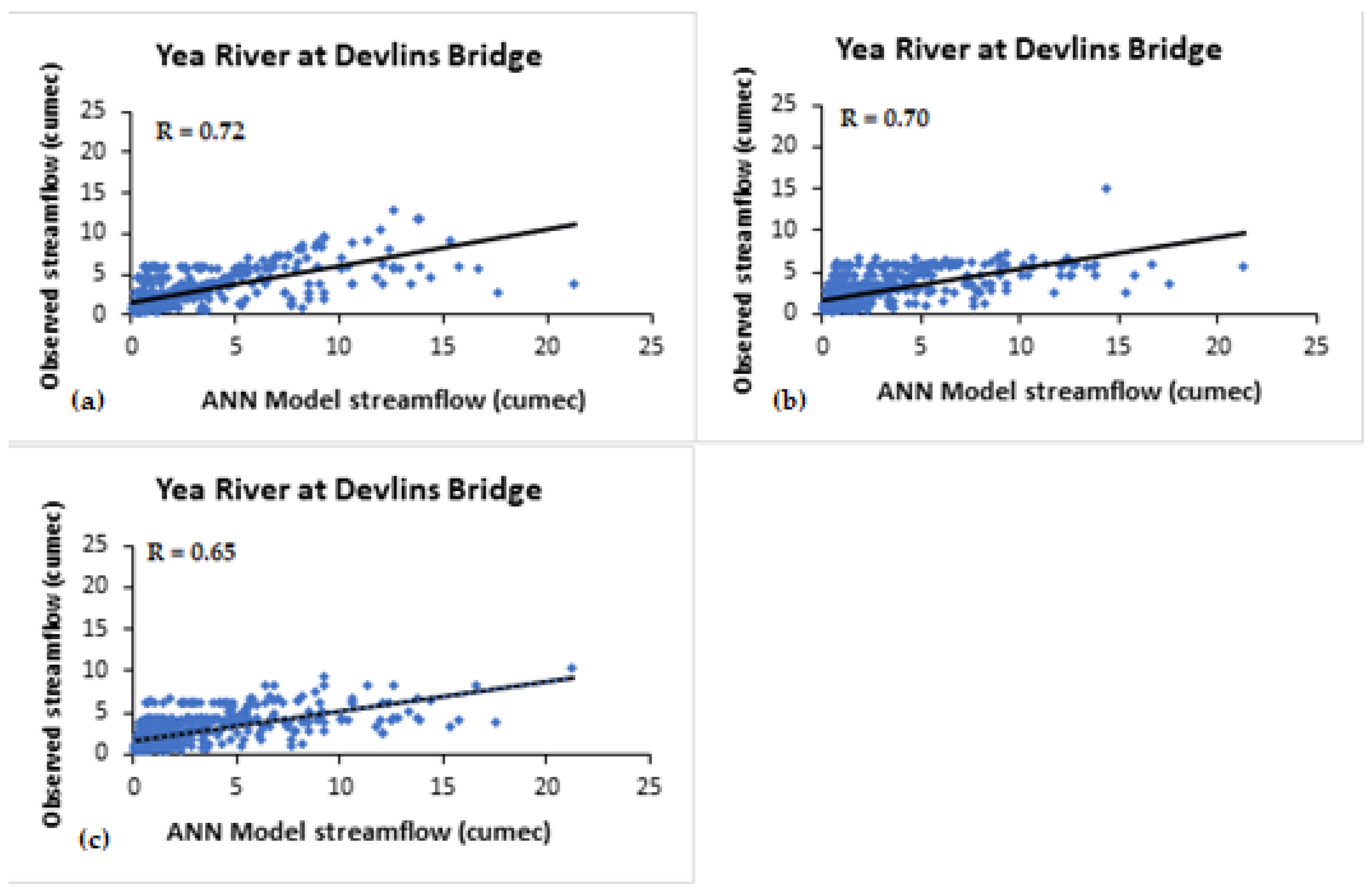
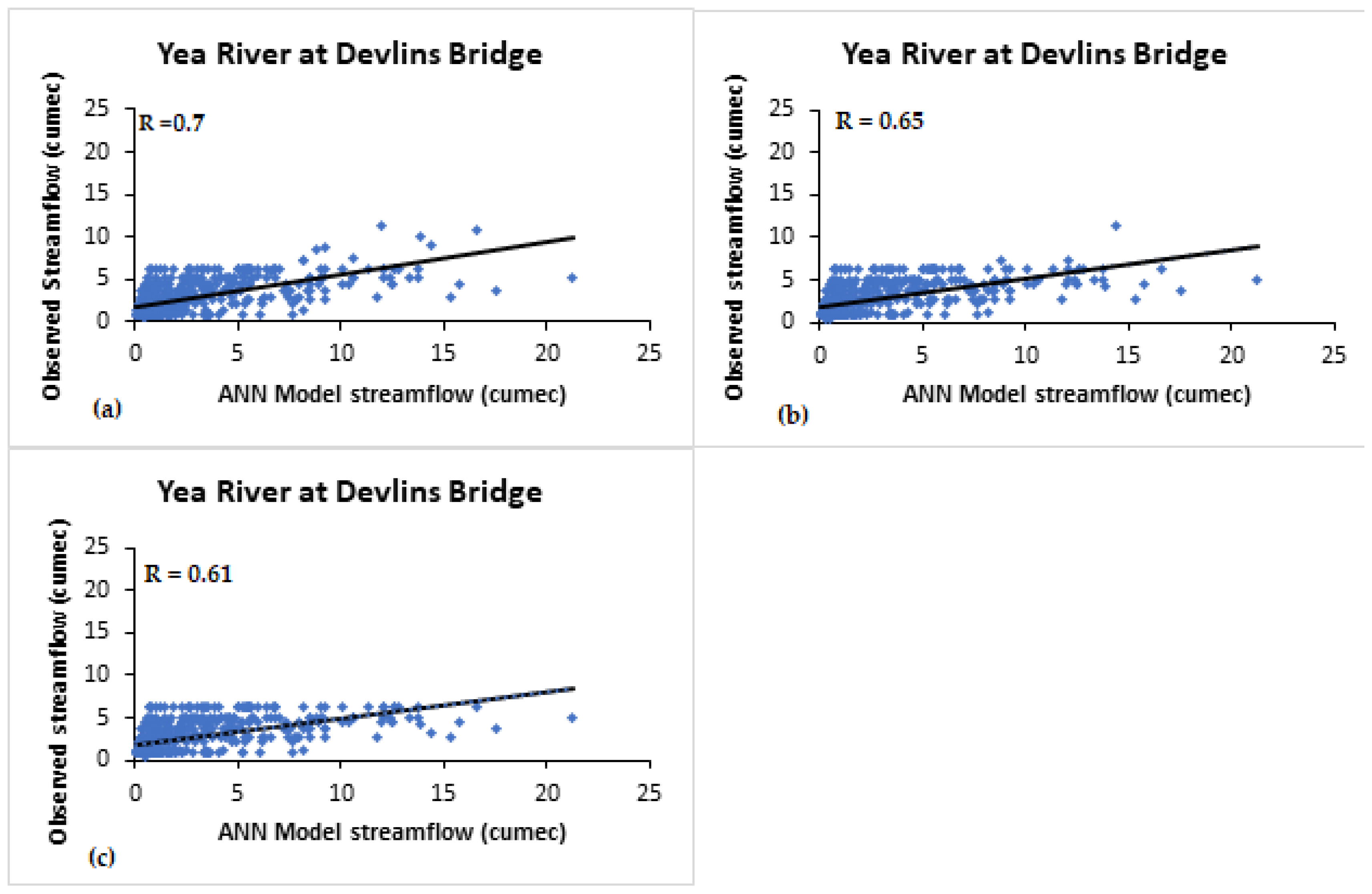
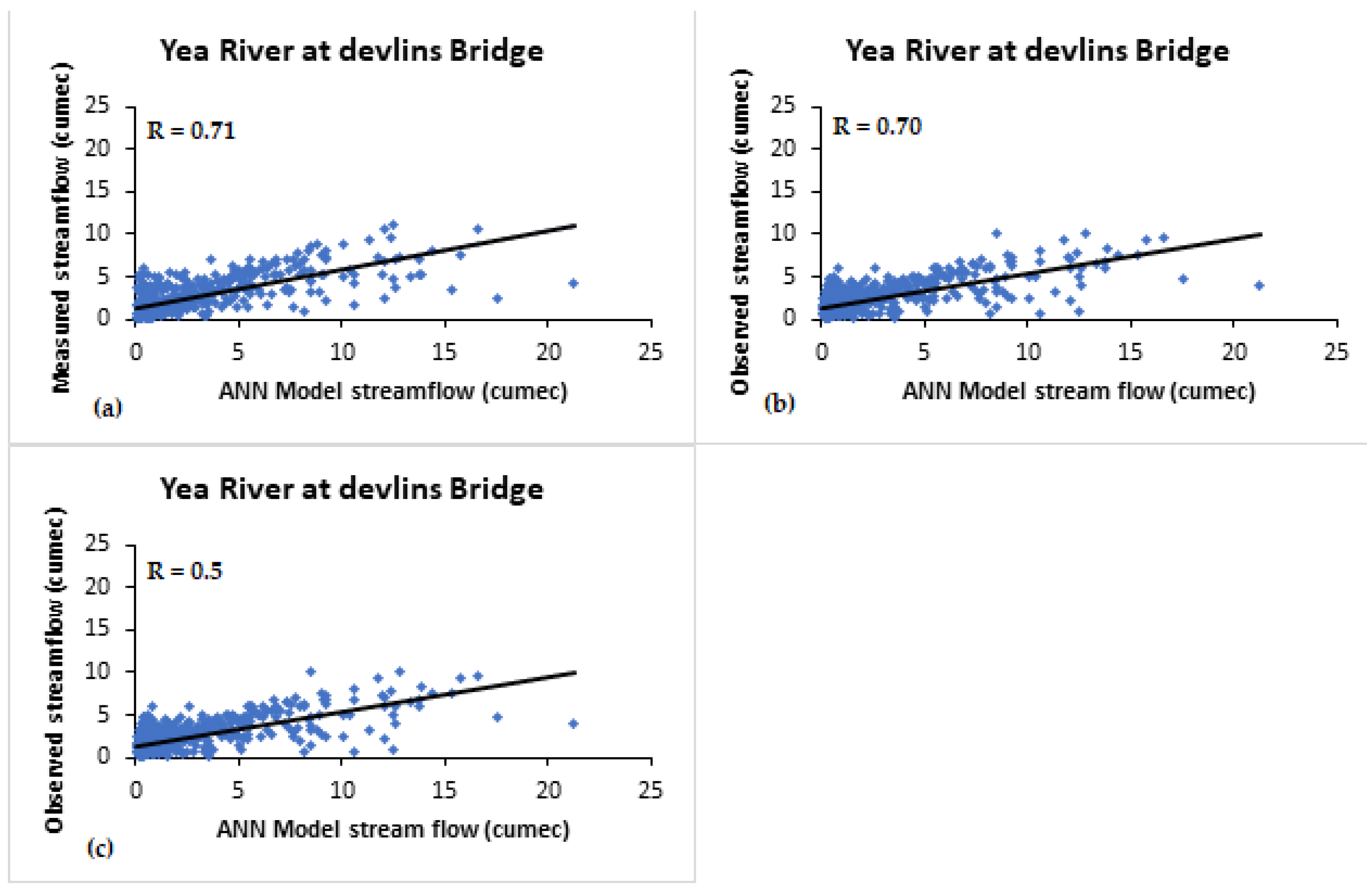
- The regression values for the Yea River models using ENSO indices varied from 0.7 to 0.74 for 1-month lag. For six-month lag, the regression values varied from 0.61 to 0.74. For all the studied cases (for Yea River), the most influencing index was Niño4.
- The time series comparisons for the models with higher correlation values were also found to be good, except that in some cases models were unable to predict the peak values. This is due to the fact that the streamflow is not only dependent on a particular climate index; it is also affected by some other local parameters. In some cases, influences of other local parameters may become superior and discrepancy with the solely index-based models may underperform.
- The performances of the developed models ascertain that such machine-learning-based models using climate indices can be used for other ungauged stations for long-term streamflow forecasting within the region. However, the current study was performed with a single index. It is likely that consideration of a combined effect of multiple indices will provide even better performance. As such, it is recommended that a future study be performed with combined indices, i.e., examining the effect of combined indices on streamflow.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akhtar, M.K.; Corzo, G.A.; Van Andel, S.J.; Jonoski, A. River flow forecasting with artificial neural networks using satellite observed precipitation pre-processed with flow length and travel time information: Case study of the Ganges River basin. Hydrol. Earth Syst. Sci. 2009, 13, 1607–1618. [Google Scholar] [CrossRef]
- Power, S.; Casey, T.; Folland, C.; Colman, A.; Mehta, V. Inter-decadal modulation of the impact of ENSO on Australia. Clim. Dyn. 1999, 15, 319–324. [Google Scholar] [CrossRef]
- Abbot, J.; Marohasy, J. Using lagged and forecast climate indices with artificial intelligence to predict monthly rainfall in the Brisbane Catchment, Queensland, and Australia. Int. J. Sustain. Dev. Plan. 2015, 10, 29–41. [Google Scholar] [CrossRef]
- Norel, M.; Katczvnski, M.; Pińskwar, I.; Krawiec, K.; Kundzewicz, Z.W. Climate Variability Indices—A Guided Tour. Geosciences 2011, 11, 128. [Google Scholar] [CrossRef]
- Duc, H.N.; Rivett, K.; MacSween, K.; Le-Anh, L. Association of climate drivers with rainfall in New South Wales, Australia, using Bayesian model averaging. Theor. Appl. Climatol. 2017, 127, 169–185. [Google Scholar] [CrossRef]
- Esha, R.I.; Imtiaz, M.A. Assessing the predictability of MLR models for long-term streamflow using lagged climate indices as predictors: A case study of NSW (Australia). Hydrol. Res. 2019, 50, 262–281. [Google Scholar] [CrossRef]
- Mekanik, F.; Imteaz, M.A.; Gato-Trinidad, S.; Elmahdi, A. Multiple regression and Artificial Neural Network for long-term rainfall forecasting using large scale climate modes. J. Hydrol. 2013, 503, 11–21. [Google Scholar] [CrossRef]
- Dutta, S.C.; Ritchie, J.W.; Freebairn, D.M.; Abawi, G.Y. Rainfall and streamflow response to El Niño Southern Oscillation: A case study in a semiarid catchment, Australia. Hydrol. Sci. J. 2006, 51, 1006–1020. [Google Scholar] [CrossRef]
- Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. 2007, 112, C11007. [Google Scholar] [CrossRef]
- Li, F.F.; Wang, Z.Y.; Qiu, J. Long-term streamflow forecasting using artificial neural network based on preprocessing technique. Sci. Total Environ. 2019, 38, 192–206. [Google Scholar] [CrossRef]
- Song, X.; Sun, W.; Zhang, Y.; Song, S.; Li, J.; Gao, Y. Using hydrological modelling and data-driven approaches to quantify mining activities impacts on centennial streamflow. J. Hydrol. 2020, 585, 124764. [Google Scholar] [CrossRef]
- Barsugli, J.J.; Sardeshmukh, P.D. Global atmospheric sensitivity to tropical SST anomalies throughout the Indo-Pacific basin. J. Clim. 2002, 15, 3427–3442. [Google Scholar] [CrossRef]
- Chattopadhyay, G.S.; Jain, R. Multivariate forecast of winter monsoon rainfall in India using SST anomaly as a predictor: Neurocomputing and statistical approaches. Comptes Rendus Geosci. 2010, 342, 755–765. [Google Scholar] [CrossRef]
- Hennessy, K.J.; Risbey, J. Trends in rainfall indices for six Australian regions: 1910–2005. Aust. Meteorol. Mag. 2007, 57, 171–173. [Google Scholar]
- MDBA, Climate and Climate Change. Available online: https://www.mdba.gov.au/importance-murray-darling-basin/environment/climate-change (accessed on 2 May 2021).
- Water NSW. Available online: https://realtimedata.waternsw.com.au (accessed on 2 August 2022).
- Jarvis, C.; Darbyshire, R.; Eckard, R.; Goodwin, I.; Barlow, E. Influence of El Niño-Southern Oscillation, and the Indian Ocean Dipole on winegrape maturity in Australia. Agric. For. Meteorol. 2018, 248, 502–510. [Google Scholar] [CrossRef]
- Chiew, F.H.; Piechota, T.C.; Dracup, J.A.; McMahon, T.A. El Niño/Southern Oscillation and Australian rainfall, streamflow and drought: Links and potential for forecasting. J. Hydrol. 1998, 204, 138–149. [Google Scholar] [CrossRef]
- Kiem, A.S.; Franks, S.W.; Kuczera, G. Multi-decadal variability of flood risk. Geophhys. Res. Lett. 2003, 30, 1035. [Google Scholar] [CrossRef]
- Sarle, W.S. Stopped training and other remedies for overfitting. In Proceedings of the 27th Symposium on the Interface of Computing Science and Statistics, Pittsburgh, PA, USA, 21–24 June 1996; pp. 352–360. [Google Scholar]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Turan, M.E. River flow estimation from upstream flow records by artificial intelligence methods. J. Hydrol. 2009, 369, 71–77. [Google Scholar] [CrossRef]
- Weather Atlas. Available online: https://www.weather-atlas.com/en/australia/acheron-climate (accessed on 7 August 2021).
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–artificial intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Campolo, M. River flood forecasting with a neural network model. Water Resour. Res. 1999, 35, 1191–1197. [Google Scholar] [CrossRef]
- Humphrey, G.B.; Gibbs, M.S.; Dandy, G.C.; Maier, H.R. A hybrid approach to monthly streamflow forecasting: Integrating hydrological model outputs into a Bayesian artificial neural network. J. Hydrol. 2016, 540, 623–640. [Google Scholar] [CrossRef]
- Ibrahim, K.S.M.H.; Huang, Y.F.; Ahmed, A.N.; Koo, C.H.; El-Shafie, A. A review of the hybrid artificial intelligence and optimization modelling of hydrological streamflow forecasting. Alex. Eng. J. 2022, 61, 279–303. [Google Scholar] [CrossRef]
- Kişi, Ö. Streamflow forecasting using different artificial neural network algorithms. J. Hydrol. Eng. 2007, 12, 532–539. [Google Scholar] [CrossRef]
- DELWP, Department of Environment, Land, Water and Planning. Available online: https://data.water.vic.gov.au/static.htm (accessed on 20 August 2022).
- Chiang, Y.M.; Chang, L.C.; Chang, F.J. Comparison of static-feedforward and dynamic-feedback neural networks for rainfall–runoff modeling. J. Hydrol. 2004, 290, 297–311. [Google Scholar] [CrossRef]
- Daliakopoulos, I.N.; Coulibaly, P.; Tsanis, I.K. Groundwater level forecasting using artificial neural networks. J. Hydrol. 2005, 309, 229–240. [Google Scholar] [CrossRef]
- Abed, M.; Imteaz, M.A.; Ahmed, A.N.; Huang, Y.F. Application of Long Short-Term Memory Neural Network Technique for Predicting Monthly Pan Evaporation. Sci. Rep. 2021, 11, 20742. [Google Scholar] [CrossRef]
- Abed, M.; Imteaz, M.A.; Ahmed, A.N.; Huang, Y.F. Modelling Monthly Pan Evaporation Utilizing Random Forest and Deep Learning Algorithms. Sci. Rep. 2022, 12, 13132. [Google Scholar] [CrossRef]
- Ruiz, J.E.; Cordery, I.; Sharma, A. Forecasting streamflows in Australia using the tropical Indo-Pacific thermocline as predictor. J. Hydrol. 2007, 341, 156–164. [Google Scholar] [CrossRef]
- Kirono, D.G.; Chew, F.H.; Kent, D.M. Identification of best predictors for forecasting seasonal rainfall and runoff in Australia. Hydrol. Process. 2010, 24, 1237–1247. [Google Scholar] [CrossRef]
- Sang, Y.F. Improved wavelet modeling framework for hydrologic time series forecasting. Water Resour. Manag. 2013, 27, 2807–2821. [Google Scholar] [CrossRef]
- Chiew, F.H.; McMahon, T.A. El Niño/Southern Oscillation and Australian rainfall and streamflow. J. Water Resour. Res. 2003, 6, 115–129. [Google Scholar]
- Britannica. “Murray River, Australia”. Available online: https://www.britannica.com/place/Murray-River (accessed on 19 May 2022).
- Elders Weather. Available online: https://www.eldersweather.com.au/climate-history/vic/yea (accessed on 20 July 2021).
- Schepen, A.; Wang, Q.J.; Robertson, D. Evidence for using lagged climate indices to forecast Australian seasonal rainfall. J. Clim. 2012, 25, 1230–1246. [Google Scholar] [CrossRef]
- Taschetto, A.S.; England, M.H. El Niño modoki impacts on Australian rainfall. J. Clim. 2009, 22, 3167–3174. [Google Scholar] [CrossRef]
- Westra, S.; Sharma, A.; Brown, C.; Lall, U. Multivariate streamflow forecasting using independent component analysis. Water Resour. Res. 2008, 44, W02437. [Google Scholar] [CrossRef]
- Ghaith, M. Hybrid hydrological data-driven approach for daily streamflow forecasting. J. Hydrol. Eng. 2020, 25, 04019063. [Google Scholar] [CrossRef]
- Yaseen, Z.M. Prediction of evaporation in arid and semi-arid regions: A comparative study using different machine learning models. Eng. Appl. Comput. Fluid Mech. 2020, 14, 70–89. [Google Scholar] [CrossRef]
- Robertson, D.E.; Wang, Q.J. A Bayesian joint probability approach to seasonal prediction of streamflows: Predictor selection and skill assessment. In Proceedings of the H2009: 32nd Hydrology and Water Resources Symposium, Newcastle: Adapting to Change, Newcastle, Australia, 30 November–3 December 2009; Engineers Australia: Barton, Australia; pp. 1545–1556.
- Whiting, J.P.; Lambert, M.F.; Metcalfe, A.V. Modelling persistence in annual Australia point rainfall. Hydrol. Earth Syst. Sci. 2003, 7, 197–211. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Sahoo, A.; Samantaray, S.; Ghose, D.K. Stream flow forecasting in Mahanadi River Basin using artificial neural networks. Procedia Comput. Sci. 2019, 157, 168–174. [Google Scholar] [CrossRef]

| Station No. | Latitude | Longitude | River Name & Data Source |
|---|---|---|---|
| 405209 | 37.32° S | 145.71° E | Acheron River at Taggerty https://realtimedata.waternsw.com.au/ # https://data.water.vic.gov.au/static.htm # |
| 405217 | 37.38° S | 145.47° E | Yea River at Devlins Bridge https://data.water.vic.gov.au/static.htm # |
| 405241 | 37.29° S | 145.82° E | Rubicon River https://data.water.vic.gov.au/static.htm # |
| Predictors | Predictor Definition | Origin | Data Source |
|---|---|---|---|
| NIÑO3 | Average SST anomaly over central Pacific Ocean (5° S–5° N, 90°–150° W) | Pacific Ocean | HadISSTI1 (http://climexp.knmi.nl/) * |
| NIÑO3.4 | Average SST anomaly over central Pacific Ocean (5° S–5° N, 120°–170° W) | Pacific Ocean | HadISSTI1 (http://climexp.knmi.nl/) * |
| NIÑO4 | Average SST anomaly over central Pacific Ocean, (5° S–5° N, 150°–200° W) | Pacific Ocean | HadISSTI1 (http://climexp.knmi.nl/) * |
| IPO | SST anomaly in North and South Pacific Ocean, (Includes south of 20° N latitude) | Pacific Ocean | HadISSTI1 (http://climexp.knmi.nl/) * |
| PDO | SSTA anomaly in North Pacific Ocean, (North of 20° N latitude) | Pacific Ocean | ERSST (http://climexp.knmi.nl/) * |
| IOD | West pole index (10° S–10° N, 50°–70° E)—East pole Index (10° S–0° N, 90°–110° E) | Indian Ocean | HadISSTI1 (http://climexp.knmi.nl/) * |
| Station | NIÑO3 | NIÑO3.4 | NIÑO4 | IPO | PDO | IOD |
|---|---|---|---|---|---|---|
| Acheron River | 0.72 ′ 0.71 ″ 0.7 ‴ | 0.9 ′ 0.82 ″ 0.70 ‴ | 0.94 ′ 0.91 ″ 0.80 ‴ | 0.4 ′ - - | 0.07 ′ - - | 0.32 ′ - - |
| Rubicon River | 0.78 ′ 0.77 ″ 0.73 ‴ | 0.83 ′ 0.73 ′ 0.73 ‴ | 0.71 ′ 0.70 ‴ 0.5 ‴ | 0.4 ′ - - | 0.05 ′ - - | 0.32 ′ - - |
| Yea River | 0.72 ′ 0.70 ″ 0.65 ‴ | 0.7 ′ 0.65 ″ 0.61 ‴ | 0.71 ′ 0.70 ″ 0.5 ‴ | 0.5 ′ - - | 0.014 ′ - - | 0.3 ′ - - |
| Station | Climate Indices | MSE | RMSE | MAE | MAPE |
|---|---|---|---|---|---|
| Acheron River | NIÑO3 | 30.48 ′ 30.57 ″ 32.0 ‴ | 5.52 ′ 5.53 ″ 5.66 ‴ | 3.60 ′ 3.60 ″ 3.74 ‴ | 62.63 ′ 62.74 ″ 66.11 ‴ |
| NIÑO3.4 | 0.0 ′ | 0.0 ′ | 2.03 ′ | 17.85 ′ | |
| 21.1 ″ | 4.59 ″ | 2.37 ″ | 19.99 ″ | ||
| 24.4 ‴ | 4.94 ‴ | 2.43 ‴ | 93.4 ‴ | ||
| NIÑO4 | 0.0 ′ | 0.0 ′ | 0.89 ′ | 143.45 ′ | |
| 4.80 ″ | 2.19 ″ | 1.06 ″ | 153.47 ′ | ||
| 33.82 ‴ | 5.81 ‴ | 3.97 ‴ | 153.5 ′ | ||
| IPO | 60.23 ′ | 7.76 ′ | 5.97 ′ | 43.39 ′ | |
| PDO | 63.55 ′ | 7.97 ′ | 6.18 ′ | 41.0 ′ | |
| IOD | 63.55 ′ | 7.97 ′ | 6.18 ′ | 43.74 ′ | |
| Rubicon River | NIÑO3 | 2.4 ′ | 1.5 ′ | 1.1 ′ | 40.67 ′ |
| 2.75 ″ | 1.66 ″ | 1.1 ″ | 47.0 ″ | ||
| 4.0 ‴ | 2.0 ‴ | 1.17 ‴ | 35.76 ‴ | ||
| NIÑO3.4 | 1.75 ′ | 1.32 ′ | 0.84 ′ | 61.54 ′ | |
| 1.91 ″ | 1.38 ″ | 0.90 ″ | 69.73 ″ | ||
| 3.11 ‴ | 1.76 ‴ | 1.17 ‴ | 81.00 ‴ | ||
| NIÑO4 | 3.44 ′ | 1.85 ′ | 1.29 ′ | 89.9 ′ | |
| 4.03 ″ | 2.0 ″ | 1.45 ″ | 93.37 ″ | ||
| 5.72 ‴ | 2.39 ‴ | 1.80 ‴ | 95.5 ‴ | ||
| IPO | 2.39 ′ | 5.70 ′ | 1.90 ′ | 114.94 ′ | |
| PDO | 6.19 ′ | 2.49 ′ | 1.97 ′ | 121.39 ′ | |
| IOD | 5.76 ′ | 2.40 ′ | 1.89 ′ | 131.53 ′ | |
| Yea River | NIÑO3 | 5.47 ′ | 2.34 ′ | 1.25 ′ | 122.28 ′ |
| 6.45 ″ | 2.54 ″ | 1.53 ″ | 127.43 ″ | ||
| 6.69 ‴ | 2.58 ‴ | 1.64 ‴ | 130.64 ‴ | ||
| NIÑO3.4 | 6.28 ′ | 2.51 ′ | 1.55 ′ | 112.16 ′ | |
| 6.97 ″ | 2.64 ″ | 1.67 ″ | 124.84 ″ | ||
| 7.38 ‴ | 2.71 ‴ | 1.74 ‴ | 104.47 ‴ | ||
| NIÑO4 | 5.29 ′ | 2.30 ′ | 1.20 ′ | 222.97 ′ | |
| 5.67 ″ | 2.32 ″ | 1.25 ″ | 309.59 ′ | ||
| 5.38 ‴ | 2.38 ‴ | 1.39 ‴ | 277.37 ‴ | ||
| IPO | 9.29 ′ | 3.04 ′ | 2.16 ′ | 37.63 ′ | |
| PDO | 10.95 ′ | 3.30 ′ | 2.51 ′ | 309.59 ′ | |
| IOD | 10.08 ′ | 3.17 ′ | 2.31 ′ | 277.37 ′ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oad, S.; Imteaz, M.A.; Mekanik, F. Artificial Neural Network (ANN)-Based Long-Term Streamflow Forecasting Models Using Climate Indices for Three Tributaries of Goulburn River, Australia. Climate 2023, 11, 152. https://doi.org/10.3390/cli11070152
Oad S, Imteaz MA, Mekanik F. Artificial Neural Network (ANN)-Based Long-Term Streamflow Forecasting Models Using Climate Indices for Three Tributaries of Goulburn River, Australia. Climate. 2023; 11(7):152. https://doi.org/10.3390/cli11070152
Chicago/Turabian StyleOad, Shamotra, Monzur Alam Imteaz, and Fatemeh Mekanik. 2023. "Artificial Neural Network (ANN)-Based Long-Term Streamflow Forecasting Models Using Climate Indices for Three Tributaries of Goulburn River, Australia" Climate 11, no. 7: 152. https://doi.org/10.3390/cli11070152
APA StyleOad, S., Imteaz, M. A., & Mekanik, F. (2023). Artificial Neural Network (ANN)-Based Long-Term Streamflow Forecasting Models Using Climate Indices for Three Tributaries of Goulburn River, Australia. Climate, 11(7), 152. https://doi.org/10.3390/cli11070152








