Microeconomics of Nitrogen Fertilization in Boreal Carbon Forestry
Abstract
:1. Introduction
2. Materials and Methods
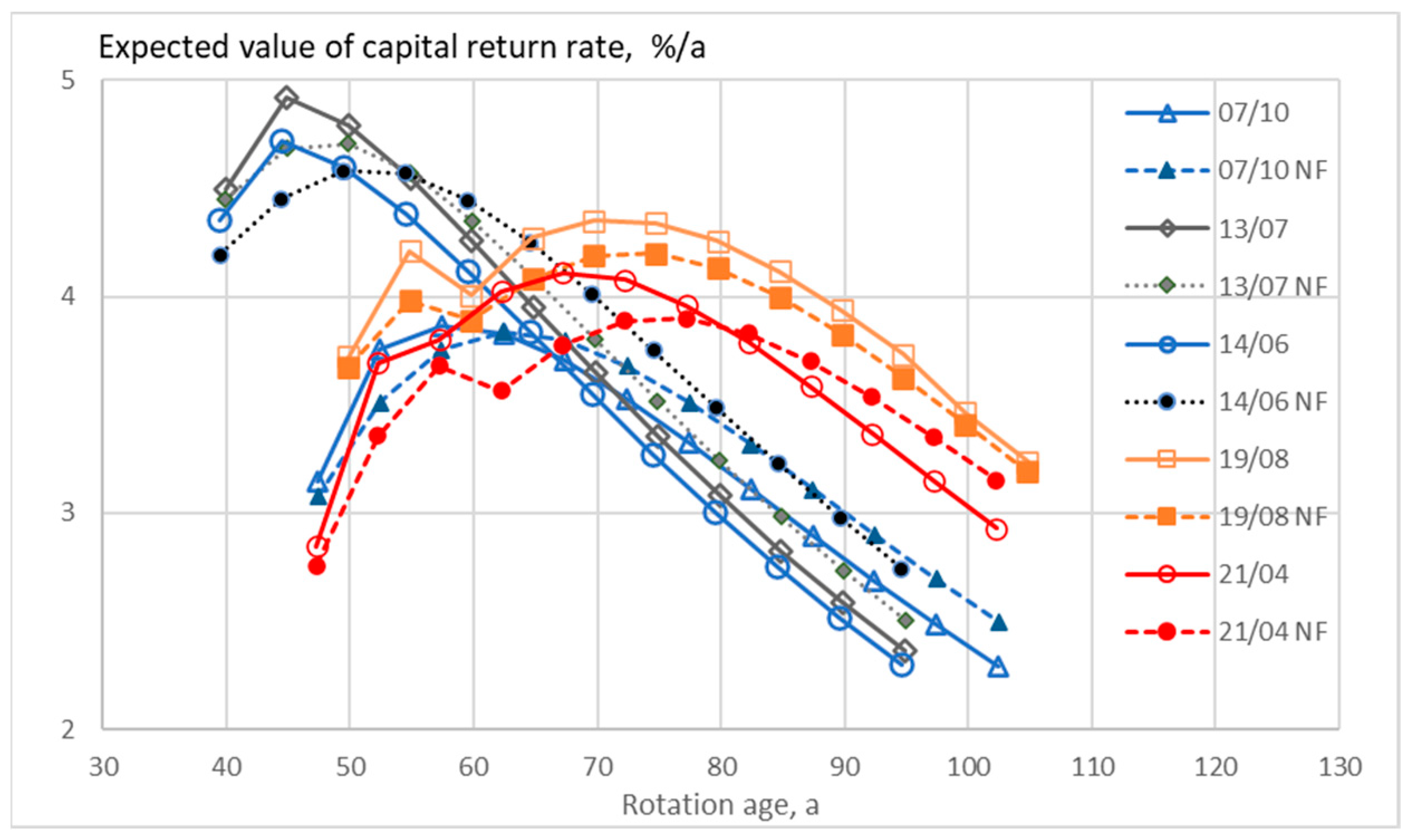
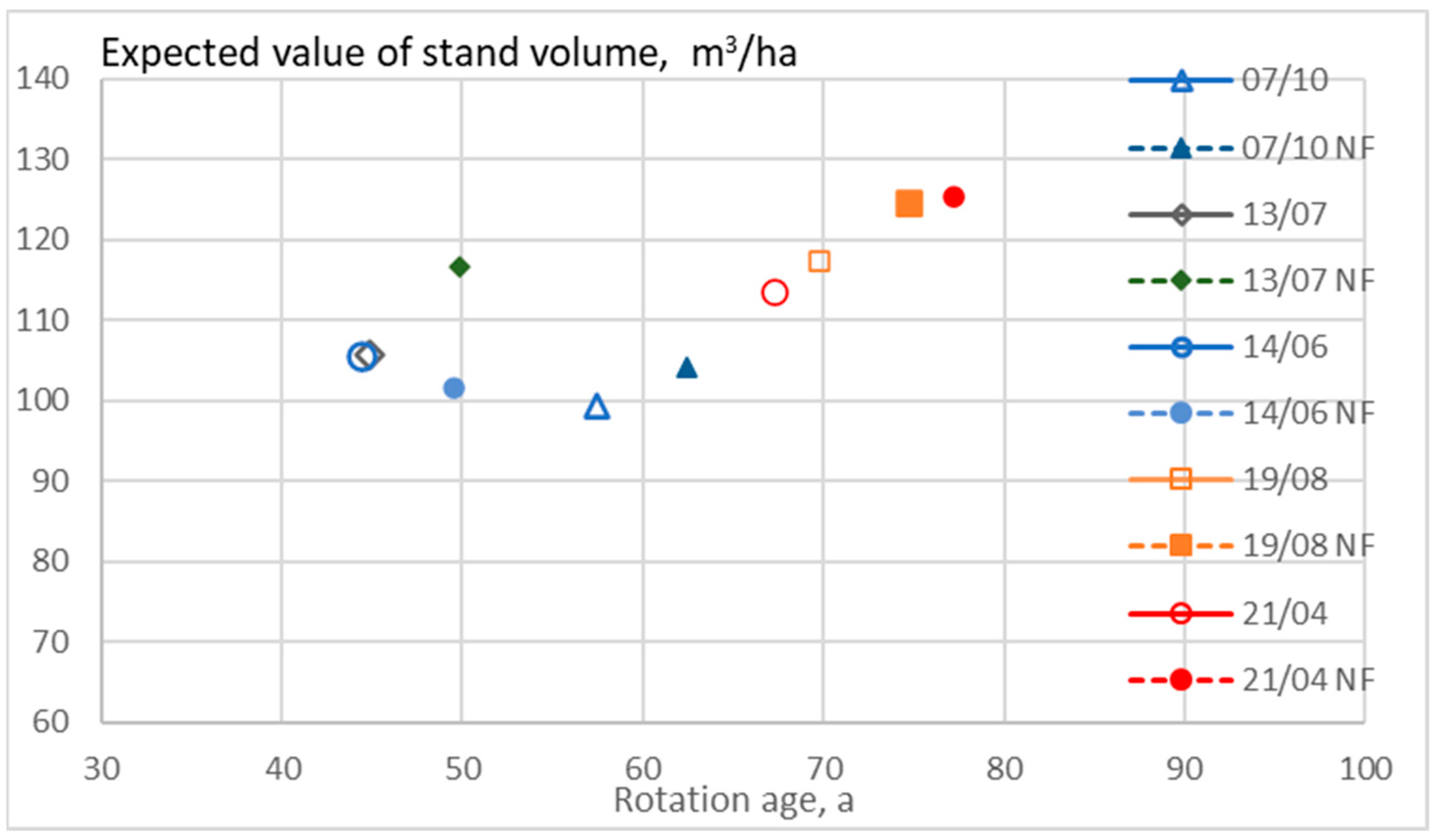
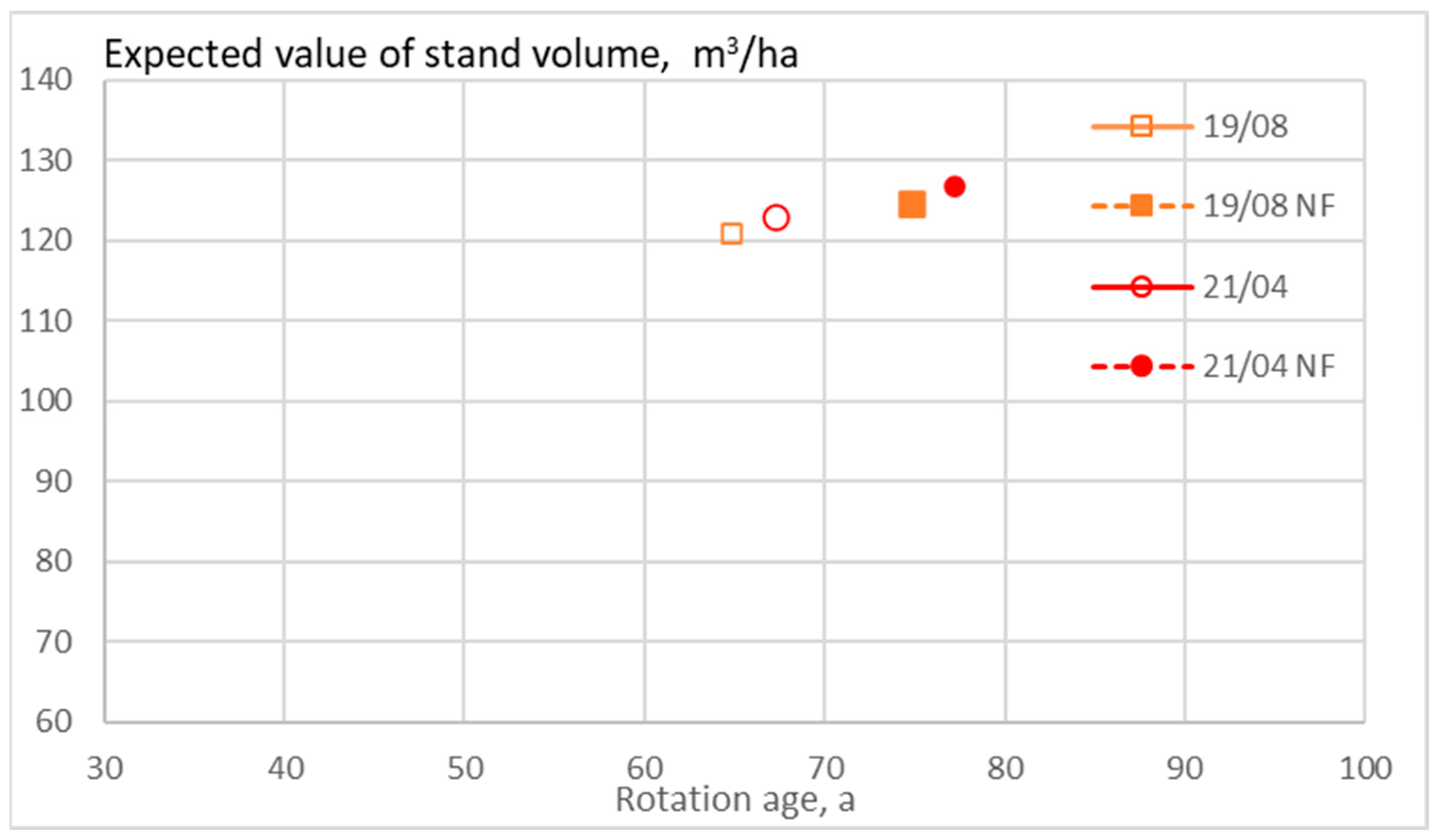
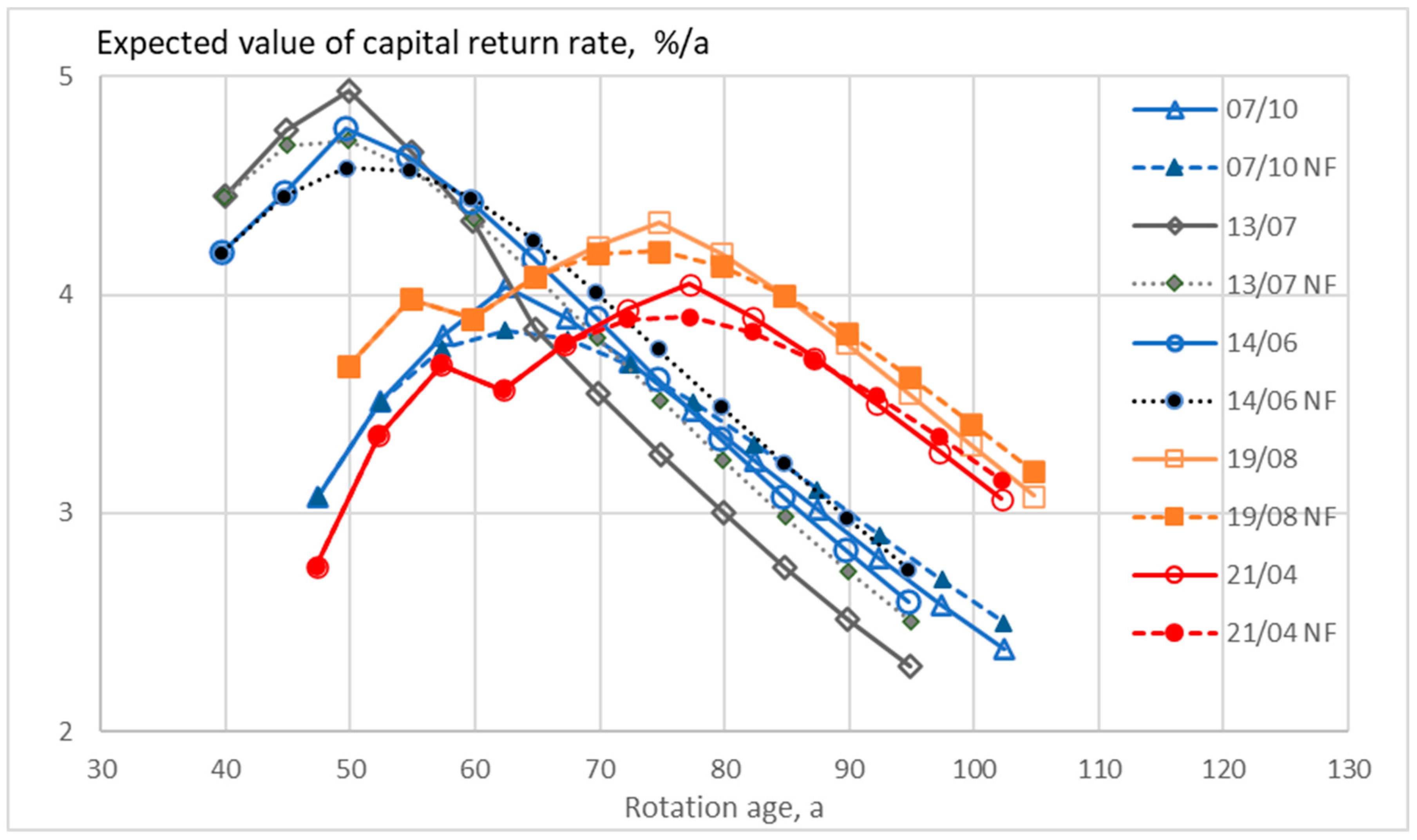
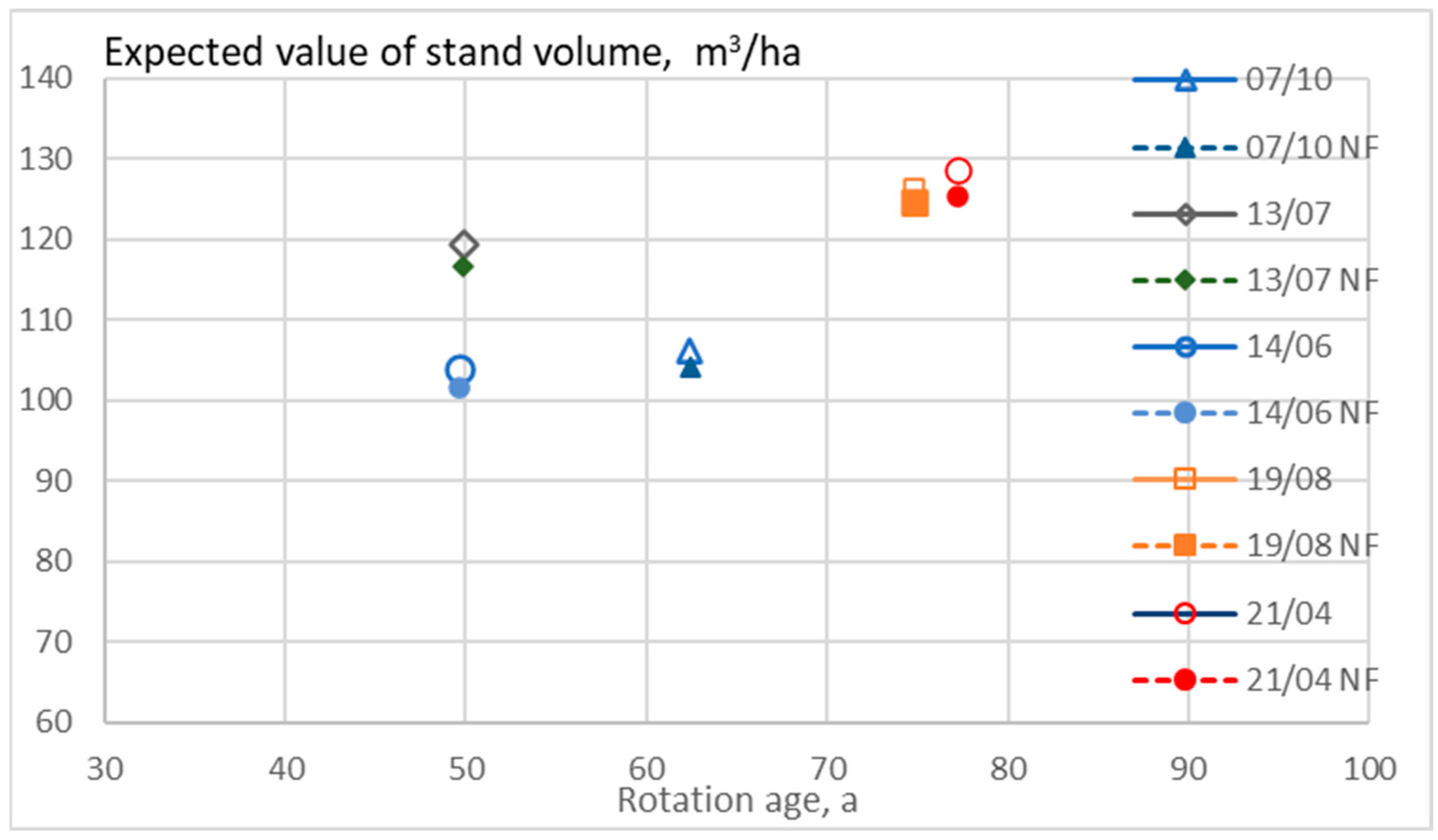
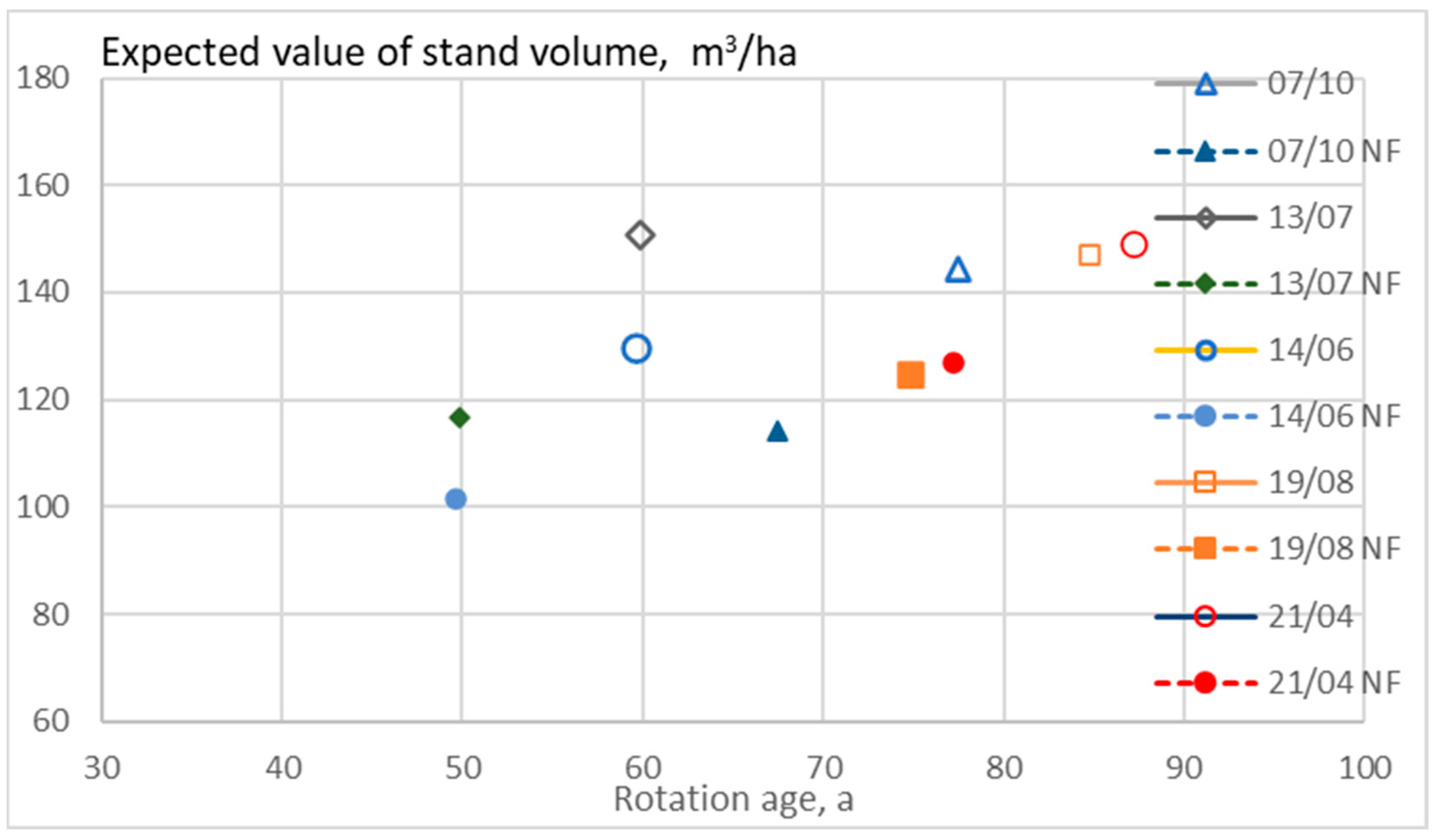
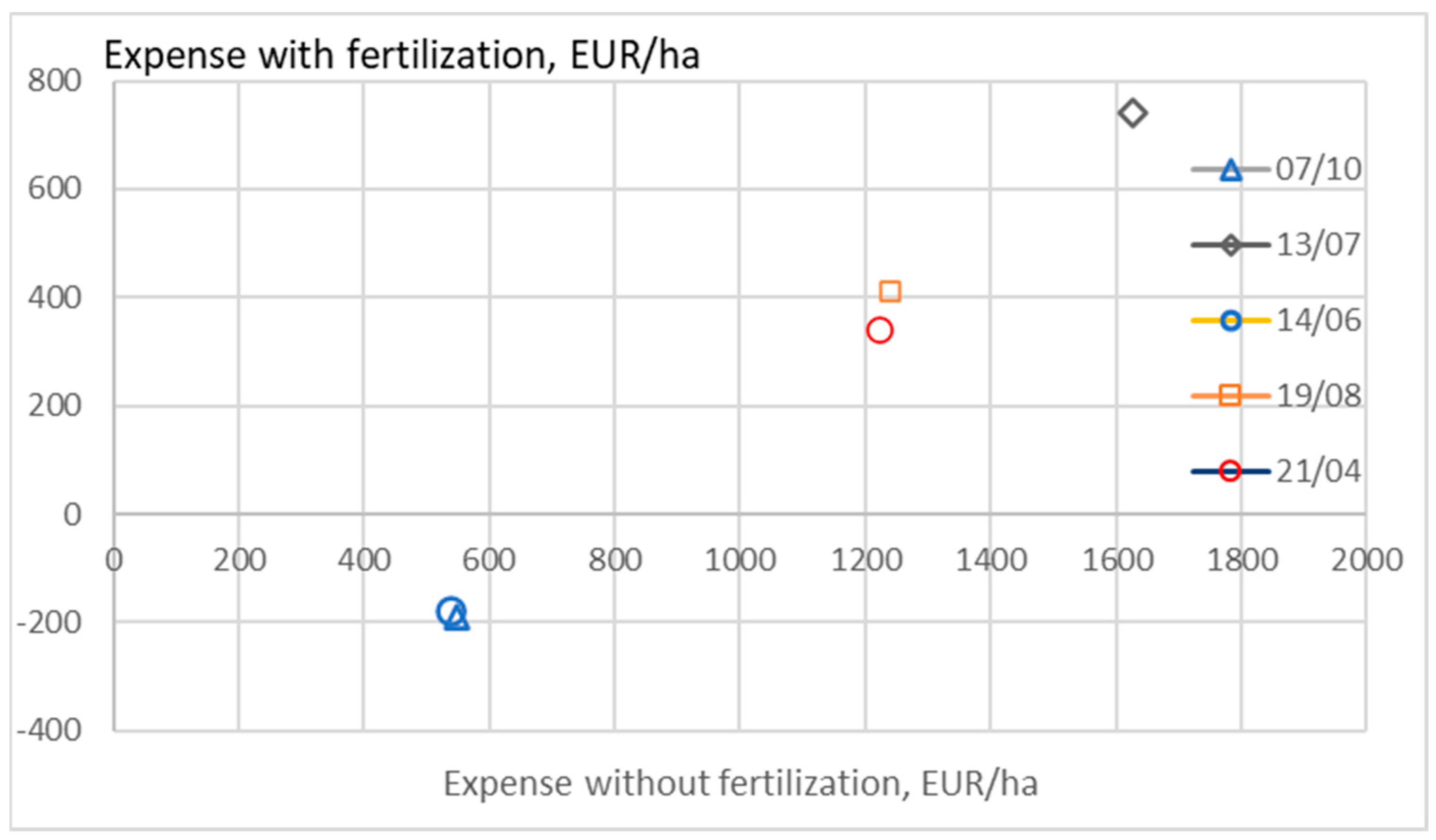
3. Results
4. Discussion
Funding
Data Availability Statement
Conflicts of Interest
References
- Friedel, M. Forests as Carbon Sinks. Available online: https://www.americanforests.org/blog/forests-carbon-sinks/ (accessed on 17 July 2021).
- Goodale, C.L.; Apps, M.J.; Birdsey, R.A.; Field, C.B.; Heath, L.S.; Houghton, R.A.; Jenkins, J.C.; Kohlmaier, G.H.; Kurz, W.; Liu, S.; et al. Forest carbon sinks in the northern hemisphere. Ecol. Appl. 2002, 12, 891–899. [Google Scholar] [CrossRef]
- Liski, J.; Lehtonen, A.; Palosuo, T.; Peltoniemi, M.; Eggersa, T.; Muukkonen, P.; Mäkipää, R. Carbon accumulation in Finland’s forests 1922-2004-an estimate obtained by combination of forest inventory data with modelling of biomass, litter and soil. Ann. For. Sci. 2006, 63, 687–697. [Google Scholar] [CrossRef]
- Adams, A.; Harrison, R.; Sletten, R.; Strahm, B.; Turnblom, E.; Jensen, C. Nitrogen-fertilization impacts on carbon sequestration and flux in managed coastal Douglas-fir stands of the Pacific Northwest. For. Ecol. Manag. 2005, 220, 313–325. [Google Scholar] [CrossRef]
- Thornley, J.H.M.; Cannell, M.G.R. Managing forests for wood yield and carbon storage: A theoretical study. Tree Physiol. 2000, 20, 477–484. [Google Scholar] [CrossRef]
- Heinonen, T.; Pukkala, T.; Asikainen, A.; Peltola, H. Scenario analyses on the effects of fertilization, improved regeneration material, and ditch network maintenance on timber production of Finnish forests. Eur. J. For. Res. 2018, 137, 93–107. [Google Scholar] [CrossRef]
- Matthews, H.D.; Zickfeld, K.; Dickau, M.; MacIsaac, A.J.; Mathesius, S.; Nzotungicimpaye, C.-M.; Luers, A. Temporary nature-based carbon removal can lower peak warming in a well-below 2 °C scenario. Commun. Earth Environ. 2022, 3, 65. [Google Scholar] [CrossRef]
- Matthews, H.D.; Zickfeld, K.; Koch, A.; Luers, A. Accounting for the climate benefit of temporary carbon storage in nature. Nat Commun 2023, 14, 5485. [Google Scholar] [CrossRef]
- Soimakallio, S.; Böttcher, H.; Niemi, J.; Mosley, F.; Turunen, S.; Hennenberg, K.J.; Reise, J.; Fehrenbach, H. Closing an open balance: The impact of increased tree harvest on forest carbon. GCB Bioenergy 2022, 14, 989–1000. [Google Scholar] [CrossRef]
- Hurmekoski, E.; Kunttu, J.; Heinonen, T.; Pukkala, T.; Peltola, H. Does expanding wood use in construction and textile markets contribute to climate change mitigation? Renew. Sustain. Energy Rev. 2023, 174, 113152. [Google Scholar] [CrossRef]
- Nilsen, P. Fertilization experiments on forest mineral soils: A review of the Norwegian results. Scand. J. Forest Res. 2001, 16, 541–554. [Google Scholar] [CrossRef]
- Kukkola, M.; Saramäki, J. Growth response in repeatedly fertilized pine and spruce stands on mineral soils. Commun. Inst. Forest Fenn. 1983, 114, 55. [Google Scholar]
- Pukkala, T. Optimal nitrogen fertilization of boreal conifer forest. For. Ecosyst. 2017, 4, 3. [Google Scholar] [CrossRef]
- Nohrstedt, H.-Ö. Response of coniferous forest ecosystems on mineral soils to nutrient additions: A review of Swedish experiences. Scand. J. Forest Res. 2001, 6, 555–573. [Google Scholar] [CrossRef]
- Hökkä, H.; Repola, J.; Moilanen, M. Modelling volume growth response of young Scots pine (Pinus sylvetris) stands to N, P, and K fertilization in drained Peatland sites in Finland. Can. J. Forest Res. 2012, 42, 1359–1370. [Google Scholar] [CrossRef]
- Saarsalmi, A.; Mälkönen, E. Forest fertilization research in Finland: A literature review. Scand. J. Forest Res. 2001, 16, 514–535. [Google Scholar] [CrossRef]
- Raulo, J. Development of dominant trees in Betula pendula Roth and Betula pubescens Ehrh. Plantations. Seloste: Viljeltyjen Raudusja Hieskoivikoidenvaltapuiden Kehitys. In Communicationes Instituti Forestalis Fenniae; Finnish Forest Research Institute: Vantaa, Finland, 1977; Volume 90. [Google Scholar]
- Oikarinen, M. Etelä-Suomen viljeltyjen rauduskoivikoiden kasvatusmallit. Summary: Growth Andyield Models for Silver Birch (Betula pendula) Plantations in Southern Finland. In Communicationes Instituti Forestalis Fenniae; Finnish Forest Research Institute: Vantaa, Finland, 1983; Volume 113. [Google Scholar]
- Hedwall, P.-O.; Gong, P.; Ingerslev, M.; Bergh, J. Fertilization in northern forests—Biological, economic and environmental constraints and possibilities. Scand. J. Forest Res. 2014, 29, 301–311. [Google Scholar] [CrossRef]
- Kilpeläinen, J.; Räisänen, M.; Mehtätalo, L.; Sutinen, S.; Rummukainen, A.; Repo, T.; Lehto, T. The longevity of Norway spruce responses to boron fertilisation. For. Ecol. Manag. 2013, 307, 90–100. [Google Scholar] [CrossRef]
- Pettersson, F.; Högbom, L. Long-term growth effects following forest nitrogen fertilization in Pinus sylvestris and Picea abies stands in Sweden. Scand. J. Forest Res. 2004, 19, 339–347. [Google Scholar] [CrossRef]
- Mälkönen, E.; Derome, J.; Kukkola, M. Effects of nitrogen inputs on forest ecosystems, estimation based on long-term fertilization experiments. In Acidication in Finland; Kauppi, P., Anttila, P., Kenttämies, K., Eds.; Springer: Berlin, Germany, 1990; pp. 325–347. [Google Scholar]
- Kärenlampi, P.P. Two Sets of Initial Conditions on Boreal Forest Carbon Storage Economics. PLoS Clim. 2022, 1, e0000008. [Google Scholar] [CrossRef]
- Kärenlampi, P.P. Two Manifestations of Market Premium in the Capitalization of Carbon Forest Estates. Energies 2022, 15, 3212. [Google Scholar] [CrossRef]
- Kärenlampi, P.P. Harvesting Design by Capital Return. Forests 2019, 10, 283. [Google Scholar] [CrossRef]
- Kärenlampi, P.P. Net present value of multiannual growth in the absence of periodic boundary conditions. Agric. Financ. Rev. 2020, 81, 39–50. [Google Scholar] [CrossRef]
- Kärenlampi, P.P. Diversity of Carbon Storage Economics in Fertile Boreal Spruce (Picea abies) Estates. Sustainability 2021, 13, 560. [Google Scholar] [CrossRef]
- Kärenlampi, P.P. Capital return rate and carbon storage on forest estates of three boreal tree species. Sustainability 2021, 13, 6675. [Google Scholar] [CrossRef]
- Kärenlampi, P.P. Empirical observations of the yield of logs from trees of the boreal region. Balt. For. 2022, 28, 1. [Google Scholar] [CrossRef]
- Kärenlampi, P.P. Estate-Level Economics of Carbon Storage and Sequestration. Forests 2020, 11, 643. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Buongiorno, J.; Gobakken, T. Predicting the growth of stands of trees of mixed species and size: A matrix model for Norway. Scand. J. For. Res. 2008, 23, 167–178. [Google Scholar] [CrossRef]
- Kärenlampi, P.P. Two strategies for boreal forestry with goodwill in capitalization. arXiv 2022, arXiv:2205.06744. [Google Scholar]
- Murray, B.C.; McCarl, B.A.; Lee, H.-C. Estimating Leakage from Forest Carbon Sequestration Programs. Land Econ. 2004, 80, 109–124. [Google Scholar] [CrossRef]
- Henders, S.; Ostwald, M. Forest Carbon Leakage Quantification Methods and Their Suitability for Assessing Leakage in REDD. Forests 2012, 3, 33–58. [Google Scholar] [CrossRef]
- Sohngen, B.; Brown, S. Measuring leakage from carbon projects in open economies: A stop timber harvesting project in Bolivia as a case study. Can. J. For. Res. 2004, 34, 829–839. [Google Scholar] [CrossRef]
- Pan, W.; Kim, M.-K.; Ning, Z.; Yang, H. Carbon leakage in energy/forest sectors and climate policy implications using meta-analysis. For. Policy Econ. 2020, 115, 102161. [Google Scholar] [CrossRef]
- Petersson, H.; Ellison, D.; Mensah, A.A.; Berndes, G.; Egnell, G.; Lundblad, M.; Lundmark, T.; Lundström, A.; Stendahl, J.; Wikberg, P.-E. On the role of forests and the forest sector for climate change mitigation in Sweden. GCB Bioenergy 2022, 14, 793–813. [Google Scholar] [CrossRef]
- Kalliokoski, T.; Bäck, J.; Boy, M.; Kulmala, M.; Kuusinen, N.; Mäkelä, A.; Minkkinen, K.; Minunno, F.; Paasonen, P.; Peltoniemi, M.; et al. Mitigation Impact of Different Harvest Scenarios of Finnish Forests That Account for Albedo, Aerosols, and Trade-Offs of Carbon Sequestration and Avoided Emissions. Front. For. Glob. Change 2020, 3, 562044. [Google Scholar] [CrossRef]
- Cosola, G.; Grigolato, S.; Ackerman, P.; Monterotti, S.; Cavalli, R. Carbon Footprint of Forest Operations under Different Management Regimes. Croat. J. For. Eng. 2016, 37, 201–217. [Google Scholar]
- Kärhä, K.; Haavikko, H.; Kääriäinen, H.; Palander, T.; Eliasson, L.; Roininen, K. Fossil-fuel consumption and CO2eq emissions of cut-to-length industrial roundwood logging operations in Finland. Eur. J. For. Res. 2023, 142, 547–563. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kärenlampi, P.P. Microeconomics of Nitrogen Fertilization in Boreal Carbon Forestry. Climate 2023, 11, 194. https://doi.org/10.3390/cli11090194
Kärenlampi PP. Microeconomics of Nitrogen Fertilization in Boreal Carbon Forestry. Climate. 2023; 11(9):194. https://doi.org/10.3390/cli11090194
Chicago/Turabian StyleKärenlampi, Petri P. 2023. "Microeconomics of Nitrogen Fertilization in Boreal Carbon Forestry" Climate 11, no. 9: 194. https://doi.org/10.3390/cli11090194
APA StyleKärenlampi, P. P. (2023). Microeconomics of Nitrogen Fertilization in Boreal Carbon Forestry. Climate, 11(9), 194. https://doi.org/10.3390/cli11090194




