Assessing Climate Change Impacts on Combined Sewer Overflows: A Modelling Perspective
Abstract
:1. Introduction
2. Materials and Methods
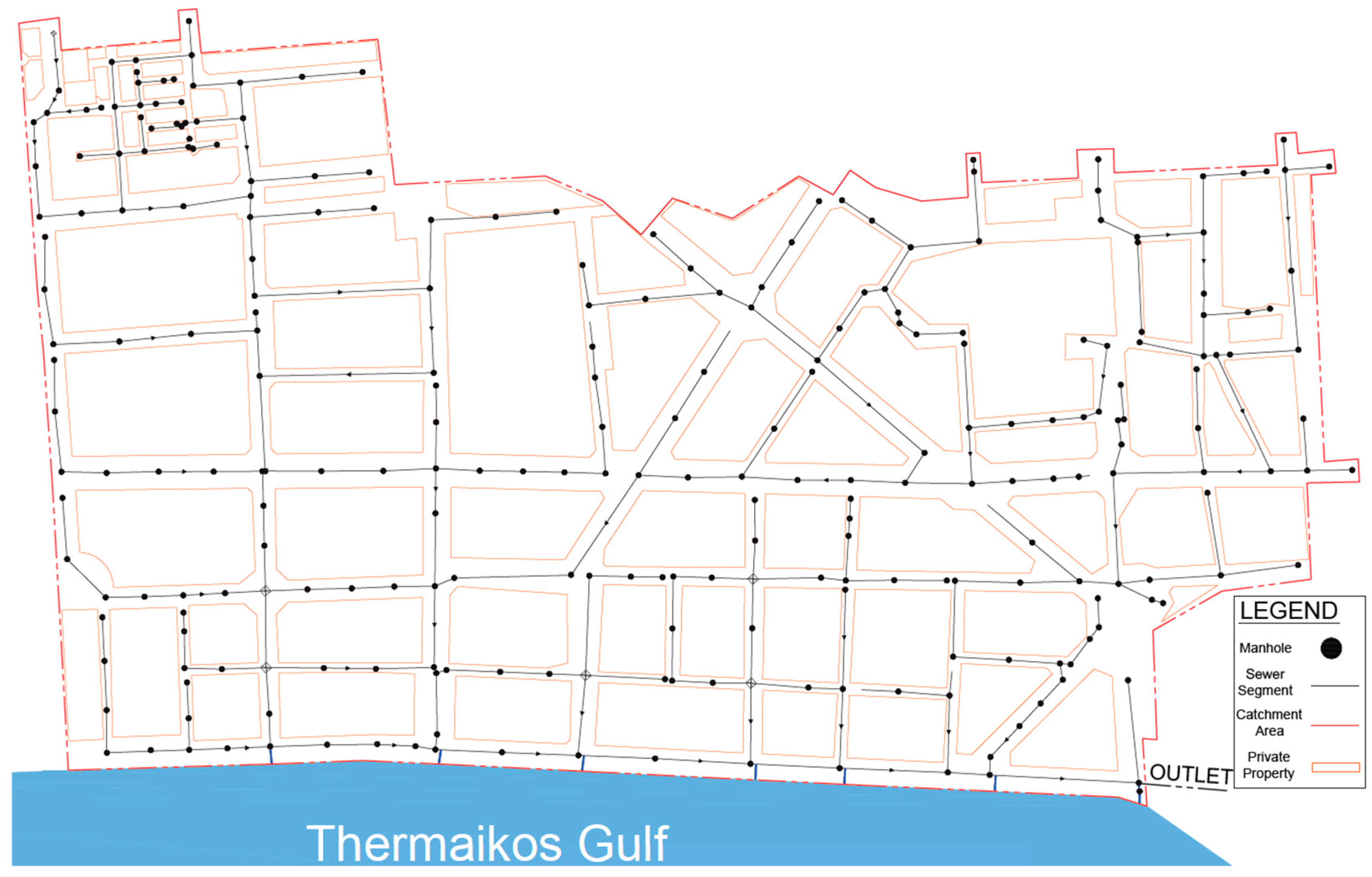
2.1. Study Area
2.2. Climate Data Assessment and Downscaling Methodology
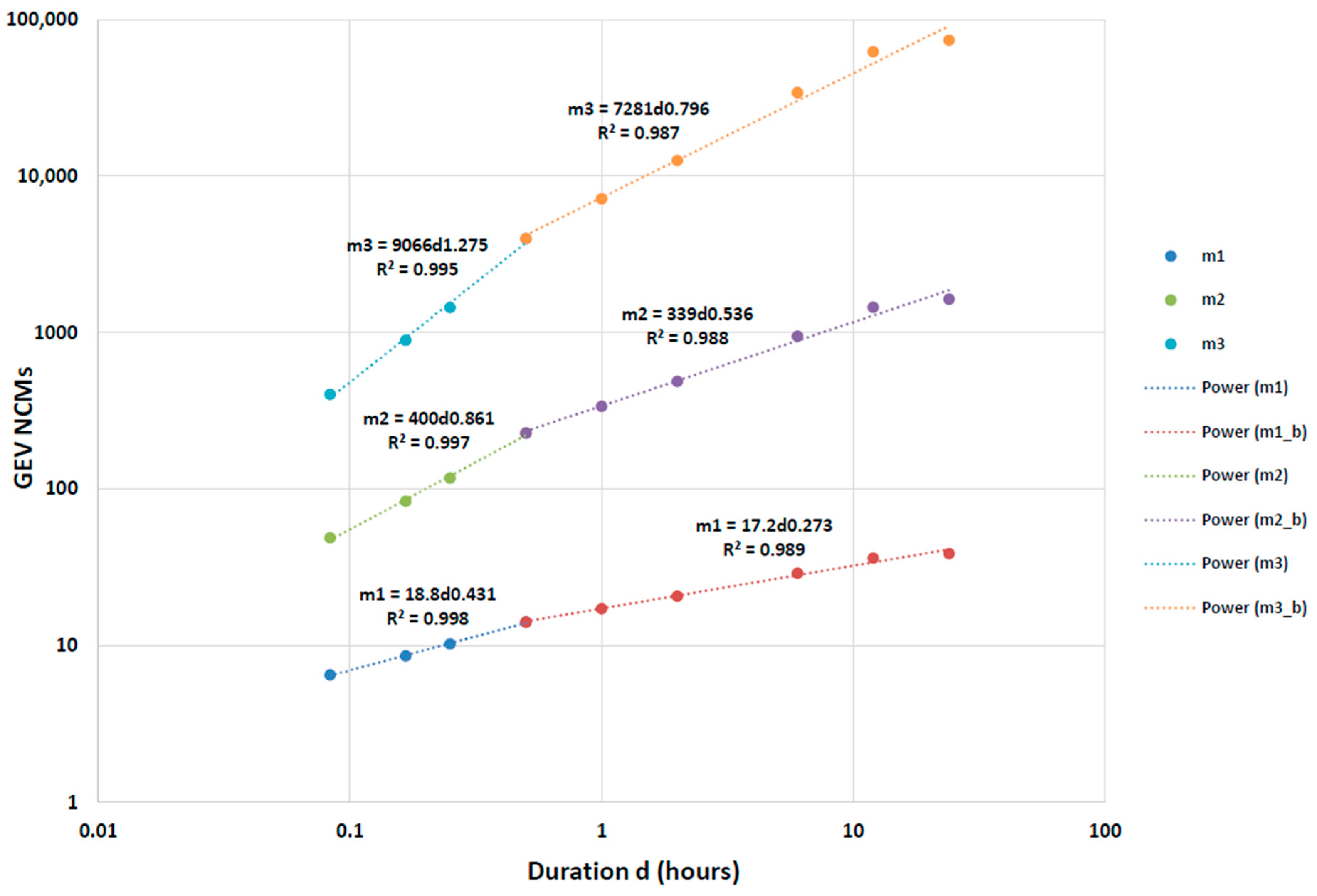
2.3. The Scaling GEV Model
2.4. Hydrologic and Hydraulic Model Configuration
3. Results
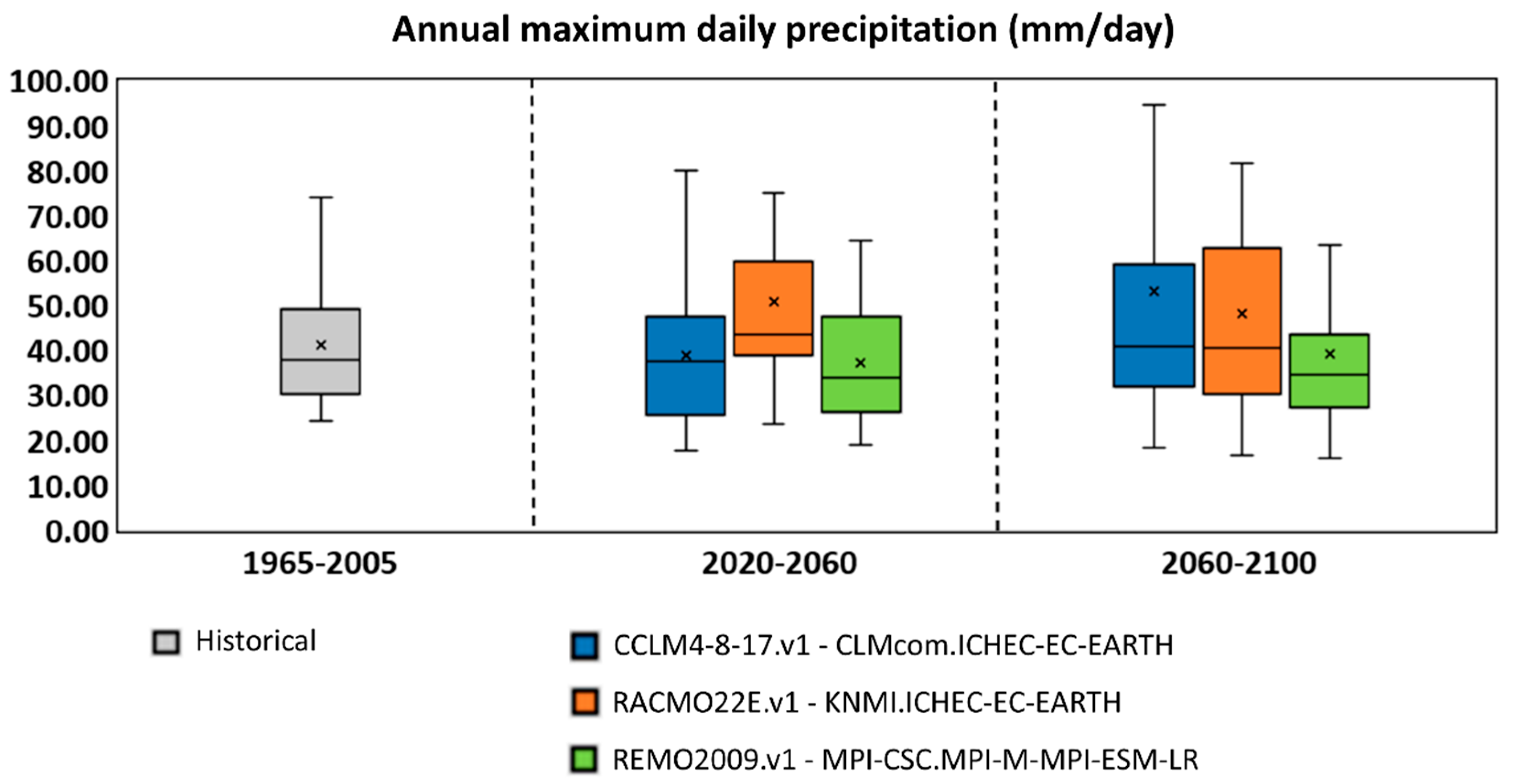
3.1. Projected Outcomes of Climate Models
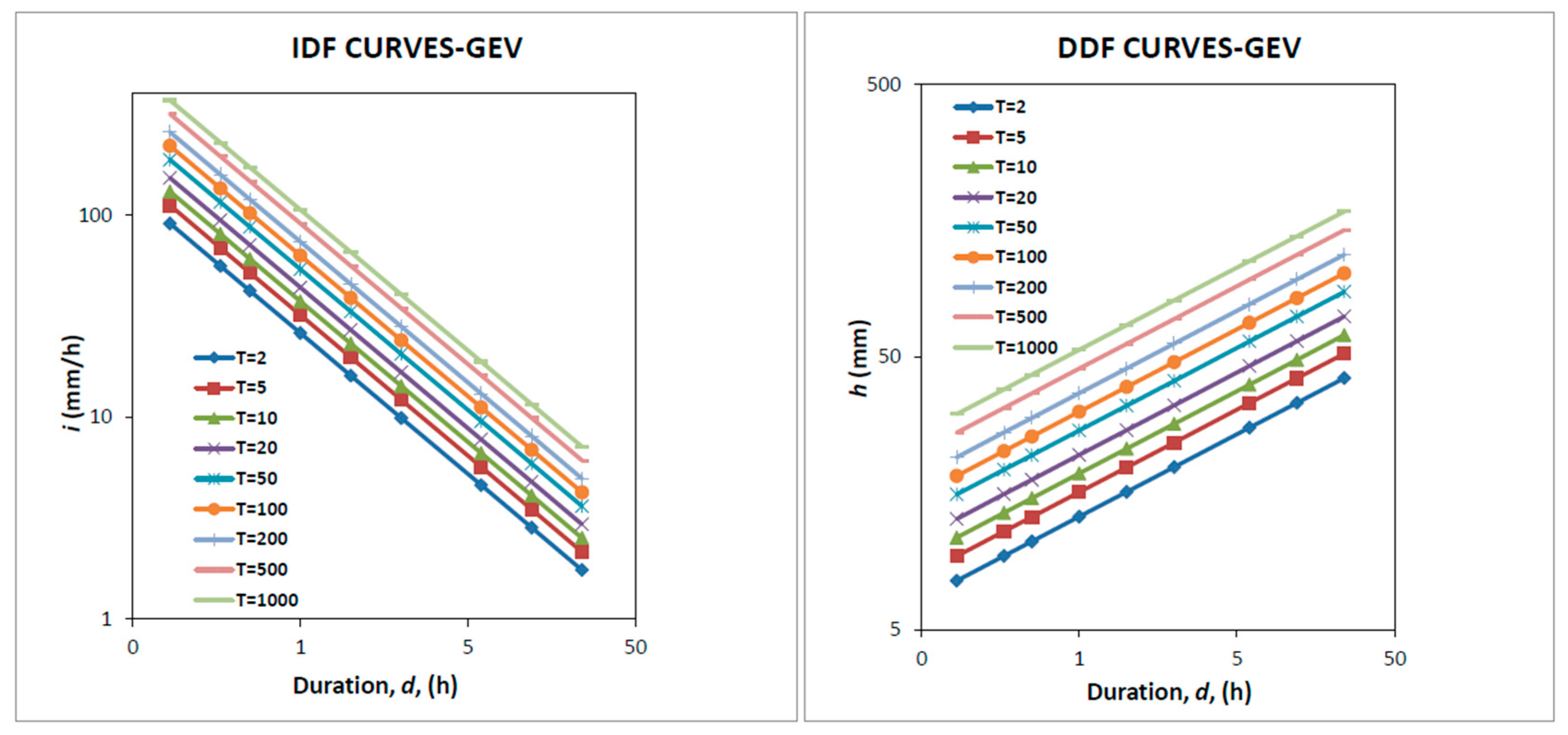
3.2. Development of IDF Curves
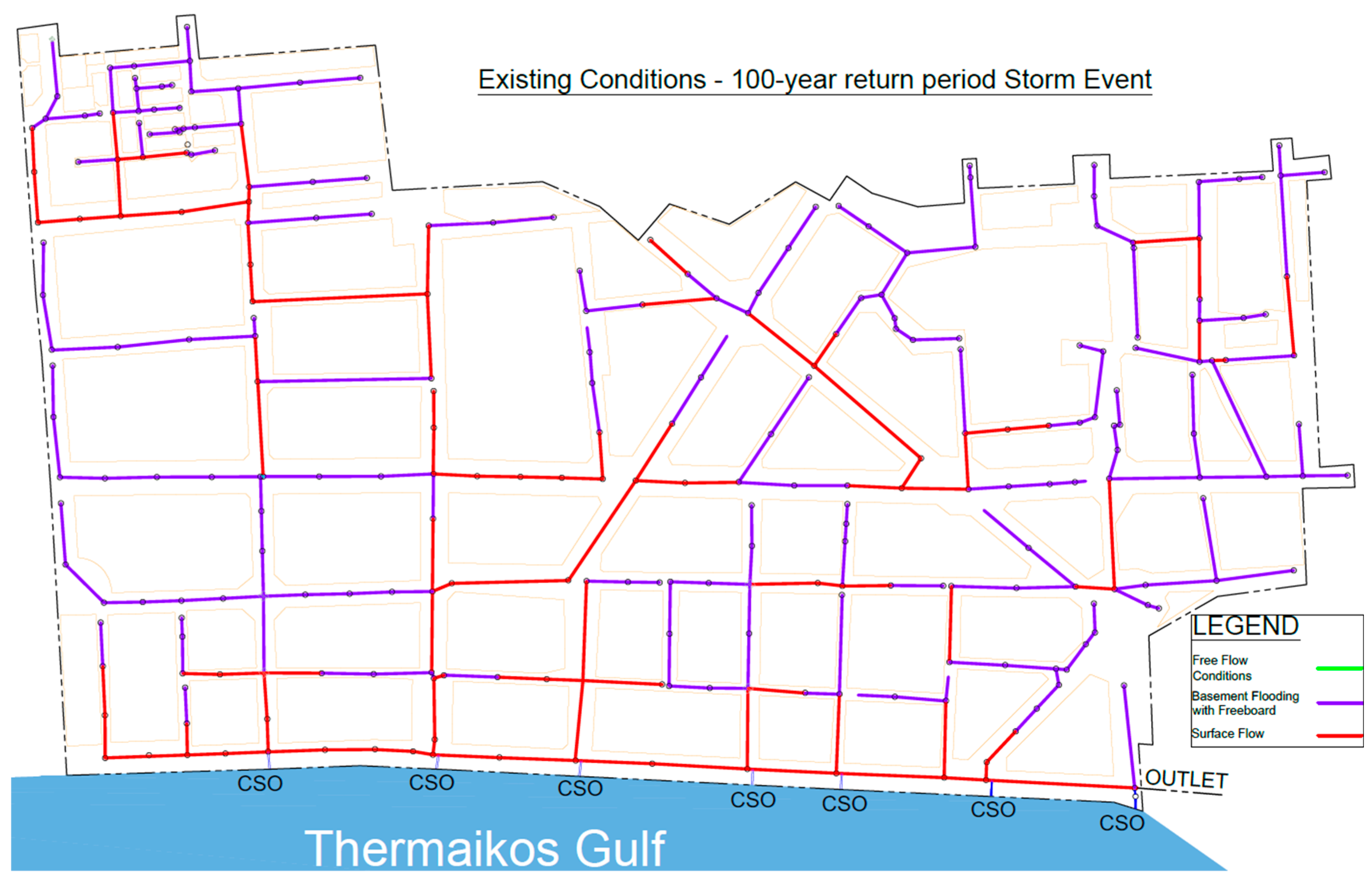
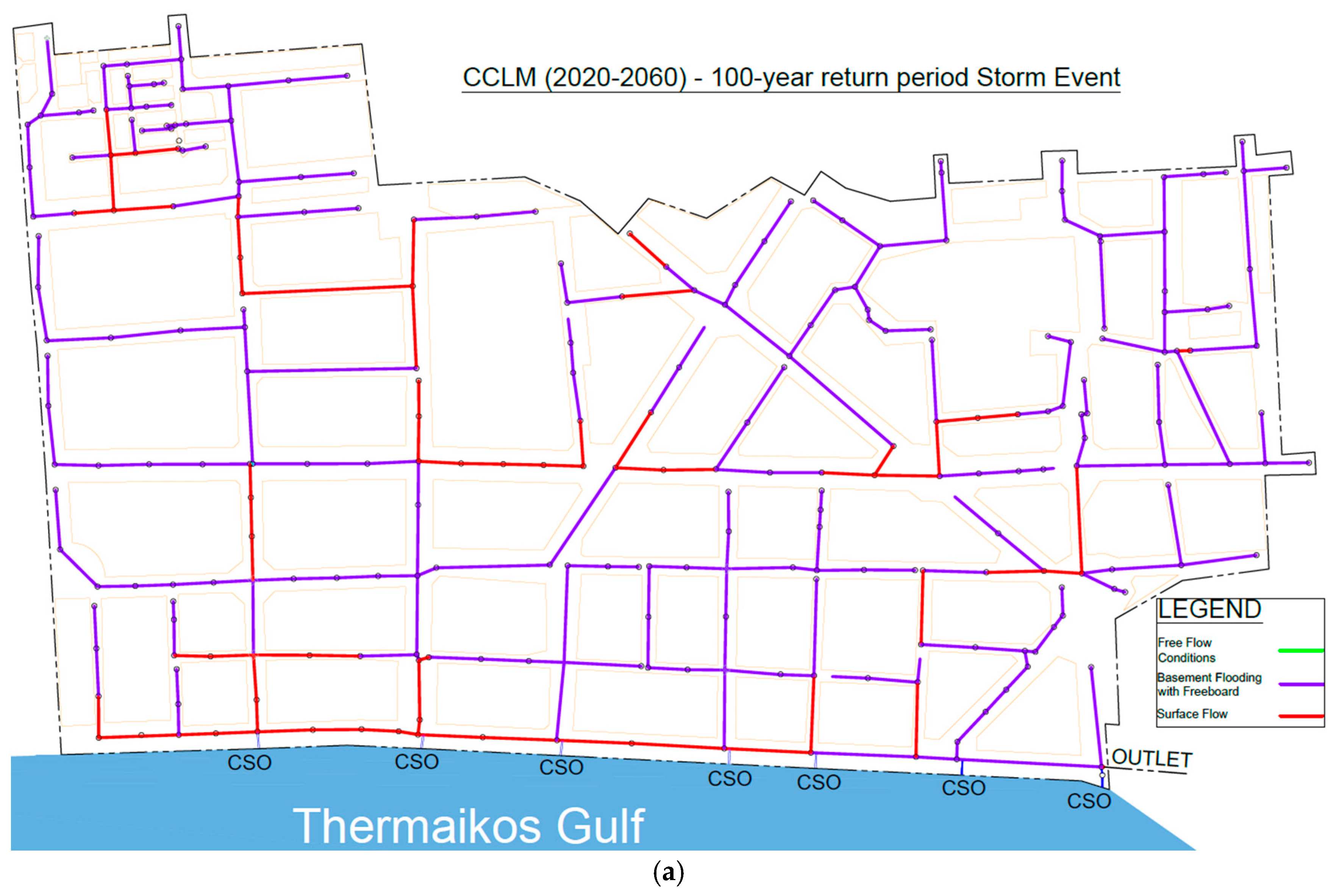
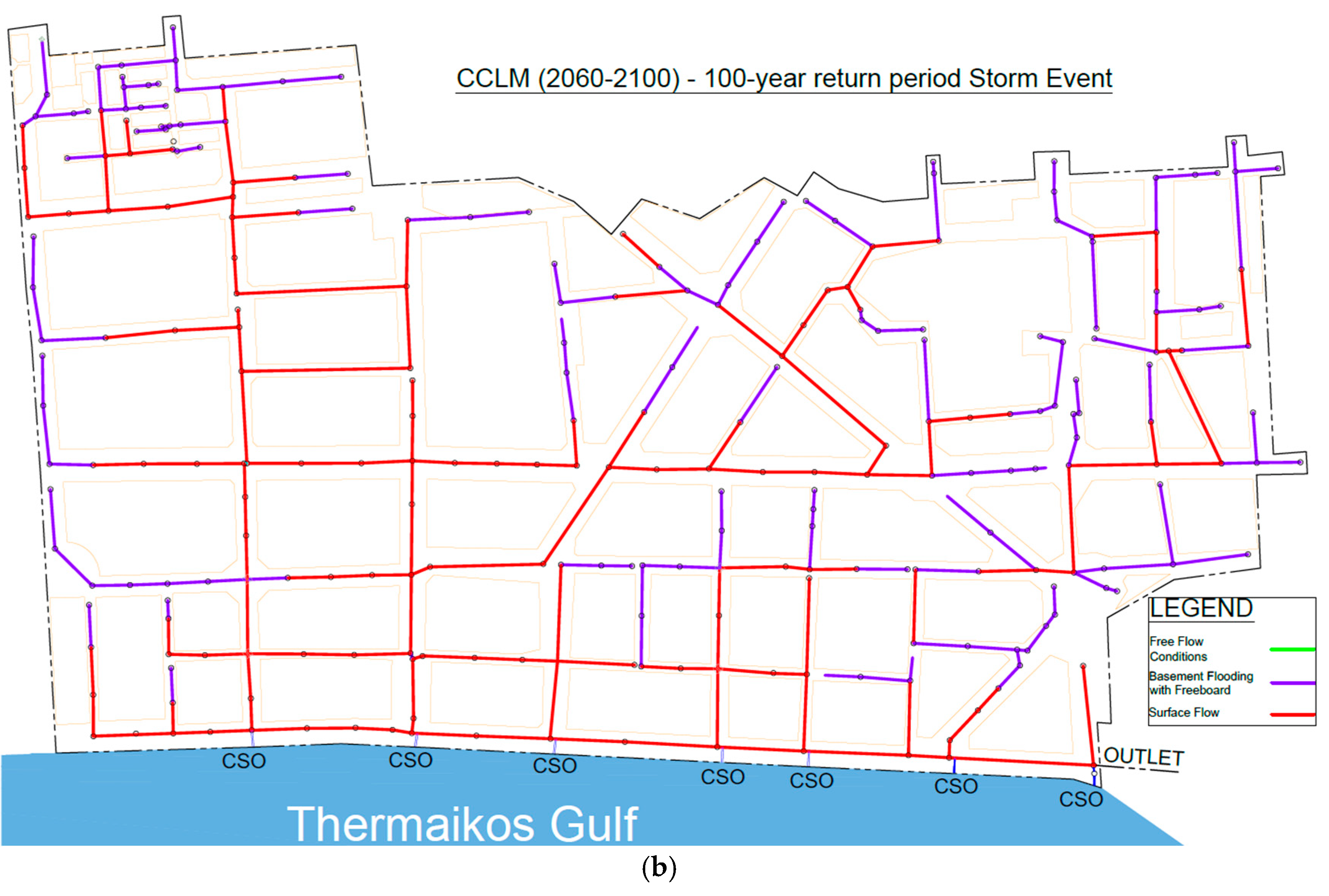
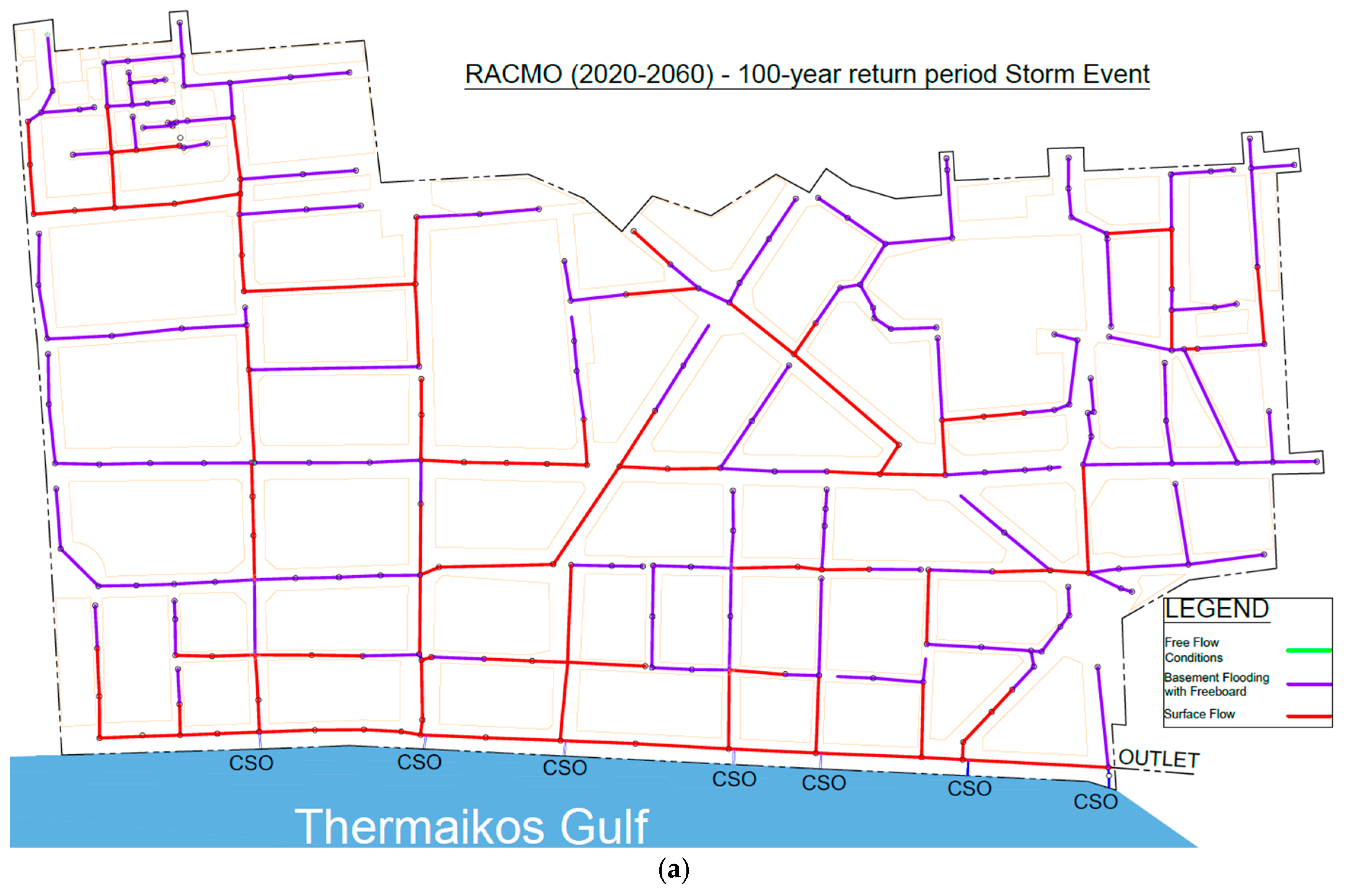
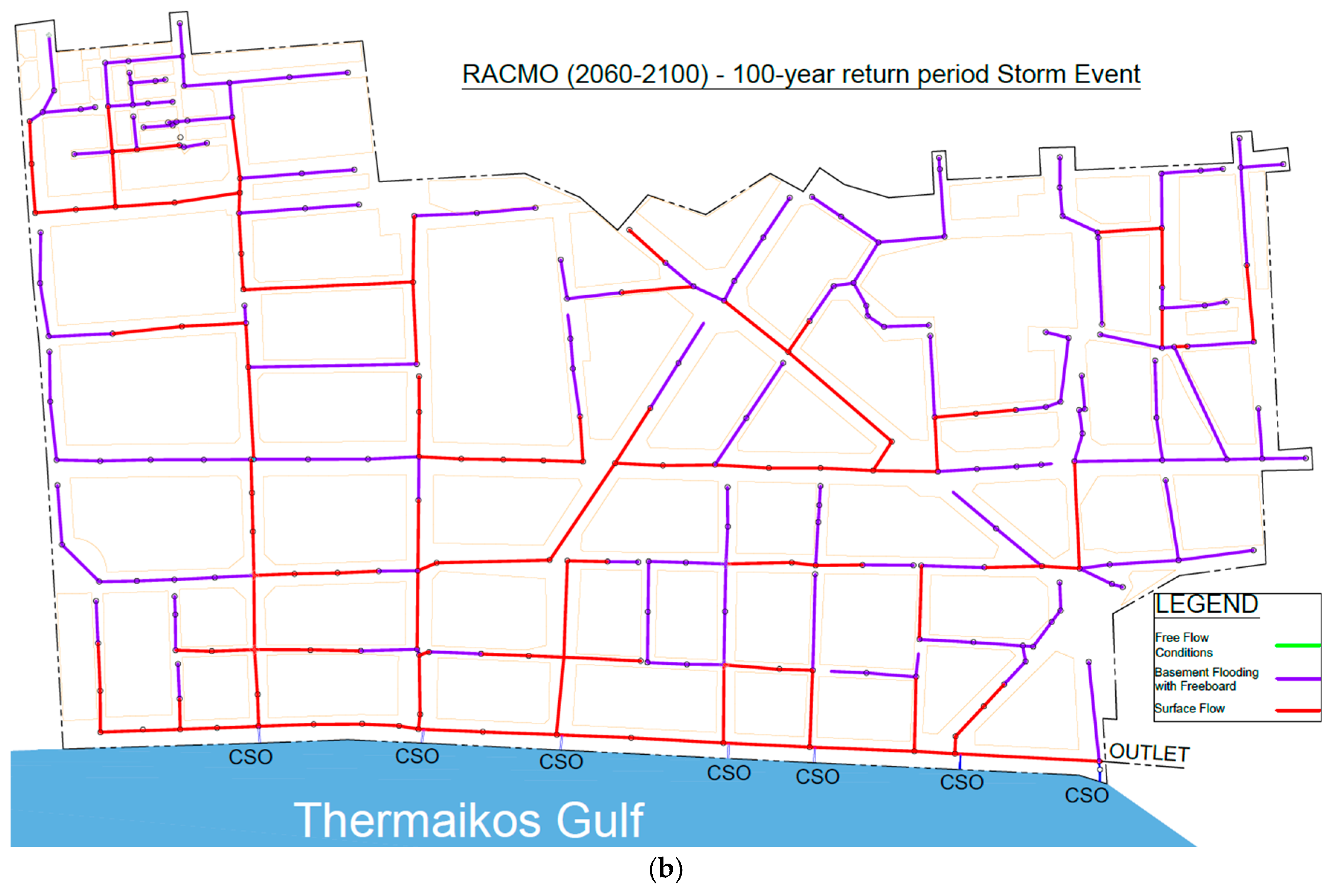
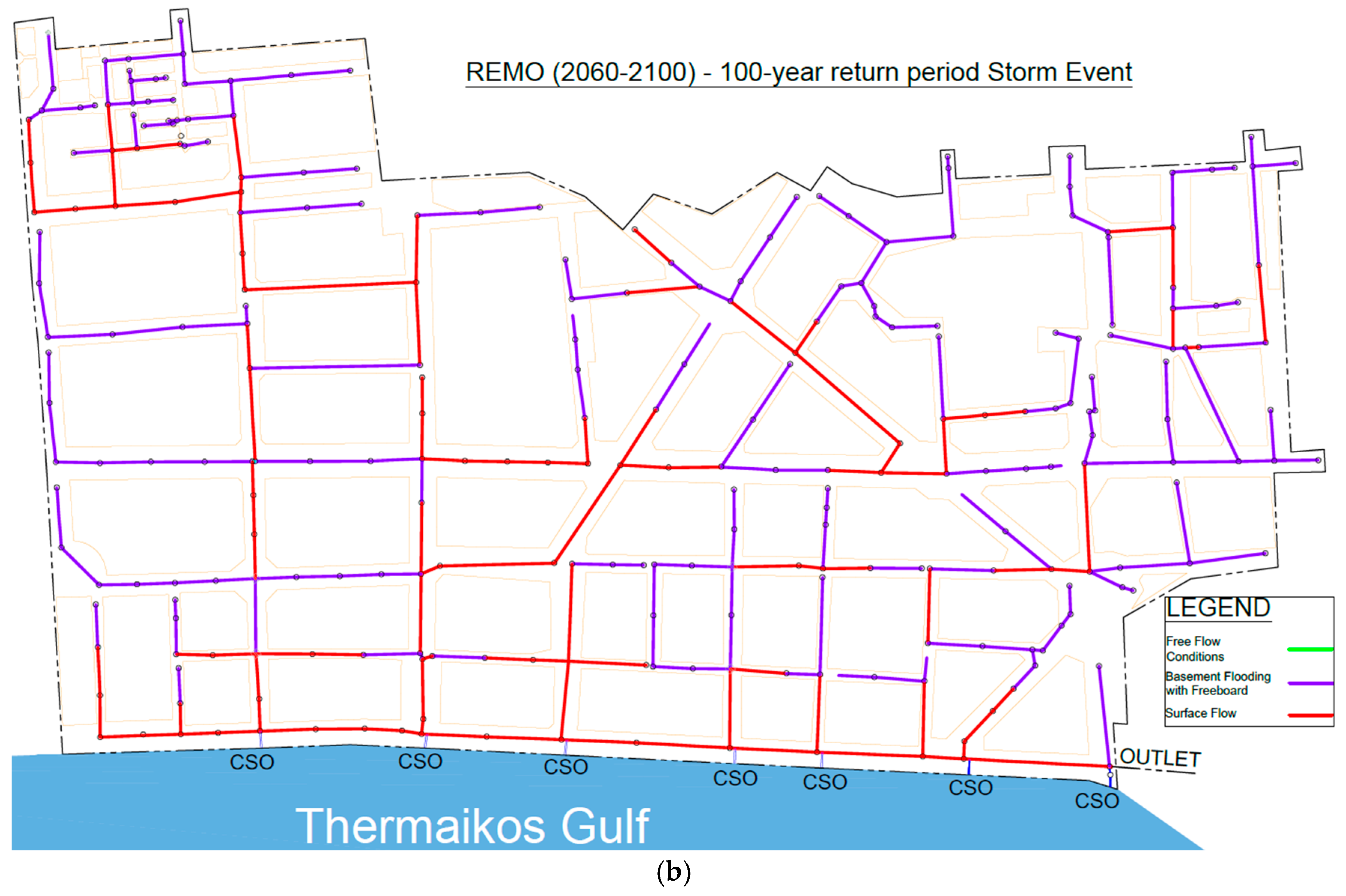
3.3. Hydraulic Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Colmet-Daage, A.; Sanchez-Gomez, E.; Ricci, S.; Llovel, C.; Borrell Estupina, V.; Quintana-Seguí, P.; Llasat, M.C.; Servat, E. Evaluation of uncertainties in mean and extreme precipitation under climate change for northwestern Mediterranean watersheds from high-resolution Med and Euro-CORDEX ensembles. Hydrol. Earth Syst. Sci. 2018, 22, 673–687. [Google Scholar] [CrossRef]
- Tramblay, Y.; Somot, S. Future evolution of extreme precipitation in the Mediterranean. Clim. Change 2018, 151, 289–302. [Google Scholar] [CrossRef]
- Berg, P.; Christensen, O.B.; Klehmet, K.; Lenderink, G.; Olsson, J.; Teichmann, C.; Yang, W. Summertime precipitation extremes in a EURO-CORDEX 0.11° ensemble at an hourly resolution. Nat. Hazards Earth Syst. Sci. 2019, 19, 957–971. [Google Scholar] [CrossRef]
- Cardell, M.F.; Amengual, A.; Romero, R.; Ramis, C. Future extremes of temperature and precipitation in Europe derived from a combination of dynamical and statistical approaches. Int. J. Climatol. 2020, 40, 4800–4827. [Google Scholar] [CrossRef]
- Di Sante, F.; Coppola, E.; Giorgi, F. Projections of river floods in Europe using EURO-CORDEX, CMIP5 and CMIP6 simulations. Int. J. Climatol. 2021, 41, 3203–3221. [Google Scholar] [CrossRef]
- Ivušić, S.; Güttler, I.; Horvath, K. Overview of mean and extreme precipitation climate changes across the Dinaric Alps in the latest EURO-CORDEX ensemble. Clim. Dyn. 2024, 62, 10785–10815. [Google Scholar] [CrossRef]
- Vautard, R.; Kadygrov, N.; Iles, C.; Boberg, F.; Buonomo, E.; Bülow, K.; Coppola, E.; Corre, L.; van Meijgaard, E.; Nogherotto, R.; et al. Evaluation of the Large EURO-CORDEX Regional Climate Model Ensemble. JGR Atmos. 2021, 126, e2019JD032344. [Google Scholar] [CrossRef]
- Boe, J.; Mass, A.; Deman, J. A simple hybrid statistical–dynamical downscaling method for emulating regional climate models over Western Europe. Evaluation, application, and role of added value? Clim. Dyn. 2022, 61, 271–294. [Google Scholar] [CrossRef]
- Ascenso, A.; Augusto, B.; Coelho, S.; Menezes, I.; Monteiro, A.; Rafael, S.; Ferreira, J.; Gama, C.; Roebeling, P.; Miranda, A.I. Assessing Climate Change Projections through High-Resolution Modelling: A Comparative Study of Three European Cities. Sustainability 2024, 16, 7276. [Google Scholar] [CrossRef]
- Cox, P.; Stephenson, D. Climate change—A changing climate for prediction. Science 2007, 317, 207–208. [Google Scholar] [CrossRef]
- Déqué, M.; Rowell, D.P.; Lüthi, D.; Giorgi, F.; Christensen, J.H.; Rockel, B.; Jacob, D.; Kjellström, E.; de Castro, M.; van den Hurk, B. An intercomparison of regional climate simulations for Europe: Assessing uncertainties in model projections. Clim. Change 2007, 81, 53–70. [Google Scholar] [CrossRef]
- Elía, R.; Caya, D.; Côté, H.; Frigon, A.; Biner, S.; Giguère, M.; Paquin, D.; Harvey, R.; Plummer, D. Evaluation of uncertanties in the CRCM-simulated North American climate. Clim. Dyn. 2008, 30, 113–132. [Google Scholar] [CrossRef]
- Kendon, E.J.; Rowell, D.P.; Jones, R.G.; Buonomo, E. Robustness of future changes in local precipitation extremes. J. Clim. 2008, 21, 4280–4297. [Google Scholar] [CrossRef]
- Gogien, F.; Dechesne, M.; Martinerie, R.; Lipeme Kouyi, G. Assessing the impact of climate change on Combined Sewer Overflows based on small time step future rainfall timeseries and long-term continuous sewer network modelling. Water Res. 2023, 230, 119504. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Z.; Cai, Y.; Qiu, J.; Huang, B. Impacts of Climate Change on Urban Drainage Systems by Future Short-Duration Design Rainstorms. Water 2021, 13, 2718. [Google Scholar] [CrossRef]
- Willems, P.; Olsson, J.; Arnbjerg-Nielsen, K.; Beecham, S.; Pathirana, A.; Gregersen, I.B.; Madsen, H.; Nguyen, V.-T.-V. Impacts of Climate Change on Rainfall Extremes and Urban Drainage; IWA Publishing: London, UK, 2012. [Google Scholar]
- Haerter, J.O.; Hagemann, S.; Moseley, C.; Piani, C. Climate model bias correction and the role of timescales. Hydrol. Earth Syst. Sci. 2011, 15, 1065–1079. [Google Scholar] [CrossRef]
- Themeɮl, M.J.; Gobiet, A.; Heinrich, G. Empirical statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Change 2012, 112, 449–468. [Google Scholar]
- Heo, J.H.; Ahn, H.; Shin, J.Y.; Kjeldsen, T.R.; Jeong, C. Probability distributions for a quantile mapping technique for a bias correction of precipitation data: A case study to precipitation data under climate change. Water 2019, 11, 1475. [Google Scholar] [CrossRef]
- Tani, S.; Gobiet, A. Quantile mapping for improving precipitation extremes from regional climate models. J. Agrometeorol. 2019, 21, 434–443. [Google Scholar] [CrossRef]
- Holthuijzen, M.; Beckage, B.; Clemins, P.J.; Higdon, D.; Winter, J.M. Robust bias-correction of precipitation extremes using a novel hybrid empirical quantile-mapping method: Advantages of a linear correction for extremes. Theor. Appl. Climatol. 2022, 149, 863–882. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations–a comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 16, 12–29. [Google Scholar] [CrossRef]
- Chandra, R.R.; Papalexiou, S.M. Precipitation Bias Correction: A Novel Semi-parametric Quantile Mapping Method. Earth Space Sci. 2023, 10, e2023EA002823. [Google Scholar]
- Nguyen, V.-T.-V.; Nguyen, T.-D.; Ashkar, F. Regional Frequency Analysis of Extreme Rainfalls. Water Sci. Technol. 2002, 45, 75–81. [Google Scholar] [CrossRef]
- Terti, G.; Galiatsatou, P.; Prinos, P. Effects of climate change on the estimation of intensity-duration-frequency (IDF) curves for Thessaloniki, Greece. In Proceedings of the 9th International Conference on Urban Drainage Modelling, Belgrade, Serbia, 3–7 September 2012. [Google Scholar]
- Ghanmi, H.; Bargaoui, Z.; Mallet, C. Estimation of intensity-duration-frequency relationships according to the property of scale invariance and regionalization analysis in a Mediterranean coastal area. J. Hydrol. 2016, 541, 38–49. [Google Scholar] [CrossRef]
- Yeo, M.H.; Nguyen, V.T.V.; Kpodonu, T.A. Characterizing extreme rainfalls and constructing confidence intervals for IDF curves using Scaling-GEV distribution model. Int. J. Climatol. 2021, 41, 456–468. [Google Scholar] [CrossRef]
- Galiatsatou, P.; Iliadis, C. Intensity-Duration-Frequency Curves at Ungauged Sites in a Changing Climate for Sustainable Stormwater Networks. Sustainability 2022, 14, 1229. [Google Scholar] [CrossRef]
- Iliadis, C.; Galiatsatou, P.; Glenis, V.; Prinos, P.; Kilsby, C. Urban flood modelling under extreme rainfall conditions for building-level flood exposure analysis. Hydrology 2023, 10, 172. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Veneziano, D.; Furcolo, P. Multifractality of rainfall and scaling of intensity-duration-frequency curves. Water Resour. Res. 2002, 38, 42-1–42-12. [Google Scholar] [CrossRef]
- Singh, V.P.; Zhang, L. IDF curves using the Frank Archimedean copula. J. Hydrol. Eng. 2007, 12, 651–662. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the concepts of return period and risk for nonstationary hydrologic extreme events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J.; Vogel, R.M. Techniques for assessing water infrastructure for nonstationary extreme events: A review. Hydrol. Sci. J. 2018, 63, 325–352. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, L.; Jiang, C.; Zhang, M.; Wang, D.; Xu, C.Y. Updating intensity–duration–frequency curves for urban infrastructure design under a changing environment. Wiley Interdiscip. Rev. Water 2021, 8, e1519. [Google Scholar] [CrossRef]
- Martel, J.L.; Mailhot, A.; Brissette, F.; Caya, D. Role of natural climate variability in the detection of anthropogenic climate change signal for mean and extreme precipitation at local and regional scales. J. Clim. 2018, 31, 4241–4263. [Google Scholar] [CrossRef]
- Schlef, K.E.; Kunkel, K.E.; Brown, C.; Demissie, Y.; Lettenmaier, D.P.; Wagner, A.; Yan, E. Incorporating non-stationarity from climate change into rainfall frequency and intensity-duration-frequency (IDF) curves. J. Hydrol. 2023, 616, 128757. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Stationarity is undead: Uncertainty dominates the distribution of extremes. Adv. Water Resour. 2015, 77, 17–36. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Kourtis, I.M.; Tsihrintzis, V.A. Adaptation of urban drainage networks to climate change: A review. Sci. Total Environ. 2021, 771, 145431. [Google Scholar] [CrossRef]
- Galiatsatou, P.; Zafeirakou, A.; Nikoletos, I.; Gkatzioura, A.; Kapouniari, M.; Katsoulea, A.; Malamataris, D.; Kavouras, I. Capacity Assessment of a Combined Sewer Network under Different Weather Conditions: Using Nature-Based Solutions to Increase Resilience. Water 2024, 16, 2862. [Google Scholar] [CrossRef]
- Al-Mukhtar, M.; Dunger, V.; Merkel, B. Runoff and sediment yield modeling by means of WEPP in the Bautzen dam catchment, Germany. Environ. Earth Sci. 2014, 72, 2051–2063. [Google Scholar] [CrossRef]
- Nasiry, M.K.; Said, S.; Ansari, S.A. Analysis of surface runoff and sediment yield under simulated rainfall. Model. Earth Syst. Environ. 2023, 9, 157–173. [Google Scholar] [CrossRef]
- Cojoc, L.; de Castro-Català, N.; de Guzmán, I.; González, J.; Arroita, M.; Besolí-Mestres, N.; Cadena, I.; Freixa, A.; Gutiérrez, O.; Larrañaga, A.; et al. Pollutants in urban runoff: Scientific evidence on toxicity and impacts on freshwater ecosystems. Chemosphere 2024, 369, 143806. [Google Scholar] [CrossRef] [PubMed]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Change 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Galiatsatou, P.; Prinos, P. Joint probability analysis of extreme wave heights and storm surges in the Aegean Sea in a changing climate. E3S Web Conf. 2016, 7, 02002. [Google Scholar] [CrossRef]
- Silva Lomba, J.; Fraga Alves, M.I. L-moments for automatic threshold selection in extreme value analysis. Stoch. Environ. Res. Risk Assess. 2020, 34, 465–491. [Google Scholar] [CrossRef]
- Galiatsatou, P.; Prinos, P. Bivariate analysis of extreme wave and storm surge events. Determining the failure area of structures. Open Ocean Eng. J. 2011, 4, 3–14. [Google Scholar] [CrossRef]
- Galiatsatou, P.; Prinos, P.; Sanchez-Arcilla, A. Estimation of extremes: Conventional versus Bayesian techniques. J. Hydraul. Res. 2008, 46, 211–223. [Google Scholar] [CrossRef]
- Desramaut, N. Estimation of Intensity Duration Frequency Curves for Current and Future Climates. Master’s Thesis, McGill University, Montreal, QC, Canada, 2008; pp. 1–75. [Google Scholar]
- InfoWorks ICM Help Documentation. Available online: https://help-innovyze.refined.site/space/infoworksicm/18219088/ (accessed on 31 May 2024).
- Sheng, J.G.; Dan, Y.D.; Liu, C.S.; Ma, L.M. Study of Simulation in Storm Sewer System of Zhenjiang Urban by Infoworks ICM. Model. Appl. Mech. Mater. 2012, 193, 683–686. [Google Scholar] [CrossRef]
- Peng, H.-Q.; Liu, Y.; Wang, H.-W.; Ma, L.-M. Assessment of the service performance of drainage system and transformation of pipeline network based on urban combined sewer system model. Environ. Sci. Pollut. Res. 2015, 22, 15712–15721. [Google Scholar] [CrossRef]
- Biswas, R.R. Modelling seismic effects on a sewer network using Infoworks ICM. Indian J. Sci. Technol. 2017, 10, 1–9. [Google Scholar] [CrossRef]
- Sidek, L.M.; Jaafar, A.S.; Majid, W.H.A.W.A.; Basri, H.; Marufuzzaman, M.; Fared, M.M.; Moon, W.C. High-resolution hydrological-hydraulic modeling of urban floods using InfoWorks ICM. Sustainability 2021, 13, 10259. [Google Scholar] [CrossRef]
- Leitao, J.; Simoes, N.; Pina, R.D.; Ochoa-Rodriguez, S.; Onof, C.; Sa Marques, A. Stochastic evaluation of the impact of sewer inlets’ hydraulic capacity on urban pluvial flooding. Stoch. Environ. Res. Risk Assess. 2017, 31, 1907–1922. [Google Scholar] [CrossRef]
- Cheng, T.; Xu, Z.; Hong, S.; Song, S. Flood risk zoning by using 2D hydrodynamic modeling: A case study in Jinan City. Math. Probl. Eng. 2017, 2017, 5659197. [Google Scholar] [CrossRef]
- Wang, K.; Chen, J.; Hu, H.; Tang, Y.; Huang, J.; Wu, Y.; Lu, J.; Zhou, J. Urban Waterlogging Simulation and Disaster Risk Analysis Using InfoWorks Integrated Catchment Management: A Case Study from the Yushan Lake Area of Ma’anshan City in China. Water 2024, 16, 3383. [Google Scholar] [CrossRef]
- Nikoletos, I.; Katsifarakis, K. The Method of Images Revisited: Approximate Solutions in Wedge-Shaped Aquifers of Arbitrary Angle. Water Resour. Res. 2024, 60, e2022WR034347. [Google Scholar] [CrossRef]
- Jin, X.; Mu, Y. Hydrodynamic Simulation of Urban Waterlogging Based on an Improved Vertical Flow Exchange Method. Water 2024, 16, 1563. [Google Scholar] [CrossRef]


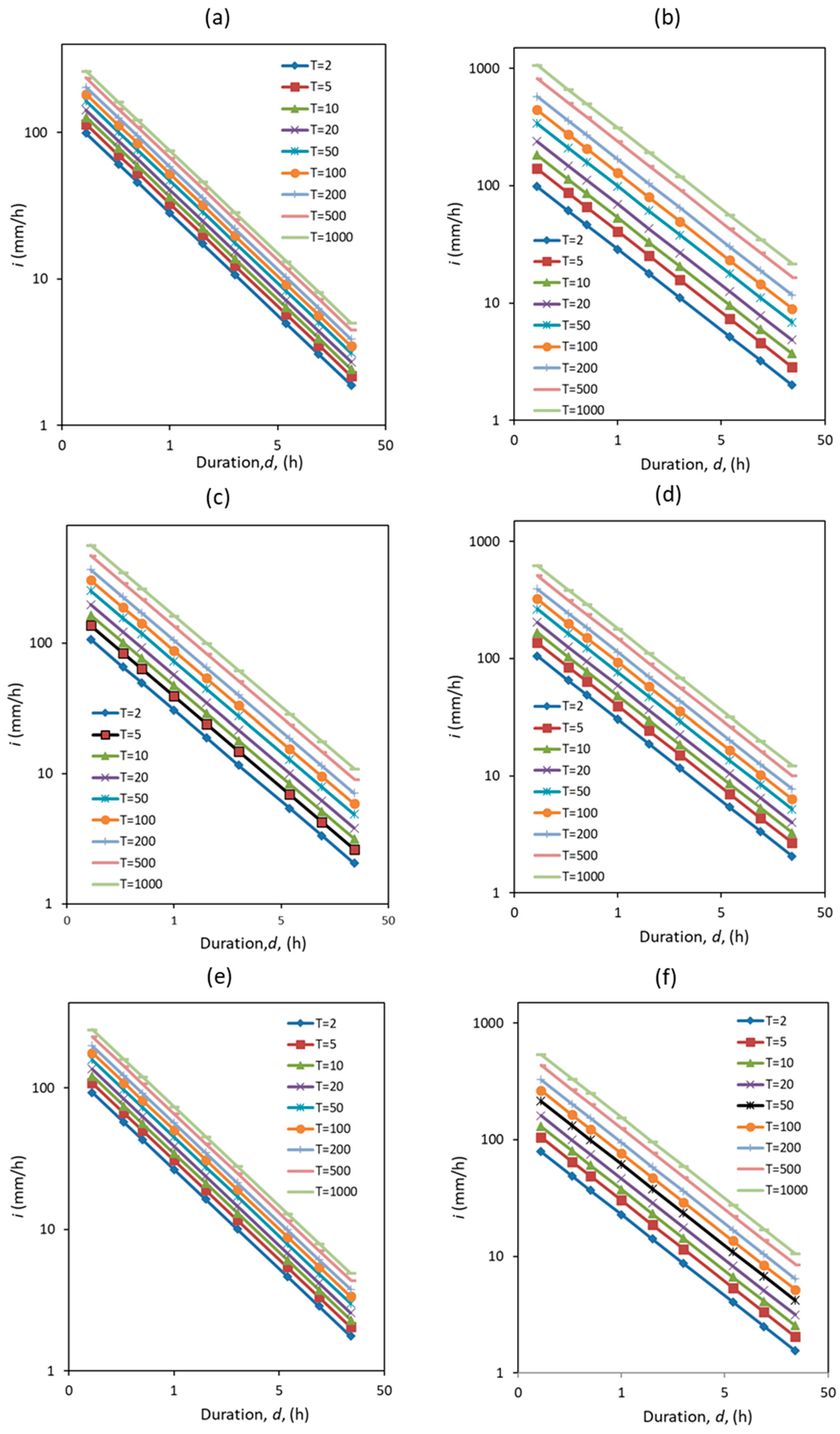

| Institute_id | RCM | Driving GCM | Realization | |
|---|---|---|---|---|
| 1 | CLMcom | CCLM4-8-17.v1 | CLMcom.ICHEC-EC-EARTH | r12i1p1 |
| 2 | KNMI | RACMO22E.v1 | KNMI.ICHEC-EC-EARTH | r12i1p1 |
| 3 | MPI-CSC | REMO2009.v1 | MPI-CSC.MPI-M-MPI-ESM-LR | r1i1p1 |
| Daily Max. | Daily Avg. | St. Dev. | |
|---|---|---|---|
| Measurements (1965–2005) | 52.23 | 1.21 | 4.22 |
|
CCLM4-8-17.v1-CLMcom.ICHEC-EC-EARTH Raw climatic data (1965-2005) | 74.73 | 1.46 | 4.61 |
|
CCLM4-8-17.v1-CLMcom.ICHEC-EC-EARTH Bias-corrected data (1965–2005) | 62.14 | 1.22 | 4.03 |
|
RACMO22E.v1-KNMI.ICHEC-EC-EARTH Raw climatic data (1965–2005) | 39.03 | 1.13 | 3.45 |
|
RACMO22E.v1-KNMI.ICHEC-EC-EARTH Bias-corrected data (1965–2005) | 50.29 | 1.22 | 4.16 |
| REMO2009.v1-MPI-CSC.MPI-M-MPI-ESM-LR Raw climatic data (1965–2005) | 59.58 | 1.42 | 4.52 |
| REMO2009.v1-MPI-CSC.MPI-M-MPI-ESM-LR Bias-corrected data (1965–2005) | 55.53 | 1.22 | 4.15 |
| Measurements (mm/day) (1965–2005) | Downscaled Climatic Data (mm/day) (2020–2060) | Downscaled Climatic Data (mm/day) (2060–2100) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Daily Min. | Daily Max. | Daily Avg. | St. Dev. | Daily Min. | Daily Max. | Daily Avg. | St. Dev. | Daily Min. | Daily Max. | Daily Avg. | St. Dev. | |
| Oct. | 0.00 | 62.70 | 1.31 | 4.68 | 0.00 | 66.28 | 1.20 | 4.51 | 0.00 | 87.92 | 1.21 | 5.09 |
| Nov. | 0.00 | 98.00 | 1.72 | 5.96 | 0.00 | 66.07 | 2.02 | 6.60 | 0.00 | 88.06 | 2.39 | 8.06 |
| Dec. | 0.00 | 54.50 | 1.62 | 4.80 | 0.00 | 35.69 | 1.31 | 2.80 | 0.00 | 22.86 | 1.63 | 2.93 |
| Jan. | 0.00 | 33.80 | 1.11 | 3.34 | 0.00 | 40.59 | 1.22 | 3.73 | 0.00 | 29.21 | 0.86 | 2.96 |
| Feb. | 0.00 | 49.20 | 1.22 | 3.88 | 0.00 | 46.24 | 1.11 | 3.48 | 0.00 | 33.76 | 0.89 | 2.70 |
| Mar. | 0.00 | 49.00 | 1.23 | 3.82 | 0.00 | 31.82 | 1.11 | 3.02 | 0.00 | 38.83 | 1.26 | 3.71 |
| Apr. | 0.00 | 54.20 | 1.25 | 3.85 | 0.00 | 35.74 | 1.16 | 3.43 | 0.00 | 34.90 | 0.85 | 3.01 |
| May | 0.00 | 38.10 | 1.53 | 4.32 | 0.00 | 51.25 | 1.56 | 3.91 | 0.00 | 86.33 | 1.67 | 4.89 |
| June | 0.00 | 39.60 | 0.89 | 3.47 | 0.00 | 63.64 | 1.06 | 4.19 | 0.00 | 109.21 | 1.11 | 4.78 |
| July | 0.00 | 60.70 | 0.92 | 4.37 | 0.00 | 49.77 | 1.03 | 4.18 | 0.00 | 155.29 | 0.86 | 5.48 |
| Aug. | 0.00 | 36.10 | 0.78 | 3.36 | 0.00 | 79.82 | 0.64 | 3.78 | 0.00 | 185.40 | 0.73 | 6.37 |
| Sept. | 0.00 | 50.90 | 0.93 | 3.93 | 0.00 | 56.68 | 0.92 | 3.47 | 0.00 | 53.08 | 0.73 | 3.30 |
| Measurements (mm/day) (1965–2005) | Downscaled Climatic Data (mm/day) (2020–2060) | Downscaled Climatic Data (mm/day) (2060–2100) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Daily Min. | Daily Max. | Daily Avg. | St. Dev. | Daily Min. | Daily Max. | Daily Avg. | St. Dev. | Daily Min. | Daily Max. | Daily Avg. | St. Dev. | |
| Oct. | 0.00 | 62.70 | 1.31 | 4.68 | 0.00 | 68.74 | 1.32 | 5.19 | 0.00 | 60.94 | 1.06 | 4.09 |
| Nov. | 0.00 | 98.00 | 1.72 | 5.96 | 0.00 | 105.42 | 2.51 | 8.75 | 0.00 | 79.22 | 2.33 | 8.18 |
| Dec. | 0.00 | 54.50 | 1.62 | 4.80 | 0.00 | 41.35 | 1.31 | 4.12 | 0.00 | 74.02 | 1.97 | 5.66 |
| Jan. | 0.00 | 33.80 | 1.11 | 3.34 | 0.00 | 28.49 | 1.04 | 2.56 | 0.00 | 19.63 | 0.74 | 2.07 |
| Feb. | 0.00 | 49.20 | 1.22 | 3.88 | 0.00 | 45.52 | 1.67 | 4.81 | 0.00 | 45.84 | 1.38 | 4.30 |
| Mar. | 0.00 | 49.00 | 1.23 | 3.82 | 0.00 | 92.80 | 1.56 | 4.88 | 0.00 | 45.06 | 1.48 | 4.49 |
| Apr. | 0.00 | 54.20 | 1.25 | 3.85 | 0.00 | 41.94 | 1.10 | 3.23 | 0.00 | 46.96 | 1.18 | 3.92 |
| May | 0.00 | 38.10 | 1.53 | 4.32 | 0.00 | 72.92 | 2.00 | 5.45 | 0.00 | 70.56 | 1.89 | 5.74 |
| June | 0.00 | 39.60 | 0.89 | 3.47 | 0.00 | 38.82 | 0.99 | 3.21 | 0.00 | 55.75 | 1.08 | 3.92 |
| July | 0.00 | 60.70 | 0.92 | 4.37 | 0.00 | 49.77 | 1.03 | 4.18 | 0.00 | 155.29 | 0.86 | 5.48 |
| Aug. | 0.00 | 36.10 | 0.78 | 3.36 | 0.00 | 30.92 | 0.53 | 2.09 | 0.00 | 29.74 | 0.79 | 2.75 |
| Sept. | 0.00 | 50.90 | 0.93 | 3.93 | 0.00 | 100.90 | 1.26 | 5.54 | 0.00 | 81.47 | 1.09 | 4.71 |
| Measurements (mm/day) (1965–2005) | Downscaled Climatic Data (mm/day) (2020–2060) | Downscaled Climatic Data (mm/day) (2060–2100) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Daily Min. | Daily Max. | Daily Avg. | St. Dev. | Daily Min. | Daily Max. | Daily Avg. | St. Dev. | Daily Min. | Daily Max. | Daily Avg. | St. Dev. | |
| Oct. | 0.00 | 62.70 | 1.31 | 4.68 | 0.00 | 49.09 | 1.29 | 4.15 | 0.00 | 36.25 | 1.18 | 3.47 |
| Nov. | 0.00 | 98.00 | 1.72 | 5.96 | 0.00 | 64.50 | 1.90 | 6.11 | 0.00 | 63.37 | 2.01 | 6.15 |
| Dec. | 0.00 | 54.50 | 1.62 | 4.80 | 0.00 | 54.92 | 1.87 | 5.43 | 0.00 | 56.46 | 1.54 | 4.93 |
| Jan. | 0.00 | 33.80 | 1.11 | 3.34 | 0.00 | 31.16 | 1.21 | 3.36 | 0.00 | 40.98 | 1.22 | 3.60 |
| Feb. | 0.00 | 49.20 | 1.22 | 3.88 | 0.00 | 59.89 | 1.24 | 3.91 | 0.00 | 55.69 | 1.39 | 4.51 |
| Mar. | 0.00 | 49.00 | 1.23 | 3.82 | 0.00 | 52.69 | 1.51 | 4.55 | 0.00 | 29.66 | 1.05 | 3.11 |
| Apr. | 0.00 | 54.20 | 1.25 | 3.85 | 0.00 | 38.33 | 1.29 | 3.67 | 0.00 | 39.17 | 1.32 | 3.90 |
| May | 0.00 | 38.10 | 1.53 | 4.32 | 0.00 | 32.42 | 1.18 | 3.13 | 0.00 | 31.66 | 0.88 | 2.50 |
| June | 0.00 | 39.60 | 0.89 | 3.47 | 0.00 | 27.13 | 0.52 | 1.92 | 0.00 | 146.11 | 0.70 | 4.68 |
| July | 0.00 | 60.70 | 0.92 | 4.37 | 0.00 | 52.09 | 0.53 | 2.94 | 0.00 | 61.20 | 0.40 | 2.73 |
| Aug. | 0.00 | 36.10 | 0.78 | 3.36 | 0.00 | 49.81 | 0.61 | 2.83 | 0.00 | 50.13 | 0.52 | 2.55 |
| Sept. | 0.00 | 50.90 | 0.93 | 3.93 | 0.00 | 28.59 | 0.80 | 3.10 | 0.00 | 42.30 | 0.59 | 2.77 |
| Climate Period and RCM | DDF Equation | IDF Equation |
|---|---|---|
| 1965–2005 Historical/Reference | 33.19T0.227d0.302 | 33.19T0.227d−0.698 |
| 2020–2060 CCLM | 28.83T0.157d0.300 | 28.83T0.157d−0.700 |
| 2020–2060 RACMO | 44.70T0.268d0.303 | 44.70T0.268d−0.697 |
| 2020–2060 REMO | 27.73T0.165d0.300 | 27.73T0.165d−0.700 |
| 2060–2100 CCLM | 61.24T0.383d0.311 | 61.24T0.383d−0.689 |
| 2060–2100 RACMO | 47.13T0.287d0.306 | 47.13T0.287d−0.694 |
| 2060–2100 REMO | 38.02T0.309d0.305 | 38.02T0.309d−0.695 |
| Scenario (100-Year Return Period) | Combined Sewer Overflow Volume (m3) |
|---|---|
| Existing Conditions | 12,273 |
| 2020–2060 CCLM | 10,735 |
| 2020–2060 RACMO | 17,117 |
| 2020–2060 REMO | 10,012 |
| 2060–2100 CCLM | 25,514 |
| 2060–2100 RACMO | 18,605 |
| 2060–2100 REMO | 15,799 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galiatsatou, P.; Nikoletos, I.; Malamataris, D.; Zafirakou, A.; Ganoulis, P.J.; Gkatzioura, A.; Kapouniari, M.; Katsoulea, A. Assessing Climate Change Impacts on Combined Sewer Overflows: A Modelling Perspective. Climate 2025, 13, 82. https://doi.org/10.3390/cli13050082
Galiatsatou P, Nikoletos I, Malamataris D, Zafirakou A, Ganoulis PJ, Gkatzioura A, Kapouniari M, Katsoulea A. Assessing Climate Change Impacts on Combined Sewer Overflows: A Modelling Perspective. Climate. 2025; 13(5):82. https://doi.org/10.3390/cli13050082
Chicago/Turabian StyleGaliatsatou, Panagiota, Iraklis Nikoletos, Dimitrios Malamataris, Antigoni Zafirakou, Philippos Jacob Ganoulis, Argyro Gkatzioura, Maria Kapouniari, and Anastasia Katsoulea. 2025. "Assessing Climate Change Impacts on Combined Sewer Overflows: A Modelling Perspective" Climate 13, no. 5: 82. https://doi.org/10.3390/cli13050082
APA StyleGaliatsatou, P., Nikoletos, I., Malamataris, D., Zafirakou, A., Ganoulis, P. J., Gkatzioura, A., Kapouniari, M., & Katsoulea, A. (2025). Assessing Climate Change Impacts on Combined Sewer Overflows: A Modelling Perspective. Climate, 13(5), 82. https://doi.org/10.3390/cli13050082









