Modelling Hydrological Components of the Rio Maipo of Chile, and Their Prospective Evolution under Climate Change
Abstract
:1. Introduction
2. Case Study and Data Base
2.1. Maipo River
2.2. Historical Weather and Hydro Data
2.3. Satellite Data
2.4. Field Campaigns
2.5. Climate Projections
3. Methods
3.1. Glacio-Hydrological Modelling
3.2. Temperature and Precipitation Correction Using Satellite Data
3.3. Snow and Ice Ablation Modelling
3.4. Downscaling of GCM Projections
3.5. Glacio-Hydrological Projections
3.6. Trend Analysis, and Correlation against Climate Drivers
4. Results
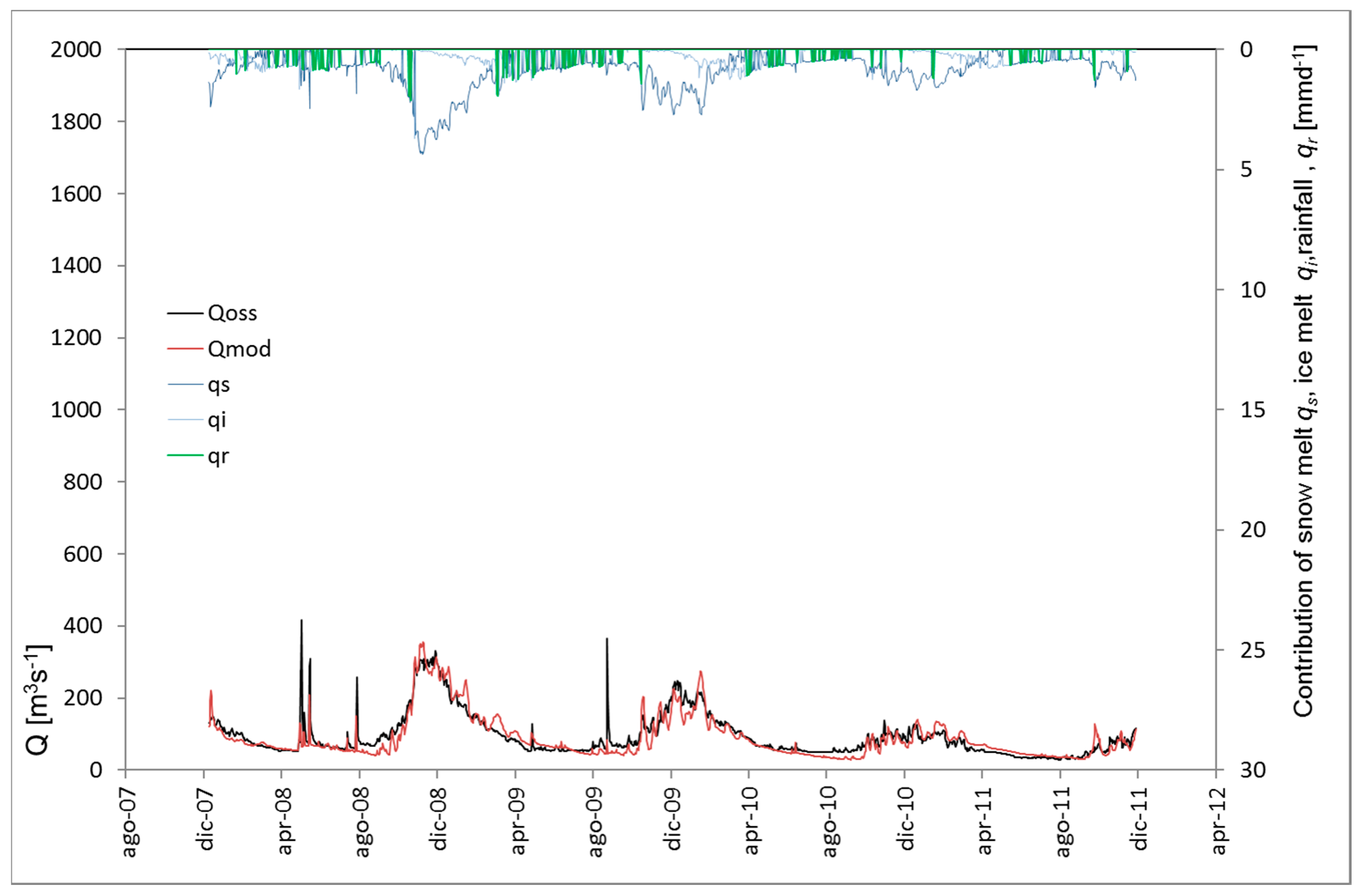
4.1. Models’ Performance
4.2. Ice Flow Model
4.3. Climate and Hydrological Projections
4.4. Glaciers’ Dynamics
4.5. Climate and Hydrological Trends until 2100
4.6. Correlation against Climate Drivers
5. Discussion
5.1. Glacio-Hydrological Trends, and Flow Components
5.2. Benchmark against the Present Literature
5.3. Limitations and Outlooks
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Rivera, A.; Acuña, C.; Casassa, G.; Bown, F. Use of remote sensing and field data to estimate the contribution of Chilean glaciers to the sea level rise. Ann. Glaciol. 2002, 34, 367–372. [Google Scholar] [CrossRef]
- Rivera, A.; Bown, F.; Acuña, C.; Ordenes, F. I Ghiacciai del Cile come Indicatori dei Cambiamenti Climatici. Chilean Glaciers as Indicators of Climatic Change. Terra Glacialis Edizione Speciale. Special Issue “Mountain Glaciers and Climate Changes in the Last Century”. 2009. Available online: http://repositorio.uchile.cl/bitstream/handle/2250/117817/113801_C11_rivera-italia.pdf?sequence=1 (accessed on 24 June 2018).
- Urrutia, R.; Vuille, M. Climate change projections for the tropical Andes using a regional climate model: Temperature and precipitation simulations for the end of the 21st century. J. Geophys. Res. 2009, 114, 2156–2202. [Google Scholar] [CrossRef]
- Bodin, X.; Rojas, F.; Brenning, A. Status and evolution of the cryosphere in the Andes of Santiago. Geomorphology 2011, 118, 453–464. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Helbing, J.; Rivera, A.; Favier, V.; Corripio, J.; Araos, J.; Sicart, J.-E.; Carenzo, M. A study of the energy balance and melt regime on Juncal Norte Glacier, semi-arid Andes of central Chile, using melt models of different complexity. Hydrol. Process. 2008, 22, 3980–3997. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Ragettli, S.; Carenzo, M.; McPhee, J. Review: Changes of glaciers in the Andes of Chile and priorities for future work. Sci. Total Environ. 2014, 493, 1197–1210. [Google Scholar] [CrossRef] [PubMed]
- Rabatel, A.; Castebrunet, H.; Favier, V.; Nicholson, L.; Kinnard, C. Glacier changes in the Pascua-Lama region, Chilean Andes (29S): Recent mass balance and 50 yr surface area variations. Cryosphere 2011, 5, 1029–1041. [Google Scholar] [CrossRef] [Green Version]
- Rabatel, A.; Francou, B.; Soruco, A.; Gomez, J.; Caceres, B.; Ceballos, J.L.; Basantes, R.; Vuille, M.; Sicart, J.-E.; Huggel, C.; et al. Current state of glaciers in the tropical Andes: A multi-century perspective on glacier evolution and climate change. Cryosphere 2013, 7, 81–102. [Google Scholar] [CrossRef] [Green Version]
- Carrasco, J.F.; Casassa, G.; Quintana, J. Changes of the 0 °C isotherm and the equilibrium line altitude in central Chile during the last quarter of the 20th century. Hydrol. Sci. J. 2005, 50, 933–948. [Google Scholar] [CrossRef]
- Masiokas, M.H.; Villalba, R.; Luckman, B.H.; Le Quesne, C.; Aravena, J.C. Snowpack Variations in the Central Andes of Argentina and Chile, 1951–2005: Large-Scale Atmospheric Influences and Implications for Water Resources in the Region. J. Clim. 2006, 19, 6334–6352. [Google Scholar] [CrossRef]
- Masiokas, M.H.; Rivera, A.; Espizua, L.E.; Villalba, R.; Delgado, S.; Aravena, J.C. Glacier fluctuations in extratropical South America during the past 1000 years. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 242–268. [Google Scholar] [CrossRef]
- Meza, F.J.; Wilks, D.S.; Gurovich, L.; Bambach, N. Impacts of Climate Change on Irrigated Agriculture in the Maipo Basin, Chile: Reliability of Water Rights and Changes in the Demand for Irrigation. J. Water Resour. Plan. Manag. 2012, 138, 421–430. [Google Scholar] [CrossRef]
- Ahumada, G.; Bustos, D.; González, M. Effect of climate change on drinking water supply in Santiago de Chile. Sci. Cold Arid Reg. 2013, 5, 27–34. [Google Scholar]
- Bocchiola, D.; Mihalcea, C.; Diolaiuti, G.; Mosconi, B.; Smiraglia, C.; Rosso, R. Flow prediction in high altitude ungauged catchments: A case study in the Italian Alps (Pantano Basin, Adamello Group). Adv. Water Resour. 2010, 33, 1224–1234. [Google Scholar] [CrossRef]
- Soncini, A.; Bocchiola, D.; Confortola, G.; Bianchi, A.; Rosso, R.; Mayer, C.; Lambrecht, A.; Palazzi, E.; Smiraglia, C.; Diolaiuti, G. Future hydrological regimes in the upper Indus basin: A case study from a high altitude glacierized catchment. J. Hydrometeorol. 2015, 16, 306–326. [Google Scholar] [CrossRef]
- Soncini, A.; Bocchiola, D.; Confortola, G.; Minora, U.; Vuillermoz, E.; Salerno, F.; Viviano, G.; Shrestha, D.; Senese, A.; Smiraglia, C.; et al. Future hydrological regimes and glacier cover in the Everest region: The case study of the Dudh Koshi basin. Sci. Total Environ. 2016, 565, 1084–1101. [Google Scholar] [CrossRef] [PubMed]
- Aili, T.; Soncini, A.; Bianchi, A.; Diolaiuti, G.; Bocchiola, D. A method to study hydrology of high altitude catchments: The case study of the Mallero River, Italian Alps. Theor. Appl. Climatol. 2018, 1–22. [Google Scholar] [CrossRef]
- Migliavacca, F.; Confortola, G.; Soncini, A.; Diolaiuti, G.A.; Smiraglia, C.; Barcaza, G.; Bocchiola, D. Hydrology and potential climate changes in the Rio Maipo (Chile). Geogr. Fis. Din. Quat. 2015, 38, 155–168. [Google Scholar]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Garreaud, R.; Aceituno, P. Interannual rainfall variability over the South American Altiplano. J. Clim. 2001, 14, 2779–2789. [Google Scholar] [CrossRef]
- Bookhagen, B.; Burbank, D.W. Topography, relief, and TRMM-derived rainfall variations along the Himalaya. Geophys. Res. Lett. 2006, 33, L08405. [Google Scholar] [CrossRef]
- Bookhagen, B.; Burbank, D.W. Towards a complete Himalayan hydrologic budget: Thespatiotemporal distribution of snow melt and rainfall and their impact on river discharge. J. Geophys. Res. 2010. [Google Scholar] [CrossRef]
- Bocchiola, D. Use of Scale Recursive Estimation for multisensor rainfall assimilation: A case study using data from TRMM (PR and TMI) and NEXRAD. Adv. Water Resour. 2007, 30, 2354–2372. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. The value of MODIS snow cover data in validating and calibrating conceptual hydrologic models. J. Hydrol. 2008, 358, 240–258. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G. Spatio-temporal combination of MODIS images-potential for snow cover mapping. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Bocchiola, D.; Diolaiuti, G.; Soncini, A.; Mihalcea, C.; D’Agata, C.; Mayer, C.; Lambrecht, A.; Rosso, R.; Smiraglia, C. Prediction of future hydrological regimes in poorly gauged high altitude basins: The case study of the upper Indus, Pakistan. Hydrol. Earth Syst. Sci. 2011, 15, 2059–2075. [Google Scholar] [CrossRef] [Green Version]
- Mihalcea, C.; Mayer, C.; Diolaiuti, G.; Lambrecht, A.; Smiraglia, C. Ice ablation and meteorological conditions on the debris covered area of Baltoro Glacier, Karakoram (Pakistan). Ann. Glaciol. 2006, 43, 292–300. [Google Scholar] [CrossRef]
- Bocchiola, D.; Senese, A.; Mihalcea, C.; Mosconi, B.; D’Agata, C.; Smiraglia, C.; Diolaiuti, G. An ablation model for debris covered ice: The case study of Venerocolo Glacier (Italian Alps). Geogr. Fis. Din. Quat. 2015, 38, 113–128. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Summary for Policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The Community Climate System Model Version. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Hazeleger, W.; Wang, X.; Severijns, C.; Ştefănescu, S.; Bintanja, R.; Sterl, A.; Wyser, K.; Semmler, T.; Yang, S.; van den Hurk, B.; et al. EC-Earth V2.2: Description and validation of a new seamless earth system prediction model. Clim. Dyn. J. 2011, 39, 2611–2629. [Google Scholar] [CrossRef]
- Stevens, B.; Giorgetta, M.; Esch, M.; Mauritsen, T.; Crueger, T.; Rast, S.; Salzmann, M.; Schmidt, H.; Bader, J.; Block, K.; et al. Atmospheric component of the MPI-M Earth System Model: ECHAM. J. Adv. Model. Earth Syst. 2013, 5, 1–27. [Google Scholar] [CrossRef]
- Groppelli, B.; Bocchiola, D.; Rosso, R. Spatial downscaling of precipitation from GCMs for climate change projections using random cascades: A case study in Italy. Water Resour. Res. 2011, 47, W03519. [Google Scholar] [CrossRef]
- Soncini, A.; Bocchiola, D.; Azzoni, R.S.; Diolaiuti, G. A methodology for monitoring and modeling of high altitude Alpine catchments. Prog. Phys. Geogr. 2017, 41, 393–420. [Google Scholar] [CrossRef]
- Groppelli, B.; Soncini, A.; Bocchiola, D.; Rosso, R. Evaluation of future hydrological cycle under climate change scenarios in a mesoscale Alpine watershed of Italy. Nat. Hazards Earth Syst. Sci. 2011, 11, 1769–1785. [Google Scholar] [CrossRef] [Green Version]
- Confortola, G.; Soncini, A.; Bocchiola, D. Climate change will affect water resources in the Alps: A case study in Italy. J. Alp. Res. 2013, 101-3, 1–19. Available online: http://rga.revues.org/2176 (accessed on 24 June 2018).
- Wallinga, J.; van de Wal, R.S.W. Sensitivity of Rhonegletscher, Switzerland, to climate change: Experiments with a one-dimensional flow line model. J. Glaciol. 1998, 44, 383–393. [Google Scholar] [CrossRef]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers, 4th ed.; Academic Press: Cambridge, MA, USA, 2010; 704p, ISBN 978-0123694614. [Google Scholar]
- Oerlemans, J. Glaciers and Climate Change; A. A. Balkema Publishers: Brookfield, VT, USA, 2001; 148p. [Google Scholar]
- DGA, Direccion General De Aguas, Gobierno de Chile, Unidad de Glaciología y Nieves. Servicio De Consultoría: Plan De Accion Para La Conservación De Glaciares Ante El Cambio Climático. Cooperación técnica no reembolsable ATN/OC-11996 –CH, Programa Plan de Acción para la Conservación de Glaciares ante Cambio Climático, DGA-BID, Sci. Coord. Diolaiuti, G., Informe Final. 2012. Available online: https://www.researchgate.net/publication/292145572_PLAN_DE_ACCION_PARA_LA_CONSERVACION_DE_GLACIARES_ANTE_EL_CAMBIO_CLIMATICO_Vol_II (accessed on 24 June 2018).
- Barros, V.; Grimm, A.M.; Doyle, M.E. Relationship between temperature and circulation in southeastern South America and its influence from El Niño and La Niña events. J. Meteorol. Soc. Jpn. 2002, 80, 21–32. [Google Scholar] [CrossRef]
- Hock, R. A distributed temperature-index ice- and snowmelt model including potential direct solar radiation. J. Glaciol. 1999, 45, 101–111. [Google Scholar] [CrossRef] [Green Version]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- DGA, Direccion General De Aguas, Gobierno de Chile, Unidad de Glaciología y Nieves. Catastro, Exploración y Estudio de Glaciares en Chile Central. 2011. Realizado Por: Geoestudios Ltda, S.I.T. N° 265. Available online: https://research.csiro.au/gestionrapel/wp-content/uploads/sites/79/2016/11/Catastro-exploraci%C3%B3n-y-estudio-de-glaciares-en-chile-central.-Volumen-2-Anexos-2011.pdf (accessed on 24 June 2018).
- Minora, U.; Bocchiola, D.; D’Agata, C.; Maragno, D.; Mayer, C.; Lambrecht, A.; Mosconi, B.; Vuillermoz, E.; Senese, A.; Compostella, C.; et al. 2001–2010 glacier changes in the Central Karakoram National Park: A contribution to evaluate the magnitude and rate of the Karakoram anomaly. Cryosphere Discuss 2013, 7, 2891–2941. Available online: http://www.the-cryosphere-discuss.net/7/2891/2013/tcd-7-2891-2013.html (accessed on 24 June 2018). [CrossRef]
- Minora, U.; Bocchiola, D.; D’Agata, C.; Maragno, D.; Mayer, C.; Lambrecht, A.; Vuillermoz, E.; Senese, A.; Compostella, C.; Smiraglia, C.; et al. Glacier area stability in the Central Karakoram National Park (Pakistan) in 2001–2010: The “Karakoram Anomaly” in the spotlight. Prog. Phys. Geogr. 2016, 40, 629–660. [Google Scholar] [CrossRef]
- Bocchiola, D.; Diolaiuti, G. Recent (1980–2009) evidence of climate change in the upper Karakoram, Pakistan. Theor. Appl. Climatol. 2013, 113, 611–641. [Google Scholar] [CrossRef]
- Bocchiola, D. Long term (1921–2011) hydrological regime of Alpine catchments in Northern Ital. Adv. Water Resour. 2014, 70, 51–64. [Google Scholar] [CrossRef]
- Archer, D.R. Contrasting hydrological regimes in the upper Indus Basin. J. Hydrol. 2003, 274, 198–210. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, N.; Arora, M. Degree-day factors for snow and ice for Dokriani Glacier, Garhwal Himalayas. J. Hydrol. 2000, 235, 1–11. [Google Scholar] [CrossRef]
- Comisión Económica para América Latina y el Caribe (CEPAL). La Economía del Cambio Climático en Chile; United Nations: Santiago, Chile, 2009; p. 88. (In Spanish) [Google Scholar]
- Krellenberg, C.; Hansjürgens, B. Climate Adaptation Santiago; Springe-Verlag: Berlin/Heidelberg, Germany, 2014; p. 221. [Google Scholar]
- Cortés, G.; Schaller, S.; Rojas, M.; Garcia, L.; Descalzi, A.; Vargas, L.; McPhee, J. Assessment of the Current Climate and Expected Climate Changes in the Metropolitan Region of Santiago de Chile; UFZ-Report 03/2012; Helmholtz Center for Environmental Research (UFZ): Leipzig, Germany, 2012. [Google Scholar]
- Ranke, J.R.; Bellisario, A.C.; Ferrando, F.A. Classification of debris-covered glaciers and rock glaciers in the Andes of central Chile. Geomorphology 2015, 241, 98–121. [Google Scholar]
- Kuchment, L.S.; Gelfan, A.N.; Demidov, V.N. A distributed model of runoff generation in the permafrost regions. J. Hydrol. 2000, 240, 1–22. [Google Scholar] [CrossRef]
- Klene, A.E.; Nelson, F.E.; Shiklomanov, N.I.; Hinkel, K.M. The N-Factor in Natural Landscapes: Variability of Air and Soil-Surface Temperatures, Kuparuk River Basin, Alaska, U.S.A. Arct. Antarct. Alp. Res. 2001, 33, 140–148. [Google Scholar] [CrossRef]
- Ohmura, A. Physical basis for the temperature-based melt-index method. J. Appl. Meteorol. 2001, 40, 753–761. [Google Scholar] [CrossRef]
- Senese, A.; Diolaiuti, G.; Mihalcea, C.; Smiraglia, C. Energy and Mass Balance of Forni Glacier (Stelvio National Park, Italian Alps) from a Four-Year Meteorological Data Record. Arct. Antarct. Alp. Res. 2012, 44, 122–134. [Google Scholar] [CrossRef] [Green Version]
- Minora, U.F.; Senese, A.; Bocchiola, D.; Soncini, A.; D’Agata, C.; Ambrosini, R.; Mayer, C.; Lambrecht, A.; Vuillermoz, E.; Smiraglia, C.; et al. A simple model to evaluate ice melt over the ablation area of glaciers in the Central Karakoram National Park, Pakistan. Ann. Glaciol. 2015, 56, 202–216. [Google Scholar] [CrossRef] [Green Version]
- Marangunic, C. Inventario de Glaciares, Hoya del rio Maipo; Direcciòn General de Aguas: Santiago, Chile, 1979; (In Spanish). Available online: http://documentos.dga.cl/GLA1046v5.pdf (accessed on 24 June 2018).
- Palazzoli, I.; Maskey, S.; Uhlenbrook, S.; Nana, E.; Bocchiola, D. Impact of prospective climate change on water resources and crop yields in the Indrawati basin, Nepal. Agric. Syst. 2015, 12, 143–157. [Google Scholar] [CrossRef]
- Fuss, S.; Canadell, J.G.; Peters, G.P.; Tavoni, M.; Andrew, R.M.; Ciais, P.; Jackson, R.B.; Jones, C.D.; Kraxner, F.; Nakicenovic, N.; et al. Betting on negative emissions. Nat. Clim. Chang. 2014, 4, 850–853. [Google Scholar] [CrossRef] [Green Version]













| Station | Altitude (m a.s.l.) | Variable | Period Available |
|---|---|---|---|
| Cerro Calan | 848 | T | (1975–2013) |
| El Manzano | 890 | P, Q | P(2012–2013), Q(1695–2013) |
| Mapocho | 966 | P | (2012–2013) |
| San Alfonso | 1040 | P | (1965–1973, 2012–2013) |
| Maitenes Bocatoma | 1143 | P | (1979–2013) |
| Rio Molina | 1158 | P | (2010–2013) |
| San Gabriel | 1266 | P | (1977–2013) |
| Le Ermita Bocatoma | 1350 | T | (1987–2011) |
| Queltehues | 1450 | T, P | T(1987–2011), P(1972–1980) |
| Las Melosas | 1527 | T, P | T(1977–1978), P(1962–2006) |
| Rio San Francisco | 1550 | P | April–July 2013 |
| Glaciar San Francisco | 2220 | T, P, HS | T(2012–2013), P(2012), HS(2012–2013) |
| El Yeso embalse | 2475 | T, P | T(1963–2013), P(1998–2013) |
| Laguna Negra | 2780 | T | T(2012–2013) |
| Yerba Loca Carvajal | 3250 | T, P, HS | T(2011–2013), P(2013), HS(2012–2013) |
| Glaciar Piramide | 3587 | T | T(March–April 2012) |
| Glaciar Echaurren | 3850 | T | T(1999–2001) |
| Model | Institute | Country | Grid Cell Size | Layers | Cells |
|---|---|---|---|---|---|
| CCSM4 | National Center for Atmospheric Research | U.S.A. | 1.25° × 1.25° | 26 | 288 × 144 |
| ECHAM6 | Max Planck Institute for Meteorology | GER | 1.875° × 1.875° | 47 | 192 × 96 |
| EC-EARTH | Europe-wide consortium | E.U. | 1.125° × 1.125° | 62 | 320 × 160 |
| Parameter | Description | Value | Method |
|---|---|---|---|
| Calibration | |||
| DD (mm °C−1·day−1) | Snow Degree Day | 5.6 | Snow data/valid vs. MODIS |
| DI (mm °C−1·day−1) | Ice Degree Day | 7.2 | Surveys/Calibration vs. flow |
| Kd (m−1·year−1) | Ice flow deformation coefficient | 0.98 × 10−16 | Ice stakes (SF, PI)/Literature |
| Ks (m−3·year−1) | Ice flow basal sliding coefficient | 1 × 10−14 | Ice stakes (SF, PI)/Literature |
| k (.) | Groundwater flow exponent | 2 | Max NSE, Min |Bias| |
| K (mm·day−1) | Hydraulic conductivity | 4 | Max NSE, Min |Bias| |
| Wmax (mm) | Max soil water content (average) | 244 | Land use analysis |
| ts (day) | Lag time surface | 3 | Max NSE, high flows |
| tg (day) | Lag time subsurface | 20 | Max NSE, low flows |
| n (.) | Number of reservoir (sup./subsup.) | 4/5 | Literature |
| Goodness of fit (Calib., Valid.) | |||
| Bias (%) | Daily average percentage error | −4.4, −4.7 | Minimization (for Calib.) |
| BiasI (%) | Percentage error ice flow vel. | −4 | Minimization (for Calib.) |
| R2I (.) | Det. Coefficient ice flow vel | 0.56 | Maximization (for Calib.) |
| NSE (.) | Daily Nash Sutcliffe efficiency | 0.81,0.79 | Maximization (for Calib.) |
| RMSE (m3·s−1) | Daily Random mean square error | 24.2,17.2 | - |
| RMSE (%) | Percentage RMSE | 23,19 | - |
| NSENS (.) | NSE without satellite correction | 0.62, 0.61 | Maximization (for Calib.) |
| RMSENS (m3·s−1) | RMSE without satellite correction | 35.0, 23.53 | - |
| NSETR (.) | NSE using only TRMM | 0.77, 0.74 | Maximization (for Calib.) |
| RMSETR (m3·s−1) | RMSE using only TRMM | 26.5, 19.5 | - |
| Flow statistics obs/mod (Calib., Valid.) | |||
| QavY (m3 s−1) | Av. stream flow yearly (±95%) | 113 ± 17.1/108, 93 ± 16/89 | |
| QavJFM (m3 s−1) | Av. stream flow JFM (±95%) | 156 ± 43/155, 121 ± 21/125 | - |
| QavAMJ (m3 s−1) | Av. stream flow AMJ (±95%) | 6 5± 8/73, 64 ± 10/66 | - |
| QavJAS (m3 s−1) | Av. stream flow JAS (±95%) | 68 ± 12/62, 58 ± 10/46 | - |
| QavOND (m3 s−1) | Av. stream flow OND (±95%) | 163 ± 40/142, 130 ± 30/119 | - |
| Qav (m3 s−1) | Average flow discharge (±95%) | 113 ± 3/108, 94 ± 3/89 | Best fitting (for Calib.) |
| σQ (m3 s−1) | Standard deviation of flow discharge | 84/83, 59/60 | - |
| CVQ (.) | Coeff. of variation of flow discharge | 0.75/0.76 | - |
| Season | P, CP | E[P] mm ·day−1 | T, CP | E[T] °C | Q, CP | E[Q] m3 s−1 | |
| CP | Year | −2.4 × 10−2 | 1.70 | 2.0 × 10−2 | 8.8 | −1.5 | 120 |
| CP | JFM | 3.3 × 10−3 | 0.15 | 2.5 × 10−2 | 14.7 | −2.6 | 167 |
| CP | AMJ | 1.7 × 10−2 | 3.01 | 4.6 × 10−2 | 6.7 | −7.8 × 10−1 | 74 |
| CP | JAS | −6.5 × 10−2 | 2.93 | 1.3 × 10−2 | 3.3 | −6.5 × 10−1 | 71 |
| CP | OND | −9.3 × 10−4 | 0.48 | −3.8 × 10−3 | 10.7 | −1.7E | 167 |
| Scenario | Season | P, PR | P, CM | T, PR | T, CM | Q, PR | Q, CM |
| CCSM4RCP26 | Year | 2.2 × 10−3 | −5.0 × 10−4 | 2.2 × 10−3 | 8.7 × 10−3 | −9.9 × 10−2 | −3.0 × 10−1 |
| CCSM4RCP26 | JFM | 1.6 × 10−3 | 1.3 × 10−3 | −2.0 × 10−2 | 1.7 × 10−2 | −1.4 × 10−1 | −5.3 × 10−1 |
| CCSM4RCP26 | AMJ | 4.1 × 10−3 | −2.4 × 10−3 | −2.1 × 10−2 | 7.6 × 10−3 | −1.1 × 10−1 | −1.0 × 10−1 |
| CCSM4RCP26 | JAS | 3.5 × 10−3 | 4.2 × 10−3 | 2.6 × 10−2 | 2.0 × 10−3 | −2.1 × 10−2 | −1.7 × 10−1 |
| CCSM4RCP26 | OND | −1.1 × 10−3 | −2.3 × 10−3 | 2.4 × 10−2 | 8.0 × 10−3 | −1.3 × 10−1 | −4.1 × 10−1 |
| CCSM4RCP45 | Year | 6.9 × 10−3 | 1.7 × 10−3 | 1.7 × 10−2 | 2.1 × 10−2 | 1.0 × 10−1 | −2.4 × 10−1 |
| CCSM4RCP45 | JFM | −1.2 × 10−4 | 4.6 × 10−4 | 3.5 × 10−4 | 3.0 × 10−2 | 7.0 × 10−2 | −4.8 × 10−1 |
| CCSM4RCP45 | AMJ | 2.3 × 10−2 | 5.6 × 10−3 | −8.3 × 10−3 | 1.9 × 10−2 | −2.5 × 10−2 | −9.8 × 10−2 |
| CCSM4RCP45 | JAS | 1.1 × 10−3 | 3.9 × 10−3 | 3.5 × 10−2 | 1.3 × 10−2 | 2.2 × 10−1 | −6.4 × 10−2 |
| CCSM4RCP45 | OND | 3.9 × 10−3 | −4.1 × 10−5 | 4.2 × 10−2 | 2.2 × 10−2 | 1.4 × 10−1 | −3.1 × 10−1 |
| CCSM4RCP85 | Year | −5.5 × 10−3 | −5.4 × 10−3 | 4.7 × 10−2 | 4.3 × 10−2 | −3.1 × 10−1 | −3.9 × 10−1 |
| CCSM4RCP85 | JFM | −2.5 × 10−5 | 3.8 × 10−4 | 3.0 × 10−2 | 5.2 × 10−2 | −5.5 × 10−1 | −7.3 × 10−1 |
| CCSM4RCP85 | AMJ | −3.0 × 10−3 | −8.0 × 10−3 | 2.1 × 10−2 | 4.0 × 10−2 | −1.2 × 10−1 | −1.1 × 10−1 |
| CCSM4RCP85 | JAS | −2.0 × 10−2 | −9.7 × 10−3 | 6.7 × 10−2 | 3.5 × 10−2 | 1.0 × 10−1 | −2.3 × 10−2 |
| CCSM4RCP85 | OND | 1.3 × 10−3 | −1.0 × 10−3 | 6.9 × 10−2 | 4.2 × 10−2 | −6.7 × 10−1 | −6.9 × 10−1 |
| ECHAMRCP26 | Year | 3.3 × 10−3 | 8.7 × 10−4 | 1.4 × 10−3 | 8.5 × 10−3 | 2.5 × 10−1 | 4.3 × 10−2 |
| ECHAMRCP26 | JFM | 1.0 × 10−3 | 1.8 × 10−4 | 3.8 × 10−3 | 5.8 × 10−3 | −8.2 × 10−2 | −3.3 × 10−1 |
| ECHAMRCP26 | AMJ | −2.9 × 10−3 | −7.6 × 10−3 | 1.9 × 10−3 | 6.3 × 10−3 | 2.3 × 10−1 | 2.0 × 10−1 |
| ECHAMRCP26 | JAS | 1.3 × 10−2 | 1.3 × 10−2 | −1.5 × 10−3 | 1.1 × 10−2 | 5.5 × 10−1 | 3.1 × 10−1 |
| ECHAMRCP26 | OND | 1.7 × 10−3 | 1.0 × 10−3 | 1.3 × 10−3 | 1.0 × 10−2 | 2.9 × 10−1 | −1.3 × 10−2 |
| ECHAMRCP45 | Year | −2.0 × 10−4 | −2.4 × 10−3 | 1.6 × 10−2 | 1.9 × 10−2 | 2.4 × 10−2 | −7.5 × 10−2 |
| ECHAMRCP45 | JFM | −9.4 × 10−4 | −4.7 × 10−4 | 1.7 × 10−2 | 1.8 × 10−2 | −1.6 × 10−1 | −3.7 × 10−1 |
| ECHAMRCP45 | AMJ | 3.0 × 10−3 | −6.6 × 10−3 | 1.5 × 10−2 | 1.3 × 10−2 | 1.1 × 10−1 | 9.4 × 10−2 |
| ECHAMRCP45 | JAS | −6.8 × 10−3 | −1.4 × 10−3 | 1.8 × 10−2 | 2.2 × 10−2 | 2.8 × 10−1 | 6.6 × 10−2 |
| ECHAMRCP45 | OND | 4.4 × 10−3 | 2.0 × 10−3 | 1.5 × 10−2 | 2.2 × 10−2 | −1.4 × 10−1 | −1.0 × 10−1 |
| ECHAMRCP85 | Year | −6.6 × 10−3 | −5.6 × 10−3 | 4.9 × 10−2 | 4.2 × 10−2 | 3.5 × 10−2 | −1.1 × 10−1 |
| ECHAMRCP85 | JFM | −9.2 × 10−4 | −2.5 × 10−4 | 5.5 × 10−2 | 4.4 × 10−2 | −3.7 × 10−1 | −6.3 × 10−1 |
| ECHAMRCP85 | AMJ | −8.2 × 10−3 | −1.3 × 10−2 | 4.6 × 10−2 | 3.6 × 10−2 | 3.1 × 10−1 | 1.6 × 10−1 |
| ECHAMRCP85 | JAS | −1.7 × 10−2 | −5.9 × 10−3 | 4.6 × 10−2 | 4.4 × 10−2 | 7.0 × 10−1 | 4.0 × 10−1 |
| ECHAMRCP85 | OND | −3.1 × 10−4 | −3.7 × 10−4 | 4.9 × 10−2 | 4.5 × 10−2 | −5.1 × 10−1 | −3.9 × 10−1 |
| EC-EarthRCP26 | Year | 2.3 × 10−3 | −1.7 × 10−3 | 5.3 × 10−3 | 1.4 × 10−2 | −8.6 × 10−2 | −7.9 × 10−2 |
| EC-EarthRCP26 | JFM | 1.3 × 10−3 | 9.7 × 10−4 | 9.1 × 10−3 | 1.2 × 10−2 | −4.9 × 10−1 | −4.6 × 10−2 |
| EC-EarthRCP26 | AMJ | 7.5 × 10−3 | 5.2 × 10−3 | 3.9 × 10−3 | 8.7 × 10−3 | −3.0 × 10−1 | −2.2 × 10−2 |
| EC-EarthRCP26 | JAS | 2.7 × 10−3 | −7.5 × 10−3 | 4.1 × 10−3 | 1.7 × 10−2 | 5.4 × 10−2 | −1.2 × 10−1 |
| EC-EarthRCP26 | OND | −3.4 × 10−3 | −2.6 × 10−3 | 4.5 × 10−3 | 1.6 × 10−2 | 3.9 × 10−1 | −1.3 × 10−1 |
| Ec-EarthRCP45 | Year | −4.0 × 10−4 | −3.4 × 10−3 | 2.2 × 10−2 | 2.6 × 10−2 | −5.4 × 10−2 | −1.6 × 10−2 |
| Ec-EarthRCP45 | JFM | 1.2 × 10−3 | 8.3 × 10−4 | 2.0 × 10−2 | 2.3 × 10−2 | −8.7 × 10−1 | −1.8 × 10−1 |
| Ec-EarthRCP45 | AMJ | −3.4 × 10−4 | 3.9 × 10−4 | 1.5 × 10−2 | 1.9 × 10−2 | −1.0 × 10−1 | 6.7 × 10−2 |
| Ec-EarthRCP45 | JAS | −3.6 × 10−3 | −1.1 × 10−2 | 3.1 × 10−2 | 3.3 × 10−2 | 2.1 × 10−1 | −1.2 × 10−2 |
| Ec-EarthRCP45 | OND | 9.3 × 10−4 | −9.0 × 10−4 | 2.1 × 10−2 | 2.8 × 10−2 | 5.4 × 10−1 | 5.6 × 10−2 |
| EC-EarthRCP85 | Year | −5.2 × 10−3 | −6.1 × 10−3 | 5.3 × 10−2 | 4.9 × 10−2 | −4.8 × 10−1 | −2.2 × 10−1 |
| EC-EarthRCP85 | JFM | −4.0 × 10−4 | 4.0 × 10−4 | 5.1 × 10−2 | 4.3 × 10−2 | −1.6 | −6.3 × 10−1 |
| EC-EarthRCP85 | AMJ | −6.4 × 10−3 | −5.1 × 10−3 | 4.8 × 10−2 | 4.3 × 10−2 | −2.8 × 10−1 | −2.4 × 10−2 |
| EC-EarthRCP85 | JAS | −1.4 × 10−2 | −1.6 × 10−2 | 6.1 × 10−2 | 5.9 × 10−2 | 2.0 × 10−1 | 5.0 × 10−2 |
| EC-EarthRCP85 | OND | 7.0 × 10−4 | −8.4 × 10−4 | 5.1 × 10−2 | 5.2 × 10−2 | −2.4 × 10−1 | −2.9 × 10−1 |
| CP | PR, CCSM4 | PR, EC-Earth | PR, ECHAM6 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RCP26 | RCP45 | RCP85 | RCP26 | RCP45 | RCP85 | RCP26 | RCP45 | RCP85 | ||
| Q-T Y | −0.32 | −0.04 | −0.10 | −0.48 | −0.17 | −0.15 | 0.00 | −0.14 | 0.16 | −0.33 |
| Q-T JFM | 0.08 | 0.22 | 0.22 | −0.32 | −0.10 | 0.23 | −0.09 | 0.29 | 0.15 | −0.13 |
| Q-T AMJ | −0.40 | 0.30 | 0.21 | −0.16 | −0.35 | −0.03 | 0.32 | 0.12 | 0.15 | 0.04 |
| Q-T JAS | −0.44 | 0.38 | 0.26 | 0.36 | −0.16 | 0.39 | 0.57 | 0.16 | 0.29 | 0.10 |
| Q-T OND | −0.26 | 0.25 | 0.15 | −0.13 | −0.15 | −0.16 | −0.18 | 0.16 | 0.14 | −0.40 |
| Q-P Y | 0.42 | 0.30 | 0.06 | 0.34 | 0.23 | 0.40 | 0.17 | 0.27 | 0.21 | 0.39 |
| Q-P JFM | 0.25 | −0.09 | −0.12 | 0.04 | −0.11 | −0.01 | 0.22 | 0.02 | 0.19 | 0.05 |
| Q-P AMJ | 0.31 | 0.18 | 0.04 | 0.26 | 0.33 | 0.35 | 0.13 | 0.18 | 0.27 | 0.32 |
| Q-P JAS | 0.66 | 0.21 | 0.18 | −0.01 | 0.15 | 0.14 | −0.17 | 0.11 | 0.21 | 0.39 |
| Q-P OND | 0.02 | 0.08 | 0.05 | −0.06 | −0.07 | 0.05 | 0.19 | −0.01 | −0.18 | 0.02 |
| P-T Y | −0.46 | −0.15 | −0.09 | −0.37 | −0.20 | −0.16 | −0.30 | −0.11 | −0.17 | −0.36 |
| P-T JFM | −0.02 | −0.15 | −0.06 | −0.06 | −0.09 | −0.05 | −0.06 | −0.36 | 0.00 | −0.07 |
| P-T AMJ | −0.03 | −0.25 | −0.14 | −0.03 | −0.25 | −0.12 | −0.29 | −0.09 | −0.15 | −0.18 |
| P-T JAS | −0.45 | −0.16 | −0.37 | −0.40 | −0.24 | −0.11 | −0.23 | −0.23 | −0.17 | −0.39 |
| P-T OND | −0.47 | 0.06 | 0.18 | 0.07 | −0.16 | −0.05 | 0.07 | −0.29 | −0.24 | −0.09 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bocchiola, D.; Soncini, A.; Senese, A.; Diolaiuti, G. Modelling Hydrological Components of the Rio Maipo of Chile, and Their Prospective Evolution under Climate Change. Climate 2018, 6, 57. https://doi.org/10.3390/cli6030057
Bocchiola D, Soncini A, Senese A, Diolaiuti G. Modelling Hydrological Components of the Rio Maipo of Chile, and Their Prospective Evolution under Climate Change. Climate. 2018; 6(3):57. https://doi.org/10.3390/cli6030057
Chicago/Turabian StyleBocchiola, Daniele, Andrea Soncini, Antonella Senese, and Guglielmina Diolaiuti. 2018. "Modelling Hydrological Components of the Rio Maipo of Chile, and Their Prospective Evolution under Climate Change" Climate 6, no. 3: 57. https://doi.org/10.3390/cli6030057
APA StyleBocchiola, D., Soncini, A., Senese, A., & Diolaiuti, G. (2018). Modelling Hydrological Components of the Rio Maipo of Chile, and Their Prospective Evolution under Climate Change. Climate, 6(3), 57. https://doi.org/10.3390/cli6030057








