Decadal Oscillation in the Predictability of Palmer Drought Severity Index in California
Abstract
1. Introduction
2. Materials and Methods
2.1. Environmental Setting and Data
2.2. Exponential Smoothing
2.3. Transfer Function Models
2.4. Model Validation Methods
3. Results and Discussion
3.1. Data Analysis
3.2. Validation Results and PDSI Time Series Predictability
3.3. Simulation Experiment
3.4. Comparison with the Transfer Function Modelling Approach
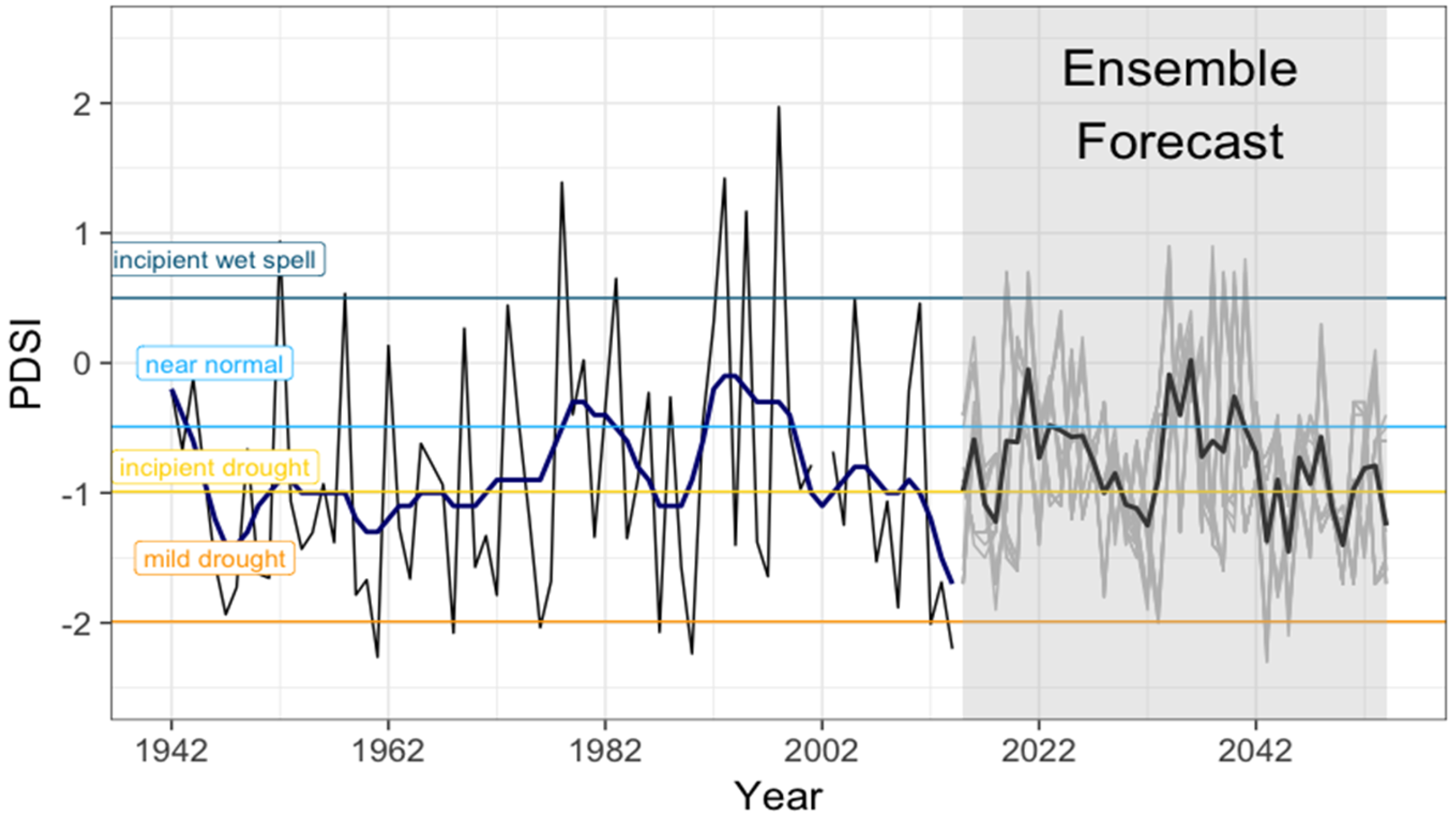
3.5. Ensemble Forecast with the Transfer Function Model
3.6. Limitations and Perspectives
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Griffin, D.; Anchukaitis, K.J. How unusual is the 2012–2014 California drought? Geophys. Res. Lett. 2014, 41, 9017–9023. [Google Scholar] [CrossRef]
- Meko, D.M.; Woodhouse, C.A.; Baisan, C.H.; Knight, T.; Lukas, J.J.; Hughes, M.K.; Salzer, W. Medieval drought in the upper Colorado River basin. Geophys. Res. Lett. 2007, 34, L10705. [Google Scholar] [CrossRef]
- Raab, L.M.; Larson, D.O. Medieval climatic anomaly and punctuated cultural evolution in coastal Southern California. Am. Antiq. 1997, 62, 319–336. [Google Scholar] [CrossRef]
- Heusser, L.; Kirby, M.E.; Nichols, J.E. Pollen-based evidence of extreme drought during the last Glacial (32.6–9.0 ka) in coastal southern California. Quat. Sci. Rev. 2015, 126, 242–253. [Google Scholar] [CrossRef]
- Cole, J.E.; Overpeck, J.T.; Cook, E.R. Multiyear La Niña events and persistent drought in the contiguous United States. Geophys. Res. Lett. 2002, 29, 25. [Google Scholar] [CrossRef]
- California Department of Water Resources. California’s Most Significant Drought: Comparing Historical and Recent Conditions; California Department of Water Resources: Sacramento, CA, USA, 2015. Available online: https://water.ca.gov (accessed on 29 December 2018).
- California’s Sustainable Groundwater Management Act. 2014. Available online: http://groundwater.ucdavis.edu/SGMA (accessed on 29 December 2018).
- Hanak, H.; Lund, J.; Dinar, A.; Gray, B.; Howitt, R.; Mount, J.; Moyle, P.; Thompson, B. Managing California’s Water. From Conflict to Reconciliation; Public Policy Institute of California: San Francisco, CA, USA, 1990; Available online: http://www.ppic.org/content/pubs/report/R_211EHR.pdf (accessed on 29 December 2018).
- Tortajada, C.; Kastner, M.J.; Buurman, J.; Biswas, A.K. The California drought: Coping responses and resilience building. Environ. Sci. Policy 2017, 78, 97–113. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E.; Karl, T.R. Global variations in droughts and west spells: 1900–1995. Geophys. Res. Lett. 1998, 25, 3367–3370. [Google Scholar] [CrossRef]
- Palmer, WC. Meteorological Drought. Research Paper No. 45; Office of Climatology, U.S. Weather Bureau: Washington, DC, USA, 1965.
- Karl, T.R.; Koscielny, A.J. Drought in the United States: 1895-1981. Int. J. Clim. 1982, 2, 313–329. [Google Scholar] [CrossRef]
- Byun, H.R.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E.; Qian, T. A global dataset of Palmer Drought Severity Index for 1870–2002: Relationship with soil moisture and effects of surface warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Shabbar, A.; Skinner, W. Summer drought patterns in Canada and the relationship to global sea surface temperatures. J. Clim. 2004, 17, 2866–2880. [Google Scholar] [CrossRef]
- Tatli, H. Detecting persistence of meteorological drought via the Hurst exponent. Meteorol. Appl. 2015, 22, 763–769. [Google Scholar] [CrossRef]
- Van der Schrier, G.; Briffa, K.R.; Osborn, T.J.; Cook, E.R. Summer moisture availability across North America. J. Geophys. Res. 2006, 111, D11102. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A self-calibrating Palmer Drought Severity Index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Flint, L.E.; Flint, A.L.; Mendoza, J.; Kalansky, J.; Ralph, F.M. Characterizing drought in California: New drought indices and scenario-testing in support of resource management. Ecol. Process. 2018, 7, 1. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 20, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Cook, E.R.; Seager, R.; Cane, M.A.; Stahle, D.W. North American drought: Reconstructions, causes, and consequences. Earth-Sci. Rev. 2007, 81, 93–134. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pie, J. Data mining: Concepts and Techniques; Elsevier: Burlington, MA, USA, 2012. [Google Scholar]
- Huang, F.T.; Mayr, H.G.; Russell, J.M., III; Mlynczak, M.G. Ozone and temperature decadal trends in the stratosphere, mesosphere and lower thermosphere, based on measurements from SABER on TIMED. Ann. Geophys. 2014, 32, 935–949. [Google Scholar] [CrossRef]
- Mossad, A.; Alazba, P. Drought forecasting using stochastic models in a hyper-arid climate. Atmosphere 2015, 6, 410–430. [Google Scholar] [CrossRef]
- Mishra, A.; Desai, V.R. Drought forecasting using stochastic models. Stoch. Environ. Res. Risk Assess. 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Cancelliere, A.; Mauro, G.D.; Bonaccorso, B.; Rossi, G. Drought forecasting using the Standardized Precipitation Index. Water Resour. Manag. 2007, 21, 801–819. [Google Scholar] [CrossRef]
- Fernández, C.; Vega, J.A.; Vega, J.A.; Fonturbel, T.; Jiménez, E. Streamflow drought time series forecasting: A case study in a small watershed in North West Spain. Stoch. Environ. Res. Risk Assess. 2009, 23, 1063–1070. [Google Scholar] [CrossRef]
- Yoon, J.; Mo, K.; Wood, E.F. Dynamic-model-based seasonal prediction of meteorological drought over the contiguous United States. J. Hydrometeorol. 2012, 13, 463–482. [Google Scholar] [CrossRef]
- Karavitis, C.A.; Vasilakou, C.G.; Tsesmelis, D.E.; Oikonomou, P.D.; Skondras, N.A.; Stamatakos, D.; Fassouli, V.; Alexandris, S. Short-term drought forecasting combining stochastic and geo-statistical approaches. Eur. Water J. 2015, 49, 43–63. [Google Scholar]
- Yan, H.; Moradkhani, H. Combined assimilation of streamflow and satellite soil moisture with the particle filter and geostatistical modeling. Adv. Water Resour. 2016, 94, 364–378. [Google Scholar] [CrossRef]
- Holt, C.C. Forecasting seasonals and trends by exponentially weighted moving averages. Int. J. Forecast. 2004, 20, 5–10. [Google Scholar] [CrossRef]
- Gardner, E.S., Jr. Exponential smoothing: The state of the art—part II. Int. J. Forecast. 2006, 22, 637–666. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- McClain, J.O. Dynamics of exponential smoothing with trend and seasonal terms. Manag. Sci. 1974, 20, 1300–1304. [Google Scholar] [CrossRef]
- Taylor, J.W. Exponential smoothing with a damped multiplicative trend. Int. J. Forecast. 2003, 19, 715–725. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecasting 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Armstrong, J.S. Combining forecasts. In Principles of Forecasting: A Handbook for Researchers and Practitioners; Armstrong, J.S., Ed.; Kluwer Academic Publishers: Norwell, MA, USA, 2001. [Google Scholar]
- Diodato, N. Storminess forecast skills in Naples, Southern Italy. In Storminess and Environmental Change; Diodato, N., Bellocchi, G., Eds.; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Diodato, N.; Bellocchi, G. Long-term winter temperatures in central Mediterranean: Forecast skill of an ensemble statistical model. Appl. Clim. 2014, 116, 131–146. [Google Scholar] [CrossRef]
- Diodato, N.; Bellocchi, G. Using historical precipitation patterns to forecast daily extremes of rainfall for the coming decades in Naples (Italy). Geosciences 2018, 8, 293. [Google Scholar] [CrossRef]
- Diodato, N.; Bellocchi, G.; Fiorillo, F.; Ventafridda, G. Case study for investigating groundwater and the future of mountain spring discharges in Southern Italy. J. Mt. Sci. 2017, 14, 1791–1800. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Allen, R.J.; Anderson, R.G. 21st century California drought risk linked to model fidelity of the El Niño teleconnection. npj Clim. Atmos. Sci. 2018, 1, 21. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Swain, D.L.; Touma, D. Anthropogenic warming has increased drought risk in California. Proc. Natl. Acad. Sci. USA 2015, 112, 3931–3936. [Google Scholar] [CrossRef]
- Box, G.E.P. Understanding exponential smoothing: A simple way to forecast sales and inventory. Qual. Eng. 1991, 3, 561–566. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Jennings, C.L.; Kulachi, M. Introduction to Time-Series Analysis and Forecasting; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wichard, J.D.; Merkwirth, C. Robust long term forecasting of seasonal time series. In Proceedings of the 8th International Work-Conference on Artificial Neural Networks, Barcelona, Spain, 8–10 June 2005. [Google Scholar]
- De Guenni, L.B.; García, M.; Muñoz, Á.G. Predicting monthly precipitation along coastal Ecuador: ENSO and transfer function models. Appl. Clim. 2017, 129, 1059–1073. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer: Berlin, Germany, 2008. [Google Scholar]
- Franses, P.H. A note on the Mean Absolute Scaled Error. Int. J. Forecast. 2016, 32, 20–22. [Google Scholar] [CrossRef]
- Addiscott, T.M.; Whitmore, A.P. Computer simulation of changes in soil mineral nitrogen and crop nitrogen during autumn, winter and spring. J. Agric. Sci. 1987, 109, 141–157. [Google Scholar] [CrossRef]
- Wessa, P. Free Statistics Software, Office for Research Development and Education. Version 1.1.23-r7. 2012. Available online: https://www.wessa.net (accessed on 29 December 2018).
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar]
- Karagiannis, T.; Faloutsos, M.; Riedi, R.H. Long-range dependence: Now you see it, now you don’t! In Proceedings of the Global Telecommunications Conference “GLOBECOM ’02”, Taipei, Taiwan, 17–21 November 2002; Volume 3. [Google Scholar]
- Karagiannis, T.; Molle, M.; Faloutsos, M. Long-range dependence: Ten years of internet traffic modeling! IEEE Internet Comput. 2004, 8, 57–64. [Google Scholar] [CrossRef]
- Belov, I.; Kabašinskas, A.; Sakalauskas, L. A study of stable models of stock markets. Inf. Technol. Control 2006, 35, 34–56. [Google Scholar]
- Yin, X.-A.; Yang, X.-H.; Yang, F.-Z. Using the R/S method to determine the periodicity of time series. Chaos Solitons Fractals 2009, 39, 731–745. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Y.Q. Robustness analysis of the estimators for noisy long-range dependent time series. In Proceedings of the ASME 2009 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009. [Google Scholar]
- Chatfield, C. Time-Series Forecasting; Chapman and Hall/CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Buishand, T.A. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point detection. J. R. Stat. Soc. C Appl. 1979, 28, 126–135. [Google Scholar]
- Daniell, P.J. Discussion following ‘On the theoretical specification and sampling properties of autocorrelated time series’ by M.S. Bartlett. J. R. Stat. Soc. 1946, 8, 88–90. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org (accessed on 29 December 2018).
- Kim, W.; Cai, W. Second peak in the far eastern Pacific sea surface temperature anomaly following strong El Niño events. Geophys. Res. Lett. 2013, 40, 4751–4755. [Google Scholar] [CrossRef]
- Ramasubramanian, V. Time-Series Analysis, Modelling and Forecasting Using SAS Software; Indian Agricultural Statistics Research Institute: New Delhi, India, 1970; Available online: http://www.iasri.res.in/sscnars/socialsci/5-TS_SAS_lecture.pdf (accessed on 29 December 2018).
- The International Telegraph and Telephone Consultative Committee. International Telephone Service Network Management, Traffic Engineering (Recommendations E.401-E.600), Volume II, Fascicle II.3; The International Telegraph and Telephone Consultative Committee: Geneva, Switzerland, 1985; Available online: http://handle.itu.int/11.1004/020.1000/4.259.43.en.1004 (accessed on 29 December 2018).
- Quian, B.; Rasheed, K. Hurst exponent and financial market predictability. In Proceedings of the 2nd IASTED International Conference on Financial Engineering and Applications, Cambridge, MA, USA, 8–11 November 2004. [Google Scholar]
- Kaklauskas, L.; Sakalauskas, L. Study of on-line measurement of traffic self-similarity. Cent. Eur. J. Oper. Res. 2013, 21, 63–84. [Google Scholar] [CrossRef]
- Dotov, D.G.; Bardy, B.G.; Dalla Bella, S. The role of environmental constraints in walking: Effects of steering and sharp turns on gait dynamics. Sci. Rep. 2016, 6, 28374. [Google Scholar] [CrossRef]
- Robeson, S.M. Revisiting the recent California drought as an extreme value. Geophys. Res. Lett. 2015, 42, 6771–6779. [Google Scholar] [CrossRef]
- Philander, S.G.H. El Niño, La Niña and the Southern Oscillation; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]
- Trenberth, K.E. The definition of El Niño. Bull. Amer. Meteorol. Soc. 1997, 78, 2771–2777. [Google Scholar] [CrossRef]
- Wang, S.; Huang, J.; He, Y.; Guan, Y. Combined effects of the Pacific Decadal Oscillation and El Niño-Southern Oscillation on global land dry-wet changes. Sci. Rep. 2014, 4, 6651. [Google Scholar] [CrossRef] [PubMed]
- Benson, L.; Linsley, B.; Smoot, J.; Mensing, S.; Lund, S. Influence of the Pacific Decadal Oscillation on the climate of the Sierra Nevada, California and Nevada. Quat. Res. 2003, 59, 151–159. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Halpert, M.S. Precipitation patterns associated with the high index phase of the Southern Oscillation. J. Clim. 1986, 2, 268–284. [Google Scholar] [CrossRef]
- Shukla, S.; Steinemann, A.; Iacobellis, S.F.; Cayan, D.R. Annual drought in California: Association with monthly precipitation and climate phases. J. Clim. 2015, 54, 2273–2281. [Google Scholar] [CrossRef]
- Spliid, H. Marima: Multivariate ARIMA and ARIMA-X Analysis. R Package Version 2.2. 2017. Available online: https://cran.r-project.org/web/packages/marima (accessed on 29 December 2018).
- Collopy, F.; Armstrong, J.S. Rule-based forecasting: Development and validation of an expert systems approach to combining time series extrapolations. Manag. Sci. 1992, 38, 1394–1414. [Google Scholar] [CrossRef]
- Chu, P.-S.; Chen, Y.R.; Schroeder, A. Changes in precipitation extremes in the Hawaiian Islands in a warming climate. J. Clim. 2010, 23, 4881–4900. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F. Global trends and variability in soil moisture and drought characteristics, 1950–2000, from observation-driven simulations of the terrestrial hydrologic cycle. J. Clim. 2008, 21, 432–458. [Google Scholar] [CrossRef]
- Esfahani, A.A.; Friedel, M.J. Forecasting conditional climate-change using a hybrid approach. Environ. Model. Softw. 2014, 52, 83–97. [Google Scholar] [CrossRef]
- Hazeleger, W.; van den Hurk, B.J.J.M.; Min, E.; van Oldenborgh, G.J.; Petersen, A.C.; Stainforth, D.A.; Vasileiadou, E.; Smith, L.A. Tales of future weather. Nat. Clim. Chang. 2015, 5, 107–113. [Google Scholar] [CrossRef]
- Ingram, W. Extreme precipitation: Increases all round. Nat. Clim. Chang. 2016, 6, 443–444. [Google Scholar] [CrossRef]













| Hurst (H) Exponent/Estimation Method | Whole Series (1801–2014) | Reduced Series (1901–2014) |
|---|---|---|
| Rescaled range (R/S) | 0.611 | 0.743 |
| Ratio variance of residuals | 0.611 | 0.550 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diodato, N.; De Guenni, L.B.; Garcia, M.; Bellocchi, G. Decadal Oscillation in the Predictability of Palmer Drought Severity Index in California. Climate 2019, 7, 6. https://doi.org/10.3390/cli7010006
Diodato N, De Guenni LB, Garcia M, Bellocchi G. Decadal Oscillation in the Predictability of Palmer Drought Severity Index in California. Climate. 2019; 7(1):6. https://doi.org/10.3390/cli7010006
Chicago/Turabian StyleDiodato, Nazzareno, Lelys Bravo De Guenni, Mariangel Garcia, and Gianni Bellocchi. 2019. "Decadal Oscillation in the Predictability of Palmer Drought Severity Index in California" Climate 7, no. 1: 6. https://doi.org/10.3390/cli7010006
APA StyleDiodato, N., De Guenni, L. B., Garcia, M., & Bellocchi, G. (2019). Decadal Oscillation in the Predictability of Palmer Drought Severity Index in California. Climate, 7(1), 6. https://doi.org/10.3390/cli7010006






