Evaluation of Daily Precipitation from the ERA5 Global Reanalysis against GHCN Observations in the Northeastern United States

Abstract

Precipitation is a primary input for hydrologic, agricultural, and engineering models, so making accurate estimates of it across the landscape is critically important. While the distribution of in-situ measurements of precipitation can lead to challenges in spatial interpolation, gridded precipitation information is designed to produce a full coverage product. In this study, we compare daily precipitation accumulations from the ERA5 Global Reanalysis (hereafter ERA5) and the US Global Historical Climate Network (hereafter GHCN) across the northeastern United States. We find that both the distance from the Atlantic Coast and elevation difference between ERA5 estimates and GHCN observations affect precipitation relationships between the two datasets. ERA5 has less precipitation along the coast than GHCN observations but more precipitation inland. Elevation differences between ERA5 and GHCN observations are positively correlated with precipitation differences. Isolated GHCN stations on mountain peaks, with elevations well above the ERA5 model grid elevation, have much higher precipitation. Summer months (June, July, and August) have slightly less precipitation in ERA5 than GHCN observations, perhaps due to the ERA5 convective parameterization scheme. The heavy precipitation accumulation above the 90th, 95th, and 99th percentile thresholds are very similar for ERA5 and the GHCN. We find that daily precipitation in the ERA5 dataset is comparable to GHCN observations in the northeastern United States and its gridded spatial continuity has advantages over in-situ point precipitation measurements for regional modeling applications.

1. Introduction

Accurate representations of precipitation across a landscape are important in the design of various engineering systems, as well as in the modeling of meteorological, hydrologic, and agricultural systems. This is especially true for the northeastern United States (hereafter Northeast). The Northeast is classified as a humid continental climate [1] and is characterized by complex terrain, a coast that borders the Atlantic Ocean, and a large number of metropolitan areas. Attempts to model hydrologic systems or draw conclusions from these models over large areas of complex topography using only in-situ precipitation gauges are subject to errors from missing data, large interpolation distances, a non-uniform distribution of gauges, and difficulty in the generalizability of results. Therefore, researchers have looked to using gridded precipitation information [2] such as the Daymet Dataset (spatial interpolation) [3], Meteorological Forcing Dataset (observation-based land surface forcings, derived surface fluxes and state variables) [4,5], the Parameter-elevation Regressions on Independent Slopes Model (PRISM; gridded precipitation estimates adjusted by physiographic factors) [6] and the ERA5 Global Reanalysis (hereafter ERA5; [7]) to address the challenges posed by in-situ observations. ERA5 is the most recent global climate reanalysis from the European Centre for Medium-Range Weather Forecasts (ECMWF) and represents an improvement over its predecessor ERA-Interim [8] in both spatial and temporal resolutions, and 2 m temperature accuracy [9]. ERA5 not only includes a robust physical and dynamic model of the atmosphere but also assimilates millions of observations into its reanalysis forecasts, making it suitable for reconstructing the climate past. Information from ERA5 allows the user to analyze continuous processes in a framework with fully coupled land, atmosphere, and ocean dynamics. With its complex topography, proximity to the Atlantic Ocean, and large population centers, the Northeast is a prime location to evaluate the utility of ERA5 for hydrologic and other applications.

Existing literature on the performance of the ERA5 dataset over the continental United States for hydrologic and precipitation studies has found that, while ERA5 performs better in hydrologic simulations than its predecessor ERA-Interim for all regions, it does not perform as well as actual observations for the eastern United States, perhaps due to the higher station density there [10]. For example, Beck et al. [11] compared 15 uncorrected precipitation datasets across the Northeast and found that ERA5 performed the best overall (with the highest Kling-Gupta Efficiency score [12,13]), especially in complex terrain when compared to the IMERGHHE V05 satellite precipitation product [14,15]. However, the opposite is true in locations dominated by small-scale convectively driven precipitation when compared to IMERGHHE V05 [11]. There are challenges in comparing an in-situ measurement of precipitation to a distributed precipitation product, such as a gridded dataset. This is primarily due to the fact that an in-situ measurement is only representative of the immediate surroundings in which it is located, whereas a distributed measurement of precipitation smooths information over a larger region. The scales on which in-situ and distributed measurements of precipitation can be applied need to be carefully considered.

In addition to using ERA5 for hydrologic modeling purposes [10] it is useful to assess how well ERA5 represents heavy precipitation events across the Northeast. Heavy precipitation events can be defined in a number of ways and generally fall in the right tail of a precipitation distribution (statistically the 75th to 99th percentile). Some studies, e.g., Huang et al. [16], Marquardt Collow et al. [17], Frei et al. [18], Guilbert et al. [19], and Hayhoe et al. [20], have found positive trends in warm season heavy precipitation, while the trends of these events in winter have been found to be decreasing, or changing very little over time in the Northeast.

The main goals of this paper are to: (1) Understand what drives the differences in the yearly average precipitation accumulations between ERA5 and US Global Historical Climate Network (hereafter GHCN) observations; (2) Quantify the seasonality of these differences and their relations to the drivers identified; (3) Compare the 90th, 95th, and 99th percentiles, and accumulation of precipitation above those percentiles between ERA5 and GHCN.

2. Materials and Methods

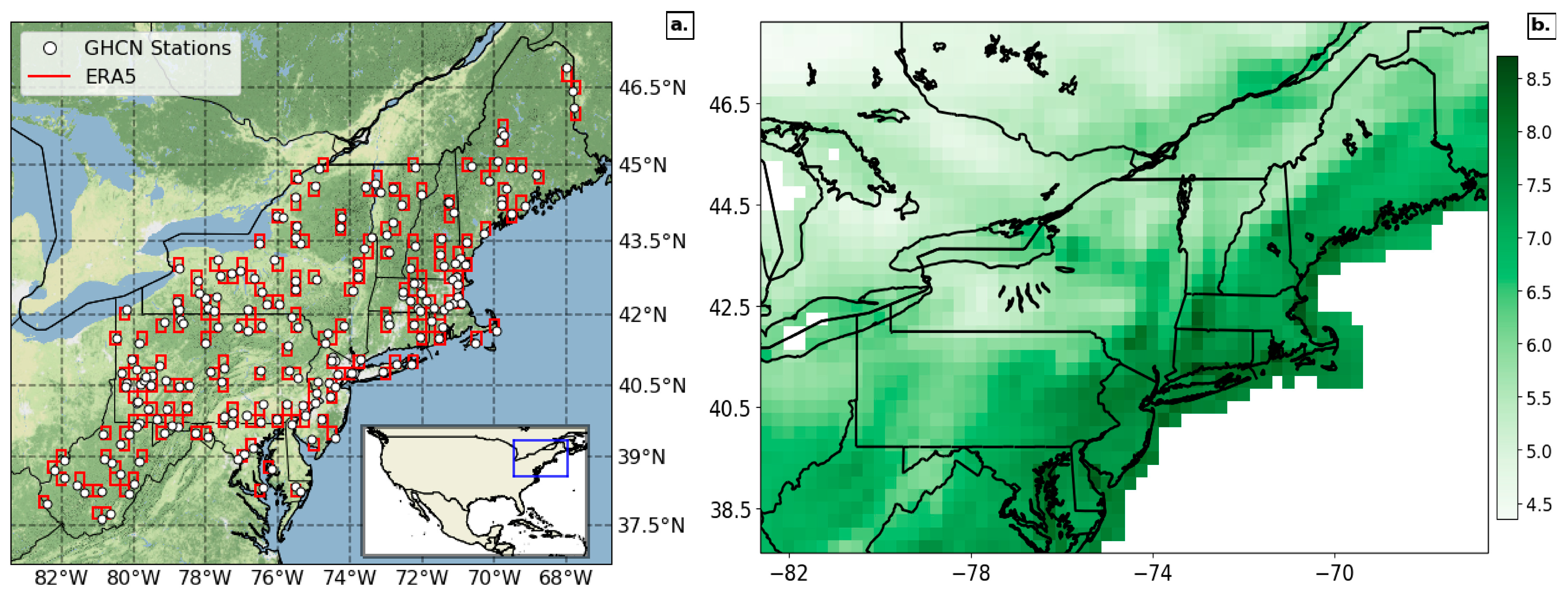
Two datasets were used in this study. Precipitation data from the GHCN dataset [21] were accessed directly at https://www.ncdc.noaa.gov/ghcnd-data-access, while the ERA5 [22] data came from https://cds.climate.copernicus.eu/cdsapp#!/home. Figure 1 shows the co-location of the 211 GHCN stations and corresponding ERA5 grid-boxes used in this study. The Northeast matches the definition of the region in the Fourth National Climate Assessment [23] as the states of Maine, New Hampshire, Vermont, New York, New Jersey, Connecticut, Massachusetts, Rhode Island, Delaware, Maryland, West Virginia, and Pennsylvania. The GHCN data are in-situ observational weather stations that report daily precipitation, whereas the ERA5 data are a gridded reanalysis product with quarter-degree spatial resolution and hourly temporal resolution. The period of record for this study is from 1979 to 2018 to match the start date of ERA5. The 2018 end date was the most recent full-year of ERA5 available at the time of data retrieval. Figure 1b shows the 40-year mean daily precipitation for the region as represented by ERA5. All subsequent analyses were carried out using Python and Excel.

There are a number of types of products available in the ERA5 dataset. One of these, the ERA5 surface forecast product, includes two separate initialization times, 06 UTC and 18 UTC. Each forecast is run for 18 h from the initialization time, resulting in a six-hour overlap between the two forecasts. This overlap produces an estimate of model spin-up in precipitation, which occurs as the model adjusts to the assimilation of new data. Over our domain of interest, we found six percent more precipitation in the 12–18 h forecasts than the 0–6 h forecasts for the same verification time. Therefore, to reduce the effects of model spin-up, we combined the 7–18 h forecast hours (valid for 13–00 UTC) from the 06 UTC analysis, and the 7–18 h forecast hours (valid for 01–12 UTC) from the 18 UTC analysis. These hourly ERA5 data were aggregated up to the daily time scale by summing the hourly precipitation accumulations from midnight-to-midnight local time, consistent with the time period over which the GHCN stations report daily precipitation.

Only GHCN stations with at least 95% or greater data coverage over their period of record were used in this analysis. For our domain of interest, 211 GHCN stations met this criterion. ERA5 is a continuous dataset with no missing data. Each of the 211 GHCN stations was then matched with the ERA5 grid box to which it was closest (Figure 1a). Due to the potential for missing data within the GHCN, and to ensure that the data coverage was over an identical time period for both datasets, any days that were missing in the GHCN were identified and were removed from the matching ERA5 grid box. Thus, for each location, we produced two datasets of matching period of record and length. In the cases where two GHCN stations fell within or were closest to a given ERA5 grid box, the latter was used as the match for both stations, although analyses that used date matching were performed separately for each GHCN station.

Wet days were defined as those on which precipitation accumulations recorded were equal to or greater than 0.3 mm/day (i.e., a trace). The GHCN stations only record daily precipitation at or above a trace amount, whereas the ERA5 precipitation estimates are a model derived product that can report accumulations which are smaller than the measurements that could be made by a standard precipitation gauge. Therefore, we removed all days with less than this trace amount of precipitation from both datasets. It should be noted, however, that although the lengths of record of wet days produced non-matching datasets, we do not believe that the difference in the number of precipitation days adversely affected the statistical results, due to the length of the period of record and the time scales considered.

The Atlantic Ocean considerably influences the weather and climate of the nine states in the Northeast that border it. We determined the distance from the coast to each ERA5 grid box using the ERA5 land-sea mask, a binary variable, where zero represents a “sea” grid point and one represents a “land” grid point. We used the Haversine formula, which computes the distance on a sphere between two points from their latitude and longitude, to determine the distance from the coast.

To examine how well ERA5 represents the heaviest precipitation across the Northeast, we compared the values of the 90th, 95th, and 99th percentile thresholds of daily precipitation of both datasets as well as the daily precipitation accumulation above the 90th, 95th, and 99th percentiles of wet day precipitation [16,24]. We first found the values of the 90th, 95th, and 99th percentiles of wet day precipitation for both datasets using all 40 years of data for each station. From there, we summed up the precipitation accumulation for any day with precipitation that fell above the percentile threshold considered. We did this for every year at each station and its corresponding ERA5 grid box. We then took the average of this yearly accumulation over a threshold over the 40-year period and used it in our analyses. We examine not only the thresholds themselves, but also the precipitation accumulation above these thresholds to get a sense of the average amount of heavy precipitation that falls each year.

We compared variables using ordinary least squares regression, zero intercept regression, multiple linear regression, and Deming regression [25]. The latter fits a line to two-dimensional data where both variables are measured with error (i.e., the line is weighted by the ratio of the variances of each dataset), and was used because both the ERA5 and GHCN datasets have some form of error, whether that be model or measurement error.

3. Results

In the following analyses, all means were taken over the 1979–2018 period of record using a seasonal or yearly aggregate of daily precipitation accumulations unless otherwise stated. Differences in precipitation and elevation were always taken as ERA5–GHCN.

3.1. Climate Comparison

We first computed yearly precipitation totals for each location and each dataset separately, and then took the mean of those yearly values for both ERA5 and the GHCN. Figure 2a shows that the relationship between the two datasets is influenced by the highest elevation points (Mounts Washington and Mansfield in New Hampshire and Vermont, respectively;

Table 1. Regression analyses for 1979–2018 annual means.

	Slope	Y-Intercept	R-Squared	p-Value on Slope
Deming Regression (mm)	0.66 ± 0.27 *	421 ± 294	0.23	1.3 × 10−2
Zero Intercept Regression (mm)	1.02 ± 0.01 *	0	–	1.5 × 10−187
Deming Regression (No Mountains; mm)	0.84 ± 0.11 *	226 ± 117	0.23	2.1 × 10−13
Zero Intercept Regression (No Mountains; mm)	1.03 ± 0.01 *	0	–	1.2 × 10−202
Precipitation Difference (mm) vs. Distance from Coast (km)	0.62 ± 0.04 *	−76 ± 11	0.51	1.3 × 10−33
Precipitation Difference (mm) vs. Elevation Difference (m)	0.57 ± 0.08 *	22 ± 9	0.20	1.04 × 10−11

* Result is significant to the 95% confidence level.

). This is not surprising given that the ERA5 grid boxes are a distributed measure of precipitation over the full quarter-degree grid box, whereas the actual location of the GHCN precipitation gauges on these two mountain peaks were 949 m and 678 m above their respective mean grid box elevations. Therefore, these two mountain-top stations were excluded from subsequent analyses in order to reduce their impact on the results (Figure 2b).

Figure 2b illustrates that the average yearly precipitation was generally higher in ERA5 than the GHCN, since more points are above the 1:1 line. The 209-station average of the annual precipitation ratio (ERA5/GHCN) was 1.06 ± 0.12 (where the ± uncertainty is the standard deviation, here and throughout the paper), and mean absolute error (MAE) of 109 ± 78 mm/year (Table S1). The average annual precipitation may be larger in ERA5 due to two reasons: (1) ERA5 on average has 22 ± 6% more wet days than the GHCN which would result in larger yearly precipitation totals; (2) the GHCN data have not been corrected for precipitation undercatch. Undercatch in standard precipitation gauges, primarily due to wind effects, has been well documented as a systematic error in observational precipitation measurements, especially with snowfall [26,27]. Errors from gauge undercatch can result in significant underrepresentation of precipitation accumulation at a site, and in this analysis may have contributed to the smaller yearly precipitation accumulations noted in the GHCN.

Figure 2c shows the dependence of the difference in mean yearly precipitation upon the distance away from the Atlantic Coast, with the linear fit shown in Table 1. On the coast, that difference was −76 ± 11 mm with a linear increase inland of 62 ± 4 mm per 100 km. Therefore, by 120 km inland from the coast, the ERA5 precipitation was larger than the GHCN, a value that continued to increase inland. This may be linked to two reasons: (1) the spatial resolution of ERA5 is not sufficient to capture local sea breeze circulations, which aid in the production of precipitation along the coast; (2) ERA5 has more precipitation inland, possibly a result of the two aforementioned issues regarding the larger number of wet days in ERA5 and the undercatch of the GHCN precipitation gauges.

The difference in the elevation between the ERA5 grid point and the GHCN station may also play a role in the differences in precipitation noted between the two datasets. While we treated the distance from the Atlantic Coast as the same for both ERA5 and the GHCN, the mean elevation of the grid point and associated station differ. Each GHCN station has a point elevation, while ERA5 has a mean value for the quarter-degree grid box. ERA5 only resolves the mean orography on the quarter-degree scale, but has additional sub-grid scale orography (at 5000 m resolution) to better represent the momentum transfers that are influenced by small-scale variations in orography [28]. The full impact of this sub-grid scale orography in regions of complex topography is unclear. The mean elevation difference between the two datasets was 53 ± 97 m, meaning that, on average, the ERA5 grid boxes have a higher elevation, although the standard deviation is large. In complex terrain, the GHCN station may be located preferentially at lower elevations.

As the elevation difference increases, so too does the difference in precipitation, with a lot of scatter in this relationship (Figure 2d, Table 1). Since the distance inland from the coast is also correlated with elevation (but not correlated with elevation difference), the combination of these two variables showed a clear improvement in the regression results. Using both the distance from the Atlantic Coast and elevation difference as explanatory variables, for predicting the difference in average annual precipitation, revealed that the R-squared value for the multiple linear regression increased to 0.60 (

Table 2. Multiple linear regression of average yearly precipitation difference between ERA5 and GHCN (mm) on the distance from the coast (km) and elevation difference (m).

Y-Intercept	Slope of the Distance from the Coast (p-Value)	Slope of the Elevation Difference (p-Value)	R-Squared
−85 ± 10	0.56 ± 0.04 (1.2 × 10−32) *	0.40 ± 0.06 (7.8 × 10−11) *	0.60

* Result is significant to the 95% confidence level.

), versus 0.51 and 0.20 for the distance from the Atlantic Coast or the elevation difference, respectively (Table 1).

3.2. Seasonal Analysis

Understanding how well ERA5 represents precipitation seasonally is also important in determining its utility for hydrologic studies across the Northeast. Seasons are defined meteorologically as: Winter: December, January, and February (DJF); Spring: March, April, and May (MAM); Summer: June, July, and August (JJA); Fall: September, October, and November (SON). We computed the total precipitation in each season of each year and then took the mean over each season. MAE for seasons were 31 ± 21 mm, 40 ± 26 mm, 27 ± 22 mm, and 29 ± 19 mm for winter, spring, summer, and fall, respectively (Table S1). Figure 3 and

Table 3. Regression analyses for the seasonal precipitation.

	Season	Slope	Y-Intercept	R-Squared	p-Value on Slope
Seasonal Precipitation: Deming Regression	Winter (DJF)	0.69 ± 0.06 *	91 ± 13	0.49	2.1 × 10−25
	Spring (MAM)	0.91 ± 0.10 *	56 ± 26	0.30	1.0 × 10−17
	Summer (JJA)	1.29 ± 0.13 *	−91 ± 40	0.34	7.8 × 10−19
	Fall (SON)	0.64 ± 0.12 *	106 ± 34	0.19	3.1 × 10−7
Seasonal Precipitation: Zero Intercept Regression	Winter (DJF)	1.06 ± 0.01 *	0	–	1.5 × 10−182
	Spring (MAM)	1.09 ± 0.01 *	0	–	5.5 × 10−190
	Summer (JJA)	1 ± 0.01 *	0	–	5.4 × 10−201
	Fall (SON)	1 ± 0.01 *	0	–	1.3 × 10−194
Seasonal Precipitation Difference (mm) vs. Distance from Coast (km)	Winter (DJF)	0.13 ± 0.01 *	7 ± 3	0.32	8.4 × 10−19
	Spring (MAM)	0.2 ± 0.01 *	11 ± 3	0.59	1.1 × 10−41
	Summer (JJA)	0.14 ± 0.01 *	29 ± 3	0.33	1.2 × 10−19
	Fall (SON)	0.16 ± 0.01 *	29 ± 3	0.41	1.8 × 10−25
Seasonal Precipitation Difference (mm) vs. Elevation Difference (m)	Winter (DJF)	0.16 ± 0.02 *	11 ± 2	0.24	4.1 × 10−14
	Spring (MAM)	0.17 ± 0.02 *	21 ± 3	0.2	1.9 × 10−11
	Summer (JJA)	0.08 ± 0.02 *	−5 ± 3	0.06	5.0 × 10−4
	Fall (SON)	0.16 ± 0.02 *	−5 ± 2	0.19	2.5 × 10−11

* Result is significant to the 95% confidence level.

compare these 40-year averages by season for ERA5 and the GHCN. ERA5 estimates were generally larger in winter, spring (both about 10%), and fall (1%) but not in summer, illustrated by where the points fell relative to the 1:1 line in Figure 3. The slightly lower precipitation in ERA5 than the GHCN in summer may be due to the convective parameterization in ERA5. Convective precipitation is the main mode of precipitation accumulation in the summer in the Northeast, whereas other larger-scale precipitation-producing systems occur in the other seasons. All slopes of the Deming regression analysis are less than one, except for in summer, indicating a change in the ERA5–GHCN relationship during this season (Table 3). Point precipitation accumulations at individual stations may also be under-sampled given the nature of scattered convective precipitation compared to large-scale precipitation events.

Next, we examined the relationship between the difference in the mean seasonal precipitation totals versus both the distance from the Atlantic Coast and elevation difference using results from the ordinary least squares regression analysis. Similar to Figure 2c, linear regressions revealed that during all seasons, as the station’s distance from the coast increased, the difference in average seasonal precipitation shifted from a negative or near zero value near the coast to a linear increase inland (Figure 4). The transition from a negative precipitation difference (ERA5 < GHCN) to a positive one (ERA5 > GHCN) occurred around 50 km inland from the coast in winter and spring, and around 200 km inland in the summer and fall. Higher precipitation totals along the coast in summer may have been due to the frequency of sea breezes. While Barbato [29] and Sikora et al. [30] found a peak sea-breeze frequency from June to August at Boston, Massachusetts and the Chesapeake Bay region in Maryland (both on the Atlantic Coast), Defant [31] found that the strongest sea breezes at mid-latitude coastal locations tend to occur in summer. Spring and summer exhibit large thermal gradients from the sea to the land which produce sea breezes. The scatterplots and regression results (R-squared values) for the winter, spring, and fall of the difference in seasonal precipitation and elevation difference (Figure 5) closely resembled those for the full-year analyses shown in Figure 2d and Table 1. Summer results showed a much smaller dependence on elevation difference and variance explained as compared to the values in Figure 3c (Figure 5c and Table 3).

Table 4. Multiple linear regression of the mean seasonal precipitation difference between ERA5 and GHCN (mm) on the distance from the coast (km) and elevation difference (m).

Season	Y-Intercept	Slope of the Distance from the Coast (p-Value)	Slope of the Elevation Difference (p-Value)	R-Squared
Winter (DJF)	−10 ± 3	0.11 ± 0.01 (6.0 × 10−17) *	0.13 ± 0.02 (2.8 × 10−12) *	0.46
Spring (MAM)	−13 ± 3	0.18 ± 0.1 (1.3 × 10−41) *	0.11 ± 0.02 (1.7 × 10−11) *	0.67
Summer (JJA)	−30 ± 3	0.13 ± 0.1 (7.0 × 10−18) *	0.04 ± 0.02 (3.6 × 10−2) *	0.34
Fall (SON)	−31 ± 3	0.14 ± 0.01 (1.0 × 10−23) *	0.11 ± 0.02 (1.4 × 10−9) *	0.51

* Result is significant to the 95% confidence level.

summarizes the results of the multiple linear regression of the mean seasonal precipitation difference on both the distance from the Atlantic Coast and the elevation difference. For all seasons, the multiple linear regression yielded a higher amount of variance explained than did the ordinary linear regression (Table 3 and Table 4). The relationship with the distance from the Atlantic Coast was weakest in the winter and strongest in the spring, where the latter season also had the largest R-squared value. This again suggests the importance of a high frequency of sea breezes along the coast in the spring. Elevation differences are equally important in winter, spring, and fall, but negligible in summer, consistent with the results of the ordinary linear regression (Table 3 and Table 4). Increases in the R-squared values in the multiple linear regression for all seasons, confirm that the coastal distance and elevation difference should not be considered individually as explanatory variables.

3.3. Heavy Precipitation

We compared heavy precipitation statistics across the Northeast between ERA5 and the GHCN.

Table 5. Regression analyses for heavy precipitation.

	Percentile Threshold	Slope	Y-Intercept	R-Squared	p-Value on Slope
Value of Percentile Threshold: ERA5 vs. GHCN (mm)	90th	0.50 ± 0.02 *	7 ± 0.4	0.81	6.5 × 10−77
	95th	0.50 ± 0.02 *	9 ± 0.5	0.82	4.2 × 10−79
	99th	0.44 ± 0.02 *	17 ± 0.9	0.78	1.3 × 10−70
Precipitation Above Threshold: Deming Regression	90th	0.63 ± 0.09 *	176 ± 41	0.26	1.4 × 10−11
	95th	0.59 ± 0.09 *	121 ± 27	0.24	2.0 × 10−9
	99th	0.53 ± 0.11 *	41 ± 10	0.14	4.5 × 10−6
Precipitation Above Threshold: Zero Intercept Regression	90th	1 ± 0.01 *	0	–	3.1 × 10−204
	95th	0.98 ± 0.01 *	0	–	3.3 × 10−201
	99th	0.95 ± 0.01 *	0	–	5.7 × 10−187
Precipitation Difference Above Threshold (mm) vs. Distance from Coast (km)	90th	0.23 ± 0.02 *	−44 ± 5	0.42	5.5 × 10−26
	95th	0.15 ± 0.01 *	−3 ± 3	0.39	3.8 × 10−24
	99th	0.05 ± 0.00 *	−15 ± 1	0.38	2.1 × 10−23
Precipitation Difference Above Threshold (mm) vs. Elevation Difference (m)	90th	0.26 ± 0.03 *	−10 ± 3	0.25	2.3 × 10−14
	95th	0.17 ± 0.02 *	−11 ± 2	0.26	5.7 × 10−15
	99th	0.06 ± 0.01 *	−7 ± 1	0.26	1.8 × 10−15

* Result is significant to the 95% confidence level.

summarizes the value of the 90th, 95th, and 99th percentiles of daily precipitation between the two datasets, as well as the sum of precipitation over these percentiles. Given the similarity in the results for the three thresholds (Table 5), only the 90th percentile value will be discussed here. Plots for the 95th and 99th percentile thresholds can be found in the Supplementary Materials (Figures S1 and S2, respectively).

Figure 6a summarizes the values of the 90th percentile thresholds for the two datasets. For the stations considered, the 90th percentile threshold value for the GHCN was greater than that for ERA5, since all of the points are below the 1:1 line (Figure 6a; MAE of 4 ± 2 mm, Table S1). However, the precipitation accumulation above the 90th percentile showed that the GHCN dataset did not have consistently higher precipitation accumulations than did the ERA5 dataset, as the zero-intercept regression line corresponds with the 1:1 line (Figure 6b; MAE 44 ± 41 mm, Table S1). Comparing histograms of the frequency of days with less than 10.3 mm/day of precipitation illustrates that there were many more days with small precipitation accumulations in ERA5 relative to the GHCN (Figure S3). The large number of smaller precipitation values in ERA5 contributed to a lower threshold value when compared to the GHCN due to the higher density of the left tail of the histogram. The value of precipitation that fell above that threshold is dependent upon individual station characteristics and daily precipitation distributions which led to both larger and smaller accumulations above the 90th percentile threshold for ERA5 (Figure 6b). The Deming regression slopes are less than one, similar to most earlier plots, decreasing slightly from the 90th to 99th percentile thresholds. Conceptually, these slopes mean that for lower precipitation values, ERA5 was greater than the GHCN, while for higher precipitation values, the GHCN was greater than ERA5. The scatterplot of the difference in the precipitation accumulation above the 90th percentile between ERA5 and the GHCN against the distance from the Atlantic Coast (Figure 6c) resembled those of Figure 2c and Figure 4, where ERA5 consistently showed less precipitation along the coast. Figure 6d shows that the difference in the precipitation above the 90th percentile generally increased with the difference in elevation, also shown in the seasonal and full-year analyses (Figure 2d and Figure 5). As aforementioned, the distance from the coast and elevation difference cannot be considered individually as explanatory variables.

Table 6. Multiple linear regression of the difference of precipitation accumulation on the distance from the coast (km), and elevation difference (m) at the 90th, 95th, and 99th percentiles thresholds (mm).

Threshold	Y-Intercept	Slope of the Distance from the Coast (p-Value)	Slope of the Elevation Difference (p-Value)	R-Squared
90th Percentile	−48 ± 4	0.20 ± 0.02 (6.2 × 10−25) *	0.19 ± 0.03 (2.3 × 10−13) *	0.55
95th Percentile	−35 ± 3	0.13 ± 0.01 (5.3 × 10−23) *	0.13 ± 0.02 (7.3 × 10−14) *	0.54
99th Percentile	−16 ± 1	0.05 ± 0.004 (2.8 × 10−22) *	0.05 ± 0.01 (2.2 × 10−14) *	0.54

* Result is significant to the 95% confidence level.

summarizes the multiple linear regression results of the precipitation accumulation difference above the 90th, 95th, and 99th percentiles on both distance from the Atlantic Coast and elevation difference. All percentile thresholds have a similar explained variance. The dependence on the distance from the coast and the elevation difference also had similar slopes, but the actual slopes decreased from the 90th to 99th percentile thresholds.

4. Discussion and Conclusions

The comparison of the yearly precipitation accumulation from the ERA5 climate reanalysis against that from GHCN stations across the Northeast provides a framework for assessing the value of ERA5 for different applications in the Northeast. Several key patterns emerged. Average annual precipitation was generally higher in ERA5 than in the GHCN. The 209-station average of the annual precipitation ratio (ERA5/GHCN) was 1.06 ± 0.12. This may be due to the 22 ± 6% more wet days in ERA5, or that the GHCN data have not been corrected for precipitation undercatch. We found a relationship between precipitation differences and both the distance from the Atlantic Coast and the difference in elevation. ERA5 consistently displayed less precipitation both along the coast and for isolated mountain peaks. Coastal precipitation shortfalls probably reflected the inability of the ERA5 parameterization to quantify sea breeze-induced precipitation at the quarter-degree spatial resolution. In regions of high terrain, ERA5 cannot resolve mountain peaks that are well above the mean grid elevation. When considered together, the distance from the coast and elevation difference provided a better fit to the differences in precipitation, implying that they should not be treated independently.

Seasonally, ERA5 showed 10% more precipitation than the GHCN in winter and spring, 1% in autumn and a trace less in summer. Similar patterns were observed in the relationship between distance from the coast and elevation difference in all seasons except summer, which was the only season in which ERA5 did not have more precipitation than the GHCN and the relationship between the difference in precipitation and the elevation difference was the weakest. We attributed these differences in the summer months to the frequency of convective precipitation events, which are parameterized in ERA5.

The forty-year 90th, 95th, and 99th percentile thresholds for daily heavy precipitation were well correlated, and the mean precipitation accumulation over these percentiles was very similar for both ERA5 and the GHCN. The structure of the heavy precipitation dependence on the distance from the coast and the elevation difference were similar to the long-term and seasonal results suggesting that the ERA5 dataset will be useful for studies of daily heavy precipitation events.

In assessing the utility of the ERA5 climate reanalysis at aggregated timescales, our study results highlight the importance of a full appreciation of the strengths and limitations of precipitation estimates being used in models to explore biogeophysical processes across the landscape. Precipitation datasets derived primarily from in-situ stations often lack uniform spatial and temporal coverage or require large interpolation distances in order to create uniform coverage. Such limitations have prompted the use of climate reanalyses, such as ERA5, which with its quarter-degree spatial and hourly temporal resolutions, we have shown to be comparable to GHCN observations of precipitation across the Northeast. The ability to utilize a full coverage, spatio-temporally consistent product such as ERA5 will allow users the increased capability to model or predict land-surface processes across large geographic regions with greater confidence. There are two important caveats. The first is the biases that exist in the ERA5 precipitation estimates in terms of their distance from the Atlantic coast and elevation difference relative to the point GHCN observations. Secondly, we acknowledge that hourly precipitation estimates, especially the extremes in heavy precipitation, can have significant impacts on engineering, hydrologic, and agricultural systems (i.e., stormwater, flood control, etc.), and may not have been represented in our aggregated approach. Therefore, future work should include an examination of how well ERA5 data represent precipitation at the hourly scale to assess its utility in applications that require high temporal resolutions.