Lorenz Atmospheric Energy Cycle in Climatic Projections
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Formulation of the Problem
2.3. Methodology
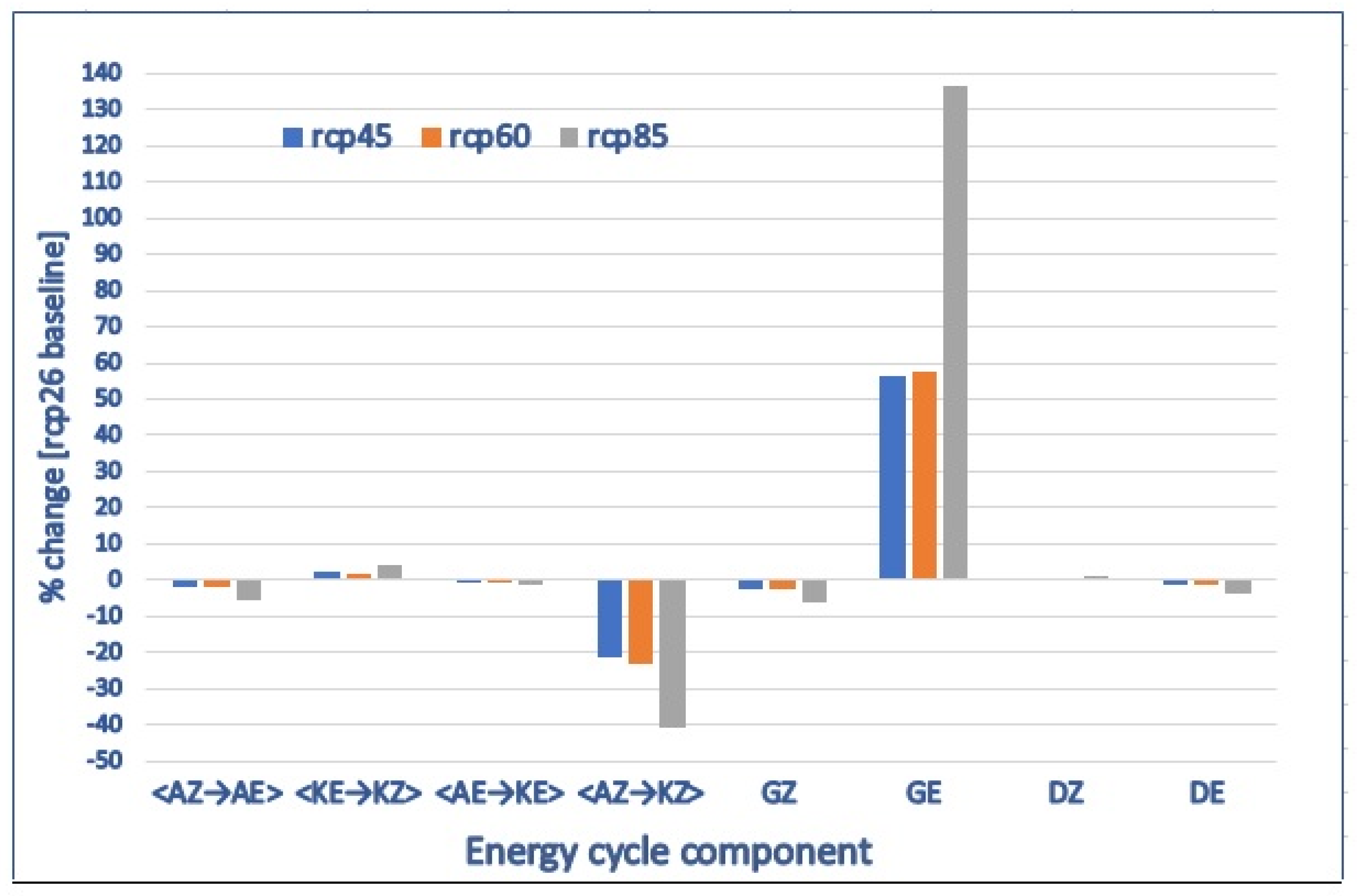
3. Results
3.1. Energy Balance
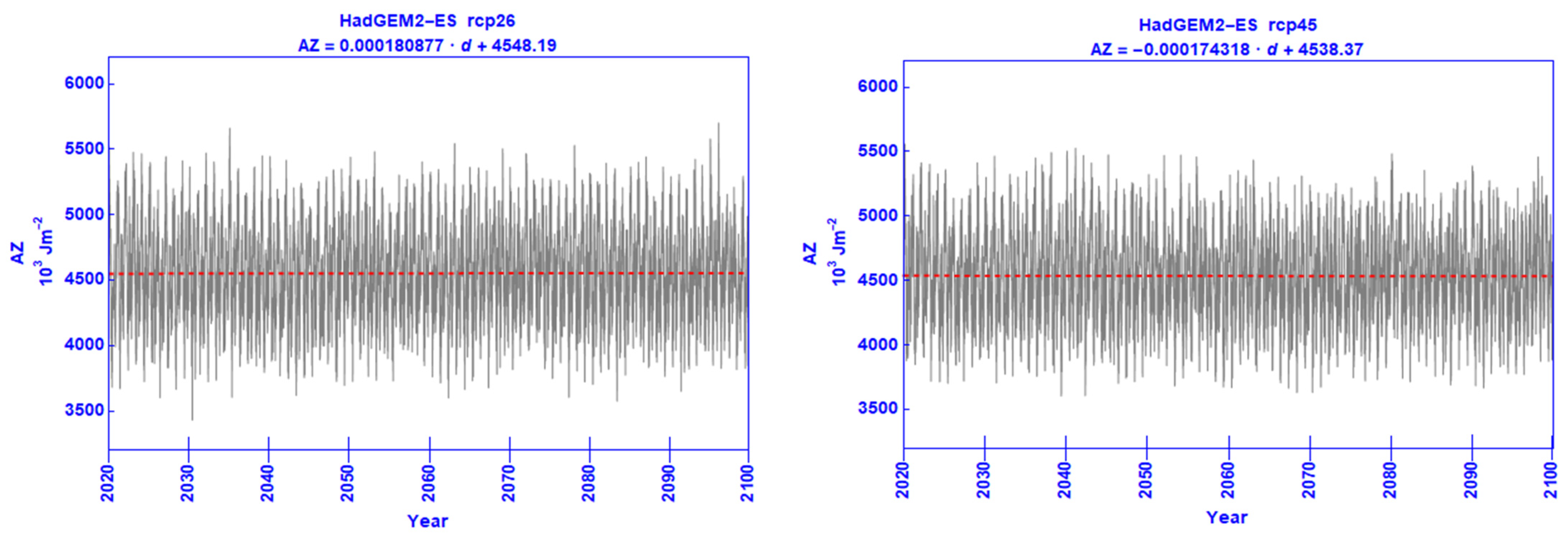
3.2. Time Series and Trends
4. Discussion
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Oort, A.H. On estimates of the atmospheric energy cycle. Mon. Weather Rev. 1964, 92, 483–493. [Google Scholar] [CrossRef] [Green Version]
- Saltzman, B. Large-scale atmospheric energetics in the wave-number domain. Rev. Geophys. 1970, 8, 289–302. [Google Scholar] [CrossRef]
- Wiin-Nielsen, A. On the intensity of the general circulation of the atmosphere. Rev. Geophys. 1968, 6, 559–579. [Google Scholar] [CrossRef]
- Margules, M. Über die Energie der Stürme (On the energy of storms—Originally published by the Imperial Central Institute for Meteorology, Vienna, Austria, 1903; pp. 1–26). In The Mechanics of the Earth’s Atmosphere—A Collection of Translations; Abbe, C., Ed.; English translation by Smithsonian Institution: Washington, DC, USA, 1904; Volume 51, pp. 533–595. [Google Scholar]
- Lorenz, E.N. Energy and numerical weather prediction. Tellus 1960, 12, 364–373. [Google Scholar] [CrossRef] [Green Version]
- Van Mieghem, J. Atmospheric Energetics; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Pearce, R.P. On the concept of available potential energy. Q. J. R. Meteorol. Soc. 1978, 104, 737–755. [Google Scholar] [CrossRef]
- Bannon, P.R. Atmospheric available energy. J. Atmos. Sci. 2012, 69, 3733–3744. [Google Scholar] [CrossRef]
- Aranha, A.F.; Veiga, J.A.P. An analysis of the spectral energetics for a planet experiencing rapid greenhouse gas emissions. Atmos. Clim. Sci. 2017, 7, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. The Nature and Theory of the General Circulation of the Atmosphere; World Meteorological Organization: Geneva, Switzerland, 1967. [Google Scholar]
- Lorenz, E.N. Available potential energy and the maintenance of the general circulation. Tellus 1955, 7, 157–167. [Google Scholar] [CrossRef] [Green Version]
- Krueger, A.F.; Winston, J.S.; Haines, D.A. Computations of atmospheric energy and its transformation for the Northern Hemisphere for a recent five-year period. Mon. Weather Rev. 1965, 93, 227–238. [Google Scholar] [CrossRef]
- Dutton, J.A.; Johnson, D.R. The theory of available potential energy and a variational approach to atmospheric energetics. Adv. Geophys. 1967, 12, 333–436. [Google Scholar]
- Wiin-Nielsen, A. On the annual variation and spectral distribution of atmospheric energy. Tellus 1967, 19, 540–559. [Google Scholar] [CrossRef]
- Oort, A.H.; Peixóto, J.P. The annual cycle of the energetics of the atmosphere on a planetary scale. J. Geophys. Res. 1974, 79, 2705–2719. [Google Scholar] [CrossRef]
- Oriol, E. Energy Budget Calculations at ECMWF—Part 1: Analyses 1980–81. Technical Report, 35; ECMWF: Reading, UK, 1982. [Google Scholar]
- Kung, E.C.; Tanaka, H. Energetics analysis of the global circulation during the special observation periods of FGGE. J. Atmos. Sci. 1983, 40, 2575–2592. [Google Scholar] [CrossRef] [Green Version]
- Ulbrich, U.; Speth, P. The global energy cycle of stationary and transient atmospheric waves: Results from ECMWF analyses. Meteorol. Atmos. Phys. 1991, 45, 125–138. [Google Scholar] [CrossRef]
- Hu, Q.; Tawaye, Y.; Feng, S. Variations of the northern hemisphere atmospheric energetics: 1948–2000. J. Clim. 2004, 17, 1975–1986. [Google Scholar] [CrossRef]
- Marques, C.A.F.; Castanheira, J.M. A detailed normal-mode energetics of the general circulation of the atmosphere. J. Atmos. Sci. 2012, 69, 2718–2732. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef] [Green Version]
- Uppala, S.M.; Kållberg, P.W.; Simmons, A.J.; Andrae, U.; da Costa Bechtold, V.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Hernandez, A.; Kelly, G.A.; et al. The ERA-40 re-analysis. Q. J. R. Meteorol. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Boer, G.J.; Lambert, S. The energy cycle in atmospheric models. Clim. Dyn. 2008, 30, 371–390. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; Van Vuuren, D.P.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef]
- Gleckler, P. The AMIP Experience: Challenges and Opportunities. Available online: https://digital.library.unt.edu/ark:/67531/metadc1406844/m1/1/ (accessed on 7 November 2021).
- Hernández-Deckers, D.; von Storch, J.S. Energetics responses to increases in greenhouse gas concentration. J. Clim. 2010, 23, 3874–3887. [Google Scholar] [CrossRef] [Green Version]
- Veiga, J.A.P.; Ambrizzi, T. A global and hemispherical analysis of the Lorenz energetics based on the representative concentration pathways used in CMIP5. Adv. Meteorol. 2013, 2013, 485047. [Google Scholar] [CrossRef] [Green Version]
- Jones, C.D.; Hughes, J.K.; Bellouin, N.; Hardiman, S.C.; Jones, G.S.; Knight, J.; Liddicoat, S.; O’Connor, F.M.; Andres, R.J.; Bell, C.; et al. The HadGEM2-ES implementation of CMIP5 centennial simulations. Geosci. Model Dev. 2011, 4, 543–570. [Google Scholar] [CrossRef] [Green Version]
- Collins, W.J.; Bellouin, N.; Doutriaux-Boucher, M.; Gedney, N.; Halloran, P.; Hinton, T.; Hughes, J.; Jones, C.D.; Joshi, M.; Liddicoat, S.; et al. Development and evaluation of an Earth-System model—HadGEM2. Geosci. Model Dev. 2011, 4, 1051–1075. [Google Scholar] [CrossRef] [Green Version]
- Martin, G.M.; Bellouin, N.; Collins, W.J.; Culverwell, I.D.; Halloran, P.R.; Hardiman, S.C.; Hinton, T.J.; Jones, C.D.; McDonald, R.E.; McLaren, A.J.; et al. The HadGEM2 family of Met Office Unified Model climate configurations. Geosci. Model Dev. 2011, 4, 723–757. [Google Scholar]
- Lorenz, E.N. Energetics of atmospheric circulation. Int. Dict. Geophys. 1965, 66, 1–9. [Google Scholar]
- Muench, H.S. On the dynamics of the wintertime stratosphere circulation. J. Atmos. Sci. 1965, 22, 349–360. [Google Scholar] [CrossRef] [Green Version]
- Muench, H.S. Stratospheric Energy Processes and Associated Atmospheric Long-Wave Structure in Winter; Office of Aerospace Research, United States Air Force: Cambridge, MA, USA, 1965. [Google Scholar]
- Reiter, E. Atmospheric Transport Processes—Part 1: Energy Transfers and Transformations; Available as TID-24868 from the Clearinghouse for Federal Scientific and Technical Information U. S. Department of Commerce; U.S. Atomic Energy Commission: Springfield, VA, USA, 1969; ISBN 9788578110796.
- Michaelides, S.C. Limited area energetics of Genoa cyclogenesis. Mon. Weather Rev. 1987, 115, 13–26. [Google Scholar] [CrossRef]
- Michaelides, S.C. A spatial and temporal energetics analysis of a baroclinic disturbance in the Mediterranean. Mon. Weather Rev. 1992, 120, 1224–1243. [Google Scholar] [CrossRef]
- Sverdrup, H.U. Der nordatlantische Passat; Geophysikalischen Instituts der Karl-Marx-Universität: Leipzig, Germany, 1917; Volume 2. [Google Scholar]
- Brunt, D. XLIII. Energy in the Earth’s atmosphere. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1926, 1, 523–532. [Google Scholar] [CrossRef]
- Holopainen, E.O. On the dissipation of kinetic energy in the atmosphere. Tellus 1963, 15, 26–32. [Google Scholar] [CrossRef]
- Kung, E.C. Large-scale balance of kinetic energy in the atmosphere. Mon. Weather Rev. 1966, 94, 627–640. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Generation of available potential energy and the intensity of the general circulation. In Dynamics of Climate; Pfeffer, R.L., Ed.; Pergamon Press: Oxford, UK, 1960; pp. 86–92. [Google Scholar]
- Marquet, P. On the concept of exergy and available enthalpy: Application to atmospheric energetics. Q. J. R. Meteorol. Soc. 1991, 117, 449–475. [Google Scholar] [CrossRef]
- Lucarini, V.; Fraedrich, K.; Lunkeit, F. Thermodynamics of climate change: Generalized sensitivities. Atmos. Chem. Phys. 2010, 10, 9729–9737. [Google Scholar] [CrossRef] [Green Version]
- Boer, G.J. Some dynamical consequences of greenhouse gas warming. Atmos. Ocean 1995, 33, 731–751. [Google Scholar] [CrossRef]
- Miao, C.; Duan, Q.; Sun, Q.; Huang, Y.; Kong, D.; Yang, T.; Ye, A.; Di, Z.; Gong, W. Assessment of CMIP5 climate models and projected temperature changes over Northern Eurasia. Environ. Res. Lett. 2014, 9, 055007. [Google Scholar] [CrossRef]
- Díaz-Esteban, Y.; Raga, G.B.; Rodríguez, O.O.D. A weather-pattern-based evaluation of the performance of CMIP5 models over Mexico. Climate 2020, 8, 5. [Google Scholar] [CrossRef] [Green Version]
- Kravtsov, S. Pronounced differences between observed and CMIP5-simulated multidecadal climate variability in the twentieth century. Geophys. Res. Lett. 2017, 44, 5749–5757. [Google Scholar] [CrossRef]
- Riahi, K.; van Vuuren, D.P.; Kriegler, E.; Edmonds, J.; O’Neill, B.C.; Fujimori, S.; Bauer, N.; Calvin, K.; Dellink, R.; Fricko, O.; et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Glob. Environ. Chang. 2017, 42, 153–168. [Google Scholar] [CrossRef] [Green Version]
- van Vuuren, D.P.; Kriegler, E.; O’Neill, B.C.; Ebi, K.L.; Riahi, K.; Carter, T.R.; Edmonds, J.; Hallegatte, S.; Kram, T.; Mathur, R.; et al. A new scenario framework for Climate Change Research: Scenario matrix architecture. Clim. Chang. 2014, 122, 373–386. [Google Scholar] [CrossRef] [Green Version]
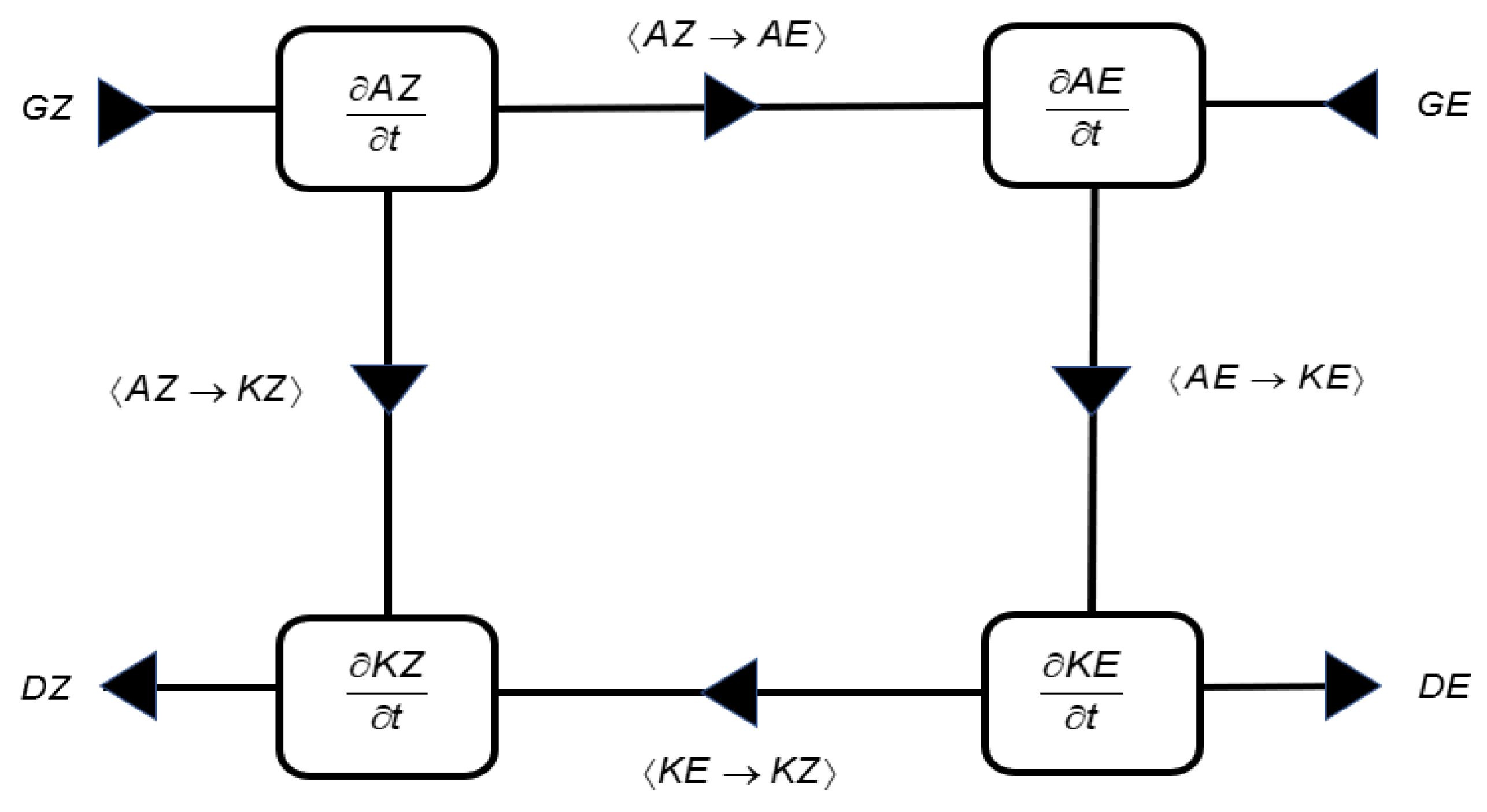
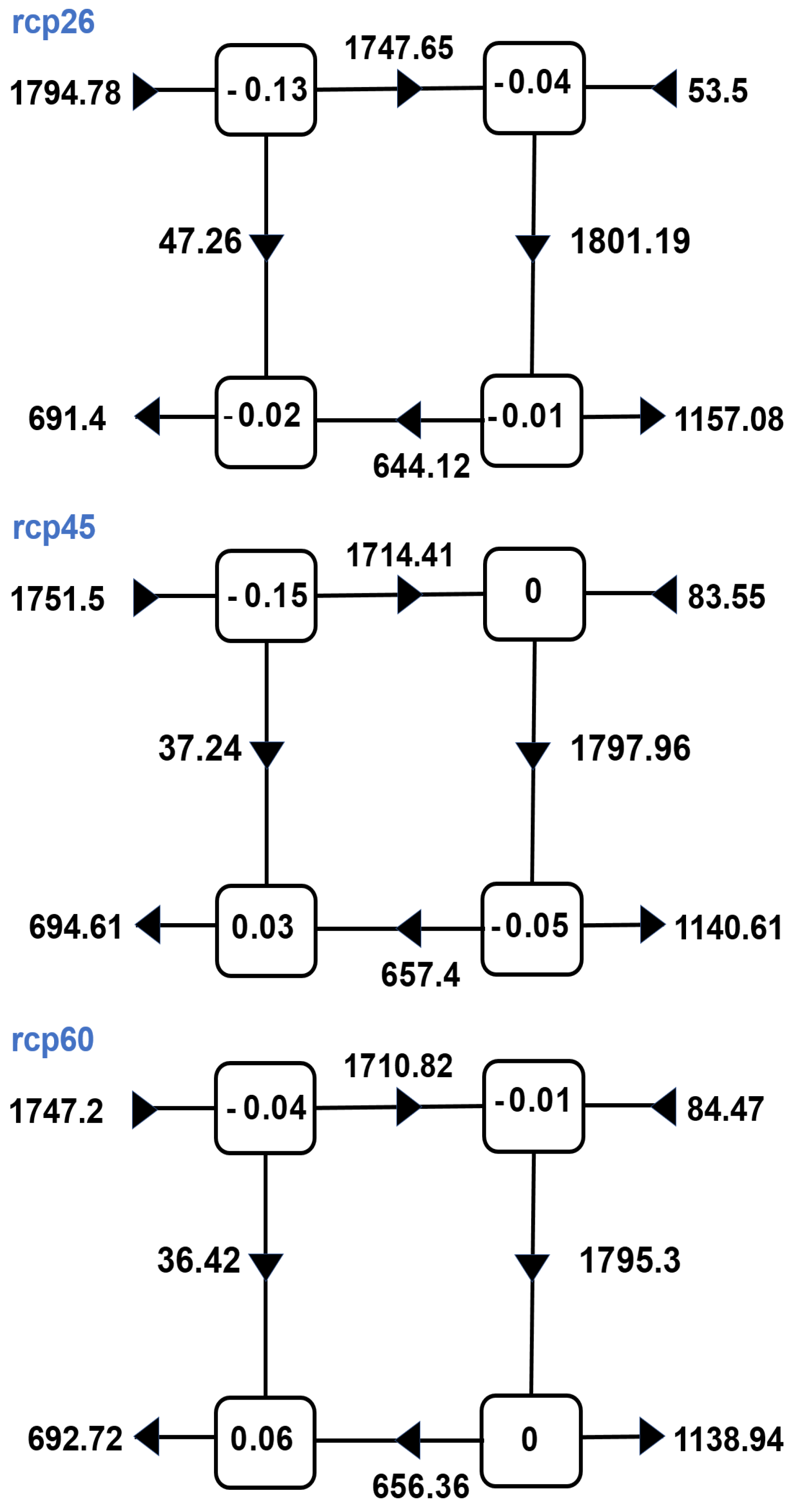
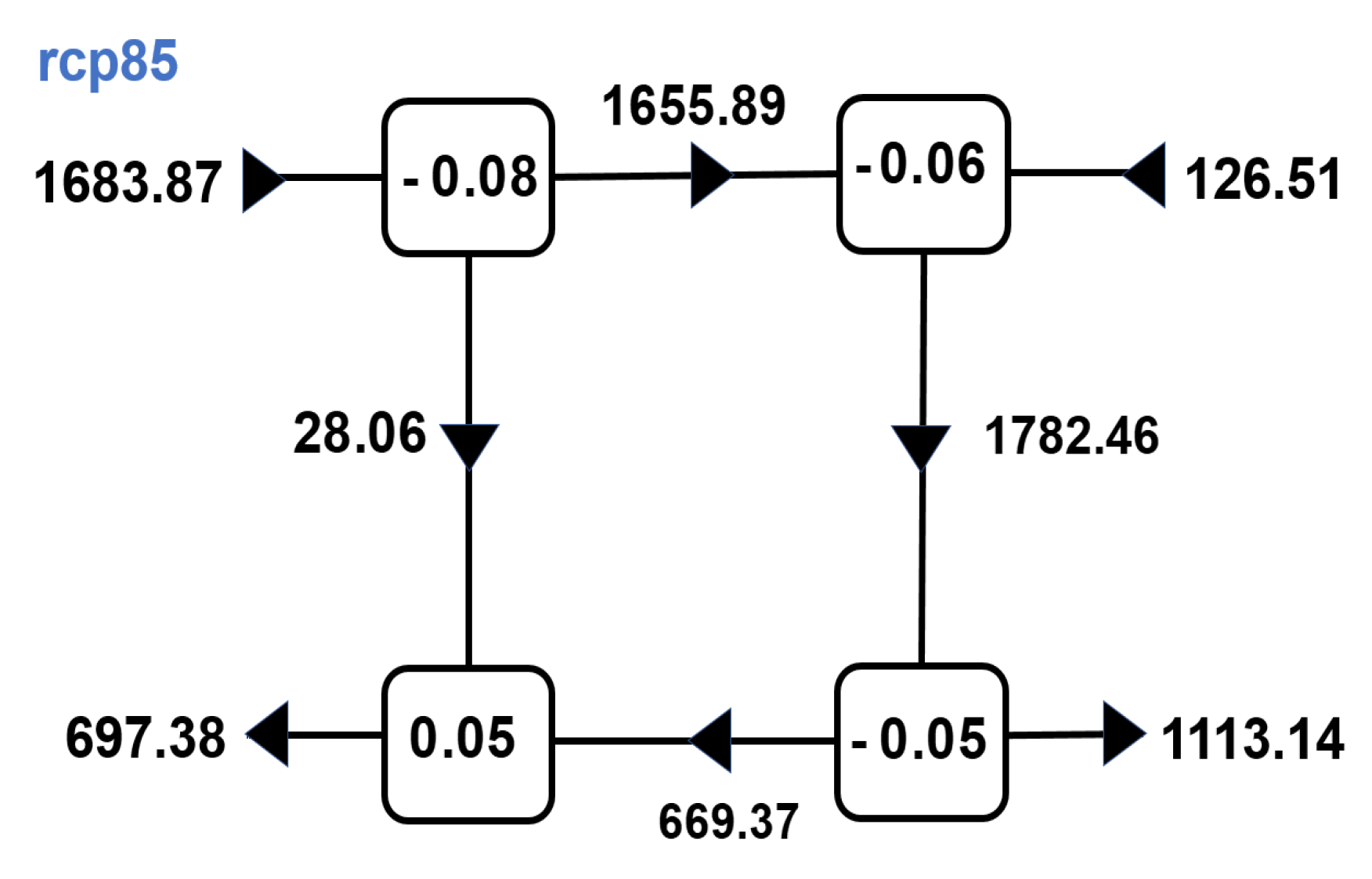
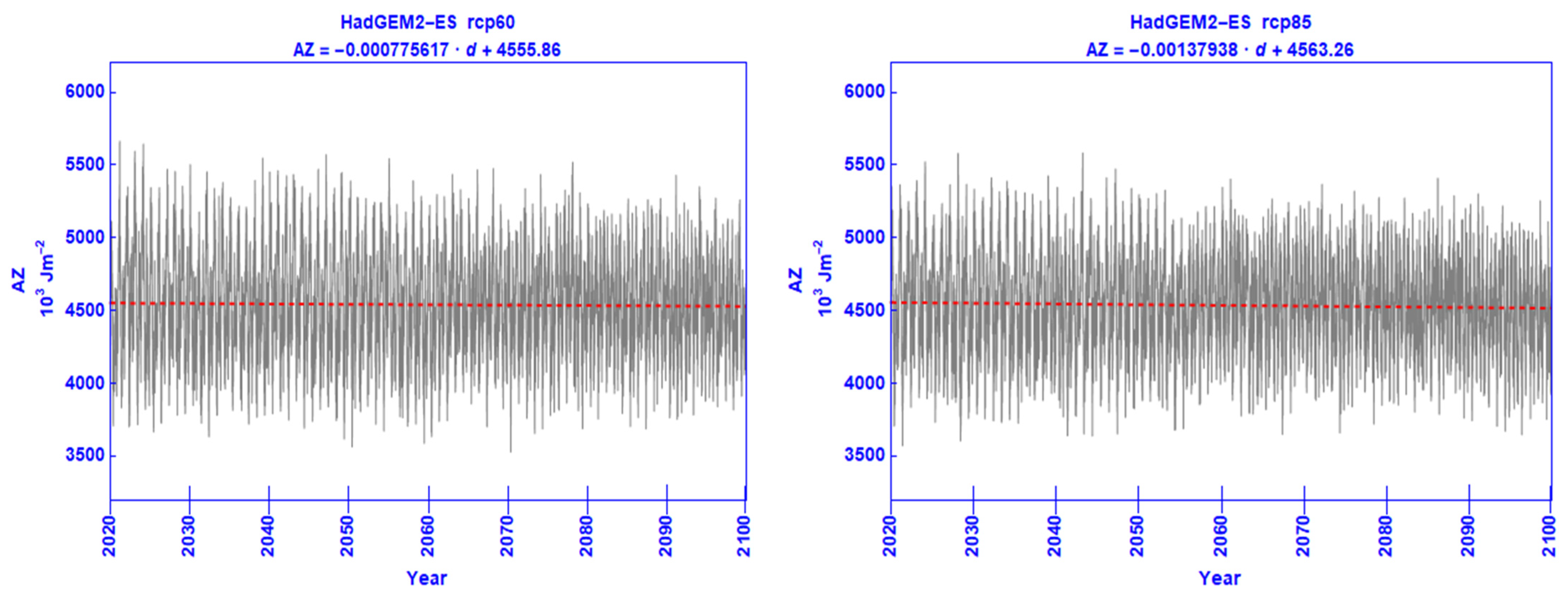

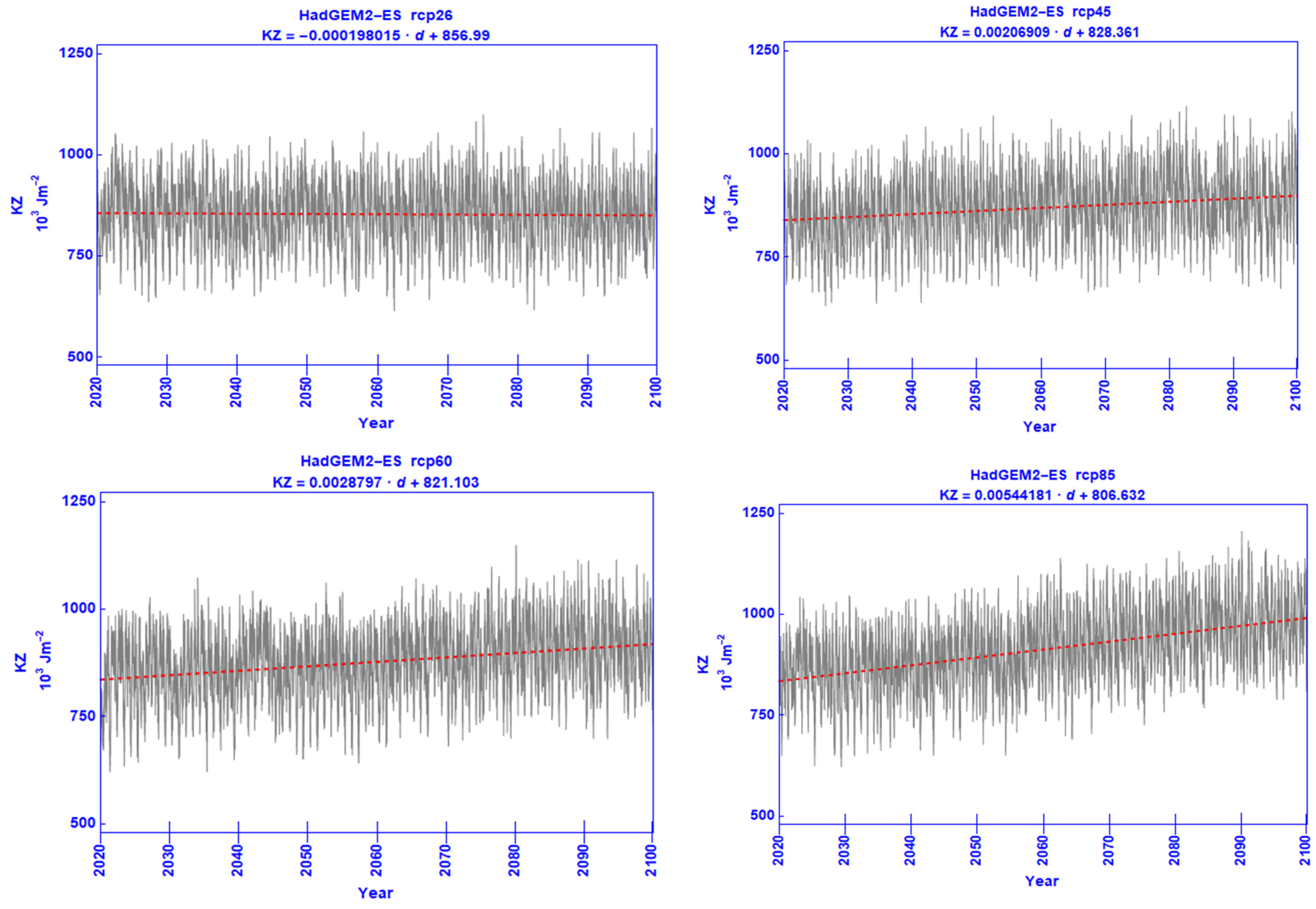
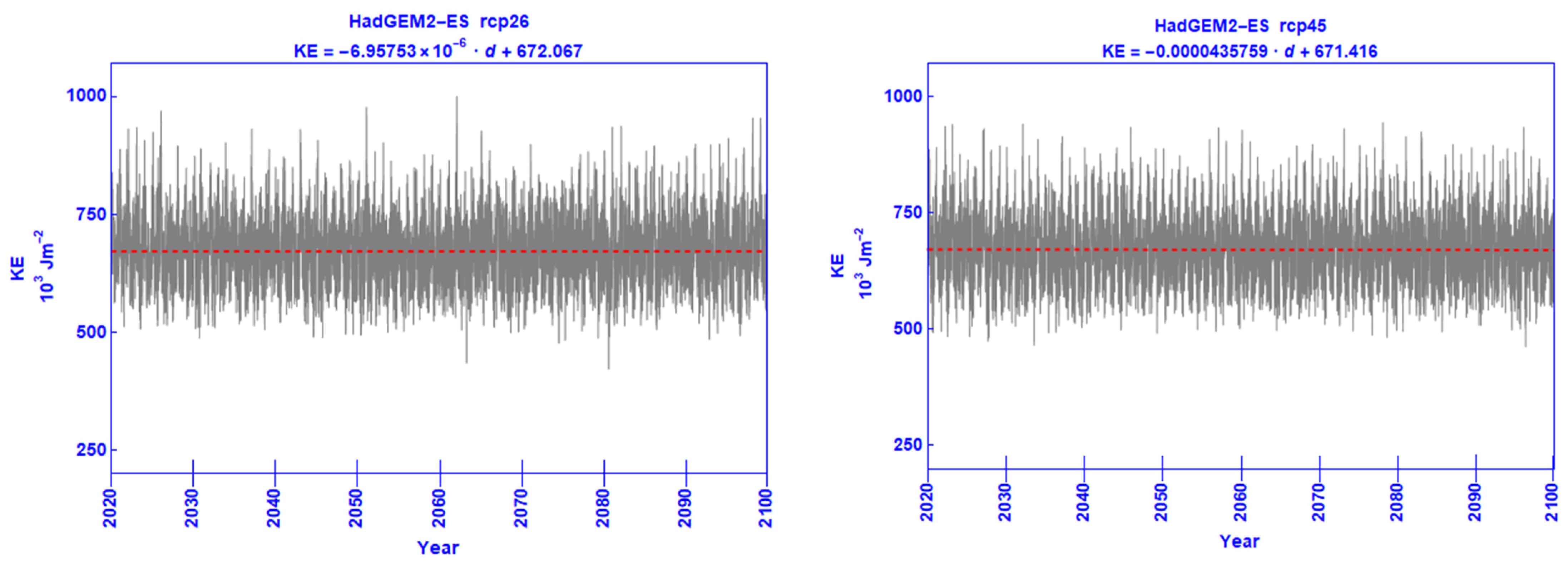
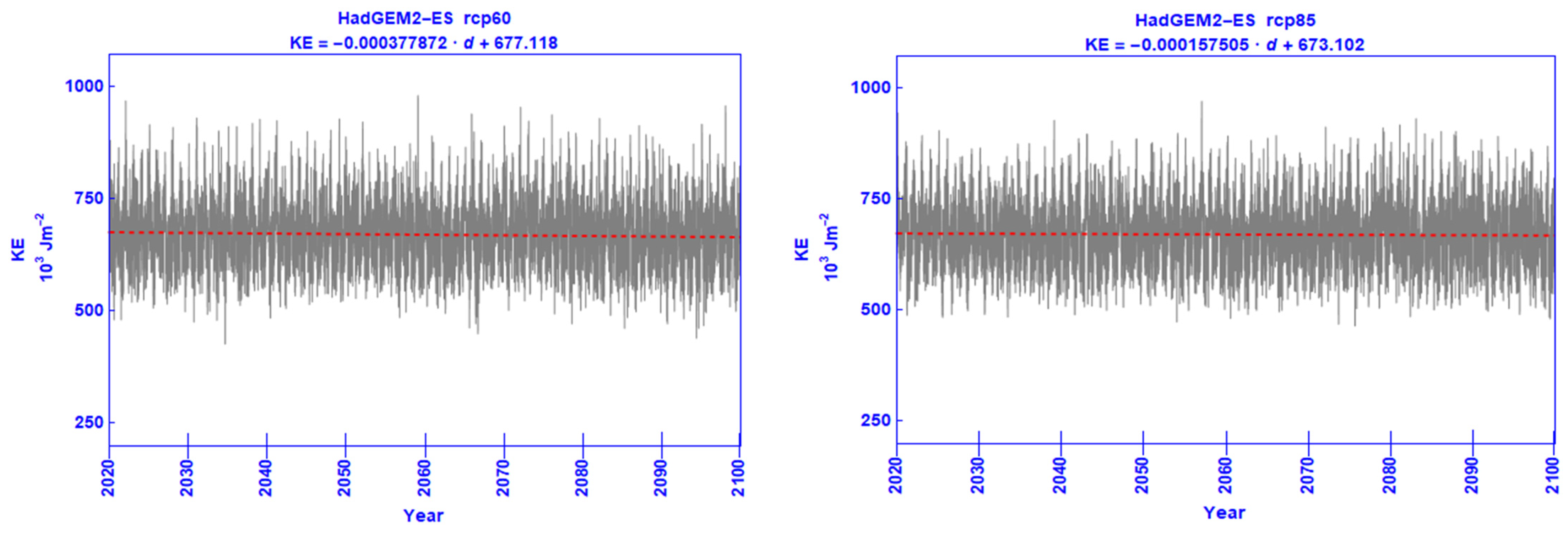
| RCP | Statistic | AZ | AE | KZ | KE | ∂AZ/∂t | ∂AE/∂t | ∂KZ/∂t | ∂KE/∂t |
|---|---|---|---|---|---|---|---|---|---|
| rcp26 | Max | 5702.00 | 892.00 | 1099.00 | 1001.00 | 5983.80 | 1076.39 | 694.44 | 1296.30 |
| Min | 3430.00 | 345.00 | 614.00 | 422.00 | −4317.13 | −1134.26 | −740.74 | −1273.15 | |
| StDev | 345.54 | 78.95 | 74.12 | 67.88 | 747.05 | 234.60 | 151.07 | 271.63 | |
| rcp45 | Max | 5560.00 | 843.00 | 1115.00 | 944.00 | 4317.13 | 1134.26 | 659.72 | 1168.98 |
| Min | 3603.00 | 328.00 | 631.00 | 462.00 | −3738.43 | −1250.00 | −648.15 | −1250.00 | |
| StDev | 334.20 | 78.24 | 77.16 | 68.52 | 746.70 | 231.63 | 149.75 | 271.66 | |
| rcp60 | Max | 5665.00 | 861.00 | 1148.00 | 980.00 | 4722.22 | 949.07 | 729.17 | 1076.39 |
| Min | 3528.00 | 322.00 | 621.00 | 426.00 | −3761.57 | −1111.11 | −717.59 | −1238.43 | |
| StDev | 346.83 | 79.24 | 79.35 | 69.81 | 754.14 | 235.13 | 152.78 | 277.14 | |
| rcp85 | Max | 5584.00 | 840.00 | 1205.00 | 970.00 | 4861.11 | 879.63 | 833.33 | 1354.17 |
| Min | 3571.00 | 319.00 | 622.00 | 464.00 | −3969.91 | −1145.83 | −694.44 | −1134.26 | |
| StDev | 323.40 | 75.93 | 89.24 | 68.17 | 737.18 | 227.13 | 155.40 | 275.54 |
| RCP | Statistic | <AZ→AE> | <AE→KE> | <KE→KZ> | <AZ→KZ> | GZ | GE | DZ | DE |
|---|---|---|---|---|---|---|---|---|---|
| rcp26 | Max | 3781.00 | 3605.00 | 2226.00 | 1183.00 | 7062.30 | 908.13 | 1448.91 | 1940.83 |
| Min | 456.00 | 633.00 | −400.00 | −1043.00 | −2183.24 | −806.80 | 144.91 | 544.94 | |
| StDev | 412.11 | 338.09 | 284.60 | 277.55 | 615.99 | 217.52 | 156.14 | 180.83 | |
| rcp45 | Max | 3707.00 | 3493.00 | 2102.00 | 1130.00 | 5819.13 | 1025.31 | 1499.94 | 2043.61 |
| Min | 231.00 | 646.00 | −612.00 | −1229.00 | −1235.26 | −829.76 | 115.82 | 465.44 | |
| StDev | 410.42 | 342.51 | 290.34 | 280.47 | 620.38 | 221.72 | 158.90 | 178.64 | |
| rcp60 | Max | 3838.00 | 3356.00 | 2050.00 | 1350.00 | 6000.91 | 943.24 | 1459.37 | 1955.83 |
| Min | 268.00 | 602.00 | −791.00 | −1081.00 | −1730.57 | −879.61 | 176.59 | 451.69 | |
| StDev | 416.45 | 344.25 | 291.76 | 281.11 | 627.65 | 222.37 | 159.345 | 181.46 | |
| rcp85 | Max | 3570.00 | 3568.00 | 2102.00 | 1255.00 | 6139.11 | 1072.39 | 1488.61 | 2001.39 |
| Min | 252.00 | 521.00 | −331.00 | −1168. | −1906.41 | −751.89 | 93.70 | 441.89 | |
| StDev | 409.87 | 345.54 | 295.75 | 291.448 | 621.44 | 228.30 | 166.437 | 182.39 |
| Energy Component | rcp26 | rcp45 | rcp60 | rcp85 | ||||
|---|---|---|---|---|---|---|---|---|
| a | b | a | b | a | b | a | b | |
| AZ | 0.000180877 | 4548.19 | −0.000174318 | 4538.37 | −0.000775617 | 4555.86 | −0.00137938 | 4563.26 |
| AE | −0.000173414 | 520.886 | −0.000855808 | 528.035 | −0.00112469 | 532.671 | −0.0139 | 530.562 |
| KZ | −0.000198015 | 856.99 | 0.00206909 | 828.361 | 0.0028797 | 821.103 | 0.00544181 | 806.632 |
| KE | −0.000006957 | 672.067 | −0.0000435769 | 671.416 | −0.000377872 | 677.118 | −0.000157505 | 673.102 |
| <AZ→AE> | −0.000727695 | 1761.81 | −0.00406241 | 1793.51 | −0.00526606 | 1813.36 | −0.0091761 | 1834.56 |
| <AE→KE> | 0.0000681611 | 1799.87 | −0.000578684 | 1809.23 | −0.000711477 | 1809.16 | −0.00188323 | 1819.13 |
| <KE→KZ> | −0.0000463435 | 645.031 | 0.0010757 | 636.46 | 0.00151958 | 626.78 | 0.00222846 | 625.985 |
| <AZ→KZ> | 0.00012192 | 44.8891 | −0.000619308 | 49.3058 | −0.00095322 | 54.9834 | −0.00134682 | 54.287 |
| GZ | −0.000603186 | 1806.53 | −0.00464604 | 1841.96 | −0.00619399 | 1867.8 | −0.0104915 | 1888.16 |
| GE | 0.000814931 | 37.6362 | 0.00350392 | 15.3122 | 0.00457072 | −4.51968 | 0.00730985 | −15.8114 |
| DZ | 0.0000805303 | 689.841 | 0.000446787 | 685.912 | 0.000579014 | 681.446 | 0.000885082 | 680.156 |
| DE | 0.000103154 | 1155.08 | −0.00166409 | 1173.02 | −0.00224273 | 1182.61 | −0.00413184 | 1193.6 |
| ∂AZ/∂t | 0.00000617363 | −0.234767 | 0.0000359286 | −0.861479 | 0.0000229027 | −0.506591 | 0.0000364437 | −0.771435 |
| ∂AE/∂t | 0.0000213124 | −0.453647 | 0.0000184446 | −0.360312 | 0.0000132693 | −0.276031 | 0.0000111378 | −0.296424 |
| ∂KZ/∂t | −0.00000413516 | 0.0599288 | 0.0000111867 | −0.194471 | −0.000013008 | 0.317168 | 0.000000572 | 0.0563835 |
| ∂KE/∂t | 0.00000907443 | −0.192631 | 0.0000100373 | −0.252894 | 0.0000121827 | −0.231162 | 0.0000181658 | −0.414366 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michaelides, S. Lorenz Atmospheric Energy Cycle in Climatic Projections. Climate 2021, 9, 180. https://doi.org/10.3390/cli9120180
Michaelides S. Lorenz Atmospheric Energy Cycle in Climatic Projections. Climate. 2021; 9(12):180. https://doi.org/10.3390/cli9120180
Chicago/Turabian StyleMichaelides, Silas. 2021. "Lorenz Atmospheric Energy Cycle in Climatic Projections" Climate 9, no. 12: 180. https://doi.org/10.3390/cli9120180
APA StyleMichaelides, S. (2021). Lorenz Atmospheric Energy Cycle in Climatic Projections. Climate, 9(12), 180. https://doi.org/10.3390/cli9120180






