Review of On-Orbit Robotic Arm Active Debris Capture Removal Methods
Abstract
:1. Introduction
2. Research Progress Analysis
2.1. Related Literature Analysis
2.2. Historical Progres Periods
2.2.1. 1983–1998 Theoretical Exploration Period
2.2.2. 1992–2007 Theoretical Supplement Period
2.2.3. 2004–2018 Theoretical Development Period
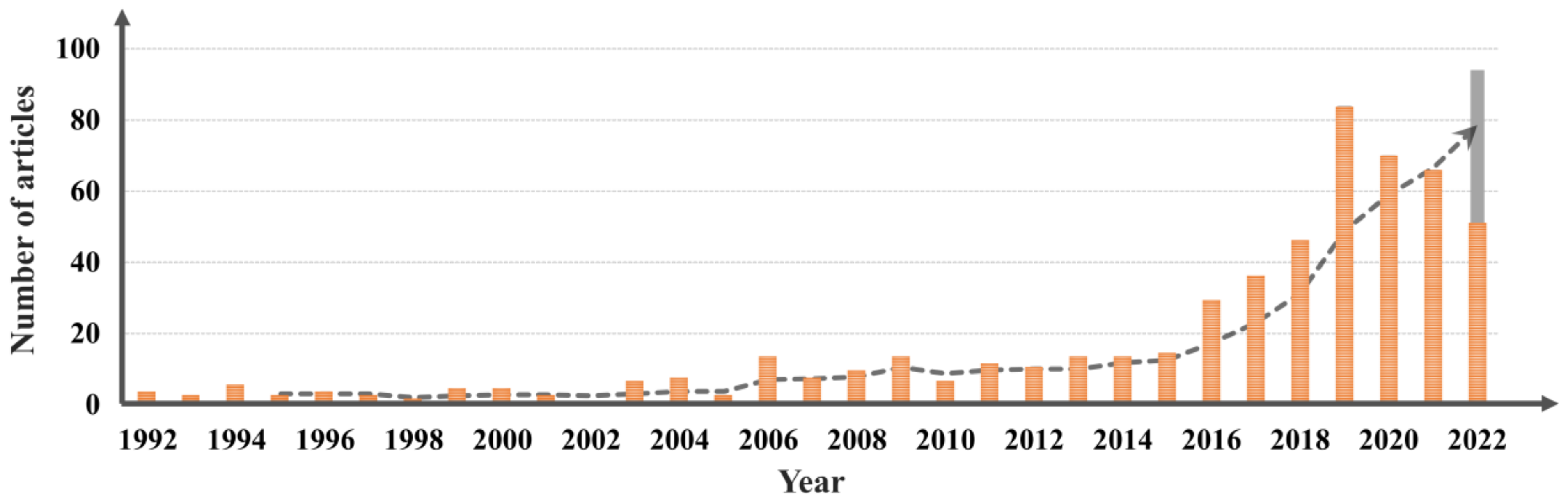
2.3. Recent Research Trends
3. Trend I: Uncertainty Identify and Reduce
3.1. Pre-Process and Identify Parameters
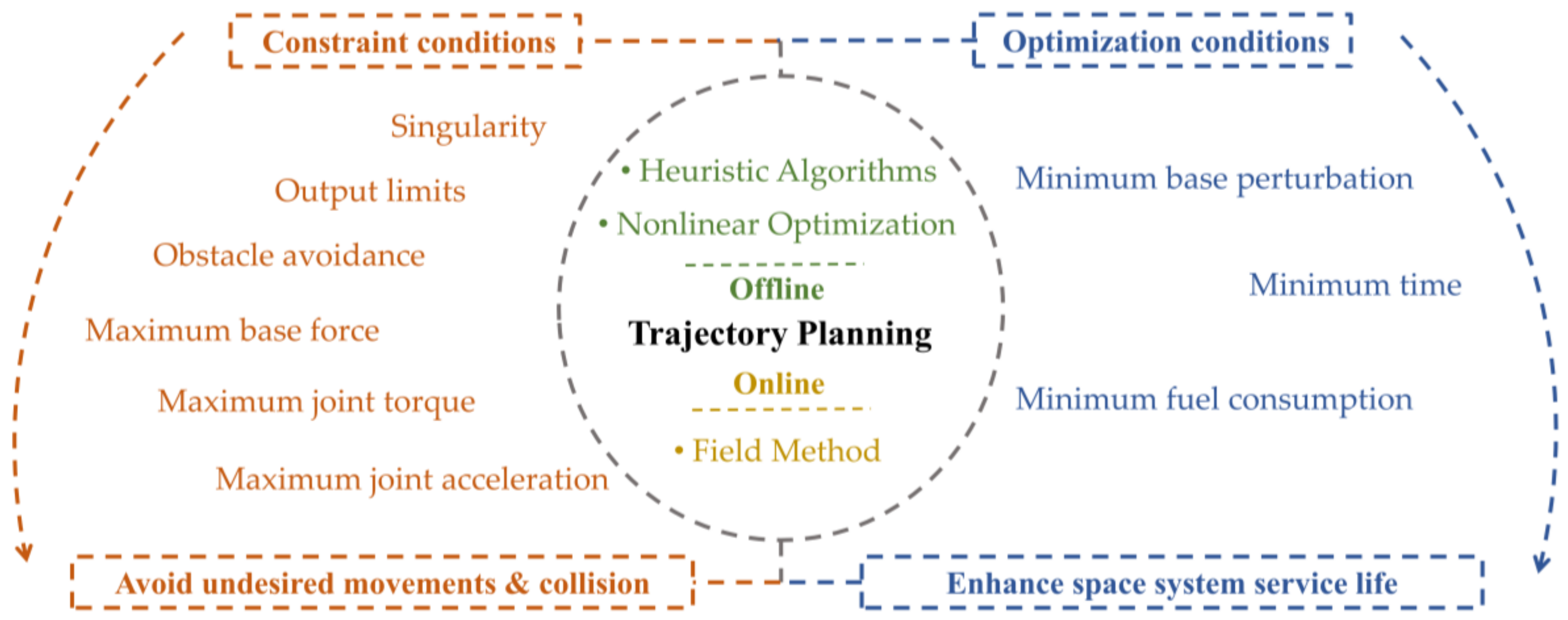
3.2. Constraints and Trajectory Planning
3.3. Trajectory Tracking and Target Capture
4. Trend II: Uncertainty Offset and Avoid
4.1. Free/Weak Model Control Approaches
4.2. High Error Margin Capture Strategy
4.3. Strong Robustness Controllers
5. Challenges and Reflections
5.1. Observation and Model Building
5.2. Transformation and Trajectory Planning
5.3. Tracking and Target Capture
6. Future Outlook
6.1. Convergence of Tendencies
6.2. Fundamental Modeling Theory
6.3. Feasibility Verification Platform
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AccPF | Acceleration potential field |
| APF | Artificial potential field |
| DM | Disturbance map |
| DMC | Distributed momentum control |
| EBA | Enhanced bidirectional approach |
| EDM | Enhanced disturbance map |
| IE | Interval excitation |
| ILC | Iterative learning control |
| MMMs | Metamorphic mechanism modules |
| MOPSO | Multi-objective particle swarm optimization algorithm |
| OVF | Obstacle vector field |
| PE | Persistent excitation |
| RA-ADCR | Robotic arm active debris capture removal |
| RL | Reinforcement learning |
| RNSC | Reaction null space control |
| RRT | Rapid-exploring random trees algorithm |
| SLAM | Simultaneous localization and mapping |
| VRFT | Virtual reference feedback tuning |
| ZRM | Zero reaction maneuver |
References
- Nishida, S.; Kawamoto, S.; Okawa, Y.; Yoshimura, S.; Terui, F.; Nakajima, A.; Kitamura, S. Development Status of an Active Space Debris Removal System. In Proceedings of the Space Debris and Space Traffic Management Symposium 2005, Fukuoka, Japan, 17–21 October 2005; Volume 112, p. 233240. [Google Scholar]
- United Nations Guidelines for the Long-Term Sustainability of Outer Space Activities. A/AC.105/C.1/L.366. Available online: https://www.unoosa.org/oosa/oosadoc/data/documents/2019/aac.105c.1l/aac.105c.1l.366_0.html (accessed on 18 June 2020).
- United Nations Office for Outer Space Affairs. 2021 Annual Report. 2022. Available online: https://www.unoosa.org/oosa/oosadoc/data/documents/2022/stspace/stspace80_0.html (accessed on 18 June 2022).
- Murtaza, A.; Pirzada, S.J.H.; Xu, T.; Jianwei, L. Orbital Debris Threat for Space Sustainability and Way Forward (Review Article). IEEE Access 2020, 8, 61000–61019. [Google Scholar] [CrossRef]
- Liou, J.-C.; Johnson, N.L. Risks in Space from Orbiting Debris. Science 2006, 311, 340–341. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liou, J.-C.; Johnson, N.L. Instability of the Present LEO Satellite Populations. Adv. Space Res. 2008, 41, 1046–1053. [Google Scholar] [CrossRef] [Green Version]
- ESA’S Space Environment Report 2022. Available online: https://www.esa.int/Space_Safety/Space_Debris/ESA_s_Space_Environment_Report_2022 (accessed on 10 May 2022).
- Kessler, D.J.; Cour-Palais, B.G. Collision Frequency of Artificial Satellites: The Creation of a Debris Belt. J. Geophys. Res. 1978, 83, 2637. [Google Scholar] [CrossRef]
- Aglietti, G.S.; Taylor, B.; Fellowes, S. RemoveDEBRIS: An in-Orbit Demonstration of Technologies for the Removal of Space Debris. Aeronaut. J. 2020, 124, 1–23. [Google Scholar] [CrossRef]
- United Nations Report of the 2019 Session of the Committee on the Peaceful Uses of Outer Space (A/74/20). Available online: https://www.unoosa.org/oosa/en/oosadoc/data/documents/2019/a/a7420_0.html (accessed on 18 June 2020).
- Nishida, S.-I.; Kawamoto, S.; Okawa, Y.; Terui, F.; Kitamura, S. Space Debris Removal System Using a Small Satellite. Acta Astronaut. 2009, 65, 95–102. [Google Scholar] [CrossRef]
- Liou, J.-C.; Johnson, N.L.; Hill, N.M. Controlling the Growth of Future LEO Debris Populations with Active Debris Removal. Acta Astronaut. 2010, 66, 648–653. [Google Scholar] [CrossRef]
- Araromi, O.A.; Gavrilovich, I.; Shintake, J.; Rosset, S.; Richard, M.; Gass, V.; Shea, H.R. Rollable Multisegment Dielectric Elastomer Minimum Energy Structures for a Deployable Microsatellite Gripper. IEEE/ASME Trans. Mechatron. 2015, 20, 438–446. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Wang, X.; Zhou, X.; An, J.; Li, Y. TDE-Based Adaptive Integral Sliding Mode Control of Space Manipulator for Space-Debris Active Removal. Aerospace 2022, 9, 105. [Google Scholar] [CrossRef]
- Shan, M.; Guo, J.; Gill, E. Review and Comparison of Active Space Debris Capturing and Removal Methods. Prog. Aerosp. Sci. 2016, 80, 18–32. [Google Scholar] [CrossRef]
- Bonnal, C.; Ruault, J.-M.; Desjean, M.-C. Active Debris Removal: Recent Progress and Current Trends. Acta Astronaut. 2013, 85, 51–60. [Google Scholar] [CrossRef]
- Meintel, A.J., Jr.; Larsen, R.L. Nasa Research in Teleoperation and Robotics. In Proceedings of the 26th Annual Technical Symposium, San Diego, CA, USA, 23 May 1983; pp. 22–31. [Google Scholar]
- Lee, S.; Bekey, G.; Bejczy, A. Computer Control of Space-Borne Teleoperators with Sensory Feedback. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, Institute of Electrical and Electronics Engineers, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 205–214. [Google Scholar]
- Vafa, Z.; Dubowsky, S. On the Dynamics of Manipulators in Space Using the Virtual Manipulator Approach. In Proceedings of the 1987 IEEE International Conference on Robotics and Automation, Institute of Electrical and Electronics Engineers, Raleigh, NC, USA, 31 March–3 April 1987; Volume 4, pp. 579–585. [Google Scholar]
- Nakamura, Y.; Mukherjee, R. Nonholonomic Path Planning of Space Robots via Bi-Directional Approach. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 1764–1769. [Google Scholar]
- Umetani, Y.; Yoshida, K. Resolved Motion Rate Control of Space Manipulators with Generalized Jacobian Matrix. IEEE Trans. Robot. Automat. 1989, 5, 303–314. [Google Scholar] [CrossRef]
- Masutani, Y.; Miyazaki, F.; Arimoto, S. Sensory Feedback Control for Space Manipulators. In Proceedings of the 1989 International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; pp. 1346–1351. [Google Scholar]
- Nanos, K.; Papadopoulos, E.G. On the Dynamics and Control of Free-Floating Space Manipulator Systems in the Presence of Angular Momentum. Front. Robot. AI 2017, 4, 26. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; Feng, J.; Liu, Y.; Ju, Z. Effective Capture of Nongraspable Objects for Space Robots Using Geometric Cage Pairs. IEEE/ASME Trans. Mechatron. 2020, 25, 95–107. [Google Scholar] [CrossRef] [Green Version]
- Papadopoulos, E.; Dubowsky, S. Coordinated Manipulator/Spacecraft Motion Control for Space Robotic Systems. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; pp. 1696–1701. [Google Scholar]
- Papadopoulos, E.; Dubowsky, S. On the Nature of Control Algorithms for Free-Floating Space Manipulators. IEEE Trans. Robot. Automat. 1991, 7, 750–758. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Moosavian, S.A.A. Dynamics and Control of Multi-Arm Space Robots during Chase and Capture Operations. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’94), Munich, Germany, 12–16 September 1994; Volume 3, pp. 1554–1561. [Google Scholar]
- Moosavian, S.A.A.; Papadopoulos, E. On the Kinematics of Multiple Manipulator Space Free-Flyers and Their Computation. J. Robot. Syst. 1998, 15, 207–216. [Google Scholar] [CrossRef]
- Moosavian, S.A.A.; Papadopoulos, E. Explicit Dynamics of Space Free-Flyers with Multiple Manipulators via SPACEMAPLE. Adv. Robot. 2004, 18, 223–244. [Google Scholar] [CrossRef] [Green Version]
- Liang, B.; Xu, Y.; Bergerman, M. Mapping a Space Manipulator to a Dynamically Equivalent Manipulator. J. Dyn. Syst. Meas. Control 1998, 120, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.H.; Sakawa, Y. Control of a Space Manipulator for Capturing a Tumbling Object. In Proceedings of the 29th IEEE Conference on Decision and Control, Honolulu, HI, USA, 05–07 December 1990; Volume 1, pp. 103–108. [Google Scholar]
- Dubowsky, S.; Torres, M.A. Path Planning for Space Manipulators to Minimize Spacecraft Attitude Disturbances. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 09–11 April 1991; pp. 2522–2528. [Google Scholar]
- Yoshida, K.; Sashida, N.; Kurazume, R.; Umetani, Y. Modeling of Collision Dynamics for Space Free-Floating Links with Extended Generalized Inertia Tensor. In Proceedings of the 1992 IEEE International Conference on Robotics and Automation, Nice, France, 12–14 May 1992; pp. 899–904. [Google Scholar]
- Matunaga, S.; Kanzawa, T.; Ohkami, Y. Rotational Motion-Damper for the Capture of an Uncontrolled Floating Satellite. Control Eng. Pract. 2001, 9, 199–205. [Google Scholar] [CrossRef]
- Dimitrov, D.N.; Yoshida, K. Momentum Distribution in a Space Manipulator for Facilitating the Post-Impact Control. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 4, pp. 3345–3350. [Google Scholar]
- Rekleitis, I.; Martin, E.; Rouleau, G.; L’Archevêque, R.; Parsa, K.; Dupuis, E. Autonomous Capture of a Tumbling Satellite. J. Field Robot. 2007, 24, 275–296. [Google Scholar] [CrossRef]
- Lichter, M.D.; Dubowsky, S. State, Shape, and Parameter Estimation of Space Objects from Range Images. In Proceedings of the IEEE International Conference on Robotics and Automation, ICRA ’04, New Orleans, LA, USA,, 26 April–1 May 2004; Volume 3, pp. 2974–2979. [Google Scholar]
- Hillenbrand, U.; Lampariello, R. Motion and Parameter Estimation of a Free-Floating Space Object from Range Data for Motion Prediction. In Proceedings of 8th International Symposium on Artificial Intelligence, Robotics and Automation in Space 2005, 10. Available online: https://elib.dlr.de/55779/1/Lampariello-isairas_05.pdf (accessed on 10 December 2021).
- Swain, A.K.; Morris, A.S. Dynamic Control of Multi-Arm Co-Operating Manipulator Systems. Robotica 2004, 22, 271–283. [Google Scholar] [CrossRef]
- Yang, G.; Liu, Y.; Jin, M.; Liu, H. A Robust and Adaptive Control Method for Flexible-Joint Manipulator Capturing a Tumbling Satellite. IEEE Access 2019, 7, 159971–159985. [Google Scholar] [CrossRef]
- Cocuzza, S.; Pretto, I.; Debei, S. Reaction Torque Control of Redundant Space Robotic Systems for Orbital Maintenance and Simulated Microgravity Tests. Acta Astronaut. 2010, 67, 285–295. [Google Scholar] [CrossRef]
- Jin, M.-H.; Zhou, C.; Liu, Y.-C.; Liu, Z.-Q.; Liu, H. Reaction Torque Control of Redundant Free-Floating Space Robot. Int. J. Autom. Comput. 2017, 14, 295–306. [Google Scholar] [CrossRef]
- Wang, M.; Luo, J.; Yuan, J.; Walter, U. Detumbling Strategy and Coordination Control of Kinematically Redundant Space Robot after Capturing a Tumbling Target. Nonlinear Dyn. 2018, 92, 1023–1043. [Google Scholar] [CrossRef]
- Xie, Y.; Wu, X.; Inamori, T.; Shi, Z.; Sun, X.; Cui, H. Compensation of Base Disturbance Using Optimal Trajectory Planning of Dual-Manipulators in a Space Robot. Adv. Space Res. 2019, 63, 1147–1160. [Google Scholar] [CrossRef]
- Wang, M.; Luo, J.; Yuan, J.; Walter, U. Coordinated Trajectory Planning of Dual-Arm Space Robot Using Constrained Particle Swarm Optimization. Acta Astronaut. 2018, 146, 259–272. [Google Scholar] [CrossRef]
- Regoli, L.; Ravandoor, K.; Schmidt, M.; Schilling, K. On-Line Robust Pose Estimation for Rendezvous and Docking in Space Using Photonic Mixer Devices. Acta Astronaut. 2014, 96, 159–165. [Google Scholar] [CrossRef]
- Sell, J.L.; Rhodes, A.; Woods, J.; Christian, J.A. Pose Performance of LIDAR-Based Navigation for Satellite Servicing. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference; American Institute of Aeronautics and Astronautics, San Diego, CA, USA, 4 August 2014. [Google Scholar]
- Volpe, R.; Palmerini, G.B.; Sabatini, M. A Passive Camera Based Determination of a Non-Cooperative and Unknown Satellite’s Pose and Shape. Acta Astronaut. 2018, 151, 805–817. [Google Scholar] [CrossRef]
- Nishida, S.-I.; Kawamoto, S. Dynamical Simulations for Space Debris Capture. In Proceedings of the SICE Annual Conference 2011, Tokyo, Japan, 13–18 September 2011. [Google Scholar]
- Nishida, S.-I.; Kawamoto, S. Strategy for Capturing of a Tumbling Space Debris. Acta Astronaut. 2011, 68, 113–120. [Google Scholar] [CrossRef]
- Ma, Z.; Ma, O.; Shashikanth, B. Optimal Control for Spacecraft to Rendezvous with a Tumbling Satellite in a Close Range. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 09–15 October 2006; pp. 4109–4114. [Google Scholar]
- Aghili, F. Optimal Control for Robotic Capturing and Passivation of a Tumbling Satellite with Unknown Dynamics. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18 August 2008. [Google Scholar]
- Aghili, F. Optimal Control of a Space Manipulator for Detumbling of a Target Satellite. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3019–3024. [Google Scholar]
- Aghili, F. A Prediction and Motion-Planning Scheme for Visually Guided Robotic Capturing of Free-Floating Tumbling Objects With Uncertain Dynamics. IEEE Trans. Robot. 2012, 28, 634–649. [Google Scholar] [CrossRef]
- Reiter, A.; Muller, A.; Gattringer, H. On Higher Order Inverse Kinematics Methods in Time-Optimal Trajectory Planning for Kinematically Redundant Manipulators. IEEE Trans. Ind. Inf. 2018, 14, 1681–1690. [Google Scholar] [CrossRef]
- Nenchev, D.; Umetani, Y.; Yoshida, K. Analysis of a Redundant Free-Flying Spacecraft/Manipulator System. IEEE Trans. Robot. Automat. 1992, 8, 1–6. [Google Scholar] [CrossRef]
- Yoshida, K.; Hashizume, K.; Abiko, S. Zero Reaction Maneuver: Flight Validation with ETS-VII Space Robot and Extension to Kinematically Redundant Arm. In Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Seoul, Republic of Korea, 21–26 May 2001; Volume 1, pp. 441–446. [Google Scholar]
- Xu, S.; Wang, H.; Zhang, D.; Yang, B. Extended Jacobian Based Adaptive Zero Reaction Motion Control for Free-Floating Space Manipulators. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 8359–8364. [Google Scholar]
- Abiko, S.; Lampariello, R.; Hirzinger, G. Impedance Control for a Free-Floating Robot in the Grasping of a Tumbling Target with Parameter Uncertainty. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 09–15 October 2006; pp. 1020–1025. [Google Scholar]
- Giordano, A.M.; Garofalo, G.; De Stefano, M.; Ott, C.; Albu-Schaffer, A. Dynamics and Control of a Free-Floating Space Robot in Presence of Nonzero Linear and Angular Momenta. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 7527–7534. [Google Scholar]
- Sabatini, M.; Gasbarri, P.; Palmerini, G.B. Coordinated Control of a Space Manipulator Tested by Means of an Air Bearing Free Floating Platform. Acta Astronaut. 2017, 139, 296–305. [Google Scholar] [CrossRef]
- Liu, Y.-Q.; Yu, Z.-W.; Liu, X.-F.; Chen, J.-B.; Cai, G.-P. Active Detumbling Technology for Noncooperative Space Target with Energy Dissipation. Adv. Space Res. 2019, 63, 1813–1823. [Google Scholar] [CrossRef]
- Liu, Y.-Q.; Yu, Z.-W.; Liu, X.-F.; Cai, G.-P. Active Detumbling Technology for High Dynamic Non-Cooperative Space Targets. Multibody Syst Dyn 2019, 47, 21–41. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Z.; Chen, Y.; Chen, S. Optimal Contact Control for Space Debris Detumbling and Nutation Damping. Adv. Space Res. 2020, 66, 951–962. [Google Scholar] [CrossRef]
- Dai, H.; Chen, H.; Yue, X. Dynamic Analysis of Detumbling a Rotating Satellite Using Flexible Deceleration Rod. Nonlinear Dyn. 2022, 108, 3331–3345. [Google Scholar] [CrossRef]
- Cheng, R.; Liu, Z.; Ma, Z.; Huang, P. Approach and Maneuver for Failed Spacecraft De-Tumbling via Space Teleoperation Robot System. Acta Astronaut. 2021, 181, 384–395. [Google Scholar] [CrossRef]
- Meng, Q.; Liang, J.; Ma, O. Identification of All the Inertial Parameters of a Non-Cooperative Object in Orbit. Aerosp. Sci. Technol. 2019, 91, 571–582. [Google Scholar] [CrossRef]
- Cheng, W.; Li, Z.; He, Y. Strategy and Control for Robotic Detumbling of Space Debris by Using Flexible Brush. In Proceedings of the 2019 3rd International Conference on Robotics and Automation Sciences (ICRAS), Wuhan, China, 01–03 June 2019; pp. 41–47. [Google Scholar]
- Chen, G.; Wang, Y.; Wang, Y.; Liang, J.; Zhang, L.; Pan, G. Detumbling Strategy Based on Friction Control of Dual-Arm Space Robot for Capturing Tumbling Target. Chin. J. Aeronaut. 2020, 33, 1093–1106. [Google Scholar] [CrossRef]
- Wang, H.; Xie, Y. Prediction Error Based Adaptive Jacobian Tracking for Free-Floating Space Manipulators. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3207–3221. [Google Scholar] [CrossRef]
- Christidi-Loumpasefski, O.-O.; Nanos, K.; Papadopoulos, E. On Parameter Estimation of Space Manipulator Systems Using the Angular Momentum Conservation. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5453–5458. [Google Scholar]
- Naveen, B.; Shah, S.V.; Misra, A.K. Momentum Model-Based Minimal Parameter Identification of a Space Robot. J. Guid. Control Dyn. 2019, 42, 508–523. [Google Scholar] [CrossRef] [Green Version]
- Felicetti, L.; Sabatini, M.; Pisculli, A.; Gasbarri, P.; Palmerini, G.B. Adaptive Thrust Vector Control during On-Orbit Servicing. In Proceedings of the AIAA SPACE 2014 Conference and Exposition; American Institute of Aeronautics and Astronautics, San Diego, CA, USA, 4 August 2014. [Google Scholar]
- Li, Y.; Wang, Y.; Xie, Y. Using Consecutive Point Clouds for Pose and Motion Estimation of Tumbling Non-Cooperative Target. Adv. Space Res. 2019, 63, 1576–1587. [Google Scholar] [CrossRef]
- Poo Gallardo, A.; Mishra, H.; Massimo Giordano, A.; Lampariello, R. Robust Estimation of Motion States for Free-Floating Tumbling Target Capture. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 02–09 March 2019; pp. 1–11. [Google Scholar]
- Peng, J.; Xu, W.; Pan, E.; Yan, L.; Liang, B.; Wu, A. Dual-Arm Coordinated Capturing of an Unknown Tumbling Target Based on Efficient Parameters Estimation. Acta Astronaut. 2019, 162, 589–607. [Google Scholar] [CrossRef]
- Li, Z.; Ge, F.; Chen, W.; Shao, W.; Liu, B.; Cheng, B. Particle Filter-Based Relative Rolling Estimation Algorithm for Non-Cooperative Infrared Spacecraft. Infrared Phys. Technol. 2016, 78, 58–65. [Google Scholar] [CrossRef]
- Pesce, V.; Haydar, M.F.; Lavagna, M.; Lovera, M. Comparison of Filtering Techniques for Relative Attitude Estimation of Uncooperative Space Objects. Aerosp. Sci. Technol. 2019, 84, 318–328. [Google Scholar] [CrossRef]
- Takeishi, N.; Yairi, T.; Tsuda, Y.; Terui, F.; Ogawa, N.; Mimasu, Y. Simultaneous Estimation of Shape and Motion of an Asteroid for Automatic Navigation. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2861–2866. [Google Scholar]
- Dor, M.; Tsiotras, P. ORB-SLAM Applied to Spacecraft Non-Cooperative Rendezvous. In Proceedings of the 2018 Space Flight Mechanics Meeting, Kissimmee, FL, USA, 8 January 2018. [Google Scholar]
- Zong, L.; Luo, J.; Wang, M.; Yuan, J. Parameters Concurrent Learning and Reactionless Control in Post-Capture of Unknown Targets by Space Manipulators. Nonlinear Dyn. 2019, 96, 443–457. [Google Scholar] [CrossRef]
- Luo, J.; Xu, R.; Wang, M. Detumbling and Stabilization of a Tumbling Target Using a Space Manipulator with Joint-Velocity Limits. Adv. Space Res. 2020, 66, 1689–1699. [Google Scholar] [CrossRef]
- Li, S.; She, Y.; Sun, J. Inertial Parameter Estimation and Control of Non-Cooperative Target with Unilateral Contact Constraint. Chin. J. Aeronaut. 2021, 34, 225–240. [Google Scholar] [CrossRef]
- Dou, B.; Yue, X.; Zhang, T. Optimal Detumbling Strategy for a Non-Cooperative Target with Unknown Inertial Parameters Using a Space Manipulator. Adv. Space Res. 2022, 69, 3952–3965. [Google Scholar] [CrossRef]
- Ma, C.; Dai, H.; Wei, C.; Yuan, J. Two-Stage Filter for Inertia Characteristics Estimation of High-Speed Tumbling Targets. Aerosp. Sci. Technol. 2019, 89, 333–344. [Google Scholar] [CrossRef]
- Ding, H.; Yi, J.; Wang, Z.; Mou, J.; Han, F. Robust Feature-Free Pose Tracking and Uncertainty-Aware Geometry Reconstruction for Spinning Non-Cooperative Targets. Comput. Graph. 2022, 102, 30–44. [Google Scholar] [CrossRef]
- Zhang, T.; Yue, X.; Yuan, J. An Online One-Step Method to Identify Inertial Parameters of the Base and the Target Simultaneously for Space Robots in Postcapture. IEEE Access 2020, 8, 189913–189929. [Google Scholar] [CrossRef]
- Zhang, T.; Yue, X.; Dou, B.; Yuan, J. Online One-Step Parameter Identification Method for a Space Robot with Initial Momentum in Postcapture. J. Aerosp. Eng. 2020, 33, 04020029. [Google Scholar] [CrossRef]
- Na, J.; Mahyuddin, M.N.; Herrmann, G.; Ren, X.; Barber, P. Robust Adaptive Finite-Time Parameter Estimation and Control for Robotic Systems: ADAPTIVE FINITE-TIME ESTIMATION & CONTROL FOR ROBOTICS. Int. J. Robust. Nonlinear Control 2015, 25, 3045–3071. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Duan, G. Integrated Design of Trajectory Tracking and Inertia Property Identification for Post-Capture of Non-Cooperative Target. Aerosp. Sci. Technol. 2019, 95, 105437. [Google Scholar] [CrossRef]
- Yang, S.; Wen, H.; Jin, D. Trajectory Planning of Dual-Arm Space Robots for Target Capturing and Base Manoeuvring. Acta Astronaut. 2019, 164, 142–151. [Google Scholar] [CrossRef]
- Yang, S.; Wen, H.; Hu, Y.; Jin, D. Coordinated Motion Control of a Dual-Arm Space Robot for Assembling Modular Parts. Acta Astronaut. 2020, 177, 627–638. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Cai, G.; Chen, J. Trajectory Planning and Coordination Control of a Space Robot for Detumbling a Flexible Tumbling Target in Post-Capture Phase. Multibody Syst Dyn 2021, 52, 281–311. [Google Scholar] [CrossRef]
- Cui, L.; Wang, H.; Chen, W. Trajectory Planning of a Spatial Flexible Manipulator for Vibration Suppression. Robot. Auton. Syst. 2020, 123, 103316. [Google Scholar] [CrossRef]
- Aghili, F. Optimal Trajectories and Robot Control for Detumbling a Non-Cooperative Satellite. J. Guid. Control Dyn. 2020, 43, 981–988. [Google Scholar] [CrossRef]
- Serrantola, W.G.; Grassi, V. Trajectory Planning for a Dual-Arm Planar Free-Floating Manipulator Using RRTControl. In Proceedings of the 2019 19th International Conference on Advanced Robotics (ICAR), Belo Horizonte, Brazil, 02–06 December 2019; pp. 394–399. [Google Scholar]
- Xie, Z.; Zhao, X.; Jiang, Z.; Yang, H.; Li, C. Trajectory Planning and Base Attitude Restoration of Dual-Arm Free-Floating Space Robot by Enhanced Bidirectional Approach. Front. Mech. Eng. 2022, 17, 2. [Google Scholar] [CrossRef]
- Yan, L.; Xu, W.; Hu, Z.; Liang, B. Virtual-Base Modeling and Coordinated Control of a Dual-Arm Space Robot for Target Capturing and Manipulation. Multibody Syst Dyn 2019, 45, 431–455. [Google Scholar] [CrossRef]
- Yan, L.; Xu, W.; Hu, Z.; Liang, B. Multi-Objective Configuration Optimization for Coordinated Capture of Dual-Arm Space Robot. Acta Astronaut. 2020, 167, 189–200. [Google Scholar] [CrossRef]
- Zhao, S.; Zhu, Z.; Luo, J. Multitask-Based Trajectory Planning for Redundant Space Robotics Using Improved Genetic Algorithm. Appl. Sci. 2019, 9, 2226. [Google Scholar] [CrossRef] [Green Version]
- Zong, L.; Luo, J.; Wang, M. Optimal Detumbling Trajectory Generation and Coordinated Control after Space Manipulator Capturing Tumbling Targets. Aerosp. Sci. Technol. 2021, 112, 106626. [Google Scholar] [CrossRef]
- Cai, P.; Yue, X.; Wang, M.; Cui, Y. Hierarchical Motion Planning at the Acceleration Level Based on Task Priority Matrix for Space Robot. Nonlinear Dyn. 2022, 107, 2309–2326. [Google Scholar] [CrossRef]
- Rybus, T.; Wojtunik, M.; Basmadji, F.L. Optimal Collision-Free Path Planning of a Free-Floating Space Robot Using Spline-Based Trajectories. Acta Astronaut. 2022, 190, 395–408. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.; Zhang, Q.; Wei, X. Obstacle Avoidance Path Planning of Space Robot Based on Improved Particle Swarm Optimization. Symmetry 2022, 14, 938. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, Z.; Wu, X.; Shi, Z.; Chen, Y.; Wu, B.; Mantey, K.A. Obstacle Avoidance and Path Planning for Multi-Joint Manipulator in a Space Robot. IEEE Access 2020, 8, 3511–3526. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, Z. Sampling-Based Motion Planning for Free-Floating Space Robot without Inverse Kinematics. Appl. Sci. 2020, 10, 9137. [Google Scholar] [CrossRef]
- Jin, R.; Rocco, P.; Geng, Y. Cartesian Trajectory Planning of Space Robots Using a Multi-Objective Optimization. Aerosp. Sci. Technol. 2021, 108, 106360. [Google Scholar] [CrossRef]
- Ni, S.; Chen, W.; Ju, H.; Chen, T. Coordinated Trajectory Planning of a Dual-Arm Space Robot with Multiple Avoidance Constraints. Acta Astronaut. 2022, 195, 379–391. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Jiang, P.; Du, Z.; Wu, Z.; Sun, B.; Huang, X. Evolutionary Multi-Objective Trajectory Optimization for a Redundant Robot in Cartesian Space Considering Obstacle Avoidance. Mech. Sci. 2022, 13, 41–53. [Google Scholar] [CrossRef]
- Rybus, T. The Obstacle Vector Field (OVF) Method for Collision-Free Trajectory Planning of Free-Floating Space Manipulator. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70, 14. [Google Scholar] [CrossRef]
- Zhan, B.; Jin, M.; Yang, G.; Zhang, C. A Novel Strategy for Space Manipulator Detumbling a Non-Cooperative Target with Collision Avoidance. Adv. Space Res. 2020, 66, 785–799. [Google Scholar] [CrossRef]
- Zhan, B.; Jin, M.; Yang, G.; Zhao, Z. A Novel Collision-Free Detumbling Strategy for a Space Robot with a 7-DOF Manipulator in Postcapturing Phase. J. Aerosp. Eng. 2022, 35, 04022008. [Google Scholar] [CrossRef]
- Li, Y.; Hao, X.; She, Y.; Li, S.; Yu, M. Constrained Motion Planning of Free-Float Dual-Arm Space Manipulator via Deep Reinforcement Learning. Aerosp. Sci. Technol. 2021, 109, 106446. [Google Scholar] [CrossRef]
- Li, Y.; Li, D.; Zhu, W.; Sun, J.; Zhang, X.; Li, S. Constrained Motion Planning of 7-DOF Space Manipulator via Deep Reinforcement Learning Combined with Artificial Potential Field. Aerospace 2022, 9, 163. [Google Scholar] [CrossRef]
- Yao, Q. Adaptive Fuzzy Neural Network Control for a Space Manipulator in the Presence of Output Constraints and Input Nonlinearities. Adv. Space Res. 2021, 67, 1830–1843. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Tang, Z.; Qi, N. Probabilistic Ensemble Neural Network Model for Long-Term Dynamic Behavior Prediction of Free-Floating Space Manipulators. Aerosp. Sci. Technol. 2021, 119, 107138. [Google Scholar] [CrossRef]
- Ma, Z.; Huang, P. Adaptive Neural-Network Controller for an Uncertain Rigid Manipulator With Input Saturation and Full-Order State Constraint. IEEE Trans. Cybern. 2022, 52, 2907–2915. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Chang, H.; Huang, P. Eddy Current De-Tumbling Large Geostationary Debris Based on Feedback Linearization Model Predictive Control. Aerosp. Sci. Technol. 2021, 112, 106641. [Google Scholar] [CrossRef]
- Dong, G.; Zhu, Z.H. Predictive Visual Servo Kinematic Control for Autonomous Robotic Capture of Non-Cooperative Space Target. Acta Astronaut. 2018, 151, 173–181. [Google Scholar] [CrossRef]
- Dong, G.; Zhu, Z.H. Kinematics-Based Incremental Visual Servo for Robotic Capture of Non-Cooperative Target. Robot. Auton. Syst. 2019, 112, 221–228. [Google Scholar] [CrossRef]
- Zhao, X.; Xie, Z.; Yang, H.; Liu, J. Minimum Base Disturbance Control of Free-Floating Space Robot during Visual Servoing Pre-Capturing Process. Robotica 2020, 38, 652–668. [Google Scholar] [CrossRef]
- Santos, R.R.; Rade, D.A.; Da Fonseca, I.M. A Machine Learning Strategy for Optimal Path Planning of Space Robotic Manipulator in On-Orbit Servicing. Acta Astronaut. 2022, 191, 41–54. [Google Scholar] [CrossRef]
- Liu, Q.; Jin, M.; Wang, B.; Liu, H. LSTM Based Model Predictive Control for Flying Space Robot to Track Uncooperative Target. In Intelligent Robotics and Applications; Liu, X.-J., Nie, Z., Yu, J., Xie, F., Song, R., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2021; Volume 13016, pp. 428–439. ISBN 978-3-030-89091-9. [Google Scholar]
- Yao, Q. Adaptive Trajectory Tracking Control of a Free-Flying Space Manipulator with Guaranteed Prescribed Performance and Actuator Saturation. Acta Astronaut. 2021, 185, 283–298. [Google Scholar] [CrossRef]
- Yao, Q.; Jahanshahi, H.; Moroz, I.; Alotaibi, N.D.; Bekiros, S. Neural Adaptive Fixed-Time Attitude Stabilization and Vibration Suppression of Flexible Spacecraft. Mathematics 2022, 10, 1667. [Google Scholar] [CrossRef]
- Wang, X.; Xu, B.; Cheng, Y.; Wang, H.; Sun, F. Robust Adaptive Learning Control of Space Robot for Target Capturing Using Neural Network. IEEE Trans. Neural Netw. Learning Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Zhu, Y.; Qiao, J.; Guo, L. Adaptive Sliding Mode Disturbance Observer-Based Composite Control With Prescribed Performance of Space Manipulators for Target Capturing. IEEE Trans. Ind. Electron. 2019, 66, 1973–1983. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, Y.; Qiao, J.; An, S. Refined Disturbance Rejection-Based Composite Control of Flexible Spacecrafts for Tracking a Tumbling Non-Cooperative Target. IEEE Access 2022, 10, 30596–30609. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Wang, J.; Cai, G. Dynamics Analysis of Flexible Space Robot with Joint Friction. Aerosp. Sci. Technol. 2015, 47, 164–176. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, X.; Cai, G. Dynamics and Control of a Flexible-Link Flexible-Joint Space Robot with Joint Friction. Int. J. Aeronaut. Space Sci. 2021, 22, 415–432. [Google Scholar] [CrossRef]
- Liu, X.-F.; Cai, G.-P.; Wang, M.-M.; Chen, W.-J. Contact Control for Grasping a Non-Cooperative Satellite by a Space Robot. Multibody Syst Dyn 2020, 50, 119–141. [Google Scholar] [CrossRef]
- Wang, X.; Shi, L.; Katupitiya, J. A Strategy to Decelerate and Capture a Spinning Object by a Dual-Arm Space Robot. Aerosp. Sci. Technol. 2021, 113, 106682. [Google Scholar] [CrossRef]
- Tao, D.; Zhang, Q.; Chu, X.; Zhou, X.; Zhao, L. Impedance-Sliding Mode Control With Force Constraints for Space Robots Capturing Non-Cooperative Objects. IEEE Access 2021, 9, 160163–160174. [Google Scholar] [CrossRef]
- Liu, X.-F.; Zhang, X.-Y.; Cai, G.-P.; Chen, W.-J. Capturing a Space Target Using a Flexible Space Robot. Appl. Sci. 2022, 12, 984. [Google Scholar] [CrossRef]
- Zhu, A.; Ai, H.; Chen, L. A Fuzzy Logic Reinforcement Learning Control with Spring-Damper Device for Space Robot Capturing Satellite. Appl. Sci. 2022, 12, 2662. [Google Scholar] [CrossRef]
- Chu, M.; Wu, X. Modeling and Self-Learning Soft-Grasp Control for Free-Floating Space Manipulator During Target Capturing Using Variable Stiffness Method. IEEE Access 2018, 6, 7044–7054. [Google Scholar] [CrossRef]
- Xu, S.; Chu, M.; Sun, H. Design and Stiffness Optimization of Bionic Docking Mechanism for Space Target Acquisition. Appl. Sci. 2021, 11, 10278. [Google Scholar] [CrossRef]
- Wei, C.; Gu, H.; Liu, Y.; Zhao, Y. Attitude Reactionless and Vibration Control in Space Flexible Robot Grasping Operation. Int. J. Adv. Robot. Syst. 2018, 15, 172988141881830. [Google Scholar] [CrossRef]
- Bu, X.; Hou, Z.; Zhang, H. Data-Driven Multiagent Systems Consensus Tracking Using Model Free Adaptive Control. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1514–1524. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.-H.; Yu, Z.-C.; Li, C.-Y.; He, M.-J.; Hua, B.; Chen, Z.-M. Reinforcement Learning in Dual-Arm Trajectory Planning for a Free-Floating Space Robot. Aerosp. Sci. Technol. 2020, 98, 105657. [Google Scholar] [CrossRef]
- Dong, G.; Huang, P.; Wang, Y.; Li, R. A Modified Forward and Backward Reaching Inverse Kinematics Based Incremental Control for Space Manipulators. Chin. J. Aeronaut. 2021, 35, 287–295. [Google Scholar] [CrossRef]
- Hu, Q.; Niu, G.; Wang, C. Spacecraft Attitude Fault-Tolerant Control Based on Iterative Learning Observer and Control Allocation. Aerosp. Sci. Technol. 2018, 75, 245–253. [Google Scholar] [CrossRef]
- Radac, M.-B.; Precup, R.-E.; Roman, R.-C. Data-Driven Model Reference Control of MIMO Vertical Tank Systems with Model-Free VRFT and Q-Learning. ISA Trans. 2018, 73, 227–238. [Google Scholar] [CrossRef]
- Gao, H.; Ma, G.; Lv, Y.; Guo, Y. Forecasting-Based Data-Driven Model-Free Adaptive Sliding Mode Attitude Control of Combined Spacecraft. Aerosp. Sci. Technol. 2019, 86, 364–374. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, G.; Lyu, Y.; Wang, P. Neural Network-Based Reinforcement Learning Control for Combined Spacecraft Attitude Tracking Maneuvers. Neurocomputing 2022, 484, 67–78. [Google Scholar] [CrossRef]
- Ai, H.; Zhu, A.; Wang, J.; Yu, X.; Chen, L. Buffer Compliance Control of Space Robots Capturing a Non-Cooperative Spacecraft Based on Reinforcement Learning. Appl. Sci. 2021, 11, 5783. [Google Scholar] [CrossRef]
- Fu, X.; Ai, H.; Chen, L. Repetitive Learning Sliding Mode Stabilization Control for a Flexible-Base, Flexible-Link and Flexible-Joint Space Robot Capturing a Satellite. Appl. Sci. 2021, 11, 8077. [Google Scholar] [CrossRef]
- Wang, S.; Cao, Y.; Zheng, X.; Zhang, T. Collision-Free Trajectory Planning for a 6-DoF Free-Floating Space Robot via Hierarchical Decoupling Optimization. IEEE Robot. Autom. Lett. 2022, 7, 4953–4960. [Google Scholar] [CrossRef]
- Xu, W.; Hu, Z.; Yan, L.; Yuan, H.; Liang, B. Modeling and Planning of a Space Robot for Capturing Tumbling Target by Approaching the Dynamic Closest Point. Multibody Syst Dyn 2019, 47, 203–241. [Google Scholar] [CrossRef]
- Xu, W.; Yan, L.; Hu, Z.; Liang, B. Area-Oriented Coordinated Trajectory Planning of Dual-Arm Space Robot for Capturing a Tumbling Target. Chin. J. Aeronaut. 2019, 32, 2151–2163. [Google Scholar] [CrossRef]
- Han, D.; Liu, Z.; Huang, P. Capture and Detumble of a Non-Cooperative Target without a Specific Gripping Point by a Dual-Arm Space Robot. Adv. Space Res. 2022, 69, 3770–3784. [Google Scholar] [CrossRef]
- Han, D.; Dong, G.; Huang, P.; Ma, Z. Capture and Detumbling Control for Active Debris Removal by a Dual-Arm Space Robot. Chin. J. Aeronaut. 2021, 35, 342–353. [Google Scholar] [CrossRef]
- Hawkes, E.W.; Jiang, H.; Cutkosky, M.R. Three-Dimensional Dynamic Surface Grasping with Dry Adhesion. Int. J. Robot. Res. 2016, 35, 943–958. [Google Scholar] [CrossRef]
- Cauligi, A.; Chen, T.G.; Suresh, S.A.; Dille, M.; Ruiz, R.G.; Vargas, A.M.; Pavone, M.; Cutkosky, M.R. DESIGN AND I-SAIRAS2020-Papers (2020) DEVELOPMENT OF A GECKO-ADHESIVE 5055.Pdf. 2020, 8. Available online: https://www.hou.usra.edu/meetings/isairas2020fullpapers/pdf/5055.pdf (accessed on 24 July 2022).
- Zhang, G.; Zhang, Q.; Feng, Z.; Chen, Q.; Yang, T. Dynamic Modeling and Simulation of a Novel Mechanism for Adhesive Capture of Space Debris. Adv. Space Res. 2021, 68, 3859–3874. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, M.; Ding, M. Space Multi-Ring Closed Chain Parallel Type Flexible Catching Device, Has Six-Rod Zoom Closed Ring Mechanism Installed at Lower End of Device, and Three First Rotating Pair and Ring Mechanism Far Away from Hinge End of Three-Phase Rotating Pair 2021. Available online: https://www.webofscience.com/wos/alldb/full-record/DIIDW:202253624J (accessed on 22 July 2022).
- Yang, J.; Ren, C.; Yang, C.; Wang, Y.; Wan, S.; Kang, R. Design of a Flexible Capture Mechanism Inspired by Sea Anemone for Non-Cooperative Targets. Chin. J. Mech. Eng. 2021, 34, 77. [Google Scholar] [CrossRef]
- Banken, E.; Schneider, V.E.; Ben-Larbi, M.K.; Pambaguian, L.; Oeffner, J. Biomimetic Space Debris Removal: Conceptual Design of Bio-Inspired Active Debris Removal Scenarios. CEAS Space J. 2022. [Google Scholar] [CrossRef]
- Li, X.; Sun, K.; Liu, H. Design of a Novel Deployable Mechanism for Capturing Tumbling Debris. Trans. Can. Soc. Mech. Eng. 2019, 43, 294–305. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Wan, W.; Deng, L. Adaptive Space Debris Capture Approach Based on Origami Principle. Int. J. Adv. Robot. Syst. 2019, 16, 172988141988521. [Google Scholar] [CrossRef] [Green Version]
- Jia, G.; Huang, H.; Li, B.; Wu, Y.; Cao, Q.; Guo, H. Synthesis of a Novel Type of Metamorphic Mechanism Module for Large Scale Deployable Grasping Manipulators. Mech. Mach. Theory 2018, 128, 544–559. [Google Scholar] [CrossRef]
- Li, G.; Huang, H.; Guo, H.; Li, B. Design, Analysis and Control of a Novel Deployable Grasping Manipulator. Mech. Mach. Theory 2019, 138, 182–204. [Google Scholar] [CrossRef]
- Li, G.; Xu, P.; Qiao, S.; Li, B. Stability Analysis and Optimal Enveloping Grasp Planning of a Deployable Robotic Hand. Mech. Mach. Theory 2021, 158, 104241. [Google Scholar] [CrossRef]
- Li, G.; Xu, P. Design and Analysis of a Deployable Grasping Mechanism for Capturing Non-Cooperative Space Targets. Aerosp. Sci. Technol. 2020, 106, 106230. [Google Scholar] [CrossRef]
- Nishida, S.; Yoshikawa, T. Space Debris Capture by a Joint Compliance Controlled Robot. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; pp. 496–502. [Google Scholar]
- ClearSpace-1. Available online: https://www.esa.int/Safety_Security/ClearSpace-1 (accessed on 26 May 2022).
- Juillard, M.; Richard-Noca, M.; Kneib, J.-P. Simulation Tool to Study High Performance Avionic for Active Debris Removal Missions. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 08–12 September 2019; pp. 1–10. [Google Scholar]
- Singh, S.; Mooij, E.; Gransden, D.I. Multibody Approach to the Controlled Removal of Large Space Debris with Flexible Appendages. In Proceedings of the AIAA Scitech 2019 Forum, American Institute of Aeronautics and Astronautics, San Diego, CA, USA, 7 January 2019. [Google Scholar]
- Singh, S.; Mooij, E. Robust Control for Active Debris Removal of a Large Flexible Space Structure. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6 January 2020. [Google Scholar]
- Xie, Z.; Sun, T.; Kwan, T.H.; Mu, Z.; Wu, X. A New Reinforcement Learning Based Adaptive Sliding Mode Control Scheme for Free-Floating Space Robotic Manipulator. IEEE Access 2020, 8, 127048–127064. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; Gao, Q.; Ju, Z. Adaptive Robust Decoupling Control of Multi-Arm Space Robots Using Time-Delay Estimation Technique. Nonlinear Dyn. 2020, 100, 2449–2467. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; Tong, Y.; Liu, Y.; Ju, Z. Attitude Decoupling Control of Semifloating Space Robots Using Time-Delay Estimation and Supertwisting Control. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4280–4295. [Google Scholar] [CrossRef]
- Shao, X. Nonsingular Terminal Sliding Mode Control for Free-Floating Space Manipulator with Disturbance. Acta Astronaut. 2021, 9, 396–404. [Google Scholar] [CrossRef]
- Dong, H.; Yang, X. Learning-Based Online Optimal Sliding-Mode Control for Space Circumnavigation Missions with Input Constraints and Mismatched Uncertainties. Neurocomputing 2022, 484, 13–25. [Google Scholar] [CrossRef]
- Liu, Y.; Yen, W.; Zhang, T.; Yu, C.; Tu, H. Trajectory Tracking for a Dual-Arm Free-Floating Space Robot With a Class of General Nonsingular Predefined-Time Terminal Sliding Mode. IEEE Trans. Syst. Man Cybern Syst. 2022, 52, 3273–3286. [Google Scholar] [CrossRef]
- Liu, E.; Yang, Y.; Yan, Y. Spacecraft Attitude Tracking for Space Debris Removal Using Adaptive Fuzzy Sliding Mode Control. Aerosp. Sci. Technol. 2020, 107, 106310. [Google Scholar] [CrossRef]
- Xie, Z.; Sun, T.; Kwan, T.; Wu, X. Motion Control of a Space Manipulator Using Fuzzy Sliding Mode Control with Reinforcement Learning. Acta Astronaut. 2020, 176, 156–172. [Google Scholar] [CrossRef]
- Mu, C.; Ni, Z.; Sun, C.; He, H. Air-Breathing Hypersonic Vehicle Tracking Control Based on Adaptive Dynamic Programming. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 584–598. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Liu, Y. Fixed-time Adaptive Sliding Mode Trajectory Tracking Control of Uncertain Mechanical Systems. Asian J. Control. 2020, 22, 2080–2089. [Google Scholar] [CrossRef]
- Seddaoui, A.; Saaj, C.M. Combined Nonlinear H∞ Controller for a Controlled-Floating Space Robot. J. Guid. Control Dyn. 2019, 42, 1878–1885. [Google Scholar] [CrossRef]
- Gangapersaud, R.A.; Liu, G.; De Ruiter, A.H.J. Detumbling a Non-Cooperative Space Target with Model Uncertainties Using a Space Manipulator. J. Guid. Control Dyn. 2019, 42, 910–918. [Google Scholar] [CrossRef]
- Liu, Q.; Shi, S.; Jin, M.; Fan, S.; Liu, H. Minimum Disturbance Control Based on Synchronous and Adaptive Acceleration Planning of Dual-Arm Space Robot to Capture a Rotating Target. Ind. Robot 2022, 49. [Google Scholar] [CrossRef]
- Shi, L.; Yao, H.; Shan, M.; Gao, Q.; Jin, X. Robust Control of a Space Robot Based on an Optimized Adaptive Variable Structure Control Method. Aerosp. Sci. Technol. 2022, 120, 107267. [Google Scholar] [CrossRef]
- He, J.; Xu, F.; Wang, X.; Yang, J.; Liang, B. Modeling and Control of Free-Floating Space Manipulator Using the T-S Fuzzy Descriptor System Approach. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 06–09 October 2019; pp. 1049–1055. [Google Scholar]
- Zong, L.; Emami, M.R.; Luo, J. Reactionless Control of Free-Floating Space Manipulators. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1490–1503. [Google Scholar] [CrossRef]
- Shao, X.; Yao, W.; Li, X.; Sun, G.; Wu, L. Direct Trajectory Optimization of Free-Floating Space Manipulator for Reducing Spacecraft Variation. IEEE Robot. Autom. Lett. 2022, 7, 2795–2802. [Google Scholar] [CrossRef]
- Zhang, L. Configuration Optimization for Free-Floating Space Robot Capturing Tumbling Target. Aerospace 2022, 9, 69. [Google Scholar] [CrossRef]
- She, Y.; Li, S. An Extra Degree-of-Freedom Model for Combined Spacecraft Attitude Control with Unilateral Contact Constraint. Acta Astronaut. 2019, 165, 54–67. [Google Scholar] [CrossRef]
- She, Y.; Li, S.; Hu, J. Contact Dynamics and Relative Motion Estimation of Non-Cooperative Target with Unilateral Contact Constraint. Aerosp. Sci. Technol. 2020, 98, 105705. [Google Scholar] [CrossRef]
- Stolfi, A.; Gasbarri, P.; Misra, A.K. A Two-Arm Flexible Space Manipulator System for Post-Grasping Manipulation Operations of a Passive Target Object. Acta Astronaut. 2020, 175, 66–78. [Google Scholar] [CrossRef]
- Santaguida, L.; Zhu, Z.H. Development of Air-Bearing Microgravity Testbed for Autonomous Spacecraft Rendezvous and Robotic Capture Control of a Free-Floating Target. Acta Astronaut. 2022, S0094576522006725. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Paraskevas, I.S.; Flessa, T.; Nanos, K.; Georgios, R.; Ioannis, K. The NTUA Space Robot Simulator: Design & Results. In Proceedings of the 10th ESA Workshop on Advanced Space Technologies for Robotics & Automation, Noordwijk, The Netherlands, 11 November 2008. [Google Scholar]
- Sabatini, M.; Farnocchia, M.; Palmerini, G.B. Design and Tests of a Frictionless 2D Platform for Studying Space Navigation and Control Subsystems. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 03–10 March 2012; pp. 1–12. [Google Scholar]
- Virgili Llop, J.; Drew, J.; Zappulla, R.; Romano, M. Autonomous Capture of a Resident Space Object by a Spacecraft with a Robotic Manipulator: Analysis, Simulation and Experiments. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Long Beach, CA, USA, 13 September 2016. [Google Scholar]
- Virgili-Llop, J.; Romano, M. Simultaneous Capture and Detumble of a Resident Space Object by a Free-Flying Spacecraft-Manipulator System. Front. Robot. AI 2019, 6, 14. [Google Scholar] [CrossRef]

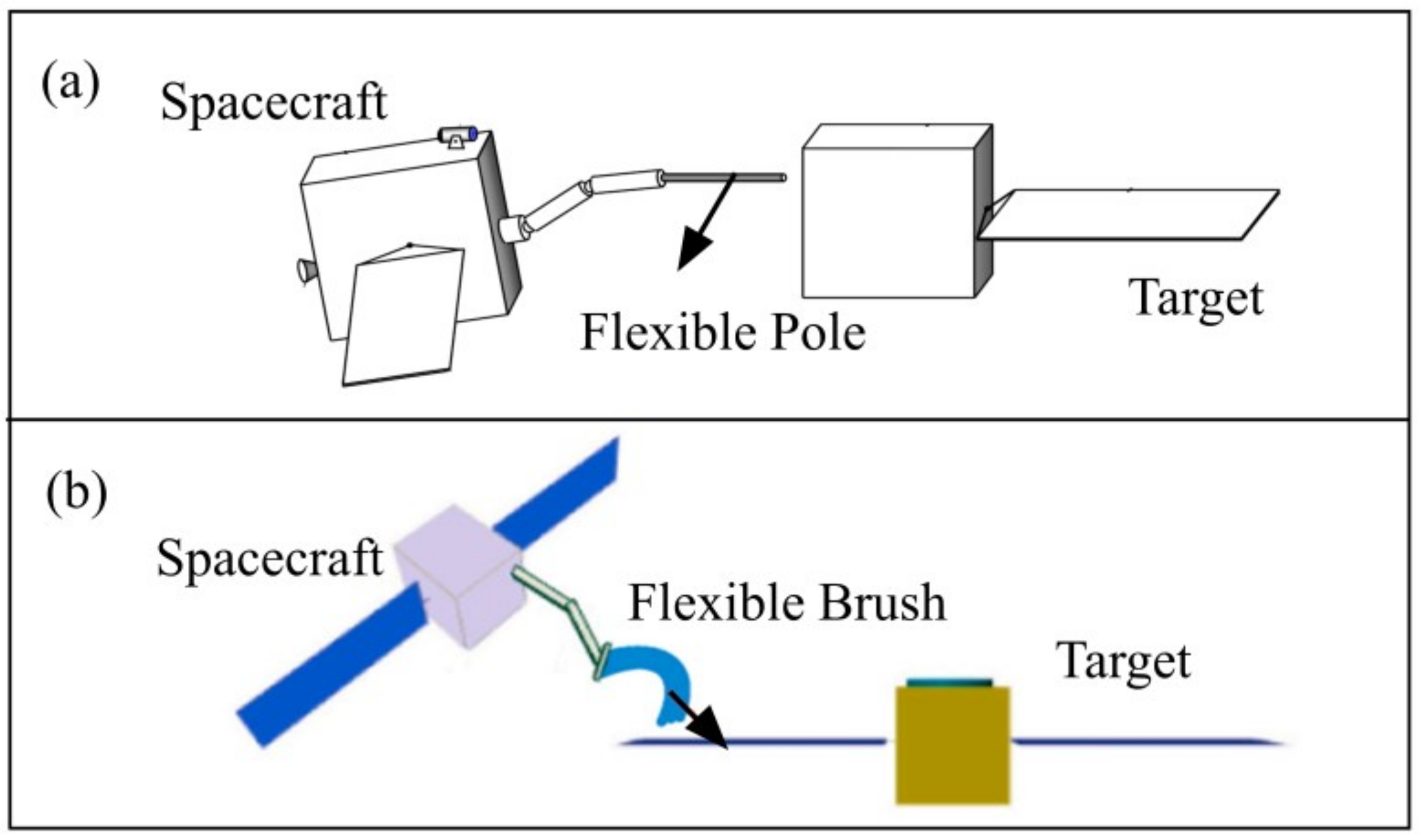
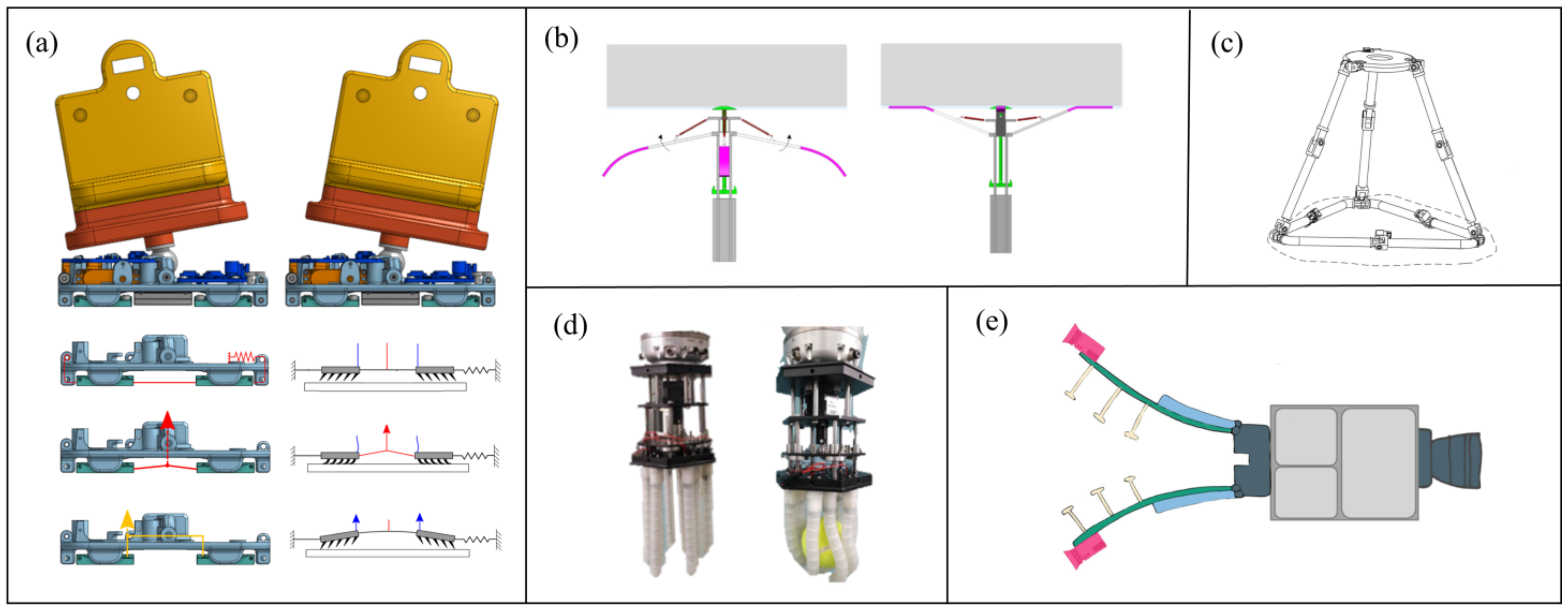

| - | Mode of Action | Contact Mode |
|---|---|---|
| Flexible rod (a) | Impact | Two-stage instantaneous |
| Flexible brush (b) | Friction | Multiple persistent |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Li, F.; Li, J.; Cheng, Q. Review of On-Orbit Robotic Arm Active Debris Capture Removal Methods. Aerospace 2023, 10, 13. https://doi.org/10.3390/aerospace10010013
Zhang W, Li F, Li J, Cheng Q. Review of On-Orbit Robotic Arm Active Debris Capture Removal Methods. Aerospace. 2023; 10(1):13. https://doi.org/10.3390/aerospace10010013
Chicago/Turabian StyleZhang, Wei, Feng Li, Junlin Li, and Qinkun Cheng. 2023. "Review of On-Orbit Robotic Arm Active Debris Capture Removal Methods" Aerospace 10, no. 1: 13. https://doi.org/10.3390/aerospace10010013
APA StyleZhang, W., Li, F., Li, J., & Cheng, Q. (2023). Review of On-Orbit Robotic Arm Active Debris Capture Removal Methods. Aerospace, 10(1), 13. https://doi.org/10.3390/aerospace10010013







