Atomization Characteristics of Kerosene in Crossflow with an Incident Shock Wave
Abstract
:1. Introduction
2. Numerical Simulation Method
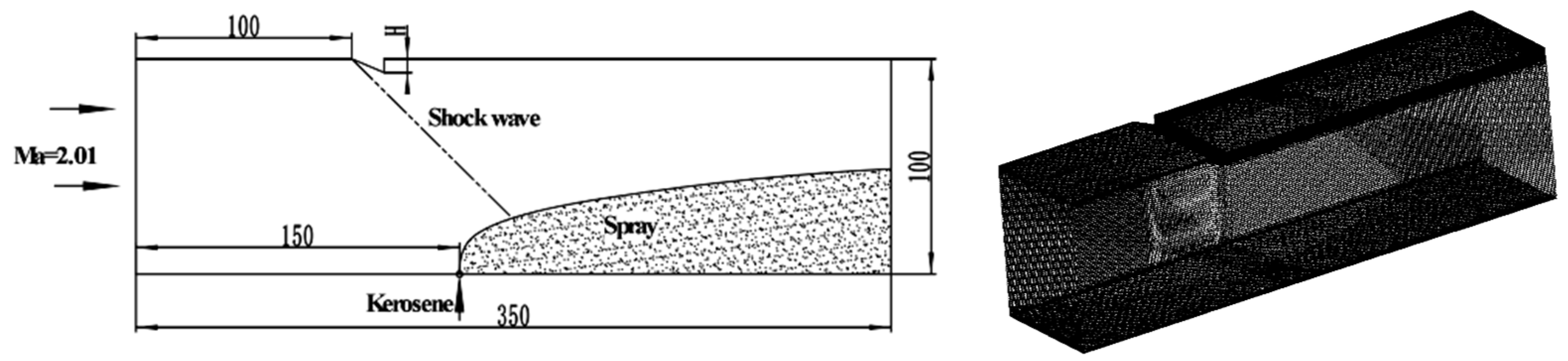
2.1. Calculation Model
2.2. Physical Model and Grid
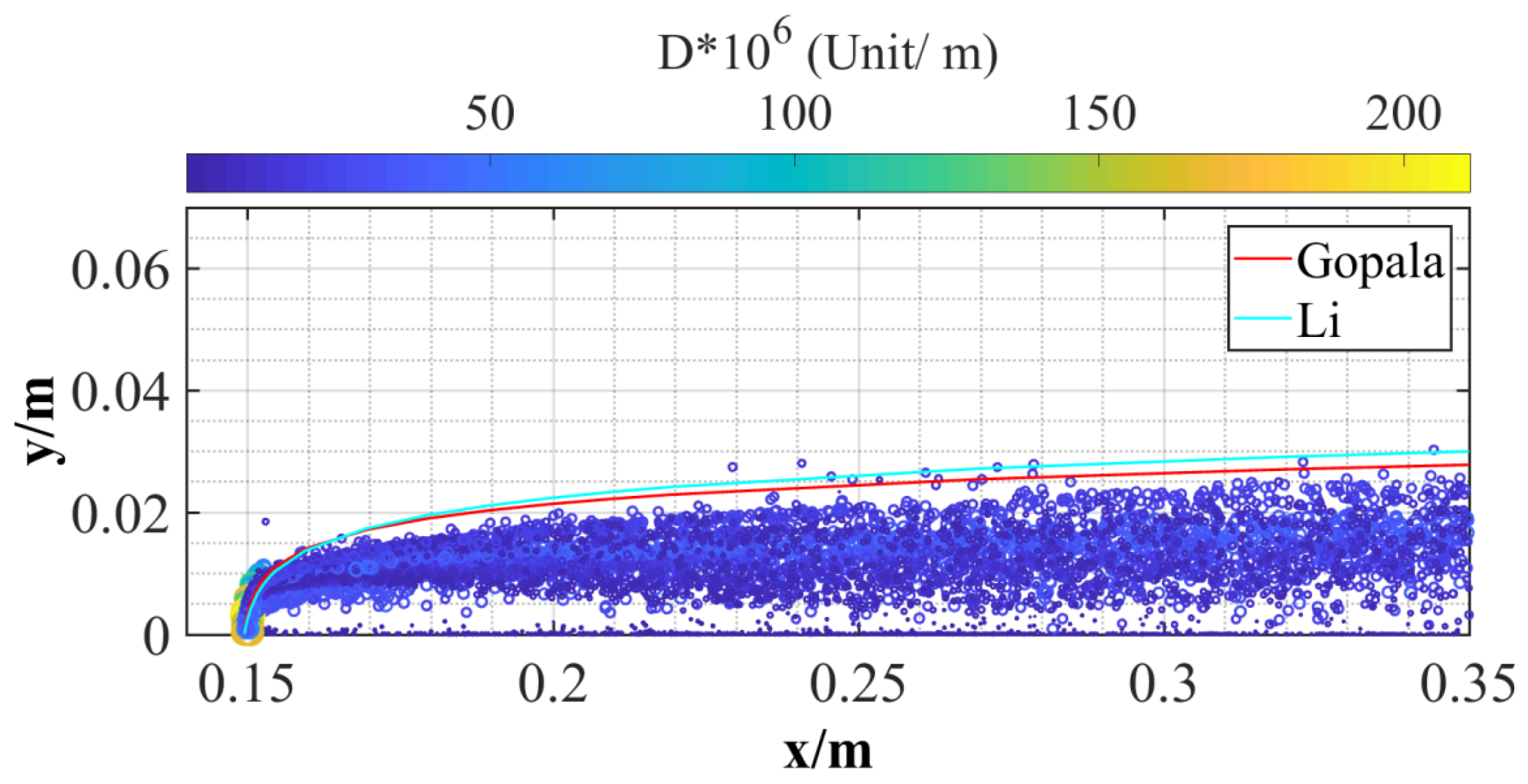
2.3. Numerical Method Verification
3. Results and Analysis
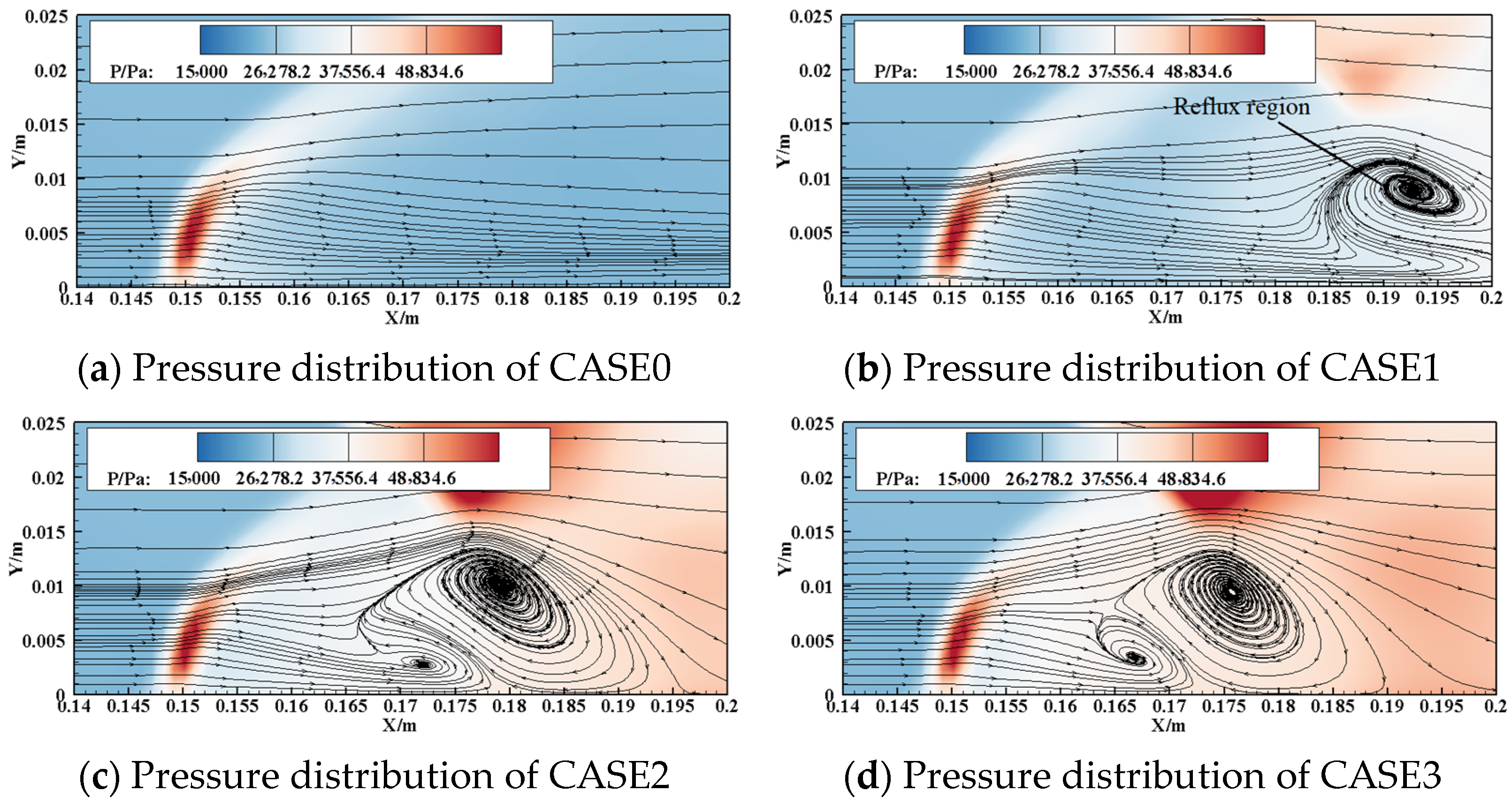
3.1. Influence of Shock Waves on Jet Characteristics in the Central Section
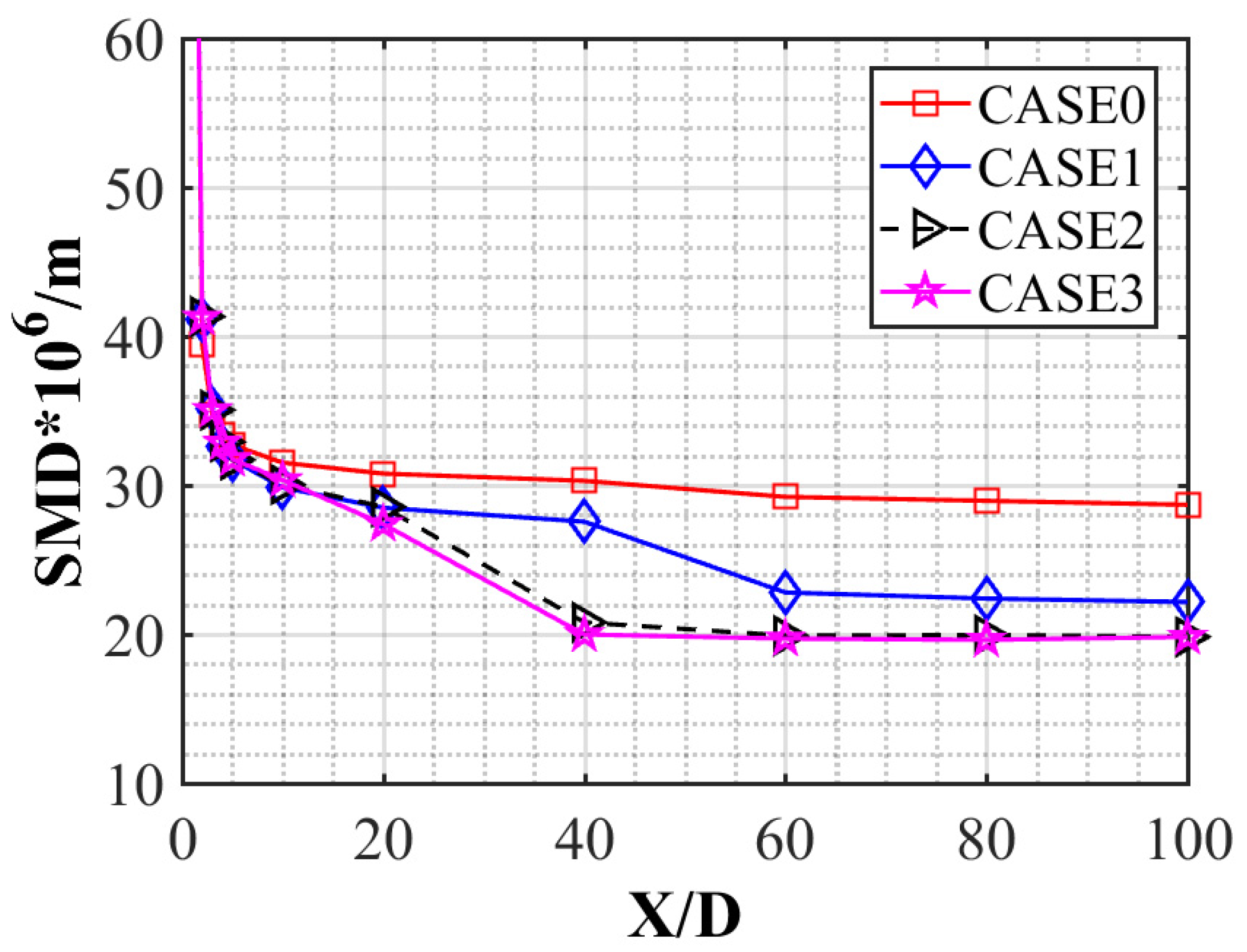
3.2. Influence of Shock Waves on Jet Characteristics in the Transverse Section
3.3. Influence of Shock Waves on Jet Characteristics in the Spanwise Section
4. Conclusions
- When there is a shock wave, the outer-edge trajectory of the jet does not change much, but the inner-edge trajectory is close to the combustion chamber wall. Additionally, the length of the pure gas zone gets shorter. With the shock wave moving upstream, the pure gas region is pushed further towards the jet root and is divided into two parts. Meanwhile, the incident shock wave changes the K-H instability of the jet. The unsteadiness of the jet root is strengthened, while the unsteadiness downstream of the jet is weakened. The main reason for the characteristic change is the change in the reflux region caused by the incident shock wave.
- Because the incident shock wave changes the momentum exchange characteristics between the mainstream and the jet, the SMD of the transverse section of the jet decreases, and the droplet distribution becomes more uniform.
- Due to the adverse pressure gradient caused by the incident shock wave, the width of the jet increases first and then decreases, and this change becomes more obvious as the shock wave moves upstream of the jet.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Charles, R. McClinton. X-43-scramjet power breaks the hypersonic barrier Dryden lectureship in research for 2006. In Proceedings of the 44th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Ronald, S. A Century of Ramjet Propulsion Technology Evolution. J. Propuls. Power 2004, 20, 27–58. [Google Scholar]
- Seiner, J.; Dash, S.; Kenzakowshi, D. Historical Survey on Enhanced Mixing in Scramjet Engines. J. Propuls. Power 2001, 17, 1273–1286. [Google Scholar] [CrossRef]
- Takahashi, H.; Masuya, G.; Hirota, M. Effects of Injection and Main Flow Conditions on Supersonic Turbulent Mixing Structure. AIAA J. 2010, 48, 1748–1756. [Google Scholar] [CrossRef]
- Rana, Z.A.; Thornber, B.; Drikakis, D. Transverse jet injection into a supersonic turbulent cross-flow. Phys. Fluids 2011, 23, 585. [Google Scholar] [CrossRef]
- Rana, Z.A.; Thornber, B.; Drikakis, D. On the importance of generating accurate turbulent boundary condition for unsteady simulations. J. Turbul. 2011, 12, N35. [Google Scholar] [CrossRef]
- Génin, F.; Menon, S. Dynamics of sonic jet injection into supersonic crossflow. J. Turbul. 2010, 11, 1–30. [Google Scholar] [CrossRef]
- Nakamura, H.; Sato, N.; Kobayashi, H.; Niioka, T.; Masuya, G. Combustion of transverse hydrogen injection with shock wave in a supersonic airstream. In Proceedings of the 5th Asia-Pacific Conference on Combustion, Adelaide, SA, Australia, 17–20 July 2005. [Google Scholar]
- Tahsini, A.M.; Mousavi, S.T. Investigating the supersonic combustion efficiency for the jet-in-cross-flow. Int. J. Hydrogen Energy 2015, 40, 3091–3097. [Google Scholar] [CrossRef]
- Shekarian, A.A.; Tabejamaat, S.; Shoraka, Y. Effects of incident shock wave on mixing and flame holding of hydrogen in supersonic air flow. Int. J. Hydrogen Energy 2014, 39, 10284–10292. [Google Scholar] [CrossRef]
- Mai, T.; Sakimitsu, Y.; Nakamura, H.; Ogami, Y.; Kudo, T.; Kobayashi, H. Effect of theincident shock wave interacting with transversal jet flow on the mixing and combustion. Proc. Combust. Inst. 2011, 33, 2335–2342. [Google Scholar] [CrossRef]
- Schetz, J.A.; Maddalena, L.; Burger, S.K. Molecular weight and shock-wave effects on transverse injection in supersonic flow. J. Propuls. Power 2010, 26, 1102–1113. [Google Scholar] [CrossRef]
- Erdem, E.; Saravanan, S.; Lin, J.; Kontis, K. Experimental investigation of transverse injection flowfield at Mach 5 and the influence of impinging shock wave. In Proceedings of the 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference, Tours, France, 24–28 September 2012. [Google Scholar]
- Huang, W.; Tan, J.G.; Liu, J.; Yan, L. Mixing augmentation induced by the interaction between the oblique shock wave and a sonic hydrogen jet in supersonic flows. Acta Astronaut. 2015, 117, 142–152. [Google Scholar] [CrossRef]
- Huang, W.; Wang, Z.G.; Wu, J.P.; Li, S.B. Numerical prediction on the interaction between the incident shock wave and the transverse slot injection in supersonic flows. Aerosp. Sci. Technol. 2013, 28, 91–99. [Google Scholar] [CrossRef]
- Gerdroodbary, M.B.; Ganji, D.D.; Amini, Y. Numerical study of shock wave interaction on transverse jets through multiport injector arrays in supersonic crossflow. Acta Astronaut. 2015, 115, 422–433. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Xing, J.-W.; Yang, Y. Three-dimensional simulation of H2O vitiation effects on combustor performance for scramjet. J. Propuls. Technol. 2011, 32, 5–10. [Google Scholar]
- Thomas, R.A.; Bussing Murmant, E.M. Finite-Volume Method for the Calculation of Compressible Chemically Reacting Flows. AIAA J. 1988, 26, 1070–1078. [Google Scholar]
- Zhai, X.F.; Bai, H.C.; Li, C. Numerical simulation of atomization of liquid jet in supersonic flow. Phys. Gases 2021, 6, 23–29. [Google Scholar]
- Gopala, Y.; Zhang, P.; Bibik, O.; Lubarsky, E.; Zinn, B. Liquid fuel jet in crossflow-trajectory correlations based on the column breakup point. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Li, L.; Lin, Y.; Xue, X.; Gao, W.; Sung, C.J. Injection of liquid kerosene into a high-pressure subsonic air crossflow from normal temperature. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012. [Google Scholar] [CrossRef]
- Inamura, T.; Nagai, N. Spray Characteristics of Liquid Jet Traversing Subsonic Airstreams. J. Propuls. Power 1997, 13, 250–256. [Google Scholar] [CrossRef]
- Wu, P.K.; Kirkendall, K.A.; Fuller, R.P.; Nejad, A.S. Spray Structures of Liquid Jets Atomized in Subsonic Crossflows. J. Propuls. Power 1998, 14, 173–182. [Google Scholar] [CrossRef]


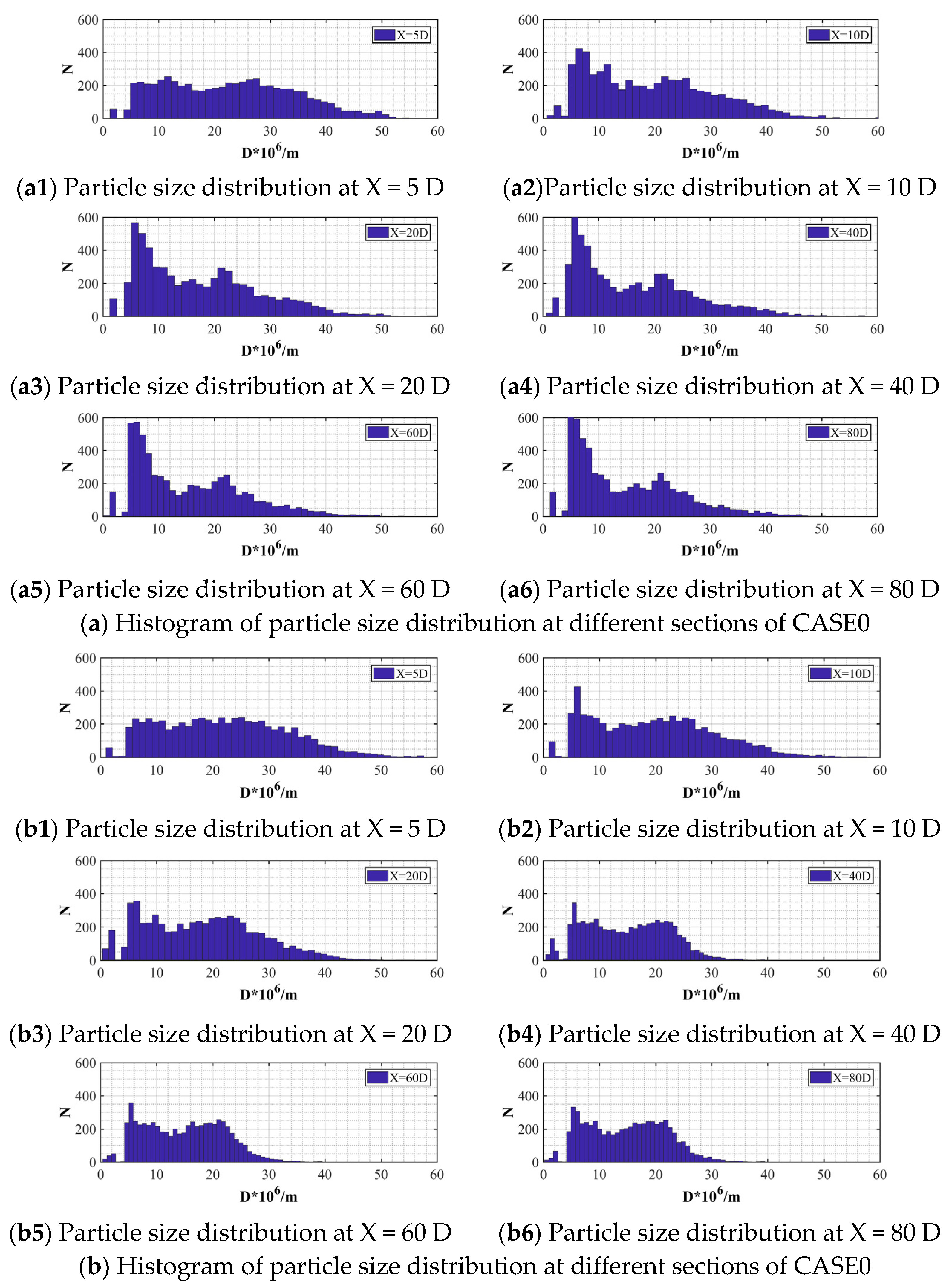


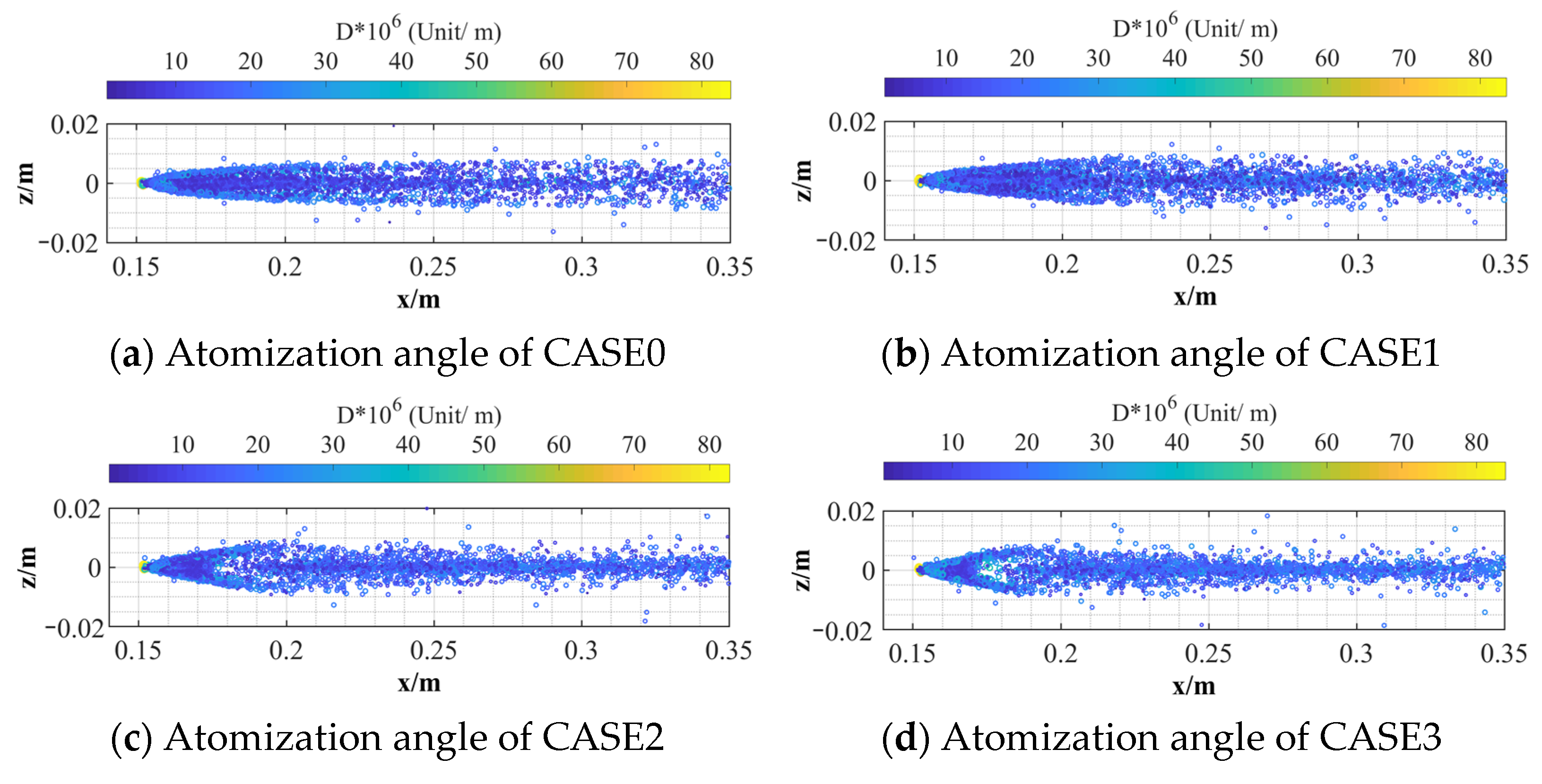
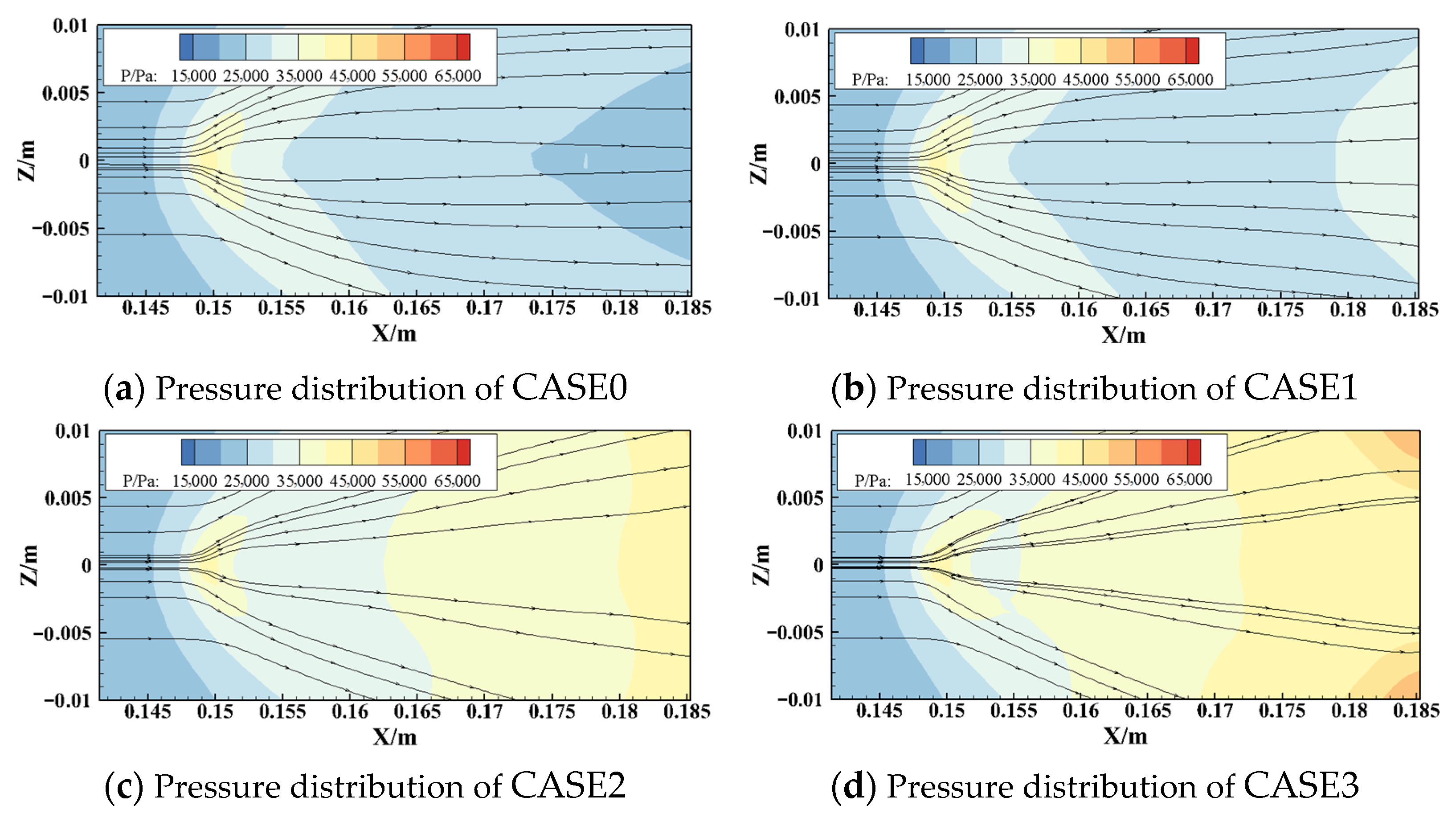
| CASE0 | CASE1 | CASE2 | CASE3 | |
|---|---|---|---|---|
| H/mm | 0 | 4.4 | 5.89 | 6.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wu, J.; Mu, X. Atomization Characteristics of Kerosene in Crossflow with an Incident Shock Wave. Aerospace 2023, 10, 30. https://doi.org/10.3390/aerospace10010030
Zhao Y, Wu J, Mu X. Atomization Characteristics of Kerosene in Crossflow with an Incident Shock Wave. Aerospace. 2023; 10(1):30. https://doi.org/10.3390/aerospace10010030
Chicago/Turabian StyleZhao, Yongsheng, Junfei Wu, and Xiangyang Mu. 2023. "Atomization Characteristics of Kerosene in Crossflow with an Incident Shock Wave" Aerospace 10, no. 1: 30. https://doi.org/10.3390/aerospace10010030
APA StyleZhao, Y., Wu, J., & Mu, X. (2023). Atomization Characteristics of Kerosene in Crossflow with an Incident Shock Wave. Aerospace, 10(1), 30. https://doi.org/10.3390/aerospace10010030






