Real-Time Implementation of an Adaptive PID Controller for the Quadrotor MAV Embedded Flight Control System

Abstract

This paper presents the real-time implementation of an altitude-embedded flight controller using proportional, integral, and derivative (PID) control, adaptive PID (APID) control, and adaptive PID control with a fuzzy compensator (APIDFC) for a micro air vehicle (MAV), specifically, for a Parrot Mambo Minidrone. In order to obtain robustness against disturbance, the adaptive mechanism, which was centered on the second-order sliding mode control, was applied to tune the classical parameters of the PID controller of the altitude controller. Additionally, a fuzzy compensator was introduced to diminish the existence of the chattering phenomena triggered by the application of the sliding mode control. Four simulation and experimental scenarios were conducted, which included hovering, as well as sine, square, and trapezium tracking. Moreover, the controller’s resilience was tested at 1.1 m above the ground by adding a mass of about 12.5 g, 15 s after the flight launch. The results demonstrated that all controllers were able to follow the reference altitude, with some spike or overshoot. Although there were slight overshoots in the control effort, the fuzzy compensator reduced the chattering phenomenon by about 6%. Moreover, it was found that in the experiment, the APID and APIDFC controllers consumed 2% and 4% less power, respectively, when compared to the PID controller used to hover the MAV.

1. Introduction

Unmanned Aerial Vehicle (UAV) control is a very challenging area of research, particularly for vertical take-off and landing (VTOL) of aircraft such as the quadrotor. A quadrotor is an unmanned aerial VTOL vehicle that belongs to the category of aerial vehicles with rotating wings. Because of its simple structure, quadrotors are a common design for small UAVs. This aerial aircraft features four motors that transmit electricity to propellers to produce propulsion thrust. By adjusting the engine rpm, this vehicle may be controlled and stabilized.

In the last few years, the state-of-the-art for quadrotor control has seen a significant development. All studies begin with the quadrotor’s fundamental dynamical model, although more complicated aerodynamic features have also been incorporated [1,2]. As a small-scale UAV, the minidrone, nano, or micro air vehicle (MAV) has attracted the attention of educators and researchers due to its dependability and safety in restricted GPS spaces, such as hallways, schools, and other indoor environments. Thus, various control strategies, such as PID controllers, LQR controllers, sliding mode controllers, intelligent controllers, adaptive controllers, and others, have been studied. For instance, numerous works deal with the modeling and control of the Crazyflie [3,4,5,6]. DJI and Parrot are two of the most well-known manufacturers who have established and commercialized quadrotor drones which cover most of the types used for educational purposes. For instance, the company created the Tello EDU, which supports iOS users, and Scratch 2.0, SDK 2.0, and Swift Playgrounds for programming, which was been used in the studies in [7,8,9]. Parrot recently created the AR Drone 2.0, the Rolling Spider, and the Mambo, all of which allow for the models to be programmed using MATLAB/Simulink. Researchers have used the AR Drone reported in [10,11,12,13], whereas other researchers have used the Rolling Spider/Parrot Minidrones, supported by MATLAB’s Simulink, as reported in [14,15,16,17].

Due to the advancement of technology, quadrotors can be utilized in performing various high risk, high intensity tasks which require a high degree of efficiency, such as military operations, agricultural applications, and express delivery [18]. These applications exhibit the inescapable issue that if the load is unknown or fluctuating, the quadrotor’s altitude control will be unstable, making it impossible to maintain stable high-altitude flight or hover in the air. To maintain the stability of the altitude and track the planned trajectory, it is crucial to build a strong altitude control system. The linear control technique is an effort at control, but its effectiveness is limited, and it depends on a number of factors. Additionally, the linear controller is unable to handle the situations of drift and hover.

Due to its straightforward control architecture and effective control performance, PID is the most common flight control algorithm used in multirotor systems. PID is therefore still the favored approach for actual control in a quadrotor UAV [17,19]. However, troubleshooting the PID controller’s settings is challenging, mainly relying on the expertise of researchers. In its application to autonomous load carrying and transport, the hovering vehicles must remain stable and balanced in flight as payload mass is added to the vehicle. Therefore, [20] investigates the impact of dynamic load disturbances caused by suddenly increasing the payload mass on a quadrotor operating under PID control. As a result, under PID control, a quadrotor will successfully reject additional load offset to a relative amount within a sizable range and allowable load position. Therefore, the control input that has a wide floating range and a slow convergence rate is deemed to be unstable.

Estimating the mass is another crucial step in altitude control. Altitude control is quite challenging if the quadrotor mass cannot be precisely approximated, since we cannot measure it directly while it is in the air. In reference [21], a mass estimation technique was suggested for estimating the inertial properties of the item being held in order to modify the controller and enhance performance while in flight. The authors of [22] suggested an adaptive robust control (ARC) to account for the parametric uncertainty for unknown payloads. However, the parameter estimate could not get close to its real value when the required output remained constant.

To track the position of a quadrotor, a linear quadratic regulator (LQR) is examined in [23,24,25]. A sliding mode control (SMC) strategy is created for a class of underactuated systems in [26,27], used to stabilize the position and attitude of a quadrotor UAV. According to simulation and experiment, the second order SMC may significantly reduce chattering when compared to regular SMC. A model free-based single dimension fuzzy SMC technique is created in [28] to enable the finite-time control of a quadrotor’s translational and rotational movements, despite perturbations. According to numerical simulation on the altitude, the comprehensive fuzzy adaptive sliding mode control in [29] is able to handle the control problems of the highly coupled nonlinear fixed-wing UAV model to address the chattering problem of classic sliding mode control.

The hybrid backstepping-based control techniques also show good performance to cater to the quadrotor trajectory tracking problem. In order to exhibit the efficacy and practicability of the suggested control approach, simulation results under several scenarios, such as parameter uncertainties under Gaussian random disturbances, constant and time-varying external disturbances are provided, as shown in [30]. In [31], a robust backstepping super-twisting sliding mode control strategy was tested on the X450 quadrotor, emphasize the improved proficiencies of the proposed control approach in terms of tracking accuracy and chattering occurrence reduction.

In a previous study, [32] implemented the control scheme and simulated it on UAV, while [33] successfully used FPGA to apply the control scheme on a DC motor. This paper focuses on the impact of the real-time implementation of PID, adaptive PID (APID), and adaptive PID with a fuzzy compensator (APIDFC) for an altitude controller on the embedded flight system of a quadrotor MAV which has a mass less than 0.1kg. Using the sliding type control as the adaptive mechanism, this technique can suppress the manual controller’s re-tuning gains in the classical PID controller. Furthermore, the effect of chattering by the sliding manifolds is removed by a fuzzy compensator. In order to display the benefits of applying the newly suggested flight control system, MATLAB software simulation and real-time hardware implementation were performed by redesigning the Flight Control System in the Simulink Support Package for the Parrot Mambo Minidrone. In conclusion, the APID and APIDFC control scheme can reduce energy usage and robust perturbation throughout, compared to PID controller.

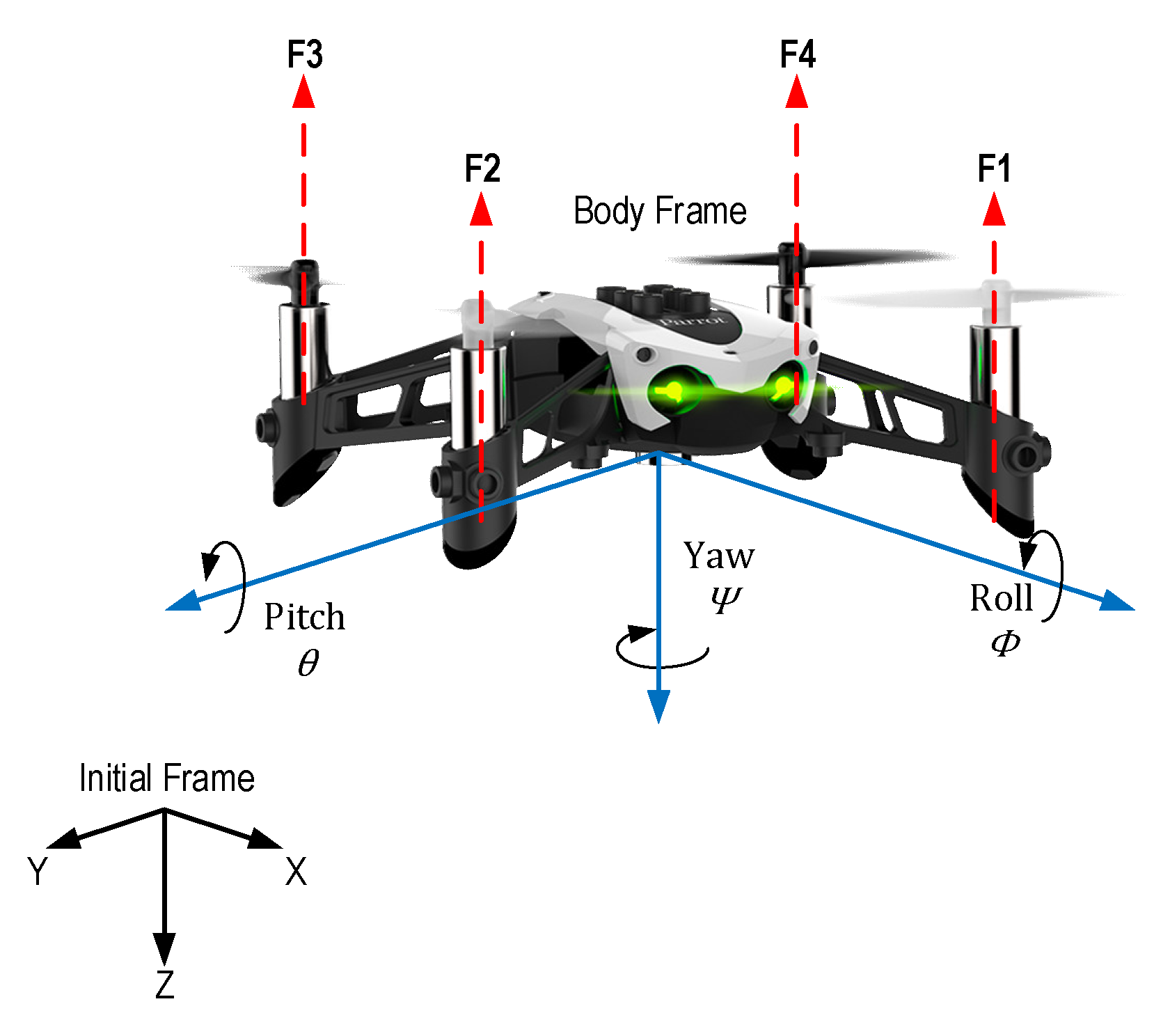
2. MAV Quadrotor Modeling

The Parrot Mambo Minidrone is a quadrotor, which falls under the category of a micro aerial vehicle (MAV). This category is actually comprised of four symmetrically arranged rotors and, as displayed in Figure 1, is independently fixed on a rigid fuselage. Rotor 1 and rotor 3 rotate in a clockwise direction, whereas rotor 2 and rotor 4 rotate in a counterclockwise direction.

The mathematical model of the aforementioned MAV is formed based on 6 degrees of freedom (DOF) ${\left[x,y,z,\varphi ,\theta ,\psi \right]}^T$, which is well accepted by the researchers of such systems. Hence, this particular model can be categorized by two coordinate subsystems. Vector ${\left[x,y,z\right]}^T$ defines the absolute positions, while vector ${\left[\varphi ,\theta ,\psi \right]}^T$ designates the orientation.

According to the general Newton–Euler formulation, quadrotor translational dynamics can be defined as:

$$\begin{array}{l}m\ddot{x}=-U_1\left(Sin\left(\psi \right)Sin\left(\varphi \right)+Cos\left(\psi \right)Sin\left(\theta \right)Cos\left(\varphi \right)\right)\\ m\ddot{y}=-U_1\left(-Cos\left(\psi \right)Sin\left(\varphi \right)+Sin\left(\psi \right)Sin\left(\theta \right)Cos\left(\varphi \right)\right)\\ \begin{array}{c}m\ddot{z}=mg-U_1\left(Cos\left(\theta \right)Cos\left(\varphi \right)\right)\end{array}\end{array}$$

(1)

where $m$ represent the mass, $g$ denotes the gravitational coefficient, and $U_1$ symbolize the total thrust force. Thus, the rotational dynamics are termed as:

$$\begin{array}{l}{I}_{xx}\ddot{\varphi }=\left(I_{yy}-I_{zz}\right)\dot{\psi }\dot{\theta }-\left(J_r{\mathsf{\Omega }}_d\right)\dot{\theta }+l{U}_2\\ I_{yy}\ddot{\theta }=\left(I_{zz}-I_{xx}\right)\dot{\psi }\dot{\varphi }+\left(J_r{\mathsf{\Omega }}_d\right)\dot{\varphi }+l{U}_3\\ \begin{array}{c}{I}_{zz}\ddot{\psi }=\left(I_{xx}-I_{yy}\right)\dot{\theta }\dot{\varphi }+U_4\end{array}\end{array}$$

(2)

where $U_2$, $U_3$, and $U_4$ represent the total torque for the roll, pitch, and yaw, respectively. $l$, on the other hand, is the lateral arm length. Meanwhile, $I_{xx}$, $I_{yy}$ and $I_{zz}$ are the moments of inertia for the quadrotor. Whereas $J_r$ is the rotor inertia, and ${\mathsf{\Omega }}_{\mathrm{d}}$ denotes the total rotor speed generated from the torque related to the control inputs as:

$$\begin{array}{l}{u}_1=b\left({\mathsf{\Omega }}_1^2+{\mathsf{\Omega }}_2^2+{\mathsf{\Omega }}_3^2+{\mathsf{\Omega }}_4^2\right)\\ u_2=b\left({\mathsf{\Omega }}_1^2-{\mathsf{\Omega }}_2^2-{\mathsf{\Omega }}_3^2+{\mathsf{\Omega }}_4^2\right)\\ u_3=b\left({\mathsf{\Omega }}_1^2+{\mathsf{\Omega }}_2^2-{\mathsf{\Omega }}_3^2-{\mathsf{\Omega }}_4^2\right)\\ u_4=d\left(-{\mathsf{\Omega }}_1^2+{\mathsf{\Omega }}_2^2-{\mathsf{\Omega }}_3^2+{\mathsf{\Omega }}_4^2\right)\\ \begin{array}{c}{\mathsf{\Omega }}_d=-{\mathsf{\Omega }}_1+{\mathsf{\Omega }}_2-{\mathsf{\Omega }}_3+{\mathsf{\Omega }}_4\end{array}\end{array}$$

(3)

where ${\mathsf{\Omega }}_i\left(i=1,2,3,4\right)$ represents the rotor speed. On the other hand, $b$ and $d$ are the thrust and drag coefficients, respectively. To summarize, the Parrot Mambo Minidrone parameters are shown in

Table 1. Parrot Mambo Model Physical Parameters [17].

Specification	Parameter	Unit	Value
Quadrotor mass	$m$	$\mathrm{kg}$	$0.0630$
Lateral moment arm	$l$	$\mathrm{m}$	$0.0624$
Thrust coefficient	$b$	${\mathrm{Ns}}^2$	$0.0107$
Drag coefficient	$d$	${\mathrm{Nms}}^2$	$0.7826400\times {10}^{-3}$
Rolling moment of inertia	$I_{xx}$	${\mathrm{kgm}}^2$	$0.0582857\times {10}^{-3}$
Pitching moment of inertia	$I_{yy}$	${\mathrm{kgm}}^2$	$0.0716914\times {10}^{-3}$
Yawing moment of inertia	$I_{zz}$	${\mathrm{kgm}}^2$	$0.1000000\times {10}^{-3}$
Rotor moment of inertia	$J_r$	${\mathrm{kgm}}^2$	$0.1021\times {10}^{-6}$

.

Translational and rotational dynamics, as shown in (1) and (2), can be expressed as second-order state-space equations:

$$\ddot{x}=f\left(x\right)+g\left(x\right)u$$

(4)

In order to create an orderly control system design method and at the same time, maintain simple notation, the state vector becomes:

$$x={\left[x_1{x}_2{x}_3{x}_4{x}_5{x}_6\right]}^T={\left[xyz\varphi \theta \psi \right]}^T$$

(5)

and the input vector $u={\left[u_1{u}_2{u}_3{u}_4\right]}^T$. The non-linear function $f\left(x\right)$ and $g\left(x\right)$ can be rewritten as:

$$f\left(x\right)=\left[\begin{array}{c}{f}_1\left(x\right)\\ f_2\left(x\right)\\ f_3\left(x\right)\\ f_4\left(x\right)\\ f_5\left(x\right)\\ f_6\left(x\right)\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ g\\ a_1\dot{\psi }\dot{\theta }-a_2{\mathsf{\Omega }}_d\dot{\theta }\\ a_3\dot{\psi }\dot{\varphi }+a_4{\mathsf{\Omega }}_d\dot{\varphi }\\ a_5\dot{\theta }\dot{\varphi }\end{array}\right]$$

(6)

$$g\left(x\right)=\left[\begin{array}{cccc}{g}_1\left(x\right)& 0& 0& 0\\ g_2\left(x\right)& 0& 0& 0\\ g_3\left(x\right)& 0& 0& 0\\ 0& g_4\left(x\right)& 0& 0\\ 0& 0& g_5\left(x\right)& 0\\ 0& 0& 0& g_6\left(x\right)\end{array}\right]=\left[\begin{array}{cccc}-\frac{1}{m}{u}_x& 0& 0& 0\\ -\frac{1}{m}{u}_y& 0& 0& 0\\ -\frac{1}{m}{u}_z& 0& 0& 0\\ 0& b_1& 0& 0\\ 0& 0& b_2& 0\\ 0& 0& 0& b_3\end{array}\right]$$

(7)

where

$$\begin{array}{l}{a}_1=\frac{I_{yy}-I_{zz}}{I_{xx}},a_2=\frac{J_r}{I_{xx}},a_3=\frac{I_{zz}-I_{xx}}{I_{yy}}\\ a_4=\frac{J_r}{I_{yy}},a_5=\frac{I_{xx}-I_{yy}}{I_{zz}},b_1=\frac{l}{I_{xx}}\\ b_2=\frac{l}{I_{yy}},b_3=\frac{1}{I_{zz}}\end{array}$$

(8)

and

$$\begin{array}{l}{u}_x=S\psi S\varphi +C\psi S\theta C\varphi \\ u_y=-C\psi S\varphi +S\psi S\theta C\varphi \\ \begin{array}{c}{u}_z=C\theta C\varphi \end{array}\end{array}$$

(9)

3. Flight Controller Design

Four controllers were designed to control the minidrone, which consist of the attitude controller, yaw controller, position controller, and altitude controller, as shown in Figure 2. The control mixer is an inverse of (3) to convert the rotation speed to force. Thereafter, a brief description of the controller’s design is mentioned, but in this work, we concentrate on the altitude controller.

3.1. Attitude and Yaw Controller

The attitude controller is designed using cascaded PID, where the proportional loop controls the pitch and roll angle, while the PID controls the angular velocity as:

$$U_i=k_P^i{e}_i+k_I^i\int e_i+k_D^i{\dot{e}}_i\left(i=\varphi ,\theta ,\psi \right)$$

(10)

where $e_i=i_d-i$ and ${\dot{e}}_i={\dot{\dot{i}}}_d-\dot{\dot{i}}$ are the error and derivate error between the desired signal and the actual signal, and $k_P^i$, $k_I^i$, and $k_D^i$ are the PID gains parameters ($i=\varphi ,\theta ,\psi )$. The yaw controller, on the other hand, used classical PID (10) as well.

3.2. Position Controller

The position controller is designed using cascade PID, where the proportional loop controls the x-y, while the PI controls the angular velocity as:

$$U_i=k_P^i{e}_i+k_I^i\int e_{i}dt\left(i=x,y\right)$$

(11)

In addition, a position error transformation is introduced for error body ($e^b)$ to error earth ($e^e)$ conversion as:

$$\left[\begin{array}{c}{e}_x^b\\ e_y^b\end{array}\right]=\left[\begin{array}{cc}\cos \left(\psi \right)& \sin \left(\psi \right)\\ -\sin \left(\psi \right)& \cos \left(\psi \right)\end{array}\right]\left[\begin{array}{c}{e}_x^e\\ e_y^e\end{array}\right]$$

3.3. Altitude Control Design

Figure 3 illustrates the block diagram of an adaptive PID scheme applied to the altitude control systems. In this control system, a PID controller and a fuzzy logic compensator are combined in the suggested method as:

$$u_1=u_{pid}+u_{fc}$$

(12)

where $u_{pid}$ is the PID controller implemented to approach the optimum controller, $u^{*}$, and $u_{fc}$ is the designated fuzzy logic compensator applied to decrease the approximation error left between both controllers.

The aim of the system is to determine a certain control law so that $x$ can track the coveted $x_d$ as close as possible. Hence, the tracking error can be defined as:

$$e=x_d-x$$

(13)

Presuming that the optimal controller is created when all the parameters in (4) are identified, this can be expressed as:

$$u^{*}=g^{-1}\left(-f+{\ddot{x}}_d+k_1\dot{e}+k_{2}e\right)$$

(14)

where $k_1$ and $k_2$ are chosen as the non-zero positive constants to adhere to the Hurwitz criterion, indicating $\underset{t\to \infty }{\lim }e=0$ for any initial starting conditions. Substituting (14) into (4) then yields:

$$\ddot{e}+k_1\dot{e}+k_{2}e=0$$

(15)

Due to the system dynamics that are normally unidentified in real-life implementation, the optimal controller $u^{*}$ in (14) is unable to be precisely acquired. Nevertheless, it is possible to use the sliding mode controller to address this matter. Before the required controller is developed, the nominal model (4) can be rephrased as:

$$\ddot{x}=f_n\left(x\right)+g_n\left(x\right)u$$

(16)

where $f_n$ and $g_n$ denote the nominal behavior of $f$ and $g,$ correspondingly. Considering uncertainties and external disturbances, (16) can be further revised as:

$$\ddot{x}=\left(f_n+\Delta f\right)+\left(g_n+\Delta g\right)u+d=f_n+g_{n}u+w$$

(17)

where $d$ is the external disturbance, i.e., wind, $\Delta f$ and $\Delta g$ are system uncertainties, $w$ is lumped with uncertainties and defined as $w=\Delta f+\Delta gu+d$, with the assumption $\left|w\right|\le W$, where $W$ is a positive constant.

The significant idea for sliding mode control is to confirm that the system meets the essential condition and is guaranteed to possess a sliding environment. Thus, a sliding surface can be stated as:

$$s=\dot{e}+k_{1}e+k_2\int edt$$

(18)

where $k_1$ and $k_2$ are both positive coefficients. The law for sliding-mode control, on the other hand, is given as:

$$u_{sc}=u_{eq}+u_{ht}$$

(19)

where $u_{eq}$ is the comparable controller and can be described as:

$$u_{eq}=g_n^{-1}\left(-f_n+\ddot{x}+k_1\dot{e}+k_{2}e\right)$$

(20)

while the hitting controller, $u_{ht}$ is designed to guarantee system stability and is described as:

$$u_{ht}=\frac{W}{g_n}sgn\left(s\right)\&wheresgn\left(s\right)\left\{\begin{array}{c}+1ifs<0\\ -1ifs>0\end{array}\right.$$

(21)

The derivative of (18) gives:

$$\dot{s}=\ddot{e}+k_1\dot{e}+k_{2}e$$

(22)

Inserting (19–21) into (17) yields:

$$\ddot{e}+k_1\dot{e}+k_{2}e=-w-Wsgn\left(s\right)=\dot{s}$$

(23)

For the purpose of stability, a Lyapunov function is expressed as:

$$V_1=\frac{1}{2}{s}^2$$

(24)

Differentiating (24) in conjunction with time reads:

$$\dot{V_1}=s\dot{s}$$

(25)

For stability $\dot{V_1}\le 0$, substituting (23) into (25) yields:

$${\dot{V}}_1=-\left(W-\left|w\right|\right)\left|s\right|$$

(26)

In short, the sliding mode control law that is established according to the Lyapunov theorem will ensure the stability of the system. However, a larger control gain, $W$, will cause a chattering effect. Furthermore, the switching function is not easily implementable because of the existence of physical limitations on the rotor deployed by the MAV.

3.3.1. PID Controller Design

A conventional PID controller can normally be defined as:

$$u_{pid}={\widehat{k}}_{p}e+{\widehat{k}}_i\int edt+{\widehat{k}}_d\dot{e}$$

(27)

where ${\widehat{k}}_p$, ${\widehat{k}}_i$, and ${\widehat{k}}_d$ are the value of proportional gain, integral gain, and derivative gain, respectively.

For stability, $\dot{s}=0$, and by using (14) and (22) it can be obtained that:

$$\dot{s}=\ddot{e}+k_1\dot{e}+k_{2}e=-f-gu+A_d$$

(28)

where $A_d={\ddot{x}}_d+k_1\dot{e}+k_{2}e$, substitute (27) into (28) and multiply by $s$,

$$s\dot{s}=-s\left[g\left(u_{pid}\right)+f-A_d\right]$$

(29)

Applying the methods of gradient and the rule of chain, ${\widehat{k}}_p$, ${\widehat{k}}_i$ and ${\widehat{k}}_d$ gains are revised using the rules as in:

$$\begin{array}{l}{\dot{\widehat{k}}}_p=s{\beta }_{p}sgn\left(g\right)e={\beta }_{p}se\\ {\dot{\widehat{k}}}_i=s{\beta }_{i}sgn\left(g\right)\int edt={\beta }_{i}s\int edt\\ {\dot{\widehat{k}}}_d=s{\beta }_{d}sgn\left(g\right)\dot{e}={\beta }_{d}s\dot{e}\end{array}$$

(30)

where ${\beta }_p$, ${\beta }_i$, and ${\beta }_d$ are the positive learning rates of ${\dot{\widehat{k}}}_p$, ${\dot{\widehat{k}}}_i$, and ${\dot{\widehat{k}}}_d$, respectively. Furthermore, the designed approach necessitates the use of the $g$ value, which can be readily attained from the physical features of the controlled system [32,33].

3.3.2. Design of Fuzzy Compensator

For the fuzzy compensator, three fuzzy rules are fixed, as outlined in (31), where P is positive, Z is zero, and N is negative.

$$\begin{array}{l}Rule1:IfsisP,the{u}_{fc}isP\\ Rule2:IfsisZ,the{u}_{fc}isZ\\ Rule3:IfsisN,the{u}_{fc}isN\end{array}$$

(31)

where the triangular and singleton functions are applied to describe the input and the output membership functions. This is shown in Figure 4a,b, correspondingly. Through the center of gravity approach, the defuzzification is achieved as:

$$u_{fc}=\frac{{{\displaystyle \sum }}_{i=1}^3{r}_i{w}_i}{{{\displaystyle \sum }}_{i=1}^3{w}_i}=r_1{w}_1+r_2{w}_2+r_3{w}_3$$

(32)

where $w_i\left(i=1,2,3\right)$ refers to the firing strength and restricted to ($0\le w_i\le 1$). The total of $w_i$ is less than or equal to one. This condition is unique in the case of the triangle membership function. In order to reduce the loading of calculations, $r_1=\widehat{r},r_2=0,\mathrm{and}{r}_3=-\widehat{r}$ settings are made. Hence, only one of the four cases, as mention in [32,33], will occur at any set value of input $s$, as in:

Case 1: Only rule 1 is triggered $(s>s_a,w_1=1,w_2=w_3=0)$

$$u_{fc}=r_1=\widehat{r}$$

(33)

Case 2: Rules 1 and 2 are triggered simultaneously ($0<s\le s_a,0<w_1,w_2\le 1,w_3=0)$

$$u_{fc}=r_1{w}_1=\widehat{r}{w}_1$$

(34)

Case 3: Rules 2 and 3 are triggered simultaneously ($s_b<s\le 0,w_1=0,0<w_2,w_3\le 1)$

$$u_{fc}=r_3{w}_3=-\widehat{r}{w}_3$$

(35)

Case 4: Only rule 3 is triggered ($s\le s_b,w_1=w_2=0,w_3=1)$

$$u_{fc}=r_3=-\widehat{r}$$

(36)

Then, (33)–(36) can be reproduced as:

$$u_{fc}=\widehat{r}\left(w_1-w_3\right)$$

(37)

Furthermore, it can be seen from [32,33]

$$s\left(w_1-w_3\right)=\left|s\right||(w_1-w_3\left)\right|\ge 0$$

(38)

3.4. Stability Analysis

By substituting (12) into (4), it is revealed that

$$\ddot{x}=f+g\left(u_{pid}+u_{fc}\right)$$

(39)

The error equation representing the system can also be acquired after direct exploitation of (14), (22), and (39), as follows:

$$\ddot{e}+k_i\dot{e}+k_{2}e=g\left(u^{*}-u_{pid}-u_{fc}\right)=\dot{s}$$

(40)

In case of any estimation error, the optimal controller equation can be readjusted as:

$$u^{*}=u_{pid}\left({\widehat{k}}_p,{\widehat{k}}_i,{\widehat{k}}_d\right)+\epsilon$$

(41)

where $\epsilon$ refers to an estimation error and is thought to be restricted by $0\le \left|\epsilon \right|\le E$, where $E$ is a positive constant. Therefore, (40) is rewritten as:

$$\dot{s}=g\left(\epsilon -u_{fc}\right)$$

(42)

A Lyapunov function can then be selected as:

$$V_2=\frac{1}{2}{s}^2$$

(43)

Differentiating (43) with regard to time, as well as deploying (37) and (42), gives:

$${\dot{V}}_2=-g\left|s\right|\left|w_1-w_3\right|\left(\widehat{r}-\frac{\left|\epsilon \right|}{\left|w_1-w_3\right|}\right)$$

(44)

If inequality occurs in

$$\widehat{r}>\frac{\left|\epsilon \right|}{\left|w_1-w_3\right|}$$

(45)

then it is probable to fulfil the sliding condition ${\dot{V}}_2\le 0$. Having the unknown lumped uncertainties causes the value $\widehat{r}$ to be unachievable in advance, for practical applications. Corresponding to (37), in order to attain the minimum sliding value, an optimal $r^{*}$ value needs to be obtained, as follows:

$$r^{*}=\frac{\left|\epsilon \right|}{\left|w_1-w_3\right|}+\kappa$$

(46)

where $\kappa$ denotes a positive constant. Thus, a direct adaptive algorithm is used to gauge the optimal value of $r^{*}$, and the expected error can be described as:

$$\tilde{r}=r^{*}-\widehat{r}$$

(47)

where, $\widehat{r}$ is the projected ideal value of $r^{*}$. Next, a new Lyapunov function can be outlined as:

$$V_3=\frac{1}{2}{s}^2+\frac{g}{2{\mathsf{\eta }}_{\mathrm{r}}}{\tilde{r}}^2$$

(48)

where, ${\eta }_r$ is a positive constant learning rate, differentiating (48) with regard to time and deploying (37), (42), and (46), gives:

$${\dot{V}}_3\le g\left|s\right|\left|\epsilon \right|-\tilde{r}g\left[s\left(w_1-w_3\right)+\frac{\dot{\tilde{r}}}{{\eta }_r}\right]-r^{*}sg\left(w_1-w_3\right)$$

(49)

The parameter tuning law is chosen as:

$$\dot{\tilde{r}}=-\dot{\widehat{r}}=-{\eta }_{r}s\left(w_1-w_3\right)$$

(50)

and by (46), (49) becomes:

$${\dot{V}}_3=-g\kappa \left|s\right|\left|w_1-w_3\right|\le 0$$

(51)

Therefore, ${\dot{V}}_3$ is negative and semidefinite, where $V_3\left(s,\tilde{r},t\right)\le V_3\left(s,\tilde{r},0\right)$. This suggests that $s$ and $\tilde{r}$ are restricted. Let function $\mathsf{\Omega }\left(\tau \right)\equiv g\kappa \left|s\right|\left|w_1-w_3\right|\le -{\dot{V}}_3$, and $\mathsf{\Omega }\left(t\right)$ is integrated with respect to time:

$${{\displaystyle \int }}_0^t\mathsf{\Omega }\left(\tau \right)d\tau \le V_3\left(s,\tilde{r},0\right)-V_3\left(s,\tilde{r},t\right)$$

(52)

Since $V_3\left(s,\tilde{r},0\right)$ is restricted, and $V_3\left(s,\tilde{r},t\right)$ is non-increasing and restricted, the following output can be acquired:

$$\underset{t\to \infty }{\lim }{{\displaystyle \int }}_0^t\mathsf{\Omega }\left(\tau \right)d\tau <\infty$$

(53)

Furthermore, since $\dot{\mathsf{\Omega }}\left(t\right)$ is restricted, as shown by Barbalat’s Lemma [33], $\underset{t\to \infty }{\lim }\mathsf{\Omega }\left(t\right)=0$, $s\to 0$ as $t\to \infty$. Therefore, the stability of the proposed APIDC system can be assured.

To conclude, if the ${\beta }_p$, ${\beta }_i$, and ${\beta }_d$ learning rate or initial ${\widehat{k}}_p$, ${\widehat{k}}_i$, and ${\widehat{k}}_d$ of PID gains are not properly picked, the state of the system will deviate. Hence, the learning rate can be tuned manually or by applying the optimization technique. Meanwhile, the fuzzy compensator in (34) plays a vital part, offering additional input for the state reversal. The algorithm to apply this control method is as described by [32,33]:

• APIDC system parameter initialization.
• Utilization of tracking error, $e=x_d-x$, and the sliding surface, $s$, as denoted in (18)
• Implementation of the PID controller, $u_{pid}$, as shown in (27), using the gains parameter ${\widehat{k}}_p,{\widehat{k}}_i\mathrm{and}{\widehat{k}}_d$, as revised by (30).
• Usage of the fuzzy compensator, as described in (37), with the parameter $\widehat{r}$ is as projected by (50).
• Application of the control law, as specified in (12).
• Return to Step 2

4. Simulation Results

Four simulations and experiments were conducted to show the proposed controller scheme performance. A comparison with a classical PID plus gravity compensator was made to show the effectiveness of proposed controller scheme. The proposed APIDC controller is designed in the Flight Control System of the Quadcopter Flight Simulation Model for the simulations and then deployed wirelessly through Bluetooth to the embedded system on the Parrot Mambo Minidrone for real-time implementation, as shown in Figure 5. The state estimation is declared beforehand in the provided package, with the sensor fusion algorithm in the Sensor Model designed by a complementary filter and a Kalman filter to process the already available onboard sensors, such as the ultrasonic sensor, IMU, air pressure sensor, and optical flow sensor [15]. The Sensor Model and the Environment Model were the perturbation injected to the Nonlinear Airframe of the Multi-copter Model.

All the gains parameters of the PID, APID, and the fuzzy compensator are listed in

Table 2. PID gains parameter.

		Position/Angle Control	Velocity Control
	Gains	Kp	Kp	Ki	Kd
State
$\mathit{Z}$: PID			0.80000	0.24000	0.5000000
$\mathit{Y}$: P-PI		0.7	0.20000	0.10000
$\mathit{X}$: P-PI		0.7	0.20000	0.10000
$\mathbf{\psi }$: PID			0.00400	0.00400	0.0012000
$\mathbf{\theta }$: P-PID		4	0.00300	0.00600	0.0001200
$\mathbf{\varphi }$: P-PID		4	0.00243	0.00486	0.0000972

and

Table 3. APID and fuzzy compensator gains parameters.

	Sliding		Learning Rate APID			Learning Rate Fuzzy Compensator
State	$k_1$	$k_2$	${\beta }_p$	${\beta }_i$	${\beta }_d$	${\eta }_{fz}$
$\mathit{Z}$	0.1	0.5	1	0.1	0.1	−0.001

, respectively. These PID gains were the default setting of the Quadcopter Flight Simulation Model, and the APID and fuzzy compensator gains were set by trial and error until we obtained the best results, both for the simulations and the experiments, which were set to last for 60 s. Four simulations and experiments were conducted to show the performance of the altitude quadrotor under various scenarios. The simulation results and experimental data for each of these scenarios are presented in the following sections.

4.1. Hovering Test

The initial condition for the test was set above ground level with the Parrot Mambo hovering at a height of 1.1 m for 60 s. The Landing Logic Algorithm will trigger 5 s before the simulation ends to let the drone land safely. Figure 6 shows the controller response during the simulation, which shows a slight overshoot for the APID and APIDFC compared to the PID controller. We consider that the learning rate takes a few seconds to adjust the parameter gains to provide good performance. In this simulation, both APID and APIDFC responses overlap with each other, and we cannot yet determine the difference between these controllers. Figure 7 shows that all controllers require the same speed of around 250 rotations/second to maintain the quadrotor hovering height.

4.2. Altitude Tracking Test

Three simulations were conducted in this tracking; sine wave, square wave, and trapezium wave tracking. Sine wave tracking is conducted to observe the smoothness of the quadrotor in following the curve signals, while square wave and trapezium wave tracking are performed to check the response of the quadrotor when the altitude changes to a certain level. From the simulations, all controllers can adequately track the desired responses with minimum error. However, the PID controller produces a slight overshoot compared to the APID and APIDFC. Both APID and APIDFC still overlap with each other, and we cannot yet determine which one is better. All the tracking responses are shown in Figure 8, Figure 9 and Figure 10.

4.3. Changing the Mass during the Hovering Test

The final simulation involves altering the mass during the hover test to assess how resilient the controls are to perturbations. A perturbation of 0.122625 N was injected into the control signal after 15 s to observe the controllers’ behaviors. From the results shown in Figure 11 and Figure 12, all the controllers perform well and can restabilize the drone within 5 s to the setting height of 1.1 m. However, the PID controller produces a slight overshoot compared to the APID and APIDFC. In this simulation, the propellor rotation speeds overlap, and the performance of the controller cannot be justified.

5. Experimental Results

The layout and test field is shown in Figure 13. Masking tape on the black surface of the floor was utilized to create contrast to improve the optical flow sensitivity for altitude estimation. All the settings and controller designs were followed for the simulation, and the “Flight Control System—Code Generator” block, highlighted with orange color in Figure 5, was built and deployed wirelessly to the Parrot Mambo Minidrone. Additionally, the experiments’ index performances were recorded, based on integral square error (ISE) and tabulated in

Table 4. Experiment performance index for PID, APID, and APIDFC.

	PID	APID	APIDFC
Hover	1.4586	1.3801	1.2877
Sine	1.6831	1.3675	1.3048
Square	1.6761	1.4327	1.3952
Trapezium	1.5323	1.2611	1.1983
Mass Change	1.4700	0.8003	0.7937

for comparison. In this experiment, the assumptions were as follows:

• The experiment is conducted in an air conditioning hall.
• The Parrot Mambo Minidrone structure is assumed to be in a good condition.
• The propellors are assumed to be in good condition, with no dents.
• All the motors are assumed to be in good condition.
• The execution starting point is always the same.
• The lighting condition is considered fair to good.

5.1. Hovering Test

Figure 14 shows the transient response of the altitude for 60 s of flight. The desired altitude is set at −1.1 m, as predefined in the “MATLAB Original Setting”. There was no overshot produced by the PID controller, but overshot was noted for the APID and APIDC. The results are still acceptable, since the adaptive mechanism needs time to compute the controller’s gain parameters, finally settling and stabilizing within 10 s. APIDC produces a 13.29% overshoot, while APID produces a 14.62% overshoot. Figure 15 shows that the controller requires the motors to rotate about 380–400 per second to maintain the altitude at −1.1 m from ground. Then, based on the ISE, Table 4 clearly shows both that the results for APID (1.3801), and APIDFC (1.2877) were better than for PID (1.4586).

5.2. Altitude Tracking Test

The experiment continues to show how the Parrot Mambo Minidrone reacts to following sine wave, square wave, and trapezium wave tracking. For all cases, the altitude cannot be set lower than 0.6 m due to the optical sensor and ultrasonic sensor limitations. As a result, the MAV can follow the dedicated references, as shown in Figure 16, Figure 17 and Figure 18. However, we can claim that the APID and APIDFC controllers provided better performance compared to the PID controller, as proved by the ISE tabulated in Table 4. During the executions, observations show that the MAV was able to follow the sine, trapezium, and square references. Figure 19 shows the motor 1 (M1) speed reactions during this execution. The spike in the figure shows the immediate change of rotation speed of the motor. Suddenly changing attitude will immediately reduce the motor speed from higher to lower, which can cause an error in altitude estimation due to the limits of the optical flow and ultrasonic sensors.

5.3. Changing Mass during Hovering Test

In this test, a cylindrical type of mass of about 12.5 g was immediately added to the Parrot Mambo after it had been hovering for about 15 s. For all cases, the PID controller, APID controller, and APID with fuzzy compensator controller managed to balance the mass and stabilized within few seconds, as shown in Figure 20. Even though there were slight spikes that occurred throughout, the steady-state error is small and acceptable for the case of quadrotor. In addition, the APID and APIDFC controllers show better reactions to stabilize the drone with less overshoot. Figure 21 shows a comparison for all motor rotation speeds of the controllers during the experiments. The results clearly show that PID requires greater speed, about 400 rotation per second, to adapt to the change in mass during hovering, compared to 300–380 rotation per second for the APID and APIDFC controllers. This shows the proposed control scheme APID, without or with fuzzy compensator, was better than the PID controller, with less energy consumption and better performance.

The control effort comparison between the controllers on $U1$ (Figure 22) clearly shows that the APID and APIDFC controllers require slightly less effort than the PID. Then even though $U2$, $U3$, and $U4$ use the same control technique, the control effort for this signal improves significantly when the altitude controller is based on APID and APIDFC. Moreover, it was found that in the experiment that the APID and APIDFC consumed 2% and 4% less power, respectively, when compared to the PID when hovering the MAV.

Figure 23 shows that the adaptive gains for both APID and APIDFC can converge to a certain point, while Figure 24 shows less chattering produced by the second-order sliding mode, with an integral or sliding manifold for both controllers. By introducing a fuzzy compensator, it reduces the occurrence of chattering phenomena on the input signal by about 6%. According to Table 4, for the mass change event during hovering, under PID control, the MAV produces 1.4700 ISE. The ISE does, however, drop by 45% under APID control and 46% while under APIDFC control. Hence, with a fuzzy compensator, the flight control system can provide additional improvement to the MAV during flight control. Thus, we can claim that both APID and APIDFC were more robust compared to the PID control scheme.

6. Conclusions

This paper presents the real-time implementation of altitude controllers using PID, adaptive PID (APID), and APID with a fuzzy compensator (APIDFC) for a MAV, specifically, for a Parrot Mambo Minidrone. The adaptive mechanism, based on a second-order sliding mode control, is utilized to alter the classical parameters of the PID controller of the altitude controller. Four experiments were conducted: hovering, as well as sine, square, and trapezium tracking. In addition, the robustness of the controller was tested by adding mass of about 12.5 g, 15 s after flight launch, at 1.1 m altitude above ground. In the experiment, the propeller rotations were about 30–60 rotations less when using APID and APIDFC controllers. Then, by introducing a fuzzy compensator, it reduces the occurrence of chattering phenomena on the input signal by about 6%, which is due to the implementation of a sliding mode control. Furthermore, both methods also consume 2% and 4% less power, respectively, when compared to the PID controller used to hover the MAV. Hence, based on this observation, the APID and APIDFC controllers were significantly robust and energy-efficient compared to the PID controller.