Digital Twin Modeling Method for Hierarchical Stiffened Plate Based on Transfer Learning
Abstract
:1. Introduction
2. Methodology
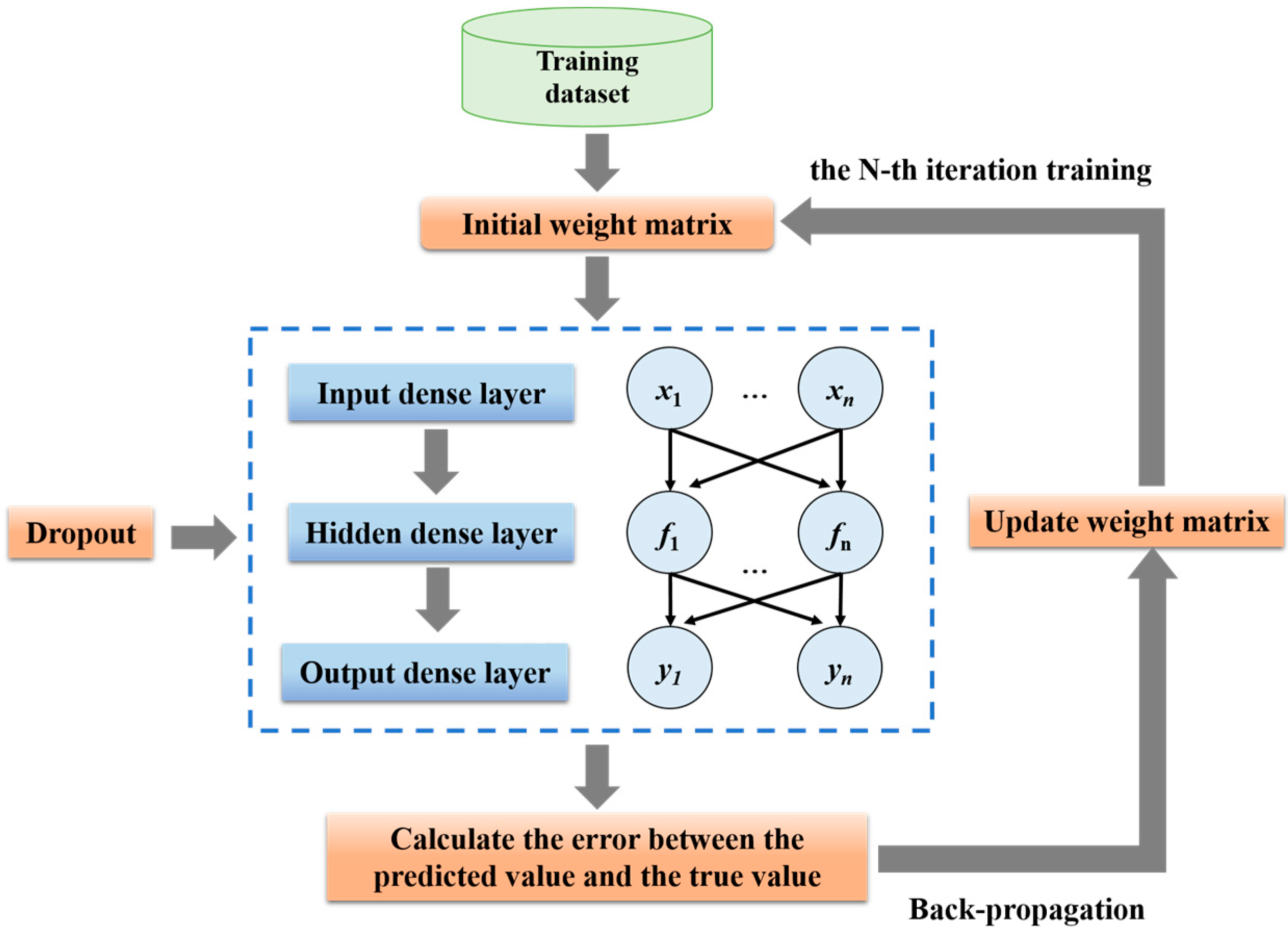
2.1. Traditional Multi-Fidelity Data Fusion Methods
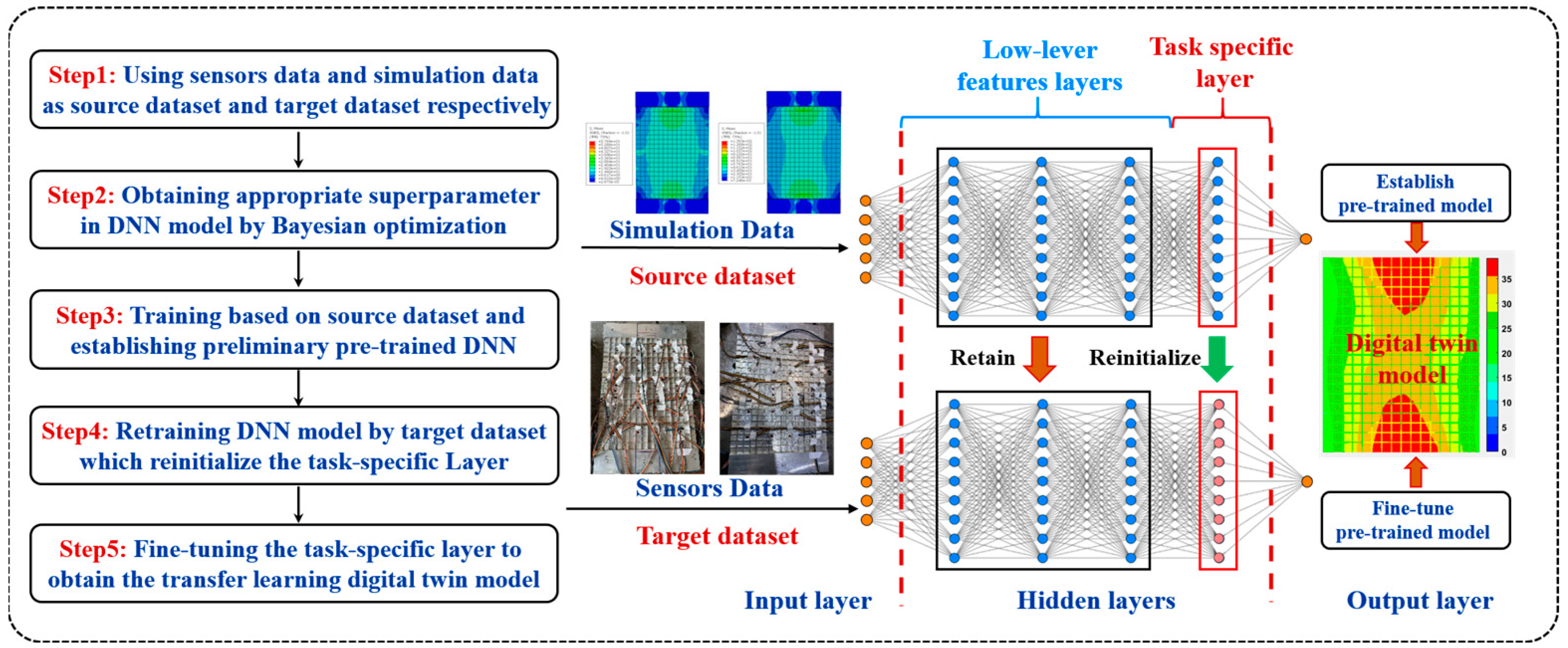
2.2. Digital Twin Modeling Method Based on Transfer Learning
3. Experiment and Discussion
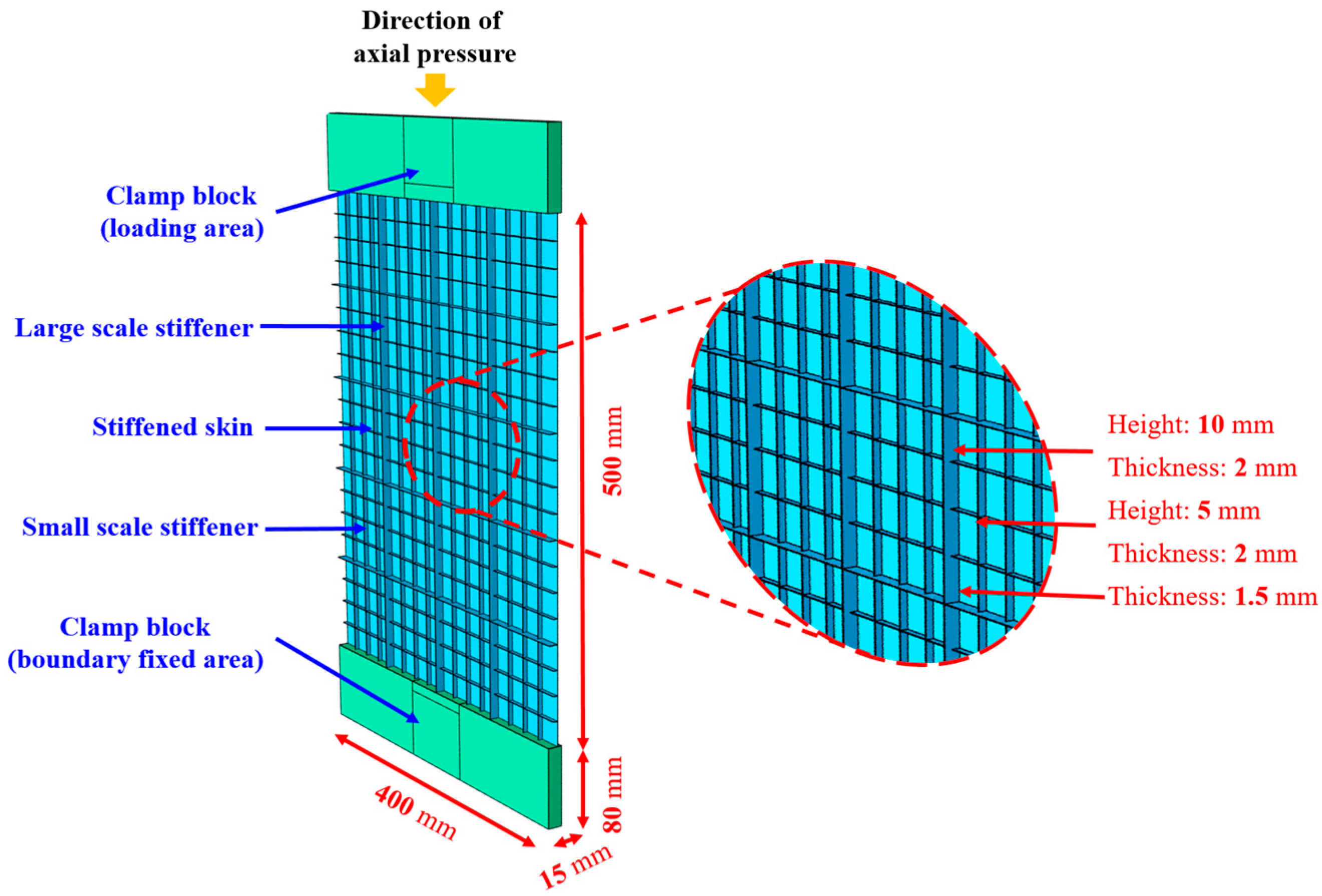
3.1. Introduction of the Simulation Results of the Hierarchical Stiffened Plate
3.2. Experimental Process of the Hierarchical Stiffened Plate
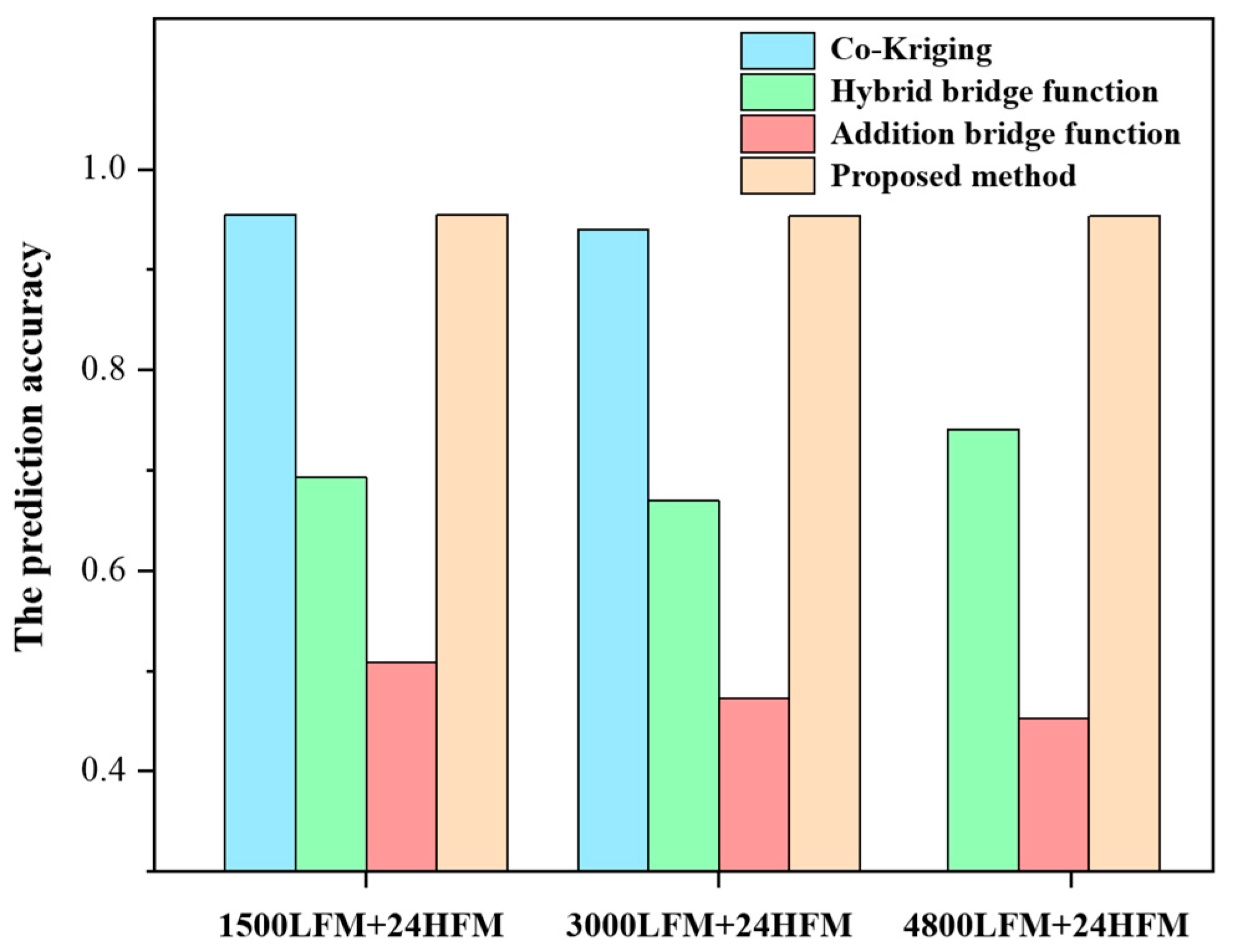
3.3. Comparison between the Proposed Method and the Traditional Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BO | Bayesian Optimization |
| DNN | Deep Neural Network |
| LHS | Latin Hypercube Sampling |
| MSE | Mean Square Error |
| SGDM | Stochastic Gradient Descent with Momentum |
| LFM | low-fidelity model |
| HFM | high-fidelity model |
References
- Tian, K.; Lai, P.; Sun, Y.; Sun, W.; Cheng, Z.; Wang, B. Efficient buckling analysis and optimization method for rotationally periodic stiffened shells accelerated by Bloch wave method. Eng. Struct. 2023, 276, 115395. [Google Scholar] [CrossRef]
- Wang, D.; Hui, J.; Cao, W.; Yang, Y.; Wan, Y.; Zuo, H.; Zhang, B. The influence of geometric imperfections on post-buckling behavior and free vibrations of a fiber-reinforced composite laminated plate under thermal loading. Compos. Struct. 2022, 306, 116568. [Google Scholar] [CrossRef]
- Ye, Y.; Yang, Q.; Yang, F.; Huo, Y.; Meng, S. Digital twin for the structural health management of reusable spacecraft: A case study. Eng. Fract. Mech. 2020, 234, 107076. [Google Scholar] [CrossRef]
- Schleich, B.; Anwer, N.; Mathieu, L.; Wartzack, S. Shaping the digital twin for design and production engineering. CIRP Ann. 2017, 66, 141–144. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.-X.; Nagano, T.; Shimoda, M. Fundamental frequency maximization of orthotropic shells using a free-form optimization method. Compos. Struct. 2017, 170, 135–145. [Google Scholar] [CrossRef]
- Liu, M.; Fang, S.; Dong, H.; Xu, C. Review of digital twin about concepts, technologies, and industrial applications. J. Manuf. Syst. 2021, 58, 346–361. [Google Scholar] [CrossRef]
- Jones, D.; Snider, C.; Nassehi, A.; Yon, J.; Hicks, B. Characterising the Digital Twin: A systematic literature review. CIRP J. Manuf. Sci. Technol. 2020, 29, 36–52. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Ghassabi, M.; Talebitooti, R. Prediction of acoustic wave transmission features of the multilayered plate constructions: A review. J. Sandw. Struct. Mater. 2022, 24, 218–293. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Ghassabi, M.; Talebitooti, R. A Review Approach for Sound Propagation Prediction of Plate Constructions. Arch. Comput. Methods Eng. 2021, 28, 2817–2843. [Google Scholar] [CrossRef]
- Liu, L.; Song, X.; Zhang, C.; Tao, D. GAN-MDF: An Enabling Method for Multi-fidelity Data Fusion. IEEE Internet Things J. 2022, 9, 13405–13415. [Google Scholar] [CrossRef]
- Jin, S.-S.; Kim, S.T.; Park, Y.-H. Combining point and distributed strain sensor for complementary data-fusion: A multi-fidelity approach. Mech. Syst. Signal Process. 2021, 157, 107725. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, S.; Li, H.; Tian, K.; Cheng, Z.; Chen, Y.; Wang, B. On-line transfer learning for multi-fidelity data fusion with ensemble of deep neural networks. Adv. Eng. Inform. 2022, 53, 101689. [Google Scholar] [CrossRef]
- Tian, K.; Li, Z.; Zhang, J.; Huang, L.; Wang, B. Transfer learning based variable-fidelity surrogate model for shell buckling prediction. Compos. Struct. 2021, 273, 114285. [Google Scholar] [CrossRef]
- Milanoski, D.; Galanopoulos, G.; Zarouchas, D.; Loutas, T. Multi-level damage diagnosis on stiffened composite panels based on a damage-uninformative digital twin. Struct. Health Monit. 2022. [Google Scholar] [CrossRef]
- Wang, S.; Lai, X.; He, X.; Qiu, Y.; Song, X. Building a Trustworthy Product-Level Shape-Performance Integrated Digital Twin with Multifidelity Surrogate Model. J. Mech. Des. 2022, 144, 031703. [Google Scholar] [CrossRef]
- Li, K.; Kou, J.; Zhang, W. Deep Learning for Multifidelity Aerodynamic Distribution Modeling from Experimental and Simulation Data. AIAA J. 2022, 60, 4413–4427. [Google Scholar] [CrossRef]
- Gano, S.E.; Renaud, J.E.; Sanders, B. Hybrid Variable Fidelity Optimization by Using a Kriging-Based Scaling Function. AIAA J. 2005, 43, 2422–2433. [Google Scholar] [CrossRef]
- Le Gratiet, L.; Garnier, J. Recursive Co-Kriging Model for Design of Computer Experiments with Multiple Levels of Fidelity. Int. J. Uncertain. Quantif. 2014, 4, 365–386. [Google Scholar] [CrossRef]
- Fernández-Godino, M.G.; Park, C.; Kim, N.H.; Haftka, R.T. Review of Multi-fidelity Models. arXiv 2016, arXiv:160907196. [Google Scholar] [CrossRef]
- Choi, S.; Alonso, J.J.; Kroo, I.M. Two-Level Multifidelity Design Optimization Studies for Supersonic Jets. J. Aircr. 2009, 46, 776–790. [Google Scholar] [CrossRef]
- Haftka, R.T. Combining global and local approximations. AIAA J. 1991, 29, 1523–1525. [Google Scholar] [CrossRef]
- Fernández-Godino, M.G.; Park, C.; Kim, N.H.; Haftka, R.T. Issues in Deciding Whether to Use Multifidelity Surrogates. AIAA J. 2019, 57, 2039–2054. [Google Scholar] [CrossRef]
- Tian, K.; Li, Z.; Huang, L.; Du, K.; Jiang, L.; Wang, B. Enhanced variable-fidelity surrogate-based optimization framework by Gaussian process regression and fuzzy clustering. Comput. Methods Appl. Mech. Eng. 2020, 366, 113045. [Google Scholar] [CrossRef]
- Han, Z.H.; Zimmermann, R.; Goretz, S. A New Cokriging Method for Variable-Fidelity Surrogate Modeling of Aerodynamic Data. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Ex-position, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Tian, K.; Li, Z.; Ma, X.; Zhao, H.; Zhang, J.; Wang, B. Toward the robust establishment of variable-fidelity surrogate models for hierarchical stiffened shells by two-step adaptive updating approach. Struct. Multidiscip. Optim. 2020, 61, 1515–1528. [Google Scholar] [CrossRef]
- Han, Z.-H.; Görtz, S.; Zimmermann, R. Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function. Aerosp. Sci. Technol. 2013, 25, 177–189. [Google Scholar] [CrossRef]
- Eckle, K.; Schmidt-Hieber, J. A comparison of deep networks with ReLU activation function and linear spline-type methods. Neural Netw. 2019, 110, 232–242. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Marei, M.; El Zaatari, S.; Li, W. Transfer learning enabled convolutional neural networks for estimating health state of cutting tools. Robot. Comput. Manuf. 2021, 71, 102145. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, W.; Ma, H. Local stress analysis of a defective rolling bearing using an explicit dynamic method. Adv. Mech. Eng. 2016, 8, 1687814016679909. [Google Scholar] [CrossRef]




| Element Seed Size/(mm) | Number of Elements | Mises Stress/(MPa) | CPU Time/s |
|---|---|---|---|
| 7 | 8032 | 67.17 | 277.7 |
| 5 | 11,640 | 61.65 | 296.3 |
| 4 | 15,888 | 63.48 | 315.8 |
| 3.5 | 21,644 | 70.62 | 326.9 |
| 3 | 32,128 | 92.3 | 638.6 |
| 2.8 | 39,024 | 106.6 | 695.4 |
| 2.4 | 46,560 | 110.1 | 714.8 |
| 2.2 | 54,736 | 111.7 | 755.1 |
| 2 | 80,860 | 112.3 | 1061.5 |
| 1.8 | 93,296 | 114 | 1237.6 |
| 1.6 | 116,864 | 115.2 | 1784.2 |
| Sensor’s Location | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 21.33 | 31.99 | 31.86 | 23.00 |
| B | 20.37 | 26.50 | 26.34 | 20.42 |
| C | 19.58 | 25.01 | 25.35 | 19.68 |
| D | 19.13 | 24.78 | 24.93 | 20.09 |
| E | 17.89 | 26.31 | 27.04 | 17.89 |
| F | 18.59 | 31.81 | 32.00 | 20.64 |
| Co-Kriging Method [24] | Hybrid BridgeFunction Method [22] | Addition Bridge Function Method [23] | Proposed Method | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Acc | CPU time/s | Acc | CPU time/s | Acc | CPU time/s | Acc | CPU time/s | ||
| 18 kN | 1500 LFM + 24 HFM | 0.9543 | 350.59 | 0.6931 | 0.36 | 0.5083 | 0.13 | 0.9546 | 24.01 |
| 3000 LFM + 24 HFM | 0.9394 | 4861.22 | 0.6697 | 0.73 | 0.4729 | 0.46 | 0.9532 | 40.46 | |
| 4800 LFM + 24 HFM | - | - | 0.7412 | 2.64 | 0.4526 | 1.32 | 0.9531 | 64.33 | |
| 15 kN | 1500 LFM + 24 HFM | 0.9471 | 339.64 | 0.6187 | 0.34 | 0.5250 | 0.14 | 0.9575 | 26.06 |
| 3000 LFM + 24 HFM | 0.9523 | 4902.6 | 0.6925 | 0.81 | 0.5422 | 0.47 | 0.9617 | 38.92 | |
| 4800 LFM + 24 HFM | - | - | 0.6572 | 2.48 | 0.4507 | 1.37 | 0.9614 | 68.58 | |
| 10 kN | 1500 LFM + 24 HFM | 0.9539 | 356.27 | 0.6280 | 0.32 | 0.4922 | 0.13 | 0.9588 | 25.29 |
| 3000 LFM + 24 HFM | 0.9559 | 4684.75 | 0.6928 | 0.69 | 0.4689 | 0.47 | 0.9592 | 42.07 | |
| 4800 LFM + 24 HFM | - | - | 0.6618 | 2.59 | 0.4201 | 1.34 | 0.9580 | 65.91 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Gao, T.; Li, Z.; Bi, Q.; Liu, X.; Tian, K. Digital Twin Modeling Method for Hierarchical Stiffened Plate Based on Transfer Learning. Aerospace 2023, 10, 66. https://doi.org/10.3390/aerospace10010066
Xu Z, Gao T, Li Z, Bi Q, Liu X, Tian K. Digital Twin Modeling Method for Hierarchical Stiffened Plate Based on Transfer Learning. Aerospace. 2023; 10(1):66. https://doi.org/10.3390/aerospace10010066
Chicago/Turabian StyleXu, Ziyu, Tianhe Gao, Zengcong Li, Qingjie Bi, Xiongwei Liu, and Kuo Tian. 2023. "Digital Twin Modeling Method for Hierarchical Stiffened Plate Based on Transfer Learning" Aerospace 10, no. 1: 66. https://doi.org/10.3390/aerospace10010066
APA StyleXu, Z., Gao, T., Li, Z., Bi, Q., Liu, X., & Tian, K. (2023). Digital Twin Modeling Method for Hierarchical Stiffened Plate Based on Transfer Learning. Aerospace, 10(1), 66. https://doi.org/10.3390/aerospace10010066







